Synchronization robustness analysis of memristive-based neural networks with deviating arguments and stochastic perturbations

1.   Introduction

The memristors were initially introduced by Chua in 1971 to describe the relationship between charge and magnetic flux ^[1]. It was predicted to be the fourth fundamental circuit element, distinct from resistors, capacitors and inductors. In 2008, the research team at HP laboratories successfully created a practical memristor device with valuable applications ^[2]. Similar to conventional resistors, the memristors can handle safe currents through the device. Furthermore, its value changes based on the amount of charge passing through it, therefore the memristors have memory functionality ^[3,4,5,6,7]. As a result, an increasing number of researchers have been using memristors instead of traditional resistors to serve as connection weights between neurons and for self-feedback connection weights, forming a state-dependent nonlinear switching system known as a memristive neural networks (MNNs). Compared to conventional artificial neural networks (NNs), MNNs possess stronger computational capabilities and information capacity, thereby enhancing the applications of NNs in associative memory, signal processing and image processing ^{[8,9,10,11,12,13]}.

The dynamic behavior of MNNs is fundamental to their applications; therefore, it necessary to analyze their dynamic characteristics ^[10,14]. Among the various dynamic behaviors of MNNs, synchronization is an important and fundamental feature. The synchronization of MNNs has garnered extensive attention from researchers due to its numerous potential applications in artificial intelligence, information science, secure communications and various other fields ^[15,16,17]. In ^[5], Du et al. derived finite-time (FNT) synchronization criteria for fractional-order MNNs with delays using the fractional-order Gronwall inequality. The FNT/fixed time (FXT) stability of MNNs was tudied in ^[18], by designing a synovial membrane controller, the MNNs reaches the sliding-mode surface in FNT/FXT. In ^{[10,11,12,13,14,15,16,17,18]}, synchronization criteria were obtained for MNNs with either delays or random interference. The above discussions mostly focus on the synchronization of MNNs with time delays, and few have considered the exponential synchronization (ESy) of MNNs with deviating arguments (DAs).

The theory of DAs differential equations was proposed by Shah and Wiener in 1983 ^[19]. In ^[20], by transforming these equations into equivalent integral equations, new stability conditions were obtained. These equations involve DAs, combining the properties of discrete and continuous equations ^[21,22,23]. During the system's operation, the relevant arguments characteristics can be altered, allowing the system to become a combination of lag and advance equations ^[24,25]. As a result, systems with DAs have broader applications compared to systems with time delays. Reference ^[26] investigates recurrent neural networks with DAs and establishes criteria for the global exponential stability. In order to further explore the impact of DAs on the exponential stability (ESt) of the systems, the robustness analysis of a fuzzy cellular neural networks with DAs and stochastic disturbance is discussed in ^[23]. The signals transmitted between MNNs are inevitably subject to stochastic perturbations (SPs) caused by environmental uncertainties ^{[27,28,29,30,31]}. For systems with SPs, the feature can significantly impact the dynamic behavior of the system, leading to either synchronization or desynchronization under certain levels of SPs ^[32,33,34]. For example, for the following simple linear systems $dx(t) = ax(t)dt$ and $dy(t) = ay(t)dt$, the error system is $de(t) = ae(t)dt$. The system is stable only when $a < 0$. However, the stability of the system is affected by SPs. Therefore, consider the following system $de(t) = ae(t)dt+be(t)dB(t)$. The system is almost surely ESt if and only if the condition $b^{2} > 2a$ is satisfied ^[35]. Then, the error system is ESt, it implies that $x(t)$ and $y(t)$ are exponential synchronization (ESy). Based on the above discussions, we reach the following conclusion: SPs can disrupt the ESy of a system that was synchronized or facilitate the ESy of a system that was initially unsynchronized. If a MNNs with SPs are ESy, can we obtain upper bounds such that the MNNs remains ESy when the SPs are smaller than the bounds?

Based on the discussion above, MNNs can lose synchronization when subjected to disturbances from external perturbations and DAs, provided that the intensity of perturbations and the width of arguments exceed certain limits. In ^{[27,30,31,32,33,34,36,37]}, there are important results regarding the synchronization of MNNs under external disturbances. In ^[21,22,23], scholars research on MNNs with DAs. It is important to note that the aforementioned literature primarily focuses on the synchronization of MNNs than its robustness. Therefore, an interesting question arises: Under the control strategy, how much argument length and perturbation intensity can MNNs with ESy endure without losing synchronization?

The major contributions of this paper include the following aspects:

$\bullet$ Compared to the references ^{[5,6,7,11,16]}, we focus on the synchronization of MNNs with DAs. The systems with DAs have broader applications compared to traditionally time-delayed systems.

$\bullet$ The references ^{[8,9,10,11,12,13,14,15,16,17]} extensively investigated MNNs with time delays, providing various stability and synchronization criteria. In references ^{[28,29,33,34]}, the robustness of ESt in systems with both time delays and SPs was further explored. In references ^[23,27], Fang et al. studied the robustness of ESt in fuzzy cellular neural networks with DAs. In contrast to the aforementioned literatures, we focus on the robustness of ESy in MNNs, utilizing the set-valued mapping method, differential inclusion theory and Gronwall inequalities, we derive the upper bounds for the DAs and SPs.

$\bullet$ Compared to the references ^{[22,23,24,25,32,33,34]}. The MNNs with state switching that we consider and results in a more complex system structure.

The paper is organized as follows. In Section Ⅱ, we introduce the model, assumptions and some preliminary lemmas. In Section Ⅲ, we present the theorems and lemmas derived in this paper. In Section Ⅵ, we provide several examples to validate the feasibility of our results. Finally, in Section Ⅴ, we have summarized the work carried out in this paper.

2.   Preliminaries

2.1.   Notation

In the paper, $\mathbb{R}^{n}$ is Euclidean space, $\mathbb{N}$ represents integers, $||\chi(t)||$ is the norm of vector $\chi(t)$, where $\chi(t)\in \mathbb{R}^{n}$ and $||\chi(t)|| = \sum_{p = 1}^{n}|\chi(t)|$, the norm $||A||$ of the matrix $A$ is given by $||A||$, where $A = \max_{1\le q\le n}\sum_{p = 1}^{n}|a_{pq}|$. For two real-valued sequences $\rho_{k}, \eta_{k}$, where $k\in \mathbb{N}$, it holds that $\rho_{k} < \rho_{k+1}$, $\rho_{k}\le\eta_{k}\le\rho_{k+1}$ for all $k\in \mathbb{N}$ with $\eta_{k}\to\infty$ as $k\to\infty$.

Let $(\Omega, \mathcal{F}, \{ \mathcal{F}_{t} \}_{t \geq t_0}, P)$ is a complete probability space with a filtration $\{ \mathcal{F}_{t} \}_{t \geq t_0}$ (the filtration contains all $P$-null sets and is right continuous). $L_{\mathcal{F}_{0}}^{P}([-\tau, 0];\mathbb{R}^{n})$ is the family of all $\mathcal{F}_{0}$-measurable $\mathbb{C}([-\tau, 0];R^{n})$, the state variable $\xi = \{\xi(s); \tau\le\xi(s)\le 0\}$ satisfies $\sup_{-\tau\le s\le 0}\mathbb{E}(||\xi(s)||^{P})\le\infty$. $\mathbb{E}(\cdot)$ is the mathematical expectation in the probability space.

2.2.   Preparation

Consider the MNNs as the derive system with the SPs,

where $p = 1, 2, \cdots, n$, $w_{p}(t)$ are the state variables, and $f_{q}\left(w_{q}(t)\right)$ are the activation functions; $d_{p} > 0$ is a self-feedback connection weights and $I_{p}(t)$ is the external inputs, $a_{pq}\left(w_{q}(t)\right)$ is the memristive connection weights, $\sigma$ is the interference intensity. $\omega_{i}(t)$ represents Brownian motion on the compete space.

For convenience, we use $w_{p}, w_{q}$, $a_{pq}\left(w_{q}\right), u_{p}$, $\omega$ to replace $w_{p}(t), w_{q}(t), a_{pq}\left(w_{q}(t)\right), u_{p}(t)$, $\omega(t)$, respectively. The initial conditions of (2.1) is

The corresponding response system,

For convenience, we use $v_{p}, v_{q}$, $a_{pq}\left(v_{q}\right), u_{p}$ to replace $v_{p}(t), v_{q}(t), a_{pq}\left(v_{q}(t)\right), u_{p}(t)$, respectively. Then, the memristive parameter of (2.1) and (2.2) are expressed as

where $i, j\in \mathbb{N}$, weights $\acute{{a}_{pq}}$, $\grave{a}_{pq}$ and switching jumps $T_{q} > 0$. The initial value of (2) are

The linear feedback controller $u_{p}$ is designed as follows

The error system between the drive system (2.1) and the response system (2.2) is defined as

Remark 1. We can observe that MNNs can be categorized as discontinuous switched systems, which necessitates considering the solution to MNNs (1) using the Filippov's sense. In the following, we will introduce certain definitions pertaining to set-valued maps and the Filippov solution.

Definition 1. (Set-valued map ^[38]) Consider a set $E\in\mathbb{R}^{n}$. A set-valued map is defined as follows: For each point $x$ in the set $E$, there exists a nonempty set $F(x)\in \mathbb{R}^{n}$ such that $x$ is mapped to $F(x)$.

Definition 2. (Differential inclusion ^[38]) For a discontinuous differential system $\dot{r}(t) = \mathbb{F}(t, r_{t})$, $t\geq 0$, the function $r_{t}$ is the solution of the differential equation in the Filippov sense, $t\in [0, t_{1}]$, $t_{1}\geq 0$, if is absolutely continuous and satisfies the following differential inclusion:

where $t\in [0, +\infty]$, $r\in \mathbb{R}^{n}$, the initial condition $r(0) = r_{0}\in \mathbb{C}([-\tau, 0], \mathbb{R}^{n})$. The $\mathbb{G}(t, r_{t})$ is a set-valued mapping, satisfies

where $\overline {\operatorname{co}}$ is the convex closure hull of a set, $\mathbb{B}(r_{t}, \varGamma) = \{x:\|x-r_{t}\| \leq \varGamma\}$, $\varGamma > 0$ and $\delta(\mathbb{N})$ is Lebesgue measure of set $\mathbb{N}$.

The set value mapps of memristive parameters is as follows:

where $p, q\in \mathbb{N}$. $K[a_{pq} (w_{q})]$ and $K[a_{pq}(v_{q})]$ are all closed, convex and compact about $w_{q}$, $v_{q}$.

According to Definitions 1 and 2, the Filippov solution of the systems (1) and (2) can be written as:

Similarly, there exist

such that

From (6), let $e_{p} = v_{p}-w_{p}$,

where $\hat{a}_{pq}(e_{q})f_{q}(e_{q}) = \bar{a}_{pq}(w_{q})f_{q}(w_{q}) -\check{a}_{pq}(v_{q})f_{q}({v_{q}})$.

The following error system without random disturbance:

The initial conditions is

The (2.7) and (2.8) can be rewritten as

where $e(t) = (e_{1}(t), \cdots, e_{n}(t))\; ^{T}$, $z(t) = (z_{1}(t), \cdots, z_{n}(t))^{T}$, $C = \operatorname{diag}\left\{\xi_{1}, \xi_{2}, \; \cdots\; , \xi_{n}\right\}$, $D = \operatorname{diag}\left\{d_{1}, d_{2}, \; \cdots\; , d_{n}\right\}$, $\hat{A} = \left(\hat{a}_{pq}\right)_{n \times n}$, $F(e(t)) = (f_{1}(e_{1}(t)), \cdots, f_{n}(e_{n}(t)))^{T}$.

The mian result of the paper are base on the following definitions, assumptions and lemmas.

Definition 3. (Exponential synchronization (ESy)) If the error system $\chi(t)$ is exponential stability (ESt). Then, the MNNs (2.1) and (2.2) are described as ESy, there exsit two nonnegative constant $\alpha$ and $\beta$,

where $\psi^{1} = (\psi^{1}_{1}, \cdots, \psi^{1}_{n})^{T}$ is any initial condition, $t\le 0$.

Definition 4. (Mean square exponential synchronization (MSESy)) The state $\chi(t)$ of system (2.7) is said to be MSESt. Then the MNNs (2.1) and (2.2) are described as MSESy, if for any $t_{0}\in\mathbb{R}^{+}$, $\psi^{1}\in\mathbb{R}^{n}$, there exist $\theta > 0$ and $\vartheta > 0$ such that

Assumption 1. The activation functions $f_{q}(\cdot)$ and $g_{q}(\cdot)$ satisfy

where $f^{*}_{q}, g^{*}_{q} > 0$ are Lipschitz constants, $w_{p}, v_{p}\in \mathbb{R}^{n}$.

Under Assumption 1, we have the following conclude: The MSESt of system (2.7) implies the almost sure ESt of system (2.7), see ^[39].

Assumption 2. $f_{q}\left(\pm T_{q}\right) = g_{q}\left(\pm T_{q}\right) = 0$.

Lemma 1. ^[14] From Assumptions 1 and 2, then

for $i, j \in \mathbb{N}$.

That is, for any $\bar{a}_{pq}\left(w_{q}\right) \in K\left[a_{pq} \left(w_{q}\right)\right], \check{a}_{pq}\left(v_{q}\right) \in K\left[a_{pq}\left(v_{q}\right)\right]$.

where $a_{pq}^{*} = \max\left\{\left|\acute{a}_{pq}\right|, \left|\grave{a}_{pq}\right|\right\}$.

Lemma 2. ^[40] (Granwall inequalities) Suppose $\vartheta(t)$, $\theta(t)$ and $u(t)$ are continuous real-valued functions, and $\theta(t)$ is integrable over the interval $I = [t_{0}, t]$, if $\vartheta (t)\geq 0$ and $u (t)$ satisfies

then,

where $t > t_{0}$.

In addition, if $\theta(t)$ is non-decreasing, then

Assumption 3. There exists a nonnegative constant $\rho$ that satisfies, $\rho_{k+1}-\rho_{k}\le \rho$, for all $k\in\mathbb{N}$.

Assumption 4. $h_{1}\rho+h_{2}\rho (1+h_{1}\rho)\exp\{h_{2}\rho\} < 1$,

where $h_{1} = ||B^{*}||||G^{*}||\rho$, $h_{2} = ||C||+||D||+||A^{*}||||F^{*}||$.

Assumption 5. $\rho(3l_{1}+9l_{2}+l_{1}^{2} +3l_{1}l_{2}) < 1$,

where $l_{1} = 9\rho^{2}||B^{*}||^{2}||G^{*}||^{2}$, $l_{2} = 3\rho(2||C||^{2} +2||D||^{2}+||A^{*}||^{2}||F^{*}||^{2}) +\theta^{2}$.

Under the influence of the linear controller, the error system (2.7) can achieve ESt, that is, systems (2.1) and (2.2) can achieve ESy. The next question is how much the SPs and DAs intensities can make the system can maintain ESy.

3.   Main results

3.1.   Effects of SPs on MNNs synchronization

Theorem 1. Let Assumption 1 hold, MNNs (2.8) is ESt. Then MNNs (2.7) is ESt, that is, the master system MNNs (2.1) and the slave system MNNs (2.2) are ESy. if $|\sigma|\le\bar\sigma$, $\bar\sigma$ is the unique nonnegative solution of the transcendental equation below.

where $\mathbb{T} > \ln(2\theta)/(4\vartheta) > 0$, $A^{*} = (a_{pq}^{*})_{n\times n}$, $F^{*} = \max_{j\in\mathbb{N}}\{f_{q}^{*}\}$, $\mathbb{T}$ is the time interval.

Proof. $z(t)$ and $e(t)$ have the same initial value, $\psi^{1} = \psi^{2}$,

The ESt of the MNNs (2.8), when $t > t_{0}$,

When $t\le t_{o}+2\mathbb{T}$, by utilizing the Cauchy-Schwarz inequalities and Lemma 1, we can conclude the following:

Then,

When $t_{0}+\mathbb{T}\le t\le t_{0}+2\mathbb{T}$, by applying Lemma 2,

When $t_{0}+\mathbb{T}\le t\le t_{0}+2\mathbb{T}$,

From (11), when $|\sigma| < \bar\sigma$,

Let

So, $\gamma > 0$,

Then, for any nonnegative integer $\mathbb{M} = 1, 2, \cdots$, when $t\geq t_{0}+(\mathbb{M}-1)\mathbb{T}$,

From (3.5) and (3.6)

where

So for $\forall t > t_{0}+\mathbb{T}$, there have a nonnegative integer $\mathbb{M}$ such that $t_{0}+\mathbb{M}\mathbb{T} \leq t \leq t_{0}+(\mathbb{M}+1)\mathbb{T}$,

The condition is also genuine when $t_{0} \leq t \leq t_{0}+\mathbb{T}$. So system (2.7) is ESt.

The following analysis considers the influence of the DAs on the ESy of the master-slave system.

3.2.   Effects of DAs on MNNs synchronization

Consider the derive system with the DAs,

where $g_{q}(w_{q}(t))$ is the activation functions with DAs, $a_{pq}(w_{q}(t))$ and $b_{pq}(w_{q}(\gamma(t)))$ are the memristive connection weights without and with DAs respectively.

The corresponding response system:

The Filippov solution of the systems (3.7) and (3.8) are

in which $w(\gamma) = w(\gamma(t))$, $v(\gamma) = v(\gamma(t))$.

The set-valued maps be defined as follows

where $\tilde{w}_{q}, \tilde{v}_{q}$ to replace $w_{q}(\gamma), v_{q}(\gamma)$. $K[a_{pq} (\tilde{w}_{q})]$ and $K[a_{pq}(\tilde{v}_{q})]$ are all closed, convex and compact about $\tilde{w}_{q}$, $\tilde{v}_{q}$.

There exist

Let $e_{p} = v_{p}-w_{p}$,

where $\hat{b}_{pq}(e_{q})g_{q}(e_{p}) = \bar{b}_{pq}(w_{q})g_{q}(w_{p}) -\check{b}_{pq}(v_{q})g_{q}({v_{p}})$.

The following error system without DAs,

The (3.11) and (3.12) can be rewritten as

where $\hat{B} = \left(\hat{b}_{pq}\right)_{n \times n}$, $G(e(t)) = (g_{1}(e_{1}(t)), \cdots, g_{n}(e_{n}(t)))^{T}$.

Lemma 3. Consider the MNNs (3.11) with DAs and the Assumptions 3 and 4 hold, the following inequality is established,

Proof. For $\gamma(t) = \eta_{k}$ and $\eta_{k} \in [\rho_{k}, \rho_{k+1}]$,

Utilizing Lemmas 1 and 2,

where $B^{*} = (b_{pq}^{*})_{n\times n}$, $G^{*} = \max_{q\in\mathbb{N}}\{g_{q}^{*}\}$, then

where $h_{1} = ||B^{*}||||G^{*}||$, $h_{2} = ||C||+||D||+||A^{*}||||F^{*}||$.

Therefore, for Assumption 4,

where $\mu = \biggl(1-(h_{1}\rho+h_{2}\rho (1+h_{1}\rho)\exp\{h_{2}\rho\})\biggr)^{-1}$, for $t \in [\rho_{k}, \rho_{k+1}]$. With regards to arbitrary values of $t$ and $k$, (3.16) holds for $t\in \mathbb{R}^{+}$.

Remark 2. When considering MNNs (3.11) on the interval $[\rho_{k}, \rho_{k+1}]$, where $k\in\mathbb{N}$, if $\rho_{k}\le t < \eta_{k}$, MNNs (3.11) behaves as an advanced system. Conversely, if $\eta_{k} < t \le \rho_{k+1}$, MMN (3.11) behaves as a retarded system.

Theorem 2. If Assumptions 1–4 hold, MNNs (3.11) is ESt. Then MMNs (3.12) is ESt, that is, the derive system MNNs (3.7) and the response system MNNs (3.8) are ESy. If $|\rho|\le \min\{\bar{\rho}, \tilde{\rho}\}$, where $\bar{\rho}$ is a unique nonnegative solution of the transcend equation:

where $\mathbb{T} > \ln(\alpha)/\beta$, $k_{1} = ||C||+||D||+||A^{*}||||F^{*}||+ \mu||B^{*}||||G^{*}||$, $k_{2} = (1+\mu)||B^{*}||||G^{*}||$.

The $\tilde{\rho}$ is a unique positive solution of the transcend equation:

Proof. Utilizing Lemmas 1 and 3, initial value $\psi^{1} = \psi^{2}$, we can conclude the following

where $k_{1} = ||C||+||D||+||A^{*}||||F^{*}||+ \mu||B^{*}||||G^{*}||$, $k_{2} = (1+\mu)||B^{*}||||G^{*}||$.

By Lemma 2, when $t_{0}+\mathbb{T}-\rho\le t\le t_{0}+2\mathbb{T}$,

So, when $t_{0}+\mathbb{T} -\rho\le t\le t_{0}+2\mathbb{T}$, from (3.19) and the global exponential stability of (3.12),

From (3.20), when $|\rho|\le\bar{\rho}$,

Let $\kappa_{1} = -(\ln (k_{2}\alpha/\beta\exp\{2k_{1}T\}+ \alpha\exp\{-\beta T\}))/\mathbb{T}, \kappa_{1} > 0$, when $t_{0}-\rho+\mathbb{T}\le t\le t_{0}+ 2\mathbb{T}$,

Consider the existence and uniqueness of the solution $e(t)$ of (8), when $t > t_{0}-\xi+(\mathbb{M}-1)\mathbb{T}$,

From (3.21) and (3.22),

where $\kappa_{2} = \sup_{t_{0}-\rho\le t\le t_{0}+\mathbb{T}} ||e(t; t_{0}, e_{0})||$.

To go a step further, there is the only scalar $m\in \mathbb{N}$ such that $t_{0}-\rho +(\mathbb{M}-1)\mathbb{T} \le t\le t_{0}+\mathbb{M}\mathbb{T}$,

Clerly, (3.23) holds for $t_{0}-\rho\le t\le t_{0}+\mathbb{T}$.

3.3.   Effects of DAs and SPs on MNNs synchronization

The following consider MNNs with SPs and DAs,

The corresponding response system,

Let $e_{p} = v_{p}-w_{p}$,

The original system is

Further,

Lemma 4. Let Assumptions 3 and 5 hold, then the following inequality

holds for all $t\in \mathbb{R}^{+}$, where $\lambda = 3(1-\varpi)^{-1}$, $\varpi = \rho(3l_{1}+9l_{2}+l_{1}^{2} +3l_{1}l_{2})$.

Proof. For $\gamma(t) = \eta_{k}$, $t\in [\rho_{k}, \rho_{k+1}]$, $\forall t\in \mathbb{R}^{+}$, $\exists k\in \mathbb{N}$, we have

Applying Lemma 2,

where $l_{1} = 9\rho^{2}||B^{*}||^{2}||G^{*}||^{2}$, $l_{2} = 3\rho(2||C||^{2} +2||D||^{2}+||A^{*}||^{2}||F^{*}||^{2}) +\sigma^{2}$.

Similarly, for $t \in [\rho_{k}, \rho_{k+1}]$,

By the Assumption 5,

where $\varpi = \rho(3l_{1}+9l_{2}+l_{1}^{2} +3l_{1}l_{2})$, $\lambda = 3(1-\varpi)^{-1}$. Therefore, (3.29) holds for $t \in [\rho_{k}, \rho_{k+1}]$. By the randomicities of $t$ and $k$, (3.29) holds for all $t\in\mathbb{R}$.

In the following, we investigate the effects of DAs and SPs on the robustness of ESy of MNNs (3.26).

Theorem 3. If {Assumptions 3–5} and {Definition 4} hold, MNNs (3.27) is ESt. Then MMNs (3.26) is ESt, that is, the derive system MNNs (3.24) and the response system MNNs (3.25) are ESy. If $|\sigma|\le \bar{\sigma}$, $|\rho| \le\min\{\bar{\rho}, \tilde{\rho}\}$ where $\bar{\rho}$ is a unique nonnegative solution of the transcend equation:

where $\upsilon_{1} = (24\mathbb{T}(||C||^{2}+||D||^{2} +2||A^{*}||^{2}||F^{*}||^{2} +2\lambda^{2}||B^{*}||^{2}||G^{*}||^{2})+4\sigma^{2})$, $\upsilon_{2} = (12\mathbb{T}(2+2\lambda^{2}) ||B^{*}||^{2}||G^{*}||^{2} +2\sigma^{2})$. The $\tilde{\rho}$ is a unique nonnegative solution of the transcend equation:

The $\bar{\sigma}$ is a unique nonnegative solution of the transcend equation:

Proof. When $t_{0}-\rho\le t\le t_{0}+2\mathbb{T}$, By applying Lemma 4, initial value $\psi^{1} = \psi^{2}$,

where $\upsilon_{1} = (24\mathbb{T}(||C||^{2}+||D||^{2} +2||A^{*}||^{2}||F^{*}||^{2} +2\lambda^{2}||B^{*}||^{2}||G^{*}||^{2})+4\sigma^{2})$, $\upsilon_{2} = (12\mathbb{T}(2+2\lambda^{2}) ||B^{*}||^{2}||G^{*}||^{2} +2\sigma^{2})$.

When $t_{0}-\rho\le t\le t_{0}+2\mathbb{T}$, By applying Lemma 2,

Then,

When $|\rho|\le\min\{\bar{\rho}, \tilde{\rho}\}$, $|\sigma|\le\bar{\sigma}$,

4.   Simulations

We demonstrate the aforementioned theoretical results through three numerical simulations.

Example 1. Consider two dimensional MNNs with SPs.

where

$w_{1} = (w_{1}, w_{2})$, $d_{1} = d_{2} = 1, q = 1, 2$, $f_{q}(w_{q}) = tanh(w_{q})$, $w_{1} = w_{2} = 0$, $\phi_{1} = (0.3, 0.35)^{T}, \phi_{2} = (0.2, 0.25)^{T}$.

The response system is

where $\varphi_{1} = (-0.1, -0.15)^{T}, \varphi_{2} = (-0.2, -0.25)^{T}$.

Let $\theta = 1.1$, $\vartheta = 0.2$, $\mathbb{T}\le\ln(\theta)/\vartheta = 0.01$, $||A^{*}|| = 0.1, ||F^{*}|| = 1, ||C|| = 0.7, ||D|| = 1$.

Solving the following transcedental equation,

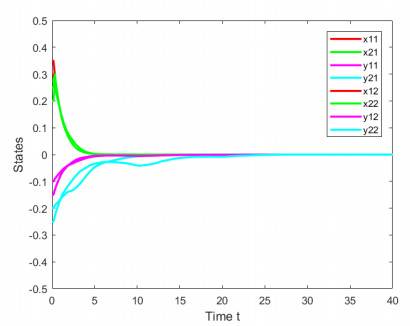
We can obtain $\bar{\sigma} = 0.1364$, let $\sigma = 0.04$, $\sigma = 0.06$, $\sigma = 0.1$, The state trajectories of MMNs (4.1) and MNNs (4.2) are shown in Figures 1–3, respectively. It can be seen from the figures that when time tends to infinity, the states of a and b tend to 0 This can show that when the perturbations intensity $\sigma$ is less than $\bar{\sigma}$, the drive-response systems can achieve Esy. When $\sigma = 0.25$, The states are illustrated in Figure 4.

Example 2. Consider two-dimensional MNNs with DAs,

where

where $\tilde{w}_{q} = w_{q}(\gamma)$, $w_{1} = (w_{1}, w_{2})$, $d_{1} = d_{2} = 1, q = 1, 2$, $f_{q}(w_{q}) = tanh(w_{q})$, $g_{q}(w_{q}) = |w_{q}+1|-|w_{q}-1|$, $w_{1} = w_{2} = 0$, $\phi_{1} = (3, 4)^{T}, \phi_{2} = (1, 2)^{T}$.

The response system is

where $\varphi_{1} = (-3, -4)^{T}, \varphi_{2} = (-1, -2)^{T}$.

Let $\alpha = 1.1$, $\beta = 0.5$, $\mathbb{T}\le\ln(\theta)/\vartheta = 0.01$, $||A^{*}|| = 0.726, ||B^{*}||^{2} = 0.1 ||F^{*}|| = 1, ||G^{*}|| = 1 ||C|| = 0.01, ||D|| = -1$.

Solving the following transcedental equations,

We can obtain $\bar{\rho} = 0.2506$, $\tilde{\rho} = 0.3314$, let $\rho = 0.2$, $\rho = 0.15$, $\rho = 0.1$, $\rho = 0.25$, when the length of the DAs in the systems is less than the calculated upper bound, we have that MNNs (4.3) and (4.4) with the controllers is ESy. The states of the MNNs (4.3) and (4.4) are shown in Figures 4–8, respectively.

Example 3. Consider two-dimensional MNNs with DAs and SPs.

All other parameters remain the same as in Example 2. The response system is,

Solving the transcedental equations. We can obtain $\bar{\rho} = 0.1567$, $\tilde{\rho} = 0.4374$, $\bar{\sigma} = 0.2463$, let $\rho = 0.1$, $\sigma = 0.04$, we have that MNNs (4.5) and (4.6) is ESy, the state trajectories are shown in Figure 9. when $\rho = 0.05$, $\sigma = 0.04$, the state trajectories are shown in Figure 10. When $\rho = 0.9$, $\sigma = 0.1$, the state trajectories are shown in Figure 11.

5.   Conclusions

In this paper, the robustness analysis of MNNs exponential synchronization problem with DAs and SPs is studied by using the Granwall inequalities and inequality techniques, and a method different from Linear Matrix Inequality method (LMI) and Lyapunov theory is used to solve the synchronization robustness of MNNs.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.