Iterative algorithm for solving monotone inclusion and fixed point problem of a finite family of demimetric mappings

1.   Introduction

Let $\psi$ be a simple, connected graph with vertex set $V(\psi)$ and edge set $E(\psi)$. The distance $d(\rho_1, \rho_2)$, $\rho_1, \rho_2 \in V(\psi)$ is the length of shortest path between $\rho_1$ and $\rho_2$. Let $Q = \{v_1, v_2, \dots, v_j\}$ be an ordered set of vertices of $\psi$. Let $\rho_1\in V(\psi)$, the representations denoted by $r(\rho_1|Q)$ is the $j$-tuple distances as $(d(\rho_1|v_1), d(\rho_1|v_2), \dots, d(\rho_1|v_j)).$ If distinct vertices of $\psi$ have distinct representation w.r.t. $Q$ then $Q$ is called the resolving set. The minimum number of $j$ in the resolving set is known as the metric dimension of $\psi$ and written as $dim(\psi).$ Motivated by the problem of determining an intruder's location in a network in a unique way, Slater introduced the definition of metric dimension in ^[27] and later independently by Harary and Melter in ^[11]. The concept of resolving set, metric basis and metric dimension appeared in the literature ^{[4,6,8,9,10,12,15,19,28,30,31]}.

A partition of a set is collection of its subsets, no pair of which overlap, such that the union of all the subsets is the whole set and partition dimension is related to the partitioning of the vertex set $V(\Omega)$ and resolvability. The partition dimension is a generalized variant of matric dimension. Another type of dimension of a graph, is called partition dimension. Let $\Gamma = \{\Gamma_1, \Gamma_2\dots, \Gamma_j\}$ and $r({\rho_1}|\Gamma) = \{d({\rho_1}, \Gamma_1), d({\rho_1}, \Gamma_2), \dots, d({\rho_1}, \Gamma_j)\}$ are named as $j$-ordered partition of vertices and $j$-tuple representations respectively. If the representations of every $\rho_1$ in $V(\psi)$ w.r.t. $\Gamma$ is different, then $\Gamma$ is the resolving partition of the vertex set and the minimum count of the resolving partition set of $V(\psi)$ is named as the partition dimension of $\psi$ and it is represented by $pd(\psi)$ ^[7]. The problem of determining the resolving set of a graph is NP-hard ^[20]. As, the problem of finding the partition dimension is a generalize version of metric dimension, therefore partition dimension is also a NP-complete problem. It is natural to think that there is a relation between metric and partition dimension, ^[7] proved for any non-trivial connected graph $\psi$,

In ^[22], fullerene graph of chemical structure is discussed and proved that the graph has constant and bounded partition dimension. For more and interesting results on constant partition dimension can see ^[16,21,24]. To find the exact value of partition dimension of a graph is not easy therefore, various results on the bounds of the partition dimension are discussed in literature, such as the partition dimension of Cartesian product operation on different graphs are studies and provided extensive bounds on partition dimension ^[29]. In ^[1] different bounds of partition dimension of subdivision of different graphs are discussed. In ^[25,26] provide bounds of partition dimension of tree and uni-cyclic graphs in the form of subgraphs.

The applications of partition resolving sets can be found in different fields such as robot navigation ^[19], Djokovic-Winkler relation ^[9], strategies for the mastermind game ^[10], network discovery and verification ^[5], in chemistry for representing chemical compounds ^[17,18] and in problems of pattern recognition and image processing, some of which involve the use of hierarchical data structures ^[23] for more applications see ^[6,11]. Following theorems are very helpful in finding the partition dimension of a graph.

Theorem 1.1. ^[7] Let $\Gamma$ be a resolving partition of $V(\psi)$ and $\rho_1, \rho_2\in V(\psi)$. If $d(\rho_1, z) = d(\rho_2, z)$ for all vertices $z \in V(\psi)\backslash (\rho_1, \rho_2)$, then $\rho_1, \rho_2$ belong to different classes of $\Gamma$.

Theorem 1.2. ^[7] Let $\psi$ be a simple and connected graph, then

● $pd(\psi)$ is $2$ iff $\psi$ is a path graph

● $pd(\psi)$ is $n$ iff $\psi$ is a complete graph,

Let $\mathbb{R}$ be a family of connected graphs $G_n: \mathbb{R} = (G_n)_{n\geq1}$, where $|V(\psi)| = \lambda(n)$ and $\lim\limits_{n\rightarrow \infty}\lambda(n) = \infty$. If there exists a constant $\alpha \geq 1$ such that $pd(\psi)\leq \alpha, n\geq 1$, then $\mathbb{R}$ has bounded partition dimension otherwise unbounded. Imran et al. ^[14] studied the metric dimension of $R_n^p,$ $D_n^p,$ and $Q_n^p,$ convex polytopes which motivates us to find the partition dimension of same families of convex polytopes. In this paper, the partition dimension of same families of convex polytopes are studied. We determine the partition dimension of $R_n^p$, in second section. In the third section, the partition dimension of the graph $D_n^p$ of a convex polytope with pendent edges is presented. The fourth section remains for the partition dimension of the graph $Q_n^p$.

2.   Results on planer graph $R_n^P$

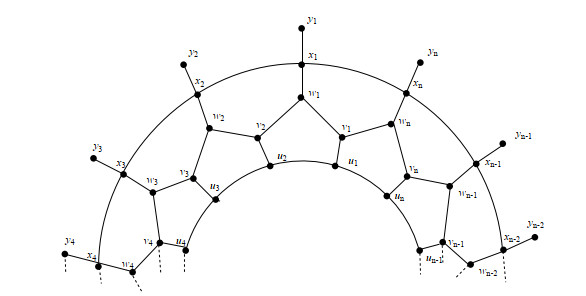
The convex polytope $R_n^p$ ($p$ for pendant edges) is a planar graph and obtained from the convex polytope $R_n$ defined in ^[13]. If we attach a pendant edge at each vertex of outer layer of $R_n$ then we obtained a new planer graph $R_n^p$ as shown in Figure 1. The vertex set of $R_n^p$, $V({R_n^P}) = \{V(R_n)\}\cup \{x_\alpha:1\leq \alpha \leq n\}$ and edge set of $R_n^p$, $E(R_n^P) = \{E(R_n)\} \cup \{w_\alpha x_\alpha: 1\leq \alpha \leq n\}$.

For calculation, $\{u_\alpha: 1\leq \alpha \leq n\}$ represents the inner cycle, the cycle induced by $\{v_\alpha: 1\leq \alpha \leq n\}$ is interior cycle, exterior cycle containing $\{w_\alpha: 1\leq \alpha \leq n\}$ set of vertices and pendant vertices named $\{x_\alpha: 1\leq \alpha \leq n\}$.

Theorem 2.1. Let $R_n^p$ be a polytopes with $n\geq 6$. Then $pd(R_n^p)\leq 4$.

Proof. We splits the proof into following two cases.

Case 1: When $n = {2\beta}, {\beta} \geq 3, {\beta} \in N.$ We partition the vertices of $R_n^p$ into four partition resolving sets $\varTheta = \{\Gamma_1, \Gamma_2, \Gamma_3, \Gamma_4\}$ where $\Gamma_1 = \{u_1\}$, $\Gamma_2 = \{u_2\}$, $\Gamma_3 = \{u_{{\beta}+1}\}$ and $\Gamma_4 = \{\forall\; V(R_n^p)| \notin\{\Gamma_1, \Gamma_2, \Gamma_3\}\}$. It suffice to show that if every vertex of $R_n^p$ have different representation w.r.t. resolving set $\Gamma$, then $pd(R_n^p)\leq4$. We give the representations of all vertices w.r.t. resolving partition set $\Gamma$ are following.

The vertices on inner cycle having the representations w.r.t. $\Gamma$ which are:

If $3\leq \alpha \leq {\beta}$, then $r(u_{\beta}|\Gamma) = (\alpha-1, \; \alpha-2, \; {\beta}-\alpha+1, \; 0)$. If ${\beta}+2\leq \alpha \leq {2\beta}$, then $r(u_{\beta}|\Gamma) = ({2\beta}-\alpha+1, \; {2\beta}-\alpha+2, \; \alpha-{\beta}-1, \; 0).$ There are no two vertices have same representation in inner cycle of $R_n^p$.

The vertices on interior cycle having the representations w.r.t. $\Gamma$ which are:

If $\alpha = 1$, then $r(v_{\beta}|\Gamma) = (1, \; 1, \; {\beta}, \; 0)$. If $2\leq \alpha \leq {\beta}$, then $r(v_{\beta}|\Gamma) = (\alpha, \; \alpha-1, \; {\beta}-\alpha+1, \; 0).$ If $\alpha = {\beta}+1$, then $r(v_{\beta}|\Gamma) = ({\beta}, \; {\beta}, \; 1, \; 0).$ If ${\beta}+2\leq \alpha \leq {2\beta}$, then $r(v_{\beta}|\Gamma) = ({2\beta}-\alpha+1, \; {2\beta}-\alpha+2, \alpha-{\beta}, \; 0).$ There are also no two vertices have same representation in interior cycle of $R_n^p$.

The vertices on exterior cycle having the representations w.r.t. $\Gamma$ which are:

If $\alpha = 1$, then $r(w_{\beta}|\Gamma) = (2, \; 2, \; {\beta}+1, \; 0)$. If $2\leq \alpha \leq {\beta}+1$, then $r(w_{\beta}|\Gamma) = (\alpha+1, \; \alpha, \; {\beta}-\alpha+2, \; 0).$ If $\alpha = {\beta}+2$, then $r(w_{\beta}|\Gamma) = ({\beta}+1, \; {\beta}+1, \; 2, \; 0).$ If ${\beta}+3\leq \alpha \leq {2\beta}$, then $r(w_{\beta}|\Gamma) = ({2\beta}-\alpha+2, \; {2\beta}-\alpha+3, \alpha-{\beta}+1, \; 0).$ Again there are no two vertices have same representation also in exterior cycle of $R_n^p$. The representations of pendant vertices w.r.t. $\Gamma$ are shown in Table 1. Again we can see that there are no two vertices have same representation of pendant vertices of $R_n^p$.

It is easy to verify that all the vertices of $R_n^p$ have unique representation w.r.t. resolving partition $\Gamma$. Its means we can resolve the vertices of $R_n^p$ into four partition resolving sets, when $n$ is even.

Case 2: When $n = {2\beta}+1, {\beta} \geq 3, {\beta} \in N.$ Again we resolve the vertices of $R_n^p$ into four partition resolving sets $\Gamma = \{\Gamma_1, \Gamma_2, \Gamma_3, \Gamma_4\}$ where $\Gamma_1 = \{u_1\}$, $\Gamma_2 = \{u_2\}$, $\Gamma_3 = \{u_{{\beta}+1}\}$ and $\Gamma_4 = \{\forall\; V(R_n^p)| \notin\{\Gamma_1, \Gamma_2, \Gamma_3\}\}$. It suffice to show that if every vertices of $R_n^p$ have different representation w.r.t. resolving set $\Gamma$, then $pd(R_n^p)\leq4$. {We give the representations of all vertices $\Gamma_4$ w.r.t. resolving set $\Gamma$ are following.

The vertices on inner cycle having the representations w.r.t. $\Gamma$ which are:

If $3\leq \alpha \leq {\beta}$, then $r(u_{\beta}|\Gamma) = (\alpha-1, \; \alpha-2, \; {\beta}-\alpha+1, \; 0)$. If $\alpha = {\beta}+2$, then $r(u_{\beta}|\Gamma) = (\beta, \; \beta, \; 1, \; 0)$. If ${\beta}+3\leq \alpha \leq {2\beta}+1$, then $r(u_{\beta}|\Gamma) = ({2\beta}-\alpha+2, \; {2\beta}-\alpha+3, \; \alpha-{\beta}-1, \; 0).$ There are no two vertices have same representation in inner cycle of $R_n^p$.

The vertices on interior cycle having the representations w.r.t. $\Gamma$ which are:

If $\alpha = 1$, then $r(v_{\beta}|\Gamma) = (1, \; 1, \; {\beta}, \; 0)$. If $2\leq \alpha \leq {\beta}$, then $r(v_{\beta}|\Gamma) = (\alpha, \; \alpha-1, \; {\beta}-\alpha+1, \; 0).$ If $\alpha = {\beta}+1$, then $r(v_{\beta}|\Gamma) = ({\beta}+1, \; {\beta}, \; 1, \; 0).$ If ${\beta}+2\leq \alpha \leq {2\beta}+1$, then $r(v_{\beta}|\Gamma) = ({2\beta}-\alpha+2, \; {2\beta}-\alpha+3, \alpha-{\beta}, \; 0).$ There are also no two vertices have same representation in interior cycle of $R_n^p$.

The vertices on exterior cycle having the representations w.r.t. $\Gamma$ which are: If $\alpha = 1$, then $r(w_{\beta}|\Gamma) = (2, \; 2, \; {\beta}+1, \; 0)$. If $2\leq \alpha \leq {\beta}$, then $r(w_{\beta}|\Gamma) = (\alpha+1, \; \alpha, \; {\beta}-\alpha+2, \; 0).$ If $\alpha = {\beta}+1$, then $r(w_{\beta}|\Gamma) = ({\beta}+2, \; {\beta}+1, \; 2, \; 0).$ If ${\beta}+2\leq \alpha \leq {2\beta}+1$, then $r(w_{\beta}|\Gamma) = ({2\beta}-\alpha+3, \; {2\beta}-\alpha+4, \alpha-{\beta}+1, \; 0).$ Again there are no two vertices have same representation also in exterior cycle of $R_n^p$.

The pendant vertices having the representations w.r.t. $\Gamma$ shown in Table 2. Again we can see that there are no two vertices have same representation of pendant vertices of $R_n^p$.

It is easy to verify that all the vertices of $R_n^p$ have unique representation w.r.t. resolving partition $\Gamma$. Its means we can also resolve the vertices of $R_n^p$ into four partition resolving sets, when $n$ is odd.

We note that from Case $1$ and $2$, there are no two vertices having the same representations implying that $pd(R_n^p) \leq 4$.

3.   Results on planer graph $D_n^P$

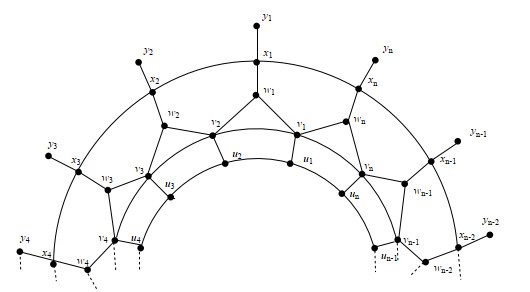
The convex polytope $D_n^P$ is a planar graph and if we attach a pendant edge at each vertex of outer cycle of $D_n$ ^[2] then we obtained a new plane graph $D_n^P$ as shown in Figure 2. The vertex and edge set $V({D_n^P}) = \{V(D_n)\}\cup \{y_\alpha:1\leq \alpha \leq n\}$, $E(D_n^P) = \{E(D_n)\} \cup \{x_\alpha y_\alpha: 1\leq \alpha \leq n\}$ are respectively. For calculation, $\{u_\alpha: 1\leq \alpha \leq n\}$ represents the inner cycle, the cycle induced by $\{v_\alpha: 1\leq \alpha \leq n\}$ is interior cycle, exterior cycle containing $\{w_\alpha: 1\leq \alpha \leq n\}$ set of vertices, $\{x_\alpha: 1\leq \alpha \leq n\}$ labeled as outer cycle and pendant vertices named for $\{y_\alpha: 1\leq \alpha \leq n\}$.

Theorem 3.1. Let $D_n^P$ be a polytopes with $n\geq 6$. Then $pd(D_n^P)\leq 4$.

Proof. We split the proof of above theorem into following two cases.

Case 1: When $n = {2\beta}, {\beta} \geq 3, {\beta} \in N.$ We partition the vertices of $D_n^p$ into four partition sets $\Gamma = \{\Gamma_1, \Gamma_2, \Gamma_3, \Gamma_4\}$ where $\Gamma_1 = \{u_1\}$, $\Gamma_2 = \{u_2\}$, $\Gamma_3 = \{u_{{\beta}+1}\}$ and $\Gamma_4 = \{\forall\; V(D_n^p)| \notin\{\Gamma_1, \Gamma_2, \Gamma_3\}\}$. It suffice to show that if every vertices of $D_n^p$ have different representation w.r.t. resolving set $\Gamma$, then $pd(D_n^p)\leq4$. We give the representations of all vertices $\Gamma_4$ w.r.t. resolving set $\Gamma$ are following.

The vertices on inner cycle having the representations w.r.t. $\Gamma$ which are:

If $3\leq \alpha \leq {\beta}$, then $r(u_{\beta}|\Gamma) = (\alpha-1, \; \alpha-2, \; {\beta}-\alpha+1, \; 0)$. If ${\beta}+2\leq \alpha \leq {2\beta}$, then $r(u_{\beta}|\Gamma) = ({2\beta}-\alpha+1, \; {2\beta}-\alpha+2, \; \alpha-{\beta}-1, \; 0).$ There are no two vertices have same representation in inner cycle of $D_n^p$.

The vertices on interior cycle having the representations w.r.t. $\Gamma$ which are:

If $\alpha = 1$, then $r(v_{\beta}|\Gamma) = (1, \; 2, \; {\beta}+1, \; 0)$. If $2\leq \alpha \leq {\beta}$, then $r(v_{\beta}|\Gamma) = (\alpha, \; \alpha-1, \; {\beta}-\alpha+2, \; 0).$ If $\alpha = {\beta}+1$, then $r(v_{\beta}|\Gamma) = ({\beta}, \; {\beta}, \; 1, \; 0).$ If ${\beta}+2\leq \alpha \leq {2\beta}$, then $r(v_{\beta}|\Gamma) = ({2\beta}-\alpha+2, \; {2\beta}-\alpha+3, \alpha-{\beta}, \; 0).$ There are also no two vertices have same representation in interior cycle of $D_n^p$.

The vertices on exterior cycle having the representations w.r.t. $\Gamma$ which are:

If $\alpha = 1$, then $r(w_{\beta}|\Gamma) = (2, \; 2, \; {\beta}+1, \; 0)$. If $2\leq \alpha \leq {\beta}$, then $r(w_{\beta}|\Gamma) = (\alpha+1, \; \alpha, \; {\beta}-\alpha+2, \; 0).$ If $\alpha = {\beta}+1$, then $r(w_{\beta}|\Gamma) = ({\beta}+1, \; {\beta}+1, \; 2, \; 0).$ If ${\beta}+2\leq \alpha \leq {2\beta}$, then $r(w_{\beta}|\Gamma) = ({2\beta}-\alpha+2, \; {2\beta}-\alpha+3, \alpha-{\beta}+1, \; 0).$ Again there are no two vertices have same representation also in exterior cycle of $D_n^p$.

The vertices on outer cycle and pendant vertices having the representations w.r.t. $\Gamma$ as shown in Tables 3 and 4. Again we can see that there are no two vertices have same representation in outer cycle and pendant vertices of $D_n^p$.

It is easy to verify that all the vertices of $D_n^p$ have unique representation w.r.t. resolving partition $\Gamma$. Its means we can resolve the vertices of $D_n^p$ into four partition resolving sets, when $n$ is even.

Case 2: When $n = {2\beta}+1, {\beta} \geq 3, {\beta} \in N.$ Again we resolve the vertices of $D_n^p$ into four partition resolving sets $\Gamma = \{\Gamma_1, \Gamma_2, \Gamma_3, \Gamma_4\}$ where $\Gamma_1 = \{u_1\}$, $\Gamma_2 = \{u_2\}$, $\Gamma_3 = \{u_{{\beta}+1}\}$ and $\Gamma_4 = \{\forall\; V(D_n^p)| \notin\{\Gamma_1, \Gamma_2, \Gamma_3\}\}$. It suffice to show that if every vertices of $D_n^p$ have different representation w.r.t. resolving set $\Gamma$, then $pd(D_n^p)\leq4$. We give the representations of all vertices $\Gamma_4$ w.r.t. resolving set $\Gamma$ are following.

The vertices on inner cycle having the representations w.r.t. $\Gamma$ which are:

If $3\leq \alpha \leq {\beta}$, then $r(u_{\beta}|\Gamma) = (\alpha-1, \; \alpha-2, \; {\beta}-\alpha+1, \; 0)$. If $\alpha = {\beta}+2$, then $r(u_{\beta}|\Gamma) = (\beta, \; \beta, \; 1, \; 0)$. If ${\beta}+3\leq \alpha \leq {2\beta}+1$, then $r(u_{\beta}|\Gamma) = ({2\beta}-\alpha+1, \; {2\beta}-\alpha+2, \; \alpha-{\beta}-1, \; 0).$ There are no two vertices have same representation in inner cycle of $D_n^p$.

The vertices on interior cycle having the representations w.r.t. $\Gamma$ which are:

If $\alpha = 1$, then $r(v_{\beta}|\Gamma) = (1, \; 2, \; {\beta}+1, \; 0)$. If $2\leq \alpha \leq {\beta}+1$, then $r(v_{\beta}|\Gamma) = (\alpha, \; \alpha-1, \; {\beta}-\alpha+2, \; 0).$ If $\alpha = {\beta}+2$, then $r(v_{\beta}|\Gamma) = ({\beta}+1, \; {\beta}+1, \; 2, \; 0).$ If ${\beta}+3\leq \alpha \leq {2\beta}+1$, then $r(v_{\beta}|\Gamma) = ({2\beta}-\alpha+2, \; {2\beta}-\alpha+3, \alpha-{\beta}, \; 0).$ There are also no two vertices have same representation in interior cycle of $D_n^p$.

The vertices on exterior cycle having the representations w.r.t. $\Gamma$ which are:

If $\alpha = 1$, then $r(w_{\beta}|\Gamma) = (2, \; 2, \; {\beta}+1, \; 0)$. If $2\leq \alpha \leq {\beta}$, then $r(w_{\beta}|\Gamma) = (\alpha+1, \; \alpha, \; {\beta}-\alpha+2, \; 0).$ If $\alpha = {\beta}+1$, then $r(w_{\beta}|\Gamma) = ({\beta}+2, \; {\beta}+1, \; 2, \; 0).$ If ${\beta}+2\leq \alpha \leq {2\beta}+1$, then $r(w_{\beta}|\Gamma) = ({2\beta}-\alpha+3, \; {2\beta}-\alpha+4, \alpha-{\beta}+1, \; 0).$ Again there are no two vertices have same representation also in exterior cycle of $D_n^p$.

The vertices on outer cycle and pendant vertices having the representations w.r.t. $\Gamma$ as shown in Tables 5 and 6. Again we can see that there are no two vertices have same representation in outer cycle and pendant vertices of $D_n^p$.

It is easy to verify that all the vertices of $D_n^p$ have unique representation w.r.t. resolving partition $\Gamma$. Its means we can also resolve the vertices of $D_n^p$ into four partition resolving sets, when $n$ is odd.

We note that from Case $1$ and $2$, there are no two vertices having the same representations implying that $pd(\mathbb{T}^p_n) \leq 4$.

4.   Results on planer graph $Q_n^P$

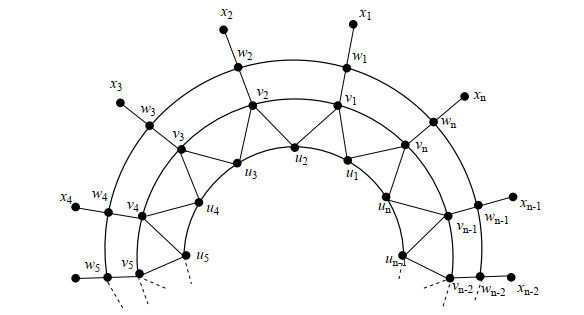
The convex polytope $Q_n^P$ is a planar graph and If we attach a pendant edge at each vertex of outer cycle of $Q_n$ ^[3] then we obtained a new plane graph $Q_n^P$ as shown in Figure 3. The vertex and edge set $V({Q_n^P}) = \{V({\alpha}_n)\}\cup \{y_\alpha:1\leq \alpha \leq n\}$, $E(Q_n^P) = \{E(Q_n)\} \cup \{x_\alpha y_\alpha: 1\leq \alpha \leq n\}$ are respectively.

For convenience, $\{u_\alpha: 1\leq \alpha \leq n\}$ represents the inner cycle, the cycle induced by $\{v_\alpha: 1\leq \alpha \leq n\}$ is interior cycle, exterior cycle containing $\{w_\alpha: 1\leq \alpha \leq n\}$ set of vertices, $\{x_\alpha: 1\leq \alpha \leq n\}$ are exterior vertices, and pendant vertices named for $\{y_\alpha: 1\leq \alpha \leq n\}$.

Theorem 4.1. Let $Q_n^P$ be a polytopes with $n\geq 6$. Then $pd(Q_n^P)\leq 4$.

Proof. Case 1: When $n = {2\beta}, {\beta} \geq 3, {\beta} \in N.$ We partition the vertices of $Q_n^p$ into four partition resolving sets $\Gamma = \{\Gamma_1, \Gamma_2, \Gamma_3, \Gamma_4\}$ where $\Gamma_1 = \{u_1\}$, $\Gamma_2 = \{u_2\}$, $\Gamma_3 = \{u_{{\beta}+1}\}$ and $\Gamma_4 = \{\forall\; V(Q_n^p)| \notin\{\Gamma_1, \Gamma_2, \Gamma_3\}\}$. It suffice to show that if every vertices of $Q_n^p$ have different representation w.r.t. resolving set $\Gamma$, then $pd(Q_n^p)\leq 4$. We give the representations of all vertices $\Gamma_4$ w.r.t. resolving set $\Gamma$ are following.

The vertices on inner cycle having the representations w.r.t. $\Gamma$ which are:

If $3\leq \alpha \leq {\beta}$, then $r(u_{\beta}|\Gamma) = (\alpha-1, \; \alpha-2, \; {\beta}-\alpha+1, \; 0)$. If ${\beta}+2\leq \alpha \leq {2\beta}$, then $r(u_{\beta}|\Gamma) = ({2\beta}-\alpha+1, \; {2\beta}-\alpha+2, \; \alpha-{\beta}-1, \; 0).$ There are no two vertices have same representation in inner cycle of $Q_n^p$.

The vertices on interior cycle having the representations w.r.t. $\Gamma$ which are:

If $\beta = 1$, then $r(v_{\beta}|\Gamma) = (1, \; 2, \; \alpha+1, \; 0).$ If $2\leq \alpha \leq {\beta}$, then $r(v_{\beta}|\Gamma) = (\alpha, \; \alpha-1, \; {\beta}-\alpha+2, \; 0).$ If ${\beta}+2\leq \alpha \leq {2\beta}$, then $r(v_{\beta}|\Gamma) = ({2\beta}-\alpha+2, \; {2\beta}-\alpha+3, \alpha-{\beta}, \; 0).$ There are also no two vertices have same representation in interior cycle of $Q_n^p$.

The vertices on exterior cycle having the representations w.r.t. $\Gamma$ which are:

If $\beta = 1$, then $r(v_{\beta}|\Gamma) = (2, \; 2, \; \alpha+1, \; 0).$ If $2\leq \alpha \leq {\beta}$, then $r(w_{\beta}|\Gamma) = (\alpha+1, \; \alpha, \; {\beta}-\alpha+2, \; 0).$ If $\alpha = \beta+1$, then $r(v_{\beta}|\Gamma) = (\alpha+1, \; \alpha+1, \; 2, \; 0).$ If ${\beta}+2\leq \alpha \leq {2\beta}$, then $r(w_{\beta}|\Gamma) = ({2\beta}-\alpha+2, \; {2\beta}-\alpha+3, \alpha-{\beta}+1, \; 0).$ Again there are no two vertices have same representation also in exterior cycle of $Q_n^p$.

The vertices on exterior cycle having the representations w.r.t. $\Gamma$ which are:

If $\beta = 1$, then $r(v_{\beta}|\Gamma) = (3, \; 3, \; \alpha+2, \; 0).$ If $2\leq \alpha \leq {\beta}$, then $r(w_{\beta}|\Gamma) = (\alpha+2, \; \alpha+1, \; {\beta}-\alpha+3, \; 0).$ If $\alpha = \beta+1$, then $r(v_{\beta}|\Gamma) = (\alpha+2, \; \alpha+2, \; 3, \; 0).$ If ${\beta}+2\leq \alpha \leq {2\beta}$, then $r(w_{\beta}|\Gamma) = ({2\beta}-\alpha+3, \; {2\beta}-\alpha+4, \alpha-{\beta}+2, \; 0).$ Again there are no two vertices have same representation also in exterior cycle of $Q_n^p$.

The pendant vertices having the representations w.r.t. $\Gamma$ as shown in Table 7. Again we can see that there are no two vertices have same representation in pendant vertices of $Q_n^p$.

It is easy to verify that all the vertices of $Q_n^p$ have unique representation w.r.t. resolving partition $\Gamma$. Its means we can resolve the vertices of $Q_n^p$ into four partition resolving sets, when $n$ is even.

Case 2: When $n = {2\beta}+1, {\beta} \geq 3, {\beta} \in N.$ Again we resolve the vertices of $Q_n^p$ into four partition resolving sets $\Gamma = \{\Gamma_1, \Gamma_2, \Gamma_3, \Gamma_4\}$ where $\Gamma_1 = \{u_1\}$, $\Gamma_2 = \{u_2\}$, $\Gamma_3 = \{u_{{\beta}+1}\}$ and $\Gamma_4 = \{\forall\; V(Q_n^p)| \notin\{\Gamma_1, \Gamma_2, \Gamma_3\}\}$. It suffice to show that if every vertices of $Q_n^p$ have different representation w.r.t. resolving set $\Gamma$, then $pd(Q_n^p)\leq4$. We give the representations of all vertices $\Gamma_4$ w.r.t. resolving set $\Gamma$ are following.

The vertices on inner cycle having the representations w.r.t. $\Gamma$ which are:

If $3\leq \alpha \leq {\beta}$, then $r(u_{\beta}|\Gamma) = (\alpha-1, \; \alpha-2, \; {\beta}-\alpha+1, \; 0)$. If $\alpha = {\beta}+2$, then $r(u_{\beta}|\Gamma) = (\beta, \; \beta, \; 1, \; 0)$. If ${\beta}+3\leq \alpha \leq {2\beta}+1$, then $r(u_{\beta}|\Gamma) = ({2\beta}-\alpha+1, \; {2\beta}-\alpha+2, \; \alpha-{\beta}-1, \; 0).$ There are no two vertices have same representation in inner cycle of $Q_n^p$.

The vertices on interior cycle having the representations w.r.t. $\Gamma$ which are:

If $\beta = 1$, then $r(v_{\beta}|\Gamma) = (1, \; 2, \; \alpha+1, \; 0).$ If $2\leq \alpha \leq {\beta}$, then $r(v_{\beta}|\Gamma) = (\alpha, \; \alpha-1, \; {\beta}-\alpha+2, \; 0).$ If $\alpha = {\beta}+2$, then $r(v_{\beta}|\Gamma) = ({\beta}+1, \; {\beta}+1, \; 2, \; 0).$ If ${\beta}+3\leq \alpha \leq {2\beta}+1$, then $r(v_{\beta}|\Gamma) = ({2\beta}-\alpha+2, \; {2\beta}-\alpha+3, \alpha-{\beta}, \; 0).$ There are also no two vertices have same representation in interior cycle of $Q_n^p$.

The vertices on exterior cycle having the representations w.r.t. $\Gamma$ which are:

If $\beta = 1$, then $r(v_{\beta}|\Gamma) = (2, \; 2, \; \alpha+1, \; 0).$ If $2\leq \alpha \leq {\beta}$, then $r(w_{\beta}|\Gamma) = (\alpha+1, \; \alpha, \; {\beta}-\alpha+2, \; 0).$ If $\alpha = {\beta}+1$, then $r(w_{\beta}|\Gamma) = ({\beta}+2, \; {\beta}+1, \; 2, \; 0).$ If ${\beta}+2\leq \alpha \leq {2\beta}+1$, then $r(w_{\beta}|\Gamma) = ({2\beta}-\alpha+3, \; {2\beta}-\alpha+4, \alpha-{\beta}+1, \; 0).$ Again there are no two vertices have same representation also in exterior cycle of $Q_n^p$.

The vertices on exterior cycle having the representations w.r.t. $\Gamma$ which are:

If $\beta = 1$, then $r(v_{\beta}|\Gamma) = (3, \; 3, \; \alpha+2, \; 0).$ If $2\leq \alpha \leq {\beta}$, then $r(w_{\beta}|\Gamma) = (\alpha+2, \; \alpha+1, \; {\beta}-\alpha+3, \; 0).$ If $\alpha = {\beta}+1$, then $r(w_{\beta}|\Gamma) = ({\beta}+2, \; {\beta}+2, \; 3, \; 0).$ If ${\beta}+2\leq \alpha \leq {2\beta}+1$, then $r(w_{\beta}|\Gamma) = ({2\beta}-\alpha+4, \; {2\beta}-\alpha+5, \alpha-{\beta}+2, \; 0).$ Again there are no two vertices have same representation also in exterior cycle of $Q_n^p$.

The pendant vertices having the representations w.r.t. $\Gamma$ as shown in Table 8. Again we can see that there are no two vertices have same representation in pendant vertices of $Q_n^p$.

It is easy to verify that all the vertices of $Q_n^p$ have unique representation w.r.t. resolving partition $\Gamma$. Its means we can also resolve the vertices of $Q_n^p$ into four partition resolving sets, when $n$ is odd.

We note that from Case $1$ and $2$, there are no two vertices having the same representations implying that $pd(\mathbb{U}^p_n) \leq 4$.

5.   Conclusions

The core of the problem of the partition dimension is deciding the resolving partition set for a graph. In this paper, we have studies the partition dimension of some families of convex polytopes graph such as $R_n^p$, $D_n^p$ and $Q_n^p$, which are obtained from the convex polytopes by adding a pendant edge at each vertex of outer cycle. In this research work, we have proved that partition dimension of these convex polytopes are bounded. Consequently, we propose the following open problems.

Conjecture 5.1. The following equalities hold:

Conflict of interest

The authors declare there is no conflict of interest.