Analysis of noise attenuation through soft vibrating barriers: an analytical investigation

1.   Introduction

The technology of commercial aviation has motivated to development of the theory of flow-generated sound to a large extent. This phenomenon is not significant only in the aircraft and ballistic missile industry, where the noise generation while taking off and landing is an important factor, but also plays a vital role in the automotive and computer industry, even in buildings and housing where noise due to air flow becomes a big deal as a selling argument. Therefore, the phenomenon of acoustic propagation and generation in fluid flow has become an important feature in the mathematical study. Concerning the defense system, the countries possessing extensive coastlines require a dire need of protection of water regions adjacent to the land and maritime borders. Foremost is the development and improvement of active and passive Sonar systems to assist the military struggle widely at sea. In an active sonar system, the transducers radiate a pulse of sound signal in water. When the object is located in the path of sound signals, on interaction with the object, the signals scatter, bounce off the object, and return to an echo to the transducer. Sonar was used to emit the acoustic signal for investigation of scattering effects of the cross board, square plate, and spherical object as geometrical markers positioned on the dam face in the underwater reservoir ^[1]. The outcomes showed that scattered sound pressure levels (SPL) due to cross board had larger values than those of due to the square plate and spherical object. An acoustic scattering model was proposed for the target-recognition procedure in sonar system ^[2]. The model predicted that acoustic scattering from the objects immersed in the water can be calculated with less cost of computation and less time as compared to numerical models, particularly in 3-Dimensional space. The scattering of acoustic waves by an elastic cylindrical obstacle produced the cylindrical pattern which made the obstacle act as an infinite target ^[3]. This model elaborated the sonar effects practically.

In recent times, noise has emerged as a significant problem for the surrounding environment. Because of this, scientists have been motivated to work on developing methods to control noise. In order to accomplish this, the barriers that each have their own unique qualities have been utilized ^[4,5]. Modeling the wave-guide structure allows for investigation into the potential for a reduction in the amount of acoustic oscillations caused by combustion engines ^[6]. Analytical methods such as the Mode-Matching Method ^[7,8], $\left(m+\frac{G^{\prime}}{G}\right)$-expansion technique ^[9], and the Wiener-Hopf technique are being incorporated for solving the acoustic problems. The Wiener-Hopf technique ^[10,11] is capable of tackling the problems of acoustic scattering by canonical structures of finite length since such types of models are configured with mixed boundary conditions: a velocity on the strip $y = 0, \text{ }p < x < q$ and pressure continuity off the strip $y = 0, \text{ }x < p, \text{ }x > q$. With such kind of two mixed conditions, one develops a Wiener-Hopf model in 1D (or scalar) form which requires multiplicative factorization of the kernel function $K\left(\alpha\right),$ that is $K\left(\alpha\right) = K_{+}\left(\alpha\right)K_{-}\left(\alpha\right)$, where the factors $K_{+}\left(\alpha\right)$ and $K_{-}\left(\alpha\right)$ are analytic in up and down regions of complex $\alpha$-plane, respectively. Analytic factorization in a few problems is very convenient like the Sommerfeld diffraction phenomenon ^[12] and diffraction by canonical structures of finite dimensions with first kind ^[13,14,15] and second kind ^[16,17] of boundary conditions, whereas little complicated in problems of such structures with third type ^[18,19,20] of boundary conditions. Wiener-Hopf formulation of acoustic problems has been devised for the noise scattering phenomena in moving fluid ^[21,22,23] as well as by vibrating planes ^[24,25,26] to inspect the acoustic attenuation by using barriers for noise control.

This study aims to investigate noise scattering by a soft plate that vibrates in a fluid in motion. The desired outcome is achieved by having the solution to separate WH-equations, and the generalized Fourier units are determined for respective vibration pattern. The scattering generated by the plate's edges includes both separated and interaction fields. This study appears to be the first effort to explore the acoustic-structure interacting the vibrating plate and the moving fluid in the context of scattering theory. Thus, the article being discussed examines the impact of fluid flow and vibration on the acoustics of a subsonic flow, which is extension of the work by Ayub et al. ^[25] which analyzes the diffraction problem via an oscillating thin strip using the Kirchhoff diffraction theory and the Wiener-Hopf technique. The current study utilizes the later for the analytical treatment of the acoustic model and also mentions the sound scattering via a soft finite barrier and the use of asymptotic computation of scattered potential integral equations. The present study shares a similar geometric structure with Ayub et al. ^[25] when the Mach number is taken to be zero, assuming that the fluid or gas is incompressible, and the wave equation simplifies to a simple wave equation. However, the assumption of incompressibility may not always be valid, especially for high-frequency sound waves or high-speed flows, in which case the full compressible wave equation should be used. Overall, the present study investigates a different problem related to noise scattering, although it shares some similarities with the work by Ayub et al. ^[25]. Moreover, the reference to Javaid et al. ^[13] serves as additional validation of the mathematical analysis performed in the current study as the findings are consistent with those of a previous study, which strengthens the reliability of the current study's results.

2.   Formulation of the problem

This model is proposed for sound scattering by finite soft plane $p < x < q,$ $y = 0,$ which is vibrating vertically with velocity $u_{0}f\left(t\right)$, and periodic function of time $t,$ $f\left(t\right)$ is revealed to be the following Fourier series in a general:

with

and

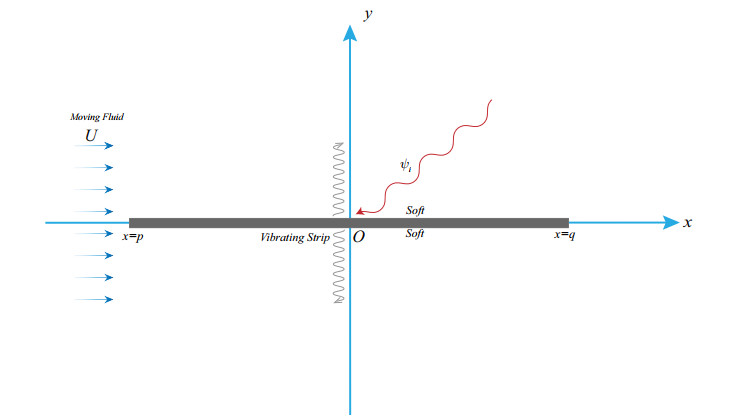
To investigate the effects of a vibrating soft plane on sound scattering in a moving fluid with $U$, we assume that sound is incident with velocity potential $\psi\left(x, y\right)\exp\left(ik_{3}z\right)$ and interacts with a finite impermeable soft plane $p < x < q,$ $y = 0$ as shown in Figure 1. The direction of oscillation of a finite plane placed horizontally is orthogonal to the direction of background mean flow with Mach number $M$ in positive $x$-direction.

The velocity potential $\psi\left(x, y, t\right)$ for irrotational sound wave is associated with $\boldsymbol{v}$ such that $\boldsymbol{v} = \nabla\psi\left(x, y, t\right)$. The pressure expression is written by

The governing convective wave equation for $\psi\left(x, y, t\right)$ is expressed as

with $\Delta$ as $2D$ Laplacian operator and $M = U/c_{s}$.

A gust with $k_{i}$ incident at $\theta_{i}$ to the vibrating plane is described by velocity potential

with $\omega _{i} = c_{s}k_{i}$.

The total field is described as

where $\psi_{s}\left(x, y, t\right)$ satisfies the wave Eq $\left(2.5\right).$

The completely impermeable body does not let the incoming wave penetrate its surface, consequently, the wave incident on the surface is entirely reflected. Therefore, the nature of vibrating plate is specified by the following boundary conditions continuous across the region $y = 0,$ $p < x < q$:

The continuity of $\psi_{s}$ and $\partial_{y}\psi_{s}$ (can be denoted by $\psi_{s}^{\prime}$) across $y = 0$ is required and is given by

It is required for $\psi_{s}$ to obey the radiation condition for outgoing waves

and the conditions near the edges of plate are here as in ^[10].

with $c_{i}$ as constants.

3.   Transformation of the problem

Let $\phi_{s}\left(x, y, \omega\right)$ be the temporal Fourier transform,

Applying the temporal Fourier transform to Eqs $\left(2.5\right)$, $\left(2.8\right)$ and $\left(2.9\right)$ yields

with $k = \omega /c_{s} = k_{R}+ik_{I},$ $k_{I} > 0$.

with

and

While having the subsonic flow assumption $\left(\vert M\vert < 1\right)$, the transformation is made such that

along with

Employing substitution $\left(3.7\right)$ together with Eq $\left(3.2\right)$ to $\left(3.6\right)$, the equation reduces to

Using same substitution with $\phi_{i}\left(x, y\right) = \Phi_{i}\left(X, Y\right)e^{-i\mathcal{K}MX}$, we have

where $\Phi_{i}\left(X, Y\right)$ is the incident on the vibrating plane and is expressed as ^[29]:

After use of substitution $\left(3.7\right)$ along with $\left(3.6\right)$ in Eq $\left(3.3\right)$, we have the result as follows:

and similarly Eq $\left(2.9\right)$ transforms to

Let the spatial Fourier transform with respect to X be defined as

with

where

The spatial Fourier transformation of $\left(3.8\right)$, $\left(3.9\right)$ and $\left(3.12\right)$ yields

with $\gamma\left(\alpha\right) = \sqrt{\alpha^{2}-\mathcal{K}^{2}}$.

where

4.   Wiener-Hopf analysis

4.1.   Formulation of Wiener-Hopf equation

The governing equation possesses the solution of the form

Now the combination of $\left(3.14\right)$ and $\left(4.1\right),$ results into

After basic algebraic operations (addition and subtraction) for the pair of Eq $\left(4.2\right)$ along with the use of condition $\left(3.21\right)$, the outcome is

and

where

The following Wiener-Hopf equation is computed through Eqs $\left(3.14\right)$, $\left(3.19\right)$ and $\left(4.1\right)$:

where

4.2.   Wiener-Hopf factorization

Equations $\left(4.3\right)$ and $\left(4.6\right)$ represent the Wiener-Hopf equations of standard form. To compute the problem, we must address Eq $\left(4.6\right)$ using the Wiener-Hopf procedure ^[10]. To do this, we require the decomposition of the kernel, which can be accomplished using the following theorem, as elaborated in ^[10,11]:

Theorem: "Suppose that $\tilde{F}\left(\alpha\right)$ is a function that is analytic in the strip $\tau_{-} < \mathfrak{I}m \, \alpha > \tau_{+}$, and $\tilde{F}\left(\alpha\right)$ approaches zero uniformly in the strip as $\vert\alpha\vert \rightarrow \infty$. Then, we can factorize $\tilde{F}\left(\alpha\right)$ as

where $\tilde{F}_{+}\left(-\alpha\right) = \tilde{F}_{-}\left(\alpha\right)$, $F_{+}(\alpha)$ is analytic in the domain $\mathfrak{I}m\{\alpha\} > \tau_{-}$, and $\tilde{F}_{-}\left(\alpha\right)$ is analytic in the domain $\mathfrak{I}m\{\alpha\} < \tau_{+}$, as shown in Figure 2."

The kernel function $\mathcal{S}\left(\alpha\right)$, which is defined by Eq $\left(4.8\right)$, can be factorized using the above theorem into two parts:

where $\mathcal{S}_{+}\left(\alpha\right)$ is regular in the upper half plane ($\mathfrak{I}m\left(\alpha\right) > -\mathfrak{I}m\left(\mathcal{K}\right)$) and $\mathcal{S} _{-}\left(\alpha\right)$ is regular in the lower half plane ($\mathfrak{I}m\left(\alpha\right) < \mathfrak{I}m\left(\mathcal{K}\right)$). This factorization is plugged in Eq $\left(4.6\right)$ to obtain the following form of Wiener-Hopf equation:

4.3.   Solution of Wiener-Hopf equation

Equation of the form $\left(4.6\right)$ has been devised through Wiener-Hopf theory ^[10] and we need to introduce a polynomial function $\mathcal{P}\left(\alpha\right)$ such that the parts of Eq $\left(4.13\right)$ analytic in the upper and lower region are equated to this entire polynomial function. $\mathcal{P}\left(\alpha\right)$ is evaluated through the extension of Liouville's theorem ^[10] and analytic continuation ^[10,11] which are stated as follows:

Liouville's Theorem: "This remarks that any function $f(\zeta)$ that is bounded by $M\vert\zeta\vert ^{p}$ as $\vert\zeta\vert\rightarrow \infty$, where $M$ and $p$ are constants, must be a polynomial of degree no greater than $\left[p\right]$. In other words, if a function grows no faster than a polynomial, then it must be a polynomial of a certain degree or less."

And

Analytic Continuation: "The principle of analytic continuation states that if two analytic functions, $f_{1}$ and $f_{2}$, defined on domains $\Omega_{1}$ and $\Omega_{2}$, respectively, agree on the intersection $\Omega_{1}\cap\Omega_{2}$, then $f_{2}$ is an analytic continuation of $f_{1}$ to $\Omega_{2}$, and vice versa. Furthermore, if such an analytic continuation of $f_{1}$ to $\Omega_{2}$ exists, it is unique."

By applying Liouville's theorem and the process of analytic continuation process (as depicted in Figure 2), we establish that $\mathcal{J}\left(\alpha \right) = 0$. As a result, we earn the subsequent outcomes.

and where

and

where $h_{-1} = e^{i\frac{\pi }{4}}$

where $z$ $= -i\left(\mathcal{K}+\alpha \right) \left(q-p\right)$.

Substituting Eq $\left(4.14\right)$ along with Eqs $\left(4.16\right)$–$\left(4.20\right)$ in Eq $\left(4.6\right)$, we get

Here, $\Phi_{s} (X, Y, \omega)$ can be sorted out while employing the inverse of the Fourier transform to Eq $\left(4.1\right)$, i.e.,

Now, $\Phi_{s} \left(X, Y, \omega \right)$ is separated as

where $\Phi _{sep}\left(X, Y, \omega \right)$ and $\Phi _{int}\left(X, Y, \omega \right)$ are as follows:

where $A_{sep}\left(\alpha, \omega \right)$ and $A_{int}\left(\alpha, \omega \right)$ can be extracted from the result $\left(4.25\right)$ as:

Both edges $x = p$ and $x = q$ of the plate generate scattering in subsonic flow which is presented by $\Phi_{s} \left(X, Y, \omega \right)$ in the frequency domain.

5.   Asymptotic results of far field

To compute the far field, we can use the integral expression $\left(4.26\right)$ and evaluate it asymptotically. In order to do this, we first make a substitution of variables, namely $X = R\cos \Theta$ and $|Y| = R\sin \Theta$. Next, we deform the contour of integration by applying a transformation to a new variable $\alpha$, which takes the form $\alpha = -\mathcal{K}\cos(\Theta + i\xi)$, where $\Theta$ ranges from 0 to $\pi$ and $\xi$ from $-\infty$ to $\infty$.

As we take $\mathcal{K}R$ to be large, the expression $\left(4.26\right)$ asymptotically simplifies, allowing us to obtain the far field. Specifically, we can evaluate the integral by using a stationary phase approximation ^[30] and the resulting expression provides a good approximation of the far field. This method is commonly used in various fields of physics, such as electromagnetism, optics, and acoustics, to study the propagation of waves and radiation.

Similarly,

and

The desired outcome of the scattered field with frequency domain can be obtained by plugging Eq $\left(5.1\right)$ in Eq $\left(3.7\right)$ as follows:

The scattered field with time domain $\psi_{s}\left(x, y, t\right)$ is computed after operating the inverse temporal transform

where

with

The desired outcome $\psi_{s}\left(x, y, t\right)$ in Eq $\left(5.6\right)$ presents the scattered field in time domain with $\zeta$ and $\eta$, as given in Eq $\left(5.7\right)$ and Eq $\left(5.8\right)$, respectively, being the coefficient functions of scattered field. One corresponds to the incident wave field and other to the vibration of plate.

Remarks: Mathematically, the current study is the extended version of finite oscillating strip problem ^[25] and scattering coefficient $A\left(\alpha, \omega\right)$ corresponding to the geometrical structure of ^[25] can be recovered by setting $M = 0$, $p = -l$ and $q = 0$ as follows:

Which is the diffraction coefficient function for the finite non-symmetric oscillating strip ^[25].

6.   Graphical results and discussion

The scattered potential function is strongly dependent on the physical parameters $\theta_{i}$, $M$, $\omega_{0}t$, $\omega_{i}t$, and corresponding results are sketched. When a sound wave encounters an oscillating object in a fluid, it can create a pressure gradient around the object, which generates a net force on the object. The magnitude and direction of this force depend on the frequency, amplitude, and phase of the sound wave as well as the geometry and material properties of the object. The incident angle of the sound wave can also affect the direction of the resulting force, as it can change the distribution of pressure around the object. To see this effect, the scattered potential for $\theta_{i} = \pi /6$, $\pi /4$, $\pi /3$ are plotted under different cases of flow. Three sharp peaks of scattered potential at $\theta = 5\pi /6$, $3\pi /4$, $2\pi /3$ for respective incident acoustic show the reflected shadow boundary as portrayed by Figures 3 and 4. One noticeable thing is that sharp peaks, coinciding near $\theta = \pi /3$ in Figure 3(a), appear in the case of mean flow (M = 0.5) whereas the same effect appears between $\theta = \pi /6$ and $\theta = \pi /3$ for M = 0.9, this happens due to the interaction of subsonic flow with scattered potential. But no such effect is seen in the case of no fluid flow (M = 0.0) as pictured in Figures 3(a) and 4(a). Moreover, the scattered potential has more oscillatory behavior in the high subsonic flow as pictured in Figures 3(c) and 4(c) as compared to that of with mean flow Figures 3(b) and 4(b) and no fluid flow Figures 3(a) and 4(a). Figures 5 and 6 elaborate the scattered potential for variation of $M$ for different frequencies of vibrating plate. In this study, the types of vibrations of plate are considered here as in ^[26,27,28]. The outcomes reveal that the amplitude of the scattered potential exhibits an incremental trend in the case of a larger frequency of vibrating plate as pictured in Figures 5(c) and 6(c). In the mean flow, the scattered potential seems to be attenuated. The impact of the vibrating plate on the scattered potential is portrayed in Figures 7 and 8. The results explore that the scattered sound gets amplified by enhancing the vibrations of the plate. Moreover, the scattered sound gets more vibrated in high subsonic flow Figures 7(c) and 8(c) as compared to the scattered sound in the mean flow Figures 7(b) and 8(b) and in no fluid flow Figures 7(a) and 8(a). The common factor of the scattered potential is nullity around $\theta = 0, \pi$. In the case of nullity at $\theta = 0$, the interference is likely constructive, meaning that the scattered waves reinforce each other and lead to a strong increase in amplitude. However, at the same time, this interference can result in a significant decrease in the scattered field at other angles, leading to the observed nullity. Similarly, at $\theta = \pi$, the interference is likely destructive, meaning that the scattered waves cancel each other out, resulting in a significant decrease in amplitude. As a result, the scattered field is significantly reduced in magnitude, leading to the observed nullity. Therefore, we can relate these interference effects to the physical properties of the oscillating plate, such as its size, shape, and material properties. We can also discuss the potential implications of these interference effects for applications such as acoustic imaging or sensing. For example, in some cases, nullity may be desirable, as it can lead to a reduction in unwanted reflections or noise in the measured signal. Overall, the presence of nullity in the scattered field of acoustic waves by a soft oscillating plate of finite length highlights the complex wave-structure interactions that occur in acoustic systems and the importance of accurately modeling and understanding these interactions for a wide range of applications.

From above observations, it is noticed that scattering of acoustic waves incident on a soft oscillating plate of finite length in a moving fluid has many practical applications. For example, it can be used to design acoustic filters and resonators, where the plate is used to selectively transmit or reflect certain frequencies of the incident wave. It can also be used in the field of acoustophoresis, where the plate is used to manipulate particles or cells suspended in the fluid by inducing acoustic radiation forces.

7.   Conclusions

The analytical study of acoustic scattering by a limited size soft oscillating plate in a flowing fluid has revealed important insights into the behavior of sound waves and their interaction with fluid and solid structures. The findings of this study indicated that the scattering of sound by a plate is significantly influenced by the physical characteristics of the plate, such as its size, shape, and material properties, as well as the properties of the surrounding fluid.

The mathematical models developed in this research have provided a valuable framework for understanding and predicting sound scattering phenomena in a broad range of practical applications. Specifically, these models can be used to better understand underwater acoustics, sonar systems, and medical imaging, among other fields. Moreover, this research suggests that further exploration of this topic could innovate the new materials and techniques for controlling and manipulating sound waves. Such advancements could have a wide range of potential applications, including noise reduction, acoustic cloaking, and ultrasonic imaging.

In summary, this research offers a comprehensive examination of sound scattering by a finite soft oscillating plate for a fluid in motion. The results provided valuable insights into the behavior of sound waves, which have practical applications across various fields. The mathematical models developed in this study also offer a useful framework for predicting sound scattering phenomena and potentially unlocking new techniques for controlling sound waves.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The financial support for this research was provided by the Ministry of Education and King Abdelaziz University, DSR, Jeddah, Saudi Arabia, through institutional fund projects under grant number IFPIP: 939-662-1443. The authors express their gratitude for the technical and financial assistance received.

Conflict of interest

We, the authors of this research article, declare that we have no conflict of interest. We have no financial or personal relationships with individuals or organizations that could inappropriately influence or bias our research.