A study of mixed generalized quasi-Einstein spacetimes with applications in general relativity

1.   Introduction

A great deal of attention has been paid to the use of mathematical tools in recent years to better describe phenomena in the world, such as nonlinear optics ^[1], network analysis ^[2], biomedical signal processing ^[3], mathematical modelling of human liver ^[4], medical imaging ^[5,6], neural networks ^[7], optimal control ^[8], a diffusive epidemic model ^[9], chemical signal concentration ^[10], attraction-repulsion ^[11], control theory ^[12], signal advancement ^[13], computational approaches in medicine ^[14], nanoscience ^[15], artificial intelligence ^[16], fractional mathematical model ^[17], wave propagation ^[18], and applied mathematical analysis ^[19]. These eras of research have attracted the attention of many scholars in both science and engineering disciplines and led to the development of many efficient numerical methods. For example, deep learning technique in ^[20], the Lyapunov functional approach in ^[21], convolutional neural network in ^[22], interpretive structural modeling in ^[23], variational methods in ^[24], fractal concepts in ^[25], the Monte Carlo analysis in ^[26], wave filters in ^[27,28]. Other methodologies include optical waveguides in ^[29], optimization methods in ^[30], high-frequency measurements in ^[31], quantitative evaluations in ^[32], carbon nanotubes computations in ^[33], microfluidics in ^[34,35], classification algorithms in ^[36]. For more applications, please refer to ^[37,38,39].

The purpose of this article is to examine an eco-epidemiological model that simulates how diseases spread in a natural environment under the influence of several factors. Recently, these types of models have gained increasing attention due to the spread and epidemic of infectious diseases. For instance, the authors of ^[40] have considered the following eco-epidemiological model:

where $\mathcal{H} _1(t), \mathcal{H} _2(t)$ and $\mathcal{H} _3(t)$ are three state variables that denote susceptible and infected prey and predator, respectively. In ^[41], the following prey-predator model with Atangana-Baleanu derivative model has been investigated:

More details of the model can be found in ^[41].

In ^[42], a three-species predator-prey model in the presence of prey social behavior given by

has been studied.

Research on infectious diseases has recently attracted a great deal of attention. For instance, the outbreak of vector-host diseases is modeled mathematically in ^[43] using a fractional model with Caputo-Fabrizio derivative. Other studies include the model for hepatitis B virus (HBV) and hepatitis C virus (HCV) co-infection in ^[44], prevalence of an infectious disease in a prey and predator system in ^[45], food chain model in ^[46], and hand-foot-mouth disease in ^[47]. During the past few decades, fractional calculus operators have become one of the effective tools for modeling various mathematical, physical and engineering problems. Probably the key reason for the increase in popularity of these operators is that they benefit from memory features as one of their main properties. Considering this valuable attribute of the operators, they are invaluable in biological modeling, since what happens in the present will be heavily influenced by what happened in the past with those variables.

In this paper, we incorporate two fractional operators, the Atangana-Baleanu-Caputo and Caputo-Fabrizio-Caputo, into a novel biological system ^[48]. These kinds of operators have been employed in many studies so far. However, their use should be accompanied by caution and compliance with some necessary conditions as outlined in ^[49].

Below is a breakdown of the remaining sections. First, some prerequisites are presented in the second part of this paper, including definitions and properties of fractional operators. The main system of the article is introduced in Section 3. A theoretical analysis of the model is presented in Section 4. The basic ideas for obtaining the numerical techniques for the model are presented in Section 5. In Section 6, we discuss the approximate solutions corresponding to the numerical methods used, as well as their implications. In the last section, we discuss several concluding remarks.

2.   An overview of fractional calculus

In this section, first, it is necessary to have a brief overview of some useful preliminary theorems in the field of differential calculus of fractional order.

Definition 2.1. The derivative and integral Caputo type ($\mathsf{Cap}$) operators are respectively given by ^[50]

and

Definition 2.2. The derivative and integral Atangana-Baleanu-Caputo ($\mathsf{ABC}$) operators are respectively given by ^[48]

where

and $\mathcal{M}_{\wp} ({\zeta})$ is the Mittag-Leffler function given by

After applying the integral operator $\mathsf{ABC}$ defined in (2.4) to the differential operator (2.3), one concludes that

The Laplace transform corresponding to the $\mathsf{ABC}$ operator defined by (2.3) is obtained as

Definition 2.3. The derivative and integral Caputo-Fabrizio-Caputo ($\mathsf{CFC}$) operators are respectively given by ^[51]

where

The Laplace transform corresponding to the $\mathsf{CFC}$ operator defined by (2.8) is obtained as ^[41]

3.   The main model

The main focus of this paper is to study the mathematical description of interactions between the populations of susceptible and infected prey given by $\mathcal{H}_1(t)$ and $\mathcal{H}_2(t)$, respectively. Moreover, $\mathcal{H}_3(t)$ denotes the predator population. The mathematical description of the interactions of these components is expressed by the following nonlinear system ^[52]:

In this model, it is assumed that the only population that is infected by infectious disease is that of the prey. Moreover, infected prey are consumed by predators, while susceptible prey do not fall under their diet. The parameters of the model are as follows: $a$ represents the birth rate of the susceptible prey, $d$ is used to explain the rate of natural death in susceptible prey, $b$ stands for the density-dependent death rate based on intra-species competition, and $\beta$ describes the contact rate between the susceptible and the infected prey. Moreover, $p$ shows the attack rate on the infected prey, and the death rate of the infected prey is presented by $\delta$, $c$ demonstrates the conversion coefficient. Also, $\mu$ shows the corresponding natural rate of the death for predator populations, and finally, the parameter $\kappa$ denotes the level of fear which drives anti-predator behavior of the prey ^[40]. A comprehensive explanation of the formation of this non-linear model can be found in ^[40].

In this paper, we will apply two more recent definitions of fractional differential calculus in the model presented by (3.1). First, let us replace standard derivatives in the model with the $\mathsf{ABC}$ fractional derivative (2.3) to get the following fractional model:

subject to initial conditions

Moreover, by applying the $\mathsf{CFC}$ fractional derivative (2.8) in the model, we arrive at the following fractional model:

4.   Mathematical analysis for model

In order to find more analytical intuition of the model (3.2), some related mathematical analyses are collected in this section.

4.1.   The basic reproduction number

In this model, the basic reproduction number $\mathcal{R}_0$ for system (3.2) is calculated as ^[52]

4.2.   The equilibrium points

The following positive equilibrium points can be calculated for the model (3.2).

● The trivial point of $\mathcal{P}_0 = \left(0, 0, 0\right)$.

● The axial point of $\mathcal{P}_1 = \left(\frac{a-d}{b}, 0, 0 \right)$. This point exists if we have $a > d$.

● The axial equilibrium point of $\mathcal{P}_2 = \left(\frac{\delta}{\beta}, \frac{a \beta -b \delta -d \beta}{\beta \left(b +\beta \right)}, 0 \right)$. This point exists if we have $a \beta -b \delta > d \beta$.

● Other equilibrium points $\mathcal{P}_i = ({{\mathcal{H}^{*}_1}}, {{\mathcal{H}^{*}_2}}, {{\mathcal{H}^*_3}})$ of the system can be evaluated by determining the positive solutions of the following nonlinear algebraic system:

The local stability for these equilibrium points $\mathcal{P}_i = ({{\mathcal{H}^{*}_1}}, {{\mathcal{H}^{*}_2}}, {{\mathcal{H}^*_3}})$ can be explored using the Jacobian matrix as

4.3.   The existence of the solution for the model (3.2)

To this end, let us employ the ${\mathsf{ABC}}$ integral operator (2.4) on the system (3.2). Then, we get

where ${\mathscr{\textbf{H(t)}}} = \left[{\mathcal{H}_1}(t), {\mathcal{H}_2}(t), {\mathcal{H}_3}(t)\right]$, and also we define

Define

and moreover

Using these assumptions, Eq (4.4) can be rewritten as

Then, from (4.6) along with ${\textbf{H}}_0(t) = {\textbf{H}_0}$, the following recursive structure is conceivable:

Considering Eq (4.7), we will have

In this position, we define

Then, it follows that

As a result, one gets

Hence, we have

Now, our main assumption will be that the nonlinear operator $\textbf{M}$ has the Leibniz condition, so we can write

Consequently, we derive the following inequality:

Further, replacing $\Vert \varrho_{n-1}(t)\Vert$, one arrives at

Also, it reads

And, finally, we obtain

Now, let us define

In addition, according to the ${\textbf{H}} (t)$ structure, it holds that

where $\theta_n (t)\rightarrow 0$ when $n (t)\rightarrow \infty$. Thus,

Now, we can write

After applying the norm of the above equation, we will have

For $n\rightarrow \infty$, we have

This will be the result for the existence of the solution.

4.4.   The uniqueness of the solution

In order to prove the uniqueness of the solution, let us assume that ${\textbf{H}_1} (t)$ and ${\textbf{H}_2} (t)$ are two solutions to the problem. So, we have

So, if we have

then by taking $n\rightarrow \infty$, we obtain

Thus, $\Vert{\textbf{H}}_1 (t)-{\textbf{H}}_2 (t)\Vert = 0$ holds. Therefore, ${\textbf{H}}_1 (t) = {\textbf{H}}_2 (t)$ results.

5.   Numerical techniques

Along with providing new differential operators in fractional calculus, the most important concern will always be the design of efficient approximate algorithms for solving those problems numerically. Thus, there is always a numerical method that needs to be developed for each new definition of an operator. There are advantages, limitations, and requirements associated with each of these numerical methods. Our objective in this section is to design two numerical techniques using the definition of the product integration rule (PI), as outlined in ^[53].

5.1.   A numerical scheme for $\mathsf{ABC}$ fractional problem (3.2)

To extract an efficient numerical technique for $\mathsf{ABC}$ fractional problems, we take the following fractional Cauchy problem:

Based on the application of the $\mathsf{ABC}$ fractional integral definition in Eq (2.4) on Eq (5.1), we derive the integral equation as follows:

Setting $t = t_{n} = t_0+n{\Delta t}$ in Eq (5.2) yields

Now, a linearized form of $\mathcal{N}({\zeta}, \mathcal{H} ({\zeta}))$ is considered as follows:

where $\mathcal{H} _{i} = \mathcal{H} (t_{i})$.

Using (5.4) in (5.3), and also by doing some algebraic calculations, we obtain ^[54,55,56]:

where

As a result of (5.5) and (5.6), one can effectively assess the approximate solution to the fractional system (5.1). In particular, to approximate the problem (3.2), we will have

These resulting schemes have implicit structures which can be solved utilizing efficient techniques in solving systems of nonlinear algebraic equations like Newton's method.

5.2.   A numerical scheme for $\mathsf{CFC}$ fractional problem (3.3)

In this part, to extract a numerical scheme for $\mathsf{CFC}$ fractional problem (3.3), we study the following fractional system:

Utilizing the corresponding fractional integral operator (2.9) on both sides of (2.8) yields

Taking $t = t_{n+1}$ in (5.9), one has

and

Inserting Eq (5.11) into Eq (5.10), we obtain

where

Thus, we get

Accordingly, the following iterative schemes are determined in order to approximate the problem (3.3) in the following manner ^[57]:

The results of scheme model (3.3) will be obtained using these explicit iterative schemes.

6.   Numerical discussions

A description of the numerical properties of the system is presented in this section. To this end, it is imperative to examine the equilibrium points for the model in more detail.

As mentioned earlier, the positive equilibrium point of

for the model is a positive solution for the following system:

From the last equation of (6.1), we immediately conclude that

Considering this result in the second equation of the system, it reads

Taking these results into account in the first equation of the system along with some simplifications, a quadratic equation for ${\mathcal{H}^{*}_3}$ is obtained as

where

The performed numerical simulations in this paper are based on the following parameters:

For these particular choices, the equilibrium point for the model will be determined as follows:

In what will come later in this section, the level of sensitivity of the model to the existing parameters will be checked. These results can be considered a confirmation of the theoretical results related to the model.

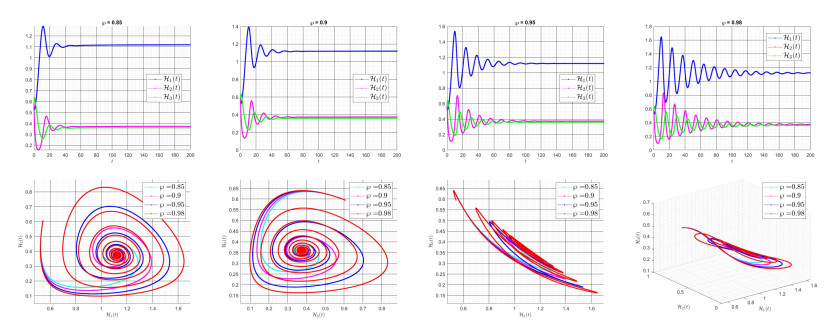
6.1.   The effects of fractional order ($\wp$)

Figures 1 and 2 demonstrate the model's sensitivity to the changes of the parameter $\wp$ in the two approximate methods of the article. Convergence of the model to equilibrium point $\left(\mathcal{H}^{**}_1, \mathcal{H}^{**}_2, \mathcal{H}^{**}_3\right)$ is evident in these graphs.

It seems that in Figure 1, for smaller values of $\wp$, the speed of convergence to the balanced point of the system occurs faster, and with its increase, the results will be more unstable and accompanied by fluctuating behavior.

It seems that in Figure 2, the oscillatory behavior increases in the model, and as a result the speed of convergence is very slow.

6.2.   The effects of fear factor ($\kappa$)

The fear parameter ($\kappa$) is one of the most important components defined in the model, and it strongly influences the type of system behavior. In ^[52], a detailed analysis of the effect of this parameter on the results is presented and can be considered a good benchmark for comparing our results. Figures 3 and 4 demonstrate the model's sensitivity with respect to the changes of parameter $\kappa$ in the two approximate methods of the article.

In this case, the positive equilibrium point is $\left(\frac{p {\mathcal{H}^{*}_3} +\delta}{\beta}, \frac{\mu}{c p}, \mathcal{H}^{*}_3\right)$ where ${\mathcal{H}^{*}_3}$ is determined from

In Figures 3 and 4, for $\kappa = 0$, with no fear factor, the equilibrium point of the system is obtained

whose Jacobian matrix is

with the following eigenvalues:

This is a clear proof of the stability of this equilibrium point.

Also, for $\kappa = 0.4$, the equilibrium point of the system is obtained

whose Jacobian matrix is

with the following eigenvalues:

With the increase of the real negative parts of the eigenvalues, the instability of the system is gradually increased, which is also clearly evident in the graphs. Finally, for $\kappa = 1$, we have a unique positive equilibrium

whose Jacobian matrix is

with the following eigenvalues:

So, a clear proof of the instability of this equilibrium point is observed.

The numerical results obtained in this case are completely consistent with the numerical properties reported in ^[52].

6.3.   The effects of the contact rate between the susceptible and the infected prey ($\beta$)

Figures 5 and 6 demonstrate the model's sensitivity with respect to the changes of parameter $\beta$ in the two approximate methods of the article. In these diagrams, it can be seen that as $\beta$ increases, the equilibrium type changes from an interior point to a planar point. For these situations, the infected predator population is on the way to extinction. For example, for $\beta = 1.2$, we have a unique positive equilibrium

whose Jacobian matrix is

with the following eigenvalues:

6.4.   The effects of the attack rate on the infected prey ($p$)

Figures 7 and 8 demonstrate the model's sensitivity with respect to the changes of the attack rate on the infected prey in the two approximate methods of the article. The important thing that can be seen from the results is that with the increase of the value for the parameter, the type of equilibrium point in the problem changes completely.

7.   Conclusions

The models in eco-epidemiology are computational tools that describe ecology and epidemiology problems in a meaningful way. The use of novel mathematical definitions in modeling eco-epidemiological scenarios can be very helpful and lead to significant results in real-world problems. The aim of this paper is to study a nonlinear predator-prey system where the prey growth rate is reduced due to anti-predator behavior. This paper employs two new definitions in fractional calculus called the $\mathsf{ABC}$ and $\mathsf{CFC}$ fractional derivatives. These two definitions are useful tools that can be used for solving the model. Our research results may be of great value to scholars in the future, when they want to apply our employed techniques to model real problems related to the epidemic and control it more efficiently.

Acknowledgments

The authors extend their appreciation to Prince Sattam bin Abdulaziz University for funding this research work through the project number (PSAU/2023/01/23035).

Conflict of interest

The authors declare that they have no competing interests.