Analysis of fractional global differential equations with power law

1.   Introduction

In the last few decades, an outstanding advancement has been witnessed in nonlinear sciences and engineering fields. Many scientists showed keen interest in finding the exact and numerical solutions for the nonlinear PDEs. Numerous techniques were devised in this regard which includes the GERFM method ^[1], modified variational iteration algorithm-II ^[3], enhanced ${(}\frac{{G}^{^{{\prime }}}}{G}$)-expansion method ^[4], the direct algebraic method ^[5], the extended trial equation method ^[6], the generalized fractional integral conditions method ^[7], the modified simple equation method ^[8], the Monch's theorem method ^[9], the extended modified mapping method ^[10], the reductive perturbation method ^[11], the new probability transformation method ^[12] and the differential transformation method ^[13]. In future work for more related extensions or generalizations of the results these references may be very helpful ^{[2,32,33,34,35,36]}.

The time fractional derivatives in the fractional reaction-diffusion model describes the process relating to the physical phenomena, physically known as the historical dependence. The space fractional derivative explains the path dependence and global correlation properties of physical processes, that is, the global dependence. The reaction diffusion equation has a dynamic role in dissipative dynamical systems as studied by various biologists ^[38], scientists and engineers ^[14]. The nonlinear form of this model has found a number of applications in numerous branches of biology, physics and chemistry ^[14,15]. This model has also been useful for other areas of science and effectively generalized by employing the theory of fractional calculus, for instance see ^[15,16]. Diffusion-wave equations involving Caputo's derivative ^[17,18], Riemann-Liouville derivatives ^[19] have been discussed by various researchers. Anomalous dispersion equations can be explained by fractional derivative ^[20]. An extensive variety of exact methods which have been applied for exact solutions of the fractional nonlinear reaction diffusion equation, for example see ^{[14,15,16,17,18,19,20]} and references there in.

To interpret numerous physical phenomena in some special fields of science and engineering, nonlinear evolution equations are extensively used as models especially in solid-state physics and plasma physics. Finding the exact solutions of NLEEs is a key role in the study of these physical phenomena ^[39]. A lot of research work has been carried out during the past decades for evaluating the exact and numerical solutions of many nonlinear evolution equations. Among them are homotopy analysis method ^[21], modified exp-function method ^[22], ${(}\frac{{G}^{^{{\prime } }}}{G}$)-expansion method ^[23], exp-function method ^[24], homotopy perturbation method ^[25], Jacobi elliptic function method ^[26], sub equation function method ^[27], kudryashov method ^[28], and so on.We can be expressed the exact solutions of FPDE via exp $(-\varphi \left(\eta \right))$.

The article is arranged as follows: Section 1 represents the introduction of the article. In section 2, we have explained the Caputo's fractional derivative. In section 3, we have interpreted the exp $(-\varphi \left(\eta \right))$-expansion method. In section 4, we use this method to explore the reaction-diffusion model. In section 5 and 6, graphical representation and physical interpretation are explained. In section 7 and 8, we have interpreted the results, discussions and conclusion.

1.1.   Caputo's fractional derivative

Property 1: ^[29] A function $f(x, t),$where $x > 0$ is considered as $C_{\alpha }$. Here $\alpha \in \mathfrak{R},$ if $\exists$ a ${\mathbb{R}}$ and $\left(p > \alpha \right),$ such that

Property2: ^[29] A function $f\left(x, t\right),$ where $x > 0$ is considered to be in space $C_{\alpha }^{m}$. Here $m\in { \mathbb{N}}\cup \left\{ 0\right\},$ if $f^{(m)}\in C_{\alpha }.$

Property3: ^[29] Suppose $f\in C_{\alpha }$ and $\alpha \geq -1$, then the Riemann Liouville integral $\mu,$ where $\mu > 0$ is given by

Property4: ^[29] A fractional Caputo derivative of $f$ with respect to $t$, where ${f\in C}_{-1}^{m}, \ m\in {\mathbb{N}}\cup \left\{ 0\right\},$is given as

Note that

1.2.   Interpretation of the method

Consider the fractional partial differential equation,

where $D_{t}^{\alpha }u, \ D_{x}^{\alpha }u, \ D_{xx}^{\alpha }u$ are derivatives, $u\left(\eta \right) = u\left(x, t\right)$. For solving Eq 1.8, we follow:

Step 1: Using a transformation, we get,

where constant $V$ is a nonzero. By substituting Eq 1.9 in Eq 1.8 yields ODE:

Step 2: Assuming the traveling wave solution

where $\varphi \left(\eta \right)$ satisfies the following equation:

where prime indicates derivative w.r.t.$\eta.$ The solutions of Eq 1.12 are written in the form of different cases.

Class1: when $\mu \neq 0$ and ${\lambda }^{2}-4\mu > 0,$ we have

where $\lambda = \sqrt{\left(-4\mu +{\lambda }^{2}\right) }$

Class 2: when, $\mu \neq 0$ and ${\lambda }^{2}-4\mu < 0,$ we have

where, $\lambda = \sqrt{\left(-4\mu +{\lambda }^{2}\right) }$

Class 3: when, $\lambda \neq 0, \mu = 0$ and ${\lambda }^{2}-4\mu > 0,$ we have

$\varphi \left(\eta \right) \mathrm{ = -ln}\left\{ \frac{\lambda }{\mathrm{-} \mathrm{1+}{\exp \left(\lambda \left(k+\eta \right) \right) \ }}\right\}.$

Class 4: when, $\lambda, \mu \neq 0$ and ${\lambda }^{2}-4\mu = 0,$ we have

Class 5: when, $\lambda, \mu = 0$ and ${\lambda }^{2}-4\mu = 0,$ we have

Step 3: Using the homogeneous balancing principal, in (10), we attain M. In view of Eq (11), Eq (10) and Eq (12), we obtain a system of equations with these parameters, a_n, $\lambda, \mu$. We substitute the values in Eq (11) and Eq (12) and obtained the results of Eq (8).

2.   Solution procedure

Suppose the reaction-diffusion equation is,

where $\delta$, $\beta$ and $\gamma$ are parameters without zero, setting, $\delta = a$, $\beta = b$ and $\gamma = c$ and changing Eq 2.1 into an ODE.

where prime represents the derivative w. r. t. $\eta$.With the help of balancing principal, $u^{\prime \prime }$ and $u^{3}$, we attain, $M = 1$.

Rewriting the solution of Eq 2.2 we get,

where $a_{0}$, $a_{1}\neq 0$ are constants, while $\lambda, \mu$ are some constants.

Substituting $u, u^{^{\prime \prime }}$ and ${u}^{3}$ in Eq 2.2, we get the solution sets as.

Solution set 1

Substituting in Eq 2.3, we get,

Substituting all the five classes in Eq 2.4, we get the solutions.

Class 1: When, ${\lambda }^{2}-4\mu > 0$ and $\mu \neq 0$,

Class 2: When, ${\lambda }^{2}-4\mu < 0$ and $\mu \neq 0,$

Solution set 2:

Substituting in Eq 2.3, we get,

Substituting equations 1.13 and 1.14 in Eq 2.6, we get the solutions.

Class 1: When, $\mu \neq 0$ and ${\lambda }^{2}-4\mu > 0,$

Class 2: When, $\mu \neq 0$ and ${\lambda }^{2}-4\mu < 0,$

Solution Set 3

Substituting in Eq 2.3, we get,

Substituting equations 1.13 to 1.15 in Eq 2.9, we get the solutions.

Class 1: When, $\mu \neq 0$ and$-4\mu +{\lambda }^{2} > 0$,

Class 2: When, $\mu \neq 0$ and$-4\mu +{\lambda }^{2} < 0$,

Class 3: When ${\lambda }\neq 0$, $-4\mu +{\lambda } ^{2} > 0$ and $\mu = 0$,

Class 4: When, ${\lambda }\neq 0$, $\mu = 0$ and $-4\mu +{ \lambda }^{2} = 0,$

Case 5: When, ${\lambda } = 0$, $\mu = 0$ and $-4\mu +{\lambda }^{2} = 0,$

3.   Graphical demonstration

Physical interpretation

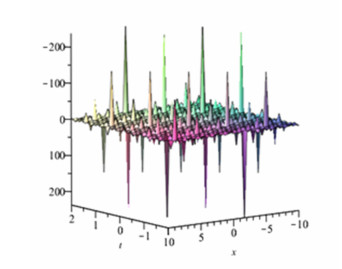
With some free parameters the proposed technique provides solitary wave solutions. By setting the specific parameters we have explained the miscellaneous wave solutions. In this study, we would explain the physical interpretation of the solutions for reaction-diffusion equation taking solution $v_{\mathrm{1}}$ for $\mu = 20 \; \lambda = 1 \; b = 11 \; a = 10 \; a_{1} = 12 \; c = -11 \; \alpha = 1,$ shows the solitary wave solution in Figure 1. Figure 2 shows Soliton wave solution with paremeters $\mu = 910 \; \lambda = 1 \; b = 11 \; a = 10 \; a_{1} = 12 \; c = -11 \; \alpha = .5.$ Figures 3, 4 and 7 interprets the singular kink solution of $v_{ \mathrm{3}}, \; v_{ \mathrm{4}}$, $v_{ \mathrm{7}}$ for $\mu = .010 \; \lambda = 1 \; b = .11 \; a = 10 \; a_{1} =$ 12 $c = -11 \; \alpha = .1, \; \mu = .0010 \; \lambda = -991 \; b = 11 \; a = 10 \; a_{1} = 102 \; c = -1 \; \alpha$= .1, $\mu = 20 \; \lambda = 1 \; b = 11 \; a = 10 \; a_{1} = 12 \; c = -11 \; \alpha = .25.$ Finally kink wave results have been obtained from $\mathrm{v}_{\mathrm{5}}, \; \mathrm{v}_{\mathrm{6}},$ $\mathrm{v}_{\mathrm{8}}$ by setting the parameters, $\mu = 3.0 \; \lambda = 1 \; b = 11 \; a = 10 \; a_{1} =$ 12 $c = -11 \; \alpha = 0.001, \; \mu = 2.0 \; \lambda = 1 \; b = 11 \; a = 10 \; a_{1} = 12 \; c =$ -11 $\alpha = 0.001, \; \mu = 20 \; \lambda = 1 \; b = 11 \; a = 10 \; a_{1} = 12 \; c = -11 \; \alpha = 0.01,$ which is presented in Figures 5, 6 and 8. The solutions gained in this article have been checked by putting them back into the original equation and found correct. From the above obtained results we have many potential applications in fluid mechanics, quantum field theory, plasma physics and nonlinear optics.

When

When

When

When

When

When

When

When

4.   Results and discussions

If we set $b = \beta, \; c = \gamma, \; \mu = r$ and $\eta = \xi$ in the obtaining solution $v_{2}$ and $v_{3}$ in this article is equal to $u_{5}$ and $u_{1}$ for case 5 respectively found in ^[31] see Table 1.

If we set $b = \beta, \; c = \gamma$ and $\eta = \xi,$ in the obtaining solution $v_{2}$ and $v_{4}$ in this article is equal to $u$ and $u$ for $c_{1}\neq 0, \; c_{2} = 0, \; \lambda = 0$ and $\mu > 0$ in ^[23] see Table 2.

If we set $b = \beta, \; c = \gamma$ in the obtaining solution $v_{2}$ and $v_{4}$ are equal to $v_{9}$ and $v_{9}$ for $\lambda = 0$ and $\mu$ is positive in $v_{9}$ found in ^[32] see Table 3.

If we set $b = -\beta, \; c = \gamma$ and $\eta = \xi$ in the obtaining solution $v_{2}$ and $v_{4}$ in this article are equal to $u_{2}$ and $u_{2}$ for $k > 0, \beta > 0$ and our $v_{1}$ and $v_{3}$ are equal to $u_{4}$ and $u_{4}$ for $k < 0, \beta < 0$ respectively founded in ^[30] see Table 4.

5.   Conclusions

In the current paper, we explore that the proposed method is effective and capable to find exact solutions of reaction-diffusion equation. The obtained solutions indicate that the suggested method is direct, constructive and simple. The proposed technique can be implemented to the other NLPDEs of fractional order to establish new reliable solutions. The exact solutions are different and new along with different values of parameters. The reduction in the magnitude of computational part and the consistency of the technique give a broader applicability to the technique. The reaction diffusion equation has a dynamic role in dissipative dynamical systems as studied by various biologists, scientists and engineers. This model has found a number of applications in biology, physics (neutron diffusi0n theory), ecology and chemistry. It has also been claimed that reaction-diffusion processes have crucial basis for procedures associated to morphogenesis in biology and may even be connected to skin pigmentation and animal coats. Other applications of this model contain spread of epidemics, ecological invasions, wound healing and tumors growth. Another aim for the consideration in reaction-diffusion systems is that although they are nonlinear partial differential equations, there are often visions for an analytical treatment. My main contribution is programming and comparisons.

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.