Improved results on an extended dissipative analysis of neural networks with additive time-varying delays using auxiliary function-based integral inequalities

1.   Introduction

Schoenberg introduced the trigonometric spline functions defined by divided differences in ^[18]. And the trigonometric spline functions have been shown to possess many B-spline-like properties. In view of this, many scholars call the trigonometric splines the trigonometric B-splines, in ^[4,8]. It is well-known that the trigonometric B-splines are piecewise functions corresponding to the spaces

for odd-order, and

for even-order. Odd-order trigonometric B-splines in $\mathcal T_{2n+1}$ form a partition of unity, a desirable property for curve design. However, even-order B-splines in $\mathcal H_{2n}$ lack this partition of unity, creating challenges in certain applications where this property is critical. As a result, extensive research has focused on the odd-order basis, particularly on its normalization. The author of ^[8] established the recurrence relation for the trigonometric B-splines of arbitrary order and derived trigonometric Marsden identity. The author of ^[20] utilized the trigonometric Marsden identity to derive the normalized odd-order trigonometric B-splines over uniform knots. Building on the trigonometric Marsden identity expansion introduced by ^[7], ^[11] explicitly derived the normalization coefficients required to ensure that the trigonometric B-spline basis functions are properly normalized. ^[15] provided the p-Bézier basis functions in the space $\mathcal T_{2n+1}$, which is defined over any interval of length $< \pi$. Those basis functions are a subcase of the normalized trigonometric B-splines. ^[2] presented the normalized Bernstein-like basis functions in the space $\mathcal T_{2n+1}$, which is defined over the interval $[0, \pi/2]$. ^[21] established the C-B spline basis. In this work, the C-B spline basis of order $3$ is just the normalized trigonometric B-spline basis corresponding to the space $\mathcal T_3$. In a more general context, the normalized trigonometric B-splines are also considered in ^[16] as a special case.

Curve and surface design is an important area in Computer Aided Geometric Design (CAGD), where trigonometric B-splines are a foundational tool. Normalized trigonometric B-splines enable enhanced construction and control of curves and surfaces, suggesting their potential applications in aircraft design ^[9]. Additionally, trigonometric B-splines show promising applications in other fields, such as physical simulations (see ^[5,12,19]).

The purpose of this paper is to introduce the integral formula for odd-order trigonometric B-splines. Given the significant applications and theoretical importance of integral formulas in Chebyshev systems for fields such as numerical analysis, signal processing, and function approximation, it is notable that the integral properties of sin and cos in trigonometric B-spline bases render them incapable of being directly derived like other bases in Chebyshev systems. The aim of this study is to provide a similar integral formula for trigonometric B-spline bases. To achieve this, this paper first constructs a novel set of even-order trigonometric B-spline curve basis functions and, through integration of these functions, successfully derives the traditional odd-order trigonometric B-spline basis functions, thereby establishing the integral formula for odd-order trigonometric B-spline bases. During this derivation process, a determinant of even order with structural symmetry is obtained. Furthermore, this study refines the conditions for knot sequences to ensure that the corresponding normalized trigonometric B-spline bases possess nonnegativity.

Our main contributions are

● A set of trigonometric spline bases corresponding to the DC component-free space is provided, along with the integral representation of normalized trigonometric B-spline bases corresponding to space $\mathcal T_{2n+1}$.

● Adjusting the conditions imposed on the knot sequence to guarantee the nonnegativity of the normalized trigonometric B-spline basis functions.

● A structurally symmetric even-order determinant is presented.

The remainder of this article is organized as follows: Section 2 reviews the related concepts and properties. The improvements to knot sequences are discussed in Section 3. In Section 4, the trigonometric spline basis corresponding to the DC component-free space and the integral formula for the normalized trigonometric B-spline basis are presented. The final conclusions are drawn in the last section.

2.   Review

In this section, we will recall some established concepts and conclusions.

^[1] has demonstrated that the knot sequences for B-spline basis functions can be finite, infinite, or bi-infinite. Analogous to the case of traditional B-spline basis functions, this paper focuses on the study of trigonometric B-spline basis functions corresponding to bi-infinite knot sequences.

The normalized trigonometric B-spline basis functions are defined in a manner analogous to the de Boor-Cox formula ^[4,7,8,11].

Definition 2.1. (Normalized trigonometric B-spline basis functions) Given a knot sequence ${\mathit{\boldsymbol{T}}} = \{t_i\}^{+\infty}_{i = -\infty}$, such that

the normalized trigonometric B-spline basis functions of order $2{\mit n}+1$ are defined as follows:

where

and the sum is taken over all permutations $\mu: \{1, 2, {\cdots}, 2n\}\to\{1, 2, {\cdots}, 2n\}$.

Remark 2.1 In ^[4,8,11], the knot sequence satisfies the condition $0 < t_{i+2n+1}-t_i < 2\pi$. However, the knot sequence described in ^[7] satisfies a slightly different condition, $0 < t_{i+2n}-t_i < 2\pi$. In the subsequent section, the conditions of the knot sequence are reiterated.

If $t_{i-1} < t_i = t_{i+1} = {\cdots} = t_{i+m_i-1} < t_{i+m_i}$, where $1\le m_i\le 2n$, the knots $t_j$, where $j = i, i+1, {\cdots}, i+m_i-1$, are referred to as knots of multiplicity ${\mit m_i}$. Especially, we set $\frac{0}{0} = 0$. The space of trigonometric spline basis is defined by

The trigonometric B-spline basis functions possess many B-spline-like properties ^[3,6,8,14].

Property 2.1. (Properties of the trigonometric B-spline basis functions) The trigonometric B-spline basis functions $N_{i, 2n+1}(t)$ defined in Eq (2.5) possess the following properties:

(1) (Local support) For any $i\in \mathbb{Z}$ and $n\in \mathbb{Z}^{+}$, there exists

(2) (Continuity) The continuous order of $N_{i, 2n+1}(t)$ at $t_j$ (where $i\le j\le i+2n+1$), denoted as $k_{i, 2n+1}^j$, can be described as

if $t_i = t_{i+1} = {\cdots} = t_{i+\xi-1} < t_{i+\xi}\le t_{i+\xi+1}\le{\cdots}\le t_{i+2n+1-\eta} < t_{i+2n+2-\eta} = {\cdots} = t_{i+2n+1}$.

3.   Condition improvement for knot sequence

In this section, we will adjust the conditions of the knot sequence to ensure the nonnegativity of the normalized trigonometric B-spline basis functions $K_{i, 2n+1}(t)$ for $i\in \mathbb{Z}$ and $n\in \mathbb{Z}^{+}$.

First, the condition (2.1) can be relaxed.

The nonnegativity of the basis function $N_{i, 2n+1}(t)$ is ensured by the condition $0 < t_{i+2n+1} - t_{i} < 2\pi$ as stated in (2.1). Since the length of the support intervals for $N_{i, 2n}(t)$ and $N_{i+1, 2n}(t)$ in Eq (2.4) is $2n$, replacing $0 < t_{i+2n+1} - t_{i} < 2\pi$ with the condition $0 < t_{i+2n} - t_{i} < 2\pi$ still guarantees the nonnegativity of $N_{i, 2n+1}(t)$. Therefore, the condition (2.1) can be relaxed to

Second, the condition to ensure the positivity of the normalized coefficients $\zeta_{i, 2n+1}$ in Eq (2.6) is presented. According to the representation in Eq (2.6), we obtain the condition to ensure the positivity of the normalized coefficient $\zeta_{i, 2n+1}$, that is

The Bézier-like basis defined in the space $\mathcal{T}_{2n+1}$ is a subcase of the trigonometric B-spline basis. In ^[13], it was noted that the space $\mathcal{T}_{2n+1}$ does not have an NTP basis when the domain of $\mathcal{T}_{2n+1}$ is $[0, \pi]$. This implies the non-existence of normalized coefficients. Consequently, we conclude that $t_{i+2n-1} - t_{i} \neq \pi$. In ^[15], it proved that there exist NTP bases provided that the domain of $\mathcal{T}_{2n+1}$ is any interval of length $< \pi$, specifically referred to as p-Bézier bases. This implies that the normalized coefficient satisfies the condition $t_{i+2n-1}-t_{i} < \pi$, in the special cases of Bézier.

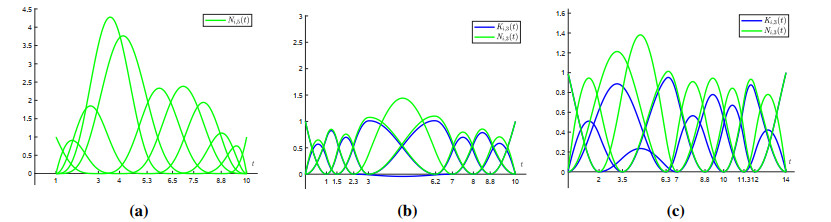
Figure 1a presents an example of the basis functions $N_{i, 2n+1}(t)$ for $i\in\mathbb{Z}$, whose corresponding knot sequence ${\mathit{\boldsymbol{T}}}$ satisfies condition (3.1) but fails to satisfy condition (2.1). Here $n = 2$ and the knot sequence ${\mathit{\boldsymbol{T}}} = \{t_i\}_{i = 1}^{16} = \{1, 1, 1, 1, 1, 3, 4, 5.3, 6.5, 7.5, 8.8, 10, 10, 10, 10, 10\}$. Figure 1b shows the trigonometric B-spline basis functions $N_{i, 3}(t)$ and $K_{i, 3}(t)$ corresponding to the knot sequence that satisfies condition (3.1) but does not satisfy condition (3.2), while Figure 1c presents the functions $N_{i, 3}(t)$ and $K_{i, 3}(t)$ corresponding to the knot sequence that satisfies both conditions (3.1) and (3.2).

Although the coefficients of the normalized trigonometric B-spline basis have already been defined in Eq (2.6), for the convenience of deriving and proving the integral formula of the normalized trigonometric B-spline basis, this paper introduces a simplified normalized coefficient expression that is equivalent to Eq (2.6).

Lemma 3.1. Let

where the sum is taken over all permutations $\gamma(1, 2, \ldots, 2n): \{m_1, m_2, \ldots, m_{2n}\} \to \{1, 2, \ldots, 2n\}$, with $m_1, m_2, \ldots, m_{2n}$ being a permutation of $1, 2, \ldots, 2n$ that satisfies $m_1 < m_3 < \ldots < m_{2n-1}$ and $m_{2r-1} < m_{2r}$ for each $r = 1, \ldots, n$. Then there exists

where $\zeta_{i, 2n+1}$ defined in Eq (2.6).

Third, a new definition for the normalized trigonometric B-spline basis that guarantees nonnegativity is presented.

Definition 3.1. (Nonnegative normalized trigonometric B-spline basis functions) Given a knot sequence ${\mathit{\boldsymbol{T}}} = \{t_i\}^{+\infty}_{i = -\infty}$, such that

the nonnegative normalized trigonometric B-spline basis functions of order $2{\mit n}+1$ are defined as follows:

where $N_{i, 2n+1}(t)$, $C_{i, 2n+1}$ is defined in Eqs (2.5) and (3.3), respectively.

4.   Trigonometric spline basis corresponding to DC component-free space

In this section, we generally set the knot sequence to be ${\mathit{\boldsymbol{T}}} = \{t_i\}^{+\infty}_{i = -\infty}$ that satisfies condition (3.4), where the multiplicity of $t_i$ is $m_i$ with $1\le m_i\le 2n$, and $k_{i, 2n+1}^j$ is defined in Eq (2.8) without further explanation. Let us define the DC component-free space as $\mathcal T_{2n}: = \text{span} \{\cos {t}, \sin {t}, {\cdots}, \cos nt, \sin nt\}$. Its corresponding piecewise trigonometric polynomial space is

Clearly, $\Gamma_{2n}[{\mathit{\boldsymbol{T}}}]$ is a linear space. We can derive the subspace of $\Gamma_{2n}[{\mathit{\boldsymbol{T}}}]$ as follows:

It can be shown that a function in the space \(\Gamma_{2n}[t_i, t_{i + 2n}]\) exhibits local support and a specific order of continuity.

4.1.   An important determinant

The following determinant and its accompanying proof are presented to facilitate future derivations.

Lemma 4.1. For any $n\in\mathbb{Z}^{+}$, then the following identity holds.

where $\gamma(1, 2, \ldots, 2n)$ defined in Lemma 3.1.

Proof. According to Euler's formula and the identity $e^{it_j}-e^{it_s} = 2ie^{\frac{i}{2}(t_j+t_s)}\sin\frac{t_j-t_s}{2},$ it follows that

For the sake of convenience, let

Therefore, it suffices to prove that

We establish the inductive hypothesis for $n$. For $n = 1$, the result is straightforward. Assume that the conclusion holds for $n\le p-1$, where \(p\) is any positive integer. Specifically, we have

where the sum is taken over all permutations $\varepsilon$:$\{m_1, m_2, {\cdots}, m_{p-1}\}\to \{n_1, n_2, {\cdots}, n_{2p-2}\}$. Here, ${n_1, n_2, \cdots, n_{2p-2}}$ represent a permutation of ${1, 2, \cdots, 2n}$ such that $n_1 < n_2 < \cdots < n_{2p-2}$, while ${m_1, m_2, \cdots, m_{p-1}}$ is a subset of ${n_1, n_2, \cdots, n_{2p-2}}$ satisfying $m_1 < m_2 < \cdots < m_{p-1}$.

Next, consider the case where $n = p$. Based on this assumption, we have

where the sum is taken over all permutations $\gamma(n_1, n_2, \cdots, n_{2p-2}):\{m_1, m_2, {\cdots}, m_{2p-2}\}\to\{n_1, n_2, \cdots, n_{2p-2}\}$, with $m_1, m_2, \cdots, m_{2p-2}$ being a permutation of $n_1, n_2, \cdots, n_{2p-2}$ that satisfies $m_1 < m_3 < \cdots < m_{2p-3}$ and $m_{2r-1} < m_{2r}$ for each $r = 1, \cdots, p-1$. Here, the sequence $\{n_1, n_2, \cdots, n_{2p-2}\}$ represents, in order, the sequences $\{1, 2, \cdots, 2p-2\}$, $\{1, 2, \cdots, 2p-3, 2p-1\}$, $\cdots$, $\{1, 3, 4, \cdots, 2p-1\}$, and \(\{2, 3, \cdots, 2p-1\}\). Eq (4.3) is valid for any positive integer $n$. Thus, the lemma is proved. □

4.2.   Constructing truncated functions

This subsection defines a set of truncated functions and demonstrates that any function in the space $\Gamma_{2n}[t_i, t_{i+2n}]$ can be expressed as a linear combination of these functions.

Let $g_{2n}(t): = \sin{\mit t}\sin^{2n-2}\left(\frac{\mit t}{2}\right)(n\in\mathbb{Z}^{+})$, the truncated functions $G_{i, 2n}(t)$, where $i\in\mathbb Z$ and $n\in\mathbb{Z}^{+}$, are defined as follows: If $t_i = t_{i+1} = {\cdots} = t_{i+\xi-1} < t_{i+\xi}$, then

Figure 2a–2c illustrate examples of the function $g_{4}(t)$ and the truncated functions $G_{i, 4}(t)$, where $i\in\mathbb Z$, over single and multiple knots, respectively.

To prove that any function in the space $\Gamma_{2n}[t_i, t_{i+2n}]$ can be represented as a linear combination of $\{G_{i, 2n}(t)\}_{i\in \mathbb Z}$, the following lemmas will be utilized.

Lemma 4.2. There exist $n+1$ real numbers $d_0, d_1, {\cdots}, d_{n}$ such that

where $d_0 = {\frac{(2n-1)!!}{(2n)!!}}$.

Proof. It is well known that

since

Thus, there are $n+1$ real numbers $d_0, d_1, {\cdots}, d_{n}$ such that

We deduce that, based on Euler's formula,

Expanding the left side of Eq (4.5) using the binomial theorem results in $d_0 = {\frac{(2n-1)!!}{(2n)!!}}$. □

Lemma 4.3. The function $G_{i, 2n}(t)$ defined in Eq (4.4) lies in $\Gamma_{2n}[\mathit{\boldsymbol{T}}]$ for any $i\in \mathbb Z, n\in\mathbb{Z}^{+}$.

Proof. First, according to Lemma 4.2, we obtain

Thus, we have

and

Second, the order of continuity of $g_{2n}(t-t_i)$ at $t_i$ is $2n-2$, because that

Third, it is easy to see that the order of continuity of $G_{i, 2n}(t)$ is $2n-\xi-1$ at $t_i$ and is $\infty$ at the other knots.

In conclusion, $G_{i, 2n}(t)\in \Gamma_{2n}[{\mathit{\boldsymbol{T}}}]$, for $i\in \mathbb Z$. □

Lemma 4.4. The functions $G_{i, {2n}}(t)$ for $i\in {\mathbb Z}$ in Eq (4.4) are linearly independent.

Proof. If $t_{i-1} < t_i = t_{i+1} = {\cdots} = t_{i+m_i-1} < t_{i+m_i}$, the ${\mit m_i}$ functions $G_{j, 2n}(t)$ for $i\le j\le i+m_i-1$ are linearly independent since they have different continuous orders at $t_i$.

For the sake of simplicity, let $r = i+m_i$ and ${t_{r-1} < t_r = t_{r+1} = {\cdots} = t_{r+m_r-1} < t_{r+m_r}}$. We can then similarly conclude that the functions $G_{j, 2n}(t)$ for $r\le j\le r+m_r-1$ are linearly independent. In addition, it is straightforward to derive that

Thus, $G_{i, 2n}(t), G_{i+1, 2n}(t), {\cdots}, G_{i+m_i-1, 2n}(t), G_{r, 2n}(t), G_{r+1, 2n}(t), {\cdots}, G_{r+m_r-1, 2n}(t)$ are linearly independent. Consequently, the functions $G_{i, 2n}(t)$ for $i\in\mathbb Z$ are linearly independent. □

From the above lemmas, we conclude that any function in the space $\Gamma_{2n}[t_i, t_{i+2n}]$ can be expressed as a linear combination of $G_{i, 2n}(t)$ for $i\in\mathbb Z$.

Theorem 4.1. For any function $F_{i, 2n}(t)\in \Gamma_{2n}[t_i, t_{i+2n}]$, there exist $2n-\eta+1$ real numbers $\nu_i, \nu_{i+1}, {\cdots}, \nu_{i+2n-\eta}$ such that

where $\eta$ is the multiplicity of $t_{i+2n}$ in the interval $[t_i, t_{i+2n}]$ and the functions $G_{j, 2n}(t)$, where $i\le j\le i+2n-\eta$, are defined in Eq (4.4).

Proof. Since $F_{i, 2n}(t)$ in space $\Gamma_{2n}[t_i, t_{i+2n}]$ is a piecewise function, it can first be linearly represented by the functions $G_{j, 2n}(t)$ for $i\le j\le i+2n-\eta$ in Eq (4.4) over a non-zero interval within its support interval.

Suppose $t_i = t_{i+1} = {\cdots} = t_{i+\xi-1} < t_{i+\xi}\le {\cdots}\le t_{i+2n-\eta} < t_{i+2n-\eta+1} = {\cdots} = t_{i+2n}$. We consider that the function $F_{i, 2n}(t)$ can be linearly represented in the interval $[t_i, t_{i+\xi})$. Thus, we prove that there exist $\xi$ real numbers $\kappa_i, \kappa_{i+1}, {\cdots}, \kappa_{i+\xi-1}$ such that

For simplicity, assume that

Based on the definition of the space $\Gamma_{2n}[t_i, t_{i+2n}]$, we know that $f_1(t)\in \mathcal T_{2n},$ which means that there exist $2n$ real numbers $x_1, x_2, \cdots, x_{2n}$ such that

and

which implies that

Let $\rho = 2n-\xi-1$, $\Omega_\rho: = \{f_1(t)|f_1(t)\in\mathcal T_{2n}, f_1^{(s)}(t_i) = 0, 0\le s\le \rho\},$ and $\Psi_\rho : = {\rm span}\{g_{2n}(t-t_i), g'_{2n}(t-t_{i+1}), {\cdots}, g^{(2n-\rho-2)}_{2n}(t-t_{i+\xi-1})\} = {\rm span}\{g_{2n}(t-t_i), g'_{2n}(t-t_{i}), {\cdots}, g^{(2n-\rho-2)}_{2n}(t-t_{i})\}$.

Since $g_{2n}(t-t_i), g'_{2n}(t-t_{i}), {\cdots}, g^{(2n-\rho-2)}_{2n}(t-t_{i})$ are linearly independent, we conclude that the dimension of $\Psi_\rho$ is $2n-\rho-1$. According to the definition of the function $g_{2n}(t)$, we obtain that $g^{(l)}_{2n}(t-t_i)\in \Omega_\rho$, $l = 0, 1, {\cdots}, 2n-\rho-2.$ Hence, it follows naturally that $\Psi_\rho$ is the subspace of $\Omega_\rho$.

The dimension of the space $\Omega_\rho$ is equal to the dimension of the solution space corresponding to the following linear equations.

Thus, the following linear equations holds:

where the corresponding coefficient matrix is given as

By performing elementary row operations, it is demonstrated that the matrix (4.8) maintains full row rank, independent of the parity of $\rho$. This result establishes that the dimension of the solution space for the linear system (4.7) is

The dimension of $\Omega_\rho$ is determined to be $2n-\rho-1$. Consequently, it follows that $\Omega_\rho = \Psi_\rho$. In other words, we know that there exist $2n-\rho-1 = 2n-(2n-\xi-1)-1 = \xi$ real numbers $\kappa_i, \kappa_{i+1}, {\cdots}, \kappa_{i+\xi-1}$ such that

According to the definition of $G_{i, 2n}(t)$, the function \(f_1(t)\) can be expressed as

Consider the non-zero interval $[t_{i+\xi}, t_{i+\xi+m_{i+\xi}})$. We define

According to the continuous order of $F_{i, 2n}(t)$ at $t_{i+\xi}$, we deduce that

This implies that

Thus, from the above analysis, it follows that there are $m_{i+\xi}$ real numbers $\kappa_{i+\xi}, \kappa_{i+\xi+1}, {\cdots}, \kappa_{i+\xi+m_{i+\xi}-1}$ such that

Consequently, we have

For every non-zero subinterval of the support interval of $F_{i, 2n}(t)$, we consider it this way. It can be concluded that there exist $2n-\eta+1$ real numbers $\nu_i, \nu_{i+1}, {\cdots}, \nu_{i+2n-\eta}$ such that

where $\nu_j$ for $i\le j\le i+2n-\eta$ is expressed as a linear combination of $\kappa_i, \kappa_{i+1}, {\cdots}, \kappa_{i+2n-\eta}$. □

4.3.   The dimension of $\Gamma_{2n}[t_i, t_{i+2n}]$

The subsection demonstrates that the dimension of $\Gamma_{2n}[t_i, t_{i+2n}]$ is 1. To support this, we first require the following lemma.

Lemma 4.5. Given an integer ${\mit i}$ and positive integers ${n, \eta}$ such that $\eta\le 2n-1$, then the determinant

where the functions $G_{j, 2n}(t)$ for $i\le j\le i+2n-\eta-1$ are defined in Eq (4.4).

Proof. Use reduction to absurdity. Assume that the determinant is equal to zero. Then, there are $2n-\eta$ real numbers $z_i, z_{i+1}, {\cdots}, z_{i+2n-\eta-1}$, which are not all equal to zero, satisfying

Let $Y(t) = \sum\limits_{l = i}^{i+2n-\eta-1}z_lG_{l, 2n}(t)$. Then, we find that the first $2n-\eta-1$ derivatives of $Y(t)$ at $t_{i+2n}$ are all zero. According to Theorem 4.1, there exist $m_{i+2n}$ real numbers, such that

Therefore,

and

According to Lemma 4.4, we obtain that $z_i = {\cdots} = z_{i+2n-\eta-1} = 0$. This conflicts with the assumption. So, the lemma is proved. □

From Theorem 4.1 and Lemma 4.5, we obtain the dimension of $\Gamma_{2n}[t_i, t_{i+2n}]$.

Theorem 4.2. The dimension of the linear space $\Gamma_{2n}[t_i, t_{i+2n}]$ is $1$.

Proof. Suppose that $u(t)$ is an arbitrary function in $\Gamma_{2n}[t_i, t_{i+2n}]$. Thus, according to Theorem 4.1, there are $2n-\eta+1$ real numbers $\nu_i, \nu_{i+1}, {\cdots}, \nu_{i+2n-\eta}$ such that

where $\eta$ denotes the multiplicity of $t_{i+2n}$ in the interval $[t_i, t_{i+2n}]$. Consider the continuous order of function $u(t)$ at $t_{i+2n}$. We have

which implies that

Thus, the equation representing the continuous order of $u(t)$s at $t_{i+2n}$ is given by

which can be expressed in matrix form as follows:

This system consists of linear equations with $\nu_i, \nu_{i+1}, {\cdots}, \nu_{i+2n-\eta}$ as variables. Based on Lemma 4.5, the coefficient matrix of these linear equations is full row rank, with a rank of $2n-\eta+1-(2n-\eta) = 1$. This indicates that the dimension of $\Gamma_{2n}[t_i, t_{i+2n}]$ is $1$. □

4.4.   Trigonometric spline basis corresponding to DC component-free space for single knot case

In this subsection, we consider single knots and assume that $t_i < t_{i+1}$ for any $i\in\mathbb Z$. Then the even-order trigonometric spline basis functions corresponding to the DC component-free space $\mathcal T_{2n}$, and the integral expression for the trigonometric B-spline basis $K_{i, 2n+1}(t)$ are presented.

According to Theorem 4.2 and the definition of $\Gamma_{2n}[t_i, t_{i+2n}]$, it is established that $F_{i, 2n}(t)\in\Gamma_{2n}[t_i, t_{i+2n}]$ and the dimension of $\Gamma_{2n}[t_i, t_{i+2n}]$ is 1. If we find a function $H(t)\in\Gamma_{2n}[t_i, t_{i+2n}]$, then it follows that $F_{i, 2n}(t) = \alpha H(t), t\in[t_i, t_{i+2n})$ for some real number $\alpha$. Thus, the following theorem is provided.

Theorem 4.3. (The function expression in the space $\Gamma_{2n}[t_i, t_{i+2n}]$ over single knots) For any function $F_{i, 2n}(t)\in\Gamma_{2n}[t_i, t_{i+2n}]$, there exists a real number $\alpha$ such that

where

and $\alpha = -\frac{1}{D(t_i, t_{i+1}, \cdots, t_{i+2n-1})}$. Here $D(t_i, t_{i+1}, \cdots, t_{i+2n-1})$ and the functions $G_{j, 2n}(t)$ for $i\le j\le i+2n$ are defined in Eqs (4.1) and (4.4), respectively.

Proof. According to Theorem 4.1, there exist $2{\mit n}$ real numbers $\alpha_i, \alpha_{i+1}, {\cdots}, \alpha_{i+2n-1}$ such that

By the continuous order of $F_{i, 2n}(t)$ at $t_{i+2n}$, it follows that

This can be expressed equivalently as a system of equations

In addition, we have

where $\beta_i, \beta_{i+1}, \cdots, \beta_{i+2n-1}$ are real numbers. Since Eq (4.14) when $t = t_{i+2n}$ is equivalent to Eq (4.13). We obtain that $\alpha_j = \beta_j, j = i, {\cdots}, i+2n-1$. Thus, we only focus on $\beta_j, i\le j\le i+2n-1$. By proving Lemma 4.3, it can be concluded that there exist $n$ numbers $\eta_{1}, \eta_2, {\cdots}, \eta_n$ such that

So we can rewrite (4.14) as follows:

Based on the properties of matrix operations, we deduce that

The coefficient matrix of (4.17) is non-zero due to the linear independence of the functions $\cos t, \sin t, {\cdots},$ $\cos nt, \sin nt$. According to Cramer's Rule, we have

We apply this result to Eq (4.11) to yield

where $G_{i+2n, 2n}(t) = 0, t\in[t_i, t_{i+2n})$. □

The linear space $\Gamma_{2n}[t_i, t_{i+2n}]$ corresponds to space $\mathcal T_{2n}$. Similarly, the space $\Gamma_{2n+1}[t_i, t_{i+2n+1}]$, which corresponds to space $\mathcal T_{2n+1}$, can be defined as follows:

We can derive the following theorem analogously.

Theorem 4.4. The dimension of the linear space $\Gamma_{2n+1}[t_i, t_{i+2n+1}]$ is $1$.

The proof is similar to the proof of Theorem 4.2.

Inspired by the method for constructing normalized B-basis in extended Chebyshev space presented in ^[10], we use the functions $F_{i, 2n}(t)$, where $i\in \mathbb{Z}$, to construct the normalized function $M_{i, 2n+1}(t)$. Therefore, the following theorem holds.

Theorem 4.5. (The normalized function) Suppose that

where $F_{i, 2n}(t)\in\Gamma_{2n}[t_i, t_{i+2n}]$ and $F_{i+1, 2n}(t)\in\Gamma_{2n}[t_{i+1}, t_{i+2n+1}]$ are defined in Theorem 4.3, with $i\in \mathbb{Z}$ and $n\in \mathbb{Z}^{+}$. Then we have

Proof. For $t \in [t_j, t_{j+1})$, there exists

□

Lemma 4.6. The function $M_{i, 2n+1}(t)$ in Eq (4.18) lies in the space $\Gamma_{2n+1}[t_i, t_{i+2n+1}].$

Proof. First, Eq (4.18) indicates that the support interval of the function $M_{i, 2n+1}(t)$ is the union of the interval of $F_{i, 2n}(t)$ and $F_{i+1, 2n}(t)$, denoted as $[t_i, t_{i+2n+1})$.

Second, since the integral operator increases the continuous order by 1, the continuous order of $M_{i, 2n+1}(t)$ at $t_j$ is greater than or equal to

So, it is natural that

□

According to Theorem 4.4 and Lemma 4.6, the normalized function $M_{i, 2n+1}(t)$ in Eq (4.18) must be equal to the trigonometric B-spline function $N_{i, 2n+1}(t)$ in Eq (2.5) multiplied by a constant. Therefore, the following theorem is established.

Theorem 4.6. (Integral representation of the normalized trigonometric B-spline basis) Given a knot sequence ${\mathit{\boldsymbol{T}}} = \{t_i\}^{+\infty}_{i = -\infty}$ satisfying

then there holds

where $K_{i, 2n+1}(t)$ and $M_{i, 2n+1}(t)$ are separately defined in Definition 3.1 and Eq (4.18).

Proof. We will demonstrate that the expression of $M_{i, 2n+1}(t)$, as defined in Eq (4.18), is identical to that of $K_{i, 2n+1}(t)$ defined in Definition 3.1. The notations $C(t_{i+1}, t_{i+2}, {\cdots}, t_{i+2n})$ in Lemma 4.1 and $U(t_i, t_{i+1}, {\cdots}, t_{i+2n})$ (see ^[17]) are used in the following proof, where

Based on Definition 2.1, it suffices to prove the explicit expression of the function $M_{i, 2n+1}(t)$ over a non-zero subinterval within its support interval. Therefore, according to Lemmas 3.1, 4.1, and 4.2, and Theorems 4.3 and 4.5, we deduce that

Since

we have

consequently

□

4.5.   Trigonometric spline basis corresponding to DC component-free space for multiple knot case

In this subsection, we consider multiple knots and assume that the multiplicity of the knot $t_i$ in the interval $[t_i, t_{i+2n})$ is $\xi$, while the multiplicity of the knot $t_{i+2n}$ in the same interval is $\eta$. Similarly to the single knot case, there exist the following theorems.

Theorem 4.7. (The function expression in the space $\Gamma_{2n}[t_i, t_{i+2n}]$ over multiple knots) Let

For any function $F_{i, 2n}(t)\in\Gamma_{2n}[t_i, t_{i+2n}]$, there exists a real number $\alpha$ such that

where

and

Here the functions $G_{j, 2n}(t)$ for $i\le j\le i+2n$ are defined in Eq (4.4).

Proof. To simplify the notation, we define

Thus, we conclude that

Similar to Theorem 4.3, there exist

Additionally, it follows that Eq (4.20) is equivalent to Eq (4.22) when $t = t_{i+2n}$. Thus, by applying the proof strategy from Theorem 4.3, we derive that

□

Theorem 4.8. (The normalized function over generalized knots) Suppose that Eq (4.18) still holds, where $F_{i, 2n}(t)\in\Gamma_{2n}[t_i, t_{i+2n}]$ and $F_{i+1, 2n}(t)\in\Gamma_{2n}[t_{i+1}, t_{i+2n+1}]$ are defined in Theorem 4.7, with $i\in \mathbb{Z}$ and $n\in \mathbb{Z}^{+},$ then

In addition, when $F_{i, 2n}(t) = 0$, we set

Theorem 4.9. (Integral representation of the normalized trigonometric B-spline basis over generalized knots) Given a knot sequence ${\mathit{\boldsymbol{T}}} = \{t_i\}^{+\infty}_{i = -\infty}$ satisfying condition (3.4), then there holds

where $K_{i, 2n+1}(t)$ and $M_{i, 2n+1}(t)$ are separately defined in Definition 3.1 and Theorem 4.8.

4.6.   Examples

This subsection presents examples of curve modeling to demonstrate that a curve possesses the convex hull property when the knot sequence satisfies condition (3.4).

Figures 3 and 4 illustrate examples of open and closed curves over different knot sequences, respectively. The red curves correspond to the knot sequences that satisfy condition (3.4) as defined in Definition 3.1, while the orange curves correspond to the knot sequences that satisfy condition (2.1) as defined in Definition 2.1. Additionally, the knot sequences in Figure 3 are ${\mathit{\boldsymbol{T}}} = \{0, 2, 3, 3, 3.5, 5.3, 6.1, 6.6, 8.4, 9.1, 9.5, 11.2, 12.2, 12.6, 14.2, 15\}$, and ${\mathit{\boldsymbol{T}}} = \{0, 0.8, 3, 3, 3.5, 5.3, 6.6, 8.6, 9.1, 9.1, 10, 12.2, 12.2, 13, 14.2, 15\}$, while those in Figure 4 are ${\mathit{\boldsymbol{T}}} = \{-8, -8, -8, -8, -8, -7, -6.3, -5.6, -4.9, -4.5, -1.2, -1.2, -1.2, 0, 1.2, 1.2$, $1.2, 4.5, 4.9, 5.6, 6.3, 7, 8, 8, 8, 8, 8\}$, and ${\mathit{\boldsymbol{T}}} = \{-8, -8, -8, -8, -8, -7, -6.3, -5.3, -4, -3.3, -1.2, -1.2$, $-1.2, 0, 1.2, 1.2, 1.2, 3.3, 4, 5.3, 6.3, 7, 8, 8, 8, 8, 8\}$. Clearly, if the knot sequence only satisfies condition (2.1), the convex hull property of the curve cannot be guaranteed.

5.   Conclusions

In the Chebyshev system, due to the integral properties of sine and cosine in the trigonometric B-spline basis, the trigonometric B-spline basis cannot be directly derived from lower-order bases through integration, which leads to an unnormal Chebyshev system. This paper successfully derives the integral formula for the normalized odd-order trigonometric B-spline basis by constructing a new set of even-order trigonometric B-spline bases. This integral formula allows for the transition from even-order to odd-order bases but cannot be obtained through stepwise integration, indicating that it is only similar to a segment of the integral formula in the Chebyshev system. Although we are currently unable to provide a direct recursive formula for integrating from lower-order trigonometric spline bases to higher-order ones, we hope to use this as a foundation for further exploration of this issue in future work.

Author contributions

Mei Li: Investigation, methodology, software, validation, writing—original draft preparation, writing—review and editing; Wanqiang Shen: Conceptualization, methodology, software, writing—original draft preparation, writing—review and editing. All authors have read and approved the final version of the manuscript for publication.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research is supported in part by the National Natural Science Foundation of China (Grant No. 61772013).

Conflict of interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.