Estimates of trapezium-type inequalities for $h$-convex functions with applications to quadrature formulae

1.   Introduction

It is familiar that the convexity has an important and key part in many areas due to its broad applications. This idea has been broadened and summed up in different directions (see, e.g., ^{[1,2,3,4,5,6,7,8]}). Sanja Varošanec present a class of convex functions ^[9] which is very helpful for the mathematicians working in the field of mathematical inequalities. There is a famous inequality for convex functions known as Hermite-Hadamard inequality (see, e.g., [10,p. 137]). This inequality provides bounds of the mean value of a continuous convex function $\Psi: (a, b)\rightarrow \mathbb{R}$.

If $\Psi: \vartriangle\rightarrow \mathbb{R}$ on an interval $\vartriangle$ of real numbers, such that ${\rho, \varrho}\in U$ with $\rho < \varrho$, we can write

Fractional calculus has vast applications in inequalities as well as in other physical sciences ^[11,12]. Recently Hermite-Hadamard inequalities have been reinvestigated and developed by many researchers by using several fractional calculus operators ^{[13,14,15,16,17,18,19,20,21,22]}. In ^[23] Sarikaya et al. studied the Hemite-Hadamard inequalities for Riemann-Liouville fractional integral (RLFI) using convex functions. Lio et al. in ^[24] investigated the said inequalities by involving RLFI operator for twice differentiable geometric-arithmetically $s$-convex functions. Such inequalities were examined by Wu et al. in ^[25] and Iqbal et al. in ^[26] for $k$-fractional operators via different convexities. Mevlut Tunc in ^[27] explored the inequality given by (1.1) for $h$-convex functions via RLFI operator. To enhance the flow of the work, we present some mathematical preliminaries of the theory of fractional calculus that are required to set up our results.

Definition 1.1. (^[24]) A function $\Psi:D\subset \mathbb{R^{+}}\to\mathbb{R^{+}}$ is known as geometric-arithmetically $s$-convex on $D$ if for $s\in(0, 1]$ and $\forall, \, \rho, \varrho\in D$ with $\nu\in[0, 1],$ we have

We utilize the class of $h$-convex $SX(h, D)$, $h$-concave $SV(h, D)$, $s$-convex in second sense $K_{s}^{2}$ and quasi convex $P(I)$ functions.

Sanja Varošanec present the following concept of convex and $h$-convex functions in ^[9] which are explained as follows:

Definition 1.2. A function $\Psi:[\rho, \varrho]\to \mathbb{R}$ is said to be convex if the inequality

holds for all $l, r \in [\rho, \varrho]$ with $\omega\in [0, 1].$

Definition 1.3. Let $h > 0$ be a function such that $h:D\subset\mathbb{R}\rightarrow \mathbb{R}$. Then the function $\Psi > 0$ is $h$-convex, if for $\Psi:D\subset\mathbb{R}\rightarrow \mathbb{R},$ the inequality

is true. The function $\Psi\in SV(h, D)$ is $h$-concave, if the inequality (1.2) is reversed.

For more detail about the classes $P(D)$ and $K_{s}^{2},$ we refer the reader to visit the article ^[28].

Definition 1.4. (^[29]) The left and right sided RLFI $I_{\rho^+}^{\alpha}\Psi$ and $I_{\varrho^-}^{\alpha}\Psi$ of order $\alpha > 0$ on an interval $[\rho, \varrho]$ are defined by

and

respectively. Here $\Gamma(.)$ represents the Euler-Gamma function defined by

The following results presented by Sarikaya et al. in ^[23] must be recalled in order to achieve our objectives.

Theorem 1.5. If $\Psi:[\rho, \varrho]\rightarrow \mathbb{R}$ is a positive convex function on $[\rho, \varrho]$ with $0\leq \rho < \varrho$ and $\Psi\in L_{1}[\rho, \varrho]$, then the inequality

holds.

Lemma 1.6. Let $\Psi:[\rho, \varrho]\rightarrow \mathbb{R}$ be a differentiable mapping on $(\rho, \varrho)$ with $\rho < \varrho$. If $\Psi^{'}\in L_{1}[\rho, \varrho]$, then the identity

holds.

The identity proved by Wang et al. in ^[30] stated as follows:

Lemma 1.7. Let $\Psi : [\rho, \varrho]\rightarrow \mathbb{R}$ be a twice differentiable mapping on $(\rho, \varrho)$ with $\rho < \varrho$. If $\Psi^{''}\in L_1[\rho, \varrho]$, then the equality

is true.

Lemma 1.8. (^[31]) For $\omega\in[0, 1]$, we have

and

Lemma 1.9. (^[19]) Assume that $\Psi:[\rho, \varrho]\rightarrow \mathbb{R}$ is twice differentiable on $(\rho, \varrho)$ with $\rho < \varrho$. If $\Psi^{''}\in L_1[\rho, \varrho]$, then the identity

is true, where

The $k$-RLFI introduced by Mubeen et al. in ^[32] is given in the following definition.

Definition 1.10. The $k$-RLFI $I_{\rho^{+}, k}^{\alpha}{\Psi}$ and $I_{\varrho^{-}, k}^{\alpha}{\Psi}$ of order $\alpha > 0,$ $k > 0$ and $\rho\geq 0$ for $\Psi\in L_{1}[\rho, \varrho]$ are defined by

and

respectively. Here $\Gamma_{k}{(.)}$ is the $k$-Gamma function and $I_{\rho^{+}, k}^{0}{\Psi}$ = $I_{\varrho^{-}, k}^{0}{\Psi}$ = $\Psi$.

The following results are given in ^[25].

Theorem 1.11. Let $\Psi:[\rho, \varrho]\rightarrow \mathbb{R}$ be a positive convex mapping for $0\leq \rho < \varrho$ and $\Psi\in L_{1}[\rho, \varrho]$, then the below inequalities

holds.

Lemma 1.12. Let $\Psi:[\rho, \varrho]\rightarrow \mathbb{R}$ be a differentiable mapping on $(\rho, \varrho)$ with $\rho < \varrho$. If $\Psi^{'}\in L_{1}[\rho, \varrho]$, then the identity for generalized RLFI

is true.

Recently, Iqbal et al. prove the following lemma's in ^[26].

Lemma 1.13. Let $\Psi : [\rho, \varrho]\rightarrow \mathbb{R}$ be a twice differentiable mapping on $(\rho, \varrho)$ with $\rho < \varrho$. If $\Psi^{''} \in L_{1}[\rho, \varrho]$, then the upcoming identity for generalized RLFI

holds.

Lemma 1.14. Assume that $\Psi:[\rho, \varrho]\rightarrow \mathbb{R}$ is twice differentiable mapping on $(\rho, \varrho)$ with $\rho < \varrho$. Let $k > 0$ and $\Psi^{''}\in L_{1}[\rho, \varrho]$, then

where

Motivated by a certain class of $h$-convex functions presented by Sanja Varošanec in ^[9] and the fractional Hermite-Hadamard inequalities ^{[23,24,25,26,27]}, we will study such inequalities for $h$-convex functions via Riemann-type integrals. Our main results are stated in sections below.

2.   Main results

This section focuses on trapezoid-type inequalities for twice-differentiable $h$-convex functions. In approximating the Riemann integral by a trapezoidal formula, such a type of inequality offers a priori error bounds. In general, they also show that the mid-point rule provides the best approximation of all Riemann sums sampled at the inside points of a given partition in the class.

Theorem 2.1. Let $I_{\rho^+}^{\alpha}\Psi$ and $I_{\varrho^-}^{\alpha}\Psi$ be the left and right sided RLFI of order $\alpha > 0$. Let $\Psi:[\rho, \varrho]\rightarrow \mathbb{R}$ be a positive mapping with $\Psi\in L_{1}[\rho, \varrho]$ and $0\leq \rho < \varrho$. If $\Psi$ is $h$-convex on $[\rho, \varrho]$, then we have the inequality

Proof. Since $\Psi$ is an $h$-convex function, so we can write

For $\omega = \frac{1}{2}$, we get

If we choose $x = \omega \rho+(1-\omega)\varrho$ and $y = \rho(1-\omega)+\varrho\omega$, then we have

Multiplying above inequality by $\omega^{\alpha-1}$ and integrating with respect to $\omega$ over $[0, 1]$, we get

which can also be written as

Now, replacing $\omega \rho+(1-\omega)\varrho = u$ and $(1-\omega)\rho+\omega \varrho = v,$ the inequality $(2.4)$ becomes

By managing the terms, we get

By replacing $x = \rho,$ $y = \varrho$ in (2.2) and (2.3) respectively, then adding, we have

Multiplying (2.6) by $\omega^{\alpha-1}$, then integrating over $[0, 1]$, we get

Combining (2.5) and (2.7), we get the desired result.

Remark 2.2. If we choose $h(\omega) = \omega$ in Theorem 2.1, then we get the result of Sarikaya et al. [23,Theorem 2].

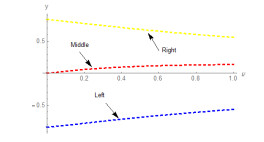
Example 2.3. By plotting graphs of double inequality (2.1) corresponding to the choice $\Psi(\wp) = e^{\wp}$ and $h(\omega) = \omega$, we prove that both inequalities are correct. Obviously

and

By utilizing these expressions into (2.1), we get

The three functions given by the double inequality on the left, middle and right sides (2.10) are plotted in Figure 1 against $\alpha\in(0, 1].$ The functions curves indicate that dual inequality is correct.

Theorem 2.4. Let $I_{\rho^+}^{\alpha}\Psi$ and $I_{\varrho^-}^{\alpha}\Psi$ be the left and right sided RLFI of order $\alpha > 0$. Let $\Psi\in SX(h, D)$, $\rho, \varrho\in D$ with $\rho < \varrho$ and $\Psi\in L_{1}[\rho, \varrho]$. Let $|\Psi^{''}|^{b}$ be $h$-convex function, then one has the following inequality

where $\frac{1}{g}+\frac{1}{b} = 1$.

Proof. By using Lemma 1.7, Definition 1.3 and Hölder's inequality respectively, we have

By utilizing the fact $(C-D)^{g}\leq C^{g}-D^{g}$ for any $C > D\geq 0$ and $g\geq1,$ we can write

This completes the proof of inequality (2.11).

Corollary 2.5. If we choose $h(\omega) = \omega$, then we get the result for convex function i.e.,

Corollary 2.6. Corresponding to the choice $h(\omega) = \omega^{s},$ where $s\in(0, 1)$, we get the result for geometric-arithmetically $s$-convex function.

Example 2.7. By plotting graphs of dual inequality in Theorem 2.4 for a convex function $\Psi(\wp) = e^{\wp},$ corresponding to $b = 2,$ $g = 2$ and $h(\wp) = \wp,$ we prove the validity of the results.

The three functions given by the double inequality on the left, middle and right sides (2.12) are plotted in Figure 2 against $\alpha\in(0, 1].$ The graphs of the functions prove the validity of dual inequality.

Theorem 2.8. Let $I_{\rho^+}^{\alpha}\Psi$ and $I_{\varrho^-}^{\alpha}\Psi$ be the left and right sided RLFI of order $\varrho > 0$. Let $\Psi\in SX(h, D)$, $\rho, \varrho\in D$ with $\rho < \varrho$ and $\Psi\in L_{1}[\rho, \varrho]$. Let $|\Psi^{''}|^{b}$ be $h$-convex, then one has inequality via fractional integrals

where $\frac{1}{g}+\frac{1}{b} = 1$.

Proof. Using Lemma 1.7, Definition 1.3, Lemma 1.8 and Hölder's inequality respectively, we have

Now, $2$-cases arise.

$\textbf{Case 1}:$ For $\varrho\in[0, 1]$, the inequality $(2.13)$ becomes

$\textbf{Case-2}$: For $\alpha\in[1, {\infty})$, the inequality $(2.13)$ can be written as:

By combining (2.14) and (2.15), we get the required result.

Corollary 2.9. If we choose $h(\omega) = \omega$ in Theorem 2.8, then we get the result for the classical convex function.

Remark 2.10. If we choos $h(\omega) = \omega^{s}$ in Theorem 2.8, where $s\in(0, 1)$, then we get the result of Liao et al. [24,Theorem 3.2].

Theorem 2.11. Let $I_{\rho^+}^{\alpha}\Psi$ and $I_{\varrho^-}^{\alpha}\Psi$ be the left and right sided RLFI of order $\alpha > 0$. Let $\Psi\in SX(h, D)$, $\rho, \varrho\in D$ with $\rho < \varrho$ and $\Psi\in L_{1}[\rho, \varrho]$. Let $|\Psi^{''}|$ be $h$-convex, then one has the following inequality

Proof. By using Lemma 1.7 and Definition 1.3 respectively, we have

Hence the inequality (2.16) holds.

Remark 2.12. By choosing $h(\omega) = \omega^{s}$, where $s\in(0, 1)$, we get the result of Liao et al. [24,Theorem 3.1].

Example 2.13. By plotting the graphs of (2.16) for a convex function $\Psi(\wp) = e^{\wp}$ corresponding to $h(\wp) = \wp,$ we prove the validity of the results.

The graphs of the functions given by the left, middle and right sides of the double inequality (2.17) are plotted in Figure 3 against $\alpha\in(0, 1]$. The functions curves indicate that dual inequality is correct.

Theorem 2.14. Let $I_{\rho^+}^{\alpha}\Psi$ and $I_{\varrho^-}^{\alpha}\Psi$ be the left and right sided RLFI of order $\alpha > 0$. Let $\Psi\in SX(h, D)$, $\rho, \varrho\in D$ with $\rho < \varrho$ and $\Psi\in L_{1}[\rho, \varrho]$. Let $|\Psi^{''}|^{b}$ be $h$-convex on $[\rho, \varrho]$ for fixed $\alpha\in(0, \infty),$ then one has the inequality

where $\frac{1}{g}+\frac{1}{b} = 1$.

Proof. By using Lemma 1.9, Hölder's inequality and Definition 1.3 respectively, we have

By simple calculation and using the fact $(1-\omega)^{\alpha+1}+\omega^{\alpha+1}\leq1$, we get

This completes the proof of Theorem 2.14.

Remark 2.15. If we choose $h(\omega) = \omega^{s}$ in Theorem 2.14, where $s\in(0, 1),$ then we get the result of Liao et al. [24,Theorem 4.2].

3.   Mid-point type inequalities for $h$-convex functions via $k$-fractional integrals

In this section, we present the estimates of mid-point type inequalities for $k$-RLFI via $h$-convex functions.

Theorem 3.1. Let $I_{\rho^+, k}^{\alpha}\Psi$ and $I_{\varrho^-, k}^{\alpha}\Psi$ be the left and right sided $k$-RLFI of order $\alpha > 0$. Let $\Psi:[\rho, \varrho]\rightarrow \mathbb{R}$ be a positive function with $0\leq \rho < \varrho$ and $\Psi\in L_{1}[\rho, \varrho]$. If $\Psi$ is $h$-convex function on $[\rho, \varrho]$, then

Proof. Since $\Psi$ is $h$-convex, then we can write

Corresponding to the choice $\omega = \frac{1}{2}$, we can write

By replacing $x = \omega a+(1-\omega)\varrho$ and $y = a(1-\omega)+\varrho\omega$, we get

Multiplying by $\omega^{\frac{\alpha}{k}-1}$ and integrating over $[0, 1]$, we get

This can also be written as:

Substituting $\omega \rho+(1-\omega)\varrho = u$ and $(1-\omega)\rho+\omega \varrho = v$, the inequality (3.3) can be written as:

which implies

Choose $x = \rho$ and $y = \varrho$ in $(3.1)$ and $(3.2)$, then adding, we get

Multiplying $(3.5)$ by $t^{\frac{\alpha}{k}-1}$ and integrating over $[0, 1]$, we obtain

Combining $(3.4)$ and $(3.6)$, we get the required result.

Remark 3.2. If we choose $h(\omega) = \omega$ in Theorem 3.1, then we get the result of Iqbal et al. [25,Theorem 2.2].

Theorem 3.3. Let $I_{\rho^+, k}^{\alpha}\Psi$ and $I_{\varrho^-, k}^{\alpha}\Psi$ be the left and right sided $k$-RLFI of order $\alpha > 0$. Let $\Psi\in SX(h, D)$, $\rho, \varrho\in D$ with $\rho < \varrho$ and $\Psi\in L_{1}[\rho, \varrho]$. Let $|\Psi^{''}|^{b}$ be $h$-convex, then the inequality

holds, where $\frac{1}{g}+\frac{1}{b} = 1$.

Proof. By using Lemma 1.13, Definition 1.3 and Hölder's inequality respectively, we can have

Using the fact $(1-(1-\omega)^{\frac{\alpha}{k}+1}-t^{\frac{\alpha}{k}+1})^{g}\leq1-(1-\omega)^{g(\frac{\alpha}{k}+1)}-\omega^{g(\frac{\alpha}{k}+1)}$ for any $\omega\in[0, 1]$, which follows from $(C-D)^{g}\leq C^{g}-D^{g}$, for any $C > D\geq 0$ and $g\geq1$.

Corollary 3.4. If we choose $h(\omega) = \omega$ in Theorem 3.3, then the result for a simple convex function is given by

Corollary 3.5. If we choose $h(\omega) = \omega^{s}$ corresponding to $s\in(0, 1)$ in Theorem 3.3, then we get the result for geometrically arithmetically $s$-convex function i.e.,

Theorem 3.6. Let $I_{\rho^+, k}^{\alpha}\Psi$ and $I_{\varrho^-, k}^{\alpha}\Psi$ be the left and right sided $k$-RLFI of order $\alpha > 0$. Let $\Psi\in SX(h, D)$, $\rho, \varrho\in I$ with $\rho < \varrho$ and $\Psi\in L_{1}[\rho, \varrho]$. Let $|\Psi^{''}|^{b}$ be $h$-convex, then one has the inequality via fractional integrals.

where $\frac{1}{g}+\frac{1}{b} = 1$.

Proof. By using Lemma 1.13, Hölder's inequality, Lemma 1.8 and Definition 1.3 respectively, we can write

Now, we have the following two cases:

$\textbf{Case 1}$: For $\alpha\in[0, 1],$ the inequality $(3.7)$ can be written as:

$\textbf{Case 2}$: For the choice of $\alpha\in[1, {\infty})$, the inequality $(3.7)$ can be written as:

Combining inequalities (3.8) and (3.9), we get the inequality (3.7).

Remark 3.7. If we choose $h(\omega) = \omega^{s}$ corresponding to $s\in(0, 1)$ in Theorem 3.6, then we get the result of Iqbal et al. [26,Theorem 2.4].

Theorem 3.8. Let $I_{\rho^+, k}^{\alpha}\Psi$ and $I_{\varrho^-, k}^{\alpha}\Psi$ be the left and right sided $k$-RLFI of order $\alpha > 0$. Let $\Psi\in SX(h, D)$, $\rho, \varrho\in D$ with $\rho < \varrho$ and $\Psi\in L_{1}[\rho, \varrho]$. Let $|\Psi^{''}|$ be $h$-convex, then the inequality

holds.

Proof. Using Lemma 1.13 and Definition 1.3 respectively, we get

This completes the proof of Theorem 3.8.

Remark 3.9. By choosing $h(\omega) = \omega^{s}$, where $s\in(0, 1)$, we get the result of Iqbal et al. [26,Theorem 2.3].

Theorem 3.10. Let $I_{\rho^+, k}^{\alpha}\Psi$ and $I_{\varrho^-, k}^{\alpha}\Psi$ be the left and right sided $k$-RLFI of order $\alpha > 0$. Let $\Psi\in SX(h, D)$, $\rho, \varrho\in D$ with $\rho < \varrho$ and $\Psi\in L_{1}[\rho, \varrho]$. If $|\Psi^{''}|^{b}$ is $h$-convex on $[\rho, \varrho]$ for $\alpha\in(0, \infty)$ and $\varrho\in(0, \infty),$ we get the inequality

where $\frac{1}{g}+\frac{1}{b} = 1$.

Proof. Using Lemma 1.14, Hölder's inequality and Definition 1.3 respectively, we have

Since $(1-\omega)^{\frac{\alpha}{k}+1}+\omega^{\frac{\alpha}{k}+1}\leq1$, therefore we can write

The proof of Theorem 3.10 is done.

Remark 3.11. If we choose $h(\omega) = \omega^{s}, \, s\in(0, 1]$ in Theorem 3.10, then we get the result of Iqbal et al. [26,Theorem 2.6].

Theorem 3.12. Let $I_{\rho^+, k}^{\alpha}\Psi$ and $I_{\varrho^-, k}^{\alpha}\Psi$ be the left and right sided $k$-RLFI of order $\alpha > 0$. Let $h : J \subset \mathbb{R}\rightarrow \mathbb{R}$ and $\Psi:[\rho, \varrho]\rightarrow \mathbb{R}$ be positive functions with $0\leq \rho < \varrho$ and $h^{b}(\omega) \in L_{1}[0, 1]$, $\Psi \in L_{1}[\rho, \varrho]$. If $|\Psi^{'}|$ is $h$-convex mapping on $[\rho, \varrho]$, then the inequality

holds, where $\alpha > 0$, $g > 0$ and $\frac{1}{g}+\frac{1}{b} = 1$.

Proof. Since $|\Psi^{'}|$ is $h$-convex, then by Lemma 1.12, we can write

Using Hölder's inequality on the right side of $(3.10),$ we get

This completes the proof of the result.

Remark 3.13. If we choose $k = 1$ in Theorem 3.12, we get the result of Tunc. [27,Theorem 5].

4.   Applications to quadrature formulas

This section is devoted to some particular inequalities which generalize some classical results such as trapezoid-type, mid-point-type and Hadamard's inequality.

Proposition 4.1. (Hadamard's inequality). Under the assumptions of Theorem 2.1 with $\alpha = 1$ and $h(\omega) = \omega,$ we get the "Hadamard's inequality"

Proposition 4.2. Let the assumptions of Theorem 2.4 be fulfilled with $\alpha = 1$ and $h(\omega) = \omega,$ then we obtain the "Trapezoid inequality"

Proposition 4.3. Let the assumptions of Theorem 2.11 be fulfilled with $\alpha = 1$ and $h(\omega) = \omega,$ then we obtain the "Trapezoid inequality"

Proposition 4.4. Under the assumptions of Theorem 2.14 with $\alpha = 1$ and $h(\omega) = \omega,$ we get the following "Mid-point inequality"

Proposition 4.5. Let the assumptions of Theorem 3.12 be fulfilled with $\alpha = 1$ and $h(\omega) = \omega,$ then we get the following "Trapezoid inequality"

5.   Conclusions

We aim at designing the generalizations of some Trapezoid-type inequalities for Riemann-type fractional integrals in the present article. We use $h$-convex function to this ends and develops numerous inequalities. We prove the validity of our results by using the examples and their graphs. The work presented consists of the formulas of quadrature as a boundary of the new inequalities. The results of these studies complement those of earlier studies. The earlier findings are supported by simple, recent studies and play an additional role in generalizations.

Acknowledgments

The authors Bahaaeldin Abdalla and Thabet Abdeljawad would like to thank Prince Sultan University for funding this research through the group: Nonlinear Analysis Methods in Applied Mathematics (NAMAM), group number RG-DES-2017-01-17.

Conflict of interest

The authors declares that there is no conflict of interests regarding the publication of this paper.