New escape conditions with general complex polynomial for fractals via new fixed point iteration

1.   Introduction

During the past few decades, singular differential equations have been widely investigated by many scholars. Singular differential equations appear in many problems of applications such as the Kepler system describing the motion of planets around stars in celestial mechanics ^[12], nonlinear elasticity ^[10] and Brillouin focusing systems ^[2]. We refer to the classical monograph ^[31] for more information about the application of singular differential equations in science. Owing to the extensive applications in many branches of science and industry, singular differential equations have gradually become one of the most active research topics in the theory of ordinary differential equations. Up to this time, some necessary work has been done by scholars, including Torres ^[31,33], Mawhin ^[17], O'Regan ^[29], Ambrosetti ^[1], Fonda ^[12,13], Chu ^[5,8] and Zhang ^[36,37], etc.

In the current literature on singular differential equations, the problem on the existence and multiplicity of periodic solutions is one of the hot topics. Lazer and Solimini ^[25] first applied topological degree theory to study the periodic solutions of singular differential equations, the results also reveal that there are essential differences between repulsive singularity and attractive singularity. In order to avoid the collision between periodic orbit and singularity in the case of repulsive singularity, a strong force condition was first introduced by Gordon ^[16]. After that, various variational methods and topological methods based on topological degree theory have been widely used, including the method of upper and lower solutions ^[9,18,19,20], fixed point theorems ^[7], continuation theory of coincidence degree ^[21,24,26], and nonlinear Leray-schauder alternative principle ^[5,6,8]. From present literature, the existence periodic solutions are convenient to prove if the singular term satisfies the strong force condition. It is worth noting that Torres obtained existence results of periodic solutions in the case of a weak singularity condition of the singular term, see the reference ^[32] for details. Until now, the work on the existence of periodic solutions with weak conditions is much less than the work with strong force conditions, see ^[22,27,32].

Because of singular Rayleigh equations are widely applied in many fields, such as engineering technique, physics and mechanics fields ^[14,30]. Singular Rayleigh equations usually have multiple regulations and local periodic vibration phenomena. Hence, periodic solutions of singular Rayleigh equation becomes one key issue of singular Rayleigh equations. However, most of the results in the references ^{[3,4,15,23,34,35]} are concerned about one solution, while fewer works are concerned about multiple periodic solutions. Therefore, it is valuable to investigate the existence of multiple periodic solutions for singular Rayleigh equations in both theory and practice.

Motivated by the above literature, the main purpose of this paper is to verify the existence and multiplicity of periodic solutions of the following singular Rayleigh equation

where $f\in C({\mathbb{R}}, {\mathbb{R}})$, $e\in C({\mathbb{R}}/T {\mathbb{Z}}, {\mathbb{R}})$, and $g\in C((0, +\infty), {\mathbb{R}})$ may be singular at the origin. We discuss both repulsive and attractive singularity with some weak conditions for the term $g$. It is said that Eq (1.1) has a repulsive singularity at the origin if

and has an attractive singularity at the origin if

The proof of the main results in this study is based on Mawhin's coincidence degree and the method of upper and lower solutions. Compared to the existing results about periodic problems of singular Rayleigh equations, the novelties lie in two aspects: (1) the singular term $g$ has a weaker force condition; (2) the existence of arbitrarily many periodic solutions are concerned.

The rest of this paper is organized as follows. Some preliminary results are presented in Section 2. The main results will be presented and proved in Section 3. Finally, in Section 4, some examples and numerical solutions are expressed to illustrate the application of our results.

2.   Preliminaries

In this section, we first recall some basic results on the continuation theorem of coincidence degree theory ^[28].

Let $X$ and $Y$ be two real Banach spaces. A linear operator

is called a Fredholm operator of index zero if

${\rm (i)\; }$ $\mbox{Im}L$ is a closed subset of $Y$,

${\rm (ii)} \ \ \mbox{dim}\; \mbox{Ker}L = \mbox{codim}\; \mbox{Im}L < \infty.$

If $L$ is a Fredholm operator of index zero, then there exist continuous projectors

such that

It follows that

is invertible and its inverse is denoted by $K_{P}$.

If $\Omega$ is a bounded open subset of $X$, the continuous operator

is said to be $L$-compact in $\bar{\Omega}$ if

${\rm (iii)}$ $K_{P}(I-Q)N(\bar{\Omega})$ is a relative compact set of $X$,

${\rm (iv)}$ $QN(\bar{\Omega})$ is a bounded set of $Y$.

Lemma 2.1. ^[28] Let $\Omega$ be an open and bounded set of $X$, $L: D(L)\subset X \rightarrow Y$ be a Fredholm operator of index zero and the continuous operator $N:\bar{\Omega}\subset X\rightarrow Y$ be $L$-compact on $\bar{\Omega}$. In addition, if the following conditions hold:

${\rm (A_{1})}$ $Lx\neq\lambda Nx, \forall (x, \lambda)\in\partial\Omega\times(0, 1)$,

${\rm (A_{2})}$ $QNx\neq0, \forall x\in {\rm Ker}L\cap\partial\Omega,$

${\rm (A_{3})}$ ${\rm deg}\{JQN, \Omega\cap {\rm Ker}L, 0\}\neq0,$

where $J: {\rm Im}Q\rightarrow {\rm Ker}L$ is an homeomorphism map. Then $Lx = Nx$ has at least one solution in $\bar{\Omega}$.

In order to apply Lemma 2.1 to Eq (1.1), let $X = C_{T}^{1}$, $Y = C_{T}$, where

Define

Clearly, $X$, $Y$ are two Banach spaces with norms $\|\cdot\|$ and $\|\cdot\|_{\infty}$. Meanwhile, let

Then

hence, $L$ is a Fredholm operator of index zero. Define the projects $P$ and $Q$ by

Obviously,

Let $L_{p} = L|_{{\rm Dom}L\bigcap{\rm Ker}P}$, then $L_{p}$ is invertible and its inverse is denoted by $K_{p}:{\rm Im}L\rightarrow {\rm Dom}L$,

Let $N:X\rightarrow Y$, such that

It is easy to show that $QN$ and $K_{P}(I-Q)N$ are continuous by the Lebesgue convergence theorem. By Arzela-Ascoli theorem, we get that $QN(\overline{\Omega})$ and $K_{p}(I-Q)N(\overline{\Omega})$ are compact for any open bounded set $\Omega$ in $X$. Therefore, $N$ is $L$-compact on $\overline{\Omega}$.

3.   Main results

For the sake of convenience, we denote

Moreover, we list the following condition

${\rm(H_{0})}$ There exist two constants $c > 0$ and $p\geq1$, such that

Obviously, we have $f(0) = 0$.

Lemma 3.1. Assume that $x$ is a $T$-periodic solution of Eq (1.1). Then the following inequalities hold

where $s_{1}$ and $t_{1}$ be the maximum point and the minimum point of $x(t)$ on $[0, T]$.

Proof. Obviously,

Combining these with Eq (1.1), we get

Then we have

3.1.   Repulsive singular case

Theorem 3.2. Assume that ${\rm(H_{0})}$ holds and Eq (1.1) has a repulsive singularity at the origin. Suppose further that

${\rm(H_{1})}$ There exist only two positive constants $\xi_{1}$ and $\eta_{1}$ with $\eta_{1} > \xi_{1} > \omega$, such that

Then Eq (1.1) has a positive $T$-periodic solution $x_{1}$ satisfies

Proof. Since Eq (1.1) can be written as an operator equation $Lx = Nx$, so we consider an auxiliary equation $Lx = \lambda Nx$,

Suppose that $x\in X$ is a periodic solution of the above equation. Multiplying both sides of Eq (3.2) by $x'(t)$ and integrating on the interval $[0, T]$, then we have

By using the Hölder's inequality, it follows from ${\rm(H_{0})}$ and the above equality that

where $\frac{1}{q}+\frac{1}{p} = 1$. Then we can obtain from the above inequality that

By Lemma 3.1 and ${\rm(H_{1})}$, we can deduce that

Then, by (3.3) and (3.4), we have

and

Combining with the above two inequalities, we get

By ${\rm(H_{0})}$ and the continuity of $f$, it is immediate to see that

Therefore, let us define two sets

and

Integrating the Eq (3.2) over the sets $I_{1}$, $I_{2}$, we get

and

which imply that

Then by (3.2), (3.7) and (3.8), we obtain

where

and $\overline{|e|}$ is the mean value of $|e(t)|$ on the interval $[0, T]$.

Obviously, $\xi_{1}$, $\eta_{1}$ and $M_{1}$ are positive constants independent of $\lambda$. Take three positive constants $h_{1}$, $h_{2}$ and $\tilde{M}_{1}$ with

and let

Obviously, $\Omega_{1}$ is an open bounded set of $X$. By the definition of $N$, we know that $N$ is $L$-compact on the $\bar{\Omega}_{1}$. By (3.7), (3.9) and (3.10), we get that

Hence, the condition ${\rm(A_{1})}$ in Lemma 2.1 is satisfied.

Next, we verify that the condition ${\rm(A_{2})}$ of Lemma 2.1 is satisfied. Clearly, if $x\in\partial\Omega_{1}\cap {\rm Ker}L = \partial\Omega_{1}\cap \mathbb{R}$, we have $QNx\neq0$. If it does not hold, then there exists $x\in\partial\Omega_{1}\cap\mathbb{R}$, such that $QNx = 0$, and $x(t)\equiv \zeta$ is a constant. That is

i.e.,

This implies that

which together with ${\rm (H_{1})}$ yield

This contradicts $x = \zeta\in\partial\Omega_{1}\cap\mathbb{R}$. Thus,

Finally, we prove that the condition ${\rm(A_{3})}$ of Lemma 2.1 is also satisfied. Define

where

Then, by (3.11), we notice that

Therefore, we have

To sum up the above discussion, we have proven that all of the conditions of Lemma 2.1 are satisfied. Therefore, Eq (1.1) has a $T$-periodic solution $x_{1}$ in $\Omega_{1}$. Moreover, by (3.4) and (3.7), we get that (3.1) holds.

Theorem 3.3. Assume that ${\rm(H_{0})}$ holds and Eq (1.1) has a repulsive singularity at the origin. Suppose further that

${\rm(H_{2})}$ There exist only four positive constants $\xi_{1}$, $\xi_{2}$, $\eta_{1}$, $\eta_{2}$ with $\xi_{2} > \eta_{2} > \eta_{1} > \xi_{1} > \omega$, such that

Then Eq (1.1) has two positive $T$-periodic solutions $x_{1}$ and $x_{2}$, which satisfy

and

Proof. From Lemma 3.1 and ${\rm(H_{2})}$, we obtain

and

Therefore, we have either

or

$\rm(1)$ If (3.14) holds, notice that

is a constant lower solution of Eq (1.1) and

is a constant upper solution of Eq (1.1). Then by the method of upper and lower solutions (see ^[11,31]), we know that Eq (1.1) has a positive $T$-periodic solution $x_{2}$ such that (3.13) holds.

$\rm(2)$ If (3.15) holds, by (3.3), analysis similar to that in (3.5) and (3.6), we have

By using similar arguments of Theorem 3.2, it follows from (3.16) that there exists a constant $M_{2} > 0$ such that

Clearly, $\xi_{1}$, $\eta_{1}$, $M_{2}$ are all independent of $\lambda$. Take three constants $u_{1}, \; u_{2},$ and $\tilde{M}_{2}$ with

and set

The remainder can be proved in the same way as in the proof of Theorem 3.2. Then, Eq (1.1) has a positive $T$-periodic solution $x_{1}$ in $\Omega_{2}$ such that (3.12) holds.

To sum up the above discussion, we plainly conclude that Eq (1.1) has at least two positive $T$-periodic solutions.

Remark 1. In Theorem 3.3, if $\eta_{1} = \eta_{2}$, we can only get that Eq (1.1) has at least one positive $T$-periodic solution.

Proof. If $\eta_{1} = \eta_{2}$, by Lemma 3.1 and ${\rm(H_{2})}$, we can only get

As in the proof of Theorem 3.3, we can prove that Eq (1.1) has a positive $T$-periodic solutions $x_{1}$ such that

Moreover, by the method of upper and lower solutions (see ^[11,31]), we can also get that Eq (1.1) has a positive $T$-periodic solution $x_{2}$ such that

But, by (3.17) and (3.18), we are not sure that $x_{1}$ is different from $x_{2}$.

Therefore, we just can assert that Eq (1.1) has at least one positive $T$-periodic solution.

Furthermore, Theorem 3.3 can be generalized to arbitrarily many periodic solutions.

Theorem 3.4. Assume that ${\rm(H_{0})}$ holds and Eq (1.1) has a repulsive singularity at the origin. Suppose further that

${\rm(H_{n})}$ There exist only $2n$ positive constants $\xi_{1}$, $\xi_{2}$, $\cdots$ $\xi_{n}$, $\eta_{1}$, $\eta_{2}$, $\cdots$ $\eta_{n}$, with

and

where $[\cdot]$ stands for the integer part, such that

Then Eq (1.1) has at least $n$ different positive $T$-periodic solutions.

Proof. The case $n = 1$ and $n = 2$, one can see Theorem 3.2 and Theorem 3.3.

Let us define the following sets

By (3.19) and (3.20), notice that $B_{i}\cap B_{j} = \varnothing$, for $i\neq j$, $\; \; i, j = 1, 2\cdots n$.

For the case $n = 3$, by Lemma 3.1 and ${\rm(H_{3})}$, we have

and

Then

or

or

By (3.21) and (3.22), as in the proof of Theorem 3.3, we can prove that Eq (1.1) has two different positive $T$-periodic solutions $x_{1}$ and $x_{2}$ with $x_{1}\in B_{1}$ and $x_{2}\in B_{2}$. By (3.23), analysis similar to that in the proof of Theorem 3.2 shows that Eq (1.1) has a positive $T$-periodic solution $x_{3}$ belonging to $B_{3}$. Then, by the facts, we get that Eq (1.1) has at least $3$ different positive $T$-periodic solutions.

Similar arguments apply to the case $n > 3$, we can prove that Eq (1.1) has $n$ different positive $T$-periodic solutions $x_{1}$, $x_{2}$, $\cdots$ $x_{n}$ with $x_{i}\in B_{i}$, $i = 1, 2, \cdots n$.

The proof is completed.

3.2.   Attractive singular case

Theorem 3.5. Assume that ${\rm (H_{0})}$ holds and Eq (1.1) has an attractive singularity at the origin. Suppose further that

${\rm(C_{1})}$ There exist only two positive constants $\xi_{1}$, $\eta_{1}$ with $\eta_{1} > \xi_{1}$, such that

Then Eq (1.1) has at least one positive T-periodic solution.

Proof. Obviously,

is a constant lower solution of Eq (1.1) and

is a constant upper solution of Eq (1.1). Then by the method of upper and lower solutions (see ^[11,31]), we know that Eq (1.1) has a positive $T$-periodic solution $x$ such that $\alpha(t)\leq x(t)\leq\beta(t)$ for every $t$.

Theorem 3.6. Assume that ${\rm (H_{0})}$ holds and Eq (1.1) has an attractive singularity at the origin. Suppose further that

${\rm(C_{2})}$ There exist only four positive constants $\xi_{1} < \eta_{1} < \eta_{2} < \xi_{2}$, such that

Then Eq (1.1) has at least two positive $T$-periodic solutions.

Proof. The proof of Theorem 3.6 works almost exactly as the proof Theorem 3.3. It is easy to get that

and

which together with Lemma 3.1 yield that

or

$\rm(1)$ If (3.24) holds, by the method of upper and lower solutions align (see ^[11,31]), we get that Eq (1.1) has at least one positive $T$-periodic solution $x$ such that

$\rm(2)$ If (3.25) holds, repeating the proof of Theorem 3.2, we can construct an open bounded set

such that Eq (1.1) has at least one positive T-periodic solutions in $\Omega_{3}$.

To sum up the above discussion, we have proved that Eq (1.1) has at least two positive $T$-periodic solutions.

Similar as in the proof of Theorem 3.4, we can generalize Theorem 3.6 to arbitrarily many periodic solutions.

Theorem 3.7. Assume that ${\rm(H_{0})}$ holds and Eq (1.1) has an attractive singularity at the origin. Suppose further that

${\rm(C_{n})}$ There exist only $2n$ positive constants $\xi_{1}$, $\xi_{2}$, $\cdots$ $\xi_{n}$, $\eta_{1}$, $\eta_{2}$, $\cdots$ $\eta_{n}$ with

and

such that

Then Eq (1.1) has at least $n$ positive $T$-periodic solutions.

4.   Example and numerical simulations

In this section, some examples and numerical solutions are given to illustrate the application of our results.

Example 1. Consider the following equation:

Conclusion: Eq (4.1) has at least one positive $2$-periodic solution.

Proof. Corresponding to Eq (1.1), we have

Obviously, $e^{*} = 5.8$, $e_{*} = -1.8$. It is easy to see that there exist only two positive constants $\xi_{1}\approx0.912$, $\eta_{1}\approx2.047$ such that

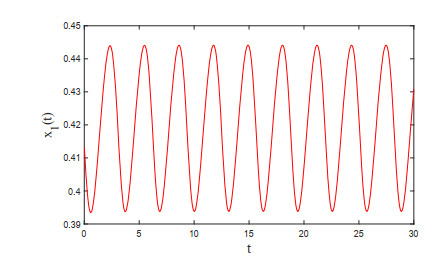
Moreover, it is easy to check that $\xi_{1} > \omega$. Then, by Theorem 3.2, we get that Eq (4.1) has at least one positive $2$-periodic solution. Applying Matlab software, we obtain numerical periodic solution of Eq (4.1), which is shown in Figure 1.

Example 2. Consider the following equation:

Conclusion: Eq (4.2) has at least two positive $\pi$-periodic solutions.

Proof. Corresponding to Eq (1.1), we have

Obviously, $e^{*} = -8.76$, $e_{*} = -17.52$. It is easy to check that exist only four positive constants $\xi_{1}\approx0.3323$, $\eta_{1}\approx0.5805$, $\eta_{2}\approx1.177$, $\xi_{2}\approx2.7$ such that

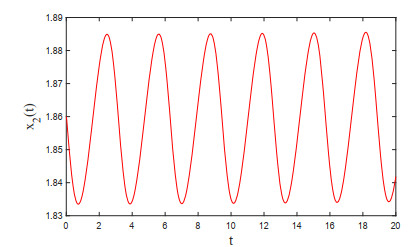
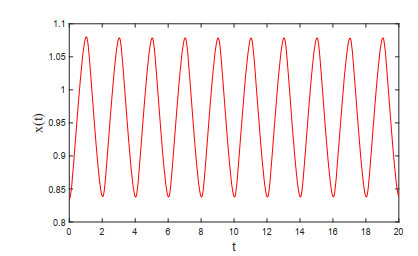
Moreover, it is easy to check that $\xi_{1} > \omega$. Then, by Theorem 3.3, we get that Eq (4.2) has at least two positive $\pi$-periodic solutions. We obtain two numerical periodic solutions of Eq (4.2), which are shown in Figures 2 and 3, respectively.

Example 3. Consider the following equation:

Conclusion: Eq (4.3) has at least one positive $2$-periodic solution.

Proof. Corresponding to Eq (1.1), we have

Obviously, $e^{*} = 5$, $e_{*} = -1$. It is easy to see that there exist only two positive constants $\xi_{1}\approx0.757$, $\eta_{1}\approx1.24$ such that

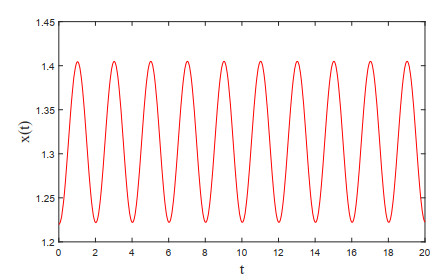
Moreover, it is easy to check that $\xi_{1} > \omega$. Then, by Theorem 3.2, we get that Eq (4.3) has at least one positive $2$-periodic solution. Applying Matlab software, we obtain numerical periodic solution of Eq (4.3), which is shown in Figure 4.

5.   Conclusions

In this paper, we study the existence and multiplicity of positive periodic solutions of the singular Rayleigh differential equation (1.1). Based on the continuation theorem of coincidence degree theory and the method of upper and lower solutions, we construct some subsets $B_{k}$, $k = 1, 2, \cdots, n$ of $C_{T}^{1}$ with $B_{i}\cap B_{j} = \varnothing$, for $i\neq j$, $\; \; i, j = 1, 2, \cdots, n$, such that the equation (1.1) has a positive $T$-periodic solution in each set $B_{k}$, $k = 1, 2, \cdots, n$. That is, the equation (1.1) has at least $n$ distinct positive $T$-periodic solutions. We discuss both the repulsive singular case and the attractive singular case, and the singular term has a weaker force condition than the literatures about strong force condition. Some results in the literature are generalized and improved. It should be pointed out that it is the first time to study the existence of arbitrarily many periodic solutions of singular Rayleigh equations. In addition, some typical numerical examples and the corresponding simulations have been presented at the end of this paper to illustrate our theoretical analysis.

Acknowledgments

We would like to express our great thanks to the referees for their valuable suggestions. Zaitao Liang was supported by the Natural Science Foundation of Anhui Province (No. 1908085QA02), the National Natural Science Foundation of China (No.11901004) and the Key Program of Scientific Research Fund for Young Teachers of AUST (No. QN2018109). Hui Wei was supported by the Postdoctoral Science Foundation of Anhui Province (No. 2019B318) and the National Natural Science Foundation of China (No. 11601007).

Conflict of interest

The authors declare that they have no competing interests concerning the publication of this article.