The purpose of this study is to establish the influence of composition on the glass transition temperature, density, enthalpy of dissolution in an acid bath and bioactivity in glasses of the molar formula 20.15[(2.038 + x)SiO2-(1.457 − x)Na2O]-2.6P2O5-25.73CaO-1.22MgO. It is also a question of correlating bioactivity and stability in this oxide glass system. Nine samples were prepared by high temperature melting followed by quenching. These samples were characterized by X-ray diffraction (XRD), differential scanning calorimetry (DSC), dissolution calorimetry and pycnometry. Their bioactivity was estimated using the Anderson model. The results indicate that the effect of magnesium composition can lead to a decrease in the glass transition temperature (Tg). These results also show that a decrease in glass stability leads to a decrease in bioactivity.
1.
Introduction
Bioactive phosphosilicate glasses are biomaterials that have biological potential in the reconstruction of diseased or damaged bone or human tissue [1,2,3,4]. They have been used in many clinical operations, including the reconstructive surgery of many injured organs of the human body such as the ossicles of the ear, teeth, knees and hips over the past twenty years. Due to their numerous clinical uses, special attention has been paid to improving their bioactivity and physicochemical properties by adding metal oxides such as MgO, Al2O3, SrO, ZnO, etc. [5,6,7,8]. Magnesium is a particularly interesting candidate because it can stimulate the proliferation of osteoblasts [9] and positively influence the bioactivity of the glasses in which it is incorporated [10,11,12].
In one study Barrere et al. [13] postulated that magnesium could affect the dissolution and physicochemical reaction of glass. It was shown that the presence of MgO in the dissolution of CaO–MgO–SiO2–P2O5 ceramic systems results in the formation of Ca2MgSi2O7 and SiO2 phases. According to this study a low degree of degradability leads to a decrease in the rate of apatite formation. This result is in line with the research of Ducheyne et al. [14] which states that the incorporation of MgO decreases the degradability of glass of CaO–MgO–SiO2–P2O5 composition. Further work by Strnad [15] and then Hill [16] proposed a theory based on the network connectivity of inorganic polymer structural parameters to predict the bioactivity of glass. Although, some studies have suggested that magnesium has no effect on apatite formation [17], other studies indicate that MgO has an adverse effect on apatite formation [10,11,12]. Oliveira et al. [18] claimed that MgO has a beneficial effect because it improves the early stages of mineralization and contributes to intimate contact with living tissue. Thus several kinetic approaches to biomineralization and the bioconsolidation of glasses are widely developed in the literature [19,20,21]. To our knowledge, there are no studies on the influence of energy quantities on the biological characteristics of glasses. Energy input (free enthalpy of formation) could also play an important role in the mechanisms of bioactivity in the same way as the dissolution kinetics of glasses in contact with physiological fluids.
The purpose of this study is to establish the influence of composition on the glass transition temperature, density, enthalpy of dissolution in an acid bath and the bioactivity in glasses of the molar formula 20.15[(2.038 + x)SiO2–(1.457 − x)Na2O]–2.6P2O5–25.73CaO–1.22MgO. It is also a question of correlating bioactivity and stability in this oxide glass system.
Methods such as X-ray diffraction (XRD), differential scanning calorimetry (DSC), dissolution calorimetry and pycnometry have been widely used to study the structure, glass transition temperature (Tg) and thermodynamic stability of glasses.
2.
Experimental procedure
2.1. Preparation of samples
Glass compositions of the molar formula 20.15[(2.038 + x)SiO2–(1.457 − x)Na2O]–2.6P2O5–25.73CaO–1.22MgO;
x varying from 0 to 1 in steps of 0.125, have been prepared using the melt quenching technique. The glasses were prepared from silica reagents SiO2 (Merck product), di-ammonium hydrogen phosphate (NH4)2HPO4 (Aldrich product), calcium carbonate CaCO3 (Prolabo product), sodium carbonate Na2CO3 (Aldrich product) and magnesium oxide MgO (Prolabo product) of high purity (99.9%) in the appropriate proportions. Mixtures of approximately 10 g were melted in platinum crucibles at 1500 ℃ in a tubular furnace for 6 h to homogenize the mixture and significantly lower its viscosity, and then tempered by dipping the bottom of the crucible in water to produce glass fragments. Nominal glass compositions are given in Table 1.
2.2. Characterizations
The glass transition temperatures (Tg) were measured by a Differential Scanning Calorimeter (DSC 111 SETERAM). Tens of milligrams of finely ground glassy powder (about 100 µm in diameter) in crimped stainless steel crucibles were used. The experiments were carried out in an argon atmosphere and at a heating rate of 5 ℃/min from 25 to 700 ℃. This technique was used by Kouyate et al. [22]. The glass transition temperature (Tg) was determined with an accuracy of ±3 ℃ for each sample.
The glass condition of the samples was checked by X-ray diffraction. Each glass composition was studied using a SIEMENS D 5000 diffractometer using CuKα (λ = 1.5406 Å) radiation at 40 kV. The data were collected between 10 and 60 ℃ (angle 2θ) with a step size of 0.02° and a scanning speed of 2°/min. The experiments were carried out at 25 ℃. A powder with a particle size of 50 µm was used.
The densities of the glass samples were measured using a pycnometer (Brand 43205) with diethylphthalate (d = 1.118) as the immersion fluid. The pycnometer consists of a glass vial with a tight-fitting ground-glass stopper, topped by an indexed capillary tube. This tube releases part of the liquid after closing the top-filled pycnometer and allows very accurate measurement of constant volume masses of liquid and solid. Care has been taken to ensure that all cast samples are free of bubbles and that the glass samples are completely wetted when immersed in the diethylphthalate (C12H14O4). The glass density was calculated using Eq 1:
where m1 is the mass of the pycnometer full of liquid, m2 is the mass of the sample alone, m3 is the mass of the pycnometer full of liquid with the sample submerged and dliq is the density of C12H14O4. The overall accuracy of the experimental density measurement is estimated to be ±0.03 g·cm−3.
The calorimetry experiments were carried out in temperature-controlled chamber with a balance calorimeter called Calset. The calorimeter and standard procedures have been described previously [23,24,25,26,27] and only a brief description will therefore be given below. Prior to dissolution, the solute and solvent are each completely isolated together in two separate compartments separated by a platinum lid and an n-decane liquid seal. Acid vapour cannot react with the solute during the thermal stabilization time of the calorimeter. After thermal equilibrium for about four hours, the sample is brought into contact with the solvent consisting of a mixture (8 mL) of HF (6 M) and HNO3 (4 M) by rotating the calorimeter. The rotation of the calorimeter is stopped as soon as the flow of energy produced by the reaction is cancelled. Data acquisition is stopped about one hour after the dissolution is complete, so that the final thermal and mechanical state of the calorimeter is identical to the initial state. This well-known dissolution method for determining the dissolution enthalpies of processed glasses has been frequently used by Kouyate et al. [22]. Dissolution lasts three hours and the effect of the heat accompanying the dissolution is measured.
3.
Results and discussion
3.1. Results
Figure 1 shows some diaffractograms of the glasses synthesized during this study. No diffraction lines were observed on any of the diffractograms. The samples are quite amorphous. The amorphous halo of the glasses was centered around 33°. Only one diffraction halo can be observed and its shift towards small angles reflects an increase in molar volume with increasing silica content.
The thermal properties of glasses of molar formula 20.15[(2.038 + x)SiO2–(1.457 − x)Na2O]–2.6P2O5–25.73CaO–1.22MgO examined by differential scanning calorimetry are shown in Table 2. These data show endothermic effects in the temperature range of 479–608 ℃.
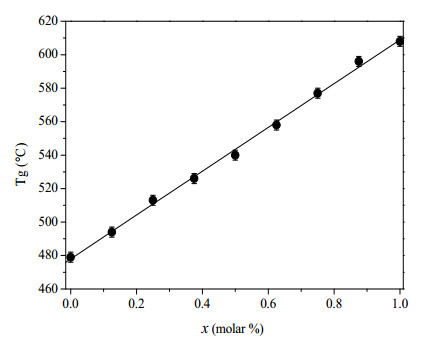
Figure 2 shows a linear increase with the silica content between 479 and 608 ℃. The addition of MgO had no significant effect on the variation in Tg compared to compositions without MgO [22].
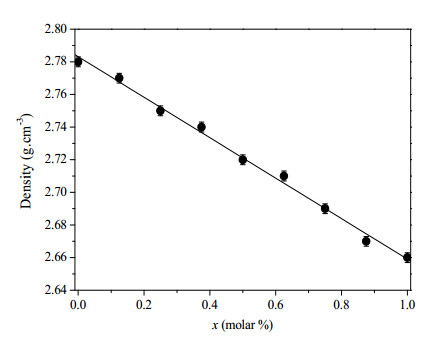
The study of the evolution of the density of the synthesized glasses is presented in Figure 3. A quasi-linear decrease in density is observed with the addition of SiO2 to the detriment of Na2O in the phosphosilicate glasses. A further significant decrease is observed with the addition of MgO. A decrease in the slope of the density curve from 2.78 to 2.66 g·cm−3 is observed when SiO2 is added in the composition.
Table 2 also shows the values of infinite dilution dissolution enthalpy at 25 ℃. These were derived by applying constrained least squares regression to all the enthalpies of dissolution of the different concentrations of the solute in the solvent (Table 3). The resulting enthalpies of dissolution at infinite dilution are negative and exothermic over the entire compositional range. The accuracy of the determination is estimated to be ±1.92 kJ·mol−1.
For a given temperature, it can be observed that the variations of free enthalpies of glass formation are strongly dependent on the composition. To calculate the enthalpies of formation of one mole of glass solution, the following reaction scheme (Table 4) is established:
where α, β, γ, δ and ε are the molar fractions of the constituent oxides with the condition α + β + γ + δ + ε = 1.
The reaction fv is the reaction of formation of glass from simple oxides. The f1–f5 reactions represent the formation reactions of the secondary references referred to simple oxides. The dv and d1–d4 reactions represent respectively the dissolutions of the glass and secondary references in the same solvent HF (6 M)–HNO3 (4 M) at 25 ℃.
Thus the enthalpy of formation sought is the sum weighted by the coefficients υi of the various formation and dissolution reactions studied (Eq 2):
The data concerning the enthalpies of dissolution at infinite dilution and the enthalpies of formation in relation to the secondary reference oxides required to calculate the enthalpy of formation of our glasses are shown in Table 5.
The enthalpies of formation referred to simple oxides are then calculated for the various compositions. They are compiled in Table 6. The entropy of formation of the glasses referred to the constituent simple oxides were calculated according to Eq 3:
where Svib, is the vibrational entropy resulting from the distribution of the vibrational energy between the constituent atoms, S°, is the standard entropy for the formation of oxides and Sid, is the entropy of chemical configuration in the glass considered as an ideal solution. Values obtained are given in Table 6.
The free enthalpies of formation at 25 ℃ relative to the oxides are deduced from the Eq 4:
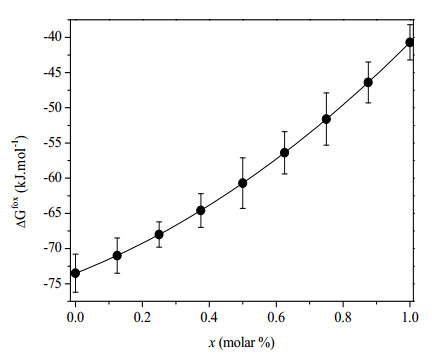
The results are shown in Table 7 and Figure 4.
The glasses of molar formula 20.15[(2.038 + x)SiO2–(1.457 − x)Na2O]–2.6P2O5–25.73CaO–1.22MgO studied have interesting biological properties [28,29]. The aim of this work is to describe the impact of the free enthalpy of glass formation in relation to the simple constituent oxides not on the physicochemical reactions induced by the immersion of the glass in the physiological fluid, but on the activities of glass through the bioactivity indices. A bioactivity index of the reaction of a glass in a physiological medium contains kinetic, energetic and morphological information. Kinetic and morphological information has been widely used to explain and improve the bioactivity of a glass.
For this purpose, we calculated the free enthalpies of formation (ΔGfox) of glasses in a solution of HF (6 M) + HNO3 (4 M) on the basis of a dissolution calorimetry study at 25 ℃ and obtained evidence of bioactivity according to the Andersson equation [30,31]:
with the proportions of the oxides in percent by weight. RN as defined by Anderson et al. is the "reaction number", a value used to define a range of bioactive glasses. The results obtained are shown in Table 7.
With the exception of glasses with compositions above 0.875, RN values indicate that all glasses are bioactive, form a hydroxyapatite layer and bind to bone (RN ≥ 5). For RN = 3.37, the silica-rich layer has formed well but the amount of precipitated CaP is too low to form a bone bond. For RN = 4.33, the CaP-rich layer has formed, but the amount of CaP is insufficient to form a strong bond to bone.
Table 7 presents the overall results of the bioactivity index calculations. All the indexes show that glasses with the lowest silica content are the most bioactive. The RN index is greater than 5 for x ≤ 0.75. It appears that the addition of 1.22% molar of MgO seems to increase the reactivity of the glass in the physiological environment and to widen the range of bioactivity.
The standard free enthalpies referred to simple oxides reflect the stability of these compounds with respect to these references (Figure 4). The formation of glasses is thermodynamically favoured from a mechanical mixture of oxides. With the exception of errors, the substitution of 1.22% molar of CaO by MgO does not induce any significant variation in the free enthalpy of formation. The stability referred to simple oxides decreases with the silica content.
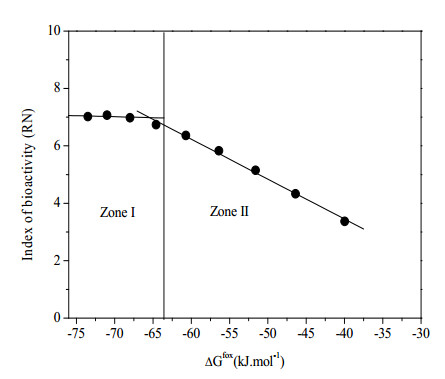
Figure 5 shows the variation of the index RN as a function of the free enthalpy of formation of the glass at 25 ℃. The first observation that should be made is that the shape of the curve can be schematically broken down into two areas characteristic of a change in the phenomenology of the reaction. Zone I, which presents almost a plateau, is very favourable to the formation of bioactive glasses. The hydroxyapatite layer binds intimately to the bone (RN > 5). Zone II, marked by a drastic decrease in the RN index with the increase in the free enthalpy of glass formation, would be favourable to the bioactive inertia. In this case, the glass does not interact with the physiological fluid and the chemical bond between the implant and the host tissue is virtually reduced or even inhibited.
3.2. Discussion
The amorphous state of the samples of all glasses of the molar formula 20.15[(2.038 + x)SiO2–(1.457 − x)Na2O]–2.6P2O5–25.73CaO–1.22MgO was checked by X-ray diffraction. On all diffractograms shown in Figure 1, no diffraction lines were observed. The samples are well amorphous [32].
The glass transition temperature (Tg) is a parameter sensitive to changes in the organization of the vitreous network, depending on the coating density of the covalent bonds, the number and the length of the bonds between cations and the oxygen atoms. In doped bioactive glasses and in glasses in general, the structure correlates with the thermal stability of the glass network [6]. A very dense structure leads to thermally stable glasses, while a slightly packed structure leads to unstable glasses. It is suggested that magnesium inhibits bioactive properties due to the low reactivity of the crystalline state and increased resistance to the ion exchange reaction [33]. Crystallinity is extremely important for the biological activity of the glass structure. Tg is also essential for bioactive glass engineering to ensure the sintering of glasses and is extremely beneficial for the design of bioactive glass for biological implants [34]. Indeed, in the present study, the glass transition temperature (Tg) increases with the addition of the content of 1.22% molar of MgO content and when the ratio x = [SiO2]/([SiO2] + [Na2O]) increases i.e. when the glass evolves from a peralkaline to parsley character is noticed (Figure 2). This increase in Tg is due to the decrease in the number of non-bridging oxygen atoms (NBO) formed in the vitreous network (increase in the degree of polymerization of the network) [35]. This result is in agreement with that of Brink et al [34] and Watts et al. [36]. The presence of MgO could be attributed to the effect of MgO4 tetrahedral groupings which cause a disturbance of the local symmetry of the structure which increases the coherence of the glass structure leading in a compact structure [37].
Moreover, in vitreous systems containing silica in the form of [SiO4]– species, increasing the SiO2 content in the glass will lead to a decrease in the amount of NBO formed in the network (increase in the degree of network polymerization) and thus induce an increase in Tg [38]. By increasing in this study, the value of x, both the quantities of modifying elements (Na2O, CaO, MgO) are decreased and that of SiO2 increased, which leads on the one hand to an increase in the polymerization of the glass network by increasing the Q4 entities and on the other hand the substitution of CaO by MgO leads to a slight decrease in Tg.
MgO therefore has a significant influence on the physicochemical properties. This influence can be positive, a decrease in the crystallization rate, which should enable them to fight more effectively against relaxation at room temperature and against crystallization, during shaping tests in the supercooled liquid range.
Density is a property that appears to be closely related to structural changes in glass [39]. Indeed, the density of the glass is directly related to the density of the elements involved in the system. It can be seen that the density of glasses of the molar formula 20.15[(2.038 + x)SiO2–(1.457 − x)Na2O]–2.6P2O5–25.73CaO–1.22MgO decreases almost linearly with the molar concentration of SiO2 from 2.78 to 2.66 g·cm−3 (Figure 3). These values were predictable in view of the very low MgO content in the processed glasses. It is important to note that MgO would weaken the network by entering the network. Consequently, a decrease in density is observed when the silica level increases. In other words, MgO's role as a network modifier leads to the breaking of Si–O–Si bonds and the formation of new Si–O–Mg bonds in the terminal oxygen silica network.
The standard free enthalpies referred to simple oxides reflect the stability of these compounds with respect to these references. The glass formation reaction is thermodynamically promoted from a mechanical mixture of oxides. The exception of errors, the substitution of 1.22% molar of CaO by MgO does not induce significant variation in the free enthalpy of formation. The stability referred to single oxides decreases with the silica content (Figure 4).
The values taken by RN provide information on the type of bonding of a material in contact with the simulated physiological environment. The slopes relative to these variations (Figure 5) can be associated with the different ways in which the glass clings to bone. Zone I, in which the RN curve as a function ΔGfox is almost constant, delimits the minimum bioactivity in the system under study. In this enthalpy zone of about −75 to −62 kJ·mol−1, the superposition of the silica-rich layer and the hydroxyapatite layer is clearly observable above the glass matrix (in solution). MgO has been shown to increase the thickness of the silica vitreous gel that forms on the surface [40]. Zone I glasses are predisposed to generate a series of physicochemical reactions that can promote the growth of apatite in contact with a biological medium, thus allowing a close chemical interfacial bond with bone. The hydroxyapatite layer binds intimately to the bone. It has been noted that the role of MgO in the formation of a rich CaP layer has been observed to be significant [17]. Zone II, on the other hand, shows decrease in the RN index with the increase in the free enthalpy of formation. It therefore appears in this case that the stable bond between the material and the host tissues is weakened or even inhibited.
This study also shows that the nature and composition of the glass are important for the biological characteristics of the material. They influence the thermodynamic properties of glass. A glass with a low silica content induces an increase in the enthalpy of formation referred to the constituent simple oxides, which is favourable to the simultaneous formation of a CaP layer and a silica-rich layer with a high reaction rate. For glasses with a low SiO2 content, the silica gel layer is formed first, then the CaP layer develops on the surface. This results in a decrease in the enthalpy of formation. For high-silica glasses, the enthalpy of formation becomes lower and lower in absolute value. In this case, the CaP layer hardly forms at all.
4.
Conclusion
This study shows the influence of composition on the thermal properties, thermodynamic stability and bioactivity of glasses of the molar formula 220.15[(2.038 + x)SiO2–(1.457 − x)Na2O]–2.6P2O5–25.73CaO–1.22MgO The results show that, contrary to the glass transition temperature, the stability referred to simple oxides decreases with the silica content. It appears that compositions low in silica have the highest free enthalpies of formation compared to the most negative simple oxides. These compositions also correspond to the products capable of forming hydroxyapatite most rapidly.
Acknowledgements
The authors thank the Environment Training and Research Unit of the Jean Lorougnon Guédé University (Côte d'Ivoire), the Physical Chemistry Laboratory of the Félix Houphouët Boigny University (Côte d'Ivoire) for their support in leading to well this research.
Conflicts of interests
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: