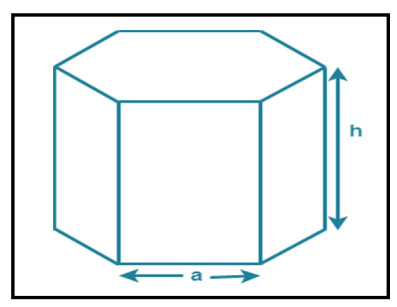
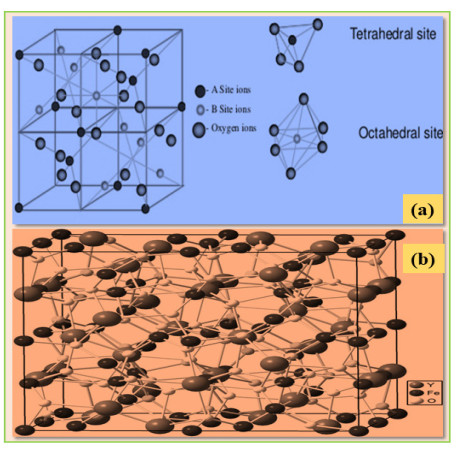
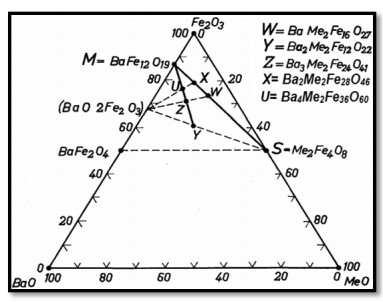
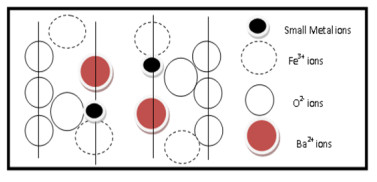
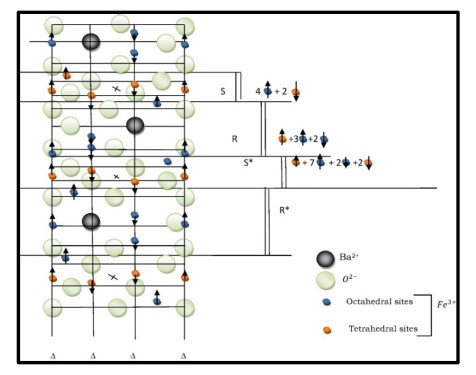
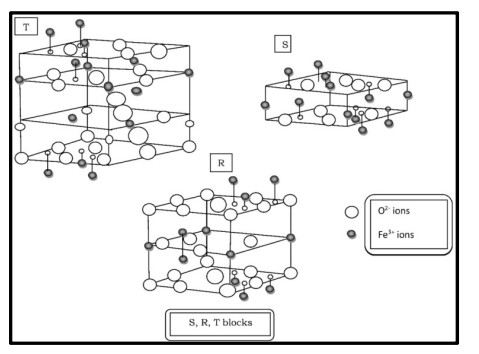
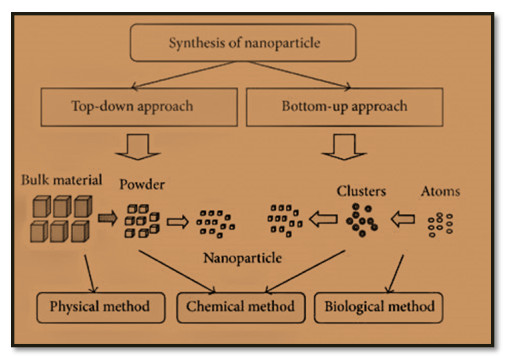
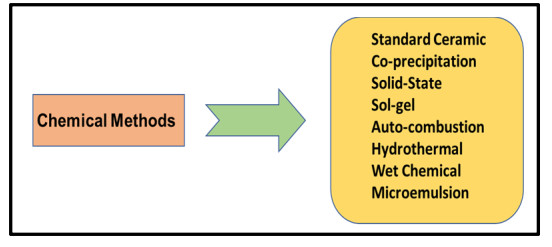
In the present review paper, we have explained the structure of Y-type hexagonal ferrite and various synthesis techniques. This paper also includes structural, electrical, magnetic properties and applications of Y-type hexaferrites and focusses on their use in antenna applications and microwave absorbing characteristic materials. Ferromagnetic nature of hexaferrites cause the induction of magnetisation within the crystal structure, which divide them into two groups: First with easy axis of magnetisation is known as uniaxial hexaferrites and second is known as ferroxplana having easy plane of magnetisation. The excellent magnetic properties of Y-type ferrites make them useful in the devices operating at high frequency range. The persistence of high refractive index upto 1 GHz enables these hexagonal ferrites useful in UHF antenna designs with small dimensions. The doping in Y-type hexaferrites affect all the properties. Current developments in Y-type hexaferrites will be explained in detail in the review of literature related to Y-type hexaferrites for the last 25 years, i.e. from 1994 to 2019 in this review paper.
1.
Introduction
The theme of fractional calculus (FC) has appeared as a broad and interesting research point due to its broad applications in science and engineering. FC is now greatly evolved and embraces a wide scope of interesting findings. To obtain detailed information on applications and recent results about this topic, we refer to [1,2,3,4,5] and the references therein.
Some researchers in the field of FC have realized that innovation for new FDs with many non-singular or singular kernels is very necessary to address the need for more realistic modeling problems in different fields of engineering and science. For instance, we refer to works of Caputo and Fabrizio [6], Losada and Nieto [7] and Atangana-Baleanu [8]. The class of FDs and fractional integrals (FIs) concerning functions is a considerable branch of FC. This class of operators with analytic kernels is a new evolution proposed in [1,9,10]. Every one of these operators is appropriate broader to cover various kinds of FC and catch diversified behaviors in fractional models. Joining the previous ideas yields another, significantly wide, which is a class of function-dependent-kernel fractional derivatives. This covers both of the two preceding aforesaid classes see [11,12].
In another context, the Langevin equations (LEs) were formulated by Paul Langevin in 1908 to describe the development of physical phenomena in fluctuating environments [13]. After that, diverse generalizations of the Langevin equation have been deliberated by many scholars we mention here some works [14,15,16]. Recently, many researchers have investigated sufficient conditions of the qualitative properties of solutions for the nonlinear fractional LEs involving various types of fractional derivatives (FDs) and by using different types of methods such as standard fixed point theorems (FPTs), Leray-Schauder theory, variational methods, etc., e.g. [17,18,19,20,21,22,23,24]. Some recent results on the qualitative properties of solutions for fractional LEs with the generalized Caputo FDs can be found in [25,26,27,28,29,30], e.g., Ahmad et al. [25] established the existence results for a nonlinear LE involving a generalized Liouville-Caputo-type
Seemab et al. [26] investigated the existence and UHR stability results for a nonlinear implicit LE involving a ϑ
-Caputo FD
The Hyers-Ulam (U-H) stability and existence for various types of generalized FDEs are established in the papers [31,32,33,34,35,36,37,38,39,40,41,42,43].
Motivated by the above works and inspired by novel developments in ϑ
-FC, in the reported research, we investigate the existence, uniqueness, and U-H-type stability of the solutions for the nonlinear fractional Langevin differential equation (for short FLDE) described by
where Dε;ϑa+ denote the ϑ-Caputo FD of order ε∈{α1,α2} such that α1∈(2,3], α2∈(1,2], ξ∈(a,b), δ>0, Iα1;ϑa+ is the ϑ-fractional integral of the Riemann-Liouville (RL) type, F:J×R→R is a continuous function, and λ,κ ∈R, ξ∈(a,b).
The considered problem in this work is more general, in other words, when we take certain values of function ϑ, the problem (1.3) is reduced to many problems in the frame of classical fractional operators. Also, the gained results here are novel contributes and an extension of the evolution of FDEs that involving a generalized Caputo operator, especially, the study of stability analysis of Ulam-Hyers type of fractional Langevin equations is a qualitative addition to this work. Besides, analysis of the results was restricted to a minimum of assumptions.
Here is a brief outline of the paper. Section 2 provides the definitions and preliminary results required to prove our main findings. In Section 3, we establish the existence, uniqueness, and stability in the sense of Ulam for the system (1.3). In Section 5, we give some related examples to light the gained results.
2.
Preliminaries and lemmas
We start this part by giving some basic definitions and results required for fractional analysis.
Consider the space of real and continuous functions U=C(J,R) space with the norm
Let ϑ∈C1=C1(J,R) be an increasing differentiable function such that ϑ′(ς)≠0, for all ς∈J.
Now, we start by defining ϑ-fractionals operators as follows:
Definition 2.1. [1] The ϑ-RL fractional integral of order α1>0 for an integrable function ω:J⟶R is given by
Definition 2.2. [1] Let α1∈(n−1,n), n∈N, ω:J→R is an integrable function, and ϑ∈Cn(J,R), the ϑ-RL FD of a function ω of order α1 is given by
where n=[α1]+1 and Dς=ddt.
Definition 2.3. [9] For α1∈(n−1,n), and ω,ϑ∈Cn(J,R), the ϑ-Caputo FD of a function ω of order α1 is given by
where n=[α1]+1 for α1∉N, n=α1 for α1∈N, and ω[n]ϑ(ς)=(Dςϑ′(ς))nω(ς).
From the above definition, we can express ϑ-Caputo FD by formula
Also, the ϑ-Caputo FD of order α1 of ω is defined as
For more details see [9,Theorem 3].
Lemma 2.4. [1] For α1,α2>0, and ω∈C(J,R), we have
Lemma 2.5. [44] Let α1>0.
If ω∈C(J,R), then
and if ω∈Cn−1(J,R), then
for all ς∈J. Moreover, if m∈N be an integer and ω∈Cn+m(J,R) a function. Then, the following holds:
Observe that from Eq (2.3), if ω[k]ϑ(a)=0, for all k=n,n+1,…,n+m−1 we can get the following relation
Lemma 2.6. [1,9] For ς>a,α1≥0, α2>0, we have
● Iα1;ϑa+(ϑ(ς)−ϑ(a))α2−1=Γ(α2)Γ(α2+α1)(ϑ(ς)−ϑ(a))α2+α1−1,
● cDα1;ϑa+(ϑ(ς)−ϑ(a))α2−1=Γ(α2)Γ(α2−α1)(ϑ(ς)−ϑ(a))α2−α1−1,
● cDα1;ϑa+(ϑ(ς)−ϑ(a))k=0,∀k∈{0,…,n−1},n∈N.
Theorem 2.7. (Banach's FPT [45]). Let (R,d) be a nonempty complete metric space with a contraction mapping G:R→R i.e., d(Gz,Gϰ)≤Ld(z,ϰ) for all z,ϰ∈R, where L∈(0,1) is a constant. Then G possesses a unique fixed point.
Theorem 2.8. (Kransnoselskii's FPT [46]). Let E be a Banach space. Let S is a nonempty convex, closed and bounded subset of E and let A1,A2 be mapping from S to E such that:
(i) A1z+A2ϰ∈S whenever z,ϰ∈S
(ii) A1 is continuous and compact;
(iii) A2 is a contraction.
Then there exists z∈S such that z=A1z+A2z.
3.
Main results
This portion interests in the existence, uniqueness, and Ulam stability of solutions to the suggested problem (1.3).
The next auxiliary lemma, which attentions the linear term of a problem (1.3), plays a central role in the afterward findings.
Lemma 3.1. Let α1∈(2,3], α2∈(1,2]. Then the linear BVP
has a unique solution defined by
where
and
with
Proof. Applying the RL operator Iα2;ϑa+ to (3.1) it follows from Lemma 2.5 that
Again, we apply the RL operator Iα1;ϑa+ and use the results of Lemma 2.5 to get
where c0,c1,c2,c3,c4∈R. By utilizing the boundary conditions in (3.1) and (3.7), we obtain c2=0,c3=0,c4=0.
Hence,
Now, by using the conditions Dα1;ϑa+z(a)=Iδ;ϑa+z(γ) and Dα1;ϑa+z(b)+κz(b)=0, we get
Substituting c0 and c1 in (3.8), we finish with (3.2).
The reverse direction can be shown easily with the help of results in Lemmas 2.5 and 2.6, i.e. Eq (3.2) solves problem (3.1). This ends the proof.
Now, we shall need to the following lemma:
Lemma 3.2. The functions μ and ν are continuous functions on J and satisfy the following properties:
(1) μ∗=max0≤ς≤b|μ(ς)|,
(2) ν∗=max0<ς<b|ν(ς)|,
where μ and ν are defined by Lemma 3.1.
Here, we give the following hypotheses:
(H1) The function F:J×R→R is continuous.
(H2) There exists a constant L>0 such that
(H3) There exist positive functions h(ς)∈C(J,R+) with bounds ‖h‖ such that
For simplicity, we denote
As a result of Lemma 3.1, we have the subsequent lemma:
Lemma 3.3. Suppose that F:J×R→R is continuous. A function z(ς) solves (1.3) if and only if it is a fixed-point of the operator G:U→U defined by
Now, we are willing to give our first result which based on Theorem 2.7.
Theorem 3.4. Suppose that (H1) and (H2) hold. If Δ<1, where Δ is given by (3.11), then there exists a unique solution for (1.3) on the interval J.
Proof. Thanks to Lemma 3.1, we consider the operator G:U→U defined by (3.13). Thus, G is well defined as F is a continuous. Then the fixed point of G coincides with the solution of FLDE (1.3). Next, the Theorem 2.7 will be used to prove that G has a fixed point. For this end, we show that G is a contraction.
Let BR={z∈U:‖z‖≤R}, where R>MΛ11−LΛ1−Λ2. Since
we obtain
which implies that ‖Gz‖≤R, i.e.,
Now, let z,ϰ∈U. Then, for every ς∈J, using (H2), we can get
Also note that
Using the above arguments, we get
As Δ<1, we derive that G is a contraction. Hence, by Theorem 2.7, G has a unique fixed point which is a unique solution of FLDE (1.3). This ends the proof.
Now, we apply the Theorem 2.8 to obtain the existence result.
Theorem 3.5. Let us assume (H1)–(H3) hold. Then FLDE (1.3) has at least one solution on J if Λ3<1, where it is supposed that
Proof. By the assumption (H3), we can fix
where Bρ={z∈U:‖z‖≤ρ}. Let us split the operator G:U→U defined by (3.13) as G=G1+G2, where G1 and G2 are given by
and
The proof will be split into numerous steps:
Step 1: G1(z)+G2(z)∈Bρ.
Hence
which shows that G1z+G2z1∈Bρ.
Step 2: G2 is a contraction map on Bρ.
Due to the contractility of G as in Theorem 3.4, then G2 is a contraction map too.
Step 3: G1 is completely continuous on Bρ.
From the continuity of F(⋅,z(⋅)), it follows that G1 is continuous.
Since
we get ‖G1z‖≤N which emphasize that G1 uniformly bounded on Bρ.
Finally, we prove the compactness of G1.
For z∈Bρ and ς∈J, we can estimate the operator derivative as follows:
where we used the fact
Hence, for each ς1,ς2∈J with a<ς1<ς2<b and for z∈Bρ, we get
which as (ς2−ς1) tends to zero independent of z. So, G1 is equicontinuous. In light of the foregoing arguments along with Arzela–Ascoli theorem, we derive that G1 is compact on Bρ. Thus, the hypotheses of Theorem 2.8 holds, so there exists at least one solution of (1.3) on J.
4.
Ulam-Hyers stability analysis for the ϑ-Caputo FLDE (1.3)
In the current section, we are interested in studying Ulam-Hyers (U-H) and the generalized Ulam-Hyers stability types of the problem (1.3).
Let ε>0. We consider the next inequality:
Definition 4.1. FLDE (1.3) is stable in the frame of U-H type if there exists cF∈R+ such that for every ε>0 and for each solution ˜z∈U of the inequality (4.1) there exists a solution z∈U of (1.3) with
Definition 4.2. FLDE (1.3) has the generalized U-H stability if there exists CF: C(R+,R+) along with CF(0)=0 such that for every ε>0 and for each solution ˜z∈U of the inequality (4.1), a solution z∈C(J,R) of (1.3) exists uniquely for which
Remark 4.3. A function ˜z∈U is a solution of the inequality (4.1) if and only if there exists a function ϱ∈U (which depends on solution ˜z) such that
1.|ϱ(ς)|≤ε,ς∈J.
2.Dα2;ϑa+(Da,ϑa+−λ)˜z(ς)=F(ς,˜z(ς))+ϱ(ς),ς∈J.
Theorem 4.4. Let Δ<1, (H1) and (H2) hold. Then the FLDE (1.3) is U-H stable on J and consequently generalized U-H stable.
Proof. For ε>0 and ˜z∈C(J,R) be a function which fulfills the inequality (4.1). Let z∈U the unique solution of
By Lemma 3.1, we have
Since we have assumed that ˜z is a solution of (4.1), hence by Remark 4.3
Again by Lemma 3.1, we have
On the other hand, for any ς∈J
Using part (i) of Remark 4.3 and (H2), we get
where Δ is defined by (3.11). In consequence, it follows that
If we let cF=((ϑ(b)−ϑ(a))α1+α2Γ(α1+α2+1)[ν∗(κ−λ)+1](1−Δ)+ν∗(1−Δ)(ϑ(b)−ϑ(a))α2Γ(α2+1)), then, the U-H stability condition is satisfied. More generally, for CF(ε)=((ϑ(b)−ϑ(a))α1+α2Γ(α1+α2+1)[ν∗|κ−λ|+1](1−Δ)+ν∗(1−Δ)(ϑ(b)−ϑ(a))α2Γ(α2+1))ε; CF(0)=0 the generalized U-H stability condition is also fulfilled.
5.
Examples
This section is intended to illustrate the reported results with relevant examples.
Example 5.1. We formulate the system of FLDE in the frame of Caputo type:
In this case we take
Obviously, the hypothesis (H1) of the Theorem 3.4 is fulfilled. On the opposite hand, for each ς∈[0,1],z,ϰ∈R we have
Hence, (H2) holds with L=0.1. Thus, we find that Δ=0.7635<1. Since all the assumptions in Theorem 3.4 hold, the FLDE (5.1) has a unique solution on [0,1]. Moreover, Theorem 4.4 ensures that the FLDE (1.3) is U-H stable and generalized U-H stable.
Example 5.2. We formulate the system of FLDE in the frame of Hadamard type:
Here
Obviously, the assumption (H1) of the Theorem 3.4 holds. On the other hand, for any ς∈[1,e],z,ϰ∈R we get
Consequently, (H2) holds with L=0.1. Besides, by computation directly we find that Δ=0.8731<1.
To illustrate Theorem 3.5, it is clear that the function f satisfies (H1) and (H3) with ‖h‖=0.1. In addition, Λ3≈0.7823<1. It follows from theorem 3.5 that the FLDE (5.2) has a unique solution on [1,e].
Example 5.3. We formulate the system of FLDE in the frame of ϑ-Caputo type:
Take
For any ς∈[0,1],z,ϰ∈R we obtain
Hence, (H2) holds with L=0.125. Moreover, by computation directly we find that Δ=0.7133<1. It follows from Theorem 3.4 that FLDE (5.4) has a unique solution on [0,1].
To illustrate Theorem 3.5, it is clear that the function F(ς,z) given by (5.5) satisfies the hypotheses (H1)–(H3) with ‖h‖=0.125. and Λ3≈0.3247<1. It follows from Theorem 3.5 that the FLDE (5.2) has a unique solution on [0,1].
6.
Conclusions
In this reported article, we have considered a class of nonlinear Langevin equations involving two different fractional orders in the frame of Caputo function-dependent-kernel fractional derivatives with antiperiodic boundary conditions. The existence and uniqueness results are established for the suggested problem. Our perspective is based on properties of ϑ-Caputo's derivatives and applying of Krasnoselskii's and Banach's fixed point theorems. Moreover, we discuss the Ulam-Hyers stability criteria for the at-hand problem. Some related examples illustrating the effectiveness of the theoretical results are presented. The results obtained are recent and provide extensions to some known results in the literature. Furthermore, they cover many fractional Langevin equations that contain classical fractional operators.
Acknowledgments
This research was funded by the Deanship of Scientific Research at Princess Nourah bint Abdulrahman University, Saudi Arabia through the Fast-track Research Funding Program.
Conflict of interest
The authors declare that there is no conflict of interests regarding the publication of this paper.














 DownLoad:
DownLoad: