|
[1]
|
Pigeon M, Pleau R (1995) Durability of Concrete in Cold climates, 1st Ed., London: CRC Press.
|
|
[2]
|
Power TC (1945) A working hypothesis for further studies of frost resistance of concrete. ACI Jour 41: 245-272.
|
|
[3]
|
Pigeon M, Marchand J, Pleau R (1996) Frost resistant concrete. Constr Build Mater 10: 339-348.
|
|
[4]
|
Hobbs PV (1974) Ice Physics, London: Oxford University Press.
|
|
[5]
|
Powers TC (1955) Basic considerations pertaining to freezing-and-thawing tests. ASTM Proceedings 55: 1132-1155.
|
|
[6]
|
Powers TC, Willis TF (1950) The air requirement of frost resistant concrete. Highw Res Board Proc 29: 184-211.
|
|
[7]
|
Litvan GG (1973) Frost action in cement paste. Mater Constr 6: 293-298.
|
|
[8]
|
Mascarenhas WJ, Akay HU, Pikal MJ (1997) A computational model for finite element analysis of the freeze-drying process. Comput Methods Appl Mech Engrg 148: 105-124.
|
|
[9]
|
Schulson EM (1998) Ice damage to concrete. USA-CRREL Special Report 98-6.
|
|
[10]
|
Penttala V (1999) Strains and pressures induced by freezing mortars exposed in sodium chloride solution. Concr Sci Eng 1: 2-14.
|
|
[11]
|
Powers TC, Helmuth RA (1953) Theory of volume changes in hardened portland-cement paste during freezing. Highw Res Board Proc 32: 285-297.
|
|
[12]
|
Léger P, Cote M, Tinawi R (1995) Thermal protection of concrete dams subjected to freeze-thaw cycles. Can J Civ Eng 22: 588-602.
|
|
[13]
|
Huon V, Cousin B, Maisonneuve O (2001) Mise en évidence et quantification des couplages thermomécaniques réversibles et irréversibles dans les bétons sains et endommagés par des cycles gel-dégel. Comptes Rendus de l'Académie des Sciences-Series ⅡB-Mechanics 329: 331-335. Available from: https://www.sciencedirect.com/science/article/pii/S1620774201013411.
|
|
[14]
|
Verbeck GJ, Landgren R (1960) Influence of physical characteristics of aggregates on frost resistance of concrete. Proceedings of ASTM International 60: 1063-1079.
|
|
[15]
|
Casbonne-Renaud F (1998) Comportement aux cycles gel-dégel des bétons de granulats calcaires [PhD's thesis]. Institut National Polytechnique de Lorraine, France. Available from: https://hal.univ-lorraine.fr/tel-01750749.
|
|
[16]
|
Bager DH, Sellevold EJ (1986) Ice formation in hardened cement paste, part I-room temperature cured pastes with variable moisture contents. Cem Concr Res 16: 709-720.
|
|
[17]
|
Bager DH, Sellevold EJ (1986) Ice formation in hardened cement paste, Part Ⅱ-drying and resaturation on room temperature cured pastes. Cem Concr Res 16: 835-844.
|
|
[18]
|
Fen-Chong T, Fabbri A (2005) Freezing and thawing porous media: experimental study with a dielectric capacitive method. C R Mec 333: 425-430.
|
|
[19]
|
Kaufmann J (1999) Experimental identification of damage mechanisms in cementitious porous materials on phase transition of pore solution under frost deicing salt attack [PhD's thesis]. Ecole polytechnique fédérale de Lausanne EPFL, Switzerland.
|
|
[20]
|
Perron S, Beaudoin JJ (2002) Freezing of water in portland cement paste-an ac impedance spectroscopy study. Cem Concr Compos 24: 467-475.
|
|
[21]
|
Setzer MJ, Liebrecht A (2002) Frost dilatation and pore system of hardened cement paste under different storage conditions, In: Setzer MZ, Auberg R, Keck H-J, 2nd Rilem International Workshop on Frost Resistance of Concrete, Cachan: RILEM Publications, 169-178.
|
|
[22]
|
Geiker MR, Laugesen P (2001) On the effect of laboratory conditioning and freeze/thaw exposure on moisture profiles in HPC. Cem Concr Res 31: 1831-1836.
|
|
[23]
|
Kruschwitz J, Bluhm J (2005) Modeling of ice formation in porous solids with regard to the description of frost damage. Comput Mater Sci 32: 407-417.
|
|
[24]
|
Hain M, Wriggers P (2008) Computational homogenization of micro-structural damage due to frost in hardened cement paste. Finite Elem Anal Des 44: 233-244.
|
|
[25]
|
Wardeh G, Perrin B (2008) Numerical modelling of the behaviour of consolidated porous media exposed to frost action. Constr Build Mater 22: 600-608.
|
|
[26]
|
Zuber B, Marchand J (2000) Modeling the deterioration of hydrated cement systems exposed to frost action-Part 1: Description of the mathematical model. Cem Concr Res 30: 1929-1939.
|
|
[27]
|
Liu Z, Yu X (2011) Coupled thermo-hydro-mechanical model for porous materials under frost action: theory and implementation. Acta Geotechnica 6: 51-65.
|
|
[28]
|
Coussy O, Monteiro PJM (2008) Poroelastic model for concrete exposed to freezing temperatures. Cem Concr Res 38: 40-48.
|
|
[29]
|
Matala S (1995) Effects of carbonation on the pore structure of granulated blast furnace slag concrete [PhD's thesis]. Helsinki University of Technology, Finland.
|
|
[30]
|
Rahman S, Grasley Z (2014) A poromechanical model of freezing concrete to elucidate damage mechanisms associated with substandard aggregates. Cem Concr Res 55: 88-101.
|
|
[31]
|
Liu L, Ye G, Schlangen E, et al. (2011) Modeling of the internal damage of saturated cement paste due to ice crystallization pressure during freezing. Cem Concr Res 33: 562-571.
|
|
[32]
|
Ng K, Dai Q (2014) Numerical investigation of internal frost damage of digital cement paste samples with cohesive zone modeling and SEM microstructure characterization. Constr Build Mater 50: 266-275.
|
|
[33]
|
Zeng Q, Fen-Chong T, Dangla P, et al. (2011) A study of freezing behavior of cementitious materials by poromechanical approach. Int J Solids Struct 48: 3267-3273.
|
|
[34]
|
Koniorczyk M, Gawin D, Schrefler BA (2015) Modeling evolution of frost damage in fully saturated porous materials exposed to variable hygro-thermal conditions. Comput Methods Appl Mech Engrg 297: 38-61.
|
|
[35]
|
Li B, Mao J, Nawa T, et al. (2017) Mesoscopic damage model of concrete subjected to freeze-thaw cycles using mercury intrusion porosimetry and differential scanning calorimetry (MIPDSC). Constr Build Mater 147: 79-90.
|
|
[36]
|
Gong F, Sicat E, Zhang D, et al. (2015) Stress analysis for concrete materials under multiple freeze-thaw cycles. J Adv Concr Technol 13: 124-134.
|
|
[37]
|
Hasan M, Okuyama H, Sato Y, et al. (2004) Stress-strain model of concrete damaged by freezing and thawing cycles. J Adv Concr Technol 2: 89-99.
|
|
[38]
|
Piltner R, Monteiro PJM (2000) Stress analysis of expansive reactions in concrete. Cem Concr Res 30: 843-848.
|
|
[39]
|
Fagerlund G (2004) A Service Life Model for Internal Frost Damage in Concrete. Lund: Lund University, 3119.
|
|
[40]
|
Hanjari KZ, Utgenannt P, Lundgren K (2011) Experimental study of the material and bond properties of frost-damaged concrete. Cem Concr Res 41: 244-254.
|
|
[41]
|
Jin S, Zhang J, Huang B (2013) Fractal analysis of effect of air void on freeze-thaw resistance of concrete. Constr Build Mater 47: 126-130.
|
|
[42]
|
Karakoç MB, Demirboğa R, Türkmen İ, et al. (2011) Modeling with ANN and effect of pumice aggregate and air entrainment on the freeze-thaw durabilities of HSC. Constr Build Mater 25: 4241-4249.
|
|
[43]
|
Štemberk P, da Silva WRL, Sýkorová J, et al. (2013) Fuzzy modeling of combined effect of winter road maintenance and cyclic loading on concrete slab bridge. Adv Eng Softw 62: 97-108.
|
|
[44]
|
Kim S, Gopalakrishnan K, Ceylan H (2009) Neural networks application in pavement infrastructure materials. Intel Soft Comp in Infra Sys Eng 259: 47-66.
|
|
[45]
|
Duan A, Tian Y, Dai JG, et al. (2014) A stochastic damage model for evaluating the internal deterioration of concrete due to freeze-thaw action. Mater Struct 47: 1025-1039.
|
|
[46]
|
Chen F, Qiao P (2015) Probabilistic damage modeling and service-life prediction of concrete under freeze-thaw action. Mater Struct 48: 2697-2711.
|










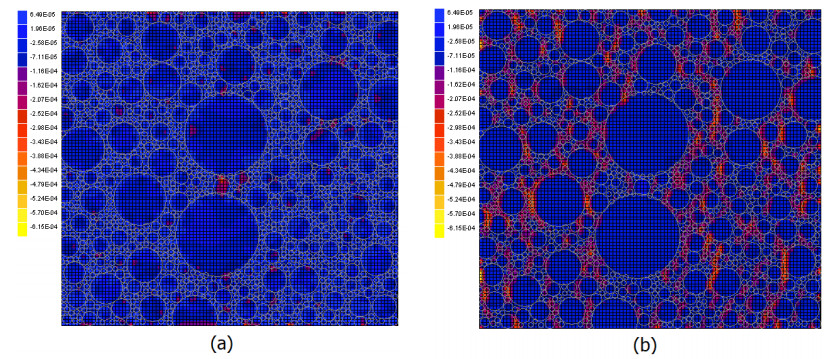
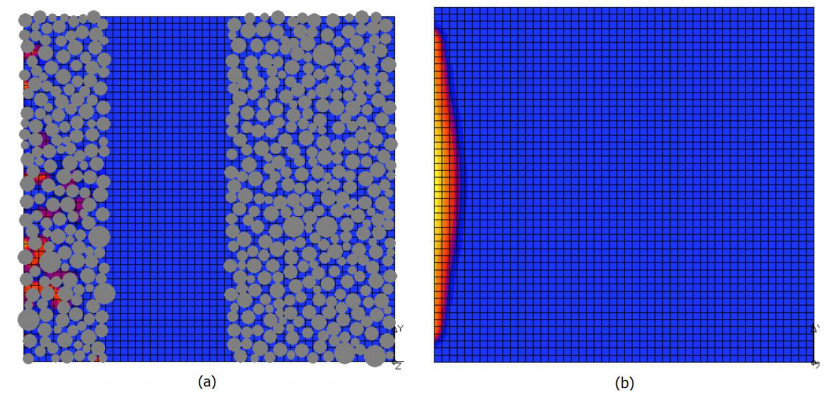


 DownLoad:
DownLoad: