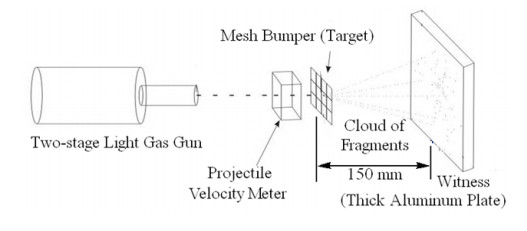
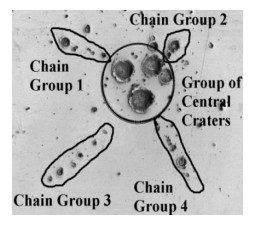
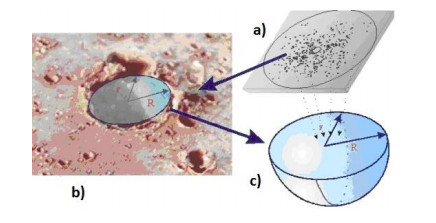
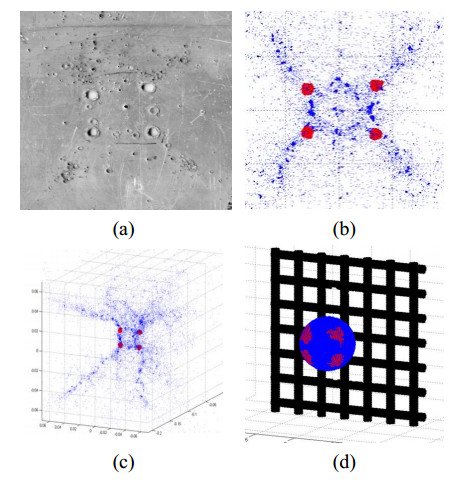
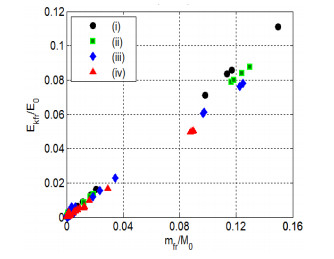
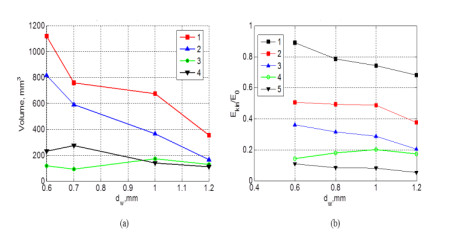
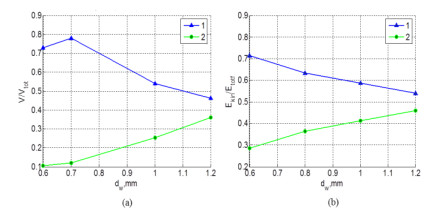
Numerical simulations of experiments (Shumikhin et al., 2014) on the fragmentation of aluminum spheres with diameter of 6.35 mm on single steel-mesh bumpers of different specific mass are carried out in the present work. Specific mass of the mesh bumpers in these experiments was varied by changing the diameter of the wire from which was woven the mesh. The spatial distribution of fragments, their mass and kinetic energy (KE) are determined. The results of the numerical simulations are in good agreement with the experimental data showing that the cloud of fragments composes of two morphologically distinct groups of fragments, which differ greatly in mass: the central group, consisting mainly of four large fragments, and four groups of linearly-distributed chains of smaller fragments. The numerical simulations in agreement with the experiments show that KE of the central group of fragments decreases relative to the total KE of the fragments cloud with increasing the specific mass of the mesh, while the relative KE of other smaller fragments increases.
1.
Introduction
Through their mRNAs, protein expression products, and other components, DNA segments in a cell interact with each other passively, forming dynamic genetic regulatory networks (GRNs) that work as a sophisticated dynamic system to govern biological processes, where the systems of regulatory linkages between DNA, RNA, and proteins comprise GRNs. Modeling genetic networks with dynamical system models, which are a useful tool for analyzing gene regulation mechanisms in living organisms, comes naturally. To examine genetic regulatory developments in life forms, the mathematical models of GRNs comprise formidable tools, which can be approximately separated into two categories, including discrete models [1,2,6,16,22] and continuous models [4,5,9,10,12]. The components in continuous models characterize the concentrations of mRNAs and proteins as continuous data, allowing for a more complete interpretation of GRNs' nonlinear dynamical behavior.
A differential equation is often used to describe a continuous model. Thus, erroneous estimates could result from theoretical models that fail to consider delays. Time delays frequently occur in various applications, and it is widely acknowledged that they can significantly impact system performance, leading to degradation and instability. This realization has sparked significant research interest in the field of stability analysis for systems with time delays over recent years, such as differential equations [35], neural networks [11,13,24], bidirectional associative memory fuzzy neural networks [36], fuzzy competitive neural networks [37], and neutral-type neural networks [14,25,27]. More accurate descriptions of GRNs are possible using differential equation models with delayed states, also called delayed GRNs, which offer a better display of the nature of life. To indicate the time needed for transcription, translation, phosphorylation, protein degradation, translocation, and posttranslational modification, time delays are often established in cellular models. Particularly for eukaryotes, delays may affect the firmness and dynamics of the whole system considerably. While there are limited quantitative assessments of the delays, developments in quantifying RNA splicing delays should be taken into account. Because the time delays in biochemical reactions align with or surpass other important time scales defining the cellular system, and the feedback loops related to these delays are robust, and these delays become pivotal for explaining transient processes. This suggests that in cases where delay durations are substantial, both analytical and numerical modeling need to consider the impact of time delays, which has led to the study of various stability forms of the system, for example, in [5,10,31,33,38]. A common type of time delay, referred to as leakage delay (i.e., the delay associated with leaking or forgetting items) might arise within the negative feedback components of networks and has a substantial impact on the dynamics, potentially resulting in instability or suboptimal performance in GRNs. In fact, various beneficial algorithms and computational tools have been devised to address this phenomenon, with numerous notable findings published in previous literature [7,17,28,29,32].
When a built system has been implemented in the field, there is typically some unpredictability; be it a windy sky or a rough road, we may encounter uncertainty in the operational area. Uncertainty can also be found in the system's defining variables, such as torque constants and physical dimensions. As a consequence of the dynamic nature of a system under investigation, one of the most critical attributes of that system is stability. In general, when a system is chaotic, or simply lacks stability, it is not especially useful. It is preferable to work with systems that are stable or offer periodic behavior, with the caveat that chaotic behavior can be readily understood in some systems, and there can also sometimes be good reasons for people to actively seek chaos in a system for various applications. Therefore, we found research that demonstrated various stability criteria such as asymptotic stability analysis, exponential stability analysis [3,34], H infinity performance [25], finite-time stability (FTS) analysis [15,23], and so on. The concept of FTS differs from classical stability in two significant ways. First, it addresses systems whose functionality is limited to a fixed finite time interval. Second, FTS necessitates predefined constraints on system variables. This is particularly relevant for systems that are recognized to operate exclusively within a finite time span and in cases where practical considerations dictate that system variables must adhere to specific bounds[8].
After thorough investigation, FTS for GRNs with delays has been studied in references [21,24,26], as well as [39]. For example, the researchers in reference [21] explored the FTS for GRNs that have demonstrated impulsive effects, employing the Lyapunov function method. In [24], the topic of FTS for switched GRNs with time-varying delays was examined through the use of Wirtinger's integral inequality. Furthermore, the effect of leakage delay has been studied in various works, including references [14,18,27]. For instance, in [14], the researchers proposed sufficient conditions that guarantee the asymptotic stability of GRNs, which have a neutral delay and are affected by leakage delay through the application of the Lyapunov functional. Additionally, in reference [18], the authors focused on global asymptotic stability analysis aimed at stabilizing switched stochastic GRNs that exhibit both leakage and impulsive effects. This stabilization has depended on both time-varying delay and distributed time-varying delay terms, utilizing contemporary Lyapunov-Krasovskii functional and integral inequality techniques. However, it has been determined that there are no studies focusing on analyzing the FTS while considering the effect of leakage delay for GRNs. The successful completion of such research could contribute to a deeper comprehension of leakage delay and potentially offer opportunities to improve the stability criteria of GRNs. This research concerns the effect of the leakage delays on FTS criteria for GRNs with interval time-varying delays. The criteria aim to consider the effect of leakage delays. Consequently, we employ the construction of a Lyapunov-Krasovskii (LK) function and estimate various integral inequalities as well as reciprocally convex techniques to establish them. These improvements enable us to specify the stability criteria concerning the effect of leakage delays on FTS. This refinement simplifies the representation of stability criteria in the form of linear matrix inequalities (LMIs). Ultimately, we offer a numerical example to demonstrate the effect of leakage delays and emphasize the significance of our theoretical findings.
The principal contributions of this research can be encapsulated as follows:
(i) Targeted focus on leakage delays: We specifically address the impact of leakage delays on the finite-time stability of GRNs, filling a gap in existing research and providing new data on the stability dynamics influenced by these delays.
(ii) Consideration of variable delay limits: We take into account the lower limits on delays, which can vary between positive values and zero, and accommodate the derivatives of delays ranging from negative to positive. This comprehensive approach allows for the one that offers a better representation of the nature of organism and modeling of real biological scenarios.
(iii) Empirical validation: A numerical example is provided to demonstrate the implications of leakage delays on the stability criteria. This example underscores the impact of leaked delays on GNRs.
(iv) Contribution to broader fields: The insights gained from this study have the potential to advance multiple fields, including systems biology, biotechnology, and medicine.
By addressing these aspects, this research significantly enhances our understanding of the interplay between leakage delays and finite-time stability in genetic regulatory networks, paving the way for future studies and applications in various scientific and medical domains.
2.
Problem formulation and preliminaries
The first step is to introduce the following symbols or notations: Rn and Rn×r represent the n-dimensional Euclidean space and the set of all n×r real matrices, respectively; G>0 (G≥0) signifies that the symmetric matrix G is positive (semi-positive) definite; G<0 (G≤0) signifies that the symmetric matrix G is negative (semi-negative) definite; The quadratic from ‖φ(t)‖2N is defined as: ‖φ(t)‖2N=φT(t)Nφ(t) or ‖φ(t)‖N=√φT(t)Nφ(t) for any state vector φ(t), and N≥0.
In this paper, we suggest the GRNs with interval time-varying delays and leakage delays in the form
where mi(⋅) and pi(⋅) are the concentrations of mRNA and protein of the ith node at time t, respectively. ai>0 and ci>0 denotes the degradation or dilution rates of mRNAs and proteins, retrospectively. di represents the translation. wij is defined as follows:
r(⋅) and h(⋅) are the feedback regulation and translation delays, respectively, which are retrospectively satisfied by
where ρa>0 and ρc>0 denote the leakage delays. gj(pj(s))=(pj(s)/Bj)Hj/(1+pj/Bj)Hj where Hj is the monotonic function in Hill form, ϵi=∑j∈Ukγij with Uk={j| the jth transcription factor being a repressor of the kth gene, j=1,…,n}, Bj>0 is a constant which the feedback regulation of the protein on the transcription. When we let (m∗,p∗)T be an equilibrium point of (2.1), the equilibrium point can be shifted to the origin by transformation: xi(t)=mi−m∗i,yi(t)=pi−p∗i, and system (2.1) can be rewritten in the vector form
where A=diag(a1,a2,...,an), C=diag(c1,c2,...,cn), W=[wij]n×n, f(y(t))=g(y(t))−p∗ with f(0)=0, ϕ(t),t∈[−max{ρa,hM},0] and ξ(t),t∈[−max{ρc,rM},0] are the initial conditions.
Assumption 1. The regulatory function f(ζ(t))=[f1(ζ1(t)),f2(ζ2(t)),...,fn(ζn(t))]T∈Rn is assumed to satisfy the following condition
where ℘−i,℘+i are real constants, and let ð−=diag(℘−1,℘−2,…,℘−n), ð+=diag(℘+1,℘+2,…,℘+n) and ℘i=diag(max{|℘−j|,|℘+j|}), ð=diag(℘1,℘2,…,℘n).
Then, the definition presented along with the several lemmas serves as a methodologies utilized to prove our primary outcomes.
Definition 2.1. (see [21]) Let G≥0 be a matrix, if
where ‖Φ(t)‖G=sup−max{ρa,hM}≤t≤0{‖ϕ(t)‖G,‖˙ϕ(t)‖G} and ‖Ψ(t)‖G=sup−max{ρc,rM}≤t≤0{‖ξ(t)‖G,‖˙ξ(t)‖G}, then the GRNs with interval time-vary delays and leakage delays (2.4) exhibits FTS concerning positive real numbers (c1,c2,T).
Lemma 2.2. Let N∈Rn×n, N=NT>0 and G∈Rn×n,G=GT be any constant matrices. Then
where the expressions "λmin(N−1G)" and "λmax(N−1G)" denote the minimum real part and the maximum real part of the eigenvalues of N−1G respectively.
Lemma 2.3. (Jensen's inequality [28]). Let G∈Rn×n, G=GT>0 be any constant matrix, δM be positive real constant and φ:[−δM,0]→Rn be vector-valued function. Then,
Lemma 2.4 (see [30]). Let G∈Rn×n, G=GT>0 be any constant matrix, δm>0,δM>0 are real constants and φ:[−δM,−δm,]→Rn be vector-valued function. Then,
Lemma 2.5 (see [20]). Let G∈Rn×n, G=GT>0 be any constant matrix, and any continuously differentiable function z:[δm,δM]→Rn. Then,
where
Lemma 2.6. (see [19]). Let κ1,κ2,…,κN:Rn→R have positive values in an open subset D of Rn. Then, the reciprocally convex combination of κi over D satisfies
subject to
Lemma 2.7. (see [11,13]). Suppose Assumption 1 is valid, let diagonal matrices Γi>0,i=1,2. Then
where Ξ1=diag(℘−1℘+1,℘−2℘+2,…,℘−n℘+n) and Ξ2=diag(℘−1+℘+12,℘−2+℘+22,…,℘−n+℘+n2).
3.
Main results
In this section, we present a theorem and a corollary related to GRNs. To begin with, the FTS result is formulated for the GRNs with interval time-varying delays, considering the effect of leakage delays.
Theorem 3.1. Given that Assumption 1 valid. For positive scalars c1,c2,T,α, ρa, ρc, hm, hM, hdm, hdM, rm, rM, rdm and rdM according conditions (2.2)–(2.3), if there exist matrices Pi>0,i=1,2,3, Qi>0,i=1,2,3,4, Ri>0,i=1,2, Si>0,i=1,2,3,4, Ui>0,i=1,2, any diagonal matrices Γi>0,i=1,2, any appropriate dimensional matrices Ei,Ni,i=1,2,3,4, satisfying the following conditions:
Then, the system (2.4) exhibits FTS concerning N>0 and positive real numbers (c1,c2,T), where Θ=∑7i=1Θi is defined as
Proof. First, we employ the Newton-Leibniz formula to modify system (2.4), which is as follows
Second, the LK functional is designed for the system (3.3) :
where
Then, taking ˙Vi(t) along the trajectory of system (3.3) with (2.2) and (2.3), we have
Utilizing the zero equation −˙x(t)−A(x(t)−∫tt−ρa˙x(s)ds)+Wf(y(t−r(t)))=0, we estimate the boundary hdm≤˙h(t)≤hdM, and the exponential function term 1=e0≤eαhm≤eαh(t)≤eαhM, −1=−e0≥−eαhm≥−eαh(t)≤−eαhM. From this, we derive the values of ˙V1(t) as follows.
Using the same method, the zero equation as −˙y(t)−C(y(t)−∫tt−ρc˙y(s)ds)+Dx(t−h(t)))=0 allows us to obtain the derivative of V2(t), which is
The derivative of V3(t) is calculated to obtain
We utilize Lemma 2.5 to estimate the amount, leading to the subsequent inequality.
The derivative of V4(t) is calculated to obtain
To facilitate our analysis, we decompose and examine the inequality in the derivative of V4(t) step by step as follows. In the first part, we use Lemma 2.5 to approximate the value, resulting in the following inequality.
Then, we estimate the values of the second part of the inequality as follows.
By utilizing Lemma 2.5 together with Lemma 2.6, we can approximate the inequality as follows
Estimating the derivatives of V4(t) along with approximating the values, in inequalities (3.6) and (3.7) is a crucial part of this analysis. We obtained consistent equations in this process as follows:
Regarding V5(t), we derived its derivative and applied Lemma 2.4 for estimation. Additionally, when approximating the exponential function where 1=e0≤eαρa, 1=e0≤eαρc, −1=−e0≥−eαρa, −1=−e0≥−eαρc, we obtain the following results
Next, by adopting Eqs (2.6) and (2.7) and let Γi>0,i=1,2 be diagonal matrices, we obtain
Additionally, we utilize the zero equation derived from the Newton-Leibniz equation: x(t)−x(t−h(t))−∫tt−h(t)˙x(s)ds=0. Let Ni,i=1,2,3,4 be appropriate dimensional matrices, resulting in the equation:
It becomes evident that, upon estimating ˙V(t) after recalling (3.1), we receive
where ˙V(t)≤χT(t)Θχ(t)+αV(t), χT(t)=[xT(t),xT(t−hm),xT(t−h(t)),xT(t−hM),˙xT(t),yT(t),yT(t−rm),yT(t−r(t)),yT(t−rM), ˙yT(t),fT(y(t)),fT(y(t−r(t))),∫tt−ρa˙xT(s)ds,∫tt−ρc˙yT(s)ds,1hm∫tt−hmxT(s)ds,1rm∫tt−rmyT(s)ds, 1h(t)−hm∫t−hmt−h(t)xT(s)ds,1hM−h(t)∫t−h(t)t−hMxT(s)ds,1r(t)−rm∫t−rmt−r(t)yT(s)ds,1rM−r(t)∫t−r(t)t−rMyT(s)ds,∫tt−h(t)˙xT(s)ds, 1h2m∫tt−hm∫tθxT(s)dsdθ,1r2m∫tt−rm∫tθyT(s)dsdθ,1(h(t)−hm)2∫t−hmt−h(t)∫t−hmθxT(s)dsdθ,1(hM−h(t))2∫t−h(t)t−hM ×∫t−h(t)θxT(s)dsdθ,1(r(t)−rm)2∫t−rmt−r(t)∫t−rmθyT(s)dsdθ,1(rM−r(t))2∫t−r(t)t−rM∫t−r(t)θyT(s)dsdθ].
By multiplying the inequality (3.11) by e−αt and integrating from 0 to t where t belongs to the interval [0,T], we derive the following result:
where
where ‖Φ(t)‖N=sup−max{ρ1,hM}≤t≤0{‖ϕ(t)‖N,‖˙ϕ(t)‖N} and ‖Ψ(t)‖N=sup−max{ρ2,rM}≤t≤0{‖ξ(t)‖N,‖˙ξ(t)‖N}, λ1=λmax((N−1P1)+β1h(N−1P2)+β2h(N−1P3)+(N−1Q1)+β1r(N−1Q2)+β2r(N−1Q3)+β3r(N−1Q4)(ðTð)+β3h(N−1R1)+β4r(N−1R2)+β3h(N−1S1)+β4r(N−1S2)+β4h(N−1S3)+β5r(N−1S4)+β1ρ(N−1U1)+β2ρ(N−1U2)), and N>0.
In the interim,
where λ2=λmin(N−1P1+N−1Q1). Let c1 be a positive real number where
Combining inequalities (3.11)–(3.13) we acquire:
where c2 be a positive real number. In accordance with Definition 2.1 of stability, finite-time stability with respect to c1,c2,T and N can be found for the GRNs (2.4). The proof is complete. □
When the interval time-varying delays h(t) and r(t) adhere to the conditions (2.2) and (2.3), and ρa=ρc=0, and V5(t)=0, the subsequent Corollary can be applied to assess the FTS of GRNs in the following system form:
as describe in Corollary 3.2.
Corollary 3.2. Given that Assumption 1 valid. For positive scalars c1,c2,T,hm, hM, hdm, hdM, rm, rM, rdm and rdM according conditions (2.2) and (2.3), if there existṁatrices Pi>0,i=1,2,3, Qi>0, i=1,2,3,4, Ri>0, i=1,2, Si>0, i=1,2,3,4, any diagonal matrices Γi>0,i=1,2, any appropriate dimensional matrices Ei,Ni,i=1,2,3,4, satisfying the following conditions:
Then, the system (3.14) exhibits FTS concerning N>0 and positive real numbers (c1,c2,T), where ˜Θ=∑6i=1Θi is defined:
Proof. The Corollary 3.2 can be derived using a similar reasoning as that employed in the proof of Theorem 3.1.
4.
Numerical examples
In this section, we employ a numerical instance to showcase the efficiency of the criteria outlined as follows:
Example 4.1. Consider the GRNs (2.4) and (3.14) with the following parameters:
The gene regulation function is represented by fi(yi)=y2i1+y2i,ð−=diag(0,0,0), and ð+=diag(0.65,0.65,0.65). The time delays h(t) and r(t) are assumed as follows: r(t)=0.5+0.7sin2t, h(t)=1+cos2t. We can derive the parameters as follows: rm=0.7,rM=1.2,rdm=−0.7,rdM=0.7, hm=1,hM=2hdm=−1hdM=1. Furthermore, we demonstrate that the system exhibits FTS by defining the parameters as follows: α=0.01,T=5,c1=0.4,andc2=6.0. It is crucial to emphasize that the Theorem 3.1 becomes feasible by utilizing MATLAB to solve LMIs (3.1) and (3.2), which enables us to attain a viable solution. As a result, the GRNs (2.4) exhibit FTS, with ρa=ρc=0.1 representing the allowable value. From this, we can derive the feasible solutions as follows:
Moreover, we found that system (2.4), under the specified conditions and Theorem 3.1, remains FTS up to T=9.9225(α=0.1).
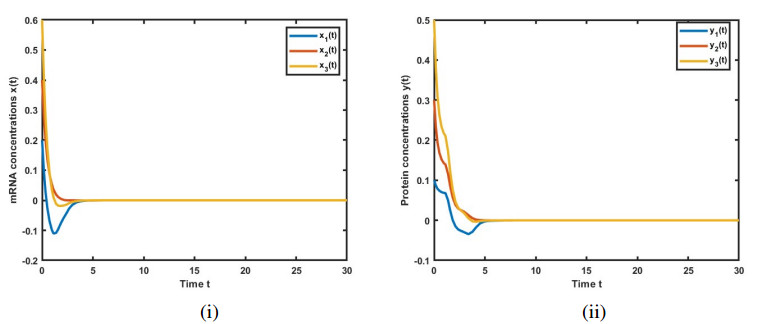
The simulation results are illustrated in Figures 1–6, depicting the trajectories of variables x(t) and y(t) for the GRNs (3.14) and (2.4). These figures showcase the impact of leakage delays on system stability. The initial conditions are set as x(0)=(0.2,0.4,0.6) and y(0)=(0.1,0.3,0.5).
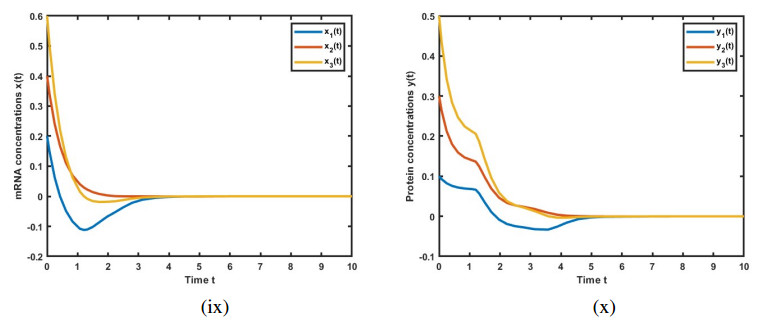
Figure 1 presents the solutions for GRN (3.14) in the absence of leakage delays. We observe that the solution for x(t) approaches 0 as t approaches 4, and the solution for y(t) approaches 0 as t approaches 5. In this case, the system converges to 0.
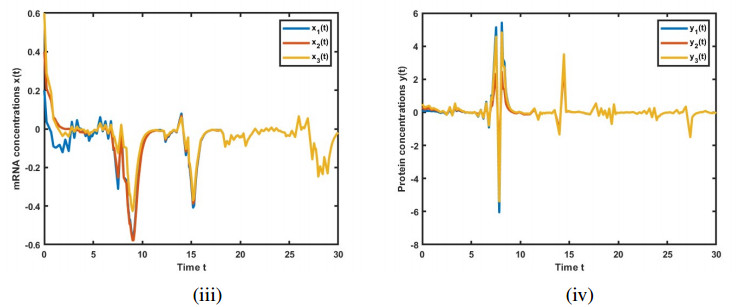
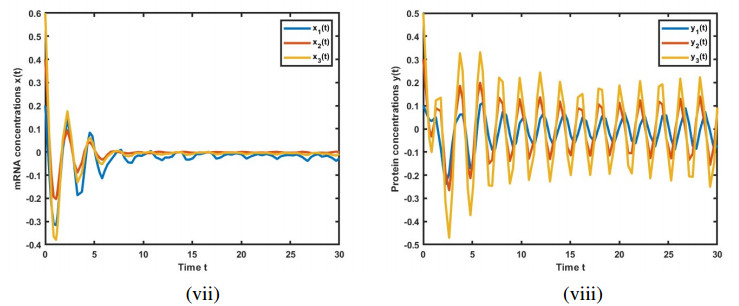
Figures 2–4 present the solutions for GRN (2.4), incorporating leakage delays. These figures clearly illustrate the interference caused by the system's leakage delays, impacting the convergence to the equilibrium point. We found that an increase in the leakage parameter has led to a corresponding rise in the frequency of the oscillations.
Figure 5 demonstrates the solutions of the GRNs (3.14) over the time interval t∈[0,10]. The solution for x(t) approaches 0 as t approaches 4, and the solution for y(t) approaches 0 as t approaches 5. In this case, the system converges to 0. While similar to Figure 1, the solution's behavior is observed over a shorter time interval in this instance.
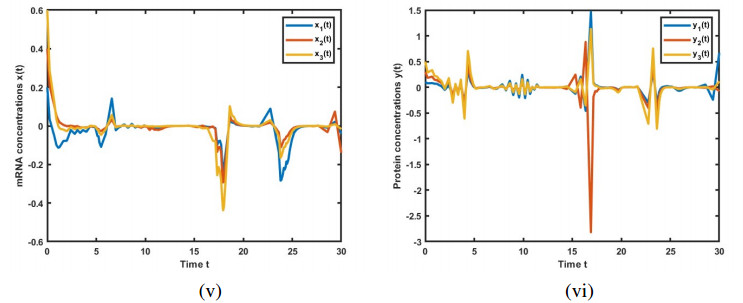
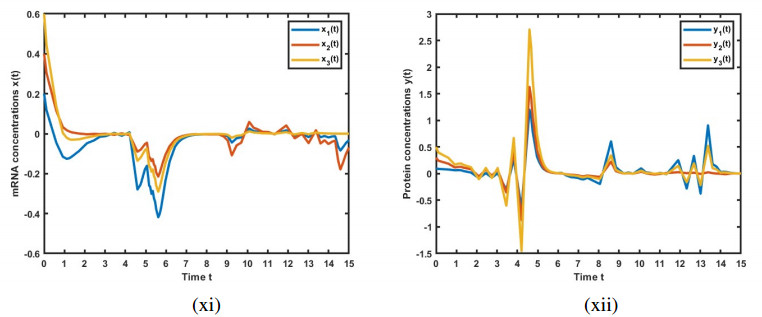
Figure 6 shows the solutions of GRN (2.4) over the time interval t∈[0,15]. Notably, a disturbance in the solution is observed around t=3, where both x(t) and y(t) begin to oscillate. Despite this disturbance, the system remains stable. This scenario shows a similar solution trajectory to Figure 3 but over a shorter time span, which reduces the frequency of oscillations.
This comprehensive analysis of the simulation results provides valuable insights into the influence of leakage delays on the dynamics of GRNs (2.4) and (3.14). The analysis demonstrates the importance of considering such delays in the design and analysis of these systems. The leakage delay has a significant effect on the dynamic behaviors of the model, often leading to instability. It is therefore crucial to study stability while taking into account the impact of leakage delays.
Additionally, we examine the leakage delays effects by substituting the following values: In Case 1, we investigate the value of hM at rm=0.7,rM=1.2,rdm=−0.7,rdM=0.7,hm=1,hdm=−1,hdM=1, α=0.01,T=5, and varying leakage delays (ρa and ρc) as shown in Table 1. In Case 2, we will explore the value of rM at rm=0.7,rdm=−0.7,rdM=0.7,hm=1,hM=2,hdm=−1,hdM=1, α=0.01,T=5, and varying leakage delays as indicated in Table 2.
We observed that as the values of leakage delays ρa and ρc increases, the times delays hM and rM both decrease. Hence, it can be stated that the effects of leakage delays lead to a decrease in the FTS boundary.
5.
Conclusions
In this paper, our focus is on investigating how leakage delays affect FTS in GRNs characterized by interval time-varying delays. To begin, we introduce GRNs that incorporate interval time-varying delays as well as leakage delays. These models consider lower bounds on delays, which may be either positive or zero, and allow for the derivatives of delays to be either positive or negative. Subsequently, we delve into the consequences of leakage delays through the construction of a LK function. We then enhance the criteria for FTS by employing estimates of integral inequalities and a reciprocally convex technique. This refinement enables us to express the new finite-time stability criteria for genetic regulatory networks in the form of LMIs. Finally, we present a numerical example to demonstrate the effect of leakage delays and validate the significance of our theoretical findings.
Author contributions
N.S. and I.K.: Conceptualization; N.S. and I.K.: Methodology; N.S. and I.K.: Software; N.S., K.M., and I.K.: Validation; I.K., N.S., and K.M.: Formal analysis; N.S., K.M., and I.K.: Investigation; N.S. and I.K.: Writing-original draft preparation; N.S., K.M., and I.K.: Writing-review and editing; N.S.and I.K.: Visualization; N.S., K.M., and I.K.: Supervision; N.S.: Project administration; N.S.: Funding acquisition. All authors have read and agreed to the published version of the manuscript.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work is supported by research and innovation funding from the Faculty of Agriculture and Technology, Nakhon Phanom University (Grant AG004/2566), and the Faculty of Engineering, Rajamangala University of Technology Isan Khon Kaen Campus.
Conflict of interest
The authors declare that there are no conflicts of interest regarding the publication of this manuscript









 DownLoad:
DownLoad: