1. Introduction

Piezoelectric materials are used in a broad spectrum of applications at present. Ceramic working elements are used in devices in the majority of cases. Piezoelectric ceramics on the base of lead zirconate-titanate (PZT) find a wide range of practical applications as sensors, electromechanical devices, transformers and converters, and ultrasound sources ^[1,2]. Currently, different kinds of sensors are used under the hardening of worldwide requirements for safe work of devices with moving working parts in industry as well as all kinds of transportation ^[3,4].

Development of new materials is carried out along three main directions:

● improvement of piezoelectric characteristics of PZT-based materials;

● development of materials based on Pb(Mg_1/3Nb_2/3)O₃–PbTiO₃ (PMN–PT) solid solutions and to a lesser extent materials based on Pb(Zn_1/3Nb_2/3)O₃–PbTiO₃ (PZN–PT) solid solutions;

● development of lead-free ceramic materials.

Here is our assessment of achievements in each of these directions. Let us start from PZT-based ceramic materials. As we noted above these are basic materials for different technological applications as of today. Use of these materials continues after more than 40 years, the manufacturing methods are extremely simple, and the materials are quite inexpensive. No one existing materials or materials under development developed material can compete with PZT-based compounds pricewise. One cannot see the availability of such materials in the short term.

During the last decade a great number of publications have appeared (after the monoclinic phases in PZT was discovered) that were "proclaiming hope" for an increase in value of piezoelectric parameters of PZT due to the presence of monoclinic phases. There are so many such publications (for the most part these are theoretical studies) that we simply do not have enough space in this article to discuss them. However, we want to say that attempts to improve parameters of PZT at the expense of monoclinic phases were unsuccessful.

If the maximum achieved value of the piezoelectric coefficient was 570–580 pC/N during the "before monoclinic" period of time then the "monoclinic" developments lifted this value to 580–600 pC/N (or just a bit larger). That's all that was achieved during 18 years.

PMN-PT-based materials have much larger values of piezoelectric parameters then PZT solid solutions but this is only true for single crystals. Ceramics with PMN–PT compositions fall short compared to PZT. Several attempts have been made to improve the piezoelectric parameters of PMN–PT ceramics by textured structures manufacturing. Using more or less simple methods for the creation of textured structures in PMN–PT ceramics did not lead to any advantage in comparison with the values of these parameters in PZT. Creation of textured structures with the help of magnetic fields created by superconducting magnetic systems does allow an increase in piezoelectric parameters of PMN–PT. However, anybody who is familiar with such superconducting systems and with methods of piezoceramics manufacturing understands that all this is good for the case of laboratory research. It is unlikely that such an approach will come about as a technological method for manufacturing ceramics with such parameters in the near future.

Thus, the technology of PMN–PT based ceramic materials manufacturing is much more complicated and expensive; their parameters are inferior to the parameters of PZT-based materials; and one does not even need to compare the prices of niobium oxide with the prices of oxides of zirconium and titanium. We do not compare the PMN–PT single crystals with PZT-based ceramics. Likely the use of single crystals will not substitute ceramic materials in 90% of applications (and maybe even more). We emphasize only one circumstance, namely, that there are fields of practical application of piezoelectric materials in which the substitution for use of the single crystals of PMN–PT and PZN–PT will not be found in the short term. However, this is a subject for other publications.

Now we want discuss the situation in lead-free ceramic materials. Barium titanate (BaTiO₃), potassium niobate (K_0.5Na_0.5)NbO₃, and sodium niobate titanate (Na_0.5Bi_0.5)TiO₃ based solid solutions serve as a basis for such compounds. Again, there are a very large number of publications devoted to each group of these materials. We will not even try to discuss here advantages or disadvantages of each group of these materials. Let us make only one statement. These materials cannot claim to be competitive with PZT-based ceramic materials at the moment. This statement is not disputed in the literature at present. Lead-free materials do not hold promise in terms of parameters compared to PZT (some of them by the working temperature interval, others by the simplicity of the technological process and price).

Speaking about lead-free materials one should take into account the following. In some respect all activities on the introduction of lead-free ceramic materials in technology are a policy. The policy was adopted by the European parliament representatives (who may not be very knowledgeable in technology of materials manufacturing). The main argument for adopting this policy and possible prohibition of lead containing PZT-based materials (that contain chemically "bounded" lead as their base) was the toxicity of lead in the process of use of these compounds. This statement is not quite right scientifically speaking. To carry out a chemical analysis of the composition of the PZT-based ceramics one has to boil its fine power in aqua regia (a mixture of a one volume part of concentrated nitric acid and three volume parts of concentrated hydrochloric acid) for one hour. This shows that PZT-based solid solutions are less active than, for example, different types of stainless steel (containing chromium, nickel, vanadium, and manganese). Namely, stainless steel is the main material for manufacturing of table ware. As for possible problems in utilization of used ceramic materials, it is well known that technological methods of their complete involvement in manufacturing of new materials on all of 100% are developed at present.

Our very short discussion of the situation with lead-free piezoelectric materials shows that there is currently no replacement for the PZT-based solid solutions. It is also confirmed by the fact that the documents allowing use of the PZT-based materials are being issued constantly in addition to the "prohibitive" directives.

The present review is devoted to one important physical mechanism that is not taken into account in the process of research and prospecting works on PZT-based solid solutions at present. This is a coexistence of the ferroelectric (FE) and antiferroelectric (AFE) phases. Based on the phase diagram of the said solid solutions it might seem that the AFE phase does not have anything to do with formation of high piezoelectric characteristics since the region of the AFE ordering and the morphotropic boundary region (where solid solutions do possess high values of piezoelectric parameters) are strongly spaced with respect to the content of PbZrO₃/PbTiO₃. Also the physical mechanisms leading to the formation of high values of piezoelectric characteristics have never been associated with the presence or absence of the AFE phase domains.

The piezoelectric coefficient is determined as:

${d_{i{{\rm \mathsf{ α} }}}} = 2{Q_{jk\alpha }}P_k^s{{\rm \mathsf{ ε} }}_{ij}^T$

(1)

For the case of the polarized piezoceramics Eq 1 is modified as follows:

${d_{33}} = 2Q{P_r}{{{\rm \mathsf{ ε} }}_{{{\rm33}}}}$

(2)

Equation 2 is a simplified form that is usually used in discussions of the properties of ceramic materials and shows the dependence of the longitudinal (along the direction of residual polarization) piezoelectric modulus d₃₃ on the permittivity measured in the same direction. Here Q is the coefficient of electrostriction. All ceramic materials that have a high piezoelectric coefficient have low Curie temperatures, which provide high permittivity.

The values of the dielectric susceptibility at frequencies up to ~10⁹ Hz are determined by the mobility of domain walls. The displacement of domain walls means the change in direction of the polarization vector within distances of such displacements. The direction of the polarization vector is reversed when the displacement of the 180-degree domain walls takes place. This process determines the response of the sample to an external electric field. This response is characterized by the dielectric permittivity (more precisely the susceptibility). Here it has to be noted that the remnant polarization varies slightly at domain wall displacements since the part of the sample within which the displacement of domain walls takes place is negligible. The same applies to the electrostriction coefficient.

Similar change in the polarization vector, and therefore an increase in the electric susceptibility (permittivity) occur when domains of the FE and AFE phases coexist. The electric field increases the stability of the FE state, and an increase of the volume fraction of the FE phase takes place due to the displacement of the interface. For substances with a narrow hysteresis loop, weak fields lead to a significant displacement of these boundaries, and, consequently, such a process can contribute to a significant increase in the dielectric constant.

The trouble is that, as a rule, the FE and AFE phases coexist when the free energies of these phases are equal. And this, in turn, means that the volume fractions of these phases are practically equal, the remnant polarization should be greatly reduced (the remnant polarization in the AFE phase is equal to zero). In addition to this, the AFE domains violate the correlation in the directions of polarization vectors of the FE domains. This leads to a drop in the remnant polarization to almost zero (even after polarization of the samples by the electric field) and to the absence of a piezoelectric response.

A natural conclusion arises that it is necessary to create conditions under which the share of the AFE phase in the sample volume will not exceed 1–2%. In this case and the remnant polarization remains practically the same (large) and the shifts of the FE–AFE domain boundaries will give an additional contribution to the piezoelectric activity of the material.

We want to note that the values of piezoelectric coefficients that are unattainable using other approaches can be achieved if the conditions for the presence of the coexisting domains of the AFE and FE phases are taken into account during the preparation of ceramics.

Within the framework of approach taking into account the phenomenon of the local decomposition of the solid solutions in the vicinity of the boundaries between the rhombohedral and tetragonal phases and the idea about the formation of nanodomains of the AFE phase inside, the said boundaries (that become much wider due to the solid solution decomposition) the piezoelectric coefficient value of more than 1200 pC/N (detailed discussion of mechanisms leading to such high values of piezocoefficient will be given in Section 5 of this article) has been achieved. As one can see, the results are disparate. However, it is not the most interesting circumstance. We have obtained the value of the d₃₃ piezoelectric modulus equal to 1200 pC/N in hard ferroelectric PZT-based ceramics with composition from the morphotropic boundary (MPB) region and a coercive field of 1900 V/mm. These results demonstrate one more time that not all the physical effects have been taken into account while interpreting experiments.

The physical basis of formation of inhomogeneous states of coexisting domains of the FE and AFE phases has been considered in a series of publications under a common title "Peculiarities of ferroelectric–antiferroelectric phase transitions" (most of these articles are cited in this paper as the material is presented). The present review contains the main results of above-mentioned publications related to the development of functional materials.

---

2. Interphase interaction and coexisting of the FE and AFE phases

---

2.1. Basic statements

Within the region of the phase diagram limited by the lability boundaries of the FE and AFE phases, the thermodynamic potential of the system has two minima (a stable and a metastable one) separated by the potential barrier. As a rule, both the AFE and the FE ordered states are realized in a substance (each taking place within its range of thermodynamic parameters), when the difference in energies of these states is small.

The local temperatures inhomogeneity T(r) ≡ T(x, y, z) takes place in any actual substance under the conditions of a real experiment (especially, at varying temperatures). The probability distribution function for values of T(r) has a finite nonzero dispersion for measurements carried out in a quasi-static regime. This fact is to be always taken into account (for instance, some phenomena caused by the distribution of local temperatures T(r) in substances with a single phase transition are considered experimentally in ^[5] and theoretically in ^[6]). In the process of cooling, a greater part of the sample's volume undergoes the transition into a state with a deeper minimum of the thermodynamic potential in the systems under consideration as a consequence of the above-discussed dispersion of local temperatures. However, some part of the crystal volume undergoes the phase transition into a state corresponding to a less deep (metastable) minimum of the thermodynamic potential. The volume of the second (metastable) phase decreases exponentially with the growth of the difference in energy of the phases. In the case when the minima of the FE and AFE phases have close values, the volumes occupied by these phases are to be approximately equal. As the temperature is lowered, the height of the barrier separating the minima increases. As a consequence, the two-phase structure at low temperatures becomes more stable towards external actions.

The thermodynamic potential for an infinite sample of a two-phase system is presented as:

$\Phi = {\xi _1}{\Phi _1} + {\xi _2}{\Phi _2} + {\Phi _{int}}$

(3)

Here Φ₁ and Φ₂ are the thermodynamic potentials of the phases; ξ₁ and ξ₂ are the volume shares occupied by each of the phases; and Φ_int describes the interaction between the domains of these phases.

The part of the thermodynamic potential describing the interaction of phases has the following form ^[7]:

${\Phi _{{\mathop{\rm int}} }} = \frac{1}{2}\left\{ {{\xi _2}\sum\limits_{i, j} {\left[ {E_{{\eta _{1, i}}}^{\left( 2 \right)}(x, y, z){\eta _{2, j}}\left( {x, y, z} \right)} \right]} + {\xi _1}\sum\limits_{i, j} {\left[ {E_{{\eta _{2, j}}}^{\left( 1 \right)}(x, y, z){\eta _{1, i}}\left( {x, y, z} \right)} \right]} } \right\}$

(4)

Here η_{1, i} and η_{2, j} are the order parameters of the first and second phases, respectively (i and j are the numbers of the order parameters of these phases); $E_{{\eta _{1, i}}}^{\left( 2 \right)}(x, y, z)$ are the fields, induced in the domains of the second phase by the nonzero values of the order parameters belonging to the domains of the first phase; $E_{{\eta _{2, j}}}^{\left( 1 \right)}(x, y, z)$ are the fields induced in the domains of the first phase by the nonzero values of the order parameters of the second phase; x, y, z are Cartesian coordinate of points inside the domains. Based on the physical nature of the order parameters (or the coexisting phases), it is evident that not all the terms in Eq 4 are nonzero. This is a consequence of the symmetry of the order parameters and the fields influencing the order parameters. The only nonzero terms in Eq 4 are those that are transformed according to the irreducible representations of the symmetry group containing the identity representation.

To determine the dependences of $E_{{\eta _{1, i}}}^{\left( 2 \right)}(x, y, z)$ and $E_{{\eta _{2, j}}}^{\left( 1 \right)}(x, y, z)$ on the order parameters of corresponding phases one must take into account the physical nature of the order parameters generating these field, the particular shape of domains of these phases, as well as the spatial distribution of order parameters in the domain's volume. Determination of $E_{{\eta _{1, i}}}^{\left( 2 \right)}(x, y, z)$ and $E_{{\eta _{2, j}}}^{\left( 1 \right)}(x, y, z)$ must be accomplished by means of a self-consistent procedure taking into account that these fields influence the spatial dependences of the order parameters which in turn define these fields. Such a program does not seem to be possible to accomplish at present. However, the solution can be found using approximations. As the most natural approximation we consider the expansion of these fields into a series of the powers of order parameters η_{α, i} of domains that generate these fields:

$E_{{\eta _{1, i}}}^{\left( 2 \right)}\left( {x, y, z} \right) = {\xi _1}C_{1, i}^{\left( 2 \right)}\left( {x, y, z} \right){\eta _{1, i}} + \cdots ,$

(5)

$E_{{\eta _{2, i}}}^{\left( 1 \right)}\left( {x, y, z} \right) = {\xi _2}D_{2, i}^{\left( 1 \right)}\left( {x, y, z} \right){\eta _{2, i}} + \cdots .$

(6)

It has to be noted that by their nature the considered fields are rather long-range and smoothly vary in space. In the case when external fields are present, they may be taken into account in Eq 3 in the usual way.

The conventional procedure of minimization of the nonequilibrium thermodynamic potential gives ^[7]:

${\xi _\alpha }(\partial {\kern 1pt} {\Phi _\alpha }/\partial {\eta _{\alpha , i}} + {E_{{\eta _{\alpha ', i}}}})\, = \, 0, \quad \quad \quad ({\xi _\alpha }\, \ne \, 0).$

(7)

${\Phi _\alpha } + {\eta _{\alpha , i}}{E_{{\eta _{_{\alpha ', i}}}}} = \lambda = const, \quad \quad \quad \alpha , \;\alpha ' = {{\rm }}1, \;2.$

(8)

As it follows from Eq 8, the condition for the existence of the thermodynamically equilibrium structure of domains of the coexisting phases is the equality of their thermodynamic potentials, taking into account the fields Eqs 5 and 6, but not the equality of the "bare" thermodynamic potentials. It also follows from Eq 8 that there is a peculiarity of the considered multiphase structure connected with the spatial dependence of the coefficients in Eqs 5 and 6. This peculiarity is observed inside the region separating the domains of the coexisting phases which is wider than the usual domain boundary. The fields $E_{{\eta _{1, i}}}^{\left( 2 \right)}(x, y, z)$ and $E_{{\eta _{2, j}}}^{\left( 1 \right)}(x, y, z)$ are spatially dependent, and their intensity decreases while moving inside the domains of the other phase. Therefore, inside these boundary regions the thermodynamic potential differs from the thermodynamic potentials characterizing the inner regions of domains. This testifies to the fact that the phase state inside the regions separating the domains will not be the same as that in the inner regions of the adjacent domains. Physical considerations allow us to conclude that this state is transient between the states of the adjacent domains.

For a particular example of the ferroelectric and antiferroelectric phases, the simplest density of the nonequilibrium thermodynamic potential has the form ^[7,8,9]:

$\Phi = \frac{{{\alpha _1}}}{2}{P^2} + \frac{{{\alpha _2}}}{4}{P^4} + \frac{{{\beta _1}}}{2}{\eta ^2} + \frac{{{\beta _2}}}{4}{\eta ^4} + \cdot \cdot \cdot + \frac{A}{2}{P^2}{\eta ^2}$

(9)

Here α₂, β₂ and А are positive values, $A > \sqrt {{\alpha _2}{\beta _2}}$ is the condition of the presence of the hysteresis region in the phase diagram, the ferroelectric and antiferroelectric phases coexist within this region. The coefficients α₁ and β₁ may change their sign at the temperatures ${T_{c, f}}$ and ${T_{c, af}}$, respectively:

${\alpha _1} = {\alpha _0}(T - {T_{c, f}});\quad \quad \quad {\beta _1} = {\beta _0}(T - {T_{c, af}}).$

(10)

Considering the thermodynamic potential in the form (Eq 9), one has to take into account that the antiferroelectric phase transition is a structural transition into the state with the order parameter η (see ^[8], for example), and the latter interacts with the polarization P, which is the order parameter of the ferroelectric state ^[8,9,10]. The thermodynamic potential in Eq 9 describes the phase transition between the paraelectric and ferroelectric states at varying temperature if ${T_{c, f}}$ > ${T_{c, af}}$. The Eq 9 describes the paraelectric–antiferroelectric transition when ${T_{c, f}}$ < ${T_{c, af}}$.

The minimum corresponding to the ferroelectric phase has the coordinates (P_{1, 0}, 0), with $P_{1, 0}^2 = - \, ({\alpha _1}/{\alpha _2})$. The equilibrium value of the energy of the ferroelectric state is ${\Phi _{1, 0}} = - (\alpha _1^2/4{\alpha _2})$. The minimum corresponding to the antiferroelectric state has the coordinates (0, η_{2, 0}), $\eta _{2, 0}^2 = - ({\beta _1}/{\beta _2})$. The equilibrium value of the antiferroelectric state energy is ${\Phi _{2, 0}} = - (\beta _1^2/4{\beta _2})$.

As it was shown in ^[7], the nonequilibrium potentials for each of the phases may be written (up to the quadratic terms) as:

${\Phi _1} = {\Phi _{1, 0}} + {U_1}{\left( {{P_1} - {P_{1, 0}}} \right)^2} + {V_1}\eta _1^2,$

(10)

${\Phi _2} = {\Phi _{2, 0}} + {U_2}{\left( {{\eta _2} - {\eta _{2, 0}}} \right)^2} + {V_2}P_2^2.$

(11)

The coefficients U_i and V_i (i = 1, 2) are expressed in terms of the coefficients from Eq 9. The fact that U_i and V_i are all positive is the most important for our consideration.

In accordance with Eqs 4–6, taking into account the restrictions imposed by the order parameters symmetry (see the remark accompanying Eq 4), the interphase interaction energy has the following form:

${\Phi _{{\mathop{\rm int}} }} = {\xi _2}{P_2}{E_{{P_1}}} + {\xi _1}{\eta _1}{E_{{\eta _2}}} = {\xi _1}{\xi _2}{C_1}{P_{1, 0}}{P_2} + {\xi _1}{\xi _2}{D_2}{\eta _{2, 0}}{\eta _1}$

(12)

Now, according to Eqs 3, 10–12, the density of the nonequilibrium thermodynamic potential of the two-phase system can be written as:

$\begin{array}{l} \Phi = {\xi _1}{\Phi _{1, 0}} + {U_1}{\left( {{P_1} - {P_{1, 0}}} \right)^2} + {V_1}\eta _1^2 + {\xi _2}{\Phi _{2, 0}} + {U_2}{\left( {{\eta _2} - {\eta _{2, 0}}} \right)^2} + {V_2}P_2^2\\ \\ \quad + {\xi _1}{\xi _2}{C_1}{P_{1, 0}}{P_2} + {\xi _1}{\xi _2}{D_2}{\eta _{2, 0}}{\eta _1}, \quad \quad \quad \quad \quad \quad \quad \quad \quad {\xi _1} + {\xi _2} = 1. \end{array}$

(13)

A conventional procedure of minimization with respect to P₁, η₁, P₂ and h₂ gives the equilibrium values of these parameters

${P_1} = {P_{1, 0}}, \;\;{\eta _1} = - \frac{1}{2}{V_1}{\xi _2}{D_2}{\eta _{2, 0}}, \;\;\;\;\;{\eta _2} = {\eta _{2, 0}}, \;\;{P_2} = - \frac{1}{2}{V_2}{\xi _1}{C_1}{P_{1, 0}}$

(14)

and the density of equilibrium energy for the two-phase system under consideration:

$\tilde \Phi = {\xi _1}\left( {{\Phi _{1, 0}} - \frac{{\xi _2^2}}{{4{V_1}}}D_2^2\eta _{2, 0}^2} \right) + {\xi _2}\left( {{\Phi _{2, 0}} - \frac{{\xi _1^2}}{{4{V_2}}}C_1^2P_{1, 0}^2} \right).$

(15)

Comparison of Eqs 15, 17 and 18 shows that the phase interaction in the form (Eq 12) lowers the energy of the system. As a final result, this two-phase state may acquire larger energy stability than a single phase state, if the difference of $(\tilde \Phi - {\Phi _{1, 0}})$ is negative. The latter condition is fulfilled in the vicinity of the ferroelectric–antiferroelectric stability line. In this case ${\Phi _{1, 0}} \cong {\Phi _{2, 0}}$, ξ₁ = ξ₂ = 1/2, and the absolute energy advantage due to the formation of the nonuniform two-phase state will be equal to:

$\Delta \Phi = - \left( {\frac{{{{{\rm \mathsf{ ξ} }}_1} \cdot {{\rm \mathsf{ ξ} }}_2^2}}{{4{V_1}}}D_2^2{{\rm \mathsf{ η} }}_{2,0}^2 + \frac{{{{\rm \mathsf{ ξ} }}_1^2 \cdot {{{\rm \mathsf{ ξ} }}_2}}}{{4{V_2}}}C_1^2P_{1,0}^2} \right)\;\xrightarrow{{{{{\rm \mathsf{ ξ} }}_1} = {{{\rm \mathsf{ ξ} }}_2} = 1/2}}\;\Delta \Phi = - \frac{1}{{32}}\left( {\frac{{D_2^2}}{{{V_1}}}{{\rm \mathsf{ η} }}_{2,0}^2 + \frac{{C_1^2}}{{{V_2}}}P_{1,0}^2} \right)$

(16)

As seen from Eqs 5 and 6, the fields $E_{{\eta _{2, j}}}^{\left( 1 \right)}$, $E_{{\eta _{1, i}}}^{\left( 2 \right)}$, and, consequently, the coefficients C₁ and D₂, are functions of the coordinates. They decrease as the distance from the interphase boundary increases. Thus, the long-range interaction fields favour the stabilization of the nonuniform state to the greatest degree. The stability of the nonuniform state is also raised by low values of the parameters V₁, V₂, U₁ and U_2.

In this article we present experimental results obtained for two series of the PZT-based solid solutions with coexisting domains of the FE and the AFE phases. The compound Pb_1−x(La_1/2Li_1/2)_x(Zr_1−yTi_y)O₃ (PLLZT) obtained by substitutions of the isovalent complex (La_1/2Li_1/2)²⁺ for lead ions in the PZT or solid solutions Pb_1−3x/2La_x(Zr_1−yTi_y)O₃ (PLZT) obtained by substitutions of the La³⁺ ions for lead. These two types of substitutions allowed achieving wide regions of the solid solution compositions within which the coexistence of the FE and AFE phases takes place.

In what follows we will used standard symbols for the solid solution compositions X/100–Y/Y, where X and Y denote the percentage content of the substituting elements (X denotes the content of ion or ion complex substituted for lead, and Y gives the Ti-content).

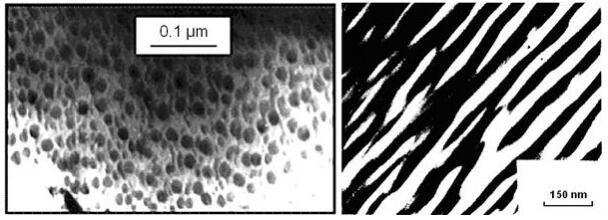
The first observations of the coexisting FE and AFE phases in different experimental conditions were presented in ^[11,12]. The TEM images of the domains of the coexisting phases are shown in Figure 1. The shape of domains depends on the experimental conditions. In particular, the shape of domains depends on the mechanical compression stresses from neighboring grains, depending on whether they are absent (the left image in Figure 1 from ^[13]) or are present (the right image in Figure 1 from ^[14]). These nonuniform states were later studied in ^[14,15], where the effect of the position of the PZT based solid solution in the diagram of phase states on the domain structure of coexisting dipole-ordered phases was studied in detail.

---

2.2. Coexistence of phases and ions segregation. Long-time relaxation

---

2.2.1. General provisions

The negative value of ΔΦ in (Eq 16) shows that the considered interphase boundary wall (IDW) possesses a negative surface energy. It seems that the negative value of this boundary's energy should have stimulated the division of the sample volume into an unlimited number of very small domains. However, it was only a simplified consideration of the problem. In particular, the effects connected with the condition of continuity for elastic medium at the interphase boundary were not taken into account.

The crossing of the IDW (from one phase to the other) goes on simultaneously with the continuous conjugation of the atomic planes (free of breaks and dislocations) ^[11,12]. This coherent IDW structure leads to an increase of the elastic energy. Such an increase is more essential the larger the difference in the configuration volumes of the FE and the AFE phases. Just this effect defines the positive value of the surface energy density for the boundaries separating ordinary domains in ferroelectrics ^[16,17]. This elastic energy restricts the increase of the area of the interphase boundaries and, consequently, the reduction in size for the domains of the coexisting phases. These stresses weaken the condition of the inhomogeneous state existence.

In the substances under consideration, that is the substances where the FE and the AFE states are possible, the equivalent crystallographic sites are occupied by ions that are different either in the size or in the value of charge or in both. In a single-phase state (inside the domains of each of the coexisting phases), the ions, forming the crystal lattice, are not subjected to the action of forces in the absence of external factors (more correctly, the resultant force affecting each ion is equal to zero). The opposite situation is observed for the ions located near the "bare" IDW. The balance of forces affecting each of these ions is upset. "Large" ions are pushed out into those domains, which have a larger configuration volume and, consequently, a larger distance between crystal planes. "Small" ions are pushed out into the domains with a smaller configuration volume and a smaller interplanar distance. The process is accompanied with both a decrease in the elastic energy concentrated along the "bare" IDW and an increase in the energy bound up with the segregation of the substance. The process of ion segregation will be completed when the new-formed IDW structure provides the energy minimum. Such a "clothed" IDW will be further called the real IDW or simply the IDW.

Thus, the formation of the heterophase structure of the coexisting domains of the FE and the AFE phases is followed by the emergence of the chemical inhomogeneity of the substance. The said process is realized owing to the ion diffusion at relatively low temperatures (T < T_c). In this case, the diffusion coefficients are too small, and the process is the long-time one. For some PZT-based solid solutions characteristic times of this process exceed 100 h at 20 ℃.

An experimental study of the kinetics of the local decomposition of a solid solution at the interphase FE–AFE boundaries was carried out in ^[18,19]. The main results of these publications are given below. The experiments were carried out according to the following scheme.

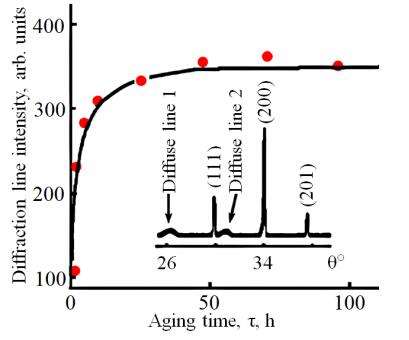
As a first step, the samples of the PLZT solid solutions were annealed at 600 ℃ for 22 h. After the annealing the samples were quenched to room temperature and then left to age at 22 ℃ (at room temperature) during the time interval τ. At the end of each time interval τ the X-ray patterns were recorded by the Debye–Scherrer method.

The X-ray patterns, which were obtained at 600 ℃ on the annealed samples, contained only the strong singlet X-ray lines caused by the coherent scattering from crystal planes of the cubic perovskite lattice. Right away after quenching (τ ≈ 0) the X-ray patterns contained only the strong singlet diffraction lines as in the high-temperature case. The structure of the X-ray patterns becomes more complicated during ageing. A splitting of the singlet lines takes place. Broadened diffuse lines (halos) with significantly lower scattering intensities appear in addition to the diffraction lines. These new lines are the result of the incoherent scattering from chaotically oriented segregates at the FE–AFE interphase boundaries ^[18,19]. We studied the behavior of the halos located in the two angle intervals θ = 25–27° (diffuse X-ray line 1) and θ = 29–32° (diffuse X-ray line 2) (the insert in Figure 2).

The intensity, the location, and the shape of the diffuse lines were changing with time. The shape and the location (position) of the diffraction Bragg-lines, which characterize the crystal structure of the solid solution under investigation, were also changing with time.

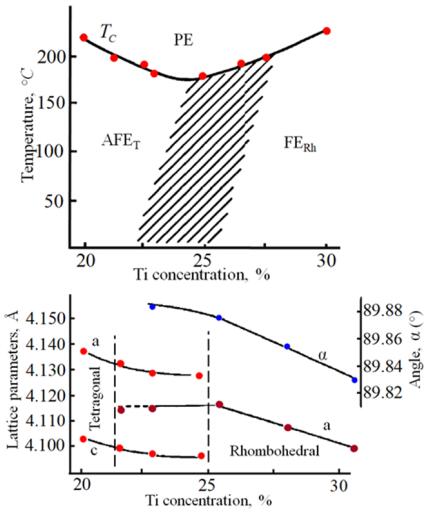
Now we consider the kinetics of the segregation process near the IDW separating domains of the FE and the AFE phases in two systems of solid solutions PLZT and PLLZT ^[18,19,20]. The phase diagrams for PLLZT solid solutions were studied in ^[21,22]. The studies of the segregation process were carried out on 6/100–Y/Y PLZT and on the 15/100–Y/Y PLLZT series. Identical results have been obtained for both series of solid solutions, namely, the phenomena described above are characteristic only for those solid solutions in which the FE and AFE phases coexist. Therefore, below the results for only one series of solid solutions 15/100–Y/Y PLLZT are presented. The phase diagram for 15/100–Y/Y PLLZT solid solutions (before they were subjected to the action of an external electric field) are presented in Figure 3.

The decomposition of the solid solution is manifested in the appearance of weak diffuse lines (diffuse lines 1 and 2 in Figure 2) the X-ray diffraction pattern. These weak diffuse lines are located near the basic diffraction lines, which are characteristic for the perovskite structure of solid solutions ^[18,21,24]. The change in the intensity of one of the diffuse lines with ageing time is presented in Figure 2. As can be seen, the decomposition process lasts no less than 40–50 hours. More precise data obtained from observations of the crystalline structure of the solid solution show that this process lasts no less than 100 hours until its final completion. More details of the process of decomposition of solid solutions near the interphase boundaries are given in papers ^[18,19].

---

2.2.2. Local decomposition of solid solutions, nanostructures and optical materials with negative refractive index

The metamaterials with negative refractive index in the near infrared and optical ranges of the spectrum are the metal-dielectric composites ^[25,26,27]. The technological approach to the manufacturing of composites mentioned in ^[25,26,27] is quite laborious and is difficult to reproduce.

An easy feasible method for obtaining the dielectric-metal composite structures with the periodic arrangement of metallic inclusions is presented in our article ^[13]. Dimensions of the said inclusions are from 8 to 12 nm, the periodicity of their arrangement is from 0.2 to 2.0 μm. This method is based on the local decomposition of the solid solution in which the structure of coexisting domains of the FE and AFE phases is realized. The decomposition of the solid solution takes place on the boundaries that separates the domains of FE and AFE phases. Such boundaries (or segregates) possess the metallic type of conductivity.

Conductivity of the majority of oxides with the perovskite crystal structure (the PZT-based solid solutions are among them) can be varied by means of ion substitutions in lattice sites in a very wide range from pure dielectric state (with resistance of the order of 10¹⁴–10¹⁶ Ω·cm) to the conducting state (with resistance of the order of 100 mΩ·cm).

The chemical composition of segregates precipitated along the interphase boundaries is slightly different from the parental composition of the base solid solution (in the domains' bulk). Special selection of the chemical composition of the maternal solid solution along with the control of the chemical composition of segregates provide the conditions at which these segregates can possess a diverse set of physical properties.

The segregates manufactured by controlled local decomposition of solid solutions with proper chemical composition can be magnetic, dielectric or conducting. In the present study we performed the decomposition of the solid solution in such a way that segregates in the vicinity of interphase boundaries had high (near-metallic) conductivity.

Samples for optical studies were manufactured by the hot pressing method (at a pressure of 30 MPa) at 1250 ℃ for 8 h. Lamellae with a thickness of 0.3 cm were cut from the sintered bars. These lamellae were grinded and polished. Before polishing, the grinded lamellas were annealed at 1200 ℃ in the presence of PbZrO₃ filling for 1 h and after that at 1100 ℃ in oxygen enriched atmosphere for 1 h. After the polishing, the lamellae were subjected to the second annealing at 850 ℃ in an oxygen enriched atmosphere for 2 h. The wavelength dependences of the light transmission coefficient were measured using a Hitachi U-4000 Spectrophotometer.

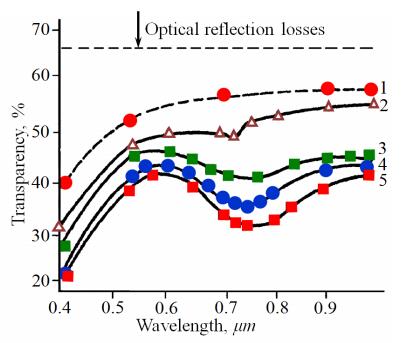
The dependences of transparency of one of the discussed materials as a function of the wave length are presented in Figure 4 as an example. The dips in the curves correspond to the presence of the negative refraction regime. The modulation depth can be controlled by changing the conductivity of segregates. It is also possible to select the optic wave length range by changing the position of the solid solution in the "composition–temperature" phase diagram of the substance. Another possibility to change the position of the solid solution in the "electric field–temperature" phase diagram is to vary the potential difference between the element's electrodes.

Additional ways of tuning the light flux appear due to the possibility to regulate the shape of the domains of coexisting phases and, as a consequence, the shape and spatial orientation of segregates. The discussed materials are characterized by a small difference in free energies of the FE and AFE states in the solid solution with specific concentrations of components (PbZrO₃ and PbTiO₃). The metastable phase domains have the shape of cylindrical domains imbedded into the stable phase matrix ^[12,28] or the shape of ellipsoids of revolution close to spheres in the bulk crystals ^[29], depending on the crystal's thickness.

However the most interesting results can be obtained using thin film structures. The change of the region of the negative refraction in this case can be achieved both by the application of the electric field to the film substrate (if the ferroelectric crystal is chosen as a substrate material) or by applying the flexural strains to the substrate. The modulation of the transmitted light has been observed in both these situations.

---

3. Two phase system in DC electric field, phase transitions via an intermediate state and tuning of piezoelectric properties

---

3.1. Theoretical model

The phase transition via the intermediate state (IS) is one of the most interesting phenomena in the physics of magnetism and superconductivity. The IS represents a thermodynamically stable state of the coexisting phases between which the first order phase transition takes place under the action of the external magnetic field. The existence of the IS in the above-mentioned substances is caused by the action of the demagnetizing field resulting from the finite size of the samples. However, it was shown in ^[30] that the IS similar to the ones in magnetic substances and superconductors is fundamentally impossible in both the FE and the AFE.

Nevertheless, it can be demonstrated that the IS that represents a thermodynamically stable structure of the coexisting domains of the FE and AFE phases may exist. The nature of this intermediate state is vastly different from the one in magnetic substances and in superconductors. The main difference of the FE and AFE substances from, for example, the magnetic materials is in how an external field is applied to the sample ^[30] (from the physics point of view this difference is explained by the different form of the Maxwell equations applied to magnetic substances and dielectrics).

The conventional procedure of minimization of the nonequilibrium thermodynamic potential (considered in Section 2.1 of the present paper) taking into account an external electric field leads to the following system of equations for the equilibrium values for the order parameters (instead of Eqs 7 and 8)

${{{\rm \mathsf{ ξ} }}_{{\rm \mathsf{ α} }}}\left( {\partial {\Phi _{{\rm \mathsf{ α} }}}/\partial {{{\rm \mathsf{ η} }}_{{{\rm \mathsf{ α} }}, i}}\, + \, {E_{{{{\rm \mathsf{ η} }}_{{{\rm \mathsf{ α} '}}, i}}}} - {E_{{{\rm \mathsf{ α} }}, i;ext}}} \right)\, = \, 0, \, \quad \quad \, ({{{\rm \mathsf{ ξ} }}_{{\rm \mathsf{ α} }}}\, \ne \, 0)$

(17)

${\Phi _{\rm \mathsf{ α} }} - \, {{\rm \mathsf{ η} }_{{\rm \mathsf{ α} }, i}}{E_{{\rm \mathsf{ α} }, i;{\mathop{\rm int}} }}\, = \, {\rm \mathsf{ λ} }\, \, = \, const,$

(18)

${E_{{{\rm \mathsf{ α} }}, i;{\mathop{\rm int}} }} = {E_{{{\rm \mathsf{ α} }}, i;ext}} - {E_{{{{\rm \mathsf{ η} }}_{{{\rm \mathsf{ α} '}}, i}}}}.$

(19)

These equations differ from Eqs 7 and 8 by the presence of the external electric fields, conjugated to the order parameters (for the case of coexisting FE and AFE phases only one order parameter, polarization, exists that must be taken into account). As seen from Eq 18, the condition for the existence of the thermodynamically balanced structure of coexisting domains of the phases is the equality of their thermodynamic potentials that takes into account the external and the internal effective fields.

The fields ${E_{{{{\rm \mathsf{ η} }}_{{{\rm \mathsf{ α} }}, i}}}}$ are spatially varied. Therefore, the AFE → FE transition may take place only in certain local regions of the sample (but not in the whole volume of the sample) at the same value of the external field${E_{\alpha , i;ext}}$. This means that, within a certain interval of the external electric field intensity, the domains of the phases, participating in the transition, coexist in the sample's volume. By analogy with magnetic materials or superconductors, such a state should be called the intermediate state in the AFE. In view of this, let us obtain a relation between the external field and the field of the phase transition for the case of a thermodynamically balanced structure of the coexisting FE and AFE phases, and define the external field intensity corresponding to the onset and the completion of the phase transition into the IS. The condition of the phase transition is the equality of the internal field within local regions of the sample to the field of the phase transition (${E_{{{\rm \mathsf{ α} }}, i;{\mathop{\rm int}} }} = {E_{pt}}$). From this condition and from Eq 19 we have the following relation:

${E_{pt}} + {E_{{{{\rm \mathsf{ η} }}_{{{\rm \mathsf{ α} '}}, i}}}} = {E_{{{\rm \mathsf{ α} }}, i;ext}}$

(20)

Now let us express ${E_{{{{\rm \mathsf{ η} }}_{{{\rm \mathsf{ α} '}}, i}}}}$ in terms of the share of the sample's volume which has undergone the transition, and put down the order parameters in accordance with (Eq 18). Thus, we obtain the dependence of the share of the phase, which has undergone the transition into the FE state, on the external field intensity within the limits of the IS existence.

Taking into account the interphase interaction energy in the form (Eq 12) ^[30]:

${\Phi _{{\mathop{\rm int}} }} = \, \, \left( {{{{\rm \mathsf{ ξ} }}_2}{P_2}} \right)\left( {{{{\rm \mathsf{ ξ} }}_1}{C_1}{P_1}} \right) + \left( {{{{\rm \mathsf{ ξ} }}_1}{{{\rm \mathsf{ η} }}_1}} \right)\left( {{{{\rm \mathsf{ ξ} }}_2}{D_2}{{{\rm \mathsf{ η} }}_2}} \right).$

(21)

we have the expression for the intrinsic field for the AFE phase domains:

${E_{2;{\mathop{\rm int}} }} = {E_{ext}} - {{{\rm \mathsf{ ξ} }}_1}{C_1}{P_1}.$

(22)

Since the equilibrium solution for P₁ for the thermodynamic potential of the two phase system is ${P_1} \cong P_{1, 0}^E$ (see Eq 14), we obtain:

${E_{2;{\mathop{\rm int}} }} \cong {E_{ext}} - {{{\rm \mathsf{ ξ} }}_1}{C_1}P_{1, 0}^E.$

(23)

For the intermediate state E_int = E_pt. Therefore, by analogy with magnetic materials we obtain:

${\xi _1} \cong \frac{{{E_{ext}} - {E_{pt}}}}{{{C_1}P_{1, 0}^E}}.$

(24)

Also by analogy with magnetic systems, for the AFE material we have the boundaries of the IS:

${E_1} \cong {E_{pt}};\, \quad \quad \quad {E_2} \cong {E_{pt}} + {C_1}{P_{1, 0}}({E_{pt}}).$

(25)

These boundaries are determined by the conditions ξ₁ = 0 and ξ₁ = 1, respectively.

Comparison of Eqs 24 and 25 with the analogous ones for the IS in the magnetic materials ^[31,32] shows that the equations which describe the IS in the AFE are similar in appearance to those for magnetic substances. However, the fields ${E_{{{\rm \eta} _{{\rm \alpha} , 1}}}}$ and H_diam (the latter is the demagnetization field in magnetic materials and it defines the nature and the range of existence of the IS in magnetic materials) differ in their physical nature. This results in some distinctions in the conditions of observation of the IS in magnetic materials and ferroelectrics or antiferroelectrics. First of all, the interval of the existence of the IS in the AFE does not depend on the geometric characteristics of the sample, whereas in magnetic substances this dependence is pronounced. Moreover, in ferroelectrics the IS may also appear in the case when the FE → AFE phase transition is induced by the hydrostatic pressure. In fact, with an increase in pressure the stability of the FE phase diminishes, but that of the AFE state increases. The thermodynamic potentials of these phases acquire the same value at some critical pressure and this leads to the emergence of the nuclei of a new AFE phase. They induce the fields ${E_{{{\rm \eta} _{{\rm \alpha} , 1}}}}$, due to which different local regions of the sample are under different conditions. This situation gives rise to the coexistence of domains of the phases participating in the phase transition.

Thus, in this section it has been shown that the presence of the IS is possible at the phase transitions induced by an electric field (or a hydrostatic pressure) in the AFE (or the FE). Such intermediate state represents the coexistence of the phases participating in the phase transition within a rather wide interval of thermodynamic parameters initiating the transition.

---

3.2. Experimental results

Of all the features of the phase transition through the intermediate state (see ^[33,34,35] for more details), we will only pay attention to the piezoelectric characteristics tuning due to such a transition. This tuning is a consequence of the phase transition induced by electric field (Figure 5).

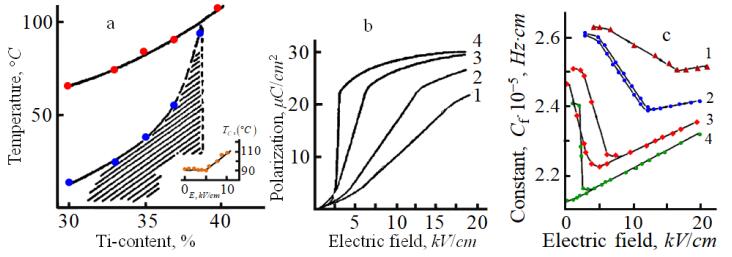
Figure 5a shows the "Ti-content–temperature" phase diagram of solid solutions characterized by the so-called narrow hysteresis loops ^[35]. Such behaviour is manifested in those substances where the domains of FE and AFE phases coexist, the difference in free energies of these phases is small and the AFE → FE phase transition induced by the electric field is realized. The dashed region in the phase diagram gives the range solid solution compositions within which the FE and AFE phases coexist. The electric field dependence of the temperature of the phase transition from the paraelectric to the dipole ordered phase is shown in the insert

This behavior was experimentally investigated in four series of the PLZT solid solutions: 6/100–Y/Y, 7.5/100–Y/Y, 8.25/100–Y/Y, and 8.75/100–Y/Y. Since the "Ti-content–temperature" diagrams of all these series are physically equivalent, below we present only the results for the 8.25/100–Y/Y series. The phase diagram of the said series is shown in Figure 5a. First of all, it should be noted that there exists a field interval within which T_c does not depend on the field intensity (insert in Figure 5a) for the solid solutions located near the FE–AFE boundary.

Figure 5b presents the dependence of polarization on the electric field intensity (the samples were previously annealed at 600 ℃). The electric field dependences of the resonance frequency (strictly speaking, the frequency constant C_f = rf, here f is the frequency of the first radial resonance, and r is the radius of the sample) of the first harmonics of radial oscillations for these samples are shown in Figure 5c. The study of the resonance characteristics also gives important information on the elastic properties of these materials; however, for the goals of this review the data presented in Figure 5 are sufficient. In contrast to the P(E) dependence, the C_f(E) dependences are nonmonotonic, therefore, they allow to fix the values of the critical field of the phase transition more precisely.

As one can see from curves 1 in Figure 5b, c, there are three intervals of the external electric field, where the properties of samples noticeably differ when the field intensity increases. At zero electric field this solid solution is in the AFE state which is preserved within the field interval 0 < E < E_cr,1. At the high fields (E > E_cr,2) the sample is in the FE state. When the field intensity is in the interval between E_cr,1 and E_cr,2 the polarization increases linearly. This interval is the region of the IS in the studied solid solutions. An increase of the Zr content in the solid solution leads to the widening of the intermediate state region. We need to note that the processes caused by the electric field are characterized by a weak hysteresis.

The measurement results discussed above allowed us to build the "composition–electric field" phase diagrams that represent the dependences E_cr,1(Y) and E_cr,2(Y). These diagrams containing the intermediate state region one can find in ^[33,35].

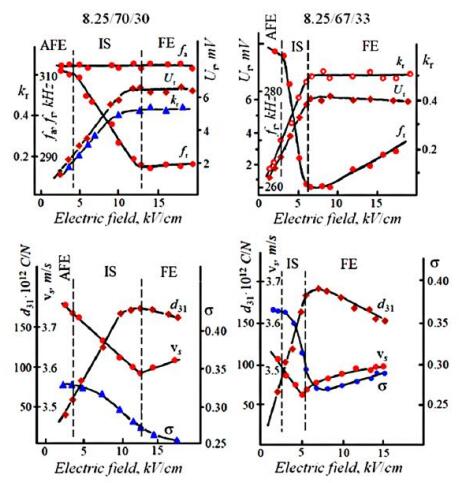
The share of the FE phase increases linearly when the external DC field increases within the interval of field intensities corresponding to the intermediate state (in compliance with Eq 24). The increase of the share of the polar phase leads to changes in the piezoelectric characteristics of samples. Experimental electric field dependences of the piezoresonance parameters such as the resonance and antiresonance frequencies (f_r, f_a) for radial resonance, the voltage on reference resistance at resonance (U_r), the piezoelectric module (d₃₁), the velocity of sound (v_s), and the Poisson coefficient (σ) are presented in Figure 6 for two series of PLZT solid solutions.

The AFE → FE phase transition through the intermediate state of the coexisting FE and AFE phases takes place as the electric field strength increases in the solid solutions shown in the Figure 6. The positions of the boundaries separating all three states (AFE, intermediate (IS), and FE) are shown by dashed vertical lines. As is seen from Figure 6, a significant and practically linear change in the piezoelectric characteristics occurs in the region of the intermediate state.

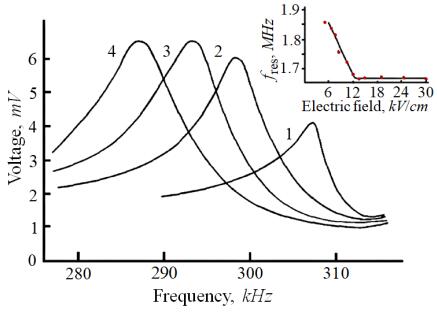
Figure 7 shows the change of resonance frequency with increasing electric field. It should be particularly emphasized here that this resonance frequency change is not linked to the change of the linear sizes of a resonator in an electric field.

The dependences of the sample deformations on the applied electric field intensity can be found in ^[34] for the solid solution compositions close to the ones studied here. The relative deformations less than 10⁻³ observed in ^[34] in the fields with intensities of the order of 10 kV/cm cannot be compared with the relative changes of the resonance frequency observed in our experiments. Moreover the relative deformations in the direction along the applied electric field and in the perpendicular direction have different signs. The dependence of the frequency of the longitudinal resonance (it is a thickness resonance for the geometry of our samples) on the applied field intensity at the phase transition via an intermediate state is given in Figure 7 for comparison. As one can see, the sign of the effect for both longitudinal and transverse (radial) resonances is the same. These data allow neglecting the changes of the resonator's linear sizes in an applied electric field during the analysis of the resonators behavior in an external electric field.

---

4. Two-phase nucleation in paraelectric phase

In Section 2.1 we have considered the stability of the two phase state at the temperatures lower than the Curie point. Some physically correct conclusions regarding the peculiarities of the behavior of the considered system may be also made for the temperatures close to T_{c, f} and the higher ones (for clarity we assume that T_{c, f} > T_{c, af}). The thermodynamic potential of the system has only one minimum within the temperature interval close to the phase transition from the paraelectric phase to the dipole ordered phase. Therefore, the substance described by such a potential is a FE, and the appearance of the AFE phase domains at the temperatures near T_{c, f} is possible only in the form of the fluctuations. The said domains, arising in the volume of the substance, interact with the FE matrix. Such interaction changes the density of the thermodynamic potential in the volume of the sample in the vicinity of the appeared AFE domain. For the other parts of the volume the density of the FE state potential remains unchanged.

Thus, for the volume, in which the interphase interaction takes place, the density of the nonequilibrium thermodynamic potential may be written as ^[7,36]:

$\Phi = \, \frac{{{{{\rm \mathsf{ α} }}_1}}}{2}{P_1}^2\, + \, \frac{{{{{\rm \mathsf{ α} }}_2}}}{4}{P_1}^4\, + \, \frac{{{{{\rm \mathsf{ β} }}_1}}}{2}{{\rm \mathsf{ η} }}_1^2\, + \, \, \frac{A}{2}{P_1}^2{{{\rm \mathsf{ η} }}_1}^2 + \frac{m}{2}P_2^2 + \frac{n}{2}{{\rm \mathsf{ η} }}_2^2 + \, C{P_1}{P_2} + D{{{\rm \mathsf{ η} }}_1}{{{\rm \mathsf{ η} }}_2}$

(26)

In this expression the first four terms correspond to the density of the nonequilibrium thermodynamic potential of the FE phase for T > T_{c, af} (b₁ > 0, so we assume that β₂ = 0), the next two terms correspond to the density of the nonequilibrium potential of the domains of the AFE phase (m > 0, n > 0) that may appear T > T_{c, af}, and the last two terms represent the interphase interaction.

The minimization of Eq 26 with respect to P₂ and η₂ yields:

${P_2} = - \, (C/m){P_1};\, \quad \quad \quad {{{\rm \mathsf{ η} }}_2} = - \, (D/n){{{\rm \mathsf{ η} }}_1}$

(27)

Substituting the obtained expression into Eq 26 we have:

$\Phi \, = \, \frac{1}{2}\left( {{\alpha _1} - \frac{{{C^2}}}{m}} \right){P_1}^2\, + \, \frac{{{{{\rm \mathsf{ α} }}_2}}}{4}{P_1}^4\, + \, \frac{1}{2}\left( {{{{\rm \mathsf{ β} }}_1} - \frac{{{D^2}}}{n}} \right){{\rm \mathsf{ η} }}_1^2\, + \, \, \frac{A}{2}{P_1}^2{{{\rm \mathsf{ η} }}_1}^2$

(28)

As one can see from the last expression, the interphase interaction leads to the renormalization and the increase of the Curie point (see the coefficient at $P_1^2$). Moreover, under certain conditions this interaction may also stabilize the AFE state in some part of the sample's volume (see the coefficient at ${{\rm \mathsf{ η} }}_1^2$). This means that there is a possibility of the existence of the two-phase (FE + AFE) domains at temperatures exceeding T_{c, f}.

It is not difficult to determine the distribution of the Curie temperatures through the crystal's volume (the dependence of T_C on the spatial coordinates). It is enough to use the standard form of the nonequilibrium thermodynamic potential (Eq 9) for the system in which the minima of thermodynamic potentials for two dipole-ordered states have close values of their depths and take into account (Eq 10)

${{{\rm \mathsf{ α} }}_1}\, = \, {{{\rm \mathsf{ α} }}_0}(T\, - \, {T_{c, f}});\, \quad \quad \quad \, {{{\rm \mathsf{ β} }}_1}\, = \, {{{\rm \mathsf{ β} }}_0}(T\, - \, {T_{c, af}}).$

(29)

As it was shown previously in Section 2.2 (Eq 16) the energy change in the region of space where the interphase interaction takes place is given by the expression (for the case ξ₁ = ξ₂):

$\Delta \Phi = - \frac{1}{{32}}\left( {\frac{{D_2^2}}{{{V_1}}}{{\rm \mathsf{ η} }}_{2, 0}^2 + \frac{{C_1^2}}{{{V_2}}}P_{1, 0}^2} \right),$

(30)

which has to be added to Eq 9. That is why the coefficients of the expansion of the thermodynamic potential are renormalized as follows:

$\begin{gathered} \,{{{\rm \mathsf{ α} }}_1}\, = \,{{{\rm \mathsf{ α} }}_0}\left[ {T\, - \,\left( {{T_{c,f}} + \frac{{{{\rm \mathsf{ ξ} }}_1^2 \cdot {{{\rm \mathsf{ ξ} }}_2}}}{4}\frac{{C_1^2(x,y,z)}}{{{V_2}}}} \right)} \right]\;\xrightarrow{{{{{\rm \mathsf{ ξ} }}_1} = {{{\rm \mathsf{ ξ} }}_2} = 1/2}}\;{{{\rm \mathsf{ α} }}_1}\, = \,{{{\rm \mathsf{ α} }}_0}\left[ {T\, - \,\left( {{T_{c,f}} + \frac{1}{{32}}\frac{{C_1^2(x,y,z)}}{{{V_2}}}} \right)} \right] \hfill \\ {{{\rm \mathsf{ β} }}_1}\, = \,{{{\rm \mathsf{ β} }}_0}\left[ {T\, - \,\left( {{T_{c,af}} + \frac{{{{{\rm \mathsf{ ξ} }}_1} \cdot {{\rm \mathsf{ ξ} }}_2^2}}{4}\frac{{D_2^2(x,y,z)}}{{{V_1}}}} \right)} \right]\;\xrightarrow{{{{{\rm \mathsf{ ξ} }}_1} = {{{\rm \mathsf{ ξ} }}_2} = 1/2}}\;{{{\rm \mathsf{ β} }} _1}\, = \,{{{\rm \mathsf{ β} }} _0}\left[ {T\, - \,\left( {{T_{c,af}} + \frac{1}{{32}}\frac{{D_2^2(x,y,z)}}{{{V_1}}}} \right)} \right] \hfill \\ \end{gathered}$

(31)

As one can see the local temperatures of the phase transition into the PE state increase and the spatial dependence of the Curie temperatures appears as a consequence of the special dependence of the coefficients C₁(x, y, z) and D₂(x, y, z). Recall that the coefficients V₁ and V₂ in Eq 31 are determined by the expansion coefficients of the thermodynamic potential (Eq 9) and are positive (see Section 2.1). That is why the spatial distribution of the Curie temperatures is determined not only by the interphase interaction but also by the "initial" properties of the system itself. In particular, the decrease of the coefficients V₁ and V₂ takes place in the systems in which the elastic potential anharmonicity manifests itself and the flattening of the minima of the thermodynamic potential (Eq 9) occurs. The widening of the temperature interval of the phase transition into the completely disordered state occurs as a result. It is also obvious that the domains in which the state of the coexisting spatially separated FE and AFE phases is realized (in the first approximation) become stable in the temperature region of the "initial" PE state.

As it follows from Eqs 28 and 31, and also from results of Section 2.1, the local regions of the crystal in the vicinity of the boundaries separating domains with the FE and the AFE orderings are characterized by the lower free energy than the main volume. At temperatures above the Curie temperature such domains appear at first as fluctuations and are stabilized later by the interphase interaction. Upon cooling from the high temperatures approaching the Curie temperature from the PE phase the domains with P ≠ 0 и η ≠ 0 appear at first and then they acquire the features of the two-phase domains in the vicinity of T_C. The temperature at which the first nuclei of the dipole-ordered state appear can exceed the Curie temperature by 100 ℃ and even more.

Our simplified approach does not take into account the effects connected with the presence of the elastic stresses caused by the phase coexistence and the interphase boundaries. Therefore some additional remarks have to be made. It is general knowledge that in the course of the PE–FE phase transition the configuration volume increases, whereas at the transition into the AFE state this parameter decreases. Therefore the existence of the domains of each phase separately at the temperatures above the Curie points is accompanied by the appearance of the substantial elastic stresses, and is not advantageous from the energy point of view.

However, the energy increase does not take place for the complex two-phase (FE + AFE) domain. In this case the configuration volume does not vary for the two-phase domain as a whole. The presence of domains with such a structure allows removal of the elastic stresses and to raise the dipole disordering temperature due to the interaction (Eq 12) as much as possible (i.e., to achieve the utmost decrease of the free energy). The ratio of the phase volumes in the two-phase domain which is present in the PE matrix of the crystal is defined by both the relative stability of the FE and AFE phases (i.e., by the relative difference of their free energies) and the changes in the elastic energy, which may be brought about by each of the phases. A characteristic property of such a domain is that it should easily match the varying external conditions: an electric field and a pressure (including those of the PE matrix). An insignificant polarization of this domain, almost complete absence of elastic stresses, and the absence of distortions in the PE matrix, where the domain arises, provide its existence at the temperatures exceeding both T_{c, f} and T_{c, af}.

For simplicity the latter phenomenon may be thought of as a complex two-phase nucleation ^[36,37,38]. It is realized in the form of a spatial domain which lies within the PE matrix of the crystal.

The microstructure of the solid solutions can be controlled by the virtue of the fact that the inhomogeneous structure and segregates along the interphase boundaries appear in the process of the phase transition. In turn, the phase transition can be easily controlled. After the phase transition the structure of segregates is preserved. Therefore, the textured structures may be created in the materials under consideration when external influences are applied to the material during the phase transition and these structures will remain stable after switching-off the external influences on the sample.

A local decomposition of the solid solution takes place near the boundaries separating these phases. The electric field, ordering the FE part of such two-phase domains, also orders the directions of the boundaries and flat-like segregates formed on them. After switching-off of the electric field, this segregate structure remains for a long time, since the diffusion of chemical elements through the crystal lattice sites at the temperatures of 200–300 ℃ is super slow (recall that we are talking about solid solutions of PZT). The said segregations also "keep on itself" an ordered domain structure after cooling the samples to room temperature. Thus, an electric field can create the texture of ceramic samples.

We emphasize that we have demonstrated how it is possible to create piezoelectrically active structures by applying (and switching-off) an electric field at the temperatures corresponding to the paraelectric state of samples. In the absence of nucleation of the two-phase domains in the paraelectric phase, such actions cannot lead to a piezoelectrically active state for ceramic samples.

Figure 8 shows the example (from ^[38]) of creation of such piezoelectrically active state by the application of the electric at the temperatures significantly exceeding the temperature of the paraelectric phase transition.

Two different regimes of the thermoelectric treatment of the samples were used to prepare samples for measurements in the above-mentioned studies. In the first case, the samples were annealed at 500 ℃ for 1 hour and after that, they were cooled at the rate of 4 degree/min. An electric field (800 V/mm) was applied to the samples at 300 ℃ (which is above the Curie point) and the cooling continued in the presence of the field until the temperature reached T_C + 20 ℃, at this temperature the electric field was switched of and the samples were cooled down to room temperature. Measurements of the piezoresonance were performed at room temperature (curve 1 in Figure 8). In the second case, the thermoelectric treatment was slightly different. After the annealing and cooling the electric field was applied to the samples at T₁ = T_C + 20 ℃ (the condition that T₁ > T_C was observed all the time). The samples were kept at this temperature in the presence of the applied electric field for 0.5 hour, after that the field was switched off and the samples were cooled down to room temperature and the resonance measurements were carried out (curve 2 in Figure 8). Recall again, all thermal treatments were carried out when samples were in the PE state.

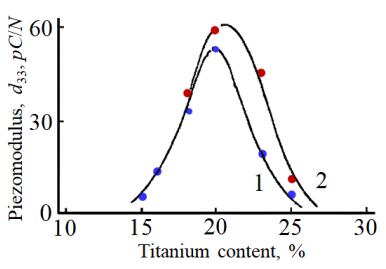
Dependences of the piezoelectric coefficient d₃₃ on the Ti-content for the 10/100–Y/Y system of PLLZT solid solutions subjected to the above-described regimes of the thermal treatment are shown in Figure 8 (curves 1 and 2 refer to the first and second regime, respectively). Both dependences have well pronounced maxima located near Y = 20 (which corresponds to 20% Ti). Solid solutions do not manifest piezoelectric properties when the Ti-content moves out from this value. Solid solutions with 20% of titanium have equal stability of the FE and AFE states (phase diagram of the said series of solid solutions with 10% of (La_1/2Li_1/2)²⁺ substituted for Pb²⁺ ions is presented in ^[21,22] and is analogous to one, presented in Figure 3 for series with 15% of (La_1/2Li_1/2)²⁺). In the volume of these solid solutions two-phase domains take place and the piezoelectric activity takes place also. In solid solutions where two-phase domains are not arisen, piezoelectric activity is absent.

---

5. Effects caused by AFE nanodomains in PZT-based coarse-grained ceramics with compositions from the morphotropic boundary region

The PZT-based solid solutions used for manufacturing of the working elements for devices have compositions located within the MPB region in the "composition–temperature diagram of phase states of PZT. For a long time, it has been considered that FE domains with the rhombohedral and tetragonal types of crystal lattice distortions exist within the sample's volume for solid solutions from this region.

The monoclinic phase in PZT solid solutions with compositions belonging to the MPB region was first reported in ^[39,40,41]. All results of research done on this topic are presented and analyzed in a series of reviews ^{[42,43,44,45]}. In the said reviews, one can find all references on original studies devoted to investigations of the MPB region in PZT.

In the case of the PZT the local decomposition of the solid solution in the vicinity of the interphase boundaries (IPB) is the unaccounted phenomenon. The boundaries between the domains of the tetragonal and rhombohedral phases coexisting within one single-crystalline grain are exactly such boundaries. These two coexisting phases are the phases with different inter-plane distances and different parameters of their crystal lattices. In the immediate vicinity of such IPBs the local decomposition of solid solution takes place to lower the elastic energy. Analogous phenomenon in the case of the PZT-based solid solutions with coexisting domains of the FE and AFE phases was considered in Section 2.2. The ions with larger ionic radii are expelled into the domain with larger parameters of the crystal lattice and the ions with smaller ionic radii are moved into the domain with smaller crystal lattice parameters (the ions in equivalent crystallographic positions are referred to here). Due to this decomposition, the chemical composition of solid solution in the vicinity of these interphase boundaries differs from the chemical composition inside the domains of both phases. As a result the segregates with the crystal lattice close to the parent solid solution composition but still different are formed.

The ions of zirconium and titanium are shifted inside the domains with different crystal lattice parameters in the process of local decomposition. As a result local zirconium-enriched regions appear. The antiferroelectric state can be realized in these local regions.

Several recent publications pointed out the possibility of the existence of AFE ordering in the PZT solid solutions with compositions from the MPB region. The results of these publications were discussed in ^[46].

The presence of segregates leads to a series of specific effects characteristic to the boundaries between the coexisting domains with the AFE and FE types of ordering (see, for example, the review ^[23]). The search for such effects and their investigations in the PZT-based solid solutions with the compositions from the MPB region of the "composition–temperature" phase diagram was the goal of ^[46]. In no case, do we try to assert the absence of the monoclinic phase in the PZT solid solutions. We only want to emphasize that there are physical effects that have not been taken into account during the interpretation of experimental results and during the identification of the crystal structure of solid solutions.

---

5.1. PZT-based coarse-grained ceramics

We have developed a procedure for the manufacturing of PZT ceramics (with different ion substitutions) with compositions located near the boundary between the tetragonal and rhombohedral phases in the "composition–temperature" phase diagram with a grain size exceeding 20 μm ^[46]. Manufactured ceramic samples are characterized by a high degree of the composition homogeneity in the bulk of the substance. This has been confirmed, first of all, by the grain size and, secondly, by the extremely small width of the MPB region (less than 0.5%) in the investigated seven-component PZT-based solid solutions with compositions (Pb_0.9Ba_0.05Sr_0.05)_0.985(Li_0.5⁺La_0.5³⁺)_0.015(Zr_1−xTi_x)O₃.

According to the data available in the literature, the grain size of the PZT ceramic samples usually used in experiments is of the order of several micrometers. That is why the rhombohedral and tetragonal phases are in different grains and until recently it has been very difficult (or even completely impossible) to investigate effects caused by the interphase domain boundaries. In this case, the grain boundaries play the role of the interphase boundaries. It is common knowledge that the inter-grain boundaries accumulate a lot of impurities as well as lattice imperfections due to impurities. It is understood that there is no gradual conjugation of crystal planes in this case. The sizes of crystal grains in our samples have been of the order of 30 to 40 microns. The domains of two phases coexisting within one crystallite are separated by the coherent interphase boundaries (CIPBs) of the atomic scale and character. There were no discontinuities of crystal plains (we have seen it using TEM) and the boundaries had a coherent character without dislocations and the concentration of the elastic stress. A high degree of the homogeneity of samples has allowed us to study the kinetics of the development of segregates in the vicinity of СIPBs along with the physical effects caused by these CIPBs.

In our opinion, it is important to note one more peculiarity of the majority of publications on the monoclinic phase in PZT-based solid solutions with compositions from the MPB region of the phase diagram. Because of the wide region of coexistence of phases, the exact phase boundaries between various phases cannot be located using diffraction data. The wide region of phase coexistence is a convincing characteristic feature of the inhomogeneity of samples. The last circumstance is an additional factor contributing to the uncertainty in the determination of the crystal structure of solid solutions.

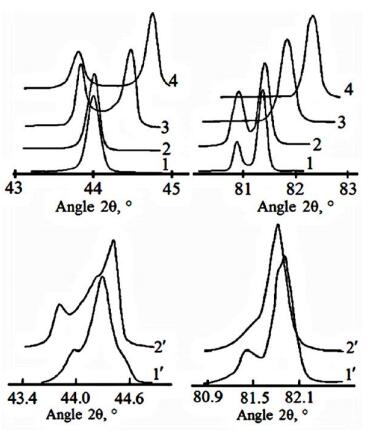
Profiles of the (200) and (222) X-ray lines for the above solid solutions with compositions from the MPB region of the phase diagram are presented in Figure 9. The coexisting domains with different types of the crystal lattice distortions are present in the bulk of these samples. Availability of such coarse-grained ceramics (let us recall, that the size of ceramic grains have been in the range of 30–40 μm) made it possible to investigate specific effects caused by the coexistence of domains with the FE and AFE orderings within a single crystalline grains.

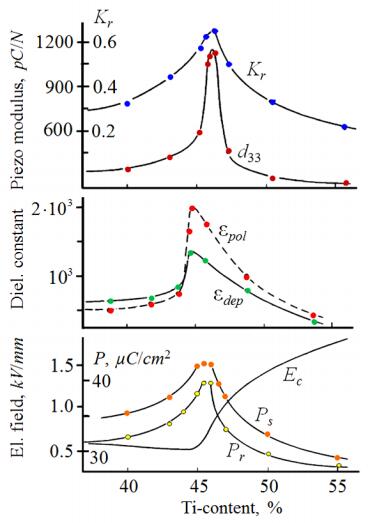
The concentration dependences of the main dielectric and piezoelectric parameters of the (Pb_0.9Ba_0.05Sr_0.05)_0.985(Li_0.5La_0.5)_0.015(Zr_1−xTi_x)O₃ system of solid solutions are depicted in Figure 10. As it seen from these dependences, all parameters have a pronounced maximum located in the MPB region of Zr/Ti compositions. On the one hand, this fact confirms the conclusions about the nature of behavior of these parameters in the vicinity of the MPB made earlier. However, a special attention has to be paid to the following fact. The MPB region of solid solutions under consideration is very narrow (not exceeding 0.5%), but the interval within which the parameters change is wide. In particular, for the coefficient of the electromechanical coupling, K_r, dielectric permittivity, ε, and polarization this interval is of the order of 10%. At the same time, the interval of high values of the piezoelectric modulus d₃₃ is narrow. We want to draw special attention to the magnitude of the piezoelectric modulus d₃₃ which reaches 1200 pC/N. Additional heat treatment leads to an additional increase of this modulus by 15–20%.

We will focus only on two physical effects among a number of others (discussed in ^[46]) caused by the presence of nanodomains of the AFE phase in the solid solutions under consideration.

---

5.2. Diffuseness of the phase transition from paraelectric to ordered state

The diffuseness parameter in FE and AFE materials defines the temperature interval above the Curie point in which domains of the ordered phase appear. In PZT based solid solutions the diffuseness of the phase transition is defined, as a rule, by the location of the composition of the considered solid solution in the phase diagram. A considerable increase of the phase transition diffuseness is characteristic of the substances, in which the difference in energies of the FE and AFE states is small and the domains of these phases coexist.

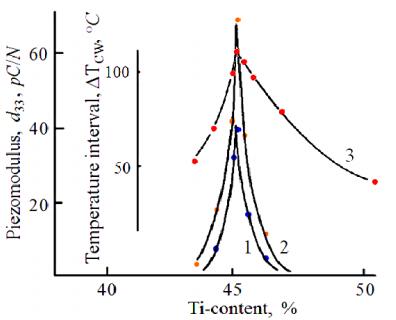
The dependence of the temperature interval, ΔT_cw, within which the deviation from the Curie–Weiss law takes place, on the Ti-content for the (Pb_0.9Ba_0.05Sr_0.05)_0.985(Li_0.5La_0.5)_0.015(Zr_1−xTi_x)O₃ system of solid solutions is given in Figure 11. This temperature interval characterizes the diffuseness of the paraelectric phase transition. As one can see the diffuseness of the paraelectric phase transition in this system of solid solutions also depends on the solid solution composition. The maximum diffuseness of the phase transition is observed in the solid solutions with Zr/Ti compositions belonging (according to the X-ray data) to the MPB region of the diagram of phase states.

---

5.3. Local decomposition of solid solutions in the paraelectric phase

The coexisting domains of the tetragonal and rhombohedral FE phases have different interplanar distances. In the said substances, equivalent sites of the crystal lattice are occupied by ions, which have different sizes and/or different charges. The A-sites of the perovskite crystal lattice are occupied by ions with different ionic sizes and charges (Pb²⁺, Ba²⁺, Sr²⁺, La³⁺, Li⁺), therefore, the local decomposition of the solid solution along IPB may be accompanied by the local disturbance of electronegativity. Thus, the formation of the heterophase structure is accompanied by the disturbance of samples' chemical homogeneity. At high temperatures, when the phases do not coexist, the samples remain homogeneous.

The local decomposition of the PZT-based solid solution in the vicinity of CIPBs leads to the appearance of the two types of local domains. One type is the local domain enriched with lead zirconate and the other type is the local domain enriched with lead titanate. The latter type of titanium-enriched domains as well as the whole matrix must exist in the FE state at the temperature below the Curie point. This is the reason why it is difficult to reveal their manifestation against the general background. However, the lead zirconate enriched domains may be in the AFE state, which differs markedly from the FE state. Thus, within the solid solution from the MPB region of compositions there exist specific FE + AFE domains formed as a pair of these phases as a result of the local decomposition of the solid solution. This system of domains of coexisting phases manifests a number of specific effects, which are not characteristic of other dipole ordered systems. This circumstance gives an opportunity to observe these characteristics experimentally.

One can easily control the microstructure of solid solutions since the inhomogeneous structure of the FE–AFE domains and segregates in the vicinity of the interphase boundaries appear in the process of the phase transition (above the Curie point) which itself can be easily controlled by an electric field or pressure. The considered physical process allows the creation of textured domain structures already in the paraelectric phase with the help of an external electric field applied to a sample at temperatures far above the Curie point. An analogous process has been considered and discussed above in the Section 4 where the case of PZT-based solid solutions from the FE–AFE region of the diagram of phase states is considered. The influence of thermal treatments in the paraelectric phase on piezoelectric modulus is demonstrated in Figure 8.

Let us now discuss the PZT-solid solutions with compositions belonging to the MPB region of the phase diagram. The results obtained as a result of special thermoelectric treatments with application of an electric field (at T > T_C) to the system of solid solutions with the (Pb_0.9Ba_0.05Sr_0.05)_0.985(Li_0.5La_0.5)_0.015(Zr_1−xTi_x)O₃ compositions are presented in Figure 11. In this case, the thermoelectric treatments have been performed at temperatures above the Curie point and an electric field E = 120 V/mm has been applied to samples at temperatures T_C(x) + 50 ℃. The samples were kept in the field during 20 min (curve 1) and 40 min (curve 2). After that, the field was switched-off, samples were cooled down to the room temperature without electric field, and then the piezoelectric coefficient d₃₃ was measured. Obtained results are analogous to the results obtained on the samples with the coexisting FE and AFE phases. The solid solutions become piezoelectrically active only if their Zr/Ti content corresponds to the MPB region of the phase diagram. This is one more experiment indicative of the existence of domains of the AFE phase in the solid solutions with compositions from the MPB region.

Both these effects are cause by the presence of the two-phase (АE + AАE) domains and their texturing by an electrical field at the temperatures above the Curie point. Such an experimental approach makes it possible to obtain high piezoelectric properties of the PZT-based solid solutions. More remarkable is the possibility of obtaining high (more than 1000 pC/N) values of the piezoelectric module in hard ferroelectric ceramic materials (surprising, in our view, from the standpoint of the established ideas is the obtaining of PZT-based materials with a quality factor Q $\cong$ 2000 and a piezoelectric module of d₃₃ $\cong$ 800 pC/N). Relying on widely advertised ideas about the monoclinic phase in morphotropic solid solutions, researchers relying on the properties of the monoclinic phase were not even able to approach such values. In our opinion, this is impossible based on widely advertised ideas about the monoclinic phase.

---

6. Conclusions

The AFE states and phase transitions involving these states have been investigated to a much lesser extent than the FE states and FE phase transitions. The physical effects caused by the coexistence of the AFE and FE phases in ferroelectric substances have been studied to a lesser degree.

Materials in which the phase transition from the FE state to the AFE state takes place have been used for the energy storage and conversion for many years. The release of energy with enormous pulse power takes place at this phase transition (caused by pulsed mechanical loads or, simply, by impact). The conversion of mechanical energy of the impact into electric energy happens when the operating FE element is depolarized. These materials are intendent mainly for special (military) applications.

In the materials discussed in this article, the initial and final states must necessarily be single-phase. The coexistence of domains of the FE and AFE phases leads to a sharp decrease in the efficiency of accumulation and conversion of energy.

We presented examples of possible applications of materials in which the inhomogeneous state of coexisting domains of the FE and AFE phases is realized. These examples include the possibility of manufacturing of materials with a negative refractive index as well as materials with controlled piezoresonance parameters.

In our opinion, the most significant for possible applications result is the demonstration of the possibility of ordering of nanodomains with the AFE structure in the PZT-based solid solutions from the morphotropic region of the phase diagram. The values of the piezoelectric characteristics obtained in such solid solutions have been impossible to achieve using methods based on existing concepts.

---

Acknowledgments

Authors are thankful to Dr. R. Corey for reading the manuscript.

---

Conflicts of interest

The authors declare no conflict of interest.

---