1. Introduction
In recent years, piezoelectric generators have been widely investigated for harvesting the kinetic energy from the ambient environment and convert it into electrical energy [1,2,3]. It has been demonstrated that the piezoelectric ceramics, such as lead-zirconium titanate (PZT), barium titanate (BaTiO3) and zinc oxide (ZnO) could be practically realized as a microelectronic and even nanoelectronic device, and the conversion efficiency could be still satisfying. Currently, many one-dimensional and two-dimensional inorganic piezoelectric nanostructures with wire, tube and branch type formations are studied to improve the yield of the miniaturized devices [4,5]. However, due to environmental issues and problems with high brittleness and poor biocompatibility, the efforts have been directed to find analogs to the piezoelectric oxide materials, mainly with polymeric [6]. One of the most studied piezoelectric polymers is polyvinylidene fluoride (PVDF) in β-phase for variety of sensing and energy harvesting applications [7,8,9]. One of its major advantages is the great durability at deformation—PVDF can stand high stress greater than 10 GPa without polymer chains damage and material degradation, because of high elasticity. It was found that high quality PVDF films could be deposited by spin coating, only if few micrometers or few hundred of nanometers thickness is required. Otherwise, the average roughness of the surface has been not satisfying. In addition, voids and other defects have occurred, making the piezoelectric element, involving such film inefficient [10]. That's why for nanosystems where thinner films are needed alternative approach for PVDF growing must be found. In this way, it is expected that the piezoelectric energy harvesting approach will be established as a reliable technology for making self-sufficient power supply for low consumable electronics, in particular flexible and stretchable electronics. For this purpose, the rest of the layers in the harvesting device must consist of suitable organic materials, as well. One of the most suitable techniques for polymer coatings deposition in this case is spray coating, due to the possibility for precise control of the temperature and aerosol/particles yield, leading to self-assembling of the polymer chains and resulting in smooth defectless films [11].
In this paper, piezoelectric polymer PVDF films were deposited by spray deposition on flexible substrate of polyethylene terephthalate (PET), coated with conductive polymer poly(3, 4-ethylenedioxythiophene) polystyrene sulfonate (PEDOT:PSS), serving as an electrode film. The effect of the deposition conditions on the microstructure and morphology of the PVDF coatings was investigated and the piezoelectric response of the system PEDOT:PSS/PVDF/Ag with single polymer/polymer interface was measured. It was found that PEDOT:PSS could serve as a suitable base for growing of uniform, well ordered layer and then piezoelectric voltage could be measured.
2. Materials and method
The PET substrate was cleaned by isopropyl alcohol in a ultrasonic cleaner for 180 s. PEDOT:PSS solution 3.0% in H2O, high-conductivity grade was spin coated on PET for producing film with thickness 120 nm, serving as a bottom contact. The samples were soft-baked at 50 ℃. PVDF granules were dissolved in methyl-ethyl-ketone (MEK) and the solution prepared was stirred 1 hour at 60 ℃, following by filtration. Solution for spraying was prepared with two different concentrations (10 wt% and 20 wt%). Each of them werepulverized simultaneously with the PEDOT:PSS coated PET sample's heating at different temperatures in the range 30–80 ℃. The rest of the spray deposition conditions were fixed—spraying pressure was set to 3.8 bars, the nozzle orifice diameter to 200 µm, temperature maintenance accuracy was 0.2 ℃. Top contacts of thermal evaporated silver films were configured through shadow mask. Their shape (rectangular with size ratio width:length = 3:1) and location on the PVDF surface (near the periphery of the substrate) were selected based on previous study, where it was found that such patterning provides the highest sensitivity [12]. Scanning electron microscopy was conducted by SEM microscope JEOL JSM-6390LV. Fourier transform infrared spectrum (FTIR) was recorded by Shimadzu spectrophotometer IRPrestige-21 in transmission mode to identify the molecular components and the typical bonds for piezoelectric phase. Films thickness and roughness profile was measured by Tencor Alpha Step 200 profiler. Vibrational tests were conducted by laboratory made stand and the generated electrical signals were monitored on oscilloscope DQ2042CN. The setup for testing is provided elsewhere [13]. The ready device is fixed to an elastic beam that performs the vibration with a certain amplitude and frequency. Using metallic wires, the electrical connection from the electrodes to the measurement equipment is set, using silver paste. The vibration frequency was 50 Hz for all measurements, but the input voltage of the electromechanical system varied from 1 V, 3 V and 5 V, where 1 V corresponded to 25 N = 2.65 g, 3 V = 29 N = 2.95 g; 5 V = 34 N = 3.45 g.
3. Results and discussion
The total eight combinations of devices with PEDOT:PSS/PVDF layers were examined by SEM with a magnification of 10000 times and compared in Figure 1. As can be seen from the microscopic images, the PVDF layer produced from 10 wt% spray deposited at 30 ℃ is non-uniform, because the solvent evaporation rate is very low. This is due to the relatively low temperature during spraying, which in turn causes the layer to leak. The layer lacks density and at 50 ℃ was still irregular. By increasing the temperature to 70 ℃, an improvement in the layer morphology was noted, with increased flatness and uniformity.
At 80 ℃, dust-like particles were observed on the substrate as a result of the very strong heat field above the PEDOT:PSS, which causes the solvent molecules to be removed quickly, before the aerosols to reach the substrate. At PVDF solution with concentration of 20 wt% higher uniformity and smoother layers were observed at lower temperatures (50 ℃) compared to 10 wt% PVDF. When spraying at temperatures of 80 ℃, it was noted that the PVDF layer is irregular with a high average roughness. On the next substrates, the PVDF layers were deposited at the optimized temperatures—at 10 wt% PVDF solution the optimal temperature of 70 ℃ was used and at 20 wt% PVDF solution the optimum was 50 ℃. These combinations of deposition conditions produced sufficiently uniform layers to form large contact area with the electrodes to be applied thereto. As a result, it is expected a uniform polarization reaction and stable piezoelectric response of the polymer. Therefore, they were used for further analyses.
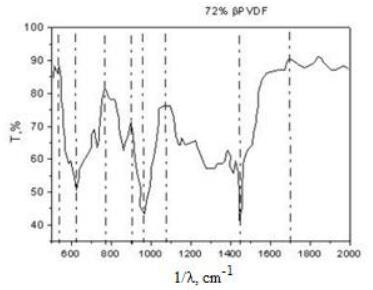
Regarding the presence of the typical piezoelectric β-phase in the PVDF polymer, FTIR analysis was conducted (Figure 2). For the sample prepared at 10 wt%, it was found that the spectrum very well coincides with the data available in the literature [14,15,16]. The characteristic absorption bands at wavenumbers 510–520,620–625,880–900, 1090, 1240, 1444, 1695 cm−1 presented and their intensity determined 72% piezoelectric phase. The rest of the bands in Figure 2 are related to α- and γ-PVDF phases, as well as some weak signal are generated due to PEDOT:PSS substrate. Some multiple overlapping bands in close range of few cm−1 are caused from impurities introduction due to the vacuum-free deposition process. For comparison, the highest reported content of β-phase in commercially available devices using PVDF is between 75% and 85% at thicker films in the micrometer range [17]. For the sample spray deposited from 20 wt% PDVF solution there was great dissipation of IR beam due to the higher roughness of the surface, which hinder the precise sweep of the transmitted bands as a function of the wavenumber. Nevertheless, we think that the results from FTIR are similar, because the voltage generated is with the same order of magnitude and close in value to the previous sample.
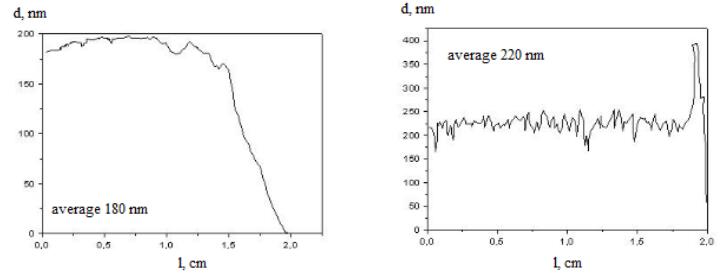
The recorded profiles of both films surfaces (Figure 3) showed PVDF film thicknesses of 186 nm and 220 nm, respectively produced from 10 wt% and 20 wt% solution concentration. The corresponding average roughness was approximately 12 nm and 25 nm across the sample length of 1 cm, which is evidence for excellent uniformity.
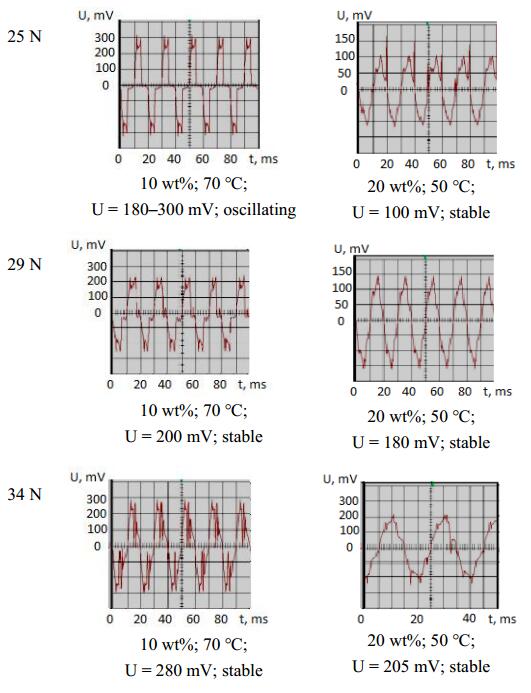
After silver contacts deposition electrical characteristics in dynamic mode for both optimal cases (10 wt%, 70 ℃ and 20 wt%, 50 ℃) are measured in case of energy harvesting application. Figure 4 shows the output voltages of the two microelements. At the sample with 10 wt% PVDF layer and 25 N input vibrations, oscillations in the output voltage were observed, probably due to the lower content of piezoelectric polymer in the layer. Increasing the input vibrations' amplitude the generated voltage increased, but the distortions in its shape also increased. If a comparison is made with the signals generated under the same input conditions, but from the sample obtained at 20 wt%, 50 ℃, it can be seen that the voltage is more stable, with a more clearly defined shape, probably because of the higher density of the layers and higher piezoelectric active polymer content. However, it has lower amplitude for each of the input stimuli. As was detected by the profiler, the surface of the sensor obtained at 20 wt% and 50 ℃ showed higher roughness, which is probably the reason for more unstable electrical contact with the electrode and loss of energy (voltage drop) at the polymer/conductive polymer interface. This could explain smaller amplitude of the generated piezoelectric voltage despite the higher concentration of PVDF. Concrete values for the amplitude of the generated piezoelectric voltage at different supplied dynamic load can be seen under each oscillogram in Figure 4.
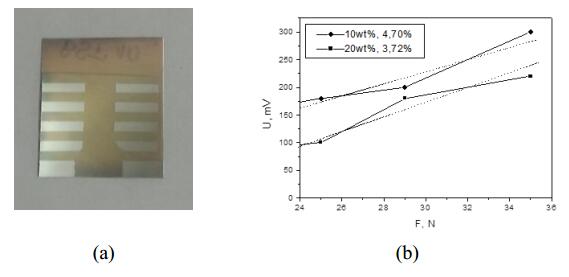
The device can perform dual functions, serving as a force (or pressure) sensor too. The dependence of the generated voltage on the applied force in static mode is shown in Figure 5b (photo of the prepared sample is shown in Figure 5a), from where the linearity of the sensor in certain force range can be determined. The mean deviation from the ideal linear response for the sample obtained at 10 wt% PVDF is 48 mV, corresponding to 4.70% non-linearity (or linearity of 95.3%). For the sample obtained at 20 wt% PVDF this value is 44.6 mV, which corresponds to non-linearity of 3.72%. Voltage was registered when the weight is released from the sample and not when applied to it, which probably means that the element is better suited for working as a tension sensor rather than to compression.
The polymer layer sensor exhibited a wider dynamic range, as compared with the PZT based sensor with similar constructive design and films thicknesses [12]. The piezoelectric response strength is comparable. At the same time, spraying technology is simpler, cheaper and faster to apply. In order to estimate the reliability of the structures with the enhanced electrical behavior (10 wt% of PVDF), they were subjected to a large number of vibration cycles. The set cycles were 6000, determined on the basis of the vibration period (the frequency of the input voltage of the electromechanical system) and the duration of vibrating. The goal was to determine the degree of degradation or sensitivity of the PEDOT:PSS/PVDF interface against repeating mechanical load. The output voltages were then measured again and it was found that there was a decrease in the amplitude reflected in Table 1. The results show excellent stability of the structures, which may ascribe to the closer Young modulus and high elasticity of both polymeric layers—piezoelectric and electrode.
Table 1. Deviation of the generated piezoelectric voltage from 10 wt% PVDF after applying multiple vibrations with different intensities.
| Parameters of the sample |
Case 1 |
Case 2 |
Case 3 |
| Mechanical load, N |
25 |
29 |
34 |
| Uo, mV |
180 |
200 |
300 |
| U6000, mV |
172 |
180 |
250 |
| Relative deviation,
% |
4.4 |
10 |
17 |
4. Conclusion
Piezoelectric structures working as both energy harvesting and force sensors have been successfully obtained by spray deposition of PVDF on flexible substrate coated with conductive polymer. The results show that for specific solution concentration (PVDF 10 wt%) if heating the substrate at 70 ℃ smooth, uniform thin film with good adhesion on the conductive polymer coating and high content of piezoelectric phase could be obtained. As a result, energy harvesting device with small non-linear distortions of the signal and force sensor with high linearity can be fabricated. The PEDOT:PSS/PVDF interface demonstrated significant mechanical durability at multiple bending, making this technology and design approach preferable for flexible and stretchable electronics.
Acknowledgments
The work is funded by BNSF, grant No DH 07/13. The author is thankful to Prof. Kostadinka Gesheva from CL-SENES, BAS for the measured FTIR spectrum and Dr. Georgi Kolev from TU-Sofia for the PVDF material provided.
Conflict of interest
The author declares no conflict of interest.










 DownLoad:
DownLoad: