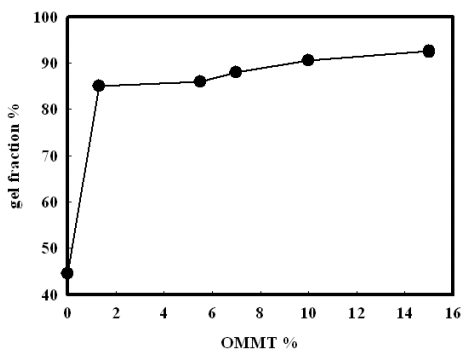
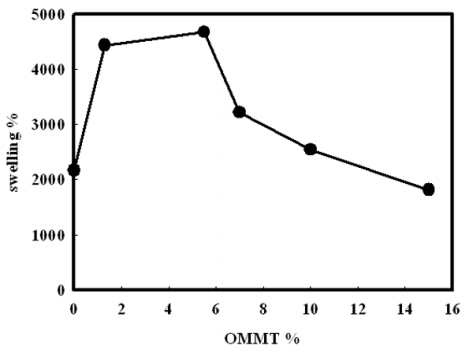
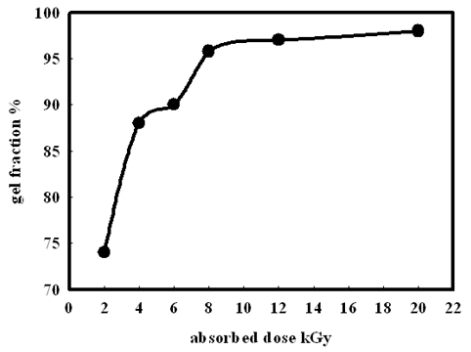
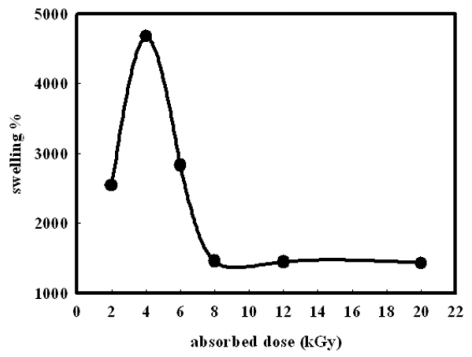
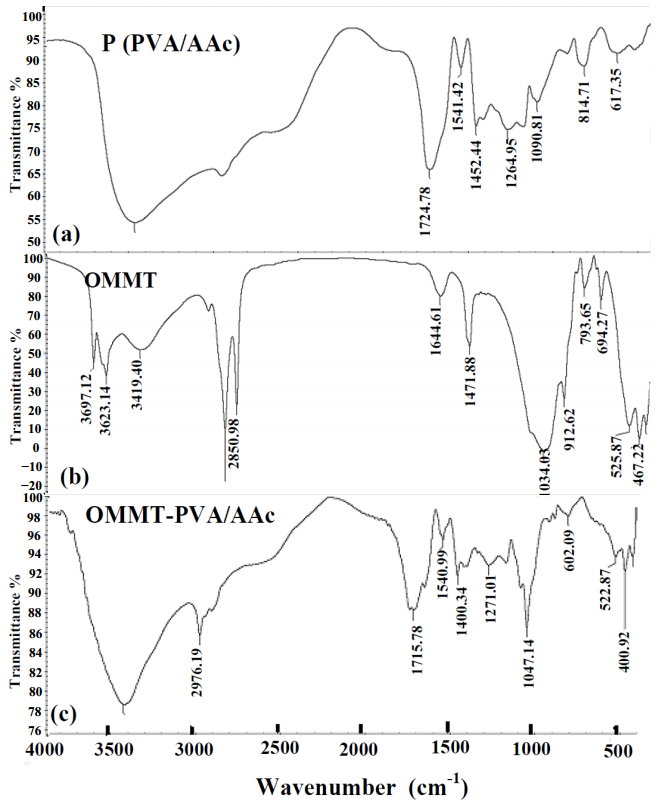
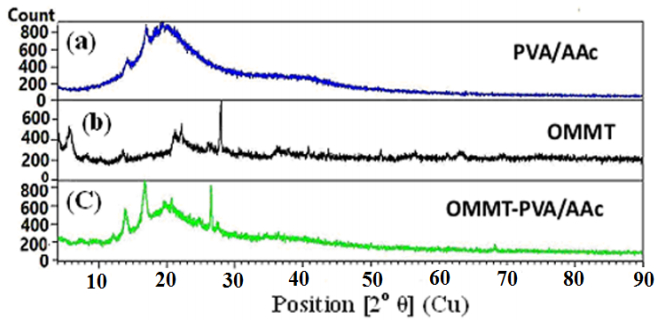
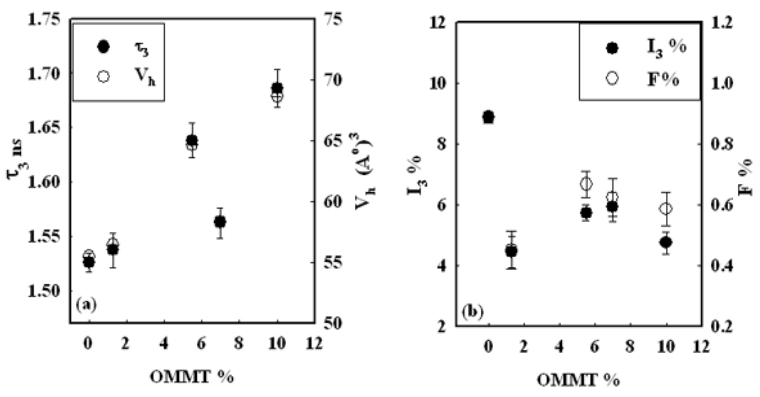
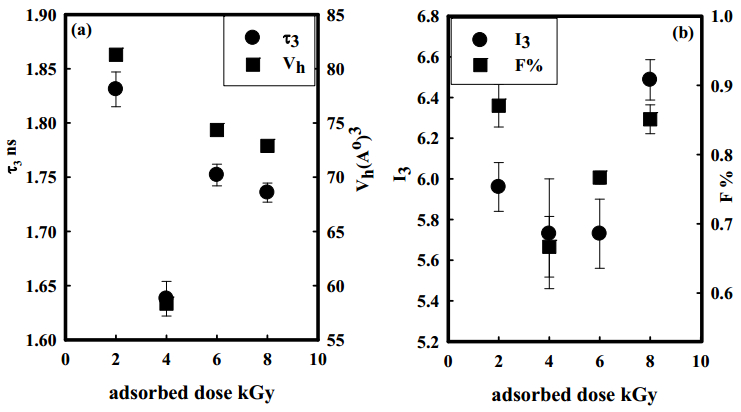
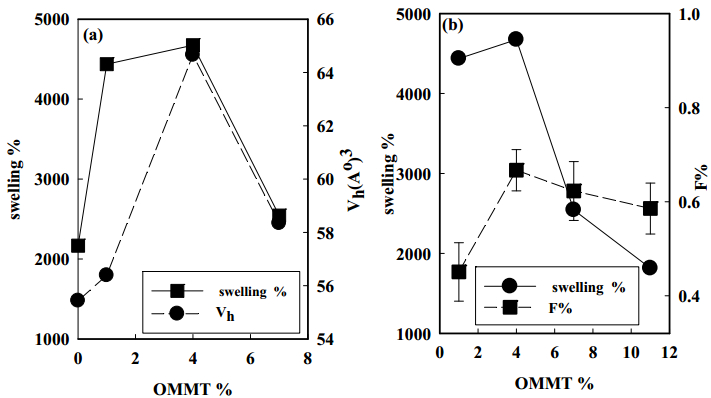
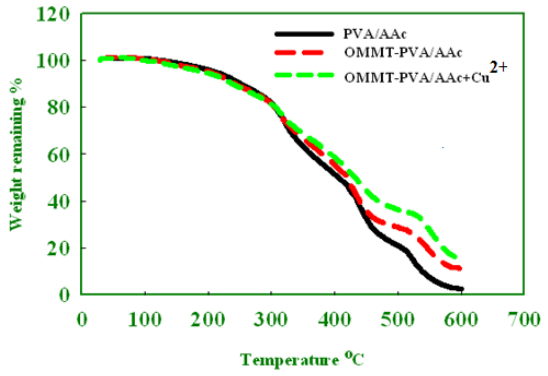
In the present work, preparation of organic montmorillonite-polyvinyl alcohol-co-polyacrylic (OMMT-PVA/AAc) nanocomposite hydrogels are performed with different OMMT ratios ranging from 1.3 to 15% using γ irradiation as initiator to induce crosslink network structure. These nanocomposites hydrogels are prepared to use in heavy metals water decontamination. The effect of clay ratio and absorbed dose on gel fraction and swelling% has been investigated. It is found that the gel fraction increases up to 92% with increasing the loaded OMMT to 15%, whereas the swelling% reaches its maximum value at a ratio of nanoscale clay of 6% and at an absorbed dose of 4 kGy. The thermal stability of PVA/AAc hydrogel and OMMT-PVA/AAc nanocomposite hydrogels has been determined by thermogravimetric analysis (TGA), which indicated a higher thermal stability of the nanocomposite hydrogel. The FTIR spectral analysis has identified the bond structure of the PVA/AAc hydrogel and the OMMT-PVA/AAc nanocomposite. The nanostructure of the composite as well as the degree of exfoliation of clay are studied by X-ray diffraction (XRD). Its free volume holes parameters (size and fraction) are investigated by means of positron annihilation lifetime spectroscopy (PALS).
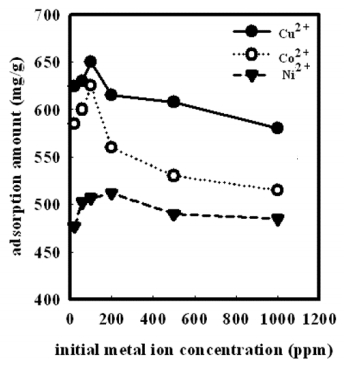
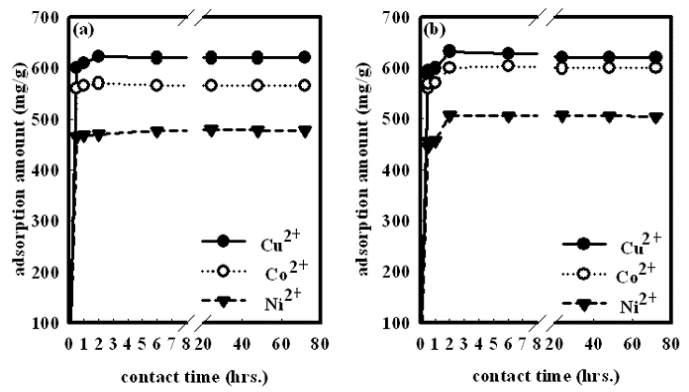
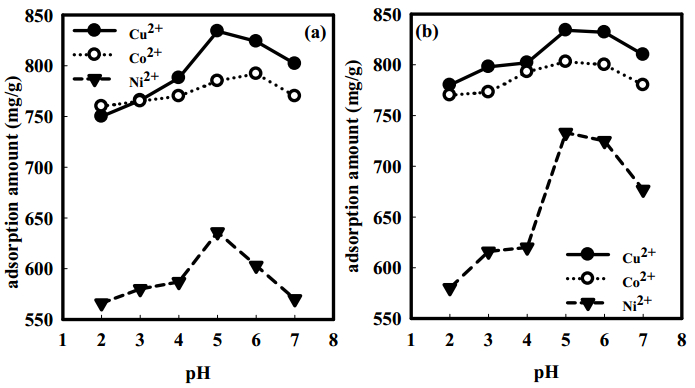
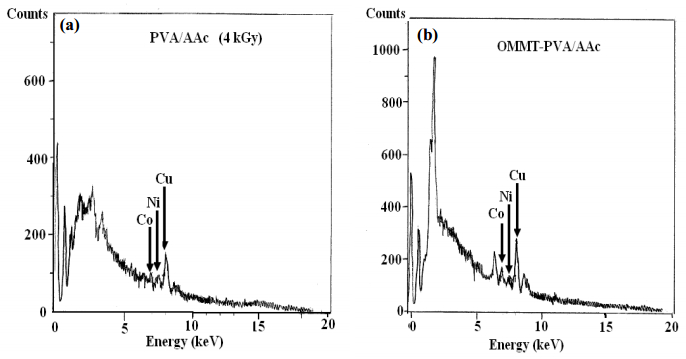
After loading the bulk and nanocomposites hydrogels with different heavy metals (Cu2+, Co2+ and Ni2+), UV spectroscopy is applied to determine the metal ion concentration before and after treatment. The distribution of heavy metals on the hydrogels is determined by energy dispersive X-ray (EDX). The factors affecting the heavy metal uptake, such as contact time, pH and metal ion concentration of solutions are studied.
The results have shown that, the presence of OMMT increases the thermal stability of PVA/AAc due to the hydrogen bond formed between them which, is confirmed by FTIR. In addition, the resulting gel fraction after irradiation with relatively low gamma absorbed dose increased by 120%, enabling the sample to be reused for several times. In addition, the metal adsorption has increased from 194, 185, 144 mg/g for Cu2+, Co2+ and Ni2+ respectively in case of previously prepared PVA/AAc hydrogel to 835, 785, 636 mg/g for Cu2+, Co2+ and Ni2+ respectively for OMMT-PVA/AAc nanocomposite.
1.
Introduction
The neural network modeling approach in the form of differential equations has been intensively applied by numerous researchers in different areas of science, engineering and medicine. The construction of a neuronal network model and its analysis are key goals in many practical applications. Indeed, the applications of such models include a variety of problems, such as optimization problems, associative memory, parallel processing, linear and nonlinear programming, including algorithms, computer vision, pattern recognition and many others [1,2].
The Cohen–Grossberg-type of neural networks [3] are an important class of neural network models that are widely used as a framework in the study of partial memory storage and global pattern formation phenomena [4,5,6]. Due to its important applications, the properties of different Cohen–Grossberg neural network models have been intensively studied, including some very recent results [7,8]. This class of neural networks also generalizes some of the essential neural network models, such as Hopfield neural networks [9] and cellular neural networks [10,11].
In order to create more adequate neural network models, researchers have generalized and extended the classical Cohen–Grossberg-type of neural networks in different directions. One line of generalization relates to the consideration of the affects of impulsive disturbances on their qualitative behavior. In fact, short-term perturbations are natural for most applications of such neural networks, and their presence may affect the dynamic properties of the models. The apparatus of impulsive differential equations [12,13,14] has been widely applied to develop and investigate impulsive neural network models. Using the impulsive modeling approach, different classes of impulsive Cohen–Grossberg neural networks have been proposed [15,16,17]. The closely related impulsive control approach [18,19] has also been examined effectively [20,21].
The fractional calculus approach has also been applied in the neural network modeling. Indeed, models with fractional order dynamics generalize the integer-order models and have numerous advantages, including universality, more flexibility and hereditary properties [22,23,24,25]. Numerous researchers contributed to the development of fractional-order Cohen–Grossberg neural network models and the study of their properties [26,27,28,29,30].
In the development of the fractional calculus fruitful direction of generalization, the most used fractional order derivatives are these of the Grunwald–Letnikov, Caputo and Riemann–Liouville types. Note that there are some restrictions when the above notions are applied to real-world models. Some of the restrictions are related to their properties and mainly to the nonexistence of a straightforward rule for the derivatives of compositions of functions. To overcome such difficulties, several researchers proposed new approaches, such as Caputo–Fabrizio [31], Caputo–Hadamard [32], including variable fractional order derivatives [33,34] without singular kernels, and generated new fractional models.
One of the recently applied extended fractional calculus approaches is based on the use of the conformable or fractional-like derivatives [35,36] which offer some computational simplifications related to derivatives of compositions of functions. Some interesting and important results for systems with conformable derivatives are proposed in [37,38,39,40]. Physical interpretations of the conformable derivatives have been given in [41,42]. Due to the advantages of such derivatives that are limit based and follow a very simple chain rule, the conformable calculus begins to be used in the modeling of several phenomena studied in economics [43], medicine [44] and forecasting [45].
The impulsive generalization is also applied to the conformable calculus approach. However, the results in this direction are very few and the theory of impulsive conformable systems is still not completed [46,47,48]. Also, to our best knowledge, the combined impulsive conformable modeling approach has not been applied to Cohen–Grossberg neural network models, and this is the main goal of this article. In fact, the proposed conformable technique seems to be very suitable for neural networks because of the simplifications in calculations offered.
In practical implementations, the global exponential stability for integer-order models [49,50] and Mittag–Leffler stability for models with fractional dynamics [51,52] are ones of the most important neural network's behaviors. Hence, there are numerous results that provided efficient asymptotic stability, exponential stability and Mittag–Leffler stability criteria for Cohen–Grossberg neural networks [3,5,6,7,15,21,26,27,30]. However, there are also cases when the classical asymptotic and Mittag–Leffler stability strategies cannot be applied [53]. In some of these cases, when the trajectories of a neural network model are not mathematically stable, but the system behavior is admissible from the practical point of view, the concept of practical stability is more relevant [54,55].
In the past decade, the practical stability concept has been rapidly developed [56,57], and has been extended to the practical stability with respect to manifolds notion [58]. Indeed, the practical stability is useful in many applied systems when the dynamic of the model is contained within particular bounds during a fixed time interval. In such cases, the global asymptotic notion is not applicable. The practical stability strategy is also very efficient when a neuronal state is unstable in the classical sense and yet, state trajectories may oscillate sufficiently near the desired state such that its performance is admissible, which does not imply stability or convergence of trajectories. In addition, there are many applied systems that are stable or asymptotically stable in the classical sense, but actually useless in practice because of the small or inappropriate stability domain or attraction domain. The stability with respect to manifolds concepts are generalizations of the stability notions for single trajectories and are related to the study of stability properties of a manifold of states. Such concepts are of considerable interest to networks capable of approaching not only one steady state. The extended practical stability with respect to manifolds concept has been applied to integer-order Cohen–Grossberg models in [59] and to some conformable models [60]. However, there is no one existing result on practical stability with respect to manifolds for impulsive conformable Cohen–Grossberg neural networks. It is clear that this task is attractive and important in the analysis of such neural network models.
The main goal of this research is to propose an impulsive conformable Cohen–Grossberg-type neural network model. Also, the adoption of the practical stability with respect to manifolds notion is an essential motivation for our study.
The innovations of this article can be described as follows:
(1) We propose a new impulsive conformable Cohen–Grossberg neural network model. The advantages of the conformable modelling approach can be used in the analysis of the properties of the introduced model. The impulsive perturbations can also be used to stabilize and control the proposed model.
(2) We introduce the practical stability with respect to manifolds notion. Using modifications of the Lyapunov technique, new criteria are proposed, which guarantee the practical stability behavior of manifolds related to the newly suggested model.
(3) The BAM generalization of the introduced model is analysed, and the corresponding sufficient conditions for practical stability with respect to manifolds are established.
(4) We verify the efficiency of the established criteria by examples.
The structuring of the rest of the paper pursue the following scheme. In Section 2 some definitions and lemmas from conformable calculus are given. The conformable impulsive Cohen–Grossberg neural network model is introduced and the practical stability with respect to manifolds concept is adopted to it. Some preliminaries related to the Lyapunov functions method are also given. Section 3 is devoted to the main practical stability results established on the basis of a Lyapunov-type analysis. The case of BAM impulsive conformable Cohen–Grossberg-type neural networks is studied, and sufficient conditions for the practical exponential stability of the trajectories are proposed in Section 4. Illustrative examples are elaborated in Section 5. Some concluding comments are stated in Section 6.
Notations: R is the set of all real numbers, the set of all nonnegative real numbers will be denoted by R+=[0,∞), Rn denotes the n-dimensional real space with the norm ||y||=∑nι=1|yι| of an y∈Rn, y=(y1,y2,…,yn)T.
2.
Basic definitions, problem formulation and preliminary results
2.1. Conformable calculus definitions and lemmas
Here, we will present some basic definitions and lemmas related to the conformable calculus. Let τ0∈R+.
Definition 1. [47,48] The generalized conformable derivative of order α, 0<α≤1 for a function y(t):[˜t,∞)→Rn, ˜t≥τ0 is defined by
Let the time instants τ1,τ2,…, are such that
and y(τ+k)=lim{y(τk+ϕ), ϕ→0+}, y(τ−k)=lim{y(τk−ϕ), ϕ→0+}.
For k=1,2,…, we have [47,48]
Any function that has an α-generalized conformable derivatives for any t∈(˜t,∞) is called α-generalized conformable differentiable on (˜t,∞), and we will denote the set of all such functions by Cα[(˜t,∞),Rn] [48].
Definition 2. [47] Let y:[˜t,∞)→Rn. The generalized conformable integral of order 0<α≤1 of y is given by
The following properties of the generalized conformable derivatives and integrals will be applied in our future analysis [46,47,48].
Lemma 3. [48] If the function y∈Cα[(˜t,∞),R] for 0<α≤1, then
Lemma 4. [48] Assume that X(y(t)):(˜t,∞)→R and 0<α≤1. If X(⋅) is differentiable with respect to y and y∈Cα[(˜t,∞),R], then for t∈[˜t,∞) and y(t)≠0, we have
where X′ is the derivative of X(⋅)
Remark 5. The result represented in Lemma 5 is a simple chain rule which is not applicable for the classical fractional-order derivatives. More results on the conformable derivatives can be found in [35,36,37,38,39,40,46,47,48].
Remark 6. To emphasize more advantages of the application of fractional derivatives, we note the following properties for α∈(0,1] and x,y∈Cα[(˜t,∞),R] which follow directly by Definition 1 [35,36,41,48]:
(a) Dα˜t(ax(t)+by(t))=aDα˜t(x(t))+bDα˜t(y(t)) for all a,b∈R;
(b) Dα˜t(tp)=ptp−1(t−˜t)1−α for any p∈R;
(c) Dα˜t(x(t)y(t))=x(t)Dα˜t(y(t))+y(t)Dα˜t(x(t));
(d) Dα˜t(x(t)y(t))=y(t)Dα˜t(x(t))−x(t)Dα˜t(y(t))y2(t);
(e) Dα˜t(x(t))=0 for any x(t)=λ, where λ is an arbitrary constant.
For the classical fractional derivatives [22,23,24,25], including the Riemann-Liouville fractional derivative
where 0<α<1 and Γ(z)=∞∫0e−ttz−1dt is the Gamma function, and Caputo fractional derivative
the properties (b)–(e) do not hold, except for the statement (e) for a fractional derivative of Caputo. The reason for this is the application of the integral in the known definitions of fractional derivatives.
2.2. The Gohen–Grossberg impulsive conformable neural network model
In this section we propose an impulsive Cohen–Grossberg-type neural network model with generalized conformable derivatives as follows
where ι=1,2,…,n, n≥2 represents the number of the units, yι(t) is the state of the ι-th node at time t, the functions aι,bι,fj,Uι∈C[R,R+] and cιj∈R+, ι,j=1,2,…,n are the system's parameters in the continuous part, aι denote the amplification functions, bι are appropriate behaved functions, fj represent the activation functions, Uι denotes the external bias on the ιth node at time t, cιj represent the connection weights, yι(τk)=yι(τ−k) and yι(τ+k) in the impulsive condition are, respectively, the neuronal states of the ι-th node before and after an impulsive perturbation at τk and the impulsive functions Pιk∈C[R,R] represent the effects of the impulse controls on the node yι at τk, ι=1,2,…,n, k=1,2,….
For τ0∈R+ we define the initial condition corresponding to the model (1) as
where y0∈Rn.
A function φ∈Rn that satisfies the system (1) and the initial condition (2) will be called a solution of the initial value problem (1), (2), and will be denoted by φ(t)=φ(t;τ0,y0), where φ(t)=(φ1(t),φ2(t),…,φn(t))T.
According to the theory of impulsive conformable systems [46,47,48], the solution φ(t) of the initial value problem (1), (2) is an α-generalized conformable differentiable function, which is piecewise continuous with points of discontinuity of the first kind τk, k=1,2,…, at which it is left continuous. At the impulsive moments, the functions φ(t) is such that
The set of all such functions will be denoted by PCα[R+,Rn].
For example, for the solution of an impulsive scalar generalized conformable neural network of the type
where u∈R, a,b∈C[R+,R+], pk∈R, k=1,2,…, we obtain
We will study some stability properties of the introduced model (1) under the following hypotheses:
H1. The continuous functions aι∈R+, ι=1,2,…,n are such that there exist positive constants a_ι and ¯aι for which 1<a_ι≤aι(χ)≤¯aι for χ∈R, and a_=min1≤ι≤naι, ¯a=max1≤ι≤naι.
H2. The continuous functions bι∈R+ are such that there exist constants βι>0 with
for any χ∈R and ι=1,2,…,n.
H3. There exist Lipschitz constants Lfj>0 such that
for all χ1,χ2∈R, j=1,2,…,n.
Remark 7. The developed Cohen–Grossberg type model (1) with generalized conformable derivatives is an extension of the existing integer-order neural network models studied in [3,5]. It also extends some impulsive models investigated in [15,16,17,20,21] to the conformable setting. Since the concept of the conformable derivative overcomes some limitations related to the classical fractional-order derivatives, the introduced model is more suitable for applications than the models considered in [26,27,29,30]. In addition, considering impulsive perturbations will allow for the application of efficient impulsive control strategies [18,19,20,21,58,59].
2.3. Practical stability with respect to manifolds formalism
In order to apply the practical stability with respect to manifolds method [55,58,59] to the model (1), we consider a continuous function H:[τ0,∞)×Rn→Rm, H=(H1,H2,…,Hm)T, m≤n which defines the following (n−m)-dimensional manifold:
The defined above manifold, will be called a H-manifold.
Consider, also
and adopt the following notions [55,56,57,58,59].
Definition 8. If for given (λ,A) with 0<λ<A, y0∈MHτ0(λ) implies y(t;τ0,y0)∈MHt(A), t≥τ0 for some τ0∈R+, then the manifold MHt is said to be practically stable for the model (1).
Definition 9. If for given (λ,A) with 0<λ<A, y0∈MHτ0(λ) implies
where 0<α<1, μ,δ>0, and Eα(ν,o) is the conformable exponential function given as [47]
then the manifold MHt is said to be practically exponentially stable for the model (1).
Remark 10. Definitions 8 and 9 generalize and extend the classical stability notions to the combined practical stability with respect to manifolds case. The combined setting increases the benefits of both approaches. In some particular cases, the defined concept can be reduced to simple practical stability notions that are used widely in the applied problems [60,61,62,63]. For example, if the function that defines the manifold H(t,y)=0 only for y=0, then definitions 8 and 9 are the classical definitions of practical stability and exponential practical stability of the zero solution of the model (1), respectively. Similarly, if the manifold MHt includes only an equilibrium state y∗, i.e., H(t,y∗)=0, then the above definitions are reduced to the practical stability and exponential practical stability definitions of y∗, respectively. Other particular cases, such as practical stability and exponential practical stability of periodic and almost periodic solutions can be considered analogously. Thus, the proposed practical stability with respect to manifolds technique offers a high-powered mechanism which can be applied not only for single solutions, but also in the cases when manifolds of solutions are attractors for the models. This technique is also appropriate to investigate such manifolds that are not stable in the classical Lyapunov sense, but their dynamic is acceptable from the practical point of view [55,58].
We will also need the following additional hypothesis related to the specifics of the stability with respect to manifolds concepts.
H4. Each solution y(t;τ0,y0) of the initial value problem (1), (2) such that
where Ω>0 is a constant, is defined on [τ0,∞).
2.4. Conformable Lyapunov functions method
Consider the sets Gk=(τk−1,τk)×Rn, k=1,2,…, G=⋃∞k=1Gk.
In the further study, we apply a modified conformable Lyapunov function approach. A class of Lyapunov-like functions Lατk is defined as [47] a set of functions L(t,y):G→R+ that are continuous on G, α-generalized conformable differentiable in t, locally Lipschitz continuous with respect to y on each of the sets Gk, L(t,0)=0 for t≥τ0, and for each k=1,2,… and y∈Rn, there exist the finite limits
with L(τ−k,y)=L(τk,y).
For a function L∈Lατk, the upper right conformable derivative is defined by [47]
Denote by F(t,y)=(F1(t,y),F2(t,y),…,Fn(t,y))T, where y=(y1,y2,…,yn)T and
for ι=1,2,…,n.
Then, the generalized conformable derivative of the function L(t,y) with respect to system (1), (2) is [47]
If L(t,y(t))=L(y(t)), 0<α≤1, the function L is differentiable on y, and the function y(t) is α-generalized conformable differentiable on [τ0,∞), then Lemma 4 can applied componentwise.
It follows from (6) and (7) that
where yk=y(τ+k), k=0,1,2,….
For more information about the conformable modifications of the Lyapunov functions approach for impulsive control models, we refer to [46,47,48].
The next Lemma from [47] will be also necessary.
Lemma 11. If for the function L∈Lατk and for t∈[τ0,∞), y∈Rn, we have:
(i)
(ii)
for δ=const>0, ϱ∈ Cα[R,R+], then
where Wα(t−τk,o−τk)=Eα(−δ,t−τk)Eα(δ,o−τk), 0<α<1, k=0,1,2,….
3.
Main practical stability with respect to manifolds criteria
In this Section, we will apply the modified conformable Lyapunov-function approach to establish our main practical stability with respect to the manifold MHt criteria for the conformable impulsive Cohen–Grossberg neural network model (1).
Theorem 12. Assume that 0<λ<A, hypotheses H1–H4 hold and:
(i) there exists a function H:[τ0,∞)×Rn→Rm, m≤n, such that
where Γ=Γ(Ω) is a constant, Γ(Ω)≥1, Γ(Ω)λ<A for any 0<Ω<∞;
(ii) the parameters and the impulsive control functions of the impulsive conformable Cohen–Grossberg neural network model (1) satisfy:
Then, the manifold MHt is practically stable for the model (1).
Proof. For the given 0<λ<A and y0∈Rn let suppose that y0∈MHτ0(λ) and consider the solution y(t;τ0,y0) of the impulsive conformable Cohen–Grossberg model (1) corresponding to the initial condition (2).
We construct a Lyapunov-type function as
From condition (11) of Theorem 12, at the impulsive control instants t=τk, k=1,2,…, we have:
for k=1,2,….
From H1-H3 and conditions (9) and (10) of Theorem 12, for t≠τk, k=0,1,2,…, we obtain:
Now, from (13) and (14), according to Lemma 11 for δ=ϱ(t)=0, t∈[τ0,∞), we have
Hence, from condition (8) of Theorem 12, we obtain
and, therefore, the manifold MHt is practically stable for the model (1). □
Next, criteria for the practical exponential stability of the manifold MHt for the model (1) will be presented.
Theorem 13. Assume that 0<λ<A, hypotheses H1–H4 hold and:
(i) there exists a function H:[τ0,∞)×Rn→Rm, m≤n, which satisfies (8) for Γ(Ω)≥1 any 0<Ω<∞;
(ii) condition (11) of Theorem 12 holds and there exists a positive δ1 such that
and
Then the manifold MHt is practically exponentially stable for the model (1).
Proof. For the given 0<λ<A and y0∈Rn let again suppose that y0∈MHτ0(λ) and consider the solution y(t;τ0,y0) of the impulsive conformable Cohen–Grossberg model (1) corresponding to the initial condition (2). Without loss generality, we can consider 1<λ<V1(t)<A, t∈[τ0,∞).
Consider again the Lyapunov-type function (12).
Following the same reasoning as in the proof of Theorem 12, at the impulsive control instants t=τk, k=1,2,…, we obtain (13).
Using H1–H3 and conditions (16) of Theorem 13, for t≠τk, k=0,1,2,…, we have
where ϱ1(t)=∑nι=1¯aιUι(t).
Now, from (13) and (18), using again Lemma 11, we have
Hence, from condition (i) of Theorem 13 and (17), and from the choice of the function L1∈Lαk, we have
Therefore,
which implies that the manifold MHt is practically exponentially stable for the model (1). □
In the next result, we will use a different Lyapunov function in order to establish more relaxed sufficient conditions for the parameters in the continuous part of model (1). The price is, more restrictive conditions for the jump functions.
Theorem 14. Assume that 0<λ<A, hypotheses H1–H4 hold and:
(i) there exists a function H:[τ0,∞)×Rn→Rm, m≤n, such that
where Γ(Ω)≥1 for any 0<Ω<∞;
(ii) there exists a positive δ such that the parameters and the impulsive control functions of the impulsive conformable Cohen–Grossberg neural network model (1) satisfy:
and
Then the manifold MHt is practically exponentially stable for the model (1).
Proof. Let 0<λ<A. No generality is lost by making the assumption 1<λ<U(t)<A, t∈[τ0,∞).
We construct a new Lyapunov-type function as
for which, we have
for any solution y(t)=y(t;τ0,y0) of the impulsive conformable Cohen–Grossberg model (1) corresponding to the initial condition (2) with y0∈MHτ0(λ).
From (21) and (24), at the impulsive control instants t=τk, k=1,2,…, we have:
for k=1,2,….
Using H1–H3, (20) and (24) from the choice of the function L∈Lαk for t≠τk, k=0,1,2,…, we have
where ϱ(t)=∑nι=1Uι(t).
Now, from (25) and (26), using again Lemma 11, we have
Hence, from condition (i) of Theorem 14 and (22), we have
Therefore,
which implies that the manifold MHt is practically exponentially stable for the model (1). □
Following the same steps as in the proof of Theorem 14, we can establish the following practical stability criteria.
Corollary 15. If in Theorem 14 condition (20) is replaced by
and condition (22) is replaced by condition (10) of Theorem 12, then the manifold MHt is practically stable for the model (1).
Remark 16. The results in this section generalize and extend many existing stability results for integer-order Cohen–Grossberg neural network models [3,4,5,6,7,8], impulsive Cohen–Grossberg neural network models [15,16,17], as well as, Cohen–Grossberg neural network models with classical fractional-order derivatives [26,27,29,30] to the generalized impulsive conformable setting. Also, since the concept of practical stability with respect to manifolds is more general, results on practical stability, stability with respect to manifolds, stability and practical stability of a single solution can be obtained as corollaries. Thus, the proposed results are very general and include many particular stability notions. For example, if in Definition 9, A=0 and the manifold MHt consists only of a single solution y∗, Theorems 13 and 14 offered criteria for exponential stability of the solution y∗ of the impulsive conformable Cohen–Grossberg neural network model (1).
Remark 17. The proposed stability of manifold results are also consistent with the results in the pioneering work of Cohen and Grossberg [3], where models capable of approaching infinitely many equilibrium points in response to arbitrary initial data, have been considered.
Remark 18. The impulsive functions Pιk, ι=1,2,…,n, k=1,2,… are the impulsive control functions in the introduced model (1). The suitable choice of these functions is crucial for the elaboration of effective impulsive control strategies that can be applied to the trajectories of the model to control their stability properties. Hence, our results contribute to the development of this direction of research. Indeed, the impulsive conformable Cohen–Grossberg neural network model (1) can be considered as a closed-loop control system represented as
where
is the control input, δ(t) is the Dirac impulsive function. The controller u(t)=(u1(t),...,un(t))T has an effect on sudden change of the states of (1) at the time instants τk where each state yι(t) changes from the position yι(τk) into the position yι(τ+k), Pιk are the functions that characterize the magnitudes of the impulse effects on the units yι at the moments τk, i.e., u(t) is an impulsive control of the conformable model without impulses
Therefore, our stability results also presents a general design method of impulsive control law u(t) for the impulse free conformable Cohen–Grossberg neural network model. The constants γιk in condition (ii) of Theorem 12 characterize the control gains of synchronizing impulses. Hence, our results can be used to design impulsive control law under which the controlled neural networks of type (1) are practically (practically exponentially) synchronized onto systems without impulses.
4.
Impulsive conformable BAM Cohen–Grossberg neural networks
BAM neural networks have attracted an increased interest of numerous researchers since their introduction by Kosko [61,62], due mainly to their important applications in many areas. Some typical applications are related to associative phenomena in two-layer hetero-associative circuits existing in biology, medicine, engineering and computer sciences.
Significant progress has been made in the theory and applications of different classes of integer-order BAM Cohen–Grossberg neural networks [63,64], including impulsive models [21,65,66]. A practical stability analysis has also been proposed for some integer-order BAM Cohen–Grossberg neural network models [67].
Correspondingly, there are not reported results in the existing literature on BAM Cohen–Grossberg neural networks with conformable derivatives. In this Section, we will propose results on practical stability of such models with respect to manifolds as corollaries of the results offered in Section 3.
We consider the following BAM Cohen–Grossberg neural network model with conformable derivatives
where t≥τ0, yι(t) and zj(t) represent the states of the ιth neuron in the first Y layer and jth neuron in the second Z-layer, respectively, at time t, fj, f∗ι are the activation functions, aι, a∗j represent the amplification functions, bι, b∗j denote well behaved functions, cjι, c∗ιj are the connection weights, the continuous functions Uι, U∗j are external inputs, ι=1,2,…,n, j=1,2,…,N. The impulsive functions Pιk,P∗jk∈C[R,R] represent the effects of the impulse controls on the nodes yι and zj, respectively, at τk, ι=1,2,…,n, j=1,2,…,N, k=1,2,….
Following the definitions of solutions of the one layer Cohen–Grossber model (1) will denote by u(t), u(t)=(y(t),z(t)), where y(t)=y(t;τ0,y0), z(t)=z(t;τ0,z0) the solution of the BAM neural network model (28) that satisfies the initial conditions:
where y0∈Rn, z0∈RN and u0=(y0,z0)∈Rn+N.
We will apply the practical stability notion with respect to a H∗-manifold
defined by a function H∗=H∗(t,u), H∗:[τ0,∞)×Rn+N→Rm, using the following definition.
Definition 19. The manifold MH∗t is called practically exponentially stable for the model (28) if given (λ,A) with 0<λ<A, u0∈MH∗τ0(λ) implies
where 0<α<1, μ,δ>0.
For the BAM neural network model (28) we can use the demonstrated Lyapunov function approach in Section 3, and obtain similar results. For example, as a corollary of Theorem 14, we can establish the following practical exponential stability criteria for the manifold MH∗t of the system (28).
Theorem 20. Assume that 0<λ<A, hypotheses H1–H4 and conditions (20), (21) of Theorem 14 hold and:
(i) the continuous functions a∗j∈R+, j=1,2,…,N are such that there exist positive constants a_∗j and ¯a∗j for which 1<a_∗j≤a∗j(χ)≤¯a∗j for χ∈R, and a_∗=min1≤j≤Na∗j, ¯a∗=max1≤j≤Na∗j;
(ii) the continuous functions b∗j∈R+ are such that there exist constants β∗j>0 with
for any χ∈R and j=1,2,…,N;
(iii) there exist Lipschitz constants Lf∗j>0 such that
for all χ1,χ2∈R, j=1,2,…,N;
(iv) there exists a function H∗:[τ0,∞)×Rn+N→Rm, m≤n, such that
where Γ(Ω)≥1 for any 0<Ω<∞;
(v) each solution u(t)=(y(t),z(t)), y(t)=y(t;τ0,y0), z(t)=z(t;τ0,z0), of the initial value problem (28), (29) such that
is defined on [τ0,∞);
(vi) there exists a positive δ∗ such that the parameters and the impulsive control functions of the impulsive conformable Cohen–Grossberg neural network model (28) satisfy:
and
Then the manifold MH∗t is practically exponentially stable for the model (28).
Remark 21. As a Corollary of Theorem 14, Theorem 20 proposes criteria for practical exponential stability of a manifold for the BAM impulsive conformable Cohen–Grossberg model (28). Similarly, criteria for practical stability of the manifold MH∗t can be established as a Corollary of Theorem 12.
5.
Illustrative examples
In this section, examples are constructed to illustrate the usefulness of the proposed results.
Example 22. We consider the 2-dimensional impulsive Cohen–Grossberg-type neural network model with generalized conformable derivatives
where α=0.98, t>0, 0=τ0<τ1<τ2<…, k=1,2,…, limk→∞τk=∞, fj(yj)=12(|yj+1|−|yj−1|), U1(t)=sint, U2(t)=1, b1(y1)=3y1, b2(y2)=2y2,
(A) If in the model (34), we have a1(y1)=2−0.5sin(y1), a2(y2)=2−0.6cos(y2), then hypotheses H1–H3 are satisfied for
Also, conditions (20), (21) and (22) of Theorem 14 are satisfied for
and ϱ(t)=1+sint.
If we consider a manifold
containing the zero solution y∗=(0,0)T of the model (34), defined by a function H:R2→R2, H=(H1,H2)T, then according to Theorem 14 the manifold (35) is practically exponentially stable for the model (34). The graphs of the trajectories of the model (34) with corresponding fixed τk are shown in Figure 1.
Note that for the particular choice of the parameters, condition (16) of Theorem 13 is not satisfied, since
Hence, the criteria provided by Theorem 13 for the parameters in the continuous part are more restrictive.
(B) If in the model (34), we have a1(y1)=a2(y2)=1.4, then, hypotheses H1–H3 are satisfied for
In this case, conditions of Theorem 13 and Theorem 14 are satisfied for δ=δ1=0.56>0. Therefore, the practical exponential stability of the manifold (35) can be provided by either one of the results.
(C) If in the model (34), we have
then condition (21) of Theorem 14 is not satisfied, however, condition (11) of Theorem 12 holds. Hence, in this case we can make some conclusions about the practical exponential behavior of the manifold (35) only by means of Theorem 12.
In addition, if
then no one of the conditions about the impulsive functions in theorems 13 and 14 are not true, and we cannot make any conclusion about the practical exponential behavior of the manifold (35).
Remark 23. The demonstrated Example 22 illustrates the validity of theorems 13 and 14 for practical exponential stability of a manifold with respect to an impulsive conformable Cohen–Grossberg neural network model of the type (1). Similar demonstration for the practical stability behavior can be provided for a particular choice of the model's parameters. We show that the conditions for the parameters in the continuous part in Theorem 14 are more relaxed than these in Theorem 13. Also, we demonstrate that the choice of the impulsive functions is very important to control the practical stability behavior of manifolds related to models of type (1).
Example 24. Consider the BAM Cohen–Grossberg impulsive conformable neural network model (28) with n=N=2, α=0.93, where t>0,
with impulsive perturbations of the type
0=τ0<τ1<τ2<…, k=1,2,…, limk→∞τk=∞.
We can verify that all assumptions of Theorem 20 are satisfied for
Therefore, according to Theorem 20, we conclude that the manifold
defined by a function H∗:R4→R4, H∗=(H∗1,H∗2,H∗3,H∗4)T=(y1−y∗1,y2−y∗2,z1−z∗1,z2−z∗2)T, where u∗=(y∗1,y∗2,z∗1,z∗2)T is a solution of the model (28), is practically exponentially stable for the model (28).
6.
Concluding comments
In this paper, using the impulsive generalization of the conformable calculus approach, an impulsive conformable Cohen–Grossberg neural network model is proposed. The introduced model extends and complements numerous existing integer-order Cohen–Grossberg neural network models [3,4,5,6,7,8], impulsive Cohen–Grossberg neural network models [15,16,17] as well as Cohen–Grossberg neural network models with classical fractional-order derivatives [26,27,29,30] to the generalized impulsive conformable setting. The proposed model possesses the flexibility of the fractional-order models. Moreover, since the conformable derivatives simplify the computational procedures, it overcomes some limitations existing in the applications of the classical fractional-order problems. We adopt the combined concept of practical stability with respect to manifolds to the introduced model. Using a Lyapunov-based analysis, sufficient conditions are derived to ensure the practical stability and practical exponential stability with respect to manifolds. The case of BAM impulsive conformable Cohen–Grossberg neural network models is also studied to contribute to the development of the stability and control theories. Two illustrative examples are given to demonstrate the effectiveness of the contributed results. The application of the proposed conformable calculus approach to more neural network models is an interesting and challenging topic for future research. Also, it is possible to extend the proposed results to the delayed case and study the delay effects on the qualitative behavior of the neuronal states. In fact, delay effects are unavoidable in most of the neuronal network models. In addition, time delays, also known as transmission delays, may affect the dynamical properties of neural networks.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Conflict of interest
The authors declare there is no conflict of interest.










 DownLoad:
DownLoad: