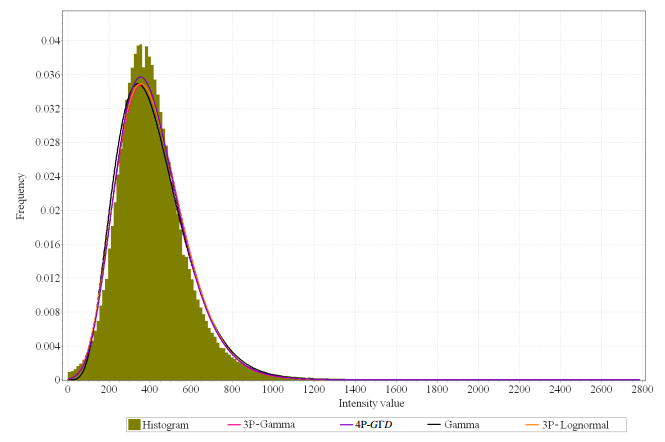
Ultrasound waves are preferably used as means to provide details about the inner structure of materials, thus providing a way to non-destructively evaluate the quality of produced components. Nevertheless, ultrasonic data are strongly affected by a multiplicative type of noise referred to as speckle noise. Within this paper, the modeling of the intensity distribution within ultrasound images and volumetric data is addressed through parametric approach modeling. The proposed model was compared with the state of the art models through measuring the corresponding goodness of fit of each model to the actual data distribution. The data were acquired on aluminum, ceramic and composite structures.
1.
Introduction
Mathematical modelling of gene-regulatory networks is a relatively new area which plays an important role in systems-biology investigations. The control and coordination of large sets of genes is intrinsic to the ability of multicellular organisms to produce specific types of cells, in the proper place and at the right time during development. The perception and integration of cellular and environmental signals are essential in controlling gene expression during development. The roles of specific proteins as gene-regulatory factors are well established; in addition, recent studies of small RNAs, particularly microRNAs (miRNAs), have generated considerable excitement. Lee et al. [1] first described this phenomenon in 1993, though the term microRNA was introduced only in 2001 [2]. MicroRNAs are a class of small non-coding RNAs. At a post-transcriptional level, they enter the RNA interference (RNAi) pathway to regulate the expression of protein-coding genes. They regulate gene expression by blocking translation (by ribosomes) and by triggering the degradation of mRNA in, for example, both Drosophila melanogaster and Caenorhabditis elegans (see [3,4,5] and references therein). MicroRNAs are, therefore, key components of an evolutionarily conserved system of RNA-based gene regulation in eukaryotes. In addition, they play crucial roles in many molecular interactions, including defence against viruses and regulation of gene expression during development, cell proliferation and apoptosis. For instance, DCL1 (DICER-LIKE 1) mRNA in plants is a miRNA target, and the defects associated with dcl1 mutants include over-proliferation of meristems (which contain pluripotent stem cells), conversion of normally determinate floral meristems into indeterminate meristems, over-proliferation of embryonic suspensor cells, delayed flower timing and leaf polarity defects [6]. Similarly, bantam miRNA, a microRNA identified in D. melanogaster, functions to repress apoptosis and to promote cell proliferation in the developing fly, by repressing the translation of the mRNA for Hid, a key activator of programmed cell death [6]. It is also believed that the alterations in miRNA expression patterns might be involved in cancer development in humans [7]; this includes evidence for cancer-related miRNAs that regulate cellular proliferation, death and tumorigenesis in a variety of tumors, including Burkitt's lymphoma, glioblastoma, colorectal, lung and breast cancers [8]. MicroRNAs can also control Nodal/activin signalling in some cases [9]. Recently, mir-34 microRNA has been identified as a key component of the DNA damage response both in the nematode C. elegans and in human breast cancer cell lines [10]. In addition, studies illustrate the role of a miRNA in well-established tumour-suppressor networks associated with p53 [11,12,13]. Moreover, microRNAs have emerged as a class of gene-expression regulators that have also been linked to environmental stress responses, such as low temperature, high-salinity and drought. Liu et al. [14] identified 14 stress-inducible miRNAs using microarray data in which the effects of abiotic stresses were surveyed in Arabidopsis thaliana. Such findings augment the current view of miRNAs as ubiquitous regulators under stress conditions.
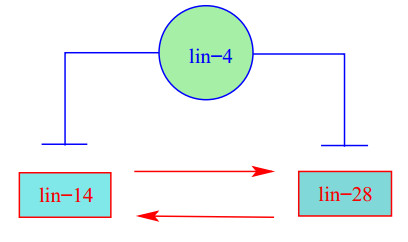
Our goal here is to study a specific regulatory module that involves three interacting genes in C. elegans, one of which encodes a microRNA (similar genetic circuity of course also arises in other contexts): lin-4 encodes a microRNA, lin-28 a RNA-binding protein and lin-14 a transcription factor, the network being shown schematically in Figure 1. In the following paragraphs we discuss their functions in C. elegans.
In the middle of the first larval stage (L1), expression of lin-4 is first observed [15]. Up-regulation of this gene results in the down-regulation of the production of LIN-14 protein, which then allows the transition from expression of L1 stage to the expression of L2 (second larval) developmental events to occur [16].
In an experimental study, Feinbaum and Ambros [15] observed that over-expression of lin-4 in the L1 stage results in precocious down-regulation of LIN-14 protein and precocious expression of larval phenotypes, and noted that most of the precocious phenotypes in lin-4 over-expressing lines were strong, consistent with a potent premature repression of LIN-14 in C. elegans. However, the L1 defects (precocious expression of L2 cell lineage patterns in the L1 stage) were relatively weak. Perhaps lin-4 is not expressed at sufficiently high levels for full repression of LIN-14 synthesis until later L1. The authors of [15] pose a question "Does lin-4 level function as a gradient or a switch?".
In the current study, we try to give a possible answer of the question posed by [15] via mathematical modelling.
In summary, several heterochronic genes, such as lin-4, lin-14 and lin-28, collaborate to control the timing of specific postembryonic developmental events in C. elegans. How these three genes interact to control a particular stage-specific event of the lateral hypodermal cell lineages is described in [17]. Here, we also focus on these specific genes: Our goal is to develop and analyse a mathematical model for a specific gene-regulatory network (described below) in which a particular miRNA plays crucial role. It is hoped that the results will be of more general relevance in enhancing the understanding of the types of phenomena just described.
2.
Assumptions and model formulation
In developing the mathematical model, we adopt the general assumption that biochemical reactions are reversible. Next we summarize the mathematical notation and existing experimental data, along with the specific assumptions upon which the mathematical model is built (see also [18]).
(A1): [N] and [L] denote the concentrations of the mRNAs of lin-14 and lin-28, respectively, and [Ψ] denotes the concentrations of the lin-4 miRNA.
(A2): Seggerson et al. [19] have suggested that lin-28 and lin-14 are repressed by lin-4 during normal development by a mechanism that acts on their respective mRNAs after translation initiation. This inhibition is reversible and seems to involve interference with the growing protein chain that is being translated from the mRNA. The microRNA interactions occur at the far (3') end of the mRNA molecule, even though the process of translation is initiated at the opposite (5') end. We denote the concentrations of the inactive complexes of [N] and of [L] with [Ψ] by [CN] and [CL], respectively. These reactions are reversible and are represented by
where ki's are the rate constants.
(A3): We treat lin-14 and lin-28 as positively regulating each other, although in both cases this is in reality mediated through two successive negative regulatory steps, see Figure 7 of Seggerson et al. [19]; it is believed that the mutual positive regulation of lin-28 and lin-14 is achieved through a two-step negative regulation involving the miRNA let-7 [19,20,21,22].
(A4): lin-4 is robustly expressed from late L1 through to peak levels at L3 and persistently into adulthood [15]. We take lin-4 to have expression rate ζ; by increasing the value of the parameter ζ we will be able to investigate its effect from the late L1 stage through to the L2 stage. Note that the numerical value of the parameter ζ is influenced by the amount of food during the time of hatching as lin-4 is repressed by starvation and activated by nutrition. In a course of time, we would be able to find that for a normal progression from L1 stage to L2 stage, an increasing value of ζ is needed (that is, a continuous nutrition is required).
A schematic diagram of the gene-regulatory network of lin-4, lin-14 and lin-28 is given in Figure 1. We model the degradation of lin-14 by the term β1[N][Ψ] and that of lin-28 by the term β2[L][Ψ].
(A5): The processes involved in the synthesis of lin-14 and lin-28 (i.e. transcription, translation and post-translational modification) are combined together, since these processes occur on a timescale of minutes to hours. The effect of a transcription factor on the transcription rate of a gene that it upregulates is taken to be described by Hill function given in the case of regulation of N by L, for example, by H([L])=[L]m[L]m+θmln. The Hill coefficient m governs the steepness of the output function (the larger m the more step-like the function) and we shall limit attention to the simplest Michaelis-Menten case m=1 . The parameters θln and λln respectively represent the threshold on a target N of the regulatory influence of L and the maximum rate of production of N induced by L. Each species spontaneously decays due to degradation, at a rate μi (i=1,2,...,5).
The resulting model then reads
Tables 1 and 2 summarise the notation.
To complete the mathematical formulation of the above model we adopt for definiteness the following initial conditions:
where N(0), L(0), Ψ(0), CN(0) and CL(0) are taken to be the steady state values that arise when lin-4 is present (we mimic the transition from L1 stage to L2 stage by introducing a non-zero ζ at t=0). The system (2.2) has two physiological meaningful steady states,
where NE, LE, ΨE, CNE and CLE are non-zero and can be obtained from an algebraic equation of order seven (see [18]). The steady state represented in Eq (2.5) denotes the early L1 stage where lin-14 and lin-28 are present and lin-4 is not yet expressed highly. The steady state in Eq (2.4) represents the L2 (or precocious L2) stage where lin-14 and lin-28 are absent and lin-4 is expressed highly.
We now introduce dimensionless quantities in according to
the timescale being based on the degradation rate of [N], which is expected to be slow.
This gives
where the dimensionless parameters are defined by
and the initial conditions (2.3) become
We note that a linear combination of (2.6c)–(2.6e) can be chosen to eliminate the (fast) complexification terms, namely
which plays a key role in describing the dynamics in the limit ϵ→0. We now indicate the basic assumption on parameter sizes in the system (2.6). Formation and dissociation of a complex typically operates on a timescale of the order of second, while it takes many minutes to a few hours for gene regulation to complete (transcription and translation) [23]; therefore we take ϵ≪1. In the limit ϵ→0 the order of system (2.6) is reduced and the associated singular perturbation problem is addressed in [18]. Here we proceed directly to the quasi-steady limit that holds for τ=O(1), the behaviour of which is significantly more accessible to analysis.
3.
The reduced system
Taking the limit ϵ→0 with τ=O(1) in (2.6) gives
at leading order, together with
where the nonlinear functions fN(N0,L0,Ψ0), fL(N0,L0,Ψ0) and fΨ(N0,L0,Ψ0) are defined by
The reduced system (3.2) subject to the initial data
determines the behaviour for τ=O(1) and we next identify a number of its properties by a linear stability analysis. We denote a steady state solution to (3.2) by (Ns,Ls,Ψs), so that
The system (3.2) has two kinds of steady states, of the form E1≡(0,0,Ψ0e) and E2=(Ne,Le,Ψe), where Ψ0e=ζμ3, and Ne, Le and Ψe are non-zero and can be obtained from a quintic equation (see [18]). Applying standard linear stability methods to E1 and E2 leads to the following propositions (details of the analysis are given in [18]).
Proposition 1. (ⅰ) The equilibrium point E1 is stable if and only if ζ>ζ[tc], where
ζ[tc]=μ3(√θln2θnl2β12μ22−2θln2θnl2β1μ2β2+θln2θnl2β22+4θlnθnlβ1β2λnlλln−(θlnθnlβ1μ2+θlnθnlβ2))2θlnθnlβ1β2.
(ⅱ) E1 becomes unstable at ζ=ζ[tc] via a transcritical bifurcation.
Proof. (ⅰ) The Jacobian matrix of the system (3.2) around E1 is given by
where
We define C1=tr(A)×M−det(A), where M is the sum of the second order principal minors of A.
Obviously, we have trA<0, and we find that for ζ>ζ[tc], detA<0 and C1<0. Hence the proof follows from Routh-Hurwitz criteria.
(ⅱ) We notice that at ζ=ζ[tc], detA=0 which means that A has one zero eigenvalue. Now when ζ=ζ[tc] the other two eigenvalues are given by −(μ3+μ2μ3+β1ζ+β2ζ)/μ3 and −μ3, that is both of them are negative. Let V and W are the eigenvectors corresponding to zero eigenvalue of the matrix A and AT, the transpose of A, respectively. We obtain that V=(v1,v2,v3)T, W=(w1,w2,w3)T, where
Next we see WT[Fζ(E1,ζ[tc])]=0, WT[DFζ(E1,ζ[tc])V]≠0 and WT[D2F(E1,ζ[tc])(V,V)]≠0, where Fζ=(∂fN∂ζ,∂fL∂ζ,∂fΨ∂ζ)T, fN=fN(N,L,Ψ), fL=fL(N,L,Ψ) and fΨ=fΨ(N,L,Ψ) are defined in (3.3), Fζ(E1,ζ[tc]) is the value of Fζ evaluated at E1 for ζ=ζ[tc], and
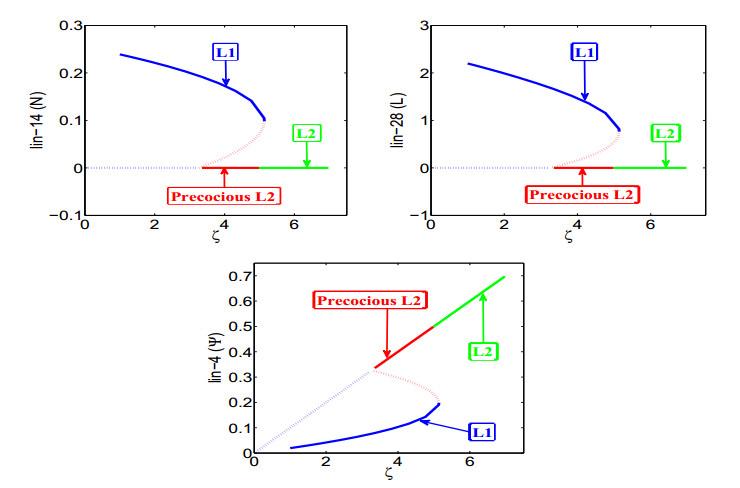
where D2F∈R3×3×3 is defined in Appendix A. Therefore, by the Sotomayor theorem [24] the system possesses a transcritical bifurcation around E1, see Figure 5.
Proposition 2. (ⅰ) For ζ[tc]<ζ<ζ[sn], the system is bistable and we denote the stable states by E1 and EI2, and the unstable one by EII2 (Figures 3 and 5). EI2 is linearly stable if Ωi<0, i=1,2,3, where the Ωi are defined in the Appendix B. (ii) E2 (or specifically EI2) experiences a saddle-node bifurcation at ζ=ζ[sn], where ζ[sn] is determined from detB(ζ[sn]) = 0, B being the Jacobian matrix of the system (3.2) at E2 (the lengthy details are again given in [18]).
Proof. (ⅰ) We examine the bistability of the system numerically (in section 4), that when the Eq (3.4) have only two real positive roots EI2 and EII2, then the system become bistable around E1 and EI2 (unstable around EII2) for ζ>ζ[tc]; (Figures 3 and 5). However the local stability of around EI2 can be shown as follows:
Let us denote the Jacobian matrix of the system (3.2) around EI2(Ne,Le,Ψe) by B=(bij)∈R3×3. Here we note that the Jacobian matrix is a full matrix. Although the Routh-Hurwitz criteria can be used, but the expressions for the conditions for local stability are even more complicated than those found for the equilibrium point E1. To analyse the stability of the system (3.2) around (Ne,Le,Ψe), we follow a different approach and get a simpler set of conditions for local stability.
To show the first claim on the asymptotic stability of the equilibrium E2, we use the method of first approximation. If B[2]=(ˉbij) be the second computed matrix of matrix B, then the matrix B[2] is given by,
Consider a diagonal matrix D=diag(Ψe,Le,Ne), then B[2] is similar to Q≡DB[2]D−1=(qij), where Q∈R3×3 with elements
Now it is easy to see that the matrix B[2] is stable if and only if Q is stable. Since the diagonal elements of the matrix Q are negative, by the Gershgorin's theorem it is stable if it is diagonally dominant in rows. Set
and ϑ∗=max{g1,g2,g3}. Obviously, when the conditions Ω1<0 and Ω2<0 are met, then ϑ∗<0, implying diagonal dominance. Next we have
In view of the third condition Ω3<0, we see detB<0, which completes the proof.
(ⅱ) Let V and U be the eigenvectors corresponding to eigenvalue 0 of the matrix B and its transpose, respectively. We obtain that V=(φ1,φ2,φ3)T, U=(u1,u2,u3)T, where φi and ui are defined in Appendix C. Next we obtain UT[Fζ(E2,ζ[sn])]≠0, UT[D2F(E2,ζ[sn])(V,V)]≠0, where D2F is given in Appendix A; therefore, system experiences saddle-node bifurcation [24] around the positive interior equilibrium E2 at ζ=ζ[sn], see Figure 5.
4.
Numerical simulations
In section 1, we report that the larval development progressions of C. elegans (whether normal or abnormal) depends on the level of expression of miRNA lin-4 [15]. The normal development progression means the transition from expression of the L1 stage to the expression of second larval stage (L2) where as an abnormal progression refers to a premature adoption of L2 (precocious L2) by skipping the first larval development stage (L1) [16].
In this section we perform numerical simulations of the reduced system (3.2) to illustrate how the current mathematical modelling reflects these two types of (i.e normal and abnormal) larval development progressions. The numerical simulations are undertaken with the set of parameter values reported in Table 3 which also convenient for verifying the properties of the system determined analytically. These computations are performed using Matlab routine ode15s and XPP-Auto for stiff ODEs. The parameter values are hypothetical; however, they are closely related to the existing literature such as [16,23].
4.1. Dynamics of the system (3.2) for constant ζ
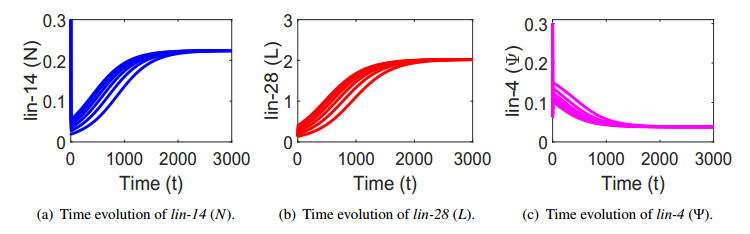
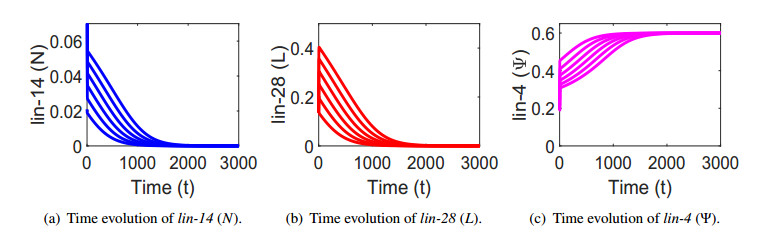
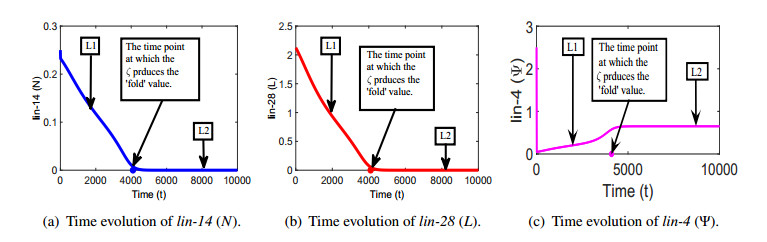
First of all we illustrate the stability of the system (3.2) around E2 for ζ<ζ[tc], see Figure 2. Note that the stability of E2 represents the early L1 larval stage where lin-4 is expressed very low and both the lin-14 and lin-28 are highly expressed. Next, we illustrate the bistability of the system (3.2) for ζ[tc]<ζ<ζ[sn]: see Figure 3. Figure 3 illustrates how the system is settling to two stable states over time depending on their initial conditions. Then, we demonstrate the stability of the system (3.2) around E1 for ζ>ζ[tc]: see Figure 4. The stability of E1 indicates the L2 larval stage where lin-4 is expressed very high and both the lin-14 and lin-28 are absent.
Figures 2-4 are obtained by varying the values of the parameter ζ only (the other parameter values are kept same and are listed in Table 3).
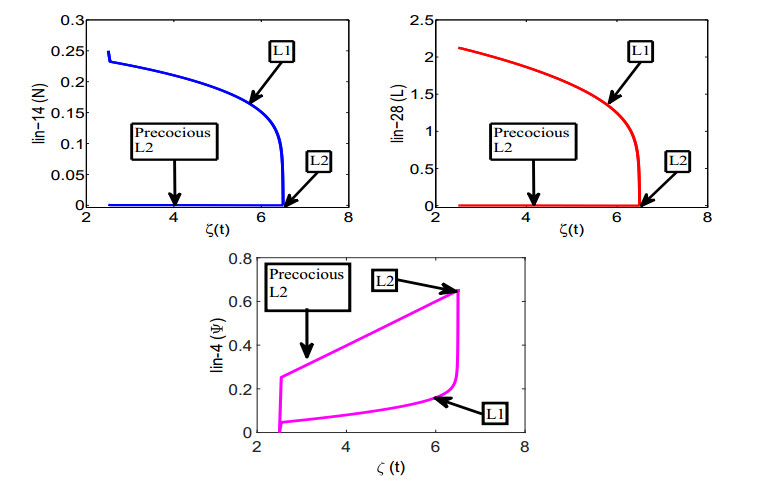
Figure 5 demonstrates the transcritical bifurcation of the system (3.2) at E1 for ζ=ζ[tc]=3.2 and the saddle-node bifurcation at E2 for ζ=ζ[sn]=5.1.
In interpreting Figures 3 and 5, we note that for the set of parameter values listed in Table 3 and 3.2<ζ=4<5.1, the system (3.2) attains the stable state EI2(0.18,1.55,0.09) if the initial conditions are N0(0)≥0.023, L0(0)=0.136 and Ψ0(0)=0.3; and it attains the stable state E1(0,0,0.4) if N0(0)<0.023 (where L0(0)=0.136 and Ψ0(0)=0.3). Therefore, certain levels of expressions of lin-14 and lin-28 are required for L1-specific fates to occur. This means certain levels of expression of lin-14 and lin-28 are required for normal progression from the L1 stage (that is from E2) through to the L2 stage (that is to E1); on the other hand, if the initial levels of expression of lin-14 and lin-28 are below the required level (that is, N0(0)<0.023 and L0(0)<0.136), then the development stage L1 is skipped (as E2 is not attained) resulting in a premature adoption of L2 (precocious L2) which illustrates an abnormal progression.
4.2. Dynamics of the system (3.2) for time-dependent ζ
In section 4.2, we noted that how the dynamics of the system (3.2) behave for the different constant values of ζ (constant over time t). It is observed that the system shows all possible scenarios (abnormal and normal progression of the larval stages) while we increase the value of ζ and (as implied by the discussion in section 1) we take an increasing value of ζ(t) to describe the up-regulation of miRNA lin-4 which causes the down-regulation of LIN-14 and LIN-28, resulting in a transition from the first developmental stage (L1) to the second developmental stage (L2) [16]. For these purposes we reinstate the initial data (2.4) and (2.5).
For definitions, we adopt the specific form ζ=A+Btanh(σt) to describe the transition between two constant values (in keeping with its biological interpretation) with σ sufficiently small that the system evolves in a quasi-steady fashion.
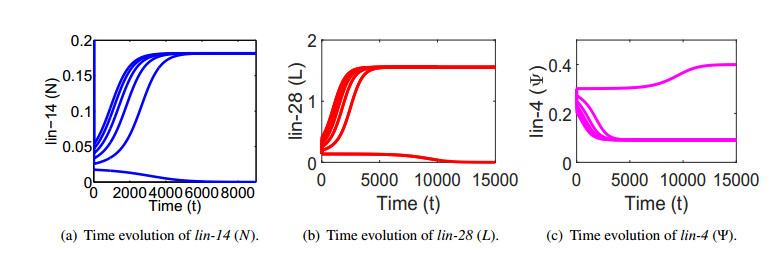
The following numerical simulations illustrate the corresponding changes in the solutions of the non-autonomous ODE system (3.2) compared to that of autonomous one. Note that the steady states E1 and E2 obtained earlier for a constant ζ will now be (slowly varying) functions of t. Figure 6 illustrates how the solution of the non-autonomous system (3.2) converges from E2 (that is from L1 stage) to E1 (that is to the L2 stage) over time for the initial conditions N0(0)=0.25, L0(0)=2.124, Ψ0(0)=2.5, rapidly moving between branches at t=4100. These initial conditions are taken in light of the initial conditions represented by Eq (2.5) of the original system (2.2).
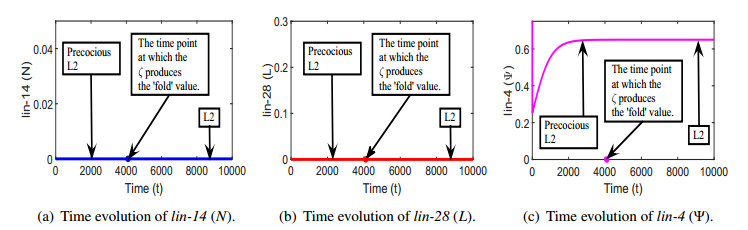
On the other hand if the initial conditions are chosen in such as way which correspond the Eq (2.4) of the original system (2.2) (for example, N0(0)=0, L0(0)=0, Ψ0(0)=2.5), then E2 converges (or E2 is not attained) to E1 very quickly, as might be anticipated. This represents an abnormal progression of the larval stages (precocious L2 to L2), see Figure 7.
Figure 8 demonstrates both the normal and abnormal progression of the larval stages in response to the time dependent ζ(t) for the both set of initial conditions used in Figures 6–7. In interpreting Figures 6-8, we again note that certain levels of expressions of lin-14 and lin-28 are necessary for a normal progression from the L1 stage to the L2 stage; otherwise, the development stage L1 is skipped and an abnormal progression takes place. These results are consistent with the results of experimental study of [25], where the authors studied the development of the larval stages of C. elegans based on genetic epistasis and expression analysis of heterochronic genes and observed that a high level of lin-14 is necessary for L1-specific fates to occur, while L2-specific fates occur only when both the lin-14 and lin-28 are at very low levels or off (Figure 5 of [25]).
5.
Discussion
We have proposed a mathematical model of a microRNA regulated gene network in C. elegans. The network consists two mutually activating heterochronic genes lin-14 and lin-28 and a microRNA lin-4 of which negatively regulates both of them. The reduced model (3.2) captures the qualitative behaviours, such as stability and bifurcation, of the full system (2.6). We summarize our numerical investigations of the steady state solutions in Table 4, the parameter values other than ζ being as in Table 3.
It has become increasingly clear that bistability is an important recurring feature in many gene-regulatory networks. Bistability may be of particular relevance to biological systems that need switch between states. Our focus lies on two mutually activating molecular species that are down-regulated by a third species.
Interestingly, in the system (3.2), we see that bistability may arise without any cooperativity of binding, in contrast to the situation familiar for two mutually repressing genes (see [26] for example).
An investigation of [27] showed that the products of the flh-1 and flh-2 genes (encoding FLYWCH Zn finger transcription factors) function redundantly in C. elegans to repress embryonic expression of the lin-4 microRNA gene, which is normally expressed only post-embryonically. However, double mutation of flh-1 and flh-2 allows derepression of target miRNAs genes (e.g. lin-4) in embryos. Mutating the flh-3 gene (encoding a third transcription factors with a FLYWCH motif) also increases precocious expression of target miRNAs. Our model provides a mathematical interpretation for this: in the early L1 larval stage lin-4 is low, that is ζ has a sufficiently small value that can be characterised (namely, ζ<ζ[tc]), both lin-14 and lin-28 are expressed. This corresponds to the stability of E2 and the instability E1 (see Figure 2 and first row of Table 4). Both lin-28 and lin-14, in turn, negatively regulate lin-29, which is believed to act as a negative regulator of early larval development, including the functions required for cell division and the expression of early larval-specific cuticle genes. Therefore, if the lin-4 microRNA expression is low, both LIN-14 and LIN-28 levels will remain high (Figure 3), and early-larval (L1-specific) stages are reiterated while later developmental events (L2-specific development) fail to occur. Conversely, if lin-4 microRNA levels remain high (ζ>ζ[sn]), then both LIN-14 and LIN-28 levels will be low (Figure 3 and first row of Table 4), resulting in the skipping of early (L1-specific) cell lineages and developmental events, while later developmental events (L2-specific) and cell lineages occur precociously, which corresponds to stability of E1 (Figure 4 and third row of Table 4). Intuitively, this means that the lin-29 gene will be turned on, resulting in the positive regulation of adult development, including the functions required for cell division and the expression for adult-specific cuticle genes; and Propositions 1 and 2 represent two important threshold values ζ[tc] and ζ[sn] of the microRNA concentration level ζ. When ζ lies between these (i.e. ζ[tc]<ζ<ζ[sn]), the system (3.2) has three steady states, namely E1, EI2 (both stable) and EII2(unstable). Figure 5 illustrates the range of ζ for which the system (3.2) attains bistability. This switching of between two stable states takes place in between early stage L1 and the later larval stages precocious L2 which depends on the initial level of expression of lin-14, lin-28 and lin-4. This switching determines whether development progresses from L1 to L2 or whether L2-precocious patterns are reiterated (Figure 5). If the system adopts the L1 then it stays with L1 development until saddle-node bifurcation point appears (and at the saddle-node bifurcation point) whereupon the system switches to L2 development stage. This is a normal progression of the first two larval stages of C. elegans development and is consistent with the current biology [25]. But if the system adopts (depending on the initial level of presence of lin-14, lin-28 and lin-4) the other stable state, then this leads to the precocious adoption of later cell fates (including L2 fates appearing during L1 and so on). These events are illustrated in Figure 5, which describes an abnormal progression through these larval stages. The numerical simulations of the current model imply that a certain level of activity of the genes lin-14, lin-28 and lin-4 is necessary to allow L1-specific fates to occur (that is to adopt a normal progression), see the initial conditions of Figure 3; and this view is also supported by the experimental biology [25]. In summary, for a normal progression of the larval stages, three things are required (ⅰ) a certain level of activity of the genes lin-14, lin-28 and lin-4, (ⅱ) a progressive decrease in their activities owing to repression by lin-4, (ⅲ) a progressive increase in lin-4 activities (that is, increasing nutrition is required). On the other hand, the absence of lin-14 and lin-28 causes an abnormal progression through these larval stages, even though there is a progressive increase in lin-4 activities. These views are consistent with the experimental biology [15,16,25].
In conclusion, we have established that the simple microRNA-regulated gene network shown schematically in Figure 1 exhibits qualitative behaviour that can be interpreted in terms of key aspects of the development of C. elegans. Its partial central edge as a subnetwork of networks containing significantly more components thus warrants investigation.
Acknowledgments
The authors are grateful to Prof. Markus Owen for valuable comments. The authors are also grateful to UK-IERI for financial support to the first author.
Conflict of interest
The authors declare that no conflict of interest arises from the contents of this paper.
Appendix
A. Notation
The notations are same as that of [28]. The value of D2F(E1,ζ[tc])(V,V) is the value of D2F(E,ζ)(V,V)=(Υ1,Υ2,Υ3)T at (E,ζ)=(E1,ζ[tc]),
where Υi's are given by
B. Values of Ωi
For completeness we give here expressions for the Ωi in section 3, determined using Maple.
C. Coefficients of the vectors V and U.
The component of vectors V(φ1,φ2,φ3) and U(u1,u2,u3) are defined by









 DownLoad:
DownLoad: