1. Introduction
The Sm5Fe17 phase is a ferromagnetic phase in the binary Sm-Fe system [1,2]. It is a metastable phase and its formation has been reported only in sputtered films [3,4]. Through the intensive studies to produce the Sm5Fe17 phase as bulk materials, it was found that the Sm5Fe17 phase can be obtained by annealing of amorphous melt-spun ribbons [5]. Sm5Fe17 melt-spun ribbon shows a large coercivity exceeding 25 kOe and a remanence of 40 emu/g, which is significantly lower than the remanence of Nd-Fe-B magnets. For the application in the motors of electric vehicles and wind-turbine generators, the temperature of the magnets rises to nearly 473 K due to the evolution of eddy currents. Nd-Fe-B magnets cannot be used for the motors and instead Nd-Dy-Fe-B magnets, which the Dy was added to increase the coercivity, are applied. At such a high temperature, the magnetic properties of the Sm5Fe17 melt-spun ribbon were almost comparable to those of the Nd-Fe-B melt-spun ribbon (The results are discussed later in the results and discussion section). Thus, the high coercivity magnets are required for the high temperature applications. Since the Sm5Fe17 melt-spun ribbon possesses the high coercivity, it can be suitable for a hard magnet component in the nanocomposite magnets, which is the most promising candidate for the new types of the permanent magnets. In any case, the increase of the remanence of the Sm5Fe17 melt-spun ribbon is almost always beneficial. There have been several efforts to increase the remanence of Sm5Fe17-type melt-spun ribbons, but the reported values are not yet satisfactory [6,7,8]. It is known that the magnetic properties of Sm-Co-based magnets can be improved by the addition of B to the Sm-Co-based alloy [9,10,11]. In this study, small amounts of B were added to Sm5Fe17 melt-spun ribbon in order to increase the remanence. The structures and magnetic properties of the Sm-Fe and Sm-Fe-B melt-spun ribbons were then examined.
2. Materials and Method
Sm5Fe17 and Sm5Fe17Bx (x = 0.5-1.5) alloy ingots were induction melted in an argon atmosphere in a quartz crucible having an orifice of 0.6 mm in diameter at the bottom. The molten metal was ejected through the orifice with argon onto a chromium-plated copper wheel rotating at a surface velocity of 40 ms−1. The resultant melt-spun ribbons were annealed under an argon atmosphere at temperatures between 773 K and 1073 K for 1 h. The phases in the specimens were examined by X-ray diffraction (XRD) using Cu Kα radiation. The microstructures of the specimens were examined using a transmission electron microscope (TEM) after ion beam thinning. The thermomagnetic properties of the specimens were examined in a vacuum using a vibrating sample magnetometer (VSM) with an applied field of 500 Oe. The magnetic properties of the specimens were measured by the VSM with a maximum applied field of 25 kOe after premagnetization in a pulsed field of 70kOe. Some of the specimens were further examined by VSM using a superconducting magnet with a maximum applied field of 100 kOe.
3. Results and Discussion
3.1. Sm-Fe melt-spun ribbon
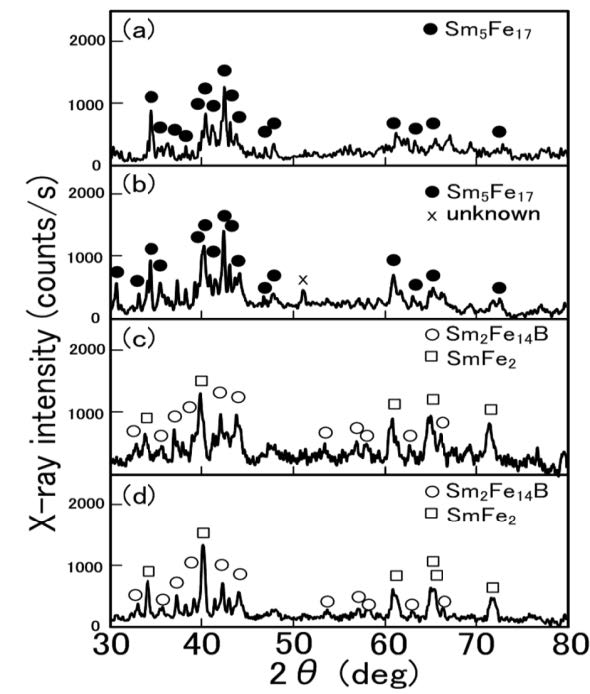
The Sm5Fe17 melt-spun ribbons were amorphous and exhibited a low coercivity value, less than 1 kOe. It is known that crystalline phases can be produced by rapid solidification processing and subsequent heat treatment [6]. In the previous studies [7,8], the annealed samples consisted of the Sm5Fe17 phase but also contained some other phase such as the SmFe12 phase and the SmFe3 phase. As the result of the extensive study of the annealing conditions, the optimal annealing condition to obtain the Sm5Fe17 phase was established in this paper. Figure 1 shows the XRD patterns of the annealed Sm-Fe melt-spun ribbons. The amorphous melt-spun ribbon should be annealed at relatively high heating rates of 0.5-1.0 K/s to 873-973 K and then kept for 1 h. As shown in Figure 1,the optimal annealed specimens consisted of the Sm5Fe17 (hexagonal) phase. However, the Sm-Fe ribbon annealed at 1073 K consisted of the SmFe3 (rhombohedral) phase together with the Sm5Fe17 phase.
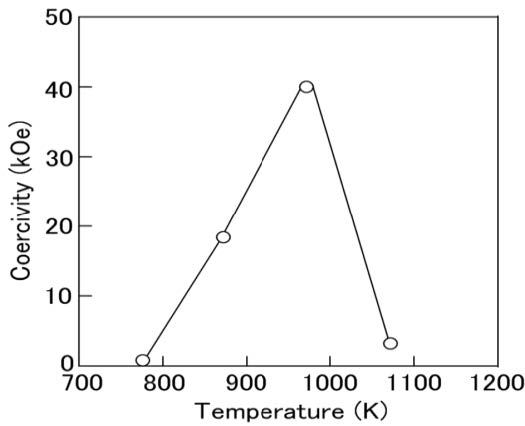
Figure 2 shows the dependence of the coercivity of the Sm5Fe17 melt-spun ribbons on the annealing temperature. The specimens annealed at 873 K and 973 K showed high coercivity values. According to the results of the XRD studies, thoseannealed melt-spun ribbon consists of the Sm5Fe17 phase. This indicates that the observed high coercivity in the annealed melt-spun ribbon is due to the existence of the Sm5Fe17 phase.
The hysteresis loops of the Sm5Fe17 melt-spun ribbon and the specimen annealed at 973 K are shown in Figure 3. Since the applied field of 25 kOe is far lower than the field required to fully saturate the Sm5Fe17 melt-spun ribbon, the hysteresis curve is not closed (i.e., it is a minor loop), and it is not symmetrical with respect to either coordinate. The actual coercivity of the annealed specimen was measured as 40 kOe using a superconducting magnet with a maximum applied field of 100 kOe.
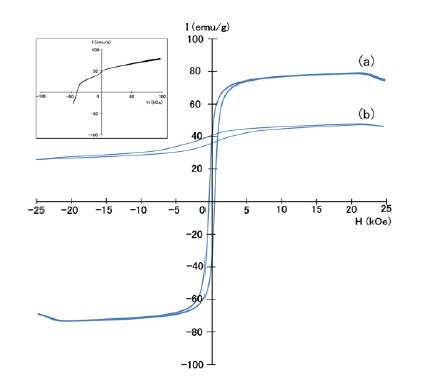
Figure 4 shows the hysteresis loops of the Sm5Fe17 melt-spun ribbon and the Nd15Fe77B8 melt-spun ribbon measured at 473 K under the applied magnetic field of 20 kOe. Although the Sm5Fe17 melt-spun ribbon ribbons showed a much smaller remanence than the Nd15Fe77B8 melt-spun ribbon at room temperature, it exhibits a much smaller difference in remanence at 473 K. Therefore, the magnetic properties of the Sm5Fe17 melt-spun ribbon are comparable to those of Nd15Fe77B8 melt-spun ribbon at 473 K.
3.2. Sm-Fe borides
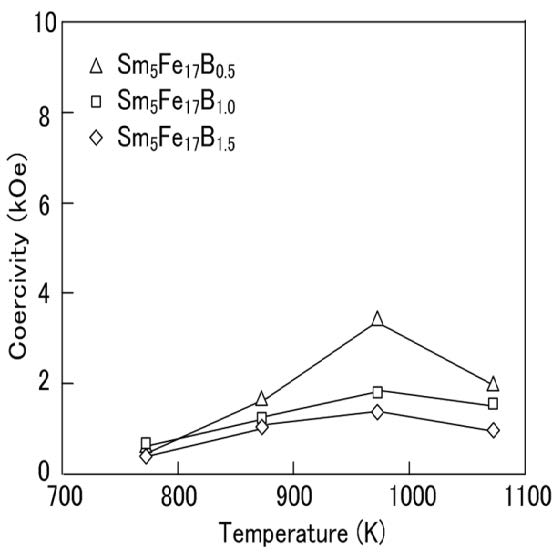
The Sm5Fe17Bx (x = 0.5-1.5) melt-spun ribbon showed a low coercivity, as was the case for the Sm5Fe17 melt-spun ribbon. Figure 5 shows the dependence of the coercivity of the Sm5Fe17Bx (x = 0.5-1.5) melt-spun ribbons on the annealing temperature. The coercivity of the Sm5Fe17Bx (x = 0.5-1.5) alloys shows a similar temperature dependence, but their maximum coercivity, achieved by annealing at 973 K, decreases with increasing B content of the alloy. This indicates that the addition of B to the Sm5Fe17 alloy results in a decrease in coercivity.
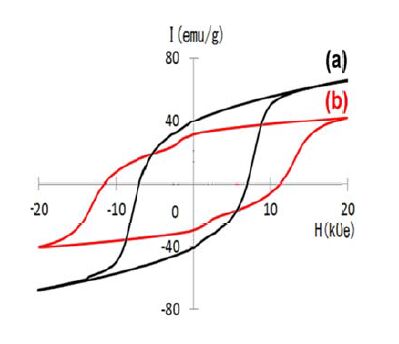
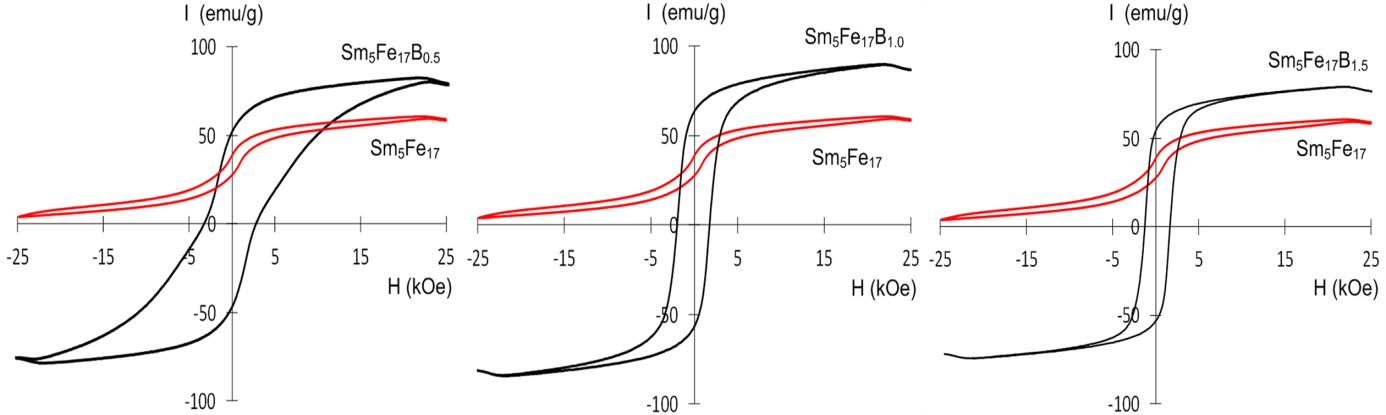
Figure 6 shows the hysteresis loops of the Sm5Fe17Bx (x = 0.5-1.5) melt-spun ribbons annealed at 973 K. For comparison, the hysteresis loop of the Sm5Fe17 melt-spun ribbon annealed at 973 K is shown in the each figure. It is found that the remanence of the Sm5Fe17Bx (x = 0.5-1.5) alloys is higher than that of the Sm5Fe17 alloy even though the coercivity of the Sm5Fe17Bx (x = 0.5-1.5) alloys is much smaller than that of the Sm5Fe17 alloy. The remanence increases with increasing B content from 40 emu/g for the Sm5Fe17 alloy to 65 emu/g for the Sm5Fe17B1.0 alloy and then decreases to 60 emu/g for the Sm5Fe17B1.5 alloy. The remanence of 65 emu/g exhibited by the annealed Sm5Fe17B1.0 alloy is much higher than that of the annealed Sm5Fe17 melt-spun ribbon.
The Sm5Fe17 and Sm5Fe17Bx (x = 0.5-1.5) melt-spun ribbons annealed at 973 K were examined by XRD and thermomagnetic studies to evaluate the differences in the coercivity value. Figure 7 shows the XRD patterns of the annealed Sm-Fe-B melt-spun ribbons. The diffraction peaks of the Sm5Fe17 alloy were determined to be the Sm5Fe17 phase. Virtually the same XRD patterns were obtained from the Sm5Fe17B0.5 alloy. This indicates that the small addition of B to the Sm5Fe17 alloy did not alter the XRD pattern. On the other hand, the XRD pattern of the Sm5Fe17B1.0 alloy is quite different from that of the Sm5Fe17 alloy. The diffraction peaks of the Sm5Fe17 alloy were determined to be the Sm2Fe14B and SmFe2 phases. The XRD pattern of the Sm5Fe17B1.5 alloy is similar to that of the Sm5Fe17B1.0 alloy, indicating that the Sm5Fe17B1.5 alloy also consisted of the Sm2Fe14B (tetragonal) and SmFe2 (cubic) phases. These results reveal that the large addition of B to the Sm5Fe17 alloy resulted in the formation of the Sm2Fe14B and SmFe2 phases instead of the Sm5Fe17 phase, and hence the decrease in coercivity.
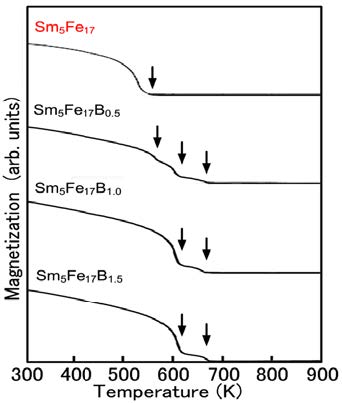
Figure 8 shows the thermomagnetic curves of the annealed Sm-Fe-B melt-spun ribbons. The thermomagnetic curve of the Sm5Fe17 alloy exhibits one magnetic transition at around 550 K, which corresponds to the Curie temperature of the Sm5Fe17 phase. Unlike in the case of the XRD studies, the thermomagnetic curve of the Sm5Fe17B0.5 alloy is quite different from that of the Sm5Fe17 alloy. The thermomagnetic curve exhibits three magnetic transitions at around 550 K, 620 K, and 680 K. It has been reported that the Curie temperatures of the Sm2Fe14B phase and SmFe2 phase are 616 K and 675 K, respectively [12,13,14]. Therefore, the Sm5Fe17B0.5 alloy contains the Sm2Fe14B and SmFe2 phases together with the Sm5Fe17 phase. The thermomagnetic curve of the Sm5Fe17B1.0 alloy exhibits two magnetic transitions at around 620 K and 680 K, indicating that the Sm5Fe17B1.0 alloy has no Sm5Fe17 phase. The Sm5Fe17B1.5 alloy also exhibits two magnetic transitions at around 620 K and 680 K, which correspond to the Curie temperatures of the Sm2Fe14B and SmFe2 phases. This is consistent with the results of the XRD studies.
Figure 9 shows TEM micrographs of the annealed Sm5Fe17B0.5 and Sm5Fe17B1.5 melt-spun ribbons. The grain size of the annealed Sm5Fe17B0.5 alloy was around 50 nm in diameter, which is almost comparable to the reported grain size of annealed Sm5Fe17 alloy [8]. Samarium and iron were detected in most of the grains of the annealed Sm5Fe17B0.5 alloy, except for the centrally located grain that were rich in samarium but poor in iron. According to the results of the thermomagnetic studies, the specimenscontained some of the Sm2Fe14B (Sm11.7 at%) and SmFe2 (Sm33.3 at%) phases together with the Sm5Fe17 (Sm22.7 at%) phase. Thus, the samarium-rich centrally located grain consisted of the SmFe2 phase and the surrounding grains were either the Sm2Fe14B or Sm5Fe17 phase. The upper-left grain region, which was rich in iron but slightly poor in samarium, may be the Sm2Fe14B phase. In the TEM micrograph of the annealed Sm5Fe17B1.5 alloy, an increase was seen in the amount of the SmFe2 phase, where is poor in iron but rich in samarium. The grain size of the SmFe2 phase was found to be larger than that in the annealed Sm5Fe17B0.5 alloy. Since the Sm5Fe17B1.5 alloy consisted of the Sm2Fe14B and SmFe2 phases, the surrounding grains are considered to be the Sm2Fe14B phase. This confirms that the addition of B to Sm5Fe17 alloy results in the formation of the SmFe2 and Sm2Fe14B phases, instead of the formation of a Sm5Fe17Bx phase. Since the Sm2Fe14B phase does not possess uniaxial anisotropy [12], the observed coercivity of the annealed Sm-Fe-B melt-spun ribbons is considered to be the fine SmFe2 phase.
4. Conclusion
The structures and magnetic properties of Sm5Fe17Bx (x = 0-1.5) melt-spun ribbons annealed at 973 K were examined. The annealed Sm5Fe17 melt-spun ribbon consisted of the Sm5Fe17 phase and exhibited a high coercivity. The annealed Sm5Fe17B0.5 melt-spun ribbon consisted of the Sm5Fe17 phase together with the Sm2Fe14B and SmFe2 phases. In contrast, the annealed Sm5Fe17Bx (x = 1.0-1.5) melt-spun ribbons consisted of the Sm2Fe14B and SmFe2 phases. The coercivity of the annealed Sm5Fe17Bx (x = 0-1.5) melt-spun ribbons decreased as the B content increased. On the other hand, the annealed Sm5Fe17Bx (x = 0.5-1.5) melt-spun ribbons exhibited a higher remanence than the Sm5Fe17 melt-spun ribbon.
Acknowledgments
The use of the facilities of the Materials Design and Characterization Laboratory at the Institute for Solid State Physics, the University of Tokyo, is gratefully acknowledged. This work was performed at High Field Laboratory for Superconducting Materials, Institute for Materials Research, Tohoku University.
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: