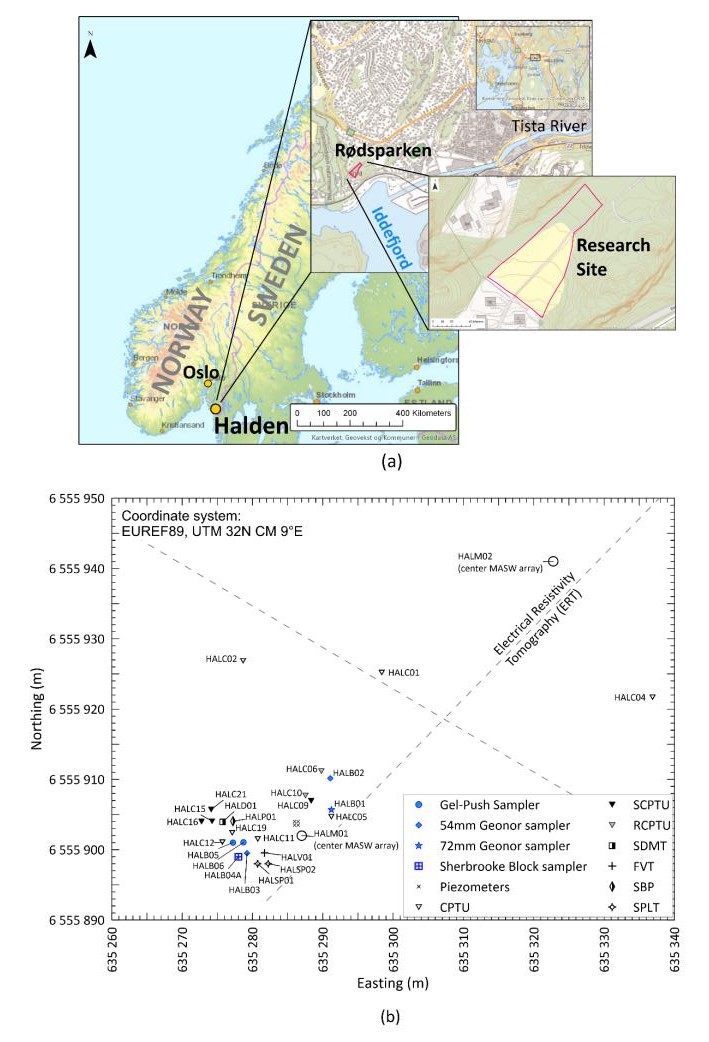
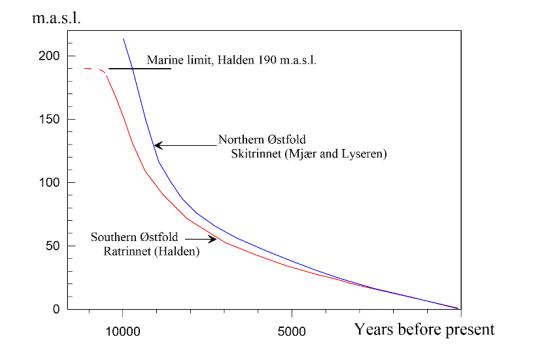
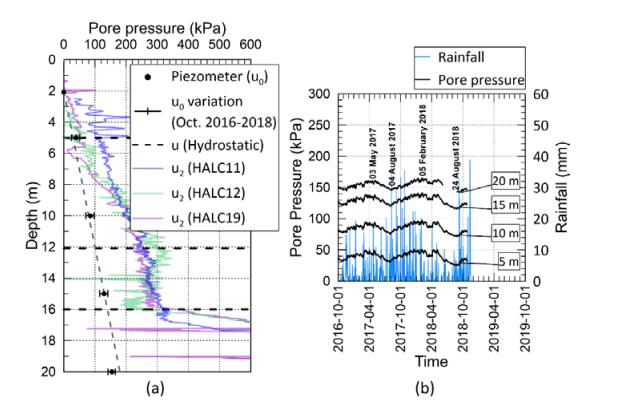
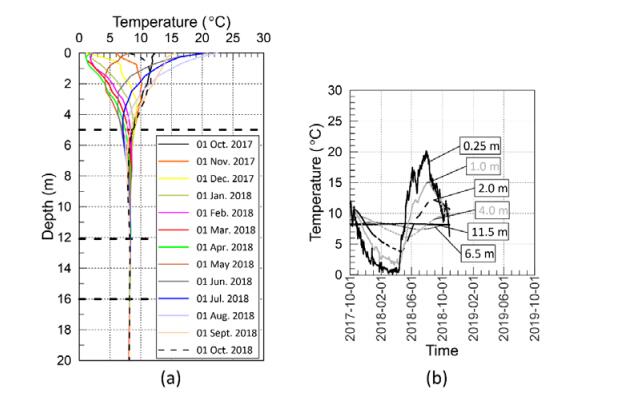
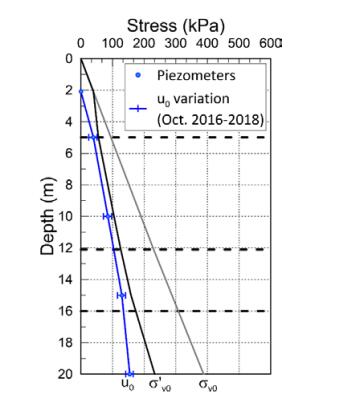
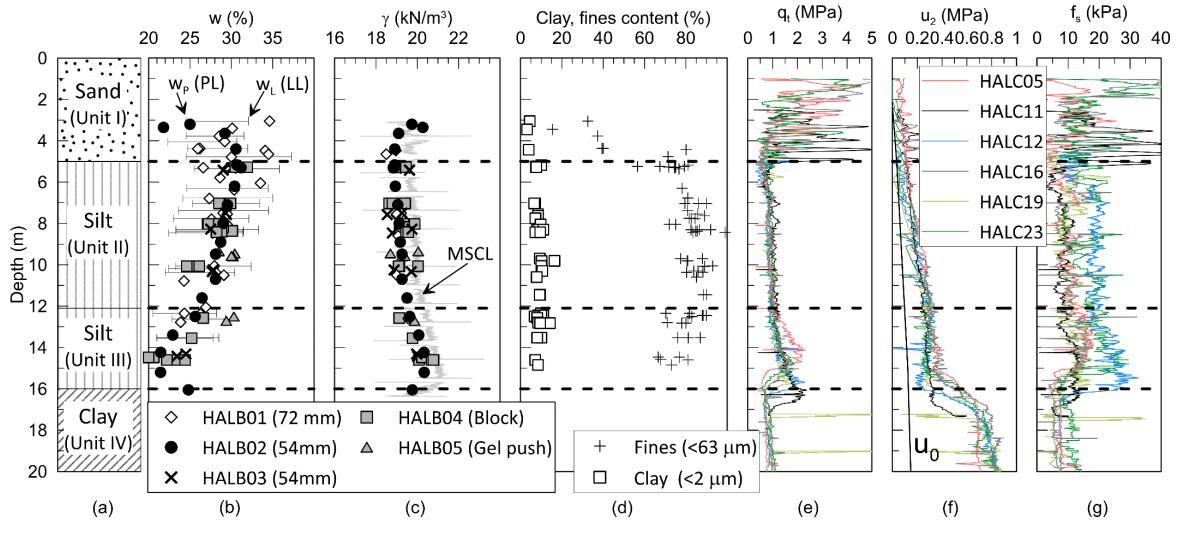
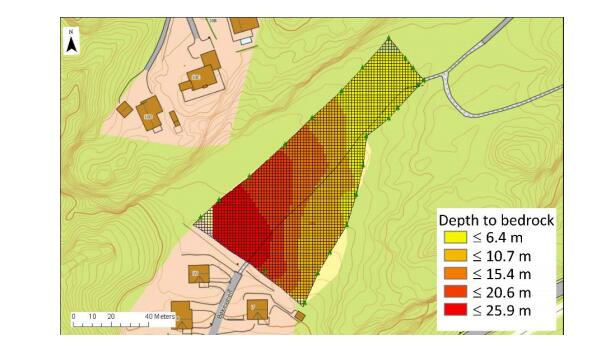
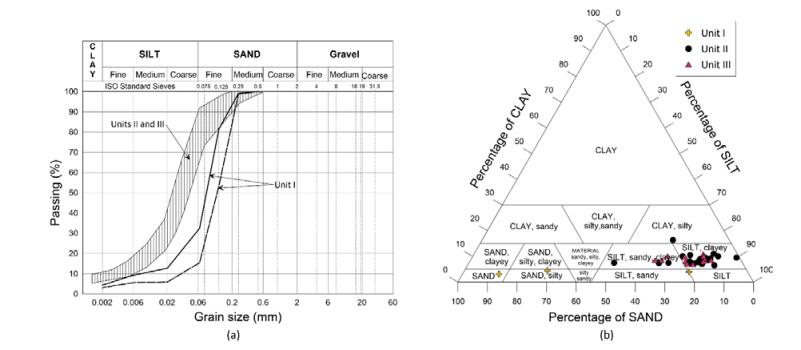
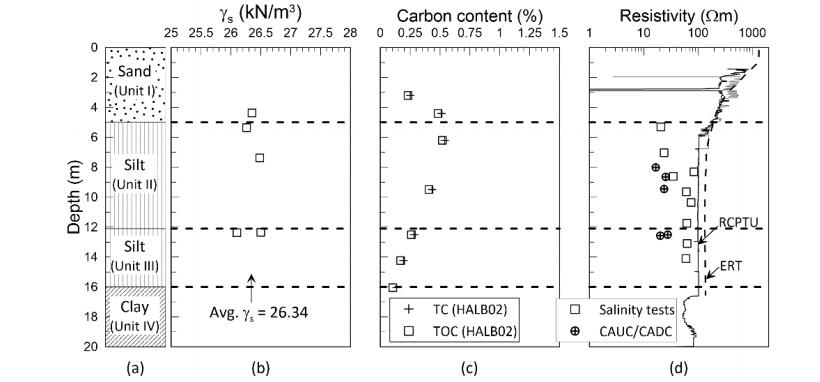
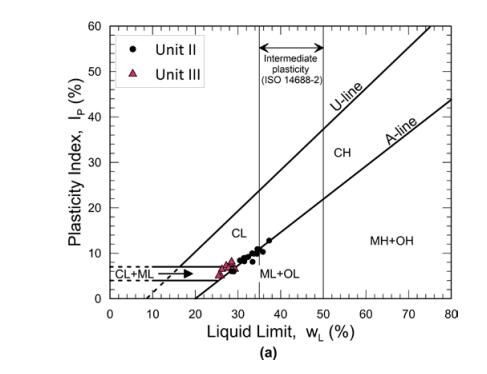
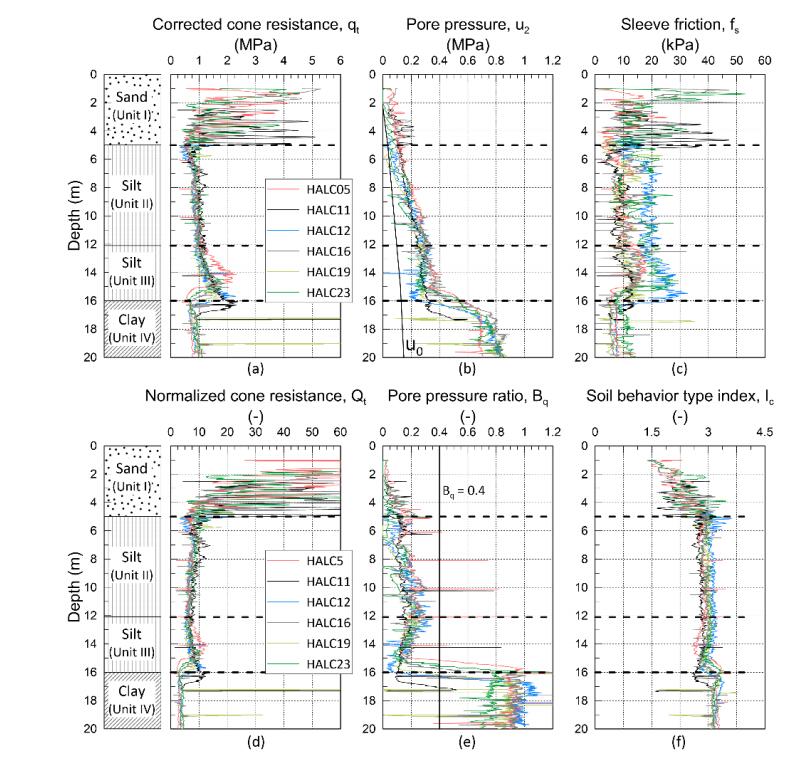
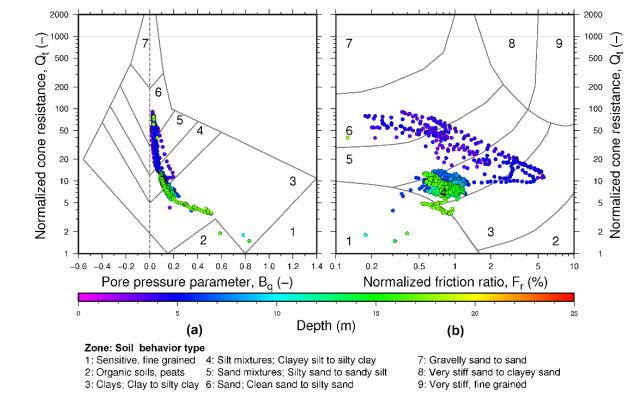
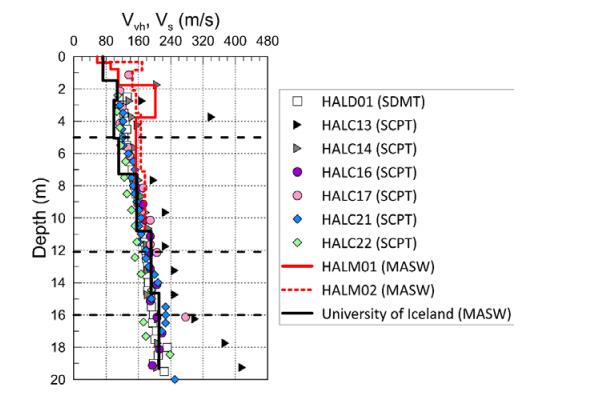
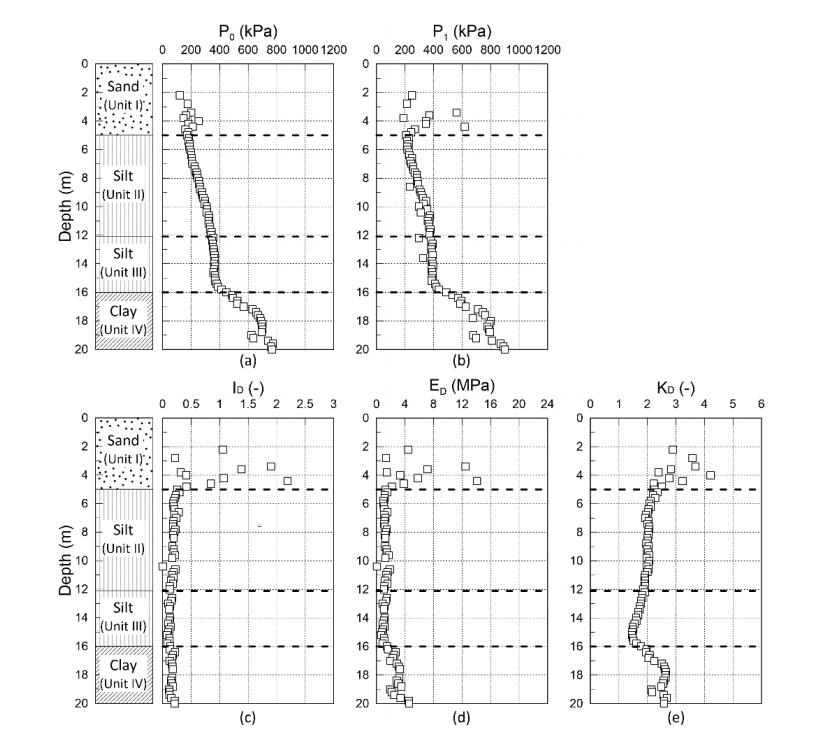
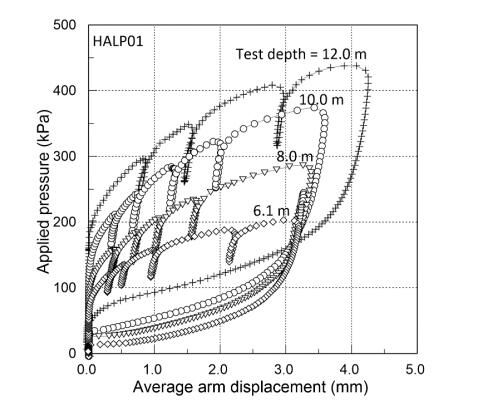
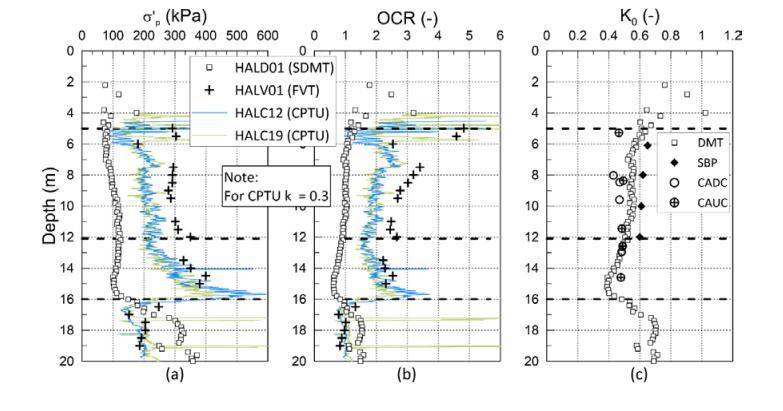
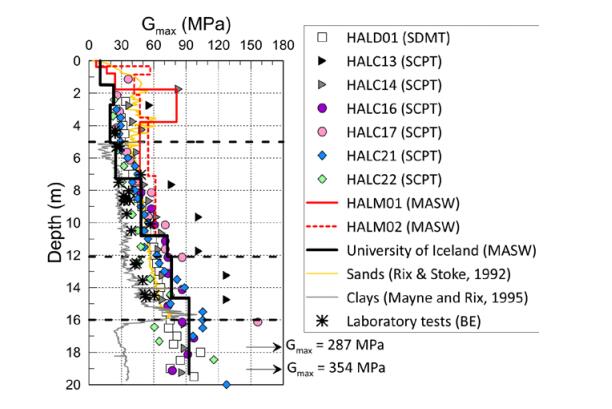
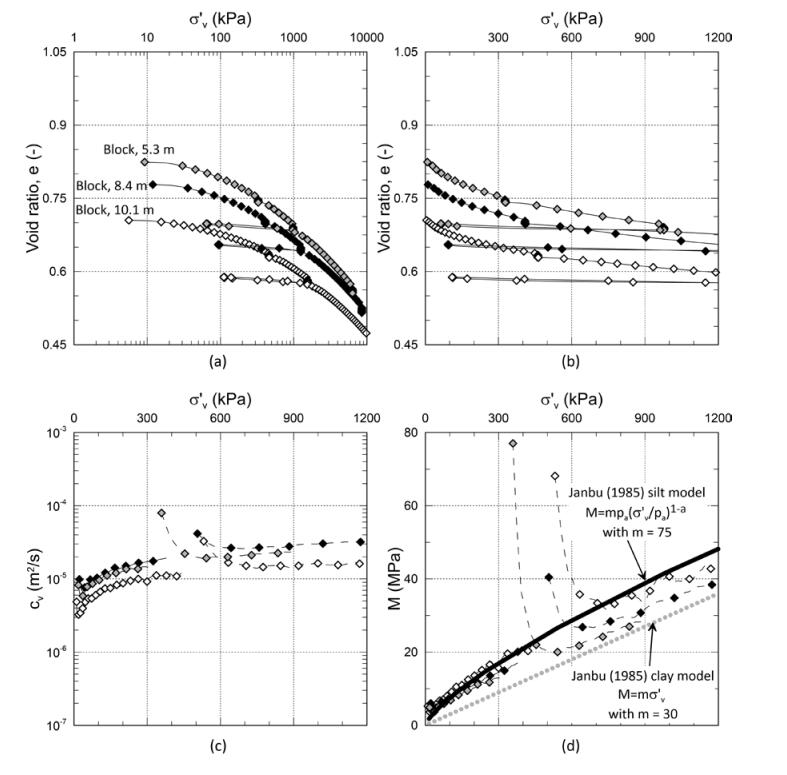
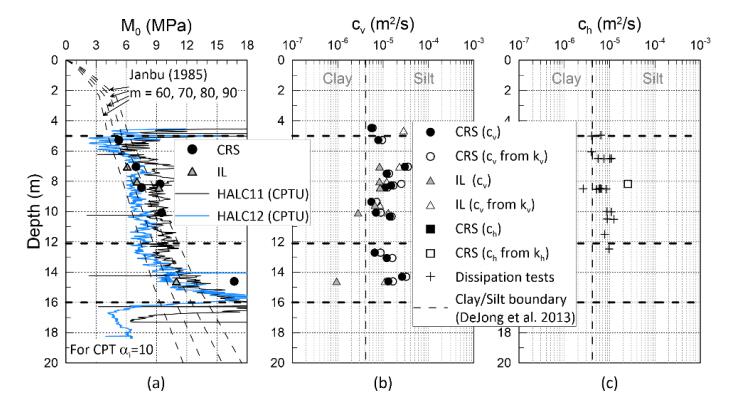
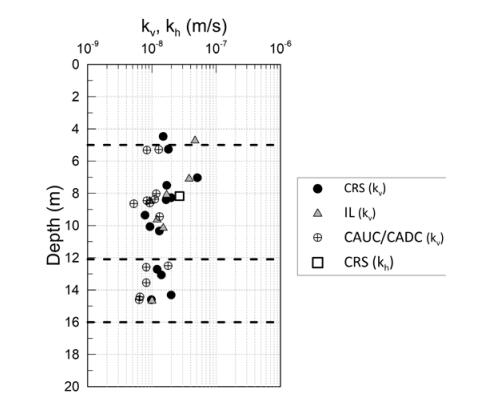
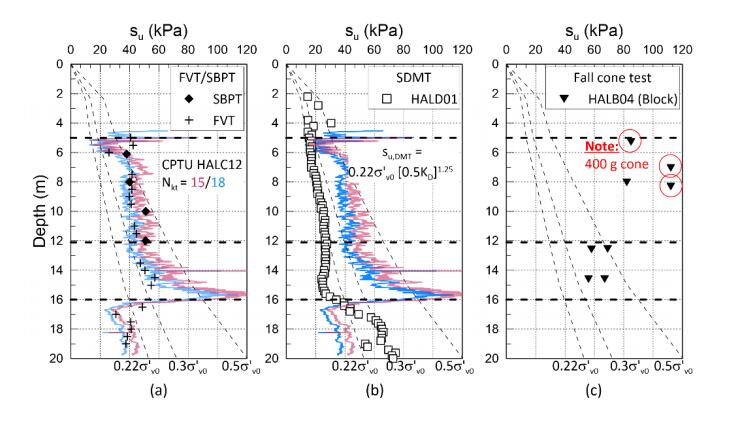
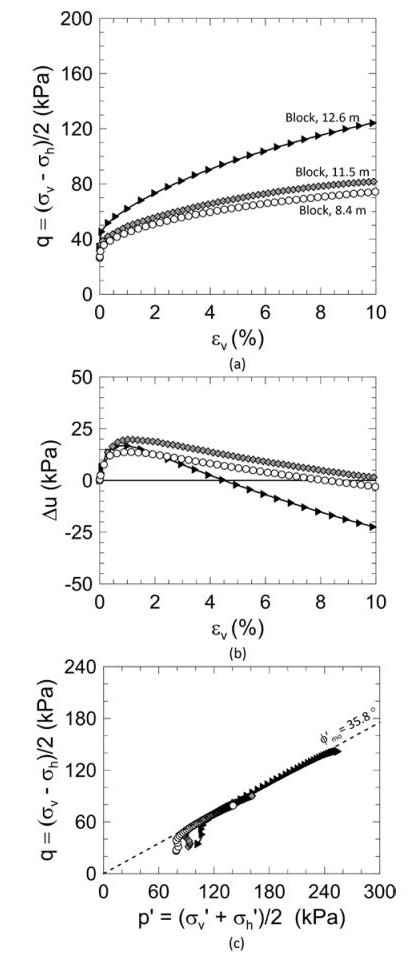
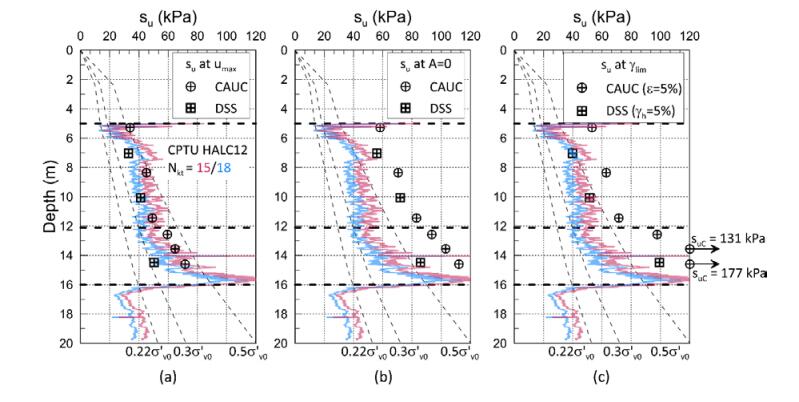
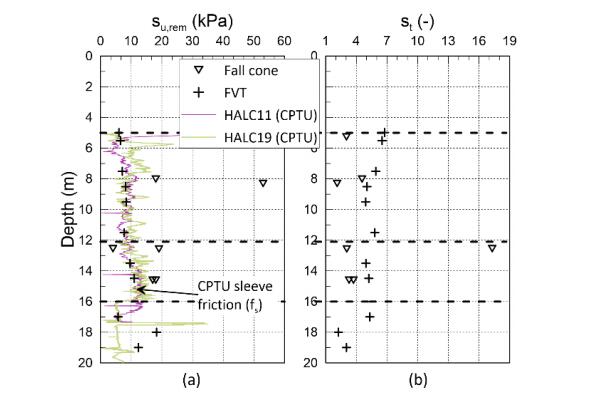
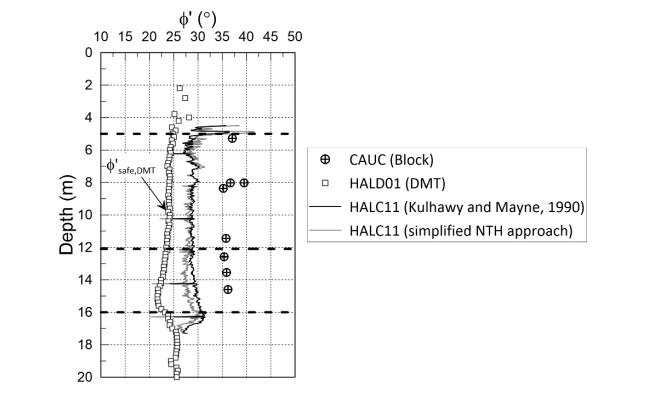
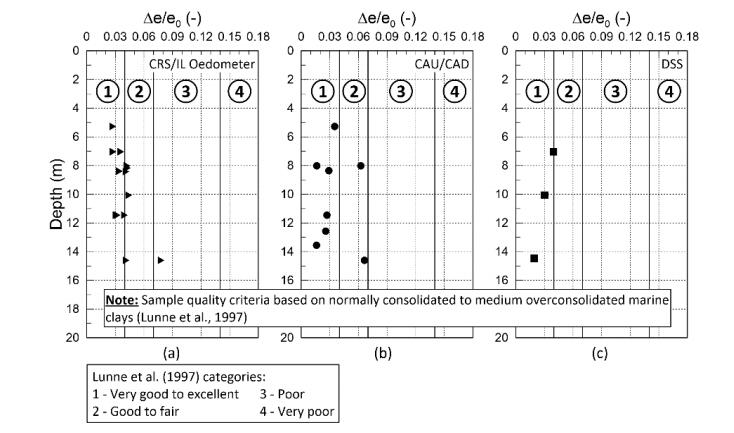
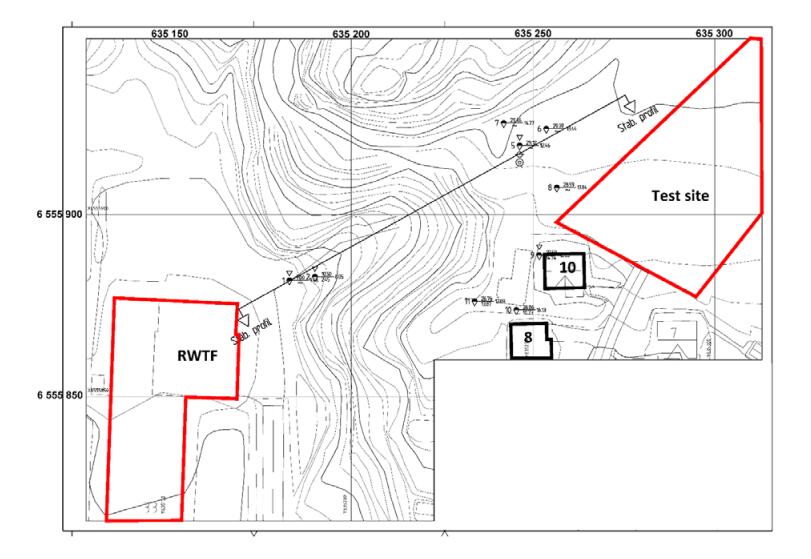
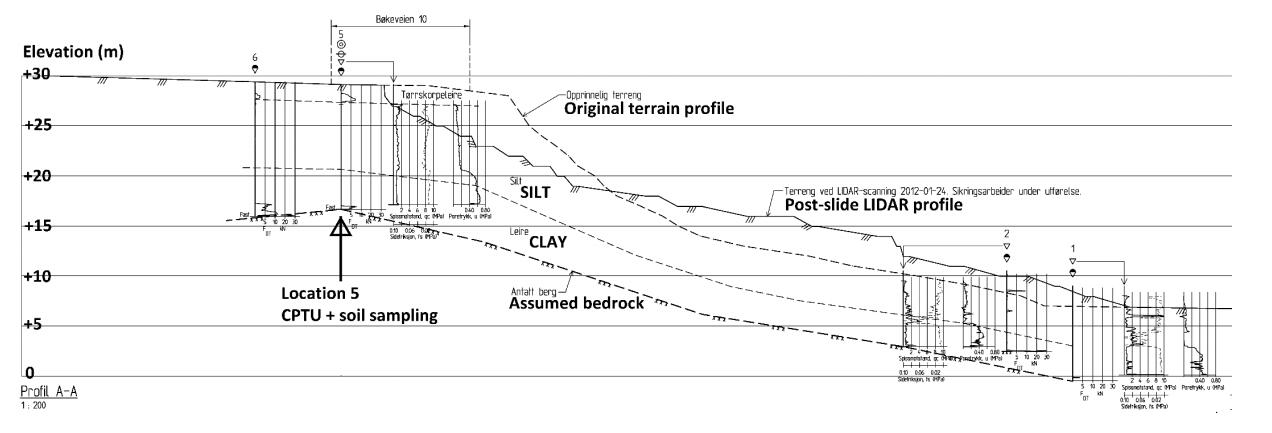
This paper describes the geology and geotechnical engineering properties of the Halden silt; a 10–12 m thick deposit of fjord-marine, low plasticity clayey silt. Over the last six years, the test site has been well characterized by combining the results from a number of geophysical and in situ tools, including; electrical resistivity tomography, multi-channel analysis of surface wave surveys, cone penetration testing, dissipation testing, in situ pore pressure measurements, seismic flat dilatometer testing, field vane testing, self-boring pressure meter testing, screw plate load testing and hydraulic fracture testing. The results from these investigations assist the interpretation of layering and in situ soil properties. Soil sampling and advanced laboratory testing have provided data for interpretation of geological setting and depositional history, soil fabric, strength, stiffness and hydraulic properties. However, interpretation of the stress history, based on oedometer tests and clay-based correlations to the cone penetration test, are unreliable. They contradict the depositional history, which suggests that the soil units at the site are near normally consolidated, except for some surface weathering and desiccation. Further, undrained shear strength interpretations are complex as the in situ tests are potentially influenced by partial drainage, and conventional undrained triaxial tests do not provide a unique (peak) undrained shear strength. Despite certain interpretation challenges the paper presents important reference data to assist in the interpretation and assessment of similar silts, and provide some guidance on important geotechnical properties for projects where limited design parameters are available.
1.
Introduction
In this modern era, hospitals are still extremely crowded, with a long line, because of the shortage of medical equipment and medical staff. An efficient and reliable patient admission scheduling (PAS) has a positive impact on hospitals, such as the availability of services, cost efficiency and social impact etc. This proposal only takes into account the average minimum waiting time for hospital admission, while it does not understand the distinctions in the in-hospital time of patients and the weak impact on the availability of hospital services caused by changes in procedures for surgery. It is also bad for hospital management performance and does not shorten the waiting time for admission to the hospital [1,2,3,4,5,6].
Due to high health needs and a competitive climate, hospitals production performance channel have begun to take strategic action on the services they provide. Operating rooms receive two-thirds of hospital revenue and account for nearly 40% of hospital expenditure [7,8]. From this perspective, in terms of both revenue and expenditure, operating rooms account for the largest share. For this reason, the rise in operating room efficiency has a major effect on hospitals' financial and ultimate ethical results. As a result, the most fascinating and desirable places in hospitals are the operating rooms [9,10]. With these changes in performance, the quality of service and patient satisfaction are growing directly in prosection.
In particular, this work offers up-to-date and basic information on health care system planning and scheduling. It discusses how service networks have taken steps to tackle the extremely high cost of medical technology and how to make better use of the available resources. Any algorithm that has been built on the process of operating room, provide us efficient results day-by-day. How much good they are, these findings are not sufficient and need to be constantly updated and the solution domain be enlarged.
In many significant and basic real-world fields, including operations research [11,12], decision making [13,14,15], the topic of risk analysis [16,17,18,19], and so on, fuzzy grading is often used. The value and significance of different options are represented as fuzzy numbers (FNs) [20,21,22] in many real cases. It is important to provide a technique to structure FNs such as real numbers to explain the choice of opportunities for each other. Chu and Tsao introduced an approach for ranking the fuzzy numbers with an area between the centroid and original points [23]. An index for order of the fuzzy numbers have been presented by Choobineh and Li [24] in 1993. In our everyday life, with the enormous problems of a system, it is very difficult for a decision-maker to obtain the best option from the collection of rational ones [25,26,27,28]. Thus, one understands the factors that can motivate decision-makers to be in charge of such an undeniable hypothesis to make the right decision.
The structure of Atanassov [29] only addresses the degree of satisfaction and dissatisfaction of elements in a set that is quite limited because human nature still has some structure of abstention and refusal problems. In 2013, Cuong [30] considered such hitches to describe the proposed picture fuzzy sets (PFS) as (P(r),I(r),N(r)) in which the elements in triplet reflect degrees of satisfaction, abstain and dissatisfaction respectively, given that 0≤P(r)+I(r)+N(r)≤1. Cuong's structure is significantly closer to human nature than that of previous definitions and is now one of the strongest areas of study. In 2014, Phong et al. [31] presented the idea of the compositions of some fuzzy relationships in the picture fuzzy setting. Ashraf et al. [32] established the algebraic norm based list of aggregation operators (AOps) under PFS environment. Singh [33] presented the idea of correlation coefficients for PFSs in 2015. Qiyas et al. [34] established the linguistic variable based novel AOps for PFS and discussed their applicability to aggregate uncertain information in DMPs. In 2016, Son [35] presented the definition of standardized picture distance measurement and proposed its applications. Khan et al. [36] established the Einstein norm based list of AOps under PFS environment. Ashraf et al. [37] presented the decision making methodology to evaluate production in gold mines utilizing distance measure under cubic PFS environment. The cosine similarity measures for PFSs was proposed by, Wei [38] in 2017. In 2017, Garg [39] implemented a PF aggregation to aggregate PF data. Khan, et al. [40] developed the novel notion of generalized PF soft sets and discussed their applicability in decision making problems (DMPs). In [41], established the novel AOps using logarithmic function under PFS environment. Although all of these approaches have drawbacks and shortcomings, there is no general model for the ranking of PFNs.
This attempt is to solve the problems and suggest a novel generalized methodology for the ranking of PFNs because of the motivation and inspiration of the above discussion. We extend the Einstein hybrid aggregation operators of FSs, IFSs and introduce PF Einstein hybrid averaging (PFEHA) and PF Einstein hybrid geometric (PFEHG) aggregation operators. Also establish the Generalized PF Einstein hybrid averaging (GPFEHA) and Generalized PF Einstein hybrid geometric (GPFEHG) aggregation operators. Utilizing the above mentioned aggregation operator we design an algorithm to rank the alternatives. The proposed approach is capable of aggregating the picture fuzzy quantities with the same mode and symmetric spreads. According to existing literature, the development of hybrid aggregation operators with a picture fuzzy environment is not observed. As a consequence of this inspiration, we construct a variety of Einstein norm based aggregation operators for picture fuzzy hybrid averaging/geometric, under the Einstein t-norm and t-conorm.
The noteworthy contributions of the present article are follows:
1) To construct novel picture fuzzy hybrid aggregation operators under picture fuzzy environment.
2) To compile a list of generalized hybrid aggregation operators based on the Einstein t-norm and t-conorm, and analyze their associated features in details.
3) To develop a DM methodology using proposed aggregation operators to aggregate the uncertain information in real-world decision making problems.
4) A numerical case study related to Patient Admission Scheduling problem as a real-world DM problem is considered to demonstrate the applicability and effectiveness of the proposed methodology.
5) Picture fuzzy TOPSIS method is employed to validate the proposed DM approach.
The remainder of the manuscript is arranged as follows: Section 2 briefly retrospects some basic concepts of fuzzy set, intuitionistic fuzzy set and picture fuzzy sets. A list of novel hybrid aggregation operators are proposed in Section 3. Section 4 highlights a list of generalized hybrid aggregation operators under picture fuzzy settings. Section 5 is devoted to a decision making methodology based on the developed aggregation operators. Section 6 presented the numerical illustration concerning the Patient Admission Scheduling problem. Further this Section deals with the applicability of the developed methodology. Section 7 establishes the PF-TOPSIS methodology to validate the established aggregation operators based MADM methodology. Section 8 concludes this manuscript.
2.
Preliminaries
This section presents the review of basic ideas associated with fuzzy sets (FSs), intuitionistic fuzzy sets (IFSs) and picture fuzzy sets (PFSs).
Definition 1. [42] In universal set M≠ϕ, a fuzzy set (FS) E is characterized as;
Pe:M→[0,1] denoted the membership degree of an element r in E.
Definition 2. [29] In universal set M≠ϕ, an IFS E is characterized as;
Pe and Ne:M→[0,1] denoted the membership and non-membership degree of an element r in E. Also it satisfy the condition that; 0≤Pe(r)+Ne(r)≤1, for all r in M.
Definition 3. [30] In universal set M≠ϕ, a PFS E is characterized as;
where the positive, neutral and negative membership degree of each r in M is represented by Pe, Ie and Ne:M→[0,1] respectively. Where the membership degrees satisfy the condition that; 0≤Pe(r)+Ie(r)+Ne(r)≤1 for all r in M.
Definition 4. [32] Let M≠ϕ be a universe set and E={Pe(r),Ie(r),Ne(r)} be a picture fuzzy set.
1) The score of E is denoted and define as follows:
where Sco(E)∈[−1,1].
2) The accuracy of E is denoted and define as follows:
where Acu(E)∈[0,1].
Definition 5. [32] Let M≠ϕ be a universe set and El={Pel(r),Iel(r),Nel(r)} and Ek={Pek(r),Iek(r),Nek(r)} be two picture fuzzy sets. Then the following conditions satisfies:
(a) If Sco(El) ≻ Sco(Ek); then El≻Ek.
(b) If Sco(El) ≈Sco(Ek); and Acu(El) ≻Acu(Ek); then El≻Ek.
(c) If Sco(El) ≈ Sco(Ek) and Acu(El)≈Acu(Ek); then El≈Ek.
Definition 6. [32] A picture fuzzy hybrid averaging aggregation operator can be defined as:
where the weight of Ep(p∈N) is τ=(τ1,τ2,...,τn)T, such that τp∈[0,1], n∑p=1τp=1.
3.
Picture fuzzy Einstein hybrid aggregation operators
In this section, we establish Einstein operational laws and a list of novel PF Einstein hybrid averaging and geometric aggregation operators under PF information.
Definition 7. Let Ek={Pek(r),Iek(r),Nek(r)} and El={Pel(r),Iel(r),Nel(r)} be the two PFNs, and τ≻0 be any real number, then
1) Ek⊕εEl=(Pek+Pel1+PekPel,IekIel1+(1−Iek)(1−Iel),NekNel1+(1−Nek)(1−Nel));
2) Ek⊗εEl=(PekPel1+(1−Pek)(1−Pel),IekIel1+(1−Iek)(1−Iel),Nek+Nel1+NekNel);
3) τ(El)=((1+Pel)τ−(1−Pel)τ(1+Pel)τ+(1−Pel)τ,2(Iel)τ(2−Iel)τ+(Iel)τ,2(Nel)τ(2−Nel)τ+(Nel)τ);
4) (El)τ=(2(Pel)τ(2−Pel)τ+(Pel)τ,2(Iel)τ(2−Iel)τ+(Iel)τ,(1+Nel)τ−(1−Nel)τ(1+Nel)τ+(1−Nel)τ).
3.1. Einstein hybrid averaging AOps
Definition 8. Let M≠ϕ be a universe set and El={Pel(r),Iel(r),Nel(r)} (l∈N) be the family of the PF values. Then PFEHA aggregation operator for n dimensions is a mapping PFEHA:PFN→PFN define as
where ¯eδ(t) is the tth largest of the weighted PF values ¯et (¯et=nτtet, t∈N),τ=(τ1,τ2,...,τn)Tis the weight of Et(t∈N), which satisfy the condition τt∈[0,1], n∑t=1τt=1, if the vector (τ1,τ2,...,τn)T became (1n,1n,...,1n)T, then the vector (nτ1e1,nτ2e2,...,nτnen)T will become (E1,E2,...,En)T, and n is the adjusting factor.
Theorem 1. Suppose M≠ϕ be a universe set and El={Pel(r),Iel(r),Nel(r)} (l=1,2,...,n)be the family of the picture fuzzy values, then by using the PFEHA operatortheir aggregated value is also a PF value and
where the weight of Et(t∈N) is τ=(τ1,τ2,...,τn)T,i.e., τt∈[0,1], n∑t=1τt=1.
Proof: To prove this Theorem we can use induction method, first we show that Eq (3.1) holds for n=2.
Then
Thus, outcome is valid for n=2; Now for n=k we consider that Eq (3.1) is true; then
If Eq (3.1) is valid for n=k, then we have to demonstrate that n=k+1 is valid for Eq (3.1), thus,
Suppose that
By putting these values in above equation, we obtain
Now putting the values in above equation we obtain
Equation (3.1) is thus valid for n=k+1. Hence, for all n, Eq (3.1) is valid.
Lemma 1. Let Et≻0,τt≻0 (t∈N) and n∑t=1τt=1, then
where equality is held if and only if (⟺) Et (t∈N)=E.
Theorem 2. Let M≠ϕ be a universe set and El={Pel(r),Iel(r),Nel(r)} (l∈N) be the family of the PF values, then
where the weight of Et(t∈N) is τ=(τ1,τ2,...τn)T i.e τt∈[0,1] and n∑t=1τt=1.
proof Since
As
Thus
Also
where equality held ⟺ P¯eδ(t)(j=1,2,...n) are equal. Again
As
So
Thus
where equality held ⟺ I¯eδ(t)(t=1,2,...n) are equal. Similarly,
As
So
Thus
where equality held ⟺ N¯eδ(t)(t=1,2,...n) are equal.
Let
And
Then Eqs (3.2)–(3.4) can be converted into the following forms: Pel≥Pεel, Iel≤Iεel and Nel≤Nεel respectively. Hence
Thus
If
then
If
Then we have
Thus
Hence from Eqs (3.5) and (3.6), we get PFEHAτ,τ(E1,E2,...,En)≤PFHAτ,τ(E1,E2,...,En), which complete the proof.
3.2. Picture fuzzy Einstein hybrid geometric (PFEHG) aggregation operator
Definition 9. Let M≠ϕ be a universe set and El={Pel(r),Iel(r),Nel(r)} (l∈N) be the family of the PF values. Then PFEHG aggregation operator for n dimensions is a mapping PFEHG:PFN→PFN define as
where ¯eδ(t) is the tth largest of the weighted PF values ¯et (¯et=nτtet, t∈N), the weight of Et(t∈N) is τ=(τ1,τ2,...,τn)T, i.e. τt∈[0,1], n∑t=1τt=1, if the vector (τ1,τ2,...,τn)T became (1n,1n,...,1n)T, then the vector (enτ11,enτ22,...,enτnn)T will become (E1,E2,...,En)T, and n is the adjusting factor.
Theorem 3. Let M≠ϕ be a universe set and El={Pel(r),Iel(r),Nel(r)} (l∈N) be the family of the PF values, then their combined value byusing the PFEHG operator is also a PF value and
where τ=(τ1,τ2,...,τn)T is theweight of Et(t∈N),i.e. τt∈[0,1], n∑t=1τt=1.
Proof The proof is identical to the Theorem 1.
Theorem 4. Let M≠ϕ be a universe set and El={Pel(r),Iel(r),Nel(r)} (l∈N) be the collection of the picture fuzzy values, then
where τ=(τ1,τ2,...τn)T is theweighted vector of Et(t∈N) such that τt∈[0,1] and n∑t=1τt=1.
Proof The proof is identical to the Theorem 2.
4.
Generalized picture fuzzy Einstein hybrid aggregation operators
In this section, we develop generalized picture fuzzy Einstein averaging and geometric hybrid aggregation operators.
4.1. Generalized picture fuzzy Einstein hybrid averaging AOps
Definition 10. Let M≠ϕ be a universe set and El={Pel(r),Iel(r),Nel(r)} (l∈N) be the family of the PF values. Then GPFEHA aggregation operator for n dimensions is a mapping GPFEHA:PFN→PFN define as
where ¯Eδ(t) is the tth largest of the weighted PF values, τ=(τ1,τ2,...,τn)Tis the weight of Et(t∈N), satisfied the condition τt∈[0,1], n∑t=1τt=1, and the balancing coefficient is n. λ be any positive real number.
Theorem 5. Let M≠ϕ be a universe set and El={Pel(r),Iel(r),Nel(r)} (l∈N) be the family of the PF values and τ=(τ1,τ2,...,τn)Tis the weight of Et(t∈N), satisfied the condition τt∈[0,1], n∑t=1τt=1. Then by using the GPFEHA aggregationoperator, the aggregated value can be indicated as follows:
Proof Theorem 1 is identical to this proof. As a result, the process has been omitted.
Theorem 6. Let M≠ϕ be a universe set and El={Pel(r),Iel(r),Nel(r)} (l∈N) be the family of the PF values, then
where τ=(τ1,τ2,...τn)T is theweight of Et(t∈N) which satisfied the condition τt∈[0,1] and n∑t=1τt=1.
Proof Theorem 2 is identical to this proof. As a result, the process has been omitted.
4.2. Generalized picture fuzzy Einstein hybrid geometric AOps
Definition 11. Let M≠ϕ be a universe set and El={Pel(r),Iel(r),Nel(r)} (l∈N) be the family of the PF values. Then GPFEHG aggregation operator for n dimensions is a mapping GPFEHG:PFN→PFN define as
where ¯Eδ(t) is the tth largest weighted of the PF values, τ=(τ1,τ2,...,τn)Tis the weight of Et(t=1,2,...,j),i.e. τt∈[0,1], n∑t=1τt=1, and the balancing coefficient is n. λ be any positive real number.
Theorem 7. Let M≠ϕ be a universe set and El={Pel(r),Iel(r),Nel(r)} (l=1,2,...,n)be the family of the PF values and τ=(τ1,τ2,...,τn)Tis the weight of Et(t=1,2,...,j), i.e. τt∈[0,1], n∑t=1τt=1. Then by using the GPFEHG operator, thecombined value can be indicated as follows:
Proof The proof is identical to the Theorem 1.
Theorem 8. Let M≠ϕ be a universe set and El={Pel(r),Iel(r),Nel(r)} (l∈N) be the family of the PF values, then
where the weight of Et(t=1,2,...,n) is τ=(τ1,τ2,...τn)T i.e. τt∈[0,1] and n∑t=1τt=1.
Proof The proof is directly related to the Theorem 2.
5.
An application of the proposed aggregation operators
Throughout this section, we illustrate how picture fuzzy Einstein hybrid operators can be used to solve the multiple criteria group decision making (MCGDM) problem.
5.1. Algorithm
Let Z={Z1,Z2,...,Zm} represent the m alternatives set, the n attributes set are represented by R={R1,R2,...,Rn}, and D={D1,D2,...,Dk} represent the k decision makers set. Let τ=(τ1,τ2,...τn)T represent the attributes weight Rt(t∈N) i.e., wt∈[0,1], n∑t=1wt=1, and consider that the weight of the decision makers Ds(s=1,2,3,...,k), is ω=(ω1,ω2,...,ωk)T i.e., ωs∈[0,1] and k∑s=1ωs=1. This approach has the following measures:
Step−1 We create the PF decision-making (DM) matrices in this step for decision, Ds=[E(s)it]m×n(s=1,2,...,k). There are benefit and cost type criteria, then the PF decision matrices, Ds=[Esit]m×n can be transformed into the normalized PF decision matrices, Rs=[r(s)it]m×n, where
j=1,2,...,n, and the complement of Esit is ¯Esit. If all of criteria are from the same kind, no normalization is needed.
Step−2 To combine all of the individual standardized PF decision matrices, use the PFEWA operator, Rs=[r(s)it]m×n (s=1,2,...,k) into a common PF decision matrix, R=[rit]m×n, where rit=(Peit,Ieit,Neit) (i=1,2,..,m,t∈N).
Step−3 To get the overall preference values, we apply ¯eit=nwteit.
Step−4 To aggregate the picture fuzzy hybrid decision matrix, using GPFEHA aggregation operator.
Step−5 Compute the ri(i=1,2,3,...m) scores function of all the aggregated alternatives. When there's no difference between the two or more than two scores, the accuracy levels of the combined preference values must be determined.
Step−6 List the scores of all alternatives in descending order, then choose the alternative with the top score value.
Figure 1 describes the proposed methodology's flow chart:
6.
Patient admission scheduling problem
The suggested ranking approach is used in this area to resolve the issue of patient admission scheduling (PAS) in the hospitals. Using proposed aggregation operators, we present a new approach to address PAS problem by assigning patients to beds randomly. The proposed methodology utilized four criteria and four alternatives strategies in the pitch adjustment stage.
6.1. Descriptions of the problem
The problem of patient admission scheduling (PAS) is an optimization and decision making problem in which we automatically allocate patients to beds for a specific interval of time while maintaining their medical needs and choices. PAS is one of the tough scheduling problems faced by many health care centers that struggle with finding an appropriate way to allocate hospital services to patients seeking hospital admission while fulfilling all the required hospital requirements (such as beds, rooms, time slots, and etc.). These hospital conditions or regulations which vary from one hospital to another, but may include that patients in a room are of the same gender, a special room request for accommodation for patients, the date of admission of patients and the period of stay, etc.. The attribute of the room is given as the quantity of beds, the unit in which the bed is situated, and medical facilities. Make sure that the therapy an unit might provide is dependent on the types of qualities of the devices located in the rooms. And the duration of stay of the patients is determined by the time slots. The patient-stay duration, for example, is provided by appointing a patient to a bed in a room and times period (night).
Doctor-patient relations are another significant fact for proper care. Improper communication between doctor and patient often delays the right treatment from being obtained. It often becomes even more difficult for a patient to find the ideal doctor's real location. According to the new conventional method, it's too complicated to appoint a doctor and patients often have to survive a lot.
For patients taking the doctor's appointment directly via mobile SMS or a smart phone device with a completely unique serial number, the main focus point is required. In the conventional time and money-wasting scheme, patients should make an appointment with a doctor. The efficient resources for both doctors and patients through the system are time to time feedback messages, both doctor and patient specific profile management with effective information, searching and locating area wise doctors list, individual patient medication management, doctor's office venue view of the assigned patients, clear and real time recommending patients to other doctors. Proper management of the profile management of individual doctors and patients is the way to improve the relationship between doctor and patient. The section on medication management is directly related to patient referral and is also necessary. The scheme is planned in a pleasant way for both doctors and patients.
The classification about each PAS problem input is given as: patient characteristics as the patient is a person with certain criteria for medication, gender, room requirement, class and age [43,44]. Suppose a group of decision-makers to conduct the assessment and choose the best PAS solution for this problem facing by patients and doctors, among the four demands of patient at the time of PAS problem are Z1, Z2, Z3 and Z4. The decision maker evaluates the demands of patient according to four attributes and describe the PAS problem whose weights are τ=(0.224,0.236,0.304,0.236)T, which are given as follows:
R1: 1) Time: Both patients and Doctors will cooperatively decide about time. A time slot that reflects the patient's day of stay; a scheduled patient stay that is the collection of all the days that the patient will spend time in the hospital; The following measure must be followed.
2) Doctors: Doctor will decide about time limit according to the health condition of patients so he/she may suggest a patient for a day, two days, month and so on. This will include stay and discharge.
3) Patients: On the basis of doctor suggestion patients will then decide the time criteria according to his/her economic and social status then he/she will take a decision for stay and discharge.
R2: Age Policy: Age policy is focused on the fact that certain hospitals determine how old a patient should be at least or at most to be admitted in a department (e.g., pediatrics department) with a PAS issue.
R3: Same Gender Patients: The same patient of the same gender matters and impacts the family and hospital environment of patients at the time of the patient admission process. So room gender policy for patient are hilighted problem, the room may have male or female patients, but they must be of the same gender, the room may be held by females only and the room may be held by males patient only.
R4: Basic needs for the patient in the room: Room requirements as each room has unique attributes, such as medical equipment, size of the room, and the unit in which the room is placed; unit as each unit has several specializations at various levels of expertise; specialty as each patient wants one or more physicians for their treatment.
Three decision makers DS(s=1,2,3), whose weight is ω=(0.3,0.3,0.4)T. The frame of the decision problem is given in Figure 2:
There are four best ways and solution for the patient-doctor to take the right decision for PAS under the fuzzy environment by using proposed list of generalized aggregation operators as follow;
Today, hospitals suffer more pressures than ever before to provide cost-effectively high-value services while providing outstanding treatment experiences are offered for their patients. Nonetheless, reducing earnings, increasing expenses, and growing demands from patients make the prospect difficult. Addressing these challenges demands that hospital managers and health care providers work together to identify forward-looking solutions without compromising quality to achieve maximum patient safety and control costs. With that in mind, here are four creative patient care improvements that will help you solve challenges and achieve your goals.
Facilitated Rooms: (Z1) Operating rooms seem to be the most significant source of hospital revenue and expenditure. Hospital management is also based on the success of timetables and schedules. For this reason, an improvement in operating room efficiency has an important effect on hospitals' financial and overall ethical results. As a result, the most fascinating and desirable places of hospitals are operating rooms. With these changes in efficiency, the quality of service and customer satisfaction are growing directly in prosection. Room temperature are the important aspect for patient because patient health depend upon on the room temperature that's why hospital management should be improve and provide the facilitated room. Some patient give preference to normal temperature, some required hot temperature room and some need cool temperature room because of there health issues.
Improve clinical documentation and Time management: (Z2) The only workable solution is to improve the standard of available bedside time. Toward this end, it is important to have better communication. A lot of time is spent on patient arrival or release by many hospital lists, but on follow-up visits scrimp. Try to ensure the providers record patient care appropriately. Better documentation means better communication within the health care team---that can facilitate patient care transitions.
Decrease length of stay: (Z3) When primary care doctors admit their patients to the hospital, they have the benefit of preexisting faith and, in many cases, a decades-long relationship with the patients and their families. Patients feel safe, believing "my doctor knows me". Hospitalists don't have this lengthy relationship with their patients, and they will be faced with the challenge of establishing a trustworthy and therapeutic relationship after just a few visits.
Appointments, updating instructions, consulting with experts, focusing on test reports, and discharging patients take up more than half of a hospitalist's time. Building trust, discussing the concerns of the patient and family, therapy, and preparing for safe discharge are all time-consuming.
Empathy: (Z4) For many patients, having admitted to the hospital tends to mean dealing with a life-threatening condition. Patients may be afraid, nervous, depressed, and sad. The underlying emotion that can manifest as anger, irritation or anxiety is very important for the doctor to fully understand. Empathy offers a very strong basis for a partnership to be established.
We are now enlisting the alternatives' suitability scores versus the four attributes listed. As per the suitability ranking for the four alternatives, Z1, Z2, Z3 and Z4 the four attributes are R1,R2,R3 and R4.
Step−1 In Tables 1–3, the construction of decision matrices can be seen:
Here R1, R3 are cost, and R2, R4 are criteria of the benefit type. So we need the decision matrices normalized. In Tables 4–6, normalized decision matrices are shown:
Step−2 Utilizing the operator of PFEWA aggregation to combine all individual normalized PF decision matrices. Table 7 show the aggregated picture fuzzy decision matrix.:
Step−3 Utilizing ¯Eij=nwjEij, we obtained
We can now find the score function as described in the Definition 4.
So we get Table 8:
Step−4 To aggregate the Table 8, we use GPFEHA and result shown in Table 9:
Step−5 We now find out the values of the score and accuracy function respectively by using the Definition 4 as, we get Table 10;
Figures 3 and 4 presented the graphical aspect of the score and accuracy functions.
Step−6 Table 11 shows the ranking result;
Different values of λ we obtain that Z1 is our best choice. Graphical aspect of score and accuracy variation using GPFEHA at different values of λ seen in Figures 5 and 6.
Graphical aspect of score and accuracy for GPFEHG Aggregation Operator at different values of λ is seen in Figures 7 and 8:
Hence we obtain that Z1 is our best alternative that help hospitals to manage the admissions of patients in a flexible manner.
7.
Comparison with TOPSIS method
Throughout this section, the proposed aggregation information compared with TOPSIS methodology under picture fuzzy environment. Hwang and Yoon [45] first developed TOPSIS methodology, the well-known classical decision making method. At the same time, it considers the distances to both positive ideal solution (PIS) and negative ideal solution (NIS) and ranks a preferred order as per their relative closeness coefficient (RCC) [46,47,48,49].
The following steps are taken to obtain the ranking results for the considered alternative;
Step−1 First, we enlist the opinions of experts in Tables 1–3. We obtained Tables 4 to 6 after normalizing the expert evaluation data.
Step−2 Utilizing the operator PFEWA to combine all individual normalized PF decision matrices. Table 7 shows the aggregated picture fuzzy information matrix.
Step−3 In this step, we findout the score result (Definition 4) of each aggregated alternative shown in Tables 12:
Step−4 Determining the relative PIS and the relative NIS for PFNs: Consider that the PFN decision matrix can be denoted as Ds=[E(s)it]m×n(s=1,2,...,k), compute PIS(s) and NIS(s) for each decision makers as follow:
and
By using Eqs (7.1) and (7.2), PIS and NIS under picture fuzzy environment is evaluted in Table 13:
{\bf{Step-5}} Determining the distance measure from R-PFPIS and R-PFNIS for PFNs: Determine the normalized Euclidean distance (NED) of each alternative from DM(N) ^{(s)} to PIS ^{(s)} and NIS ^{(s)} which are denoted and described as follows:
and
Now, using Eqs (7.3) and (7.4), we evalute the distance measures of aggregated picture fuzzy information (Table 7) and R-PFPIS & R-PFNIS(Table 13) shown in Table 14.
{\bf{Step-6}} Determining the relative closeness coefficient (RCC) to the PF ideal solutions: The RCC of each alternative is constructed and listed as,
Table 15 shows the RCC Eq (7.5) of each alternative:
{\bf{Step-7}} Alternatives ranking: Depending on the RCC, the higher values of RCC^{s} indicate the better alternative. Z_{1} is selected as the most best solution for the PAS problem. The methods suggested in this paper are obviously more general, more precise and more applicable.
7.1. Comparison with existing operators
Here, our proposed aggregation information is compared with existion aggregation information. Garg [39] in 2017, introduce the picture fuzzy averaging aggregation operators. Obviously, the methods proposed in this paper are more general and more flexible. Since Garg aggregation operators are built on algebraic t-norms, the proposed aggregation operators in this paper are built on instein t-norm operators. More important idea is that when \lambda = 1 , then the GPFEHA and GPFEHG aggregation operators proposed in this work can be reduce to PFEHA and PFEHG aggregation operators, respectively. We obtain distinct ranking results if we update the value of parameter \lambda .
Garg [39] in 2017, the PF aggregation operators were introduced to aggregate the PFNs; in this section of the analysis, we compare the proposed PF Einstein aggregation operators to existing operators as follows:
After, using proposed aggregation information, we obtained the comparison Table 17:
The best alternative is Z_{2} .
We conclude that the ranking lists are the same based on the results of the proposed operators and the existing method [39]. The generalized and novel approach to address uncertainty in DM problems based on novel picture fuzzy Einstein aggregation information under the PNS environment. Einstein norm based aggregation operators under picture fuzzy environment are more flexible and efficient as compared to existing aggregation operators to evaluate the best alternative in real-world problems.
8.
Conclusions
Aggregation of information is an important technique to tackle decision-making problems. Atanassov's construction of intuitionistic fuzzy sets is of prodigious reputation, but decision makers are somehow restricted in assigning values due to the condition on membership grades. To deal with such kinds of circumstances, Cuong proposed a new structure by defining PFSs as a generalization of FSs and IFSs. We have introduced some aggregation operators in this paper, namely the PFEHA, PFEHG, GPFEHA, and GPFEHG aggregation operators. In order to illustrate the use, applicability, and benefits of the proposed ranking approach, we presented a Patient Admission Scheduling (PAS) model and utilized proposed aggregation information to solve this problem. Patient admission scheduling is a crucial topic, not only because it is a genuine issue, but also because it involves human organizational authority. A realistic example of an arrangement of drive frameworks to verify the methodology built and to demonstrate its common uses and adaptability compared to traditional methods was outlined. A leading role in promoting PAS program is essential for health care professionals because they will allow us to identify and address service and resource shortages in our institutions as well as the requirements of patients. Therefore, I recommend that you understand more about this critical initiative and take the best steps to shorten waiting times and increase all patients' accessibility to treatment.
The direction of future research could involve improving the performance of aggregation information and decision making algorithms, and also more neighborhood structure can be embedded in them to improve the quality of the solution.
Acknowledgments
The author Muhammad Aslam extends his appreciation to the Deanship of Scientific Research at King Khalid University, Abha 61413, Saudi Arabia for funding this work through research groups program under grant number R.G. P-2/98/43.
Conflict of interest
The authors declare that they have no conflicts of interest to report regarding the present study.










 DownLoad:
DownLoad: