Numerical analysis and simulation of the compact difference scheme for the pseudo-parabolic Burgers' equation

1.   Introduction

In this paper, we consider connected simple and finite graphs, and refer to Bondy and Murty ^[4] for notation and terminologies used but not defined here.

Let $G$ be a connected graph with vertex set $V(G)$ and edge set $E(G)$, $|V(G)| = n$ and $|E(G)| = m$. We denote $G-v$ and $G-uv$ the graph obtained from $G$ by deleting a vertex $v\in V(G)$, or an edge $uv\in E(G)$, respectively. Similarly, $G+uv$ is obtained from $G$ by adding an edge $uv\notin E(G)$, where $u, v \in V(G)$. An edge $uv$ of a graph $G$ is called a cut edge if the graph $G-uv$ is disconnected. For a vertex $u\in V(G)$, its degree $d_{G}(u)$ is equal to the number of vertices in $G$ adjacent to $u$; the neighborhood of $u$ is denoted by $N_{G}(u)$, or $N(u)$ for short. The symbols $\Delta(G)$ and $\delta(G)$ represent the maximum degree and the minimum degree of $G$. We use $T_n$, $C_{n}, \ P_{n}$ and $S_{n}$ to denote the tree, cycle, path and star of order $n$, respectively.

Gutman^[13] defined a new vertex-degree-based graph invariant, called Sombor index. Precisely, for a graph $G$, it is denoted by $SO(G)$ and is defined as

He proved that for any tree $T$ with $n\geq 3$ vertices,

with left side of equality if and only if $T\cong P_{n}$, and with the right side of equality if and only if $T\cong S_{n}$. Chen etal. ^[5] determined the extremal values of the Sombor index of trees with some given parameters, including matching number, pendant vertices, diameter, segment number, branching number, etc. The corresponding extremal trees are characterized completely. Deng etal. ^[11] obtained a sharp upper bound for the Sombor index among all molecular trees with fixed numbers of vertices, and characterize those molecular trees achieving the extremal value. Cruz etal. ^[8] determined the extremal values of Sombor indices over trees with at most three branch vertices. Li etal. ^[19] give sharp bounds for the Sombor index of trees with a given diameter. Das and Gutman ^[9] present bounds on the Sombor index of trees in terms of order, independence number, and number of pendent vertices, and characterize the extremal cases. In addition, analogous results for quasi-trees are established. Sun and Du ^[30] present the maximum and minimum Sombor indices of trees with fixed domination number, and identified the corresponding extremal trees. Zhou etal. ^[36] determined the graph with minimum Sombor index among all trees with given number of vertices and maximum degree, respectively, among all unicyclic graphs with given number of vertices and maximum degree.

Cruz and Rada ^[7] investigate the Sombor indices of unicyclic and bicyclic graphs. Let $U(n, p, q, r)\in \mathcal{G}(n, 1)$, where $p\geq q\geq r\geq 0$ and $p+q+r = n-3$, be a unicyclic graph obtained from 3-cycle $C_{3}$ with $V(C_{3}) = \{u, v, w\}$, adding $p$, $q$ and $r$ pendent vertices to the vertices $u$, $v$ and $w$, respectively. They showed that for a unicyclic graph with $n\geq 3$ vertices,

The lower and upper bound is uniquely attained by $G\cong C_{n}$ and $G\cong U(n, n-3, 0, 0)$, respectively. Alidadi etal. ^[2] gave the minimum Sombor index for unicyclic graphs with the diameter $D\geq 2$.

Aashtab etal. ^[1] studied the structure of a graph with minimum Sombor index among all graphs with fixed order and fixed size. It is shown that in every graph with minimum Sombor index the difference between minimum and maximum degrees is at most 1. Cruz etal. ^[6] characterize the graphs extremal with respect to the Sombor index over the following families of graphs: (connected) chemical graphs, chemical trees, and hexagonal systems. Liu etal. ^[21] determined the minimum Sombor indices of tetracyclic (chemical) graphs. Das and Shang ^[10] present some lower and upper bounds on the Sombor index of graph $G$ in terms of graph parameters (clique number, chromatic number, number of pendant vertices, etc.) and characterize the extremal graphs. For the Sombor index of a connected graph with given order, Horoldagva and Xu ^[16] presented sharp upper and lower bounds when its girth is fixed, a lower bound if its maximum degree is given and an upper bound in terms of given number of pendent vertices or pendent edges, respectively. In ^[29], Shang observe power-law and small-word effect for the simplicial networks and examine the effectiveness of the approximation method for Sombor index through computational experiments.

Relations between the Sombor index and some other well-known degree-based descriptors ^{[14,24,25,33]}. A number of application of Sombor index in chemistry were reported in ^[3,20,27]. Besides, the relationship between the energy and Sombor index of a graph $G$ is studied in ^{[12,15,26,28,31,32]}.

Some variations of Sombor index, for instance, the reduced Sombor index, average Sombor index, are investigated. Redžepović ^[27] examined the predictive and discriminative potentials of Sombor index, the reduced Sombor index, average Sombor index. Liu etal. ^[23] obtained some bounds for reduced Sombor index of graphs with given several parameters (such as maximum degree, minimum degree, matching number, chromatic number, independence number, clique number), some special graphs (such as unicyclic grahs, bipartite graphs, graphs with no triangles, graphs with no $K_r+1$ and the Nordhaus-Gaddum-type results). A conjecture related to the chromatic number in the above paper was verified to be true by Wang and Wu ^[34]. Liu etal. ^[22] ordered the chemical trees, chemical unicyclic graphs, chemical bicyclic graphs and chemical tricyclic graphs with respect to Sombor index and reduced Sombor index. Furthermore, they determined the first fourteen minimum chemical trees, the first four minimum chemical unicyclic graphs, the first three minimum chemical bicyclic graphs, the first seven minimum chemical tricyclic graphs. Finally, the applications of reduced Sombor index to octane isomers were given. Wang and Wu ^[35] investigated the reduced Sombor index and the exponential reduced Sombor index of a molecular tree solving a conjecture ^[23] and an open problem ^[11].

A vertex of degree 1 is said to be a pendant vertex. Further, an edge is said to be a pendant edge if one of its end vertices is a pendant vertex. A connected graph that has no cut vertices is called a block, the blocks of $G$ which correspond to leaves of its block tree are referred to as its end blocks. A cactus is a connected graph in which every block is either an edge or a cycle. Let $\mathcal{G}(n, k)$ be the family of all cacti with $n$ vertices and $k$ cycles. Clearly, $|E(G)| = n+k-1$ for any $G\in\mathcal{G}(n, k)$. Note that $\mathcal{G}(n, 0)$ is the set of all trees and $\mathcal{G}(n, 1)$ is the set of all unicyclic graphs. Gutman ^[13] characterized the tree with extremal value Sombor index.

It is our main concern in this paper to study the extremal value problem of Sombor index on $\mathcal{G}(n, k), \ k\geq 2$. In this paper, we will determine the maximum Sombor index of graphs among $G\in\mathcal{G}(n, k)$, and also characterize the corresponding extremal graphs. Later, we will determine the minimum Sombor index of graphs with given conditions among $G\in\mathcal{G}(n, k)$, and also characterize the corresponding extremal graphs.

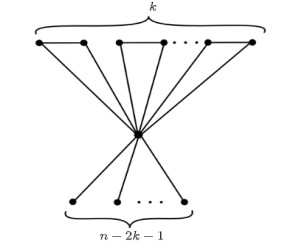
Let $G_{0}(n, k)\in\mathcal{G}(n, k)$ be a bundle of $k$ triangles with $n-2k-1$ pendent vertices attached to the common vertex, as illustrated in Figure 1.

By a simple computation, we have $SO(G_{0}(n, k)) = (n-2k-1)\sqrt{(n-1)^{2}+1}$ $+2k\sqrt{(n-1)^{2}+2^{2}}+2\sqrt{2}k$. We will see that $G_{0}(n, k)$ has the maximum Sombor index among $\mathcal{G}(n, k)$.

Theorem 1.1. Let $k\geq1$ and $n\geq3$. For any $G\in \mathcal{G}(n, k)$,

with equality if and only if $G\cong G_{0}(n, k)$.

Let $\mathcal{C}^{*}(n, k)$ denote the set of the elements $G$ of $\mathcal{G}(n, k)$ with the following properties:

(1) $\delta(G) = 2$ and $\Delta(G) = 3$;

(2) a vertex is a cut vertex if and only if it has degree 3, and there are exactly $2k-2$ cut vertices;

(3) at least $\lceil\frac{k-3} 2\rceil$ internal cycles with all three degrees are triangles;

(4) at most one vertex not belong to any cycle;

(5) the three degree vertices on the cycle are adjacent.

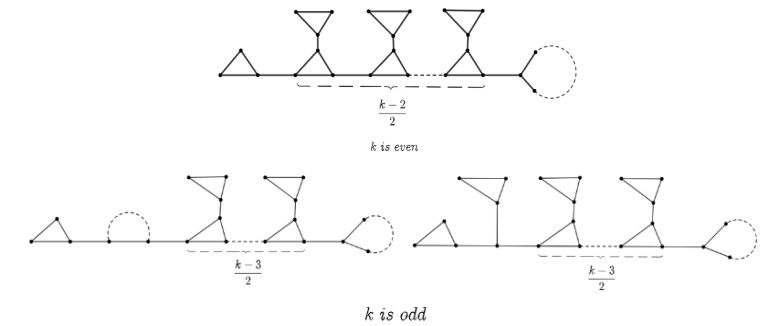
Generally speaking, if $k$ is even, an element of $\mathcal{C}^{*}(n, k)$ obtained from a tree $T$ of order $k$ with each vertex having degree 1 or 3 by replacing each vertex of degree 3 with a triangle and replacing each vertex of degree 1 with a cycle. If $k$ is odd, an element of $\mathcal{C}^{*}(n, k)$ obtained from a tree $T$ of order $k$ with exactly a vertex having degree 2 by replacing two (adjacent) vertices of degree 3 with a cycle, and other vertices having degree 1 or 3 by replacing each vertex of degree 3 with a triangle, replacing each vertex of degree 1 with a cycle or an element of $\mathcal{C}^{*}(n, k)$ obtained from a tree $T$ of order $k$ with each vertex having degree 1 or 3 by retention one vertex of degree 3, and by replacing other vertices of degree 3 with a triangle and replacing each vertex of degree 1 with a cycle.

Three elements of $\mathcal{C}^{*}(n, k)$ are shown in terms of the parity of $k$ in Figure 2.

Theorem 1.2. Let $k\geq2$ and $n\geq 6k-3$. For any $G\in\mathcal{G}(n, k)$, we have

with equality if and only if $G\in\mathcal{C}^{*}(n, k)$.

The proofs of Theorems 1.1 and 1.2 are given Sections 2 and 3, respectively.

2.   The maximum Sombor index of cacti

In this section, we will determine the maximum value of the Sombor index of cacti with $n$ vertices and $k$ cycles, and characterize the corresponding extremal graph. We start with several known results, which will be used in the proof of Theorem 1.1.

Lemma 2.1 (Horoldagva and Xu ^[16]). If $uv$ is a non-pendent cut edge in a connected graph $G$, then $SO(G') > SO(G)$, where $G'$ is the graph obtained by the contraction of $uv$ onto the vertex $u$ and adding a pendent vertex $v$ to $u$.

In 1932, Karamata proved an interesting result, which is now known as the majorization inequality or Karamata's inequailty. Let $A = (a_{1}, a_{2}, \cdots, a_{n})$ and $B = (b_{1}, b_{2}, \cdots, b_{n})$ be non-increasing two sequences on an interval $I$ of real numbers such that $a_{1}+a_{2}+\cdots+a_{n} = b_{1}+b_{2}+\cdots+ b_{n}$. If $a_{1}+a_{2}+\cdots+a_{i}\geq b_{1}+b_{2}+\cdots+ b_{i}$ for all $1\leq i\leq n-1$ then we say that A majorizes B.

Lemma 2.2 (Karamata^[18]). Let $f:I \rightarrow \mathbb{R}$ be a strictly convex function. Let $A = (a_{1}, a_{2}, \cdots, a_{n})$ and $B = (b_{1}, b_{2}, \cdots, b_{n})$ be non-increasing sequences on $I$. If A majorizes B then $f(a_{1})+f(a_{2})+\cdots+f(a_{n})\geq f(b_{1})+f(b_{2})+\cdots+f(b_{n})$ with equality if and only if $a_{i} = b_{i}$ for all $1\leq i\leq n$.

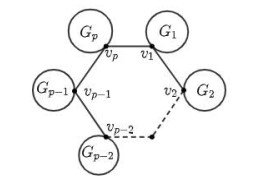
Lemma 2.3. Let $G$ be a connected graph with a cycle $C_{p} = v_{1}v_{2}\cdots v_{p}v_{1}\ (p\geq 4)$ such that $G-E(C_{p})$ has exactely $p$ components $G_1, G_2, \ldots, G_p$, where $G_{i}$ is the component of $G-E(C_{p})$ containing $v_{i}$ for each $i\in\{1, 2, \cdots, p\}$, as shown in Figure 3. If $G' = G-\{v_{p-1}v_{p}, uv_{p}|\ u\in N_{G_{p}}(v_{p})\}+\{v_{1}v_{p-1}, uv_{1}|\ u\in N_{G_{p}}(v_{p})\}$, then $SO(G') > SO(G)$.

Proof. Let $N_{G}(v_{1})\backslash\{v_2, v_{p}\} = \{x_{1}, x_{2}, \cdots, x_{s}\}$, $N_{G}(v_{p})\backslash \{v_{1}, v_{p-1}\} = \{y_{1}, y_{2}, \cdots, y_{t}\},$ where $s = d_{G}(v_{1})-2$ and $t = d_{G}(v_{p})-2$. Hence, by the definition of $SO(G)$, we obtain

Since $s\geq 0, t\geq 0$, we have $[(s+t+3)^{2}+1^{2}]-[(s+2)^{2}+(t+2)^{2}] = 2st+4s+2t+2 > 0$, implying that $SO(G') > SO(G)$.

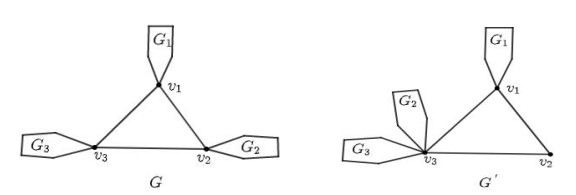
Lemma 2.4. Let $n$ and $k$ be two nonnegative integers with $n\geq 2k+1$. If $G\in \mathcal{G}(n, k)$ has a triangle $v_1v_2v_3v_1$ with $d_{G}(v_{3})\geq d_{G}(v_{2})\geq 3$ as shown in Figure 4, then $SO(G') > SO(G)$, where $G' = G-\{v_{2}u|\ u\in N_{G_{2}}(v_{2})\}+\{v_{3}u|\ u\in N_{G_{2}}(v_{2})\}$.

Proof. Let $N_{G}(v_{3})\backslash\{v_{2}\} = \{v_{1}, x_{1}, x_{2}, \cdots, x_{s}\}$, $N_{G}(v_{2})\backslash \{v_{3}\} = \{v_{1}, y_{1}, y_{2}, \cdots, y_{t}\}$, then $s = d_{G}(v_{3})-2, \ t = d_{G}(v_{2})-2$. Defined according to $G'$, $d_{G'}(v_{3}) = s+t+2$. Assume that $d_{G'}(v_{1}) = d_{G}(v_{1}) = p$, $\sqrt{(s+t+2)^{2}+2^{2}}+\sqrt{(s+2)^{2}+(t+2)^{2}} = q$.

Let us consider a function $f(x) = \sqrt{1+x^{2}}$ and it is easy to see that this function is strictly convex for $x\in [0, +\infty)$. Since $A = \{\frac{s+t+2}{p}, \ \frac{2}{p}\}$ majorizes $B = \{\frac{s+2}{p}, \ \frac{t+2}{p}\}$, By Karamata's inequality, $f(\frac{s+t+2}{p})+f(\frac{2}{p}) > f(\frac{s+2}{p})+f(\frac{t+2}{p})$. Combining this with (2.1), it follows that $SO(G') > SO(G)$.

Now, we are ready to present the proof of Theorem 1.1.

Proof of Theorem 1.1:

Let $G$ be a cactus with the maximum Sombor index value among $\mathcal{G}(n, k)$. By Lemma 2.1, each cut edge of $G$ is pendent. By Lemma 2.3, every cycles of $G$ is a triangle. Furthermore, by Lemma 2.4, $G\cong G_{0}(n, k)$. Thus, the maximum Sombor index of cacti among $\mathcal{G}(n, k)$ is

3.   The minimum Sombor index of cacti

In this section, we determine the minimum Sombor index of graphs in $\mathcal{G}(n, k)$, and characterize the corresponding extremal graphs.

First, we introduce some additional notations. For a graph $G$, $V_i(G) = \{v\in V(G)|\ d(v) = i\}, \ n_i = |V_i(G)|, \ E_{i, j}(G) = \{uv\in E(G)|\ d(u) = i, \ d(v) = j\}$ and $e_{i, j}(G) = |E_{i, j}(G)|$. Obviously, $e_{i, j}(G) = e_{j, i}(G)$. If there is no confusion, $e_{i, j}(G)$ is simply denoted by $e_{i, j}$. For any simple graph $G$ of order $n$, we have

and

Let

it follows easily from (3.1) and (3.2) that

Let $G\in\mathcal{G}(n, k)$ with $n\geq 2k+1$ and $k\geq 1$. It implies that $e_{1, 1}(G) = 0$ and $e_{i, j}(G) = 0$ for any $1 \leq i\leq j \leq n-1$ with $i+j > n+k$. Let $L_{n, n}^{k} = \{(i, j)\in L_{n, n} : i+j \leq n+k\}$, $L_{n, n}^{k'} = L_{n, n}^{k}-\{(2, 2), (2, 3), (3, 3)\}$. By a simple calculation we obtain the following result.

Lemma 3.1. For any graph $G\in\mathcal{G}(n, k)$ ($k\geq 1$),

where

Proof. For any $G\in\mathcal{G}(n, k)$,

Relations (3.5) and (3.6) can be rewritten as

Combining the above, we have

$g(2, 2) = g(2, 3) = 0$, $g(3, 3) = (5\sqrt{2}-2\sqrt{13}) < 0.$ Thus,

Lemma 3.2 (Chen, Li, Wang ^[5]). Let $f(x, y) = \sqrt{x^{2}+y^{2}}$ and $h(x, y) = f(x, y)-f(x-1, y)$, where $x, y \geq 1$. If $x, y \geq 1$, then $h(x, y)$ strictly decreases with $y$ for fixed $x$ and increases with $x$ for fixed $y$.

Since $f(x+k, y)-f(x, y) = \sum_{i = 1}^{k}[f(x+i, y)-f(x+i-1, y)] = \sum_{i = 1}^{k}{h(x+i, y)}$ for any $k\in \mathbb{Z^{+}}$, we have the following corollary.

Corollary 3.1. If $x, y \geq 1$ and $k\in \mathbb{Z^{+}}$, then $f(x+k, y)-f(x, y)$ strictly decreases with $y$ for fixed $x$ and increases with $x$ for fixed $y$.

Let $P_l = u_{0}u_{1}\cdots u_{l}, \ l\geq 1$ be a path of $G$ with $d(u_{0})\geq 3$, $d(u_{i}) = 2$ for $1\leq i \leq l-1$ when $l > 1$. We call $P_l$ an internal path if $d(u_{l})\geq 3$, and a pendent path if $d(u_{l}) = 1$.

Lemma 3.3. Let $G$ be a cactus graph of order $n\geq 4$. If there exists two edges $uu', v_{1}v_{2}\in E(G)$ such that $d(u) = 1$ and $\min\{ d_{G}(v_{1}), \ d_{G}(v_{2})\}\geq 2$. Let $G' = G-uu'-v_{1}v_{2} + uv_{1}+uv_{2}$, then $SO(G') < SO(G)$.

Proof. Let $N_{G}(u') = \{u, w_{1}, w_{2}, \cdots, w_{t-1}\}$, where $t = d(u')(t\geq 2)$. By the assumption, $d_{G'}(u) = 2$ and $d_{G'}(u') = t-1$. Since $G$ is a cactus graph, then $d(w_{i})\leq n-t+1(i = 1, \cdots, t-1)$, $d(v_{j})\leq n-t+1(j = 1, 2)$, $t < n-1$. Thus,

A repeated application of the above lemma result in the following consequence.

Corollary 3.2. If $G$ is a cactus has a pendent path $P_l = u_{0}u_{1}\cdots u_{l}$ with $d(u_{l}) = 1$ and $v_{1}v_{2}\in E(G)$, $\min\{ d_{G}(v_{1}), \ d_{G}(v_{2})\}\geq 2$, then $SO(G') < SO(G)$, where $G' = G-u_{0}u_{1}-v_{1}v_{2}+u_{1}v_{1}+u_{l}v_{2}$.

The following result is immediate from the above corollary.

Corollary 3.3. Let $k\geq 1$. If $G$ is a cactus has the minimum Sombor index among $\mathcal{G}(n, k)$, then $\delta(G)\geq 2$.

The following result is due to Jiang and Lu ^[17], which is a key lemma in the proof of Theorem 1.2.

Lemma 3.4 (Jiang and Lu ^[17]). Let $k$ and $n$ be two integers with $k\geq 2$ and $n \geq 6k-4$. If $G\in \mathcal{G}(n, k)$ with $\delta(G)\geq 2$, then there exists a path $x_{1}x_{2}x_{3}x_{4}$ of length $3$ in $G$ such that $d(x_{2}) = d(x_{3}) = 2$ and $x_{1} \neq x_{4}$.

Lemma 3.5. Let $k$ and $n$ be two integers with $k \geq 2$ and $n \geq 6k - 3$. If $G$ has the minimum Sombor index among $\mathcal{G}(n, k)$, then $\Delta(G) \leq 3$.

Proof. By contradiction, suppose that $\Delta(G)\geq 4$. Let $v \in V(G)$ with $d_{G}(v) = \Delta(G)$. Since $n \geq 6k - 3$, by Lemma 3.4, there exists a path $x_{1}x_{2}x_{3}x_{4}$ in $G$ such that $d_{G}(x_{2}) = d_{G}(x_{3}) = 2$ and $x_{1} \neq x_{4}$. Let $G_{1} = G-x_{1}x_{2}-x_{2}x_{3}+x_{1}x_{3}$. Clearly, $G_{1} \in \mathcal{G}(n-1, k)$ and $d_{G_{1}} (u) = d_{G}(u)$ for all $u \in V(G_{1})$.

Since $n-1\geq 6k-4$, by Lemma 3.4, there exists a path $y_{1}y_{2}y_{3}y_{4}$ in $G_{1}$ such that $d_{G_{1}}(y_{2}) = d_{G_{1}}(y_{3}) = 2$ and $y_{1}\neq y_{4}$. Let $G_{2} = G_{1}-y_{1}y_{2}-y_{2}y_{3}+y_{1}y_{3}$. Then $G_{2} \in \mathcal{G}(n-2, k)$ and $d_{G_{2}}(u) = d_{G_{1}} (u)$ for all $u\in V(G_{2})$. Since $d_{G}(v)\geq 4$, $v\notin\{x_{2}, y_{2}\}$ and $d_{G}(v) = d_{G_{1}}(v) = d_{G_{2}}(v)$.

For convenience, let $t = \Delta(G)$. Let $N_{G_{2}}(v) = \{w_{1}, \cdots, w_{t}\}$. Assume that $w_{1}, w_{2}$, $v$ are in the same block if $v$ is contained in a cycle in $G_{2}$. Let $G' = G_{2}-vw_{1}-vw_{2}+vx_{2}+x_{2}y_{2} +y_{2}w_{1}+y_{2}w_{2}$. Then $G' \in \mathcal{G}(n, k)$, $d_{G^{'}}(v) = t-1, \ d_{G'}(x_{2}) = 2, \ d_{G'}(y_{2}) = 3$ and $d_{G'}(u) = d_{G_{2}}(u) = d_{G}(u)\geq 2$ for all $u \in V(G_{2})\setminus\{v\}$. Next, by showing $SO(G') < SO(G)$, we arrive at a contradiction.

By the construction above, $SO(G_{1}) = SO(G)-\sqrt{2^{2}+2^{2}} = SO(G)-2\sqrt{2}$ and $SO(G_{2}) = SO(G_{1})-\sqrt{2^{2}+2^{2}} = SO(G)-4\sqrt{2}$. Thus,

Hence, to show $SO(G') < SO(G)$, it suffices to show that $f(t) > 0$ for $t\geq 4$, where $f(t) = \sqrt{2}t^{2}-2\sqrt{3^{2}+t^{2}}-(t-2)\sqrt{(t-1)^{2}+t^{2}}-\sqrt{(t-1)^{2}+2^{2}}+4\sqrt{2}-\sqrt{13}$. One can see that for any $t\geq 4$,

Hence, $f(t)$ is an increasing function with respect to $t\in [4, n-1]$, implying $f(t)\geq f(4) = 20\sqrt{2}-4\sqrt{13}-10 > 0$. This contradicts the minimality of $G$.

Lemma 3.6. Let $k\geq2$ and $n\geq 6k-3$. If $G$ has the minimum Sombor index in $\mathcal{G}(n, k)$, then it does not exist a path $v_{1}v_{2}\cdots v_{l} (l\geq 3)$ in $G$ such that $d_{G}(v_{1}) = d_{G}(v_{l}) = 3$ and $d_{G}(v_{i}) = 2 \ (i = 2, \cdots, l-1)$, where $v_{1}$ and $v_{l}$ are not adjacent. Thus,

(1) if a cycle $C$ is not an end block of $G$, then all vertices of it have degree three in $G$, or it contains exactly two (adjacent) vertices of degree three.

(2) any vertices of degree two lie on a cycle.

Proof. Suppose that there exist a path $P_{l} = v_{1}v_{2}\cdots v_{l}\in G$ as given in the assumption of the lemma. From Corollary 3.3 and Lemmas 3.5, we have $2\leq d(v)\leq 3$ of any vertex $v$ in $G$. By Lemma 3.1, in equation (3.9), $L_{n, n}^{k'} = \emptyset$,

Let $C_{s}$ be an end block of $G$, $w_{1}, w_{2}\in V(C_{s})$, $w_{1}w_{2}\in E(C_{s})$, $d_{G}(w_{1}) = d_{G}(w_{2}) = 2$. Let $G' = G-v_{1}v_{2}-v_{l-1}v_{l}+v_{1}v_{l}-w_{1}w_{2}+w_{1}v_{2}+w_{2}v_{l-1}$. Clearly,

Thus, $SO(G') < SO(G)$, a contradiction.

Thus, (1) and (2) is immediate.

Lemma 3.7. Let $k\geq2$ and $n\geq 6k-3$. Let $G\in \mathcal{G}(n, k)$ has the minimum Sombor index, then $e_{3, 3}(G)\leq \lfloor\frac{5k}{2}\rfloor-4 = 2k+\lfloor\frac{k}{2}\rfloor-4$, the equality holds if and only if $G\in \mathcal{C}^{*}(n, k)$.

Proof. By Corollary 3.3 and Lemma 3.5, we have $2\leq d(v)\leq 3$ of any vertex $v$ in $G$.

Let $n_3$ be the number of vertices with degree 3 not belongs to a cycle, $c_1$ the number of end blocks, and $c_2$ the number of cycles with exactly two (adjacent) vertices of degree three in $G$. Clearly $n_3\geq 0$ and $c_2\geq 0$. By Lemma 3.6 (1), there are $k-c_1-c_2$ remaining cycles, denoted by $C_1, \ldots, C_{k-c_1-c_2}$, all vertices of which have degree three. Let $d_i$ be the length of the cycle $C_i$.

Let $T_{k+n_3}$ be the tree obtained from contracting each cycle of $G$ into a vertex. By the hand-shaking lemma, we have

Since $d_i\geq 3$ for each $i\in\{1, \ldots, k-c_1-c_2\}$, by (3.10), we have

relation (3.11) can be rewritten as

implying that

On the other hand, by Lemma 3.6,

It follows from (3.10) and (3.14) that

Combining (3.13) and (3.15), it yields

Since $n_3\geq 0$, $c_2\geq0$,

If $k$ is even,

the equality holds if and only if $n_3 = c_2 = 0$, $d_1 = d_2 = \cdots = d_{k-c_1-c_2} = 3$, that is, $G\in \mathcal{C}^{*}(n, k)$.

If $k$ is odd,

the equality holds if and only if $n_3+c_2 = 1$, $d_1 = d_2 = \cdots = d_{k-c_1-c_2} = 3$, then $n_3 = 0, c_2 = 1$ or $n_3 = 1, c_2 = 0$, that is, $G\in \mathcal{C}^{*}(n, k)$.

Proof of Theorem 1.2: Assume that under which $k\geq2$ and $n\geq 6k-3$ condition $G$ has the minimum Sombor index in $\mathcal{G}(n, k)$. By Corollary 3.3 and Lemma 3.5, $2\leq d_G(v)\leq 3$ for any vertex $v$ in $G$. By Lemma 3.1,

Thus, by Lemma 3.7,

with equality if and only if $G\in\mathcal{C}^{*}(n, k)$.

4.   Conclusions

Recall that $\mathcal{G}(n, k)$ denotes the set of cacti of order $n$ and with $k$ cycles. In this paper, we establish a sharp upper bound for the Sombor index of a cactus in $\mathcal{G}(n, k)$ and characterize the corresponding extremal graphs. In addition, for the case when $n\geq 6k-3$, we give a sharp lower bound for the Sombor index of a cactus in $\mathcal{G}(n, k)$ and characterize the corresponding extremal graphs as well. We believe that Theorem 1.2 is true for the case when $3k\leq n\leq 6k-4$.

Conjucture 4.1. Let $k$ and $n$ be two integers with $n\geq 3k$ and $k\geq 2$. For any graph $G\in\mathcal{G}(n, k)$,

with equality if and only if $G\in\mathcal{C}^{*}(n, k)$.

Acknowledgments

The research of cactus graph is supported by the National Natural Science Foundation of China(11801487, 12061073).

Conflict of interest

The authors declare no conflict of interest.