1.
Introduction
Lung cancer is one of the leading causes of cancer deaths globally, accounting for 24% cases of all cancer deaths [1,2]. The mortality-to-incidence ratio of lung cancer is 0.87 globally, indicating the poor outcomes of lung cancer [3]. Non-small cell lung cancer (NSCLC) accounts for about 85% cases of lung cancers, of which lung adenocarcinoma (LUAD) is the most common subtype [4]. Lung cancer is often diagnosed at a late stage with concomitant poor prognosis [5]. The prognosis of lung cancer is associated with lymph node metastasis (LNM). It was reported that 5-year survival of lung adenocarcinoma patients with LNM was only 26–53% while 5-year survival of early-stage lung adenocarcinoma without LNM was over 95% [6,7]. Therefore, screening specific markers of lymph node metastasis of early-stage lung adenocarcinoma would be helpful for cancer diagnosis and treatment.
Various biomolecules such as proteins, mRNA, miRNA, methylated DNA, lncRNA, etc. have been implemented as cancer biomarkers. Among which miRNA is emerging as a useful tool. The miRNAs are a class of non-coding RNAs that post-transcriptionally control gene expression via either translational repression or mRNA degradation. Evidence reveals that miRNAs play significant roles in regulatory mechanisms including tumorigenesis [8,9]. Multiple studies have shown that tumor-derived miRNAs can persist in human plasma in a very stable form, thus serving as potential biomarkers to facilitate the early detection of lung cancer [10,11]. Compared with single miRNA biomarker, a miRNA signature comprising multiple miRNAs may improve prediction accuracy and would be more powerful in classifying cancer subtypes [12,13]. To our knowledge, no studies have worked on LNM prediction in LUAD using miRNA signatures. Therefore, we constructed a miRNA signature to predict metastasis of lymph node in LUAD and hypothesized that the signature achieves high accuracy for prediction.
2.
Methods
2.1. TCGA microRNA expression profiles
Transcriptome data including microRNA expression and mRNA expression for lung adenocarcinoma patients were downloaded from The Cancer Genome Atlas (TCGA) (https://portal.gdc.cancer.gov/) on July 3rd 2019. Tumor staging, sex and other corresponding clinical data were obtained from TCGA clinical information. MiRNA expressions were available for 342 patients without distant metastases. Only miRNAs with a trimmed mean of 95% larger than 5 counts were retained in the profile.
2.2. Model construction and validation
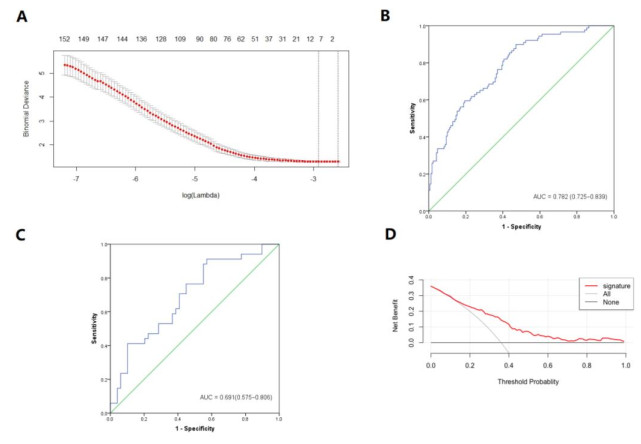
Patients were randomly partitioned into training and validation cohorts, with t-test, Fisher's exact test and chi-square test proving no significant difference of patients' characteristics between two cohorts. Least absolute shrinkage and selection operator (LASSO) regression analysis was used in training cohort to minimize multicollinearity [14]. The 10-fold cross validation was applied in LASSO to select the optimal tuning parameters (λ) via the minimum criteria, and the optimal λ value of 0.054 with log(λ) = −1.268 was chosen. Logistic regression model was used to construct the final miRNA disease signature to determine patients with lymph node metastasis. The logistic regression formula formed in the training cohort was then applied to validation cohort. Receiver operator characteristic (ROC) curve was constructed and the area under ROC curve (AUC) value was calculated to validate the performance of LMN prediction. To evaluate the clinical application value of signature, decision curve analysis (DCA) was conducted by R studio. A heatmap was plotted using TB tools (https://github.com/CJ-Chen/TBtools) to differentiate miRNA expression between the patients with or without LMN [15]. All statistical analysis were conducted using SPSS Version 23.0 software or package "rmda" within the R statistical software version 3.6.0. Two-tailed tests and p values < 0.05 for significance were used.
2.3. Gene signature analysis
miRWalk database (http://www.umm.uni-heidelberg.de/apps/zmf/mirwalk/) was used to predict the transcriptional target-genes of identified miRNAs [16]. We conducted miRNA-target gene interaction networks with miRNA-target gene interacting pairs, and the miRNA-mRNA interaction network was visualized by Cytoscape (version 3.7.1) software (http://cytoscape.org/) [17].
3.
Results
3.1. Characteristics of patients in the training and the validation cohorts
TCGA-LUAD cohort was randomly divided into a training set (n = 259) and a validation set (n = 83). The mean age of all patients in the study was 65.2 ± 9.9,174 (50.9%) females, 168 (49.1%) males and 123 (36.0%) had lymph node metastasis. The demographics of training and validation cohorts were well balanced, as shown in Table 1.
3.2. Construction of miRNA disease signature
In the training cohort, a total of 387 miRNAs were put into the LASSO logistic regression program and 10 of them had non-zero coefficients as potential predictors (Figure 1A). The selected 10 miRNAs were hsa-miR-30d, hsa-miR-338, hsa-miR-582, hsa-miR-378a, hsa-miR-3065, hsa-miR-664a, hsa-miR-552, hsa-miR-3653, hsa-miR-4728 and hsa-miR-376b. To simplify the signature, each miRNA was removed from the disease signature sequentially to analyze AUC in testing cohort. Based on the fact that the removal of has-miR-3653 led to greater AUC, we excluded it in our signature. Given hsa-miR-598 [18], hsa-miR-891a [19], hsa-miR-509-3 [20] and hsa-miR-133a [21] have been reported to have significant prognostic value in LUAD, we then included them. A 13-miRNA signature was established using logistic regression. The patient risk score was derived by the summation of each miRNA expression levels times its corresponding coefficient. The risk score for lymph node metastasis was calculated as follows: Risk score = (0.00002 × miR-30d) + (-0.000053 × miR-338) + (0.000113 × miR-582) + (0.000412 × miR-378a) + (-0.000767 × miR-3065) + (-0.002072 × miR-664a) + (-0.006408 × miR-598) + (-0.002753 × miR-552) + (0.002608 × miR-891a) + (0.007073 × miR-5093) + (-0.016114 × miR-133a1) + (-0.009681 × miR-4728) + (0.042837 × miR-376b) - 0.456838.
3.3. The prediction accuracy of miRNA disease signature in training cohort and validation cohorts
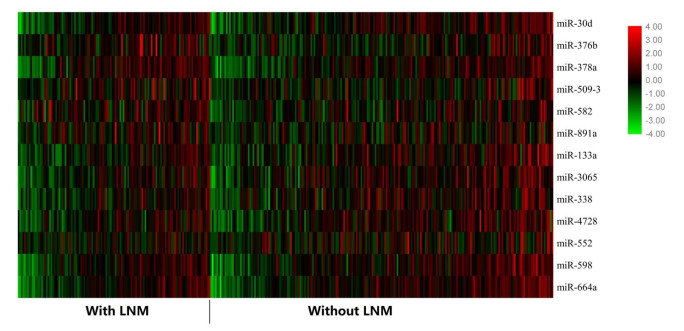
We evaluated the accuracy of the 13-miRNA signature in training cohort and validation cohort, the area under the curve (AUC) value were 0.782 (95% CI, 0.725–0.839) and 0.691 (95% CI, 0.575–0.806) respectively (Figure 1B, C). We calculated the AUC values of different sex, age and T-stage subetaoup to validate the performance of our miRNA signature in these diverse subsets. As shown in Table 2, the AUC value was high in all subetaoups ranging from 0.600 to 0.811. Notably, the AUC value reached 0.811 in patients aged over 80 years old. Hence, the signature showed good performance in both training and validation cohorts. Decision Curve Analysis (DCA) is shown in Figure 1D. If the threshold probability of a patient was between 0.2 and 0.6, the miRNA signature for predicting LNM would be more beneficial than the strategies "treat all" or "treat none". For example, at the 0.25 threshold, the net benefit was 14.6% (95% CI, 7.6–22.0%) in the treat-all model, 20.7% (95% CI, 15.7–27.0%) in our disease signature model. The net benefit of the disease signature model was significantly higher compared with the treat-none strategy at thresholds ≤ 0.63. Thus, our signature was considered clinically valuable. The differences of thirteen-miRNA expression between patients with LNM or without LNM were shown in Figure 2. The expression levels of miR-30d, miR-376b, miR-378a, miR-503-9, miR-582 and miR-891a in patients with LNM were relatively higher than patients without LNM, while the expression levels of the miR-133a, miR-3065, miR-338, miR-4728, miR-552, miR-598 and miR-664a were lower in patients with LNM. Therefore, the results of DCA and gene expression distribution both proved our miRNAs signature had good predict validation.
3.4. The construction and analysis of differentially expressed mRNAs and miRNAs regulatory network associated with lung adenocarcinoma metastasis
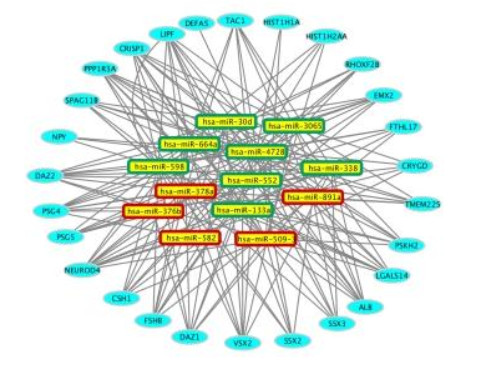
A total of 8968 mRNAs were identified from the TCGA database, of which 325 mRNAs were differentially expressed between lung adenocarcinoma patients with LNM and those without LNM (fold change > 20, P < 0.05). The next step was to deduce mRNAs targeted by miRNAs. We focused on the 13 miRNAs in our signature and 27 out of 325 differentially expressed mRNAs were identified as potential targets using miRWalk database.
Based on the data collected, we constructed a miRNA-mRNA regulatory network using Cytoscape 3.7 (Figure 3). A total of 184 interactions were identified in this network. Among them, hsa-miR-378a, hsa-miR-4728, hsa-miR-598, hsa-miR-3065, hsa-miR-338, hsa-miR-509-3, hsa-miR-552, hsa-miR-664a, hsa-miR-891a regulated the most target mRNAs. LIPF, NEUROD4, PSG4, PPPIR3A, DAZ2, CRAISP1 were putatively regulated by most miRNAs and may have a potential role in lymph node metastasis in lung adenocarcinoma patients.
4.
Discussion
Lung cancer is a leading cause of cancer deaths worldwide, contributing to 1.8 million deaths in 2018 alone [22,23]. Involvement of the regional lymph nodes is a characteristic feature of early stage of tumor growth in NSCLC, and "N status" is a major factor clinical management of this subtype [24]. NSCLC patients with LNM often have poor prognosis and high mortality. It was reported that 5-year survival of lung adenocarcinoma patients without LNM was over 95% while 5-year survival of mid-stage or late-stage cancer patients with LNM was only 30% [7]. Therefore, lymph node metastasis is closely associated with prognosis of lung adenocarcinoma and its accurate prediction is helpful to instigate early treatment to improve patient outcomes.
MiRNA signatures of lung cancer are commonly used to predict the survival time of cancer patients [25,26]. However, survival time is easily swayed by healthcare qualities, psychological condition and treatment options etc. Lymph nodes metastases is just a status of cancer disease, which is highly related to gene expressions. Thus, prediction of lymph nodes metastases with miRNA is more reasonable and objective compared to prediction of survival time. For the first time, we developed a miRNA disease signature to predict lymph node metastasis in patients with lung adenocarcinoma. Although previous studies have identified miRNA signatures that correlate with overall survival, their clinical use was limited owing to LUAD patients' significant heterogeneity from multiple aspects like pathology, treatment plans, surgical options, healthcare services and psychological conditions. Each of these aspects may significantly influence patients' overall survival rates, thus contributing to the unreliability of survival prediction. Using the TCGA lung adenocarcinoma cohort, we constructed a 13-miRNA signature with satisfying AUC values to predict LNM of LUAD. Our signature focused on the factors associated with lymph node metastasis instead of overall survival, whose evaluation were more objective, thereby conceiving great clinical value. More importantly, the prediction of lymph node metastasis serves as a distinct approach to the evaluation of patients' prognosis and could be implemented as an important indicator for physicians to pick proper treatment plans. For patients at T1 and T2 stage, the signature had AUC values of 0.697 and 0.765 respectively, indicating its good performance in early stage lung adenocarcinoma. And the higher T stage, the better prediction accuracy was achieved. In addition, our signature worked better in elder populations, as patients above 50 years old had a higher AUC value compared to younger patients.
The miRNAs in our signature were known to function in oncogenesis in lung cancer, or have reported to have prognostic value. In our signature, miR-582, miR-378a, miR-891a, miR-509-3, miR-376b were upregulated in LUAD patients with lymph node metastasis. Fang et al. reported that in NSCLC, miR-582-3p had an activating effect on Wnt/β-catenin signaling and the overexpression of which targets several negative receptors, AXIN2, DKK3 and SFRP1, in the pathway, thereby promoting tumorigenesis and tumor recurrence [27]. Contrarily, miR-582-5p was also reported to suppress the growth and invasion of NSCLC cell by targeting NOTCH1 and MAP3K2 [28,29]. MiR-378 overexpression could decrease the expression of HMOX1 and p53 while enhancing that of MUC5AC, vascular endothelial growth factor, interleukin-8, and Ang-1, thereby promoting proliferation, migration, and stimulation of endothelial cells in NSCLC cell lines [30]. Overexpression of miR-891a was observed in NSCLC and it negatively regulated HOXA5, a tumor suppressor gene whose gene product could up-regulate the expression of the TP53 tumor suppressor gene [31]. The result was further proved by a study, showing miR-891a-5p was found to present at significantly higher level in lung cancer compared with control sample [32]. MiR-509-3 could repress PLK1 expression for inhibiting cancer proliferation and sensitizes cells to DNA damage agents, which provides insights into future optimization of chemotherapy [33]. In breast cancer and renal cell carcinoma, miR-509-3 played a similar role in suppressing cell invasion and migration [34,35]. Korkmaz et al. found that overexpression of miR-376b lowered the levels of ATG4C and BECN1 to control autophagy [36].
On the other hand, miR-30d, miR-338, miR-3065, miR-664a, miR-598, miR-552, miR-133a-1, mirR4728 were down-regulated in LUAD patients with lymph node metastasis. MiR-30d-5p, an often down-regulated miRNA in NSCLC tissues, could target cyclin E2 (CCNE2) to inhibit the growth, distribution and motility of NSCLC cells [37]. Similarly, miR-338-3p could suppress the migration and invasion of NSCLC cells by targeting integrin β3, a metastasis related protein or Sox4, an epithelial-mesenchymal transition (EMT)-related transcription factor [38,39]. A negative correlation was observed between the expression of miR-338-3p and insulin receptor substrate 2, an oncogene, suggesting a new way for miR-338-3p to suppress tumor [40]. MiR-3065 was reported to target some lung squamous cell carcinoma lncRNAs, but its role in oncogenesis has not yet been studied in lung adenocarcinoma [41]. The presence of miR-664 may enhance the proliferation and migration in lung cancer cell lines while inhibiting apoptosis [42]. Overexpression of miR-598 could inhibit tumor cell metastasis in NSCLC in vivo and negatively regulates Derlin-1 and EMT to suppress cancer cell invasion and metastasis in vitro [43]. Inhibitory effect of miR-598 overexpression to LNM was also observed in NSCLC cells by targeting zinc finger E-box-binding homeobox 2 [44]. Xu et al. found a positive feedback loop between LINC01296, Twist1 and miR-598, indicating a potential target for therapeutic strategy [45]. MiR-552 was mainly reported in colorectal cancer as a negative prognostic indicator and may potentially be used to predict the origin of lung carcinoma, namely differentiating primary lung adenocarcinoma and colorectal cancer metastases [46–48]. Studies have also concluded that overexpression of miR-133a could suppress cell proliferation, invasion and metastasis in lung cancer cell lines by suppressing the expressions of matrix metalloproteinase MMP14 and oncogenic receptors including insulin-like growth factor 1 receptor (IGF-1R), TGF-beta receptor type-1 (TGFBR1), and epidermal growth factor receptor (EGFR) [49,50]. Clinical studies also confirmed that the expression of miR-133a negatively associated with the status of N classification and MMP-14 expression [51]. The role of mir-4728 in lung cancer has yet been reported, but it served as a negative regulator for of MAPK signaling through directly targeting the ERK upstream kinase MST4 to suppress cancer cell proliferation in vitro [52].
These studies demonstrated the association between expression of these miRNAs and lymph node metastasis. Identified miRNAs in our signature and the interactions between miRNA and mRNA is helpful to increase our understanding for the pathogenesis and lymph node metastasis of LUAD. Moreover, determination of these miRNAs and pathways could serve as potential therapeutic targets for treatments in lung cancer and provide insights into future clinical use.
It should be noted that although miRNAs in our signature have demonstrated functions in cell migration, invasion and other developmental processes, there was little overlap between our miRNAs and the ones reported in other signatures that predicted overall survival, possibly due to different methodology and distinct expected outcomes. Concerning that mRNAs reported in our miRNA-mRNA regulatory network have yet been reported, investigations are warranted to look into these genes. One other limitation is that both our training and validation cohorts were obtained from TCGA database. External validation sets and experimental validation in biological function of these miRNAs may suggest further implications of lymph node metastasis in lung adenocarcinoma.
Acknowledgements
This work was supported by Zhejiang Medical and Health Project (2019334185), Zhejiang Natural Sciences Foundation Grant (LQ17H160011, LY17H160029, LY18H160007), the National Natural Science Foundation of China (81602635, 81703072), Zhejiang Medical Innovative Discipline Construction Project-2016 and the Innovation research grant program for 8-year-system medical students at Zhejiang University (No.119000-5405A1).
Conflict of interest
The authors declare no competing interests.









 DownLoad:
DownLoad: