Harnack inequality for a p-Laplacian equation with a source reaction term involving the product of the function and its gradient

Dedicated to the 50th birthday of Professor Giuseppe Mingione, with high feelings of admiration for his notable contributions in Mathematics and great affection.

1.   Introduction

The last decades have seen an evolution in scientific understanding and human capabilities concerning new isolated nanoparticles set up into hybrid composite materials, not ordinarily found in nature, whose properties are specifically planned and controlled not only by the constituent phases, but also by their morphology, spatial anisotropy and relative proximity with respect to one other and the host matrix. The worldwide scientific focus on hybrid systems, based on synthetic or natural polymers combined with metal, ceramic or carbon nanosctructures, represents a truly revolutionary change in the society way of thinking and allows us to create high–performance materials, underpinning the development of previously unrealizable applications. Further details can be found in ^[1] and its references. Indeed, in ^[1] nonlocal problems have been investigated, with the aim of describing the elastic behavior of complex structures composed by two or more different phases having extremely efficient mechanical features, to employ in a wide range of fields as civil engineering and architecture. The insurgence of nonlocality in composites made of several layer of alternating stiff and soft phases as been shown in ^[17].

The analysis of a nonlocal elastic medium has been recently tackled with the tools of fractional calculus, which essentially are based on a fractional gradient elasticity model. By means of fractional operators, it is possible to associate a mechanical model to the equation involving fractional terms, consisting of points connected not only to adjacent ones but also to all the others by springs: the springs themselves have stiffness which decrease with the distance according to a power–law.

The mixed problem discussed in this paper involves in its nonlocal part the so called peridynamics, which is a nonlocal continuum model in solid mechanics introduced by Silling ^[18]; we refer to ^[4,5,6] for a detailed discussion. The main difference with the usual Cauchy–Green elasticity relies on the nonlocality, which is reflected in the fact that points separated by a positive distance exert a force upon each other. Mathematically, deformations are not assumed to be weakly differentiable, in contrast with classical continuum mechanics, and in particular hyperelasticity, where they are required to be Sobolev. This makes peridynamics a suitable framework for problems where discontinuities appear naturally, such as fractures, dislocations, or, in general, multiscale materials.

In particular, the balance equation for a one-dimensional solid (a rod) in classical (local) mechanics is given by

where $\sigma$ is the stress, $f$ are distributed forces possibly depending on $x$ and ${}'$ denotes first derivative. The constitutive elastic law for the rod affirms that

where $E$ is the modulus of elasticity and $\varepsilon$ is the deformation, related to the displacements $u$ by the compatibility law

Therefore, in classical local mechanics we have

where $\Delta$ is the Laplacian. In ^[9] Eringen considered the stress depending on the strain not only locally but also on the strain in all the point along the rod length $\mathscr{L}$, introducing the following constitutive law

where $\alpha$ is a weight (kernel) function that assess the influence of the strain in distance points to the stress. Anyway, this approach still requires the differentiation in the equation of motion, as highlighted by Silling ^[18], which could be a problem in the case of presence of discontinuities. Therefore, following the approach of Silling with which he introduced the peridynamics, where the equilibrium equation is written including a nonlocal operator $L_u$ as in the following

we assume that the peridynamic equation of motion in statics can be written as

where $(-\Delta)_\mathscr{L}^s$ is the regional fractional Laplacian which is a nonlocal operator (see later) and $k$ is a suitable parameter. Anyway, since it has been found (see ^[20]) that in the case of composites with nonlocal behaviour it is better to consider two phases, a local one and a nonlocal one, the problem can be written as

where $c$ is a suitable parameter (equivalent to $E$ in the purely local case) and $V$ account for the possible presence of external linear spring forces. It is worth noting that the previous problem is similar to that which appears in preceding papers of some of the authors ^[2,3,10] but with a different operator, the fractional Laplacian defined in an unbounded domain, and with a different approach based on the original work of Eringen using fractional derivatives. The problem of the rod in a peridynamic context has been considered in literature (see for example ^[13,19]) but with a different approach. For the regularity properties of the solutions of mixed local and nonlocal problems we refer to the recent paper ^[8] by De Filippis and Mingione, as well as its wide bibliography.

More specifically, the first problem we consider in details is linear and given by

where $c, \, k > 0$ are physical coefficients and usually, but not in this paper, are supposed to satisfy the convex restriction $c+k = 1$, the additional term $V(x)u$ represents external springs whose stiffness is related to the position of the point along $\Omega_0$, and the nonnegative potential $V$ is in $L^\infty(\Omega_0)$, while $f$ is a perturbation of class $L^2(\Omega_0)$. The operator

is the so called regional fractional Laplacian. Throughout the paper we denote by $B(x_0, r)$ the open ball in $\mathbb R^N$ of center $x_0$ and radius $r > 0$. When $x_0 = 0$ we simply denote $B(0, r)$ by $B_r$.

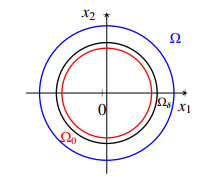
Here and in what follows $\Omega \subset \mathbb{R}^N$ is a bounded domain, with smooth boundary $\partial\Omega$. Moreover, $\Omega$ is divided into two parts, that is $\Omega = \Omega_0 \cup \Omega_1$, where $\Omega_0$ is an open set, with smooth boundary $\partial\Omega_0$ and $\Omega_0 \cap \Omega_1 = \emptyset$. Furthermore, the open enlargement $\Omega_\delta = \Omega_0+B_\delta$, for a suitable small radius $\delta > 0$, is assumed to be a subset of $\Omega$. In this way, the remaining set $\Omega_1\supset\partial\Omega_0$ and $\Omega_1$ can be seen as the nonlocal boundary of $\Omega$, see Figure 1.

In the present paper we first interpret the problem $(P_L)$ which models the behavior of an elastic body, with a linear peridynamical approach, and enrich it with additional terms in order to widen its mechanical meaning and give the conditions under which one unique solution exists. Then we prove multiplicity results for the nonlinear version of $(P_L)$, namely for problem

Finally, we treat $(P_L)$ and $(P_N)$ also numerically, estimating the regional fractional Laplacian by means of its singular integral representation. For both problems, a numerical estimation of the solutions is obtained, using in the nonlinear case an approach involving a random variation of an initial guess of the solution. Moreover, in the linear case a parametric analysis is made in order to study the effects of the parameters involved in the model, with a particular emphasis on the order of the fractional Laplacian and on the mixture law between local and nonlocal behavior.

2.   Preliminaries

Let $\Omega$, $\Omega_0$, $\Omega_1$ and $\Omega_\delta$ be as stated in the Introduction. The natural solution functional space associated to $(P_L)$ is

where $H_0^1(\Omega_0)$ is the completion of $C_c^\infty(\Omega_0)$ with respect to the norm $\|\nabla\, \cdot\, \|_{L^2(\Omega_0)}$ and $H_0^s(\Omega)$ is the completion of $C_c^\infty(\Omega)$, with respect to the Gagliardo seminorm

The canonical Hilbertian norm on $\mathbb{H}_{0, \Omega}^s$ is

which, since $V\in L^\infty(\Omega_0)$, is equivalent to the Hilbertian norm

being

where $C_P$ is the Poincaré constant. It is convenient for later purposes to endow $\mathbb{H}_{0, \Omega}^s$, with the Hilbertian norm

which is equivalent to $\|\, \cdot\, \|_{ \mathbb{H}_{0, \Omega}^s}$, since $c, k > 0$, being $\kappa\|u\|_{ \mathbb{H}_{0, \Omega}^s}\le\|u\| \le K\|u\|_{ \mathbb{H}_{0, \Omega}^s}$ for all $u\in \mathbb{H}_{0, \Omega}^s$, where $\kappa = \min\{c, \, k, \, 1\}$ and $K = \max\{c, \, k, \, 1\}$.

3.   Existence results

3.1.   The linear problem

The first problem that we consider is

where $c, \, k > 0$ and $f\in L^2(\Omega_0)$.

Definition 3.1. We say that $u\in \mathbb{H}_{0, \Omega}^s$ is a (weak) solution of problem $(P_L)$ if

for every function $v\in \mathbb{H}_{0, \Omega}^s$. $

In light of the variational structure of problem $(P_L)$, the critical points of the underlying $C^1$ functional $J: \mathbb{H}_{0, \Omega}^s \to \mathbb{R}$, defined as

are exactly the (weak) solutions of $(P_L)$. Thanks to the linearity of $(P_L)$, existence and uniqueness are obtained by standard arguments.

Proposition 3.1. Let $f\in L^2(\Omega_0)$ and $s\in (0, 1)$. Then there exists a unique solution $u\in \mathbb{H}_{0, \Omega}^s$ of problem $(P_L)$. If $f$ is nontrivial, then also the solution is nontrivial.

Proof. First, it is easy to show that the functional $J$ is coercive, since

Moreover, $J$ is $C^1$, strictly convex and coercive in the Hilbert space $\mathbb{H}_{0, \Omega}^s$, so that the Weierstrass Theorem, see Corollary 3.23 of ^[7], the functional $J$ has a global minimum in $\mathbb{H}_{0, \Omega}^s$, which is also a critical point of $J$, and hence a solution of $(P_L)$.

Uniqueness of solutions of $(P_L)$, that is uniqueness of critical points of $J$ follows from the strict convexity of $J$. This completes the proof.

3.2.   The nonlinear model

This subsection deals with the nonlinear problem

where $f:\Omega_0\times \mathbb{R}\to \mathbb{R}$ is a Carathéodory function such that $f(\cdot, 0) = 0$ a.e. in $\Omega_0$. Let us introduce the notation $2^*$ for the Sobolev exponent, that is

In addition, we assume the following conditions coming from ^[16], as improvements of those in ^[15] and ^[12]:

($f_1$) there exist $a\in L^q(\Omega_0)$, $b\in L^\infty(\Omega_0)$, with $a\geq 0$, $b > 0$ and $q\in((2^*)', 2)$, and $r\in (2, 2^*)$ such that

($f_2$) ${\lim_{t\to \pm \infty}\dfrac{F(x, t)}{|t|^2}} = \infty$ uniformly for a.e. $x\in \Omega_0$, where $F(x, t) = \int_0^t f(x, \tau)d\tau$;

($f_3$) there exist $\theta\geq 1$ and $\beta\in L^1(\Omega_0)$, $\beta\geq 0$, such that

where $\sigma(x, t) = f(x, t)t-2F(x, t)$ in $\Omega_0\times \mathbb{R}$;

($f_4$) ${\lim_{t\to 0}\dfrac{f(x, t)}{|t|}} = 0$ uniformly for a.e. $x\in \Omega_0$.

Remark 3.1. An example of a function satisfying conditions $(f_1)-(f_4)$ is given by

with $b\in L^\infty(\Omega_0)$ and $b(x) > 0$ a.e. in $\Omega_0$. Clearly, $f(x, 0) = 0$ a.e. in $\Omega_0$, and $(f_1)$ is satisfied for $N < 6$ as

for a.e. $x \in \Omega_0$, recalling that $\log(1+|t|)\leq |t|$ for every $t\in \mathbb{R}$. To show the validity of $(f_2)$, we first compute

then a simple computation of the limit is enough. Since

it is easy to see that $(f_3)$ is satisfied for $\theta = 1$ and $\beta = 0$. Finally, the computation of the limit shows that $(f_4)$ is satisfied.

Definition 3.2. With the same assumption on $f$ as above, we say that $u\in \mathbb{H}_{0, \Omega}^s$ is a (weak) solution of problem $(P_N)$ if

for every function $v\in \mathbb{H}_{0, \Omega}^s$.

From this definition and from the variational nature of $(P_N)$, the critical points of the corresponding functional $I: \mathbb{H}_{0, \Omega}^s \to \mathbb{R}$, defined as

are exactly the (weak) solutions of $(P_N)$.

Before proving the main existence theorem for $(P_N)$, let us give some preliminaries. It is useful to introduce the functionals

where $u^+$ and $u^-$ are the classical positive part and negative part of $u$.

Our aim is to prove that both $I_\pm$ satisfy the Cerami condition, (C) for short, which states that any sequence $(u_n)_n$ in $\mathbb{H}_{0, \Omega}^s$ such that $(I_\pm(u_n))_n$ is bounded and $(1+\|u_n\|)I'_\pm(u_n)\to 0$ as $n\to \infty$ admits a convergent subsequence.

Proposition 3.2. Under assumptions $(f_1)$–$(f_3)$, the functionals $I_\pm$ satisfy the (C) condition.

Proof. We give the proof for $I_+$, the proof for $I_-$ being analogous.

Let $(u_n)_n$ in $\mathbb{H}_{0, \Omega}^s$ be such that

for some $M_1 > 0$ and all $n$, and

From (3.2) we have

for every $h\in \mathbb{H}_{0, \Omega}^s$, where $\varepsilon_n\to 0$ as $n\to \infty$. That is,

Taking $h = u_n^-$ in (3.3), we get for all $n$

Since

we get

and so

Now, taking $h = u_n^+$ in (3.3), we obtain

From (3.1) we have

for $M_1 > 0$ and all $n$. Hence, together with (3.4), this leads to

for some $M_2 > 0$ and all $n$. Adding (3.6) to (3.7), we obtain

for some $M_3 > 0$ and all $n$, that is

To prove that $(u_n^+)_n$ is bounded in $\mathbb{H}_{0, \Omega}^s$, we argue by contradiction. Passing to a subsequence if necessary, we assume that $\|u_n^+\|\to \infty$ as $n\to \infty$ and that for some $v\geq 0$

for every $q\in(2, 2^*_s)$.

First, we deal with the case $v\neq 0$. We define the set

so that $|\Omega_0\setminus Z(v)| > 0$ and $u_n^+\to \infty$ for a.e. $x\in \Omega_0\setminus Z(v)$ as $n\to \infty$. By hypothesis ($f_2$) we have

for almost every $x\in \Omega_0\setminus Z(v)$. On the other hand, by Fatou's Lemma

which leads to

From (3.1) we have

for some $M_4 > 0$ and all $n$. Recalling that $\|u_n\|^2\leq 2(\|u_n^+\|^2+\|u_n^-\|^2)$, from (3.5) we obtain

for some $M_5 > 0$. Dividing by $\|u_n^+\|^2$,

Passing to the limit, we get

for some $M_6 > 0$. This contradicts (3.10), and concludes the case $v\neq 0$.

Now we deal with the case $v\equiv 0$. We consider the continuous functions $\gamma_n:[0, 1]\to \mathbb{R}$, defined as $\gamma_n(t) = I_+(tu_n^+)$, with all $t\in [0, 1]$ and all $n$. Thus, we can define $t_n$ such that

Now we define $w_n = (2\lambda)^\frac{1}{2}v_n \in \mathbb{H}_{0, \Omega}^s$ for $\lambda > 0$. From (3.9), $w_n\to 0$ in $L^q(\Omega_0)$ for all $q\in (2, 2^*_s)$. Performing some integration from ($f_1$) we have

which implies

Since $\|u_n^+\|\to \infty$, there exists $n_0$ such that $(2\lambda)^\frac{1}{2}/\|u_n^+\|\in(0, 1)$ for all $n\geq n_0$. Then, from (3.11),

for all $n\geq n_0$. Thus,

Then (3.12) implies that

and since $\lambda$ is arbitrary we have

Clearly, $0\leq t_nu_n^+\leq u_n^+$ for all $n$, so that from ($f_3$) we know that

for all $n$. Clearly, $I_+(0) = 0$. In addition, (3.1) and (3.4) imply that $I_+(u_n^+)\leq M_7$ for some $M_7 > 0$. Together with (3.13) this implies that $t_n\in (0, 1)$ for all $n\geq n_1\geq n_0$. Since $t_n$ is a maximum point, we get

and recalling that

we have

Adding (3.15) to (3.14), we obtain

that is

Hence, (3.13) implies that

Combining (3.8) and (3.16) we obtain the contradiction, which concludes the case $v\equiv 0$.

In conclusion, $(u_n^+)_n$ is bounded in $\mathbb{H}_{0, \Omega}^s$, and (3.5) gives that $(u_n)_n$ is bounded in $\mathbb{H}_{0, \Omega}^s$. Hence, upto a subsequence, if necessary, there exists $u\in \mathbb{H}_{0, \Omega}^s$ such that

Taking $h = u_n-u$ in (3.3), we have

From ($f_1$) and (3.17) we know that

Passing to the limit in (3.18) we obtain

This implies that $\|u_n\|\to \|u\|$, so that $u_n\to u$ in $\mathbb{H}_{0, \Omega}^s$. Then $I_+$ satisfies the (C) condition, which concludes the proof.

We are now able to give the proof of the main existence theorem for $(P_N)$.

Theorem 3.3. If $(f_1)$–$(f_4)$ hold, then problem $(P_N)$ admits at least two nontrivial constant sign solutions.

Proof. Let us apply the Mountain Pass Theorem to $I_+$. From Proposition 3.2 we know that $I_+$ satisfies the (C) condition, so that we only have to verify the geometric conditions.

From ($f_1$) and ($f_4$), for every $\varepsilon > 0$ there exists $C_\varepsilon$ such that

for a.e. $x\in \Omega_0$ and all $t\in \mathbb{R}$. Then

From this we kwon that, if $\|u\| = \rho$ is small enough,

Now, let $u\in \mathbb{H}_{0, \Omega}^s$ be positive in $\Omega_0$ and let $t > 0$. Then

By Fatou's Lemma

so that ($f_2$) implies that

Consequently,

Therefore, there exists $e\in \mathbb{H}_{0, \Omega}^s$ such that $\|e\| > \rho$ and $I_+(e) < 0$.

Now, thanks to Proposition 3.2 and the Mountain Pass Theorem, the functional $I_+$ possesses a nontrivial critical point $u$ at the minimax level

In particular, $u$ is a nontrivial solution of $(P_N)$ and, taking $v = u^-\in \mathbb{H}_{0, \Omega}^s$ as test function

Recalling that

we obtain

and so $u^-\equiv 0$. Hence, $I_+(u) = I(u)$. This gives at once that $u\geq 0$ is a nontrivial solution of $(P_N)$.

Arguing in the same way for $I_-$, we find a second nontrivial nonpositive solution of $(P_N)$.

4.   Numerical approximation of the problems

For an arbitrary function $f$ it could be not simple to find a closed-form solution for the problems $(P_L)$ and $(P_N)$, therefore we resort to find a numerical approximation of the solution itself.

In particular, if the domain $\Omega_0 \cup \Omega_1$ is the interval $(-L, L)$ and $\Omega_0$ is $(-L_0, L_0)$, we discretize it in a finite number, $n$, of points denoted as $x_i$ with $i = 0, 2, \ldots, n-1$, as shown in Figure 2. we have that

with

The corresponding value of $u$ in the points $x_i$ will be denoted $u_i = u(x_i)$.

The Laplacian $\Delta u$ is approximated by means of the central difference formula

in all the points except when $i = 0$ and $i = n-1$ forward difference and backward difference formulas, respectively, are used.

In order to approximate $(-\Delta)_\Omega^s u$, the approach proposed in ^[11] is used. We recall that, in the present case

with

The idea of the approach is to split the integral over $\Omega$ in two contributions, the first is the sum of the integrals in the intervals $(-L, x_i-h)$ and $(x_i+h, L)$ and the second is the (improper) integral in the interval $(x_i-h, x_i+h)$ which contains the singularity.

For the second contribution, we use the result in Section 2.2 of ^[11] and therefore

For the first contribution, as suggested in ^[11] an exact integration is made using the following interpolant of the terms $u(x_i) - u(x_i-y)$:

with

Combining the two contributions, the regional Fractional Laplacian can be evaluated numerically as

with

where

The function $F$ is such that

The discretized form of $(P_L)$ is therefore

where the points in $\Omega_0$ are $x_i$, with $i = j, j+1, \ldots, k$.

Now the problem is to find the values of $u_i$ for each $i$ in order to find the zeros of the following function $g$ expressed in discretized form

This problem can be solved numerically. In particular, we use the Python programming language and its procedure "solve", based on the Powell hybrid method, as implemented in MINPACK, see ^[14].

4.1.   Results for linear case

The following values have been taken:

The value of $\kappa$ is chosen so that for $s = 1$ the contribution due to the ordinary Laplacian and the regional Fractional Lapalacian are equal, with $c$ equal to the half of modulus of elasticity of the material.

The first case studied consist in a rod loaded by two forces in opposite direction symmetrically with respect to the midspan, as shown in Figure 3.

The response of the rod when $d = \pm 2\, \mathrm{mm}$ and magnitude $F_0 = 1000\, \mathrm{N}$ is shown in Figure 4.

The effect of the variation of the step $h$ is shown, and it can be appreciated that even for quite large values of $h$ the solution is sufficiently accurate.

It is interesting to note that for $s \to 1$ the purely local response is obtained, as shown in Figure 5.

In this case, the displacements are linear in each interval $(-L_0, -d)$, $(-d, d)$ and $(d, L_0)$ and the maximum displacement for $x = -d$ is given by

With the value recalled before, this gives $u(-d) = 0.065\, \mathrm{mm}$, as obtained numerically.

Subsequently, we study the response of the rod under the effect of a distributed load $f$ given by the following expression

as shown in Figure 6.

The results are shown in Figure 7.

Again, the effect of various values of $h$ is shown and the same considerations as before are valid.

4.1.1.   Parametric analysis

A parametric analysis is performed to show the effect of the variation of mechanical parameters on the response.

At first the values of $c$ and $\kappa$ are varied according to the following rules:

with $\beta_1 + \beta_2 = 1$. The values of $\beta_1$ and $\beta_2$ can be though of as the weight of the contribution of the local and nonlocal behavior respectively. For $\beta_1 = \beta_2 = 0.5$ the preceding case is recovered.

The results are shown in Figure 8.

As can be appreciated, as the value of $\beta_1$ increases, the behavior approximates that of a purely local material, as expected. Moreover, the variation of the maximum displacement with $\beta_1$ is no monotonic, having and initial decrement followed by a successive pronounced increment.

The values of $s$ vary in the interval $(0.5, 1)$ and produce the results shown in Figure 9.

Also in this case a non-monotonic variation of the displacement with respect to $s$ can be appreciated. Subsequently, the effect of the contribution of $V(x) u$ is analyzed. The results are shown in Figure 10.

4.2.   Results for nonlinear case

The same mechanical parameters of the linear case have been assumed. In this case, we choose a non symmetric function

Anyway, in the nonlinear case, we note that the trivial function $u\equiv0$ is always a solution of the problem.

In order to find a different non-trivial solution, the numerical procedure starts with an initial guess $u_0$ which, in the applications, we assume as

where $W$ is a function which gives Gaussian white noise.

The effect of the initial guess in retrieving the non-trivial solution is shown in Figure 11, where the blue curve (the trivial solution) was obtained with $\delta_1 = 1\, \mathrm{mm}$ and $\delta_2 = 0.1\, \mathrm{mm}$, while the orange curve (the nontrivial solution) was obtained with $\delta_1 = 0\, \mathrm{mm}$ and $\delta_2 = 0.1\, \mathrm{mm}$.

It is worth noting that $W$ is different in the two curves since they are from two different random generation.

The effect of different values of $s$ is highlighted in Figure 12.

Moreover, since we know that at least two different solutions exist, we give an estimation of these solutions in Figure 13. The solutions were obtained using a suitable choice of $u_0$, in particular the blue curve was obtained with $\delta_1 = 1\, \mathrm{mm}$ and $\delta_2 = 0.1\, \mathrm{mm}$, while the orange curve was obtained with $\delta_1 = -1\, \mathrm{mm}$ and $\delta_2 = 0.1\, \mathrm{mm}$.

Acknowledgments

F. Cluni, V. Gusella and E. Proietti Lippi were partly supported by the Italian Ministry for University and Research within P.R.I.N. National Grant 2017, Project title "Modelling of constitutive laws for traditional and innovative building materials", Project code 2017HFPKZY; University of Perugia Research Unit.

D. Mugnai, E. Proietti Lippi and P. Pucci are members of the Gruppo Nazionale per l'Analisi Matematica, la Probabilità e le loro Applicazioni (GNAMPA) of the Istituto Nazionale di Alta Matematica (INdAM). D. Mugnai and E. Proietti Lippi were partly supported by the INdAM – GNAMPA Project PDE ellittiche a diffusione mista (CUP_E55F22000270001). P. Pucci was partly supported by the INdAM – GNAMPA Project Equazioni alle derivate parziali: problemi e modelli (Prot_U-UFMBAZ-2020-000761).

Finally, D. Mugnai was also partly supported by FFABR Fondo per il finanziamento delle attività base di ricerca 2017 and by the HORIZON_EU_DM737 project 2022 COntrollability of PDEs in the Applied Sciences (COPS) at Tuscia University.

Conflict of interest

All authors declare no conflicts of interest in this paper.