1.
Introduction
Neuronal activities generate the electrical current in the brain, and further result in the potential changes over the scalp. Electroencephalography (EEG) is a technique used to record the potential changes on the scalp. Even though fMRI, PET, MEG and other brain-imaging tools are widely used in brain research, they are limited by low spatial/temporal resolution, cost, mobility and suitability for long-term monitoring. For example, fMRI has the advantage of providing spatially-resolved data, but suffers from an ill-posed temporal inverse problem, i.e., a map with regional activations does not contain information about when and in which order these activations have occurred [1]. In contrast, EEG signals have been successfully used to obtain useful diagnostic information (neural oscillations and response times) in clinical contexts. Further, they present the advantage to be highly portable, inexpensive, and can be acquired at the bedside or in real-life environments with a high temporal resolution. Because of the lack of significant patient risks, EEG is additionally suited for long-term monitoring.
EEG offers the possibility of measuring the electrical activity of neuronal cell assemblies on the sub-millisecond time scale [2,3,4]. EEG source imaging further identifies the positions or distributions of electric fields based on EEG signals collected on the scalp [5]. This new tool is widely used in cognitive neuroscience research, and has also found important applications in clinical neuroscience such as neurology, psychiatry and psychopharmacology [6,7]. In cognitive neuroscience, the majority of the studies investigate the temporal aspects of information processing by analyzing event related potentials (ERP). In neurology, the study of sensory or motor evoked potentials is of increasing interest, but the main clinical application concerns with the localization of epileptic foci. In psychiatry and psychopharmacology, a major focus of interest is the localization of sources of certain EEG frequency bands. Localizing the activity sources of a given scalp EEG measurement is achieved by solving the so-called inverse problem [8]. These kinds of inverse problems are usually ill-posed and their solutions are non-unique [9,10].
Leahy et al. [11] investigated the accuracy of forward and inverse techniques for EEG and MEG dipole localization using a human skull phantom. El Badia and Ha-Duong [12] established an algebraic method to identify the number, locations and moments of electrostatic dipoles in 2D or 3D domain from the Cauchy data on the boundary. Chafik et al. [13] further provided an error estimate without proof. Nara and Ando [14] provided a new projective method for 3D source reconstruction by projecting the sources onto a Riemann sphere. Kang and Lee [15] proposed an algorithm for solving the inverse source problem of a meromorphic function and apply their method to an electrical impedance tomography (EIT) problem. El Badia [16] established a uniqueness result and a local Lipschitz stability estimate for an anisotropic elliptic equation, assuming that the sources are a linear combination of a finite number of monopoles and dipoles. The author also proposed a global Lipschitz stability estimate for dipolar sources. Baratchart et al. [17] solved the inverse source problem by locating the singularities of a meromorphic function from the 2D boundary measurements using best rational or meromorphic approximations.
Chung and Chung [18] proposed an algorithm for detecting the combination of monopolar and multipolar point sources for elliptic equations in the 2D domain from the Neumann and Dirichlet boundary data. Kandasmamy et al. [19] proposed a novel technique, called "analytic sensing", to estimate the positions and intensities of point sources in 2D for a Poisson's equation. Analytic sensing also used the reciprocity gap principle, but with a novel design of an analytic function which behaved like a sensor. The authors evaluated their estimation accuracy by Cramér-Rao lower bound. Nara and Ando [20] proposed an algebraic method to localize the positions of multiple poles in meromorphic function field from an incomplete boundary. They investigated the accuracy of the algorithm for the open arc or the closed arc, and for the arc enclosing the poles or not enclosing the poles. El Badia and Nara [21] established the uniqueness and local stability result for the inverse source problem of the Helmholtz equation in an interior domain, assuming the source is composed of multiple point sources.
Clerc et al. [22] applied best rational approximation techniques in the complex plane to EEG source localization and offered stability estimates. Mdimagh and Ben Saad [23] identified the point sources in a scalar problem modeled by Helmholtz equation, using reciprocity gap principle and assuming the sources are harmonic in time. They proved local Lipschitz stability by two methods: one was derived from the Gâteaux differentiability, and the other used particular test functions in the reciprocity gap functional. Vorwerk et al. [24] studies the important role of head tissue conductivity in EEG dipole reconstruction. Rubega et al. [25] estimated EEG source dipole orientation based on singular-value decomposition. Michel and Brunet provided a thorough review on EEG source imaging. There exist several reconstruction methods, such as minimum norm estimates (MNE) [26], low resolution electrical tomography (LORETA) [27,28] or multiple-signal classification algorithm (MUSIC) [29,30], etc.
Recently, Muñoz-Gutiérrez et al. [31] managed to improve the accuracy of EEG source reconstruction by decomposing the EEG signals into frequency bands with different methods, such as empirical mode decomposition (EMD) and wavelet transform (WT). Kaur et al. [32] presented a new method of EEG source localization using variational mode decomposition (VMD) and standardized the low resolution brain electromagnetic tomography (sLORETA) inverse model. Their VMD-sLORETA model could locate EEG sources in the brain in a very accurate way. Oikonomou and Kompatsiaris [33] developed a novel Bayesian approach for EEG source localization. They incorporated a new sparse prior for the localization of EEG sources with the variational Bayesian (VB) framework and obtained more accurate localization of EEG sources than state-of-the-art approaches.
In our study we need new methods to detect small changes in EEG source for which dipole methods have advantage. We followed the analytic dipole method by El Badia and Ha-Duong [12] and derived a new error estimate for this source localization method. We provided a mathematical proof of this estimate. We then use simulated data to validate the method. The simulation results support our error estimation, which has a different distance power than a similar error estimate in [22].
We organize the rest of the paper as follows. In section 2, we introduce the method and its formulation. In section 3, we provide the error estimate of an inverse EEG source localization problem in a bounded domain and its mathematical proof. In section 4, we use simulated data to valid the method and error estimate. A brief conclusion and discussion is in Section 5.
2.
Mathematical model of EEG problem
2.1. Mathematical model
The electric field E is the negative gradient of the potential u.
The quasi-static approximation means all time derivatives in the equation are set to zero. By quasi-static approximation of Maxwell equation ∇×H−∂D∂t=J, we have
where H is the magnetizing field, J is the total current density, and D is the displacement field.
Since the divergence of a curl is always zero, we have
EEG problem can be modeled by a Poisson equation.
where σ is the conductivity, Jp is the primary current density, and F is the source term.
2.2. Source model
If we assume the source is composed of a finite number of point charges, then by linear combination, we have
where m is the number of point charges, qk are values of charges, and rk are the locations of the point charges.
If we assume the source is composed of a finite number of dipoles, we have
where m is the number of dipoles, pk are the moments (or strengths) of the dipoles, and rk are the centers of dipoles.
2.3. The harmonic function method of identifying dipolar sources
The dipolar source reconstruction problem can be viewed as a Poisson problem.
where f and φ are known, and ν is the outer unit normal vector.
We will use the concept of reciprocity gap functional [34]:
where v is a harmonic function in Ω:
By Green's formula, we have
Let m be the number of dipoles in the brain. Assume m≤M in our problem, i.e., there is an upper bound for the number of dipoles.
Let us consider the harmonic polynomials
Then, in 2D case
We define
Let
and
Then,
The number m of dipoles is estimated as the rank of Z1.
Now we can reduce the size of the matrix by recalculating βj and ηj with M replaced by m. Then, the m vectors η1,...,ηm are independent.
To get the estimates of the positions we need to construct an m×m matrix T such that ηj+1=Tηj,j=1,...,m. Then,
So,
The positions of dipoles are estimated as the eigenvalues of T.
We now show that the eigenvalues of T are the positions of dipoles. Let us first look at an example η2=Tη1.
where pk=pk1+ipk2,k=1,2,...,m is the moment and Sk=xk+iyk,k=1,2,...,m is the position.
where pk=pk1+ipk2,k=1,2,...,m is the moment and Sk=xk+iyk,k=1,2,...,m is the position.
Since [1S1⋮Sm−11],[1S2⋮Sm−12],...,[1Sm⋮Sm−1m] are independent and the results are similar for ηj+1=Tηj,j=1,2,...,m, we know S1,S2,...,Sm are just the eigenvalues of T.
Now the question is how to get T. Only η1 and η2 are not enough to determine T because vectors have no inverse. So, we use the redundant information to construct the matrices Z1 and Z2 such that T=Z2Z−11, where Z1 is invertible because η1,...,ηm are independent.
To estimate the moments of dipoles we will write Eq (2.9) in matrix form. Notice that now we use m instead of M.
where pk=pk1+ipk2,k=1,2,...,m is the moment and Sk=xk+iyk,k=1,2,...,m is the position.
We can write Eq (2.11) in matrix form
where b=[β1β2⋮βm],S=[S01S02⋯S0mS11S12⋯S1m⋮Sm−11Sm−12⋯Sm−1m], and p=[p1p2⋮pm]. Then, the moments of dipoles in 2D are estimated as
2.4. Optimization of linear operator
Equation (2.13) works in the ideal case of no noise. In reality, due to the noise in the measurements and in the sources, we need find a linear operator L to estimate the moments, i.e.,
where ˜p represents the estimates of the moments, and b represents the quantities obtained from the measurements.
Considering the noise accompanied in the measurements, we rewrite Eq (2.12) as
where n is a random vector of mean 0. Let N be the covariance matrix of n. Also, assume that ˜p is normally distributed with mean p and its covariance matrix is P.
Using multiple measurements and the statistical estimation theory we can find the linear operator L which minimizes the expected difference ErrL between the estimated moments ˜p and the exact moments p.
Setting the gradient of ErrL to 0 and solving for L, we get the optimal linear operator
Then, by Eq (2.14) we get the best estimates of the moments.
2.5. Uniqueness of solutions
Theorem 2.1 (Uniqueness of solutions). Let ui,i=1,2 be the solutions of the problems
such that
then
The solution of Poisson equation is the convolution of the fundamental solution of Laplace equation and the source function.
3.
Error estimates of positions
As EEG imaging data are typically noisy, especially determining the rank of a near singular matrix is very unstable, the error of the numerical reconstruction method needs to be studied. Chafik et al. [12,13] proposed that when the norms of the perturbations (g=˜f−f,h=˜φ−φ) are small in H1/2×H−1/2, there exist a>0 and b>0 such that ∀k=1,2,...,m,
where Sk=xk+iyk is the exact position of the kth dipole, ˜Sk=˜xk+i˜yk is the estimated position of the kth dipole, d is the minimal distance between Sk and ˜Sk, and R≠1 is a real number bigger than the norm of any point on Γ. However, the analysis is not given by Chafik et al.
Here we present a new error estimate and provide a proof.
Theorem 3.1. Suppose m dipoles are enclosed in a circular boundary of radius R. The potential f on the boundary and the gradient of the potential φ perpendicular to the boundary are known. If T is the measurements without noise, and ˜T is the measurements with noise, then the error estimate is given by
where p is the moment of dipoles and d is the smallest distance between any two dipoles.
Proof. We define
Then,
where
Here, (m1,m2,...,mm) is any permutation of (1,2,...,m) and τ(m1,m2,...,mm) is the sign determined by the permutation.
The maximum absolute row sum norm is defined by
where A is a matrix. When A is a vector, ‖A‖∞=maxi|ai|.
In the following proof we will use an important inequality:
where a(x) and b(x) can be scalar, vector, or matrix.
By Cauchy-Schwarz inequality, we have
where R>1.
Let
where Z1=[β1β2⋯βmβ2β3⋯βm+1⋮βmβm+1⋯β2m−1] and Z2=[β2β3⋯βm+1β3β4⋯βm+2⋮βm+1βm+2⋯β2m].
We can view R(vj) as the measurement obtained by the "detector" vj, while βj is just a constant multiple of R(vj). So, βj is still a measurement of another form, which contains the information about the moment and the position of the dipole source. Since Z1 and Z2 are constructed by different measurements βj, T is also a matrix of measurements.
Assume T is the measurements without noise, and ˜T is the measurements with noise. Then,
We will analyse the four norms in the above inequality one by one.
To find ‖Z−11‖∞ we need to estimate ‖adj(Z1)‖∞. We first observe the results for m=3, then prove the results to the arbitrary m using mathematical induction.
If Z1=[β1β2β3β2β3β4β3β4β5], then the absolute value of the first element of adj(Z1) would be
Then,
Assume when m=n−1, we have
In fact, this inequality is also true for other minors with matrix size (n−1)×(n−1).
Then, when m=n we have
Then, for any m we have
Thus,
where d is the smallest distance between any two dipoles.
Notice that
Based on the above results, we have
We can further simplify it as
where
When 0<E<1, the error in the position estimate is mainly controlled by E; when E>1, the error in the position estimate is mainly controlled by E2.
4.
Numerical simulation results
4.1. Numerical simulation for 2D
Let Ω be a circular disk centered at the origin and of radius r=1. Then, the numerical implementation can be simplified as follow.
where f is a function of θ on the boundary. We do not need to know the explicit form of f, but we can measure as many points as possible on the boundary to get enough discretized function values of f. Then, the above integral can be approximated by a Riemann sum.
The measurable values we want to use in the following are
The Romberg algorithm is used to calculate the integral numerically.
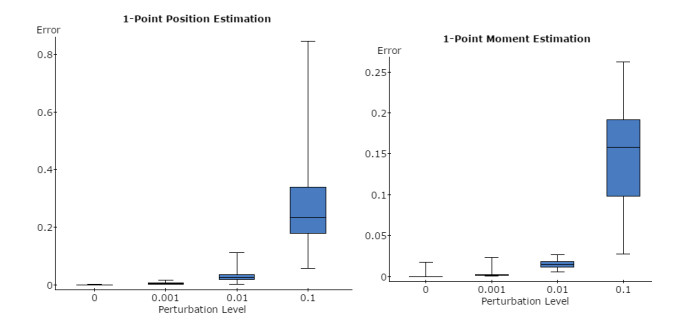
We compare the efficacy of the harmonic function method in dipolar source reconstruction when the perturbation level is 0,0.001,0.01,0.1 and the number of dipoles is 1,2,3,4,5. It is shown that as the perturbation level increases, the reconstruction error increases (see Figures 1–5).
In the following we show the results of source estimation, assuming there are 3 dipolar sources (m=3).
● Dipole 1: position (0.3,−0.3) and moment (0,1).
● Dipole 2: position (0.6,0.2) and moment (1,1).
● Dipole 3: position (−0.5,0.4) and moment (2,2).
In the graphs (see Figure 6) we use a small circle and a red line segment to indicate the true value, and use a cross sign and a green line segment to indicate the reconstructed values.
From error estimates we know that as the distance between two dipoles gets closer, the reconstruction error for the positions of dipoles gets larger (see Table 1 and Figure 7). This is verified by the numerical simulations.
We randomly assign two dipoles with fixed distance, say 0.1, in the unit disk, then reconstruct their positions. We fix the noise level for all experiments at σ=0.001.
Let di (i=1,2) be the distance between the ith exact dipole and the ith estimated dipole, and dmax be the largest d.
We repeat the experiment 10 times and show their performance on average over different dipole distances.
The above experiment also provides a numerical example to show that the estimate given by us in Theorem 3.1 provides a better error bound when the two poles are very close.
When the number of dipoles is m=2, Chafik's estimate is bounded by C1d (see Inequality (3.1)), while our estimate is bounded by C2d2 (see Inequality (3.4) and Eq (3.5)) where d is the smallest distance between two dipoles and Ci (i=1,2) are constants independent of d. That is, when the distance is halved, the error bound will be amplified by 2 in Chafik's estimate and by 4 in our estimate.
From the data simulation, we see that
For example, when the distance between the two dipoles is reduced from 0.10 to 0.05, by Chafik's estimate the error should be amplified by 2, but in fact, the error is amplified by 2.57, which is bounded by 4 in our estimate.
5.
Conclusions
In this paper we studied a harmonic function method for the dipolar source reconstruction, derived error estimate for the harmonic function method and compared our result with Chafik's estimate. By numerical simulations it is shown that the harmonic function method can quickly and accurately locate active regions in EEG source reconstruction. In the future, we plan to extend the harmonic function method to 3D case and applied this method to some real EEG data. The brain's conductance variation in different brain regions also leads to additional challenges in source localization [35]. Although these tissue properties can be quantified through MRI methods, numerical methods such as finite element method will be needed to solve the inverse problems. Since the estimation of the number of dipoles relies on the calculation of the rank of the measurement matrix, which is significantly affected by the noise, we hope to find some way to solve or circumvent this problem. In addition, the situation that the number of exact dipoles is not equal to the estimated value could also be considered. Furthermore, when two dipoles get close enough, it may be better to regard them as an equivalent dipole to avoid increased error.
Acknowledgments
We thank anonymous reviewers for providing us with valuable suggestions.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad:








