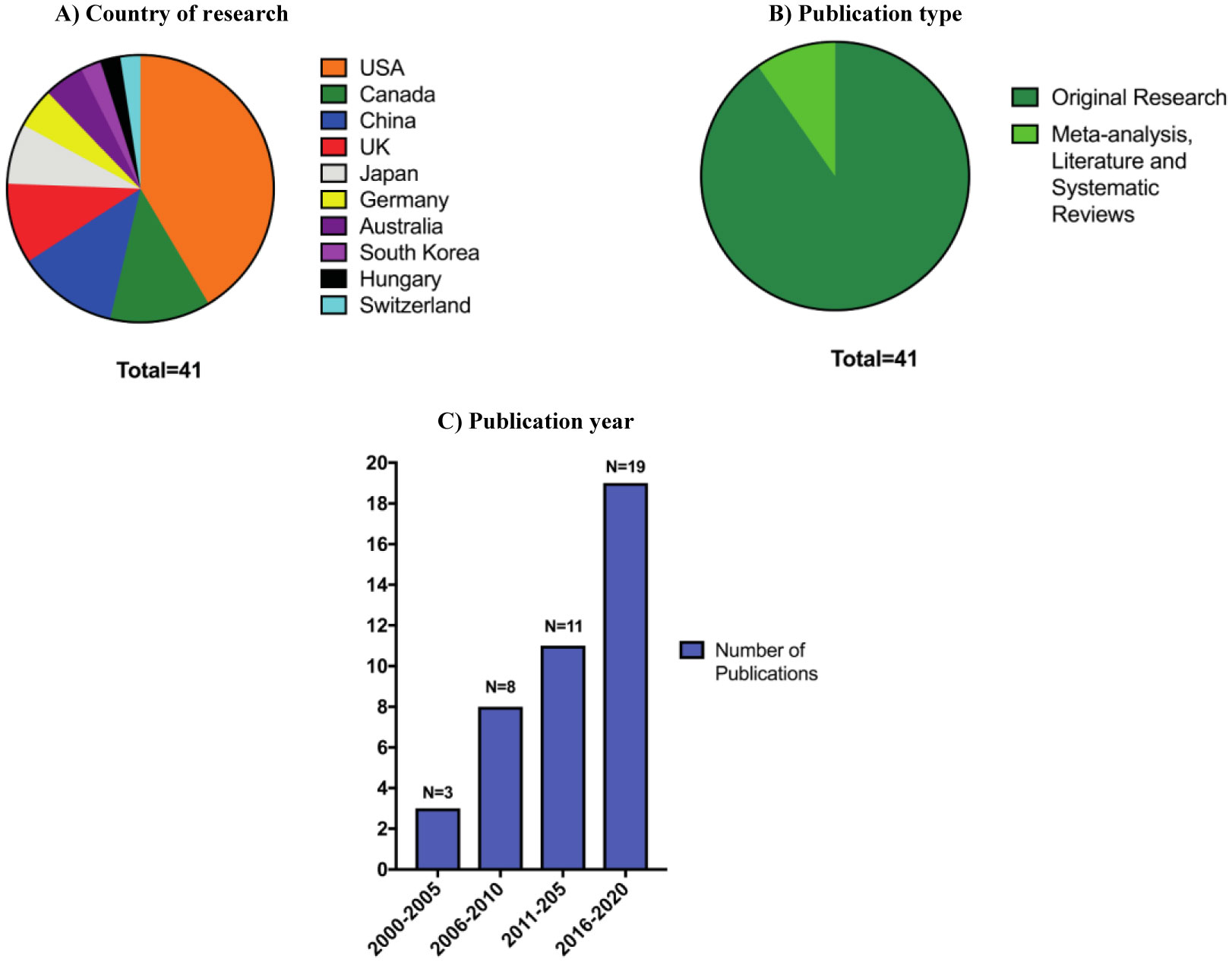
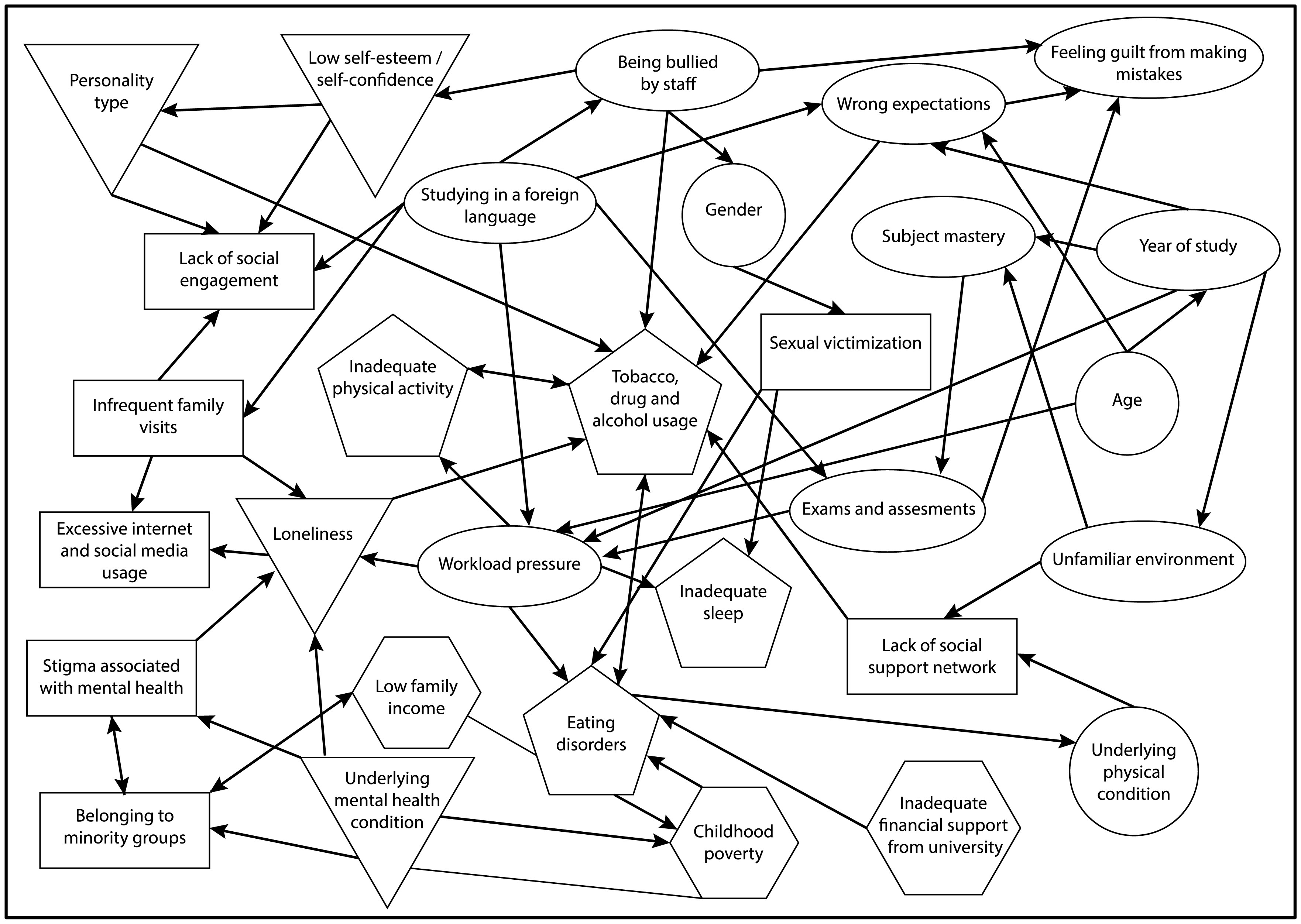
| 1.
|
Jiyoung Yoon, Eunjung Hur,
An Exploratory Study of Factors That Affect Psychological Well-Being of 4-Year College Freshmen in South Korea,
2021,
13,
2071-1050,
5230,
10.3390/su13095230
|
|
| 2.
|
Gabrijela Vrdoljak, Ana Kurtović, Ana Babić Čikeš, Marina Hirnstein,
Gender and educational stage moderate the effects of developmental assets on risk behaviours in youth,
2023,
28,
0267-3843,
10.1080/02673843.2023.2183872
|
|
| 3.
|
Andreia Vieira, Paula Sousa, Alexandra Moura, Lara Lopes, Cristiane Silva, Nicola Robinson, Jorge Machado, António Moreira,
The Effect of Auriculotherapy on Situational Anxiety Trigged by Examinations: A Randomized Pilot Trial,
2022,
10,
2227-9032,
1816,
10.3390/healthcare10101816
|
|
| 4.
|
Thanh Xuan Tran, Thi Thuy Tien Vo, Chen Ho,
From Academic Resilience to Academic Burnout among International University Students during the Post-COVID-19 New Normal: An Empirical Study in Taiwan,
2023,
13,
2076-328X,
206,
10.3390/bs13030206
|
|
| 5.
|
María Buenadicha-Mateos, María Isabel Sánchez-Hernández, Óscar Rodrigo González-López,
Analysis of the Emotional Exhaustion Derived From Techno-Stress in the Next Generation of Qualified Employees,
2022,
13,
1664-1078,
10.3389/fpsyg.2022.792606
|
|
| 6.
|
Pierpaolo Limone, Giusi Antonia Toto,
Factors That Predispose Undergraduates to Mental Issues: A Cumulative Literature Review for Future Research Perspectives,
2022,
10,
2296-2565,
10.3389/fpubh.2022.831349
|
|
| 7.
|
Britany Princella Sanchez Soncco, Víctor Santiago Viguria Condori,
Estrés académico durante la pandemia por COVID-19 en estudiantes de enfermería de una Universidad Privada, 2021.,
2022,
2,
2789-2506,
3,
10.53684/csp.v2i1.35
|
|
| 8.
|
Qinliang Ning, Junyan Shi,
Psychological adaptation level optimization to attain the goal of sustainable education,
2022,
0090-4392,
10.1002/jcop.22942
|
|
| 9.
|
Takemune Fukuie, Koshiro Inoue, Akihiko Yamaguchi,
Lifestyle Elements for Improving Mental and Physical Health in Japanese University Students: Subjective Sleep Quality is a Common Key Factor,
2023,
1559-8276,
155982762311565,
10.1177/15598276231156546
|
|
| 10.
|
Jian Zhao, Elaine Chapman, Stephen Houghton,
Key Predictive Factors in the Mental Health of Chinese University Students at Home and Abroad,
2022,
19,
1660-4601,
16103,
10.3390/ijerph192316103
|
|
| 11.
|
Shefali Liyanage, Kiran Saqib, Amber Fozia Khan, Tijhiana Rose Thobani, Wang-Choi Tang, Cameron B. Chiarot, Bara’ Abdallah AlShurman, Zahid Ahmad Butt,
Prevalence of Anxiety in University Students during the COVID-19 Pandemic: A Systematic Review,
2021,
19,
1660-4601,
62,
10.3390/ijerph19010062
|
|
| 12.
|
Beata Gavurova, Samer Khouri, Viera Ivankova, Martin Rigelsky, Tawfik Mudarri,
Internet Addiction, Symptoms of Anxiety, Depressive Symptoms, Stress Among Higher Education Students During the COVID-19 Pandemic,
2022,
10,
2296-2565,
10.3389/fpubh.2022.893845
|
|
| 13.
|
Aldana Sol Grinhauz, Sergio Héctor Azzara, Susana Azzollini,
Can Character Strengths Predict College Adjustment? A Study Carried Out in Nursing Students in the Argentine Republic,
2022,
2358-1883,
10.1007/s43076-022-00215-1
|
|
| 14.
|
Beata Gavurova, Viera Ivankova, Martin Rigelsky, Tawfik Mudarri, Michal Miovsky,
Somatic Symptoms, Anxiety, and Depression Among College Students in the Czech Republic and Slovakia: A Cross-Sectional Study,
2022,
10,
2296-2565,
10.3389/fpubh.2022.859107
|
|
| 15.
|
Keren Nitzan, Matthew O. Parker, Alon Shamir, Gang Chen, Ravid Doron,
Editorial: The burden of stress and depression – new insight into faster and efficient treatment,
2022,
16,
1662-5153,
10.3389/fnbeh.2022.998307
|
|
| 16.
|
Siew Chein Teo, Anthonysamy Lilian, Ah Choo Koo,
Examining the effects of academic motivation and online learning on Malaysian tertiary students’ psychological well-being and perceived learning performance,
2023,
10,
2331-186X,
10.1080/2331186X.2023.2186025
|
|
| 17.
|
Merita Shala, Pranvera Jetishi Çollaku,
Coping Strategies, Anxiety and Mental Health Among Female Undergraduate Students in Kosova,
2022,
8,
23940913,
19,
10.35940/ijmh.I1488.058922
|
|
| 18.
|
Shaun Liverpool, Mohammed Moinuddin, Supritha Aithal, Michael Owen, Katie Bracegirdle, Meggie Caravotta, Rachel Walker, Ciaran Murphy, Vicky Karkou, Chung-Ying Lin,
Mental health and wellbeing of further and higher education students returning to face-to-face learning after Covid-19 restrictions,
2023,
18,
1932-6203,
e0280689,
10.1371/journal.pone.0280689
|
|
| 19.
|
Saliha YURTÇİÇEK EREN, Ömer YILDIRIM, Fatih ŞAHİN,
INVESTIGATION OF DEPRESSION, ANXIETY AND STRESS LEVELS OF FRESHMAN AT VOCATIONAL SCHOOL OF HEALTH BASED ON VARIOUS VARIABLES,
2022,
6,
2619-9475,
1187,
10.47525/ulasbid.1176721
|
|
| 20.
|
Emma Davies, John Read, Mark Shevlin,
The impact of adverse childhood experiences and recent life events on anxiety and quality of life in university students,
2022,
84,
0018-1560,
211,
10.1007/s10734-021-00774-9
|
|
| 21.
|
Yu Wang, Shuo Zhang, Xiaogang Liu, Hongye Shi, Xuyang Deng,
Differences in central symptoms of anxiety and depression between college students with different academic performance: A network analysis,
2023,
14,
1664-1078,
10.3389/fpsyg.2023.1071936
|
|
| 22.
|
Nay Chi Nway, Supapak Phetrasuwan, Wimolnun Putdivarnichapong, Nopporn Vongsirimas,
Factors contributing to depressive symptoms among undergraduate nursing students: A cross-sectional study,
2023,
68,
14715953,
103587,
10.1016/j.nepr.2023.103587
|
|
| 23.
|
Mohammad Mofatteh, Mohammad Sadegh Mashayekhi, Saman Arfaie, Yimin Chen, Kasra Hendi, Angela Tian Hui Kwan, Faraz Honarvar, Arad Solgi, Xuxing Liao, Keyoumars Ashkan,
Stress, Anxiety, and Depression Associated With Awake Craniotomy: A Systematic Review,
2023,
92,
0148-396X,
225,
10.1227/neu.0000000000002224
|
|
| 24.
|
Zhaohui Su, Dean McDonnell, Junaid Ahmad, Ali Cheshmehzangi,
Disaster preparedness in healthcare professionals amid COVID-19 and beyond: A systematic review of randomized controlled trials,
2023,
14715953,
103583,
10.1016/j.nepr.2023.103583
|
|
| 25.
|
Kacper Witek, Karolina Wydra, Małgorzata Filip,
A High-Sugar Diet Consumption, Metabolism and Health Impacts with a Focus on the Development of Substance Use Disorder: A Narrative Review,
2022,
14,
2072-6643,
2940,
10.3390/nu14142940
|
|
| 26.
|
Sabine Polujanski, Thomas Rotthoff, Ulrike Nett, Ann-Kathrin Schindler,
First-year Medical Students’ Varying Vulnerability to Developing Depressive Symptoms and Its Predictors: a Latent Profile Analysis,
2023,
1042-9670,
10.1007/s40596-023-01757-x
|
|
| 27.
|
Nguyen Thi Thang, Dao Thi Dieu Linh, Ta Nhat Anh, Nguyen Thị Phuong, Nguyen Duc Giang, Nguyen Xuan Long, Dao Thi Cam Nhung, Khuong Quynh Long,
Severe Symptoms of Mental Disorders Among Students Majoring in Foreign Languages in Vietnam: A Cross-Sectional Study,
2022,
10,
2296-2565,
10.3389/fpubh.2022.855607
|
|
| 28.
|
Xuyang Deng, Tiantong Mu, Yu Wang, Yuqi Xie,
The Application of Human Figure Drawing as a Supplementary Tool for Depression Screening,
2022,
13,
1664-1078,
10.3389/fpsyg.2022.865206
|
|
| 29.
|
Susan M. McNaughton, Brenda Flood, Jane Morgan,
Enablers and barriers of first-year common semesters and semester-long courses aimed at interprofessional collaborative practice capability development: A scoping review,
2022,
1356-1820,
1,
10.1080/13561820.2022.2080192
|
|
| 30.
|
Mohammad Mofatteh,
Neurosurgery and artificial intelligence,
2021,
8,
2373-7972,
477,
10.3934/Neuroscience.2021025
|
|
| 31.
|
Daniel Mayo, Benjamin Le,
Perceived discrimination and mental health in college students: A serial indirect effects model of mentoring support and academic self-concept,
2021,
0744-8481,
1,
10.1080/07448481.2021.1924725
|
|
| 32.
|
Wei Shan Cheong, Karunanithy Degeras, Khairul Rizuan Suliman, Mohan Selvaraju, Kavitha Subramaniam,
The prevalence of depression among students in higher education institution: a repeated cross-sectional study,
2022,
21,
1746-5729,
331,
10.1108/JPMH-12-2021-0152
|
|
| 33.
|
Alireza Salmani, Jahangir Maghsoudi, Bahareh Yousefi, Seyed Reza Mousavi,
Relationship Between Stress and Anxiety Regarding COVID-19 with Some Individual-Familial Characteristics Among First-Semester Students,
2023,
12,
2322-3758,
10.5812/jjcdc-133066
|
|
| 34.
|
Hakima El Madani, Ibtissam El Harch, Nabil Tachfouti, Samira El Fakir, Rachid Aalouane, Mohamed Berraho,
Estrés psicológico y sus factores relacionados entre estudiantes de enfermería marroquíes: un estudio transversal,
2023,
11308621,
10.1016/j.enfcli.2022.11.004
|
|
| 35.
|
Irtiqa Ahmed, Cassie M. Hazell, Bethany Edwards, Cris Glazebrook, E. Bethan Davies,
A systematic review and meta-analysis of studies exploring prevalence of non-specific anxiety in undergraduate university students,
2023,
23,
1471-244X,
10.1186/s12888-023-04645-8
|
|
| 36.
|
Mohammad Mofatteh, Mohammad Sadegh Mashayekhi, Saman Arfaie, Yimin Chen, Armaan K. Malhotra, Georgios P. Skandalakis, Mohammed Ali Alvi, Fardad T. Afshari, Shakila Meshkat, Famu Lin, Ebtesam Abdulla, Ayush Anand, Xuxing Liao, Roger S. McIntyre, Carlo Santaguida, Michael H. Weber, Michael G. Fehlings,
Anxiety and Depression in Pediatric-Onset Traumatic Spinal Cord Injury: A Systematic Review,
2024,
184,
18788750,
267,
10.1016/j.wneu.2023.12.092
|
|
| 37.
|
Evans Musonda, Petro Petlovanyi, Anatolii Tsarkov, Crecious Phiri, Gabriel Mpundu, Erick Musala Kunda, Rhoda Kunda, Fabian Lungu, Nathan Kamanga,
The Psychological Impact and Associated Factors of the COVID-19 Pandemic on Health Care Providers at Chainama Psychiatry Hospital, Lusaka, Zambia,
2023,
5,
2593-8339,
11,
10.24018/ejmed.2023.5.4.1771
|
|
| 38.
|
Alessandro Carollo, Sonia De Marzo, Gianluca Esposito,
Parental care and overprotection predict worry and anxiety symptoms in emerging adult students,
2024,
248,
00016918,
104398,
10.1016/j.actpsy.2024.104398
|
|
| 39.
|
Maria Cristina Yaselga Antamba, Johanna Paola Sanmartin Sanmartin, Sophya Natalia Peñafiel Limaico, Mariam Susana Zapata Chacón, Stalin Vladimir Robles Collahuazo,
Bienestar mental y desempeño académico: una relación directa,
2024,
3,
2773-7640,
113,
10.69583/inndev.v3n1.2024.95
|
|
| 40.
|
Xinyi Wei, Huiling Zhou, Qiaoyi Zheng, Lei Ren, Niya Chen, Pengcheng Wang, Chang Liu,
Longitudinal Interactions between Problematic Internet Gaming and Symptoms of Depression Among University Students: Differentiating Anhedonia and Depressed Mood,
2025,
160,
03064603,
108184,
10.1016/j.addbeh.2024.108184
|
|
| 41.
|
Tianqing He, Wei Huang,
Automatic identification of depressive symptoms in college students: an application of deep learning-based CNN (Convolutional Neural Network),
2024,
9,
2444-8656,
10.2478/amns-2024-2435
|
|
| 42.
|
Yinghua Wang,
An interactive online educational environment to reduce anxiety, improve emotional well-being, and critical thinking for college students,
2024,
248,
00016918,
104347,
10.1016/j.actpsy.2024.104347
|
|
| 43.
|
Sumita Sharma, Lipilekha Patnaik, Trilochan Sahu,
Effect of lifestyle interventions to reduce depression, anxiety and stress among married women of reproductive age group: A non-randomised controlled trial in urban slums of Bhubaneswar,
2023,
12,
2277-9531,
10.4103/jehp.jehp_1149_22
|
|
| 44.
|
Ramin Shiraly, Ashrafalsadat Roshanfekr, Abdolrahim Asadollahi, Mark D. Griffiths,
Psychological distress, social media use, and academic performance of medical students: the mediating role of coping style,
2024,
24,
1472-6920,
10.1186/s12909-024-05988-w
|
|
| 45.
|
Edward W. Ansah, Mawuli Adabla, Norgbedzie Jerry, Eric A. Aloko, John E. Hagan,
Investigating sedentariness and health status of primary school teachers in Ghana,
2023,
23,
1472-6963,
10.1186/s12913-023-09925-3
|
|
| 46.
|
Alaa Abd-alrazaq, Mohannad Alajlani, Reham Ahmad, Rawan AlSaad, Sarah Aziz, Arfan Ahmed, Mohammed Alsahli, Rafat Damseh, Javaid Sheikh,
The Performance of Wearable AI in Detecting Stress Among Students: Systematic Review and Meta-Analysis,
2024,
26,
1438-8871,
e52622,
10.2196/52622
|
|
| 47.
|
Mugambikai Magendiran, Geeta Appannah, Nor Aishah Emi, Yit Siew Chin, Zalilah Mohd Shariff, Azriyanti Anuar Zaini, Nurainul Hana Shamsuddin, Subapriya Suppiah, Suraini Mohamad Saini, Subashini C. Thambiah, Siew Mooi Ching,
Prospective associations between an empirically derived dietary pattern and life satisfaction in Malaysian adolescents,
2024,
21,
1743-7075,
10.1186/s12986-024-00832-w
|
|
| 48.
|
He Bingge, Ooi Boon Keat,
Investigating the impact of stressors on stress level among the chinese’s students: the moderating role of chinese painting experience,
2024,
3,
2953-4860,
10.56294/sctconf2024.1242
|
|
| 49.
|
Vanessa Ferraz Leite, Moisés Kogien, Margani Cadore Weis Maia, Marina Nolli Bittencourt, Larissa de Almeida Rézio, Samira Reschetti Marcon,
Indicadores de sofrimento emocional e atenção plena em estudantes universitários: estudo transversal,
2024,
77,
1984-0446,
10.1590/0034-7167-2023-0499pt
|
|
| 50.
|
Eugene K. M. Darteh, Jerry Paul K. Ninnoni, Joshua Okyere, Florie Darteh, Johannes John-Langba, Kwamena Sekyi Dickson,
Perceived discrimination, anxiety and mood disorders among university students during the COVID-19 era: evidence from a cross-sectional survey in a Ghanaian public university,
2024,
14,
1664-1078,
10.3389/fpsyg.2023.1274585
|
|
| 51.
|
Andrea L. Tanner, Jane R. von Gaudecker, Janice M. Buelow, Ukamaka M. Oruche, Wendy R. Miller,
Adolescents' Perceptions of Functional Seizure Self-Management Strategies, Facilitators, and Barriers in the School Environment,
2023,
61,
0279-3695,
19,
10.3928/02793695-20230424-04
|
|
| 52.
|
Edwin Gustavo Estrada-Araoz, Guido Raúl Larico-Uchamaco, Jair Emerson Ferreyros-Yucra, Silvia María Revilla-Mendoza, José Octavio Ruiz-Tejada,
Assessment of predictors of satisfaction with life in pre-service teacher education students,
2024,
4,
2796-9711,
834,
10.56294/saludcyt2024834
|
|
| 53.
|
Hayder Mahjoubi, Ahlem Mtiraoui, Manel Mallouli, Chakib Zedini, Jaafar Nakhli,
Discrimination, Heterosexism and Perceived Stress Among Young LGBT Tunisians: Unveiling the Moderation Effects of Self-Esteem,
2024,
36,
1931-7611,
636,
10.1080/19317611.2024.2399119
|
|
| 54.
|
Feras Jirjees, Mohanad Odeh, Anfal Al-Haddad, Raneem Ass’ad, Yousra Hassanin, Hala Al-Obaidi, Zelal Kharaba, Yassen Alfoteih, Karem H. Alzoubi,
Test anxiety and coping strategies among university students an exploratory study in the UAE,
2024,
14,
2045-2322,
10.1038/s41598-024-59739-4
|
|
| 55.
|
Linet Imbosa Muhati-Nyakundi,
2024,
Chapter 7,
978-3-031-72519-7,
103,
10.1007/978-3-031-72520-3_7
|
|
| 56.
|
Tyler L. Renshaw, Jacqueline R. Anderson, Erik J. Reinbergs, Caleb D. Farley, Breanna King, Ashley Taylor,
Validating an Internalizing Psychopathology Screener for Use with College Students,
2024,
0748-1756,
1,
10.1080/07481756.2024.2422123
|
|
| 57.
|
Rolien Terblanche, Dorcas Khumalo,
The impact of biophilic design in university study areas on students' productivity,
2024,
2631-6862,
10.1108/ARCH-10-2023-0288
|
|
| 58.
|
Ebtihag O. Alenzi, Shahad Khalid A. Bedaiwi, Rahma Hamayun, Abdulaziz Salamah T. Alanazi, Manal S. Fawzy,
Key modifiable risk factors for self-medication among university students: An observational study,
2024,
15,
26672766,
100483,
10.1016/j.rcsop.2024.100483
|
|
| 59.
|
Raissa Dwifandra Putri, Laila Indra Lestari, Syabiilah Azzahroh,
''There is a Rainbow After The Rain'': The Role of Hope in Increasing Resilience Among Students of Universitas Negeri Malang,
2024,
2518-668X,
10.18502/kss.v9i30.17518
|
|
| 60.
|
Qi-Yue Zhang, Min-Cheol Kim, Mona Chang,
The impact of SNS and Covid-19-related stress of Chinese students in Korea based on the transaction theory of stress and coping,
2024,
10,
24058440,
e24111,
10.1016/j.heliyon.2024.e24111
|
|
| 61.
|
Bahareh Afsharnejad, Ben Milbourn, Cherylee Brown, Rhonda Clifford, Kitty‐Rose Foley, Alexandra Logan, Stephan Lund, Tawanda Machingura, Tomomi McAuliffe, Beth Mozolic‐Staunton, Nicole Sharp, Maya Hayden‐Evans, Ellie Baker Young, Melissa Black, Frank Zimmermann, Viktor Kacic, Sven Bölte, Sonya Girdler,
Understanding the utility of “Talk‐to‐Me” an online suicide prevention program for Australian university students,
2023,
53,
0363-0234,
725,
10.1111/sltb.12978
|
|
| 62.
|
Kazuto Hishida, Maya Yanase, Yu Sakagami,
Why do students who have mental health issues decide to study abroad? Qualitative research on mental health issues as a push factor for international students in Japan,
2024,
103,
01471767,
102069,
10.1016/j.ijintrel.2024.102069
|
|
| 63.
|
Stipe Vidović, Slavica Kotromanović, Zenon Pogorelić,
Depression, Anxiety, and Stress Symptoms Among Students in Croatia During the COVID-19 Pandemic: A Systematic Review,
2024,
13,
2077-0383,
6240,
10.3390/jcm13206240
|
|
| 64.
|
Mary McNaughton-Cassill, Stella Lopez, Aaron Cassill,
What If the Faculty Are Not Alright? Burnout and Compassion Fatigue in Higher Education,
2023,
55,
0009-1383,
23,
10.1080/00091383.2023.2235250
|
|
| 65.
|
Anita Maharani, Dewi Tamara,
The occupational stress and work-life balance on turnover intentions with job satisfaction as mediating,
2024,
22,
2071-078X,
10.4102/sajhrm.v22i0.2369
|
|
| 66.
|
Sarah Caimano, Albert Malkin, Patricia Monroy, Denise Horoky, Jina J. Y. Kum,
A Scoping Review of Acceptance and Commitment Therapy in Higher Education,
2024,
74,
0033-2933,
101,
10.1007/s40732-024-00586-0
|
|
| 67.
|
Soheila Zakizadeh, Alireza Heidari, Behnam Makvandi, Parviz Asgari,
Relationship of depression symptoms with emotional maturity and dysfunctional attitudes in married students: The mediating role of emotional divorce,
2024,
26,
2717-0071,
61,
10.34172/jsums.876
|
|
| 68.
|
Nur Dini Kamilia Norazizi, Muhammad Asyraf Che Amat, Nor Hafizah Mohammad Hanafi, Firman Firman, Syahrul Nizam Salam,
Influence of Depression and Loneliness on Suicidal Behaviour Among Public University Students in Malaysia,
2024,
32,
2231-8534,
55,
10.47836/pjssh.32.S3.04
|
|
| 69.
|
Fayyaz Qureshi, Sarwar Khawaja, Katarina Sokić, Mirjana Pejić Bach, Maja Meško,
Exploring Intrinsic Motivation and Mental Well-Being in Private Higher Educational Systems: A Cross-Sectional Study,
2024,
12,
2079-8954,
281,
10.3390/systems12080281
|
|
| 70.
|
Nik Daliana Nik Farid, Nuraini Aziz, Muhammad Yazid Jalaludin, Hazreen Abdul Majid,
A Longitudinal Study of Psychological Distress Among Youth in Peninsular Malaysia and Associated Factors,
2024,
36,
1010-5395,
628,
10.1177/10105395241273106
|
|
| 71.
|
Angela Bielefeldt,
2024,
Case Study: Civil Engineering Student Mental Health and Watching Football?,
10.18260/1-2--48446
|
|
| 72.
|
Hakima El Madani, Ibtissam El Harch, Nabil Tachfouti, Samira El Fakir, Rachid Aalouane, Mohamed Berraho,
Psychological stress and its related factors among Moroccan nursing students: A cross-sectional study,
2023,
33,
24451479,
205,
10.1016/j.enfcle.2023.02.001
|
|
| 73.
|
Shuaib Abolakale Muhammed, Tosin Emmanuel Akinduyo, Habeebat Olaitan Adebayo, Nancy Phyllis Makhosazane Mabaso,
Help-Seeking Attitude of Nigerian Undergraduates Toward Mental Health Issues,
2024,
6,
2656-1050,
10.51214/002024061014000
|
|
| 74.
|
Lu Li, Xin Ma, Xiangping Liu, Zijian Yao, Linpu Feng, Long Huang,
The association between helicopter parenting and college freshmen’s depression: Insights from a cross-sectional study,
2024,
43,
1046-1310,
19446,
10.1007/s12144-024-05770-7
|
|
| 75.
|
Amani Safwat ElBarazi, Farah Mohamed, Maram Mabrok, Ahmed Adel, Ahmed Abouelkheir, Rana Ayman, Maram Mustfa, Mohamed Elmosallamy, Raneem Yasser, Fatima Mohamed,
Efficiency of assertiveness training on the stress, anxiety, and depression levels of college students (Randomized control trial),
2024,
13,
2277-9531,
10.4103/jehp.jehp_264_23
|
|
| 76.
|
Shea E. Ferguson, Jackie A. Nelson, Melissa C. Duffy,
Stress and Mental Health: Social-Emotional Protective Factors by Gender and First-Generation College Student Status,
2024,
2836-7138,
1,
10.1080/28367138.2024.2393394
|
|
| 77.
|
Eda Açıkgöz Atay, Nermin Olgun, Zehra Boztepe,
Determining the Level of Depression Stigma of University Students: A Descriptive Study,
2024,
3,
2822-6445,
35,
10.59312/ebshealth.1462815
|
|
| 78.
|
Shkurti Enkelejda, Shtiza Diamant,
Health Behaviors of Albanian Students at the University of Medicine During the Coronavirus Disease 2019 Pandemic,
2023,
24,
1735-1391,
10.5812/semj-137263
|
|
| 79.
|
Xiaobing Xian, Tengfei Niu, Yu Zhang, Xilin Zhou, Xinxin Wang, Xin Du, Linhan Qu, Binyi Mao, Ying He, Xiyu Chen, Mengliang Ye,
The relationship between appearance anxiety and depression among students in a medical university in China: a serial multiple mediation model,
2024,
12,
2167-8359,
e17090,
10.7717/peerj.17090
|
|
| 80.
|
Elisa Delvecchio, Giulia Cenci, Adriana Lis, Jian-Bin Li, Alexander T. Vazsonyi, Sofya Nartova-Bochaver, Magdalena Zadworna, Claudia Mazzeschi,
Anxiety and Stress among American, Chinese, Italian, and Russian Emerging Adults: Does Uncertainty Avoidance Matter?,
2023,
11,
2227-9032,
3101,
10.3390/healthcare11243101
|
|
| 81.
|
Asma Alshanqiti, Ohood Alharbi, Dana Ismaeel, Leen Abuanq,
Social Media Usage and Academic Performance Among Medical Students in Medina, Saudi Arabia,
2023,
Volume 14,
1179-7258,
1401,
10.2147/AMEP.S434150
|
|
| 82.
|
Guwani Liyanage, D. P. R. W. Rajapakshe, D. R. Wijayaratna, J. A. I. P. Jayakody, K. A. M. C. Gunaratne, A. M. A. D. K. Alagiyawanna, Md Nazmul Huda,
Psychological distress and sleep quality among Sri Lankan medical students during an economic crisis,
2024,
19,
1932-6203,
e0304338,
10.1371/journal.pone.0304338
|
|
| 83.
|
Mohammad Mofatteh, Mohammad Sadegh Mashayekhi, Saman Arfaie, Yimin Chen, Armaan K Malhotra, Mohammed Ali Alvi, Nicholas Sader, Violet Antonick, Mostafa Fatehi Hassanabad, Alireza Mansouri, Sunit Das, Xuxing Liao, Roger S McIntyre, Rolando Del Maestro, Gustavo Turecki, Aaron A Cohen-Gadol, Gelareh Zadeh, Keyoumars Ashkan,
Suicidal ideation and attempts in brain tumor patients and survivors: A systematic review,
2023,
5,
2632-2498,
10.1093/noajnl/vdad058
|
|
| 84.
|
Malakeh Z. Malak, Ahmed.H. Shuhaiber, Ahmed Alsswey, Anwar Tarawneh,
Social support as the mediator for the relationship between internet gaming disorder and psychological problems among university students,
2023,
164,
00223956,
243,
10.1016/j.jpsychires.2023.06.007
|
|
| 85.
|
Lizy Sonia Benjamin, Kawther Eltayeb Ahmed Mohammed,
Test anxiety and academic performance: A correlational study among nursing college students,
2023,
2,
2827-8100,
173,
10.55048/jpns80
|
|
| 86.
|
Alfredo Daza, Nemias Saboya, Jorge Isaac Necochea-Chamorro, Karoline Zavaleta Ramos, Yesenia del Rosario Vásquez Valencia,
Systematic review of machine learning techniques to predict anxiety and stress in college students,
2023,
43,
23529148,
101391,
10.1016/j.imu.2023.101391
|
|
| 87.
|
Yuenan Jin, Zhaowu Yu, Gaoyuan Yang, Xihan Yao, Mingming Hu, R.P. Remme, P.M. van Bodegom, Joeri Morpurgo, Yunfeng Huang, Jingyi Wang, Shenghui Cui,
Quantifying physiological health efficiency and benefit threshold of greenspace exposure in typical urban landscapes,
2024,
362,
02697491,
124726,
10.1016/j.envpol.2024.124726
|
|
| 88.
|
Hina Illyas, Rehana Mushtaq, Sadia Saleem,
Eating Problems in Young Adults: The Role of Unbalanced Family Cohesion and Difficulties in Emotion Regulation,
2024,
1066-4807,
10.1177/10664807241289144
|
|
| 89.
|
Folake Olubukola Asejeje, Olalekan Bukunmi Ogunro,
Deciphering the mechanisms, biochemistry, physiology, and social habits in the process of aging,
2024,
1,
29503078,
100003,
10.1016/j.aggp.2023.100003
|
|
| 90.
|
Othman A. Alfuqaha, Uday M. Al-masarwah, Randa I. Farah, Jehad A. Yasin, Leen A. Alkuttob, Nour I. Muslieh, Mouath Hammouri, Afnan E. Jawabreh, Duaa A. Aladwan, Randah O. Barakat, Nida’a H. Alshubbak,
The Impact of Turkey and Syria Earthquakes on University Students: Posttraumatic Stress Disorder Symptoms, Meaning in Life, and Social Support,
2023,
13,
2076-328X,
587,
10.3390/bs13070587
|
|
| 91.
|
Ofra Walter, Jonathan Kasler, Surekha Routray,
2024,
Chapter 4,
978-981-97-5048-1,
55,
10.1007/978-981-97-5049-8_4
|
|
| 92.
|
Jimmy Nelson Paricahua-Peralta, Edwin Gustavo Estrada-Araoz, Lesy Berly León-Hancco, Basilide Avilés-Puma, Cesar Elias Roque-Guizada, Percy Amilcar Zevallos-Pollito, Libertad Velasquez-Giersch, Alhi Jordan Herrera-Osorio, Dany Dorian Isuiza-Perez,
Assessment the mental health of university students in the Peruvian Amazon: A cross-sectional study,
2024,
4,
2796-9711,
879,
10.56294/saludcyt2024879
|
|
| 93.
|
Niliarys Sifre, Rianna Deringer, Lukkamol Prapkree, Cristina Palacios,
Disordered Eating Attitudes and Their Association with Age, BMI, Stress, and Diet in College Students,
2024,
21,
1660-4601,
766,
10.3390/ijerph21060766
|
|
| 94.
|
Fareeda Abo-Rass, Anwar Khatib, Sarah Abu-Kaf, Ora Nakash,
Association between mental health literacy and formal help-seeking behaviors among students from the Palestinian-Arab minority in Israel,
2024,
53,
08839417,
158,
10.1016/j.apnu.2024.10.018
|
|
| 95.
|
Dauda Salihu, Muhammad Chutiyami, Umar Muhammad Bello, Surajo Kamilu Sulaiman, Kabiru Kasamu Dawa, Annie Hepworth, Khadijat Kofoworola Adeleye, Mowanes Majed Alruwaili,
A meta-review of systematic reviews on the effectiveness of music therapy on depression, stress, anxiety and cognitive function in adult's with dementia or cognitive impairment,
2024,
60,
01974572,
348,
10.1016/j.gerinurse.2024.09.014
|
|
| 96.
|
Neda Mahdieh, Farzaneh Hooman, Saeed Bakhtiarpour, Parviz Asgari,
The Mediatory Role of Stress in the Structural Relationship of Mindfulness and Self-construal with the Academic Performance of Medical Students,
2023,
In Press,
1735-3998,
10.5812/jme-138327
|
|
| 97.
|
Dominik Havsteen-Franklin, Jasmine Cooper, Shafeena Anas,
Developing a logic model to support creative education and wellbeing in higher education,
2023,
10,
2331-186X,
10.1080/2331186X.2023.2214877
|
|
| 98.
|
Yu Jin, Shicun Xu, Zhixian Shao, Xianyu Luo, Yinzhe Wang, Yi Yu, Yuanyuan Wang,
Discovery of depression-associated factors among childhood trauma victims from a large sample size: Using machine learning and network analysis,
2024,
345,
01650327,
300,
10.1016/j.jad.2023.10.101
|
|
| 99.
|
А. V. Petrov, М. М. Petrova, D. S. Kaskaeva, N. А. Shnayder,
SCREENING OF ANXIETY AND DEPRESSIVE DISORDERS IN MEDICAL STUDENTS,
2024,
1998-6173,
81,
10.52485/19986173_2024_1_81
|
|
| 100.
|
Ayşin Çetinkaya Büyükbodur, Ayşegül Kılıçlı, Murat Genç, Ümmet Erkan,
Capacity to Striving for Goals and Coping with Earthquake Stress in University Students After the Kahramanmaraş Earthquakes,
2024,
21,
2791-9862,
300,
10.26466/opusjsr.1529740
|
|
| 101.
|
Marouf Noorzai, Shafiq Ahmad Joya, Rovaisa Mohseni, Aziz-ur-Rahman Niazi,
Staying Active, Minding Health: Does Exercise Influence Depression and Anxiety in Herat University's Education Students?,
2024,
03,
2957997X,
47,
10.70436/nuijb.v3i02.322
|
|
| 102.
|
Dean M. Rockwell, Sasha Y. Kimel,
A systematic review of first-generation college students’ mental health,
2023,
0744-8481,
1,
10.1080/07448481.2023.2225633
|
|
| 103.
|
Mohai Menul Biswas, Kailas Chandra Das, Illias Sheikh,
Psychological implications of unemployment among higher educated migrant youth in Kolkata City, India,
2024,
14,
2045-2322,
10.1038/s41598-024-60958-y
|
|
| 104.
|
Junqiang Dong, Jianyong Chen, Yong Li, Xiaofang Huang, Xing Rong, Liang Chen,
Relationship Between Freshmen’s Psychological Health and Family Economic Status in Chinese Universities: A Latent Profile Analysis,
2023,
Volume 16,
1179-1578,
3489,
10.2147/PRBM.S424798
|
|
| 105.
|
Kate Molloy, Clare Thomson,
2023,
18,
978-1-80511-127-6,
397,
10.11647/obp.0363.17
|
|
| 106.
|
Ghazaleh Bahrami, Noushin Mohammadifard, Fahimeh Haghighatdoost, Ali Emamjomeh, Farid Najafi, Hossein Farshidi, Masoud Lotfizadeh, Tooba Kazemi, Sania Shafiei, Hamidreza Roohafza, Mohammadreza Sabri, Nizal Sarrafzadegan,
The association between soft drinks consumption and risk of mental disorders among Iranian adults: The LIPOKAP study,
2024,
363,
01650327,
8,
10.1016/j.jad.2024.07.033
|
|
| 107.
|
Hacer Yalniz Dilcen, Yeliz Çakır Koçak, Güleser Ada, Feyza Demir Bozkurt, Hanifi Dülger,
Determinants of Psychosocial Health Status in Pregnant and Postpartum Women Experiencing Earthquake in Turkey,
2024,
18,
1935-7893,
10.1017/dmp.2024.11
|
|
| 108.
|
Ninuk Hariyani, Tantry Maulina, Rahul Nair,
The Association between Dental Pain and Psychological Symptoms: Evidence from a Population-Based Study in Indonesia,
2024,
18,
1305-7456,
563,
10.1055/s-0043-1774320
|
|
| 109.
|
Takemune Fukuie, Koshiro Inoue, Akihiko Yamaguchi,
Lifestyle and well-being of university students in Japan: a cross-sectional study,
2024,
1,
2997-9196,
10.20935/MHealthWellB7327
|
|
| 110.
|
Tyler Prochnow, Jeong-Hui Park, Megan S. Patterson,
Intramural sports social networks and implications for college student physical activity, sense of community, and retention,
2023,
0744-8481,
1,
10.1080/07448481.2023.2239367
|
|
| 111.
|
Neda Shooshtari, Rezvan Homaei, Fariba Hafezi,
Roles of Family Functioning and Cognitive Failure in Predicting High-risk Behaviors Among Students with a History of Learning Disability,
2024,
12,
2252-0465,
10.5812/ermsj-145881
|
|
| 112.
|
Ian Marie Atasha Serrano, Anne Marie Nicole Cuyugan, Krischel Cruz, Jan Mae Ann Mahusay, Rowalt Alibudbud,
Sociodemographic characteristics, social support, and family history as factors of depression, anxiety, and stress among young adult senior high school students in metro Manila, Philippines, during the COVID-19 pandemic,
2023,
14,
1664-0640,
10.3389/fpsyt.2023.1225035
|
|
| 113.
|
Meghan Owenz, Laura Cruz,
Addressing Student Test Anxiety through Universal Design for Learning Alternative Assessments,
2023,
8756-7555,
1,
10.1080/87567555.2023.2245945
|
|
| 114.
|
Sarah J. Chavez, Nicole A. Hall, Mary M. Tomkins, Angelo M. DiBello, Clayton Neighbors, Kate B. Carey,
Perceived belonging on campus predicts depression among heavy drinkers: A test of three moderators,
2023,
0744-8481,
1,
10.1080/07448481.2023.2266037
|
|
| 115.
|
Mario Marendić, Diana Aranza, Ivan Aranza, Silvija Vladislavić, Ivana Kolčić,
Differences between Health and Non-Health Science Students in Lifestyle Habits, Perceived Stress and Psychological Well-Being: A Cross-Sectional Study,
2024,
16,
2072-6643,
620,
10.3390/nu16050620
|
|
| 116.
|
Mohammad Hassan Novin, Saba Shokri, Fatemeh Eslamdoust-Siahestalkhi, Ali Pourramzani,
Frequency of Smoking, Alcohol Consumption, and Substance Use in Relation to General Health Indicators in Guilan University of Medical Sciences,
2023,
15,
2008-4633,
266,
10.34172/ahj.2023.1432
|
|
| 117.
|
Samer O. Alalalmeh, Omar E. Hegazi, Moyad Shahwan, Nageeb Hassan, Ghala Rashid Humaid Alnuaimi, Raghd F. Alaila, Ammar Jairoun, Yomna Tariq Hamdi, Mina Thamer Abdullah, Roaa Mohammed Abdullah, Samer H. Zyoud,
Assessing mental health among students in the UAE: A cross-sectional study utilizing the DASS-21 scale,
2024,
32,
13190164,
101987,
10.1016/j.jsps.2024.101987
|
|
| 118.
|
Sandra Constanza Cañón Buitrago, Juan Manuel Pérez Agudelo, Mariela Narváez Marín, Olga Lucia Montoya Hurtado, Gloria Isabel Bermúdez Jaimes,
Predictive model of suicide risk in Colombian university students: quantitative analysis of associated factors,
2024,
15,
1664-0640,
10.3389/fpsyt.2024.1291299
|
|
| 119.
|
Xinkai Zhang, Zhaobo Dou, Fengying Yang, Lin Luo, Jie Yang,
Exploring the relationship between sleep patterns and depression among Chinese middle school students: a focus on sleep quality vs. sleep duration,
2024,
12,
2296-2565,
10.3389/fpubh.2024.1383884
|
|
| 120.
|
Ailin Anto, Rafey Omar Asif, Arunima Basu, Dylan Kanapathipillai, Haadi Salam, Rania Selim, Jahed Zaman, Andreas Benedikt Eisingerich,
Exploring the Impact of Social Media on Anxiety Among University Students in the United Kingdom: Qualitative Study,
2023,
7,
2561-326X,
e43037,
10.2196/43037
|
|
| 121.
|
Maureen Tang, Tamara Galoyan, Shannon Capps,
2023,
Board 34: Work in Progress: Simple, Scalable Interventions to Address Academic and Mental-Health Barriers in Engineering Undergraduates,
10.18260/1-2--42956
|
|
| 122.
|
Vinciya Pandian, Manoranjitham Sathiyaseelan, Angela Chang Chiu, Vinitha Ravindran, Karan Kverno, Sheela Durai, Patty Wilson, Alice Sony, Tamar Rodney, Katherine Rediger, Ida Nirmal, Bala Seetharaman, Natalie G. Regier, Helen Sujatha Charles, Maria Docal, Jason Farley, Vathsala Sadan, Nancy R. Reynolds,
Leveraging a Global Partnership to Address COVID‐19‐Related Mental Health Challenges,
2024,
1351-0126,
10.1111/jpm.13115
|
|
| 123.
|
Nizamettin Burak Avcı, Betül Çiçek Çınar,
The correlation between self-reported sleep quality, anxiety levels, and balance confidence among university students,
2024,
54,
0081-2463,
210,
10.1177/00812463241241309
|
|
| 124.
|
Jiao Chen,
2024,
Student Mental Health Risk Prediction Based on Apriori Algorithm in the Context of Big Data,
979-8-3503-9563-1,
615,
10.1109/EDPEE61724.2024.00120
|
|
| 125.
|
Nkopodi Nkopodi, Maria Jakovljevic, Patricia Photo,
Criteria for enhancing student wellbeing in STEM classrooms: ICT and indigenous knowledge in South African higher education,
2024,
3,
2731-5525,
10.1007/s44217-024-00251-2
|
|
| 126.
|
Ana María González-Martín, Agustín Aibar-Almazán, Yulieth Rivas-Campo, Yolanda Castellote-Caballero, María del Carmen Carcelén-Fraile,
Mindfulness to improve the mental health of university students. A systematic review and meta-analysis,
2023,
11,
2296-2565,
10.3389/fpubh.2023.1284632
|
|
| 127.
|
Bistara Nobel, Susanti Susanti, Satriya Pranata, Mustamu Cherry,
The acceptance and commitment therapy (ACT) reduce stress in patients with type 2 diabetes mellitus,
2023,
54,
2490-3329,
329,
10.5937/scriptamed54-45794
|
|
| 128.
|
Yusen Zhai, Yixin Zhang, Zhicong Chu, Baocheng Geng, Mahmood Almaawali, Russell Fulmer, Yung‐Wei Dennis Lin, Zhaopu Xu, Aubrey D. Daniels, Yanhong Liu, Qu Chen, Xue Du,
Machine learning predictive models to guide prevention and intervention allocation for anxiety and depressive disorders among college students,
2024,
0748-9633,
10.1002/jcad.12543
|
|
| 129.
|
Jacqueline S. Stephen,
2024,
Chapter 6,
978-3-031-54438-5,
77,
10.1007/978-3-031-54439-2_6
|
|
| 130.
|
Jiaqi Li, Yu Jin, Shicun Xu, Xianyu Luo, Amanda Wilson, Hui Li, Xiaofeng Wang, Xi Sun, Yuanyuan Wang,
Anxiety and Depression Symptoms among Youth Survivors of Childhood Sexual Abuse: A Network Analysis,
2023,
11,
2050-7283,
10.1186/s40359-023-01275-3
|
|
| 131.
|
Emad Shdaifat, Amira Alshowkan, Friyal Alqahtani, Hoda Alebiary, Mona AL-Qahtani, Nagla Alsaleh, Neama Kamel,
Flourishing levels among health and non-health profession students in Saudi Arabian colleges,
2024,
15,
1664-0640,
10.3389/fpsyt.2024.1469845
|
|
| 132.
|
Rаul-Ioаn Muntean, Valentina Stefanica, Daniel Rosu, Alexandru Boncu, Iulian Stoian, Mihaela Oravitan,
Examining the interplay between mental health indicators and quality of life measures among first-year law students: a cross-sectional study,
2024,
12,
2167-8359,
e18245,
10.7717/peerj.18245
|
|
| 133.
|
Pamela Atieno Ooko,
2023,
chapter 3,
9798369307083,
37,
10.4018/979-8-3693-0708-3.ch003
|
|
| 134.
|
Firras Garada, Holly Shan,
2023,
Chapter 36,
978-3-031-27724-5,
587,
10.1007/978-3-031-27725-2_36
|
|
| 135.
|
Min-Ning Yu, Yu-Ning Chang, Ren-Hau Li,
Relationships between Big Five Personality Traits and Psychological Well-Being: A Mediation Analysis of Social Support for University Students,
2024,
14,
2227-7102,
1050,
10.3390/educsci14101050
|
|
| 136.
|
Linus P. Rweyemamu, Christopher H. Mbotwa, Joseph I. Massawe, Rosemary P. Mramba,
Mental distress and associated factors among undergraduate students: evidence from a cross-sectional study at the University of Dodoma, Tanzania,
2024,
4,
2731-4383,
10.1007/s44192-024-00098-x
|
|
| 137.
|
Yun-Ju Lai, En-Yun Tsai, Ploypapus Jarustanaput, Yi-Syuan Wu, Yi-Hau Chen, Samantha E. O’Leary, Sumatchara Manachevakul, Yuan Zhang, Jiabin Shen, Yan Wang,
Optimism and mental health in college students: the mediating role of sleep quality and stress,
2024,
15,
1664-1078,
10.3389/fpsyg.2024.1403146
|
|
| 138.
|
Bala Ganesh Pichamuthu, Kalpana Kosalram, Sathya Thennavan, Sharmila Govardhanan,
Assessment of Depression Among Students Studying in Higher Educational Institutions Using PHQ 9 in Tamil Nadu—A Cross-sectional Study,
2024,
2197-3792,
10.1007/s40615-024-02221-8
|
|
| 139.
|
Shelley Viskovich, James A. Fowler, Kenneth I. Pakenham,
Fluctuations in mental health in students accessing a university-wide online mental health promotion intervention before and during the COVID-19 pandemic,
2023,
58,
0005-0067,
373,
10.1080/00050067.2023.2212150
|
|
| 140.
|
Rhenan D. Estacio, Marietta D. Subida, Ma. Victoria Bagaforo, Ma. Cristy Abuyuan, Naomi Yvonne Dionisio, Shupiwe Chisomo Letso,
The mental health of college students in the transition of post-pandemic era in Pampanga, Philippines: an input for psychoeducation programme,
2023,
14,
2150-7686,
86,
10.1080/21507686.2023.2281430
|
|
| 141.
|
Papassara Changklang, Onggan Ranteh,
The effects of cognitive behavioural therapy on depression, anxiety, stress, and self-esteem in public health students, Thailand,
2023,
12,
2277-9531,
10.4103/jehp.jehp_1274_22
|
|
| 142.
|
Michelle Andriacchi, Casey Hopper, Anne Stein, Rachel Nye, Katie Taylor,
Animal-Assisted Interventions on a College Campus to Improve Wellness: Adventures With the Northern Michigan University Wildpups,
2023,
62,
0148-4834,
631,
10.3928/01484834-20230906-05
|
|
| 143.
|
Daniel Opotamutale Opotamutale, Fillemon Shekutamba Albanus,
2023,
chapter 5,
9798369328330,
66,
10.4018/979-8-3693-2833-0.ch005
|
|
| 144.
|
Francisca Beroíza-Valenzuela,
The challenges of mental health in Chilean university students,
2024,
12,
2296-2565,
10.3389/fpubh.2024.1297402
|
|
| 145.
|
Hussein Alhawari, Sameeha Alshelleh, Osama Alzoubi, Asim Khanfar, Reem Akiely, Bayan Abdallah, Nada Hajjaj, Saja Alkhalaileh, Yousef Khader,
Comparison of Baseline and Test Day Cardiovascular Parameters, Anxiety Scores and Coffee Consumption Among Medical Students Undergoing Objective Structured Clinical Examinations in Jordan,
2023,
Volume 16,
1178-7074,
4249,
10.2147/IJGM.S432157
|
|
| 146.
|
Rafi Alnjadat, Mohammad Etoom,
Factors Affecting Nursing and Midwifery Students Knowledge Regarding Preoperative Nursing Care,
2024,
Volume 15,
1179-7258,
161,
10.2147/AMEP.S441145
|
|
| 147.
|
Vanessa Ferraz Leite, Moisés Kogien, Margani Cadore Weis Maia, Marina Nolli Bittencourt, Larissa de Almeida Rézio, Samira Reschetti Marcon,
Indicators of emotional distress and mindfulness in undergraduate students: a cross-sectional study,
2024,
77,
1984-0446,
10.1590/0034-7167-2023-0499
|
|
| 148.
|
Muhammad Ikhwan Mud Shukri, Halimatus Sakdiah Minhat, Norliza Ahmad, Fatin Ismail, Chandramalar Kanthavelu, Dina Nurfarahin, Wan Syahirah Wan Ghazali, Nor Afiah Mohd Zulkefli, Syed Far Abid Hossain,
Prevalence and factors associated with depression, anxiety and stress in Malaysia during COVID-19 pandemic: A systematic review,
2023,
18,
1932-6203,
e0288618,
10.1371/journal.pone.0288618
|
|
| 149.
|
Fatemeh Kokabisaghi, Mina Sadat Mousavi Emadi, Amirmohammad Tajik, Farshad Sharifi, Elaheh Houshmand, Mehdi Varmaghani,
The prevalence and causes of self‐medication among medical university students in Iran during COVID‐19 outbreak and its implications for public health and health systems: A cross‐sectional study,
2024,
7,
2398-8835,
10.1002/hsr2.1983
|
|
| 150.
|
Bruno Luis Schaab, Lara Finkler Cunha, Desiree Cordoni Silveira, Pamela Carvalho da Silva, Kellen Greff Ballejos, Gabriela Bertoletti Diaz, Vanessa Kaiser, Prisla Ücker Calvetti, Sílvio César Cazella, Helena Maria Tannhauser Barros, Caroline Tozzi Reppold,
A pilot study of a new app based on self-compassion for the prevention and promotion of mental health among Brazilian college students,
2024,
15,
1664-1078,
10.3389/fpsyg.2024.1414948
|
|
| 151.
|
Victoria E. Rodriguez, Laura E. Enriquez, Annie Ro, Cecilia Ayón,
Immigration-Related Discrimination and Mental Health among Latino Undocumented Students and U.S. Citizen Students with Undocumented Parents: A Mixed-Methods Investigation,
2023,
64,
0022-1465,
593,
10.1177/00221465231168912
|
|
| 152.
|
Ece Atik, Johannes Stricker, Magnus Schückes, Andre Pittig,
Efficacy of a Brief Blended Cognitive Behavioral Therapy Program for the Treatment of Depression and Anxiety in University Students: Uncontrolled Intervention Study,
2023,
10,
2368-7959,
e44742,
10.2196/44742
|
|
| 153.
|
Tina M. Olsson, Malin Broberg, Sylva Frisk, Arne F. Wackenhut, David Kjellin, Sofia Gullstrand, Stephanie Rost, Therése Skoog,
Health‐Promoting Learning Environments in Higher Education: A Scoping Review of Structural Interventions to Protect Student Mental Health,
2024,
0141-8211,
10.1111/ejed.12772
|
|
| 154.
|
Peter J. O. Aloka,
Social comparison and overall adjustment among freshmen in one public university,
2024,
2504-5571,
46,
10.21303/2504-5571.2024.003359
|
|
| 155.
|
Haishi Yu, Juan Yu, Yang Wang,
2023,
Chapter 30,
978-2-38476-067-1,
224,
10.2991/978-2-38476-068-8_30
|
|
| 156.
|
Enrique Macías Arias, Jorge Parraga-Alava, David Zambrano Montenegro,
2024,
Stress Detection among Higher Education Students: A Comprehensive Systematic Review of Machine Learning Approaches,
979-8-3503-6553-5,
1,
10.1109/ICEDEG61611.2024.10702055
|
|
| 157.
|
Claudia Lombardo, Emanuele Capasso, Giuseppe Li Rosi, Monica Salerno, Mario Chisari, Massimiliano Esposito, Lucio Di Mauro, Francesco Sessa,
Burnout and Stress in Forensic Science Jobs: A Systematic Review,
2024,
12,
2227-9032,
2032,
10.3390/healthcare12202032
|
|
| 158.
|
Aditya Sharma, Md. Aftab Alam, Awaneet Kaur, Shaweta Sharma, Shikha Yadav,
Psychopharmacological Treatment of Depression and Anxiety and
their Different Drug Delivery Targets,
2024,
20,
26660822,
297,
10.2174/2666082219666230822140902
|
|
| 159.
|
Wura Jacobs, Weisiyu Qin, Tennisha N. Riley, Erik S. Parker, Arthur H. Owora, Adam Leventhal,
Race/ethnic differences in the association of anxiety, depression, and discrimination with subsequent nicotine and cannabis use among young adults: A prospective longitudinal study,
2024,
153,
03064603,
107979,
10.1016/j.addbeh.2024.107979
|
|
| 160.
|
Hatice Deveci Şirin, Rana Şen Doğan, Hüseyin Serçe, Eda Bayrakcı, Selahattin Alan,
A Cross-Sectional and Longitudinal Investigation of Hopelessness Among University Students in the Aftermath of the COVID-19 Pandemic,
2024,
14,
2158-2440,
10.1177/21582440241245273
|
|
| 161.
|
XiaoJie Dai, WeiJun Yu,
Students’ physical activity and psychological state: psychological approaches with virtual technologies,
2024,
1046-1310,
10.1007/s12144-024-07025-x
|
|
| 162.
|
Natali Barragan, Amanda Batista, Deborah Hall, Yasin Silva,
Social Identity, Social Media Use, and Mental Health in Adults: Investigating the Mediating Role of Cyberbullying Experiences and the Moderating Effects of Gender and Age,
2024,
Volume 17,
1179-1578,
4009,
10.2147/PRBM.S466965
|
|
| 163.
|
Mohammad Mofatteh,
Examining the association between traumatic brain injury and headache,
2021,
20,
0219-6352,
10.31083/j.jin2004109
|
|
| 164.
|
Renjian Kan, Haibo Xu,
Impact of Learning Adjustment Dimensions on Depressive Symptoms Among Chinese Nursing Freshmen: The Mediating Role of Psychological Capital,
2024,
Volume 17,
1179-1578,
4063,
10.2147/PRBM.S494784
|
|
| 165.
|
Manuel Gonçalves-Pereira,
Mental Health as a Polysemic Construct? Revisiting the Debate about University Students’ Unmet Needs,
2024,
2504-3137,
1,
10.1159/000542629
|
|
| 166.
|
Kelsey Van, Sana Tasawar, Elaina B. K. Brendel, Camille Law, Anisha Mahajan, Carissa Brownell‐Riddell, Natalia Diamond, Kerry Ritchie, Jennifer M. Monk,
Using a ‘Students as Partners’ model to develop an authentic assessment promoting employability skills in undergraduate life science education,
2024,
2211-5463,
10.1002/2211-5463.13941
|
|
| 167.
|
Alli Gillespie, Zahyyeh Abu-Rubieh, Lily Coll, Manar Matti, Carine Allaf, Ilana Seff, Lindsay Stark,
“
Living their best life
”: PhotoVoice insights on well-being, inclusion, and access to public spaces among adolescent refugee girls in urban resettlement
,
2025,
20,
1748-2631,
10.1080/17482631.2024.2431183
|
|
| 168.
|
Mohammad Mofatteh,
In Reply to the Letter to the Editor Regarding “Anxiety and Depression in Pediatric-Onset Traumatic Spinal Cord Injury: A Systematic Review”,
2024,
191,
18788750,
359,
10.1016/j.wneu.2024.08.110
|
|
| 169.
|
S Subatraa Subramaniam, , Asong Joseph, Mimi Fitirana, Walton Wider, Surianti Lajuma,
The Break-up Experience of Romantic Relationship and Post-traumatic Growth Among Vicenarian Adults,
2024,
32,
2231-8534,
1247,
10.47836/pjssh.32.4.01
|
|
| 170.
|
Ali Aldirawi, Fadwa Alhalaiqa, Abdallah Alwawi, Samer Abuzerr,
Psychological stress among hypertensive male patients in Jordan: prevalence and associated factors,
2024,
24,
1471-2458,
10.1186/s12889-024-20733-0
|
|
| 171.
|
Holly Coates McDowall, Kaili Rimfeld, Saloni Krishnan,
Cognitive Reappraisal Reduces Academic Anxiety in University Students With Dyslexia,
2024,
1751-2271,
10.1111/mbe.12434
|
|
| 172.
|
Jim Warren, Lin Ni, Ben Fry, Melanie Stowell, Chelsey Gardiner, Robyn Whittaker, Taria Tane, Rosie Dobson,
2024,
Predicting Heart Rate Variability from Heart Rate and Step Count for University Student Weekdays,
979-8-3503-7149-9,
1,
10.1109/EMBC53108.2024.10781904
|
|
| 173.
|
Fariba Gadari, Azita Amirfakhraei, Saeid Kiani,
Adaptation and Psychometric Features of the Korean Medical Academicians Stress Questionnaire for Iranian Medical Academicians,
2024,
12,
2423-4451,
10.5812/mejrh-150041
|
|
| 174.
|
Jahid Hasan Rony, MM Mahbubul Syeed, Razib Hayat Khan, Kaniz Fatema, Md Shakhawat Hossain, Mohammad Faisal Uddin,
2024,
Predicting Depression Among University Students: a Comparative Assessment of ML & DL models using XAI,
979-8-3503-5395-2,
175,
10.1109/ISCIT63075.2024.10793544
|
|
| 175.
|
Katie Harrold, Anne Kathrin Fett, Corinna Haenschel,
The Effects of Social Identity Incompatibility on Student Mental Health,
2024,
14,
2227-7102,
1407,
10.3390/educsci14121407
|
|
| 176.
|
Khanh Duy Dang, Hao Yen Tran, Tien Minh Nguyen, Phuong Ha Lai, Khoa Thien Huynh, Khoa Anh Nguyen, Khoa Dang Ly,
Post-COVID-19 symptoms and the development of mental disorders in pharmacy students: a cross-sectional study,
2025,
12,
2331-1908,
10.1080/23311908.2024.2445875
|
|
| 177.
|
Said El-Ashker, Abdulmajeed Alharbi, Somaya Mahmoud, Feras Al-Awad, Ahlam Alghamdi, Nouf Alaqeel, Mohammed Al-Hariri,
Unraveling the threads of depressive symptoms: Enhancing predictions of depression among university junior students,
2025,
13,
2050-3121,
10.1177/20503121241310912
|
|
| 178.
|
Mohamed Hussein Ramadan Atta, Shimmaa Mohamed Elsayed, Heba Emad El‐Gazar, Naglaa Gamal Eldien Abdelhafez, Mohamed Ali Zoromba,
Role of violence exposure on altruistic behavior and grit among emergency nurses in rural hospitals,
2025,
72,
0020-8132,
10.1111/inr.13086
|
|
| 179.
|
Jehad Feras AlSamhori, Diala Ra’Ed Kamal Kakish, Abdel Rahman Feras AlSamhori, Ahmad Feras AlSamhori, Noor Rajeh Abu Hantash, Afnan Firas Abu Swelem, Mamoun Hamed Ali Abu-Suaileek, Hazar Mohammed Arabiat, Mohammad Anwer Altwaiqat, Radwan Banimustafa, Abdallah Barjas Qaswal, Abdulqadir J. Nashwan,
Anxiety, depression, and insomnia among medical and non-medical students in Jordan: a cross-sectional study,
2024,
31,
2090-5416,
10.1186/s43045-024-00493-8
|
|
| 180.
|
Herbert Situmorang, Reynardi Larope Sutanto, Kevin Tjoa, Rivaldo Rivaldo,
Association between primary dysmenorrhoea on quality of life, mental health and academic performance among medical students in Indonesia: a cross-sectional study,
2025,
15,
2044-6055,
e093237,
10.1136/bmjopen-2024-093237
|
|
| 181.
|
Maria Efstathiou, Varvara Kakaidi, George Tsitsas, Stefanos Mantzoukas, Mary Gouva, Elena Dragioti,
The prevalence of mental health issues among nursing students: An umbrella review synthesis of meta-analytic evidence,
2025,
00207489,
104993,
10.1016/j.ijnurstu.2025.104993
|
|
| 182.
|
Mohammad Ahsan, Turki Abualait,
Investigation of the relationship between mental health and physical activity among university students,
2025,
15,
1664-1078,
10.3389/fpsyg.2024.1546002
|
|
| 183.
|
Yinjuan Zhang, Fang Liu, Jin Ma, Jing Wu, Chao Shen, Fengjiao Chang, Wendong Hu, Hongjuan Lang,
Psychological stress and depression symptoms in nursing undergraduates: the chain mediating effect of cognitive reappraisal and ruminate thinking,
2025,
24,
1472-6955,
10.1186/s12912-024-02604-6
|
|
| 184.
|
Shoebul Haque, Farah Asif, Pragya Pandey, Rakesh Kumar Dixit,
Revolutionizing pharmacology education: Comparing escape rooms and traditional learning on student engagement and well-being,
2025,
0,
2584-136X,
1,
10.25259/FH_61_2024
|
|
| 185.
|
Muhammad Aledeh, Adewale Allen Sokan-Adeaga, Habib Adam, Sulaiman Aledeh, Yasuhiro Kotera,
Enhancing the Mental Health and Well-being of Family Caregivers Providing Informal Care in Ghana and Nigeria: A Commentary,
2025,
2198-9834,
10.1007/s40737-024-00447-7
|
|
| 186.
|
Gintarė Lübeck, Michael K. Seery, Barry J. Ryan,
Supporting female and gender diverse students in undergraduate STEM courses through enhancing self-efficacy,
2025,
1356-2517,
1,
10.1080/13562517.2025.2449660
|
|
| 187.
|
Vanessa Kaiser, Prisla Ücker Calvetti, Millena Holz Waskow, Aline Wolfart, Gabriela Bertoletti Diaz, Cleidilene Ramos Magalhães, Joana R. Casanova, Leandro Almeida, Caroline Tozzi Reppold,
Self-regulation of learning and positive psychology in University students,
2025,
1046-1310,
10.1007/s12144-024-07100-3
|
|
| 188.
|
Ernesto López-Gómez, Raúl González-Fernández, Buratin Khampirat,
Psychometric study of the Maslach Burnout Inventory-Student Survey on Thai university students,
2025,
15,
2045-2322,
10.1038/s41598-024-84829-8
|
|
| 189.
|
Leila Jasmine Dizon, Liezel Moises Abrea, Angelia Eunice Cruzada, Simon Ledz Erguiza, Alvin Ralphe Grape, Geo Dela Roca,
Utang na loob, perceived parental academic pressure and mental health status among Filipino college students,
2025,
2042-8308,
10.1108/MHSI-11-2024-0206
|
|
| 190.
|
Tobias Weinmann, Razan Wibowo, Felix Forster, Jessica Gerlich, Laura Wengenroth, Gudrun Weinmayr, Jon Genuneit, Dennis Nowak, Christian Vogelberg, Katja Radon, Britta Herbig,
Association of chronic stress during studies with depressive symptoms 10 years later,
2025,
15,
2045-2322,
10.1038/s41598-025-85311-9
|
|
| 191.
|
Rachel Wesley, Hoang Pham,
2025,
Chapter 13,
978-3-031-72635-4,
267,
10.1007/978-3-031-72636-1_13
|
|
| 192.
|
Wing W.Y. Ho, Yan H.Y. Lau,
Role of reflective practice and metacognitive awareness in the relationship between experiential learning and positive mirror effects: A serial mediation model,
2025,
157,
0742051X,
104947,
10.1016/j.tate.2025.104947
|
|
| 193.
|
Md. Jonaied Alam, Mahmudul Islam Khan Pratik, Abid Hasan Khan, Muhammad Shahidul Islam, Muhammad Millat Hossain,
Prevalence and level of stress among final-year students at a health science institute in Bangladesh,
2025,
5,
2731-4383,
10.1007/s44192-025-00136-2
|
|
| 194.
|
Abdelaziz Mahmoud Abdelaziz, Sara Sallam,
The indirect effect of communication skills on the relationship between emotional maturity and mental health disorders among a sample of Egyptian university students,
2025,
1046-1310,
10.1007/s12144-024-07236-2
|
|
| 195.
|
Juan Herrán-Alonso, David Winter, Alejandro Sanfeliciano, Luis Ángel Saúl,
Indicators of Event Integration in Repertory Grids and Ladders,
2025,
1072-0537,
1,
10.1080/10720537.2025.2452944
|
|
| 196.
|
Agnė Buivydienė, Lolita Rapolienė, Marija Truš, Agnė Jakavonytė-Akstinienė,
Connections between job satisfaction and depression, anxiety, and stress among nurses,
2025,
16,
1664-1078,
10.3389/fpsyg.2025.1548993
|
|
| 197.
|
Mohammad Mofatteh, Abdulkadir Mohamed, Mohammad Sadegh Mashayekhi, Georgios P. Skandalakis, Clemens Neudorfer, Saman Arfaie, ArunSundar MohanaSundaram, Mohammadmahdi Sabahi, Ayush Anand, Rabii Aboulhosn, Xuxing Liao, Andreas Horn, Keyoumars Ashkan,
Deep brain stimulation of the hypothalamic region: a systematic review,
2025,
167,
0942-0940,
10.1007/s00701-025-06430-w
|
|
| 198.
|
Megan Cairns, Erna Marais, Danzil Joseph, M. Faadiel Essop,
The Role of Chronic Stress in the Pathogenesis of Ischemic Heart Disease in Women,
2025,
15,
2040-4603,
10.1002/cph4.70000
|
|
| 199.
|
Marini Samaratunga, Imriyas Kamardeen,
Modelling Work–Study Conflict Effects on Built Environment Students’ Well-Being, Health, and Academic Performance,
2025,
15,
2075-5309,
406,
10.3390/buildings15030406
|
|
| 200.
|
Bashiru Garba, Samiro Ali Mohamed, Maria Mowlid Mohamed, Hodo Aideed Asowe, Najib Isse Dirie, Yushau Umar, Jamal Hassan Mohamoud, Mohamed Hussein Adam, Jihaan Hassan, Fartun Abdullahi Hassan Orey, Abdullahi Abdirahman Omar, Ibrahim Abdullahi Mohamed, Mohamad Mustaf Ahmed, Samira Abdullahi Moalim,
Prevalence of depression and its correlates among undergraduate health science students in Mogadishu, Somalia: a cross-sectional study,
2025,
25,
1471-244X,
10.1186/s12888-025-06553-5
|
|
| 201.
|
May Hamdan, Souzan Zidan, Fatima Al-Amouri, Hiba Niroukh, Manar Abu Dawod, Sajeda Ashour, Shahd Sameer Dweik, Manal Badrasawi,
Factors associated with caffeine intake among undergraduates: a cross-sectional study from Palestine,
2025,
44,
2072-1315,
10.1186/s41043-024-00723-z
|
|
| 202.
|
Alejandra López, Olaia Fontal Merillas, Pablo De Castro Martín,
El patrimonio cultural como espacio terapéutico: impacto de la fotografía y los relatos de vida en el bienestar de personas con enfermedad mental,
2025,
20,
1988-8309,
e98911,
10.5209/arte.98911
|
|
| 203.
|
Poh Gee Leng, Foong Ming Mak, Muhammad Fazli Taib Saearani, Muchammad Bayu Tejo Sampurno ,
The Effectiveness of Improvisational Dance in Decreasing Stress Levels among Tertiary Students in Malaysia,
2025,
20,
1988-8309,
e97816,
10.5209/arte.97816
|
|
| 204.
|
2024,
10.12794/metadc2332662
|
|
| 205.
|
Anmut Endalkachew Bezie, Giziew Abere, Girum Tareke Zewude, Belay Desye, Chala Daba, Eyob Tilahun Abeje, Awoke Keleb,
Prevalence of stress and associated factors among students in Ethiopia: a systematic review and meta-analysis,
2025,
13,
2296-2565,
10.3389/fpubh.2025.1518851
|
|
| 206.
|
Rizwana Khan, Fahmida Akter, Musarrat Rahman, Nuhu Amin, Mahbubur Rahman, Peter J. Winch,
Socio-demographic factors associated with mental health disorders among rural women in Mymensingh, Bangladesh,
2025,
16,
1664-0640,
10.3389/fpsyt.2025.1446473
|
|
| 207.
|
Maria Komariah, Theresia Eriyani, Laili Rahayuwati, Hana Rizmadewi Agustina, Furkon Nurhakim, Irman Somantri, Shurouq Ghalib Qadous, Aurawan Janmanee, Nina Gartika,
Quality of Life, Self-Esteem, and Stress among First-Semester Student Nurses in Indonesia: A Cross-Sectional Study,
2025,
11,
2377-9608,
10.1177/23779608251317805
|
|
| 208.
|
Francisco Lepe-Salazar, Fabián Preciado-Martínez,
2024,
Game-Based Prevention of Depression in Students,
979-8-3503-5054-8,
1,
10.1109/HealthCom60970.2024.10880808
|
|
| 209.
|
Sheriff Tolulope Ibrahim, Madeline Li, Jamin Patel, Tarun Reddy Katapally,
Utilizing natural language processing for precision prevention of mental health disorders among youth: A systematic review,
2025,
188,
00104825,
109859,
10.1016/j.compbiomed.2025.109859
|
|
| 210.
|
Francisco Lepe-Salazar, Oscar Nazarit-Campos, Nadia Cortés-Álvarez, César Vuelvas-Olmos,
2024,
Impact of Serious Game on Depression in Students,
979-8-3503-5054-8,
1,
10.1109/HealthCom60970.2024.10880792
|
|
| 211.
|
Raquel Simões de Almeida, Andreia Rodrigues, Sofia Tavares, João F. Barreto, António Marques, Maria João Trigueiro,
Mental Health and Lifestyle Factors Among Higher Education Students: A Cross-Sectional Study,
2025,
15,
2076-328X,
253,
10.3390/bs15030253
|
|
| 212.
|
Lingjiang Huang, Jialin Li, Jian Kang, Fangfang Liu, Ming Yang, Yawei Zhang,
Understanding the Nexus Between Anxiety and Acoustic Perception in University Students: A Quasi-Experimental Study During Pandemic-Induced Lockdown,
2025,
15,
2076-328X,
262,
10.3390/bs15030262
|
|
| 213.
|
Shuoyu Jing, Wan Ahmad Munsif Wan Pa, Mohd Mahzan Awang,
Anxiety and depression among Chinese international student-athletes during study abroad: a psychological network approach,
2025,
29,
2308-7250,
27,
10.15561/20755279.2025.0103
|
|
| 214.
|
Sarah W. Bisconer, Kate Van Houten,
A Three-Year Examination of U.S. Undergraduates Attending a High-Ranking Public College During COVID-19: Contributions to the Field’s Understanding of Psychological Adjustment,
2025,
2836-7138,
1,
10.1080/28367138.2025.2459092
|
|
| 215.
|
Jaegoo Lee, Jeoung Min Lee, June-Yung Kim, Dasha Shamrova,
The association of adverse childhood experiences and generalized anxiety in college students: Roles of perceived social support and resilience,
2025,
1091-1359,
1,
10.1080/10911359.2025.2473626
|
|
| 216.
|
Erinn C. Cameron, Ashraf Kagee,
Psychological, Experiential, and Behavioral Predictors of Climate Change Anxiety Among South African University Students,
2025,
2358-1883,
10.1007/s43076-025-00444-0
|
|
| 217.
|
Serap Güngör, Ipek Kose Tosunoz,
Levels of Nursing Students’ Exposure to Colleague Violence and Affecting Factors: A Multicenter Cross-Sectional Study,
2024,
115,
2532-1080,
e2024024,
10.23749/mdl.v115i4.15606
|
|
| 218.
|
Jacqueline Hua, Michael Vang, Jennifer L. Howell, Yopina Pertiwi, Andrew L. Geers, Brandon Boggs,
Health regulatory focus and college student outcomes following healthcare visits,
2025,
0744-8481,
1,
10.1080/07448481.2025.2467325
|
|
| 219.
|
Erhan Dağ, Yaşar Demir, Zuhal Kayar, Mustafa Nal,
Relationship between digital health literacy, distrust in the health system and health anxiety in health sciences students,
2025,
25,
1472-6920,
10.1186/s12909-025-06903-7
|
|
| 220.
|
Amani ELBARAZI,
Association Between Depression, anxiety, stress, and vaping among University Students,
2025,
7,
2654-1459,
10.18332/popmed/202345
|
|
| 221.
|
Sindhu C.V., Devaseelan S.,
Mind Over Matter: A Comprehensive Review of Academic Anxiety, Psychological Constructs, and Interventions in Nursing Education,
2025,
2581-6411,
12,
10.47992/IJHSP.2581.6411.0128
|
|
| 222.
|
Social Media and Mental Health: Understanding the Association between SNS Addiction and Depression in Students,
2025,
3,
2960-2807,
698,
10.70749/ijbr.v3i2.787
|
|
| 223.
|
Gengchen Liu, Jiandan Hu, Ilona Kostikova,
Music therapy and its impact on anxiety and mental well-being of Chinese students: An experimental comparison of traditional and VR approaches,
2025,
255,
00016918,
104898,
10.1016/j.actpsy.2025.104898
|
|
| 224.
|
Marini Samaratunga, Imriyas Kamardeen, Bogahawaththage Nishadi Madushika Chathurangi,
Work–Study Conflict Stressors and Impacts: A Cross-Disciplinary Analysis of Built Environment Undergraduates,
2025,
15,
2075-5309,
973,
10.3390/buildings15060973
|
|
| 225.
|
Sailaa Sunthararajah, Lucia Valmaggia, Tasnim Uddin, Simon Riches,
Virtual reality relaxation for student wellbeing: a systematic review,
2025,
2976-8756,
10.1108/MHDT-12-2024-0035
|
|
| 226.
|
Asnea Tariq, Yumeng Yang, Ziqiao Liu, Siu Ching Wong, Elaine Gray, Angela L. McLaughlin, Caden J. Arthur, Stella W. Y. Chan,
Effects of the Soothe Vision well-being tool on university students’ mood: a pilot study,
2025,
1046-1310,
10.1007/s12144-025-07649-7
|
|
| 227.
|
The Burden of University Life: Stress, Anxiety, and Depression in Undergraduates,
2025,
14,
2278-2540,
47,
10.51583/IJLTEMAS.2025.14030007
|
|
| 228.
|
Sam Leewis, John van Meerten, Koen Smit, Ha Bui,
2024,
Emotion Detection in International Students Using a Social Robot,
9798400712463,
1,
10.1145/3715885.3715892
|
|
| 229.
|
Kabir Alabi Sulaiman, Mulikat Adenike Salaudeen, Suliyat Oyindamola Salam, Farouk Mayowa Salami-Tade, Oluwatomilayo Sanni,
Information searching habit of LIS undergraduate students in selected universities in Nigeria,
2025,
0955-7490,
10.1177/09557490251335957
|
|
| 230.
|
Wael Abuhasan, Osama Mohamed Elsayed Ramadan, Zulfiqar Ullah Siddiqui, Ziyad Kamal M. Mohammad, Ahmad Rafiq Mohammad Abu Arrah, Suhail Ahmad Dar, Ishrat Munawer, Fayez Mahamid, Fakher Nabeel Mohammad Khalili, Lavanya Rajakumar,
Uncovering the Link Between Perceived Stress and Health Related Quality of Life (HRQOL) among Dentistry Students of the Arab American University-Palestine,
2025,
34,
2344-8644,
29,
10.15446/rcp.v34n1.112120
|
|
| 231.
|
Ben Singh, Hunter Bennett, Aaron Miatke, Dorothea Dumuid, Rachel Curtis, Ty Ferguson, Jacinta Brinsley, Kimberley Szeto, Emily Eglitis, Mason Zhou, Catherine E.M. Simpson, Jasmine M. Petersen, Joseph Firth, Carol A. Maher,
Systematic Umbrella Review and Meta-Meta Analysis: Effectiveness of Physical Activity in Improving Depression and Anxiety in Children and Adolescents,
2025,
08908567,
10.1016/j.jaac.2025.04.007
|
|
| 232.
|
Mohammad Esmaeelzadeh, Seyyed Abolfazl Vagharseyyedin, Zahra Zamaninasab, Sajede Soleimani,
Investigating the psychometric properties of the Persian version of Psychological Emptiness Scale (PES) among nursing students,
2025,
24,
1472-6955,
10.1186/s12912-025-03024-w
|
|
| 233.
|
Alaa Eldin Moustafa Hamed, Mohga Fathy Hamza, Nahla Abdallah Abd El-Tawab, Ahmed Abdellah Othman, Abeer Moustafa Barakat, Mohamed Hussein Ramadan Atta,
Exploring the mediation role of hardiness in the relationship between feedback sensitivity and test anxiety among nursing students: a multi-site inquiry,
2025,
24,
1472-6955,
10.1186/s12912-025-02946-9
|
|
| 234.
|
Gracie Wilson,
“If I’m not stressed, why am I even here?”: exploring narratives of student mental health and belonging on campus,
2025,
0744-8481,
1,
10.1080/07448481.2025.2486415
|
|
| 235.
|
Yoy Bergs, Yannick Griep, Pascale Peters, Xander Lub, Rob Blomme,
Understanding the role of perfectionism standards and discrepancy in longitudinal patterns of anxiety and depression: a latent class growth analysis approach,
2025,
0729-4360,
1,
10.1080/07294360.2025.2492123
|
|
| 236.
|
Jia Hang Lim, Mahadir B. Ahmad, Kususanto D. Prihadi,
Examining the role of psychological flexibility and unconditional self-acceptance as mediators in the relationship between new media literacy and psychological wellbeing among Gen Z,
2025,
14,
2277-9531,
10.4103/jehp.jehp_1077_24
|
|
| 237.
|
Hlengiwe D. Seshabela, Simangele Shakwane,
Impact of anxiety-related conditions on nursing students’ academic excellence,
2024,
47,
2223-6279,
10.4102/curationis.v47i1.2571
|
|
| 238.
|
Emma Brown, Eden Morley,
Feeling Like a Fraud: Exploring How the Impostor Phenomenon Manifests in Neurotypical and Neurodivergent First-Year Undergraduate Students in the UK Using the Impostor Phenomenon Assessment,
2025,
2836-7138,
1,
10.1080/28367138.2025.2493896
|
|
| 239.
|
Nor Hidayah Jaris, Salmi Razali, Fatimah Sham, Iman Mohamed Ali,
From Home to Campus: How family dynamics influence anxiety in Malaysian university students,
2025,
10,
2398-4287,
195,
10.21834/e-bpj.v10i32.6715
|
|
| 240.
|
Fengbin Hu, Zixue Tai, Jianping Liu,
The Positive Effect of Video Game Play During COVID-19 Shelter-in-Place Lockdowns: Anxiety and Depression Symptoms Among College Students in China (Preprint),
2024,
2291-9279,
10.2196/58857
|
|
| 241.
|
Neha Sharma, Chander Prabha, Firoz Khan, Nitin Rakesh, Sumedha Bali, ,
2025,
The Impact of Digital Platforms on Learner Lives and Educational Success,
979-8-3315-1208-8,
902,
10.1109/ICICCS65191.2025.10984511
|
|
| 242.
|
Mario Eduardo Castro Torres, Pablo Marcelo Vargas-Piérola, Aarón Marco Layme Mamani, Andrea Katerine Murillo Toro, Aneydith Ribera Domínguez, Carlos F. Pinto,
Effects of Social Capital on Depression in University Students,
2025,
15,
2254-9625,
83,
10.3390/ejihpe15050083
|
|
| 243.
|
Nkasi Stoll, Sunehna Kayn, Heidi Lempp, Stephani Hatch,
Impact of racial discrimination in education and other adverse childhood experiences on black students’ mental health and wellbeing: an interpretative phenomenological analysis study,
2025,
20,
1748-2631,
10.1080/17482631.2025.2507754
|
|
| 244.
|
Nazish Imran, David M. Ndetei, Rodrigo Nel Cordoba Rojas, Afzal Javed,
High school teachers’ awareness of anxiety and depression in adolescents: cross-country analysis,
2025,
2056-4740,
1,
10.1192/bji.2025.17
|
|
| 245.
|
İrfan Akkoç, Ebru Dığrak, Tülay Yavan, Filiz Ogce Aktas,
The mediating role of psychological well-being in the association between intolerance of uncertainty and academic life satisfaction among university students,
2025,
1046-1310,
10.1007/s12144-025-07937-2
|
|
| 246.
|
Yitong Liu, Richard J. Siegert, Wendy Wrapson,
2025,
Chapter 72-1,
978-3-030-89738-3,
1,
10.1007/978-3-030-89738-3_72-1
|
|
| 247.
|
Robi Hendra, Akhmad Habibi, Ahmad Ridwan, Dian Arisandy Eka Putra Sembiring, Tommy Tanu Wijaya, Denny Denmar, I Wayan Widana,
The Impact of Perfectionism, Self-Efficacy, Academic Stress, and Workload on Academic Fatigue and Learning Achievement: Indonesian Perspectives,
2025,
7,
2544-7831,
10.1515/edu-2025-0071
|
|
| 248.
|
V.A. Serhiyenko, V.B. Sehin, V.I. Pankiv, A.A. Serhiyenko,
Features of short-term heart rate variability in internally displaced people with type 2 diabetes mellitus,
2025,
21,
2307-1427,
243,
10.22141/2224-0721.21.3.2025.1534
|
|
| 249.
|
Bylhah Mugotitsa, Reinpeter Momanyi, Joseph Kuria, David Amadi, Jacob Masai, Eric Angula, Benjamin Tsofa, Jay Greenfield, Jim Todd, Agnes Kiragga,
Understanding mental health among university students in Kenya: what role do family support and age play?,
2025,
13,
2296-2565,
10.3389/fpubh.2025.1557058
|
|
| 250.
|
2025,
10.56902/ETDCRP.2025.14
|
|
| 251.
|
Poppy Elisano Arfanda, Ians Aprilo, Arimbi Arimbi, M. Imran Hasanuddin, Retno Farhana Nurulita,
Impact of Video-Based Aerobic Dance on Higher Students' Endurance and Concentration,
2025,
4,
2809-3682,
469,
10.51574/ijrer.v4i3.3015
|
|
| 252.
|
Yeny Dyah Cahyaningrum, Yoyo Suhoyo, Gandes Retno Rahayu,
Facilitating clinical reasoning for medical students in clinical settings: a scoping review,
2025,
37,
2005-727X,
163,
10.3946/kjme.2025.333
|
|
| 253.
|
Aybike Çavdar, İnci Boyacioglu,
Predictive Effects of Intolerance of Uncertainty, Perceived Uncertainty and Need for Autonomy on Depression and Anxiety Levels of University Students in the Post‑COVID‑19 Era,
2025,
11,
2149-1488,
148,
10.30613/curesosc.1552509
|
|
| 254.
|
Garima Rajan, Mehar Sandhu,
Investigating the Efficacy of an Integrative Positive Psychology Intervention (PPI) in Indian College Students: An Eclectic Approach Combining Mindfulness meditation, Guided Imagery, and Gratitude Journaling,
2025,
2836-7138,
1,
10.1080/28367138.2025.2513954
|
|
| 255.
|
Phillip Olla, Ashlee Barnes, Lauren Elliott, Mustafa Abumeeiz, Venus Olla, Joseph Tan,
Deploying a Mental Health Chatbot in Higher Education: The Development and Evaluation of Luna, an AI-Based Mental Health Support System,
2025,
14,
2073-431X,
227,
10.3390/computers14060227
|
|
| 256.
|
I-Ting Hsieh, Leonardo Bevilacqua,
Social distancing measures and mental Well-being outcomes of UK young adults during the pandemic: the mediating role of social connectedness,
2025,
22,
3005-0774,
10.1186/s12982-025-00722-3
|
|
| 257.
|
Caitlyn R. Flemmer, Abigail Hatcher, Alyssa Avallone, Clare Cuenya, Sharon Thompson,
Mental health problems in an academic setting among undergraduates,
2025,
1746-5729,
10.1108/JPMH-01-2025-0013
|
|
| 258.
|
Muhammad Ikhwan Mud Shukri, Anisah Baharom, Ahmad Iqmer Nashriq Mohd Nazan,
Self-esteem and stress: a structural equation modelling of biosocial determinants, psychological mediators and anxiety among Malaysian undergraduates,
2025,
13,
2167-8359,
e19304,
10.7717/peerj.19304
|
|
| 259.
|
Dorothy A. Thompson, Heidi L. Dent, Monica B. Fine,
Mental health stigma of American college students: Business student perceptions,
2025,
0883-2323,
1,
10.1080/08832323.2025.2518078
|
|
| 260.
|
Amani Safwat ElBarazi,
The effect of emotion regulation training on anxiety in college students in Egypt (Randomized control trial),
2025,
14,
2279-9036,
10.1177/22799036251347030
|
|
| 261.
|
Raif Alan, Arslan Terlemez, Hasan Bakay, Şakir Gıca, Esra Ercan,
Examination of Factors Affecting Mental Distress Among Dental Students: A Cross-Sectional Study,
2025,
15,
2459-1459,
280,
10.33808/clinexphealthsci.1458804
|
|
| 262.
|
Towhid Hasan, Nibadita Majumder, Marjia Sultana, Md. Mahmudul Hasan Shohag, Nishat Subah Tithi, Md. Hasan Al Banna,
Association of stress with nutrition literacy, eating behavior, and physical activity: A cross-sectional study of university students in Bangladesh,
2025,
20,
1932-6203,
e0326269,
10.1371/journal.pone.0326269
|
|
| 263.
|
Elisabeth Margarete Weiss, Mona Harder, Siegmund Staggl, Bernhard Holzner, Verena Dresen, Markus Canazei,
Evaluation of the effectiveness of a 7-week minimal guided and unguided cognitive behavioral therapy-based stress-management APP for students,
2025,
25,
1471-2458,
10.1186/s12889-025-23399-4
|
|
| 264.
|
Gad Namndiro, Jean Tine, Abdourahmane Sow, Ibrahima Seck,
Factors Associated with Stress, Anxiety, and Depression Among Management School Students in Senegal
,
2025,
11,
2575-5781,
113,
10.11648/j.cajph.20251103.13
|
|
| 265.
|
Jiale Wang, Jinyin Peng, Junwei Dong, Haiou Peng, Zhenxiu Yi, Yang Liu, Wenxi Tang,
The Relationship Between Physical and Psychological Maltreatment and Internet Addiction among College Students: A Moderated Mediation Model,
2025,
0885-7482,
10.1007/s10896-025-00924-y
|
|
| 266.
|
Umar Haruna, Abdul-Raheem Mohammed, Mary Braimah,
Understanding the burden of depression, anxiety and stress among first-year undergraduate students,
2025,
25,
1471-244X,
10.1186/s12888-025-07069-8
|
|
| 267.
|
Syprine Oyoo, Rosemary Akinyi Olendo,
2025,
Chapter 14,
978-3-031-88792-5,
263,
10.1007/978-3-031-88793-2_14
|
|
| 268.
|
Divya Raghavan, Anandhi Deva Amirtharaj,
Mapping learning preferences in nursing education: A cross-sectional study among generation Z students,
2025,
14,
2277-9531,
10.4103/jehp.jehp_1629_24
|
|
| 269.
|
S. V. Kucher, U. O. Mudra, I. I. Hanberher, M. S. Mysula, Yu. I. Mysula, V. H. Dzhyvak, R. S. Vastyanov,
INVESTIGATION OF INCREASED LEVELS OF ANXIETY AND DEPRESSION IMPACT ON THE QUALITY OF LIFE IN PATIENTS WITH IRRITABLE BOWEL SYNDROME,
2025,
21,
2079-8334,
89,
10.26724/2079-8334-2025-2-92-89-94
|
|
| 270.
|
Alberto Fouilloux Morales, Mariana Fouilloux Morales, Ileana Petra Micu, Beatriz Zamora López, Silvia Aracely Tafoya,
Calidad de sueño percibida y su asociación con el estrés en estudiantes del área de la salud en México: estudio longitudinal,
2025,
6,
2675-5459,
e5549,
10.46932/sfjdv6n7-012
|
|
| 271.
|
Fathia Ahmed Mersal, Shereen Ahmed Elwasefy, Amal Ahmed Elbilgahy,
Art healing and play: Reducing pain and anxiety in hospitalized children during venipuncture,
2025,
85,
08825963,
22,
10.1016/j.pedn.2025.07.009
|
|
| 272.
|
Neha Bhatt, C. G. Devi,
Effectiveness of Academic Stress Management Program on Reduction of Academic Stress Level in B.Sc. Nursing Students: A Randomized Control Trial,
2025,
22,
2231-1505,
38,
10.4103/iopn.iopn_19_24
|
|
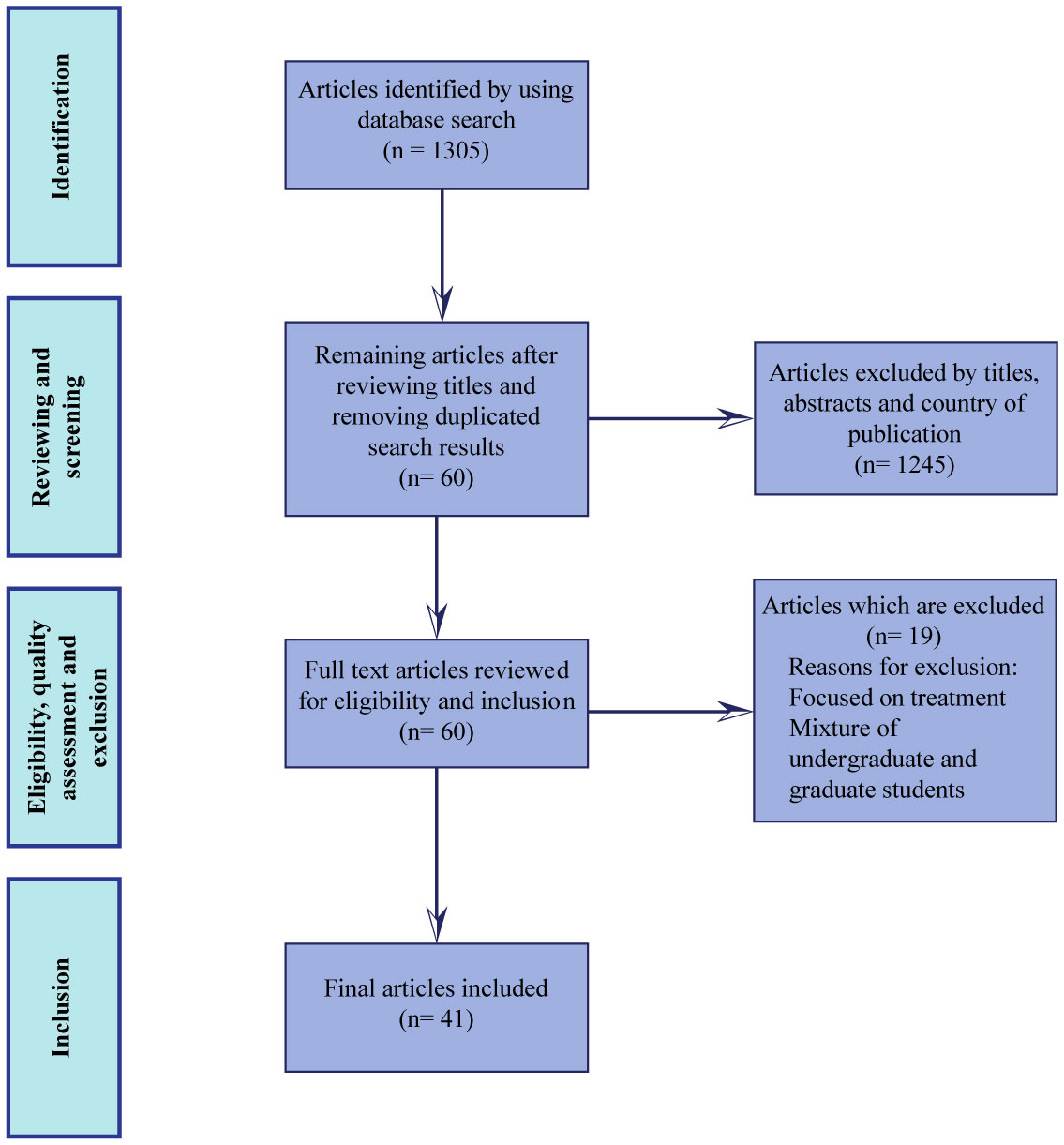









 DownLoad:
DownLoad: