1.
Introduction
Environmental pollution, artificial waste, is a synthetic polymer material from plastics [1,2]. Plastics can be produced for various versatile materials because they have low production costs, and limited natural materials so far can be reduced by their availability [3,4,5]. This can be seen from the demand for plastic production, which is increasing every year. Microplastics are often found in the soil every year, such as polypropylene and polyethylene [6]. However, limitations and inaccuracies in the recovery of plastic waste have caused the rate of polymer accumulation in the environment to increase. Thus, the plastic has been systematically fragmented, especially in the presence of ultraviolet radiation and mechanical abrasion [2,7,8]. Microplastics can be found everywhere, especially in the environment, drink bottles, food, and even the human body [9,10,11,12]. These microplastics have attracted the attention of scientists because some facts about microplastics have begun to be revealed.
In general, plastic particles, which are microplastics, have a size of < 5 mm [13,14]. The environment is a very appropriate research subject studied in recent years [15,16,17,18]. Plastic waste is commonly disposed of and produced on land. It is not surprising that recent microplastic research has embraced the terrestrial system. Where is the place where microplastic waste is disposed of for a long time is on the ground [19,20,21]. Previous studies found that fibrous microplastics can be found in soil globally [22]. Recently, detected microplastics found in field soil are highly fragmented [23], where the accumulation of microplastics in agricultural land can be done by applying sewage sludge. Microplastics that accumulate in the soil can be utilized by plants and transferred through the food chain [12]. This includes the absorption of pollutants by microplastics. However, the potential for microplastics that enter the soil is very diverse and can involve compost or sewage sludge [24,25]. In addition, the origin and potential sources of waste are also obtained from plastic mulch, irrigation, indiscriminate disposal, and atmospheric deposition [5,6,14,26]. Vulnerability to microplastic pollution in agricultural and urban soils is due to frequent contact with artificial activities and microplastic input [27]. many studies have proved that microplastics are present in soil globally. However, most people still think that microplastics found in the soil are still said to be fragmented [28]. Using sample collection with methodologies and quantification aimed at process and analysis does not yet have standardization. Thus, it cannot be comprehensively compared when microplastics occur from different research communities [8,29,30]. Therefore, a critical review through the methodology as a sampling and analytical protocol for microplastics in the soil is very important. The discovery of pathways and sources found in the soil, and the environment is important to be clarified in depth [30].
This study aims to confirm the current research status and gaps in knowledge regarding microplastics in the soil and to standardize future research. Thus, a knowledge system can be implemented regarding the recovery, reduction, and control of microplastics. In addition, this research can provide an in-depth evaluation of the development of analytical methodologies for sampling. The development of this methodology can also be used in the purification, identification, extraction, and characterization of microplastics. Analysis and pre-treatment of samples can be determined more accurately whether they are sensitive at low or high costs. Plastic polymers found in soil can be further clarified, such as occurrence, appearance, and abundance, such as color, shape, and size to identify microplastics. A critical overview of the pathways and potential sources of microplastics entering the soil can be provided. The potential risks of microplastics in the soil can be revealed with current knowledge technology.
2.
Previous research
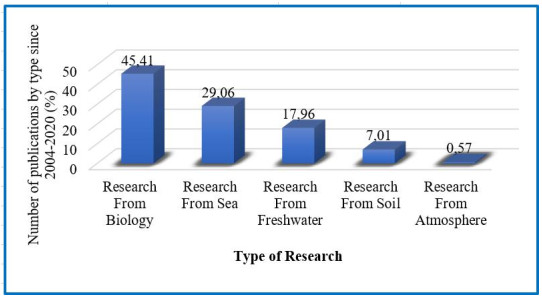
The literature collected from 2004–2020 related to microplastic research in soil ecosystems is 51 articles. The data collection for this research literature was taken from the Scopus, WOS, Google Scholar, and Science Direct databases, as shown in Figure 1. Search the various kinds of literature in this study used the keywords Microplastics directly related to the environment, waters, and soil. Determination of taking the literature only based on and included in the categories related to the monitoring of microplastics in the environment, sources of microplastics, potential risks from microplastic pollution, and analytical and technological innovations. In addition, some literature closely related to this work was taken. Meanwhile, the examination related to the bibliography of the literature was also studied. There were 51 studies on microplastic monitoring in soil among the 136 research papers collected.
3.
Methodology
3.1. Analysis of sample
The application of several methods for analyzing microplastics in both marine and freshwater has been carried out. However, complex studies are insufficient to pre-treat standard analytical methodologies for microplastics in the soil. The availability of analytical methods that can be applied to the environment is essential to be adapted to soil samples [12,31,32]. The relative stability of the aggregate formed from soil particles can wrap and cover the microplastic particles as the result of the analysis [21]. Organic content with a higher complex composition is a problem that needs to be analyzed so that the analytical method used for microplastic analysis can be applied to the environment [33]. Analysis of microplastics in the soil can be divided into three categories: soil samples must be sieved and dried first, adhering organics mixed with microplastic and organic particles in the soil must be removed, and most of the matrix in the microplastic particle samples separated and density separation is the most commonly used strategy [21,33,34]. In the end, the potential recognition of microplastics visually with a microscope can be verified employing Fourier transform infrared and Raman spectroscopy, as shown in Table 1.
3.2. Aggregation of sample
The soil sampling system process is the same as sediment. However, human interaction is very easy to influence heterogeneous metrics. Even representative samples are challenging to obtain. Samples on single sites and sample compositions can be collected as research results [21]. This is because the distribution of microplastics is not homogeneous in the soil to be disturbed by soil changes. Sampling composition from agricultural land by combining homogenization can be used as a sample. 13 previous studies have applied this method, of which there has been more focus on agricultural land. A total of 12 sampling studies were conducted at a single site. Individually target depth and fundamental level can be selected because certain characteristics that have been formed are more attractive [35]. The most suitable locations for sampling are land and non-agriculture because they have little effect on human activities.
A sampling of soil and sediment on riverbanks or lakesides uses the same tools. Soil sample collection can be done with a stainless steel trowel, steel corer, Lens sampler, and soil auger [1,23,43,44,24,36,37,38,39,40,41,42]. Soil sampling for research is generally small sampling with a size of 5×5 cm, 10×10cm, and 20×20cm [37,39,41,43,44,45,46,47]. Meanwhile, the collection is through sampling with a large area of 5×5 cm [36,47]. Sampling using the dial method is still an obstacle to be used as a quantitative analysis of microplastics in the overall environmental matrix [21]. However, the matrix on the soil system collects data through or the use of small samples, so that comparisons of pollution on microplastics in sediments are more likely to be carried out. [48]. On the contrary, the soil samples collected from depth are more than in other environmental matrices. Recommendations for sampling on agricultural soils as deep as 0–30 cm, including the processing layer [48]. At the same time, the soil samples taken are shallower, ± 5 cm. Deeper pollution must be better understood, and the extraction system must be adapted to the soil profile. At the time of vertical distribution of microplastics after cultivation, the depth of the sample taken can be adjusted to the type of cultivation [5,49]. The soil sampling system is carried out over the quantities necessary to quantify microplastics, so that additional samples can allow for repeatability in determining sample recovery and moisture analysis [21]. Soil samples are usually stored in Ziploc containers, glass bottles, etc. However, it is recommended that the tools used are not made of plastic, such as aluminum bags and glass bottles. Better storage devices should be heated to high temperatures to remove the potential for microplastics.
3.3. Drying and sieving
Soil sample collection is generally stored in a room with a temperature of 4℃ and drying is done naturally. This is done to compare the actual microplastic concentrations without any influence from soil moisture. Most of the research reviewed shows that drying the sample is possible through a natural system. Several studies report that heating samples with an oven-dry is faster than the natural method at a level of 40℃–70℃. However, microplastic changes can change shape and break easily when the thermal deformation temperature of the plastic exceeds [8]. Most polymers have a lower thermal deformation temperature so that microplastics such as PA and PE will be disturbed [50]. In this case, heating and drying the sample are not good if the temperature exceeds 50℃.
3.4. Purification
A considerable volume of organic matter may be an issue in the extraction of microplastics from the soil, which cannot be accomplished using density separation [5,20,29]. The most common investigations carried out on the efficiency of reagents, such as 30% H2O2, 65% HNO3, 50% NaOH, 96% H2SO4, and 13% KClO, aim to remove organic fractions in the soil. Where as much as 65% HNO3 found in the 90℃ sample shows a higher level of efficiency [29]. It can remove the majority of biological matter in a short period of time [29]. Polyamide (PA), Polyester (PET), and polymethyl methacrylate will partially decompose when exposed to HNO3 (PMMA) [29]. The removal efficiency of hydrogen oxide (H2O2), which is most typically employed to remove organic pollutants from environmental matrices, has been questioned due to the time-consuming method [50]. However, in the examined research (n = 11), 30% H2O2 is still the most commonly utilized chemical reagent. Fenton's reagent is a more advanced oxidation method that uses H2O2 in the presence of a catalyst Fe2+ to remove organic molecules more effectively and with less damage [8,50].
3.5. Extraction
Microplastics obtained from the soil matrix also need to be extracted after purification. Extraction of microplastics in the soil is a common method [51]. This is shown from the 26 studies reviewed, 90% of which uses the extraction method. The most commonly used separation of microplastics is through sodium iodide, zinc chloride, calcium chloride, sodium chloride, and distilled water. The separation rates in this method are NaI, 1.8 g/cm3, ZnCl2, 1.6 g/cm3, CaCl2, 1.5 g/cm3, NaCl, 1.2 g/cm3, and 1.0 g/cm3, respectively. It theoretically shows that the distilled water method is the easiest and harmless. However, the separation is only on some types of plastic with a density of less than 1.0 g/cm3 NaCl. This is because the NaCl distilled water technique is easier to obtain, non-toxic, Na is more conducive to particle dispersion, and the price is lower. However, high-density microplastics such as polyvinyl chloride (PVC), polymer (PET), and NaCl are still very low [22,29,33,52]. ZnCl2 has a higher density solution level and is often used, but the aqueous solution is toxic and corrosive. The level of solution density in NaI is calculated to be the highest but has a fairly high price. Based on the density perspective, CaCl2 separates microplastics because of its lower cost and environmental friendliness. However, the charge of organic molecules can be helped in the presence of Ca2+ [29]. This organic matter accumulates and fluctuates in the filter membrane which interferes with identification and calculation, which can be bridged by Ca2+
[8]. Recent research on evaluating sodium bromide (NaBr) with reagent as a separator is non-toxic, economical, and non-corrosive to soil [53].
The density separation method used today is still very limited, as reported in the study [24]. Meanwhile, the verified saline solution for efficient use of microplastic separation can be influenced by the shape and size of the capture of microplastics. Salt solutions such as high-density NaI can separate the fibers in microplastics in an effective and high-density manner. However, it was significantly indistinguishable, especially in the microplastic fragments and bulk. Meanwhile, recommendations for sodium chloride as a density solution can be made in some solutions. In addition, general solutions such as PET and PVC can play a very limited role in microplastic fractions with large samples, and their storage area also does not require a large space [29]. Thus, the solution for its separation needs to be selected by creating and adapting to local plastic demand conditions. The distribution of microplastics described as a whole has not shown clarity for a better solution. The density separation developed today has shown quite good results. Multi-stage separation is a strategy to reduce limitations so that the best separation effect is obtained. Density separation using sodium chloride, water, and zinc chloride three times has also been investigated [44,54]. Meanwhile, the application of the ZnCl2, NaCl, and NaI separation systems by combination method has also been studied [55,56]. In comparison, applying a mixing separation system with the aim of cost efficiency and extraction is also considered. A mixture using NaI and saturated NaCl in a ratio of 1:1 to provide a flotation solution with a density of 1.5 g/cm3 can be used 5 times through a filtration system [52]. Thus, more efforts to improve density separation are needed.
In general, microplastics can be wrapped using soil aggregate. Several procedures can be used to remove the ultrasonic treatment, stirring, continuous flow, centrifugation, and aeration [33,52,57]. Recently developed methods have demonstrated advantages for the extraction and separation of microplastics. The alternative method used for the separation of microplastics has the lipophilic nature of the polymer [8]. Separation of microplastics using olive, canola, and castor oil has been carried out [58,59,60]. This is because the method used does not depend on the type of polymer. However, this method has limitations in extracting microplastics for small particle sizes < 200 m. One of the new methods for separating microplastics is electrostatics [61]. The cohesive nature of the soil sample will form microplastic clumps that are not easily released in the soil, so the use of this soil method still needs to be verified [21]. Great gravity is possible due to microplastic adhesion to metal walls. Thus, more verification for the recovery of small particles is needed. The increased extraction pressure of the liquid can provide many possibilities for the extraction of microplastics in soil [57]. This can provide a low and efficient analysis component to be disturbed by various human activities automatically. The number of extracted samples used for a single analysis is so small, leading to their accuracy and quantification are challenging [33]. In addition, information on the particle size required for mobility and toxicity of microplastics has failed to be maintained [29].
Taking microplastics of various sizes as dry soil samples usually has to pass through several stainless steel filters with a size of 1–2 mm [62]. Agglomerated soil samples can be crushing with a hammer/rolling pin so that external forces can avoid further crushing of microplastic particles. Meanwhile, rarer soil samples can be sifted directly. Soil samples found on roads and grass usually contain a lot of roots and weeds, making them very difficult to clean. The removal of this dirt must manually go through the filter several times. Microplastics remaining on the filter are re-sorted and collected for further characteristics and identification [63]. Microplastic sieving using a 5 mm sieve is more suitable in some cases than when using a 1 and 2 mm sieve [7]. Soil samples containing many roots and other impurities difficult to remove for the purification process can be carried out using 1 and 2 mm sieves [51]. However, the sieving system must be clearer and can be stated during the analysis process. The sieve model with a one, two, and three-level system is used depending on each research objective. The reviews of previous studies show that the commonly used sieves are 1 mm, 2 mm, 5 mm.
3.6. Characterization
Microplastics separated and purified from the environmental matrix are further quantified and identified [20]. Most of the analytical techniques developed in this study have given enormous advantages and limitations, as shown in Table 1. The first microplastics identification is carried out clearly and possible through a microscope through spectroscopic methods, and Fourier transforms infrared thermodynamics. In addition, it can also be done by chromatography and Raman spectroscopy through gas pyrolysis and mass spectrometry [8,49,64]. The most important equipment for recording microplastics can be an optical microscope or, more specifically, a stereo microscope [65]. Determination of particles in microplastics with morphological characteristics can be done by identifying shape, surface texture, and color [7]. Several criteria have been proposed for microplastic research [66]. Guidelines for identifying microplastics as published by the marine and environmental research institute (MERI), aim to help filter and identify the use of hot needles. Criteria defined by the research community is for a larger environmental sample as reported in the study [17,30,67].
Visual inspection can elicit uncertain positivity levels, especially in the smaller fibers. Therefore, optimization with technologies such as -micro-FTIR, focal plane array (FPA-FTIR), and total reflectance attenuation FTIR (ATR-FTIR) can further characterize microplastics [3,7]. Detection of microplastics using infrared spectroscopic devices is possible to analyze microplastics with a length of 5–10 m [8,68]. ATR-FTIR can detect Microplastics up to 10 m thick. Utilization with a strong signal-to-noise ratio with spectrum can be via ATR-FTIR [8]. However, to contact the target pressure, the ATR-FTIR material must be equipped with a probe because it can cause damage and damage microplastics. When applying FTIR, microplastics can be transferred automatically by filtering some polymer samples [69,70]. At the same time, other technologies such as Raman spectroscopy can identify more promising microplastics. Incorporating microscopes can detect microplastics of smaller sizes. In addition, the combined microscope can also detect with a spatial resolution up to the sub-micron level as reported in the study [65,71,72,73]. Raman spectroscopy has the greater advantage that wet samples can be simultaneously analyzed and identified [74,75]. Polymer and organic additives pose a problem to the environment because they can produce spectra and hinder the identification of polymers. Some researchers are trying to build weathered plastic containers so they can be identified [76].
Microplastics can be identified with the latest solutions through the three-mass spectrum analysis technique [77,78]. Several previous researchers identified and measured with different techniques such as Pyr-GC-MS, TGA-MS, and TED-GC-MS [7,79,80,81]. Analytical thermal technology does not have to treat the initial sample. Limited particle size can be analyzed and processed by manually feeding the pyrolysis tube [75]. However, application through this technique can damage microplastics' size, shape, and color information, which are important elements in identifying microplastics. A new solution for size-independent analysis of microplastics was recently proposed by [82]. The polymerization method used for heating with the help of polyethylene terephthalate (PET) and alkali microplastic polycarbonate (PC) can measure and determine the compound making up the block [82]. This technique is the best step for separation, identification, and calculation of microplastics [77]. However, plastics containing major structural and compound compounds require further verification when using this method.
Alternatives to high-throughput microplastic analysis can be performed with several technologies such as 1H NMR spectroscopy, technologies including NIR spectroscopy (NIRS), and hyperspectral imaging [83,84,85]. However, the use of technology requires little treatment on the initial sample. In addition, this technology has weaknesses to limit the time of its application [7]. Its specific specifications and sensitivity coupled with NIR spectroscopic chemometrics have been unsuccessful [83]. At the same time, the 1H NMR method under ideal conditions can remove organic matter and avoid signal fluctuations from the sample [85]. Organic matter in environmental samples is completely impossible to remove without damaging the microplastics. While the application of 1HNMR for microplastic analysis in soil, the analysis system is still questionable [21]. Size distribution to determine the chemical composition of microplastics can be informed using secondary ion mass spectrometry time-of-flight (TOF-SIMS) [37,86]. However, only the known composition of microplastics can be analyzed by this method.
3.7. Sampling and analysis problems
There are various strategies for analysis to raise debates in several analyses, especially mass/volume. Most of the analytical tests used are statistical problems, especially those related to the level of accuracy and cost of analysis, which has resulted in this testing strategy being chosen. If the number of selected analysis samples is the smallest, then the result of the representative is the worst. However, on the other hand, further identification can be costly and time-consuming for analysis. The results of the review carried out in this work indicate that very few recommend a minimum representative sample size for extrapolation and reasonable analysis [21]. Density separations reviewed in several previous studies show that the mass of samples selected for analysis varies widely, ranging from 10 g to 1 kg. In most studies, the mass of the tested sample is not determined, and the analytical volume of the sample being measured is also not determined. The results of the alkaline sediment test analyzed by weighing have been discussed in [87]. The sediment analysis tested usually uses a weight of 50 g, 100 g, and 200 g, which is a reference in analyzing microplastics in the soil.
Furthermore, it is explained that the mass used can be in the form of items/kg (dw), and the mass of the sample being tested is a number that can be divided by 1 kg. On the other hand, the concentration level of microplastics produced from various places varies greatly. Therefore, the regional background has a value that must be considered in determining the test results with a minimum number of samples.
Identification of the definition of microplastic can be done very well but has different variations and sizes based on the technique of analyzing samples from the environment. The variability is not limited to the edges, but the microplastic size must be taken from the bottom. The use of filters through meshes often has different purposes, especially during the pre-treatment of microplastics, for example, during the selection and removal of microplastics of limited size. The sieving system is not enough to do with 5 mm but must go through 1 mm and 2 mm, which can meet the definition of microplastic. In general, the definition of soil should be given more attention and requires sieving of 2 mm according to the upper sand limit as is done in some countries even less than 1 mm [5]. However, if this analysis was carried out on microplastics, it will be possible to remove some parts of the microplastics. To ensure comparability with data from the reported environment, it is recommended to sieve < 5 mm and < 1 mm soil samples [5]. Furthermore, the abundance and size of microplastics recorded in several analytical studies are carried out depending on the size of the microplastics [64]. The FTIR size limitation is practiced according to the size of the microplastic transferred and captured through tweezers.
Meanwhile, for microplastics with a size of ± 1 m, the Raman spectrum can be used. The microplastic analysis is currently targeted to reach a size of ± 25 m using the TOF-SIMS method. TOF-SIMS is carried out after going through pre-treatment and then filtering the microplastics through a membrane filter. However, filtering using a microplastic membrane appears to have a significant difference. The most commonly used membranes are polytetrafluoroethylene (PTFE), metal filters, fiberglass, nylon, and quartz. The comparison between nylon, glass fiber, and PTFE membranes lies in filtering because it is very difficult to filter through water. This is because the surface characteristics are hydrophobic [24]. In addition, PTFE can harm the environment, so using a filter membrane is more advisable. The recommended filter member is only intended for microplastic samples identified by heating. The glass and quartz membrane fibers found in a recent study showed that they could be released during the filtration process, which could cause a major disturbance in the identification of microplastic [24]. Thus, it is advisable to use metal filters such as Anopore, especially during the microplastic filtration.
The potential risk of contamination from microplastic samples is very possible because microplastics are ubiquitous, especially in the environment. Plastic samples taken from the environment are the highest as reported in several studies [8,21]. Thus, it is necessary to take precautions to apply to all processing procedures. Microplastic analysis requires a clean room since there are so many microplastics in the air, and they cannot be stopped. The equipment must be cleaned first using ultrapure water through heating at high temperatures to remove the potential for microplastics [8]. In addition, the use of plastic should be avoided; otherwise, a blank test is necessary. During analysis and sample processing, exposure of the sample to air should be minimized, and it is recommended to cover it with aluminum foil [18]. The use of synthesis for all stages of the process is also avoided, and it is preferable to use nitrile or cotton jumpsuits [88]. Determination of the concentration level of microplastics must be carried out properly. Pollution descriptions based on the abundance in microplastic/kg soil samples or via mass concentration of microplastics/kg may be considered. A review in this study shows that abundance in characterizing microplastic pollution was more prevalent in previous studies. However, it is recommended to report the abundance of microplastic mass in soil matrix samples. As in most cases, comparability considerations are made through the sample pollutant in the environment. This statement can provide experiments and simulations on exposure to microplastic concentrations in the room, making it easier to do in the laboratory [48]. However, the comparison of the concentration of microplastics from different soil types and areas with different sampling systems and direct analysis can cause an effect on the concentration, so it needs to be studied further.
Analytical methods that can be used for microplastic analysis are currently developing rapidly. However, it has not been fully able to overcome the challenges posed by microplastics from a more complex environmental matrix, so further improvements need to be made. The reported concentration levels of microplastics must be more scientific and thorough so that data repetition does not occur. Thus, the procedure for sampling and analysis is recommended for microplastics in the soil, as shown in Figure 2.
4.
The latest in soil microplastic technology
4.1. Type of microplastics in soils
Microplastics found from various sources can be absorbed by the soil. However, the types of microplastics were found to reflect the use and local activity of making them close to the atmosphere [89]. The emergence of microplastics with correlations and types is found from regional human activities, so that it has provided various possibilities in studying the sources of microplastics in the soil. On a spatial or temporal scale, sampling locations, dispersion distances, and sources are very likely to experience shorter transfers to the atmosphere [72,90]. Furthermore, the type of microplastic greatly determines the impact produced when the terrestrial system [91,92]. The effects of microplastic films are very common on agricultural land [93]. In addition, the different characteristics of microplastics can cause transportation to be disrupted [63,64].
4.1.1. Fractions
Microplastics have a fairly complicated size because the definition of microplastics itself has sensitivity through researchers' analysis and extraction methods. Targeting microplastics in early studies, especially in the environment, can provide a clearer definition of microplastics. The particle size of microplastics is less than 5 mm. However, the minimum microplastic particle size is associated with the method used in collecting, identifying, and pre-treatment of the sample [8,63]. After taking the soil sample, it is sieved first, and the minimum microplastic size is 0.1–2 mm based on the mesh size used, as shown in Table 1. The separation of the microplastic particle size from the soil during the pre-treatment process must be determined by the size of the filter pores used. The use of filter pores with a certain size aims to vary the transfer with a size of 1–2 mm.
Meanwhile, filter nets are carried out for smaller filtration, i.e., 1.6–2 m. The recording of fractions of various sizes of microplastics shows several different variations, as shown in Figure 3. Microplastic particle size smaller than ± 1 mm is the most studied previously, especially in the soil environment. Meanwhile, the 0.5 mm microplastic size shows 99.8% of the particles obtained from several places on the city's outskirts [56]. The size of 150–250 m is the largest collection in Spain, especially around the city of Valencia [23]. Meanwhile, the size of microplastic < 100–300 m is to collect 32.1%–69.3% and particles from cultivated soil by 18.3%–48.2%. The size of microplastics and as their number increases, the trend of microplastics also decreases [94]. Most of the microplastics found on agricultural land are 0–0.49 mm or 81% [36]. The results are similar to those found in the Tiber plateau, the Swiss floodplain, the farmlands of Nanjing and Wuxi, and the Chinese city of Wuhan. Where smaller sizes of microplastics are more commonly found than soil samples [24,29,38,56]. Smaller sizes of microplastics can be dangerous, especially at orgasm, because they have a larger surface area to absorb toxic chemicals so they tend to be eaten by living creatures quickly if it is not conducted carefully [95].
4.1.2. Identification
Sources of pollution from microplastics need to be traced by careful identification. In general, there are several types of polymers found in the soil, such as polyester (PET), polystyrene (PS), polyethylene (PE), polyamide (PA), polyvinyl chloride (PVC), and polypropylene (PP). The most common polymers found are PP and PE, as shown in Figure 4. PE plastic mulch is the most common microplastic found in agricultural land in China, especially Xinjiang [28,39]. Meanwhile, the most common microplastics found in the plains of Switzerland are PE and followed by PA, PS, and PVC [29]. Total polymer donated from PE reached 75%, PP 18%, and PA 5% found in Hangzhou [55]. Meanwhile, the most common plastic polymers in Shanghai and Franconia are PP and PE [40,43]. The most commonly used polymers, especially in agriculture, are PP, PVC, PET, and PE [96]. Agricultural sources can link polymer types such as PET, PVC, and PE to become more transparent, green, and black that can be used for agriculture. It is widely produced and used as chemical fiber since polyester can be used for product packaging and plastic bottles. The application of polyamide can be carried out on synthetic fibers as found in some areas of Wuhan 32.5%, Boding 30.2%, and Hebei 28% [2,37]. The proportion of PVC present in microplastics in the soil is the highest at any waste facility in Sydney [57]. In addition, the definition of the compound was not found from the results of the identification of microplastics reviewed from several kinds of literature, such as synthetic rubber, natural latex, and plastic [1,29,42].
4.1.3. Shape
Observations of the commonly classified microplastics types include fiber/line, pellet/spherule, film, and fragment/sheet [8,95]. 22 studies show various benthic microplastics in the soil, as shown in Figure 5. Most studies state the highest proportion is fragments and fiber. Microplastics are currently largely fragmented by contributing 86% of microplastic particles, especially in the resilient agriculture tab [23]. Numerically dominant fragments have also been found in agricultural land in Shihezi city by 80.6%, cultivated land in Yunnan of 60.6%, Hangzhou of 52.3%, and Wuhan of 51.3% [28,55,56,94]. Plastic waste and packaging are easy to associate with microplastic fragments. Large plastic debris is easier to decompose and break in the presence of mechanical forces, biodegradation, and ultraviolet radiation. Experiments with weathering in the laboratory show that exposure to UV between 12 and 2 months of mechanical abrasion and for PP pellets could produce as much as 6084 and 1061 pellet particles [55]. In addition, bottles and plastic bags can be used for fertilizers and pesticides commonly found on agricultural land.
Sources of fragmented microplastics in the soil are also very likely to contribute. The discovery of very dominant fibers in samples and mud has provided evidence of the accumulation of microplastics, especially in agricultural land from sludge disposal [44]. The findings on soils around Washington, DC are predominantly fiber reaching 77%–94%, in Lake Dian of 92%, and Nanjing of 42%–87%; so, it is very possible to have a relationship with increased production of synthetic materials such as upholstery, clothing, and carpets. Fragmentation and fiber in microplastics have the same proportions in the soil as reported [52]. Meanwhile, the Lahn river plain, Germany, Franconia, and the Tibetan plateau have many fiber for all microplastics [1,38,96]. The association of films with mulch and plastic packaging has become a global agricultural practice. Some areas have used it for more than 30 years so that microplastics can be a major source, especially on cultivated land [28]. Meanwhile, the abandoned salt field shows that microplastic pellets are more abundant, reaching 76.3% than other forms [97]. The association of pellet particles with these care products such as cosmetics, cleaners, and industry [95]. In addition, fiber balls made with the new grade are made because these fibers are often spherical. These fibers come in many colors and usually appear in bundles [1].
4.1.4. Color
The color division of microplastics in this study is divided into four categories. Microplastics with various colors and dominant colors were significantly more varied in several previous studies, as shown in Figure 6. Microplastics with transparent color collected from the soil reached 51.68% [38]. Cultivated soil collected from Yunnan was significantly more transparent in color and was 46.3% as reported in the study [94]. Meanwhile, the contribution of bleaching colored plastics, single-use plastics, and plastics from fisheries such as nylon nets and fishing lines can be used as sources of microplastics with transparent colors [8,95]. Microplastics belonging to the white group obtained from the soil around Nanjing reached 38%–70.4% [24]. However, most of the colored microplastics were obtained from the suburbs of Shanghai [40]. Meanwhile, microplastics collected from Nanjing and Yunnan farmlands with highlands contributed to colored microplastics [24,94]. The colored microplastics collected by Franconia reached 40% [96]. The production of color-added plastics has attracted consumer interest [95]. The possible differences between microplastics found in deep and shallow soils need to be studied. The collection of microplastics around the city of Shanghai with black proportions on shallow soils showed a higher 39.39% compared to other particles. Meanwhile, microplastics collected from deep soil with transparent particles reached 46.30% [40].
4.2. Microplastic from aquatic system
Global garbage disposal into the sea by humans is mostly plastic waste [14,98,99,100,101]. Microplastics have polluted the sea and fresh water and penetrated the environment for the most part [30,102,103]. The environment can become mixed into microplastics from a variety of sources. Meanwhile, soil plays a bigger role in storing microplastics. The characteristics of microplastics present in the environmental matrix can reveal several different facts when it comes to the distribution and source of microplastics. Fibers and microplastic fragments have small particle sizes, especially PE and PP, commonly found in the environment [3,8,67,104]. The discovery of microplastics in the soil matrix has physicochemical, composition, and morphology and has similarities with those in the environment. Fibers and fragments are microplastics commonly found in the soil environment and have a chemical composition, especially in PP and PE. In addition, microplastic particles with a size of 1 mm were more commonly found in the soil as the particle size increased, so the trend indicated by microplastics decreased [8]. Microplastics found in soil environments have varying colors. Meanwhile, transparent and white colors have a higher proportion, especially samples from soil and environments.
The composition and characteristics of microplastics obtained from the environment and soil have the same pathways and interconnections [22]. The main correlation of the microplastic components of the soil and environment has the same population source [105]. In addition, the soil environments are major sources of waste and sludge which have undergone inadequate recycling [6,105,106]. Irrigation, a source of water from reservoirs, rivers, and soil can transfer the content of microplastics into agricultural land through irrigation flows. However, a detailed understanding of the associated resources has not been accepted with knowledge of the sources and interconnections in the soil and water environment. In addition, interactions related to quantitative data information are also still a step.
It should be noted that the size of the microplastic particles is highly dependent on the size of the sample being analyzed [8,30]. Samples of seawater, surface water, and fresh water were obtained from the volume of water and plankton, and the filter results can be around 100 or 330 μm [14]. Soil and sediment sampling does not necessarily require a filter. However, most of the microplastics with a size of 1 mm are found in the soil and water environment, so it is very likely to have a relationship with the operation of detection technology. Some particle sizes in microplastics are so small, which are impossible to record or detect. Microplastic analysis using TOF-SIMS below 35 m found in the city of Baoding which has a small size of ± 15 m by 49% [37]. Therefore, overall comparisons can be made with a more mature analysis of microplastic technology. Several previous studies stated that the concentration of microplastics was too high because the sample collection and analysis methods were not sufficient. In addition, partial nanometers on microplastics and polymer types were not tested on all suspected particles. Most of the studies noted that microplastic pollution could be based on the number of concentrations with the size of the population data information could be studied better. The types of microplastics to be analyzed should also be further clarified.
5.
Microplastics' sources and transfer
5.1. Source of microplastic
The very large microplastics present in the soil can lead to accumulation. However, these microplastic accumulation level can be easily detected without having to stop them, as presented in Figure 7. The technologies widely used for agricultural production globally are polyethylene (PE) and polyvinyl chloride (PVC). The economic benefits obtained are better, especially for fruit quality, larger, and using water more efficiently. Plastic film for agriculture is a global market with an estimated yield of 4 million tons in 2016, and by 2030 it is predicted to increase by 5.6 million tons [28]. Agricultural land around the world that has been covered by plastic mulch is estimated at 20 million hectares and the largest is found in China which accounts for about 90%. Removing all the mulch film present on agricultural land is difficult and takes long. Therefore, a more effective way is to place horses, especially females, on land covered with mulch film. The correlation level of microplastic residues and plastic mulch on agricultural land globally was significantly R2 = 0.61, and p < 0.001. This implies that plastic film mulch is the most important source on agricultural land [28]. Documentation of transparent and white microplastics collected on-farm soil surfaces has been reported by [1]. In addition, agricultural land in south-eastern Germany found 206 microplastic items/ha and ± 0.34–0.36 microplastic items/kg. Most of the microplastics that have been identified are PE film types [96]. Meanwhile, a significant increase in the concentration of microplastics occurred in each period. The increase in the abundance of microplastics in Shihezi city was in line with the increase in mulch in the same period since the last 5–30 years with a range of 10.10–61.05 mg/kg [39].
Plastic mulch debris with large pieces remaining spontaneously on agricultural land surfaces can be exposed to ultraviolet which can cause photodegradation and is very brittle [28,105,107]. Plastic waste found on agricultural land has a shear force and will occur when cultivated so that fragile microplastics will be easily fragmented [96]. Plastic fragments that have been destroyed will be buried in the land to form a thawing and freezing cycle. Moreover, the resulting interactions with orgasm are buried in the ground and subsequently become destructive. Eventually, the soil will store enough microplastics to threaten wildlife and food security [28]. However, global application in recent years has grown very rapidly, and the hidden dangers for microplastics deposited in the soil can be reduced even more.
Microplastic debris has been found in various ways in the soil environment because plastics can grow more and more. Meanwhile, the management system is inadequate or unplanned [14,20]. Microplastics found in soil are the same as those in waters, which are large amounts of plastic waste [5,108]. In 1950 and 2015, it was estimated that ± 6.3 billion tons of waste from plastic sources were produced worldwide. Whereas much as 4.97 billion tons were collected from landfills and neighborhoods adjacent to cities [109]. Waste management that is not carried out with general garbage found on the side of the road, illegal garbage dumps, etc. [18]. Previous researchers found many used bottles and plastic waste and fertilizer waste scattered on agricultural land. Microplastics generally have morphological characteristics, especially on agricultural land. This is because the agricultural land has undergone weathering to prove the hypothesis in this work [39]. However, the calculation for the amount of microplastic from illegal or indiscriminate dumping of waste on the ground is still very small. Microplastics that enter the soil can be through wind, flooding, and runoff. Thus, the literature has not found quantitative studies on microplastics that have changed and become soil due to illegal disposal.
Wastewater and sewage sludge are the main causes of pollution and accumulate in the soil with repeated use of mud [48]. Microplastic wastewater treatment systems can be found from various sources [32]. Care products, cleaners, and polymer fibers produced from textile washing are sources of microbeads waste. In addition, processing plastic from leaky factories and microplastic from car tires can be environmental pollution waste. The management process of this type of microplastic can lead to deposition and drainage. This is because the management system is through waste disposal. Most of the separation of these microplastics can go through a sedimentation process to be carried into the mud [32]. Mud which has trace elements and organic matter, which is the final product of the factory, can usually be used for fertilizers that can be applied to agricultural land. The utilization of sewage sludge is 50% for agriculture, while disposal of sewage sludge on agricultural land in Finland and Ireland reached 72% [5]. In addition, the disposal of sludge with an improper system can harm microplastic pollution in the soil environment. The collection and management of 28 waste samples carried out in China was around 1.60–56.4 × 103 items/kg with an average 22.7–12.1 × 103 items/kg [110]. The concentration of microplastics in the soil in one year can reach 3.5 particles/g after being deposited 5 times with a sample size of 200 dry tons/ha [54]. Meanwhile, in a different study, it was reported that the incentives shown on agricultural land in China reached 23 tons/ha of sewage sludge per hectare and the concentration level reached 7–43 microplastic particles/g [47]. Evaluations in various fields carried out with various sewage sludge applications have shown a fairly large amount of microplastic content [23]. The amount of increased light density of microplastics in the soil from each application reached 280 and 430 items/kg, respectively [23]. Although reports of microplastics have different results, the facts say that the sludge used can produce pollution and microplastic pollution.
Compost from soil amendments can provide microplastic pathways in the soil. The application of organic waste to agricultural land for nutrients after fragmentation can be re-established. Agricultural production through this method is an environmentally friendly system. Meanwhile, compost sourced from biological waste can contain plastic and is indicated as a result of improper and inadequate waste disposal and classification [5]. The composting carried out at the factory contains a lot of plastic fragments that can be seen with the naked eye reaching 2.38–180 mg/kg. Meanwhile, the presence of microplastics in organic compost is also described in [5]. The organic fertilizers produced from biological waste contained many microplastics with a small size of about 1 mm with 14895 [111]. The high export level of microplastics occurs due to the use of biosolid applications even though they follow applicable laws [41]. A recent study that found the total concentration level of microplastics in soil reported around 545.9 out of 87.6 items/kg after the release of compost sludge at around 15–30 tons/ha and was significantly the highest in soils [64]. This amount has made compost one of the most important microplastics that enter the soil. In addition, compost around the world, in general, can be transported into compost sludge that cannot be ignored.
Water sources with microplastics, especially in irrigation canals, have been well confirmed [36,112,113]. Irrigation canals are a source that can drain microplastics because they can involve reservoirs, groundwater, lakes, and rivers globally. Water sources found in some areas are not found because waste water uses a lot of irrigation channels [5]. Most microplastics can be removed by processing and treating waste that still has a high concentration of microplastics [110,114]. Extensive and detailed research on microplastics in rivers, groundwater, reservoirs, and lakes is still very high [8,33,115]. The transfer of microplastics hidden in the soil can be done by irrigation canals, forming a source of microplastics. In addition, irrigation can also be through flooding and runoff, which is the most important route for transportation for the accumulation of microplastics to the soil [5,49]. Indiscriminate garbage disposal on the side of the road can cause flooding and road runoff so that the roadside can experience abrasion. In addition, it may contain synthetic polymers and rubber that enter the soil [49]. Some of these microplastics can turn into microplastics that enter the soil environment in various ways. The largest microplastics found on the surface of road dust are found in several countries such as Japan, Nepal, and Vietnam [116]. Meanwhile, wear emissions calculated on the road network in Germany show that roadside haulage reaches 66%–76% or 57,300–65,400 t/a including road flows and runoff [117].
One of the most important ways of deposition can be done by the atmospheric transmission of microplastics to the soil as reported by [30]. Meanwhile, the reported estimates of fibrous microplastic deposits outdoors can reach around 0.3–1.5 fibers/m3 [106]. Mountain catchment in remote areas has a daily relative number of 249 fragments, 44 fibers, and 73 sheets of film stored daily [6]. Confirmed atmospheric deposition from microplastics has been reported in several studies. However, large sampling rates and long-term monitoring still need to be determined so that the contribution of microplastics and their transmission to the soil is better. Some previous researchers have roughly reported the presence of microplastics. The degree of degradation and the driving forces for the generation of secondary microplastics for pre-treatment is unknown, especially in the soil environment [72]. The degree of physical force may have differences, especially for radiation and shear forces on the ground surface. It is still under pressure because it is still buried deeper underground [96]. Simulations through experiments to determine the level of degradation of microplastics still need to be carried out because of the different strengths and environmental conditions.
5.2. Microplastics in soil transport
The link is a way of migration that can expand for the influence of microplastics in the soil to involve vertical and horizontal migration, especially for non-biological and biological transportation [95]. Loss of soil surface can be caused by microplastics that enter through surface runoff and are also blown by the wind [33]. Soil filled with microplastics has proved that microplastics can migrate to the bottom [40]. The pores of the farm make it possible to transport microplastics by several meters. Meanwhile, microplastics with large sizes with strong resistance to biological disturbances and agricultural activities can form parts in migrating into the soil. Bioturbation sourced from plant roots in the soil can affect microplastics in migrating, including (such as root expansion, root water extraction, root movement, and others). The contribution of fauna in the soil to microplastics' horizontal and vertical transport has been described in [48]. System transfer through collemba species and worms in the spread of microplastics can be through extraction and adhesion [91,118]. In addition, the soil leveling that appears due to the dry climate can provide access for microplastics into the soil [33].
6.
Microplastics' effects and dangers involved in soil ecosystems
Microplastics can affect biophysical properties, especially for soil structure, soil nutrients, pH, fertility, and aggregates in the soil [4]. Gradually microplastics are integrated into soil aggregates to varying degrees of integration, especially some types of fragments and types of tightly [12]. Soil structures with aggregates have an important role in shaping the habitat of soil organisms [19,119]. Microplastics with a low density for low yields have an indirect effect based on the overall different soil systems, as shown in Figure 8.
Too much and available information about plants will respond to the presence of microplastics. The addition of microplastics by altering the physical properties of the soil has been studied recently, where the hydrodynamics and the activity affected can change several soil physical parameters, depending on the size and shape of the microplastic particles [91]. The addition of high-density polyethylene PET, PS, PP, (PEHD), and Polyester (PES) found in the soil decreased. At the same time, the density is shown in the rhizosphere increases [91]. The properties of leaves and roots of plants with total biomass changed by PS will cause a significant increase in root biomass. Meanwhile, observations on plants exposed to PET, PP, and PEHD decreased more [91]. Exposure experiments used to observe significantly different groundwater aggregates can be compared with the control system [73]. Microplastics that accelerate groundwater evaporation can be carried through water movement channels, and the water concentration level increases [120]. Accumulated microplastics can damage the integrity and structure of the soil [120]. The addition of microplastics can change the pH in the soil. Exposure to HDPE planted with Lolium after 30 days showed that the soil pH decreased by about 0.62 [73].
Composite pollutants found in the environment are part of microplastics because other chemical pollutants are often combined into heavy metals, persistent organic pollutants, and dioxins [7,20]. The adverse effects found in plants are a combination of polymer additives [19,56]. The frequently used additives can be defined and can present major risks such as plasticizers, antioxidants, heat stabilizers, and flame retardants [8]. The soil's parameters and physical chemistry can change in the presence of microplastics, especially in the stadia and adhesive system, so that plant growth can be affected [55]. The PE film residue level has around 584–2284 pesticides/g than soil 13–32 pesticides/g [121]. Simulations with earthworm experiments in which ryegrass is grown show the impact of pollution from microplastics on the top and bottom of the soil [73]. Biodegradable polyethylene and polylactic acid sourced from microplastics have high density and fiber with decreased ryegrass growth rates [73]. Genotoxicity and ecotoxicity investigations on microplastics can be reported that microplastic concentrations of 100 mg/L can significantly inhibit the growth of Vicia faba and have the potential to inhibit cell wall pores of nutrients [122]. Different studies reported that microplastic mulch film and polyethylene and macroscopic residues harmed wheat growth [123]. At the same time, research on root biomass is greater when it is contained in HDPE [91]. The level of biomass obtained will be higher for individuals who are getting less and fewer water resources, nutrients, and space in plants [91].
Health and ecology can be at risk due to exposure to microplastics and have become an issue of great concern today [12,20,49,124]. Studies on the food chain confirmed the hypothesis that microplastics could transfer food at low nutrients. In addition, transfers can also be made to predators for higher nutrients through the food chain [12,32]. The transfer system of microplastics from the soil to traditional zoos, especially in those that have been proven in research [25]. The abundance of microplastics showed an increase from 0.87–1.9 grains/g to 14.8–28.8 grains/g to worms and 82.3–129.8 grains/g to chickens [25]. Evidence in fuzzy studies of microplastic transfer systems with terrestrial food chains is rare. The greenhouse factorial tested with microplastics for four different sizes reported that earthworms could increase microplastics. At the same time, small PE microspheres can be transported downwards to a large degree [119]. The discovery of microplastics through small invertebrates such as springtails, mice, snails, and nematodes, has suggested the natural transfer of microplastics [125,126,127]. Microplastics that enter the soil can also be carried out by these animals, possibly through egestion, casts, and burrows from host parts [119]. Movements with potential consequences for exposure of microorganisms to microplastics during their stay until they enter groundwater [64,119,128]. The detection of microplastics was recently carried out in human faces, which confirmed that microplastics had been present in the human digestive tract [129,130]. The food chain is found in the human digestive tract. The source and path can move. However, through other routes, it is also possible to eat salt, breathe air, food, and drink water contaminated by microplastics [30,131,132]. Microplastics may pose unclear human health risks [130]. The effects of microplastics on the human gut are very, very bad [133,134,135]. Consumption of microplastics on health risks will also be exposed in poultry such as oxidative stress, inflammation, and particulate toxicity that can give tumors [25,136]. However, the risk of microplastics in the food chain, especially humans, is the most urgent trait to be addressed immediately [56].
7.
Conclusion
The microplastics pollution will continue to increase in the future due to the increasing production of plastic along with handling and very disproportionate actions. The review of this study has investigated specifically the potential sources, methodology, predictions, and occurrences of microplastic contamination in soil. In addition, research on the recovery, reduction, and control of microplastics in the soil is discussed. The emergence of microplastics occurs everywhere, especially in the environment. However, there is very little global monitoring of microplastics in soil. Difficulties and inappropriate technicalities in performing complex particle analysis are barriers to microplastic research. The research on microplastics in the soil is mostly focused on agricultural areas. The microplastics in soil have an abundance of 1–5 orders depending on the size of the region. The highest abundance is 18,000–41,000 items/kg with an average of 24.00 items/kg obtained from the mud of the Chilean region. Fragment and fibers in microplastics such as PP and PE have < 1 mm particles, the most common microplastics found in soil. The appearance of microplastics in soil has many kinds and different colors. There are several similarities in the composition and characteristics of microplastics found in soil environments. These microplastics are found from various sources and are very important to be quantified. Only recently recognized sources of microplastics are sewage sludge, litter, compost, atmosphere, and irrigation. The nature of microplastics and environmental factors have interactions in controlling the retention and migration of microplastics in the soil. The type of land used influences the concentration of microplastics. At the same time, soil properties such as dissolved organic content, pH, and heavy metals are not the main factors in influencing the abundance of microplastics. The multiple migration behavior and mechanisms of microplastics in soil and water environments also need to be determined. Quantification and carbon of microplastics and regional emissions of microplastics in soils are very important issues to be discussed.
Acknowledgments
This research is supported by the LPPM Universitas Syiah Kuala, Research institutions, and community service with the contract number of (721/UN11/KPT/2021).
Conflict of interest
All authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.









 DownLoad:
DownLoad:









