1. Introduction
Breakwaters are maritime structures whose main objective is to shelter harbour basins, harbour entrances and water intakes against waves and currents. Its principal function is to dissipate wave energy and /or reflection of wave energy back into the sea [1]. Figure 1 illustrates two rubble-mound breakwaters whose armour layer consist on tetrapods 1(a) and Antifer cubes 1(b).
During the design process of these structures, scale model tests are required many times, in order to evaluate their hydraulic and structural behaviour. Examples of this are stability and overtopping physical model tests, where the breakwater design is optimized, with respect to crest level dimensions, size and density of the armour layer units. During stability tests, damage progression is assessed for different incident wave conditions, making use of visual observation, video and photographic techniques, or mechanical profilers when profile surveys are needed. In most cases and in the majority of the testing facilities, visual inspection is the most common technique.
However, there are also some drawbacks in damage assessment. Accounting for armour unit displacements and movements, just based on visual inspection, is a task very dependent on the experience of the technician. Moreover, tests performed by different technicians will always have differences in damage evaluation, since each person has his/her own interpretation despite following prescribed criteria and guidelines. Additionally, the problem with profile surveys using a mechanical profiler, is the number of surveys to be carried out which is always limited, since the procedure is very time-consuming. Therefore, image processing tools based on the use of photogrametric methods can be a good alternative in order to ease and speed up those tasks.
Photogrammetry is being increasingly used in many scientific and technological areas, which for example, may range from the characterization of geographical and geodesical systems to the archaeological and anthropological subjects, from engineering branches such as structural, civil and mechanical engineering to medical and biomedical sciences, to name just a few. From the literature review carried out we can find different illustrations of this increasing trend, independently of the specific features associated to the data acquisition systems. A brief study concerning the possibilities of using less expensive mid-range cameras in applications of close-range photogrammetry was presented by [2]. The focus of its work is the creation of virtual spatial models of constructions, historical buildings and facades, models of small objects industrial equipment, reconstruction of traffic accidents and crime sites and the modeling of the human body. An integrated view of systems that combine laser scanning and close range photogrammetry technologies was presented by [3]. In that work special attention is devoted to the estimation of systems uncertainties. The understanding of the basic theory and best practices associated to laser range scanners, digital photogrammetry, processing, modelling are also aspects addressed, in the main context of information augmentation and uncertainty management. The progressively decreasing field of view, with some critical aspects such as the depth of field becoming narrower, heavily affects the possibility of accurately calibrated cameras. This is a problem that was addressed in the work presented by [4] through a comparison of several calibration patterns included into an open source software library. As for more focused works in the engineering field we can refer among others, to [5] and [6]. In the first case, digital elevation models from soil surfaces with high spatial and temporal resolution were generated using digital photogrammetry, with the purpose of measuring erosion rates on complex-shaped soil surfaces under laboratory rainfall conditions, whereas in the second, the authors studied the vertical deflection measurement of bridges using digital close-range terrestrial photogrammetry. The measurement goal is an important objective in photogrammetry, and in many practical applications we can find a perfect illustration of it. Measuring building features and topographic environments constitute examples of technical fields where photogrammetry has an important role, as we may conclude from the works by authors [7-10]. The possibility to obtain three-dimensional representations, and together with the use of additive manufacturing technology, producing replicas of original cultural, historic and geological artifacts, can also be closely related to a preliminary process of acquiring the geometric characteristics of the object through photogrammetric methods. Alternatively the goal may be the constitution of a documentation repository of this valuable heritage. The works presented by [11] and [12] illustrate perfectly well the cross-link between the use of photogrammetric techniques and the wide area of social sciences. Another different field wherein the photogrammetric techniques are applied with success is related to the biometric applications. Illustrating these applications we can refer the work developed by [13] where a specifically designed photogrammetric 3D scanner of the human body, consisting of eight cameras with a resolution equal to five megapixel, equipped with sixteen millimeter wide angle lenses; with four white light illuminators, of one hundred watt each. The authors carried out tests on entire dummy and human bodies, to demonstrate the profitability of the technique for textile applications.
From the literature review carried out concerning the specific subject of the present paper, it is possible to conclude that there is an effective need to developing research studies in order to improve the detection and characterization of damage on this type of modelled structure. Very recently, it is possible to refer to a few published works in this field. [14] presented a design exercise of upgrading a typical rock armoured revetment by modifying the structure profile and adding structure elements. A simple comparative cost optimization analysis of the various upgrading solutions was carried out, and conclusions were drawn concerning the preferred upgrading concept valid for the structure studied and the uncertainties related to upgrading design.
The importance of physical model tests is underlined due to the lack of reliable desk study tools for rubble mound upgrade design. Wave basin tests have been performed by [15] to assess the effects of oblique waves on the stability of rock slopes and the stability of cube armoured rubble mound breakwaters. Physical model tests were focused on wave directions between perpendicular and parallel. The damage to the armour layers was recorded by taking digital overlay photographs before and after each test and counting the number of stones and cubes that were displaced more than one unit diameter. A number of tests with rock surveys of the armour layer envelope were also performed with a mechanical profiler.
In [16] a study is described of the performance of a laser scanner Faro Focus 3D on the detection of short-term changes in Cubipod armoured breakwater round heads. From the tests carried out using physical models, they concluded that terrestrial LiDAR (Light Detection And Ranging) can be considered an accurate technique for damage monitoring in breakwaters. It was considered that further research would be required to establish whether this approach is applicable to other LiDAR datasets and also for data acquired in real scale breakwaters.
Despite the good results obtained in the above discussed studies, it can be said that damage assessment depends mainly on the armour unit visual counting method or on very expensive equipment.
The main objective of the present work was to develop a photogrammetric method in order to obtain a robust tool for damage assessment and quantification of rubble-mound armour layers during physical scale model tests. The procedures underlying this method were implemented using an open source code in order to enable an effective dissemination of this computational tool.
The proposed method only requires two digital photos, taken respectively before and after the scale model test. The present paper follows on by considering in section 2 an overview of the case study physical modelling aspects. The methodology used to proceed with the photogrammetric analysis in section 3, will is then be introduced. The results of the application of this approach are present in section 4. Finally, conclusions and upcoming works are presented in section 5.
2. Physical modelling case study
Physical modelling is undoubtedly the closest representation of the real world, allowing the analysis of the complex physical processes involved in wave propagation and interaction with structures. In fact, physical modelling allows the simulation of wave refraction, diffraction, breaking, reflection, run-up, overtopping, as well as of wave interaction with structures or with moored ships [17]. In Portugal, different types of two-and/or three-dimensional physical model tests of harbour and coastal protection structures (Figure 2) are performed on a regular basis, such as: stability and overtopping tests; tests where wave induced pressures or forces on structures are measured; and wave disturbance or resonance tests (Figure 3). A significant part of physical scale model tests for Portuguese ports are carried out in the National Laboratory for Civil Engineering (LNEC). Up to the present, the Harbours and Maritime Structures Division (NPE) of LNECs Hydraulic Department has performed more than 250 physical scale model tests both in Portugal and in foreign countries.
Economical and logistical considerations require the selection of the smallest geometric model scale consistent with the desired accuracy of model results. The degree of accuracy which can be obtained by use of scale models is determined by laws of similitude, the detail of the model construction and the accuracy with which the incident wave can be generated and measured. Model and prototype must behave in a similar way as far as to geometry, kinematic or dynamic forces are concerned. The similarity of certain dimensionless numbers (such as Froude, Reynolds, Cauchy and Weber) in model and in prototype ensures these criteria are fulfilled. Since in maritime hydraulics, dominant forces are usually gravity and pressure, Froudes similarity law is commonly used for these types of models. Reynolds number is verified to ensure turbulent flow. In general, stability model tests use scales up to 1:50 being the values range 1:30-1:40 the most common ones. As previously mentioned, the main objective of the present work was to develop an effective tool for image analysis in order to assess damage evolution on the rubble-mound armour layer, during physical scale model tests. An important restriction associated to the test process was related to the fact that only two digital photographs were available, denoting the time instants before and after the test. In order to record these instant situations, it was used a DSLR (Digital Single-Lens Reflex) camera (Canon EOS 600D) fitted with fixed focal length lenses (Canon EF 35mm /2) was used. This setup is capable of acquiring images ranging from 0.35 megapixel to 18 megapixel. Three-dimensional physical model tests of stability and overtopping were performed in one of the LNECs wave basins, approximately 40 m long and 23 m wide. The model was reproduced at a geometrical scale of 1:30 (Figure 4), according to Froudes similarity law [18].
At the trunk, the primary armour layer consisted of a double layer of 4 6 t rock blocks both on the seaward and on the lee sides. At the head, the primary armour layer consisted of a double layer of 3 t Antifer cubes. Tests comprised two prototype still-water levels: (0.0)CD and +3.1 m (CD). Irregular waves according to a mean JONSWAP (Joint North Sea Wave Observation Project) spectrum were employed with significant wave heights (Hs) and peak periods (Tp), measured in front of the wave maker, ranging from 1 to 3 m and 8 s to 15 s in prototype values. Several photos of the breakwater head, obtained during this scale model study, were subsequently, subject to an image analysis, in order to identify armour units removal or movements, using an innovative photogrammetric technique. It is also important to note that images did not suffer any previous digital manipulation, such as for example, light correction.
3. Methodology for photogrammetric analysis
Digital photography is a powerful tool in the identification of the affected areas of the breakwater model. Additionally, the availability of computational resources, promotes an increasing use of image tools in the most various scientific areas of engineering and science, wherein a great research investment in new approaches and applications can be observed.
The digital image information is stored in pixel, which is the smallest unit of an image. An image can thus be conceptually thought of as a pixel’s hypermatrix structure constituted by the superposition of different individual matrix structures, whose significance depends on the system used. In the present work the RGB system has been considered.
In the following subsections, the methods developed to identify the areas where displacements take place will be presented.
3.1. Weighted conversion to grayscale
A grayscale image usually results from light intensity calculation of each pixel and can be represented by a matrix in which, each element has a real value between 0 and 255. However, in order to ease image reading and analysis, values are normalized by dividing them by 255. This yields values in the range 0-1, where 0 represents black and white is represented by 1. As referred, color image analysis would imply considering the existing information in the three matrices associated to each of the colour system primary colours. Working this colour structure would be very expensive and time-consuming from the computational perspective. For that reason, it is reasonable to convert these images into grayscale, converting the hyper-matrix structure into a single matrix with the same number of lines and columns. The most common conversion formula, often chosen due to its simplicity and speed is given by:
The result obtained is the average of the three primary colours and despite being a fast and simple way to convert to gray it is not very effective in the representation of luminosity. Taking into account that the colour perception of the human eye is obtained by the three colours average, it is of major importance to distribute the perception sensitivity according to the predominant colour. This predominance is given by the following descending order: green, red and blue. The conversion approach used in various image processing software like Photoshop or GIMP is given as:
|
Gray=0.3R+0.59G+0.11B
|
(2)
|
More recently, the colour distribution relation used by Scilab and SIVP pack [19,20] for grayscale conversion, is defined by:
|
Gray=0.299R+0.5587G+0.114B
|
(3)
|
According to [21] the difference between equations (2) and (3) is negligible.
By consequence the RGB color system can be interpreted as a finite vectorial space, where {R, G, B} is the basis, where a kind of”Gray”results from a linear combination on the basis {R, G, B}.
All conversion formulas in gray levels are designed with a specific goal, a kind of”Gray”, in the next section we will study a linear combination at the basis {R, G, B} to obtain the isolation of primary colors.
3.2. Primary colours isolation
The present case study involves the use of artificial armour units painted with blue and red primary colours (Figure 5).
The isolation of these two colours is of utmost importance to detect changes between photos of two consecutive experiments. It consists of the conversion of a primary colour to a grayscale level in order to detect the removed armour layer units. From the experiments carried out, this conversion was the best method to reduce the reflex effect present in several photos.
For a certain primary colour it is necessary to determine its c1, c2 and c3 coefficients
|
Primary colour=c1R+c2G+c3B,
|
(4)
|
which will, additionally, minimize the white colour resulting from the light reflection on the water and on the armour units (Figure 6).
Taking Figure 5 as an example, one can isolate the blue colour using
|
BW(i,j)=−0.5M(i,j,1)−0.5M(i,j,2)+1.5M(i,j,3)
|
(5)
|
Where BW is the grayscale level and-0.5, -0.5 and 1.5 are respectively the coefficients c1, c2 and c3, for the blue colour. The resulting image is illustrated in Figure 7.
With the grayscale conversion formula, one can isolate the primary colours in the photo.
3.3. Stratification
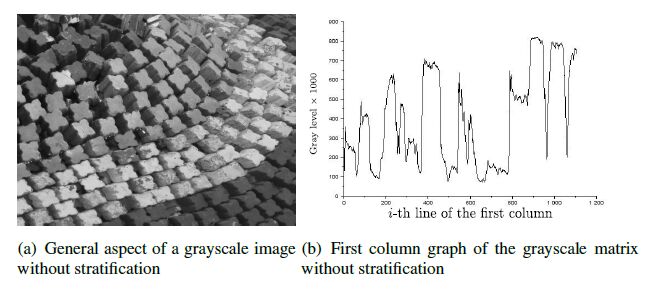
As previously mentioned, a grayscale image can be represented by a matrix, whose elements vary between 0 and 1. Figure 8 represents the original grayscale image, as well as its grayscale graphic for column 1, where the matrix elements have a continuous variation. The objective of the stratification is to convert grayscale values to previously defined level classes. An example of a class, composed of six elements ranging from 0 to 1, is given as
|
C6={0,0.2,0.4,0.6,0.8,1}.
|
Figure 9 illustrates the stratified image and its corresponding grayscale graphic for the first column of the grayscale matrix. It is worth noting that the original image quality is not compromised by stratification.
Stratification is an additional technique that may be useful for further undergoing types of analysis, which is the possibility of using grayscale levels that are not being used on the image composition, as markers.
At the moment, this technique is not perfect for stability evaluation experiments due to the difficulty of tracking the armour units with only two photos. However, it can be applied for the calculation of displacements, distances or rotations.
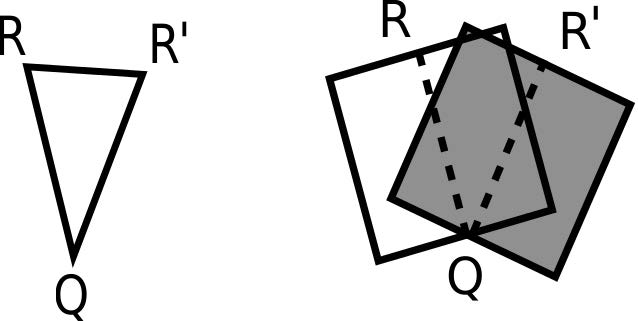
To illustrate this approach, we will consider a specific cube where a rotation is detected and we mark the same point, in both images (before and after rotation Figure 10), with a gray level not used in stratification (for instance, the correspondent to 0.3). In these images the marker is almost invisible, because it is only one pixel of colour, but very appropriate to the numerical detection because the gray level marker, we have taken, is only in two pixels (R and R') for the entire image matrix. Once two points are known we can estimate its distance.
Fixing an Antifer cube, photographed from the same point at different instants, as shown in Figure 10, and applying the stratification technique it is possible to evaluate the displacement of a point over the cube, from an initial position R to a final position R', ¯RR′=2.6 cm, by using photogrammetric measuring techniques. Here we applied a comparison with the cube’s edge. This displacement, results from the rotation of the cube over a fixed point at its basis (represented by the point Q at the outline-Figure 11).
When submitted to a wave force, applied over the breakwater model, the Antifer cube can rotate over a foothold, represented by the schematic layout illustrated in Figure 11. An initial point R is displaced to the position R' by rotation of the Antifer block over the point Q.
This stratification technique, enables us to evaluate the length ¯RR′. Once the chosen Antifer cube is subject only to a rotation, we have ¯QR=¯QR′=h, the cube’s height. From the cosines law we can write:
|
¯RR′2=h2+h2−2hhcos(ˆQ)
|
(6)
|
Simplifying (6), we get
and finally
|
ˆQ=arccos[1−12(¯RR′h)2](rad)
|
(8)
|
or
|
ˆQ=arccos[1−12(¯RR′h)2]180π(degrees)
|
(9)
|
Using h=3.2 cm (the Antifer cube height), for ¯RR′=2:6cm, using equation (9), we get the rotation angle ˆQ≈ 47.94°.
3.4. Detection of modified areas
As previously mentioned, one of the main objectives of this study was the detection of modified/damaged areas on the breakwater armour layer, between two photos representing the initial and final moments of a physical scale model test. Therefore for those two images, it was necessary to proceed to their preliminary grayscale conversion.
|
BWi(i,j) initial grayscale matrix
|
(10)
|
|
BWf(i,j) final grayscale matrix,
|
(11)
|
for i∈{1,⋯,nl},j∈{1,⋯,nc}
After the conversion of these images, the relevant differences between the two resulting image matrices were analysed, considering a matrix P, with the same size as the BW matrices, where its entries are defined as following: If the difference between the initial and final images is relevant, the entry of the P matrix will be 1, otherwise it will be 0. This relevance is defined as a threshold value, ε
|
P(i,j)={1⇐|BWi(i,j)−BWf(i,j)|≥ε0⇐|BWi(i,j)−BWf(i,j)|<ε
|
(12)
|
The most significant modified areas will be assessed by calculating the matrix norm, which in this case study was considered to be the unit norm defined by
|
‖A‖1=max1⩽j⩽sr∑i=1aij
|
(13)
|
for an arbitrary matrix A=[aij]r×s.
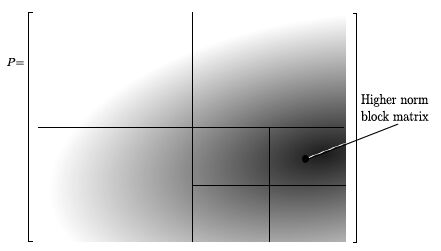
Figure 12 represents graphically the position matrix P. The entries corresponding to most significant modified areas are equal to 1, and are represented through a darker colour.
The Algorithm of the quadrisection method was used to identify the location of the most modified zone. The matrix block with the most modified area corresponds to the higher entries equal to one, i.e. with a higher matrix norm. This search process is performed iteratively, starting on the entire position matrix, dividing it into four blocks, after which, the one which has a higher matrix norm is chosen, and divided again into four blocks, and so on, until a pre-defined stopping criteria is achieved. To better illustrate the algorithm, the corresponding pseudocode will now be presented.
Algorithm of the quadrisection method
1. Begin the loop ℓ=0 by decomposing
2. Let k the index of the maximum ‖Pi‖1,i=1,2,3,4
3. Do P=Pk, ℓ=ℓ+1 and return to 1:
4. Stop when ℓ=m
Given a matrix A representing a gray-level picture, the quadrisection method produces a sequence {A0,A1,A2,…,Am}, with A0=A, and Aℓ+1=(Pk of Aℓ), the number of iterations m is chosen by the user and depends on the image resolution and the photographed object size.
We use Am matrix also to estimate the changed area. As every matrix entry corresponds to a pixel, we estimate the area of the scene using photogrammetric measurement techniques and therefore the changed area.
3.5. Images correlation
Taking the initial and the final images, represented by matrices I and F, the quadrisection method produces two sequences {I0,I1,I2,…,Im} and {F0,F1,F2,…,Fm} for each search done with m iterations. At the beginning the images I0 and F0 are quite similar, despite the differences produced by the damage. We expect that the couple Im and Fm represent the part of the image with more damage. We can evaluate this using the correlation coefficient [22].
The correlation coefficient ρ of two images described by the matrices A and B is given as
|
ρ=∑ri=1∑sj=1(A(i,j)−μA)(B(i,j)−μB)√[∑ri=1∑sj=1(A(i,j)−μA)2][∑ri=1∑sj=1(B(i,j)−μB)2]
|
(14)
|
with μArs=∑ri=1∑sj=1A(i,j) and μBrs=∑ri=1∑sj=1B(i,j) and the coefficient ρ∈[−1,1]. If ρ is close to 1 indicates that the two images are very similar, while a value close to 1 indicates that they are highly dissimilar.
In consequence, we expect the correlation coefficient begin near 1 to the couple I0 and F0, and decreases to-1 with the iterations of the quadrisection method.
4. Tests and results
The previously presented methodologies will be applied on two sets of photos obtained during scale model tests. On the first set of photos, Test 1, the damage is almost imperceptible. To the contrary, Test 2 the second set of photos presents an important damaged area of the breakwater armour layer. In these two sets of photos, the damaged zone was identified and measured. The calculations were carried out over a Hewlett-Packard with a 2xintel(R) Core(TM) CPU.
4.1. Primary colours isolation
For both tests, an appropriate conversion to grayscale levels was used to isolate primary colours blue and red. Figure 13 illustrates both the initial and final photos, for Test 1, where damage progression is almost imperceptible.
Figures 14 and 15 show the results of the primary colours isolation operations for the initial and final images, as well the difference matrix.
Figure 16 illustrates both the initial and final photos of Test 2, where severe damage occurred. Primary colours isolation and differences are illustrated in Figures 17. In this set of figures it can be clearly noticed that, at the end of the tests, significant displacements of the blue armour units occurred. Concerning the red armour units, damage was not so significant as in the previous case (Figure 15).
The difference in resolution between Test 1 and Test 2 clearly illustrate that the coefficients (5) must be adapted to the photo’s resolution, not depending only on the elementary color to isolate.
4.2. Detection and quantification of affected areas
The detection and quantification of affected areas, is based on the initial and final photos, is also developed upon the use of grayscale levels and of an auxiliary matrix structure-the position matrix. Figure 18 shows the differences between the initial and final photos, as well as the position matrix. For each entry, the position matrix associates a flag, identifying the occurrence of a difference or not, such as a negative representation of the differences matrix image.
This procedure will carry out an iterative search process, by considering a subdivision of the image into rectangular areas, to localize the most affected areas. The size and number of rectangles are defined by the number m of loops previewed at Algorithm of the quadrisection method. This increases the accuracy to a certain value depending on cube’s size and of the number of pixels by image. By increasing the number of iterations, one can refine the search for the most modified area (Figure 19).
This procedure output also includes the quantification (in cm2 and in percentage) of the total modified area. Once a search is achieved (the iteration sequence ℓ=m was performed), it is possible to begin a search of another damaged zone, producing the effect shown in Figure 19 and Figure 21, and yielding one rectangle per each search.
Figure 20 illustrates the grayscale differences between Test 2 photos, as well as the corresponding position matrix.
Some results of the affected areas detection procedure for Test 2 is presented in Figure 21.
The precision of the obtained regions can be increased with a higher number of searches, as illustrated at the sequence of Figures 19 and 21 a) to d). The idea is considering the rectangles as small as the precision we need, since all these procedures are very fast, about 60.375 s, for the entire procedure: from the gray conversion to the damaged zone detection, for case a) at Figure 21. The modified area illustrated by Figure 18 can be estimated, using final position matrix, and we obtain 271.46 cm2, corresponding to 2.67 percent of visible area.
As shown in Tables 1 and 2, the correlation coefficient presents a decreasing trend, as the quadrisection method progresses towards the more damaged area. Due to the imperceptible differences at the pair of the matrices (I0, F0) for the Test 1, the correlation coefficient begins near 1, however this is not the case for the Test 2, where there are significant displacements of the blue armour. By analysis of the tables, it is clear the path for each search procedure which often passes through more similar areas, before the end of the zone with larger differences, where damage is higher.
Table 1.Correlation coefficient for Test 1.
| Iter 0 | Iter 1 | Iter 2 | Iter 3 | Iter 4 | Iter 5 | Iter 6 |
| Search 1 | 0.947087 | 0.926323 | 0.913985 | 0.872203 | 0.758322 | 0.451739 | 0.283826 |
| Search 2 | 0.947087 | 0.926323 | 0.913985 | 0.858205 | 0.552522 | -0.038770 | -0.068101 |
| Search 3 | 0.947087 | 0.926323 | 0.913985 | 0.872203 | 0.758322 | 0.822742 | 0.275619 |
| Search 4 | 0.947087 | 0.926323 | 0.913985 | 0.858205 | 0.552522 | 0.352487 | 0.172954 |
Table 2.Correlation coefficient for Test 2.
| Iter 0 | Iter 1 | Iter 2 | Iter 3 | Iter 4 | Iter 5 | Iter 6 |
| Search 1 | 0.911807 | 0.869939 | 0.810046 | 0.603696 | 0.197405 | -0.033160 | -0.318687 |
| Search 2 | 0.911807 | 0.869939 | 0.810046 | 0.746957 | 0.633125 | 0.796093 | 0.557960 |
| Search 3 | 0.911807 | 0.869939 | 0.810046 | 0.603696 | 0.574248 | 0.329327 | 0.133452 |
| Search 4 | 0.911807 | 0.869939 | 0.810046 | 0.603696 | 0.197405 | 0.294357 | -0.605731 |
5. Conclusions
With this study, an innovative method for the analysis of physical scale models of breakwaters was developed. To this purpose, mathematical techniques were applied, allowing the assessment of differences between two photos taken at the beginning and at the end of scale model tests of rubblemound breakwaters. The presented procedures allow the detection and successful identification of modified areas, as well as its quantification in area units or percentage of the total photographed area. It is also possible to quantify movements of the armour layer units. Nevertheless, this attempt was conditioned by the existence of only two photos for each test. The effectiveness of the presented procedures is confirmed through the evolution of the correlation coefficient used in conjunction with the quadrisection method. This procedure replaces the previous count technique with human intervention and therefore with high subjectivity factor.
The results obtained offer the possibility of the development of a computational tool, as an alternative damage analysis, aiming to eliminate the subjective damage accounted for during these type of tests. Furthermore, its open-source platform allows an easier dissemination of the analysis tool.
From an economical perspective, the technique makes use of a simple, cost-effective commercial camera. On the other hand, it is based on an open-source, free development platform, which provides an inexpensive approach to answer scale model tests needs. Although some photogrammetric techniques had already been used for armour layer units movement detection [23] and [24], their application is not always easy, requiring the drainage of the wave basin at the end of each test.
During the literature review, it was not found a similar type of image analysis tool, applied to physical model tests of harbours and coastal protection structures.
Acknowledgments
The authors wish to acknowledge the financial support given by FCT/MEC through Project PTDC/ATP-AQI/5355/2012 and Project LAETA-UID/EMS/50022/2013.
Conflict of interest
All authors declare no conflicts of interest in this paper.










 DownLoad:
DownLoad: