Tissue distribution patterns of solubilized metals from internalized tungsten alloy in the F344 rat

1.   Introduction

Halyomorpha halys (Stål) (Hemiptera: Pentatomidae) is an invasive stink bug introduced from Asia into North America, Europe, and Chile ^[1,2,3]. In Italy, invasion may have occurred from two different pathways, both from Switzerland and from Asia and/or North America ^[4]. In the invaded areas, H. halys has become an important pest of many crops, causing severe economic losses due to its feeding activity mainly on developing fruits and seeds, such as apples, pears, peaches, nectarines, tomatoes, peppers, sweet corn, soybean and hazelnuts ^[1,5]. In particular, in Italy, under the current climatic conditions, the species is able to complete two generations per year and has shown very high reproductive rates for both generations, with massive outbreaks starting from the summer, confirming that it is a threat for agricultural production in southern Europe ^[6]. Control of the pest mainly relies on multiple applications of broad-spectrum insecticides, nullifying the integrated pest management programs largely adopted in Italy, and causing secondary pest outbreaks ^[5]. For this reason, as a long-term solution, classical biological control based on the use of parasitoids has been considered in the United States and Europe ^[1]. Parasitoids are insects with a parasitic larval stage (juveniles) that develops by feeding on another insect called the host, and in our case feeding on a single egg of H. halys. Unlike parasites, at the end of their development, parasitoid larvae kill their host like a predator, but they only need one host to complete their development. Then, the resulting adult is a free-living insect. Therefore, a parasitoid adult, and not a stink bug nymph, will emerge from an egg attacked by Anastatus bifasciatus (Geoffroy) (Hymenoptera: Eupelmidae) or by Trissolcus japonicus (Ashmead) (Hymenoptera: Scelionidae) ^[7]. Indeed, in Europe, an indigenous egg parasitoid, A. bifasciatus, is able to attack H. halys eggs, but without achieving effective containment of pest populations ^[8,9]. In the native area, egg parasitoids are the primary natural enemies of H. halys, and T. japonicus is considered the predominant species among the egg parasitoid complex of H. halys in China and Japan ^[10,11]. Therefore, T. japonicus has been selected as a candidate for classical biological control both in North America and Europe ^[12,13,14].

Currently, field releases of T. japonicus have been authorized in Italy starting from 2020. However, before any field release, adventive populations of T. japonicus were detected in North Italy from 2018, as well as adventive populations of Trissolcus mitsukurii (Ashmead) (Hymenoptera: Scelionidae) ^[9,15]. This latter species, known as an egg parasitoid of H. halys in Japan ^[11], has been found in Northern Italy since 2016 ^[16], and has also been considered as a promising candidate for biological control ^[17]. Both T. japonicus and T. mitsukurii have successfully established in Northern Italy, even before the release of T. japonicus was authorized as a part of the national classical biological control program, and contribute to the H. halys control together with the native A. bifasciatus ^[18]. The indigenous and exotic parasitoids can act synergistically in the biological control of H. halys and, in case of competition, T. japonicus and A. bifasciatus have been shown to be counterbalanced, the former being a superior extrinsic competitor (by guarding eggs), the latter being a superior intrinsic competitor, successfully emerging from eggs that were previously parasitized by T. japonicus ^[19]. Finally, a hyperparasitoid, Acroclisoides sinicus (Huang and Liao) (Hymenoptera: Pteromalidae), which develops in H. halys eggs previously parasitized by the Trissolcus species, is also present in Northern Italy ^[20,21]. Hyperparasitoids, or secondary parasitoids, act as parasitoids, but develop on primary parasitoids: an A. sinicus female lays eggs in the H. halys eggs that have already been attacked to develop on the larvae of Trissolcus spp. The offspring of the hyperparasitoid causes the death of the primary parasitoid. An A. sinicus adult will emerge from the attacked H. halys eggs, ^[22]. The interaction between parasitoids and hyperparasitoids can play a key role in determining the overall effectiveness of biological control of H. halys. As little information has yet been available on the Trissolcus spp. impact on H. halys populations, and on the A. sinicus impact on Trissolcus spp. populations, field surveys were carried out in Piedmont, North-western Italy, from 2017 to 2021 to assess the impact of parasitoids and hyperparasitoids. Both the data from the five-year surveys and those available in the literature are used in the model proposed here.

The paper is organized as follows. Section 2 contains all the various steps in the model construction, starting from the description of the field data gathering. It is followed by the overview of the simulations organization. Their results are presented and thoroughly discussed in Section 4. Section 5 reports the main findings on the equilibria of the model. Some remarks on the results obtained and the model limitations conclude the paper. The mathematical details of the feasibility and stability of the equilibria of the general model are presented in the Appendix B, while its Subsection B.3 analyzes a special simplified situation.

2.   Model formulation

2.1.   Data collection

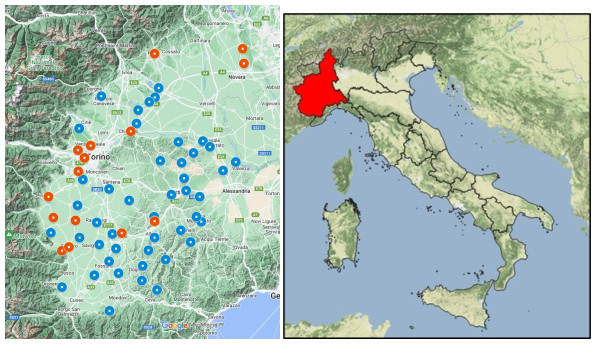
Seasonal abundance of H. halys adults was monitored weekly from May to October, at 40 sites with pheromone-baited traps (Dead-Inn Pyramid Trap - 4 ft. height, AgBio Inc., baited with Pherocon BMSB Dual Lure, Trécé Inc.), from 2018 to 2021. The traps were placed in the same locations, distributed throughout Piedmont, NW Italy, and captures were checked weekly from May to October. The collection points are reported in Figure 1, where the red dots represent the eggs collection points and the blue ones the location of the traps. Seasonal abundance of the parasitoids Trissolcus spp., A. bifasciatus, and the hyperparasitoid A. sinicus was monitored monthly from June to August from 2017 to 2021 by collecting field-laid H. halys eggs with one-hour visual inspection, at 6 sites in 2017, at an additional 3 sites (9 in total) in 2018 and at an additional 6 sites (15 in total) in 2019, 2020 and 2021. All eggs were reared in laboratory, and the number of ⅰ) H. halys nymphs, ⅱ) A. bifasciatus adults, ⅲ) Trissolcus spp. adults, and ⅳ) A. sinicus adults which emerged from eggs were counted, discarding unhatched or preyed eggs.

2.2.   Basic interactions

The mutual interactions of H. halys and its parasitoids, described in the Introduction are summarized in Figure 2. We use $ I $ to denote the hyperparasitoid A. sinicus, $ A $ to indicate the indigenous parasitoid A. bifasciatus, $ T $ to denote the combined populations of the parasitoids T. japonicus and T. mitsukurii, while $ C $ indicates the invasive pest H. halys. In addition, because parasitization occurs on H. halys eggs, these must be accounted in the formulation. Because the life cycle of these insects can be expressed in weeks, as illustrated in Tables 2 and 3, we chose the week as the time unit. A further consequence is that a discrete dynamical system formulation naturally arises, instead of a possible continuous one.

The various population dynamics are essentially represented by three terms, denoting reproduction $ R^X $, intraspecific competition $ b_X $, and natural mortality $ m_X $, where $ X \in \{I, A, T, C \} $ indicates the specific population under consideration. Natural mortality represents the mortality rate within a population, in this case of adult insects, that occurs in the absence of external factors such as natural enemies, diseases, or human intervention. It is obtained as the reciprocal of the average lifetime of a healthy insect, respectively. The H. halys reproduction function will be derived from field-collected egg data, and therefore must be time-dependent. The reproduction function for the other insects are based on H. halys egg counts, so that they are also time-dependent. As mentioned above, recall that the mortalities are easily obtained as the reciprocal of the average lifetimes of each species, which are known from the literature, ^[27,28] for $ A $, ^[23,30] for the two $ T $ species and ^[24] for $ C $. For each population $ X \in \{ I, A, T, C \} $ let $ X_n $ denote its value at time $ t = n $ and let $ \Delta X_n = X_{n+1}-X_n $ be the increment over the time interval $ [n, n+1] $. The discrete model can thus be written as

The model represents the parasitoid-host interactions shown in Figure 2. However, note that no terms for these interactions appear in the equations formulation. This is due to the fact that the damage that some insects cause to the other ones occurs only via the parasitization of their eggs. Therefore, it is very important that this mechanism be correctly depicted in the model, as we show in the next section.

2.3.   Egg parasitization

The main effort in the model construction lies in the mathematical description of the egg parasitization. Let $ s_C $ denote the sex ratio of A. sinicus. Eggs laid by a female H. halys are $ C_f = s_C C $. However, not all of them are "healthy"; $ E $ represents the per capita fraction of healthy eggs that are available for parasitization, so that their total number is $ EC_f $. To obtain those that hatch and give new H. halys individuals, from these we need to subtract those parasitized by Trissolcus spp. and A. bifasciatus, indicated by the terms $ r_T $ and $ r_A $ in the equation below. We thus obtain

Further, since only females lay eggs, it is important to consider the sex ratio. The parameter $ s_T $ denoting the sex ratio (females over the whole population) for Trissolcus spp. is known, $ s_T = 0.87 $ ^[23]. For H. halys in general the sex ratio is assumed as $ s_C = 0.5 $ ^[24].

We now discuss the parasitization process.

Considering for the moment that parasitization is due to Trissolcus spp., the total number of parasitized eggs would be obtained by multiplying the per capita parasitization $ \widetilde r_T $ of $ T $ with the total female population of Trissolcus spp. $ T_f = s_T T $, where $ s_T $ denotes the sex ratio of Trissolcus, namely $ R_T = E C_f \widetilde r_T T_f $. In this way, however, if the parasitization rate were higher than one, i.e, $ \widetilde r_T T > 1 $, the total number of emerging Trissolcus adults would exceed the total number of eggs laid by H. halys, which of course cannot be. Therefore, we need to correct this approach.

For this purpose, we need to consider the parasitization rate as a function of the parasitizing agent population. In the discussion above, this corresponds to taking $ \widetilde r_T = r_T(T) $. The function $ r_T(T) $ should have a specific form, namely it should be bounded from above. Such choice is represented by a Holling type Ⅱ-like function, i.e.,

where $ q_T^{-1} $ represents the slope at the origin of the parasitization rate. In this way, $ 0 \le r_T < 1 $. Here, $ 0 \le \beta_T \le 1 $ represents the reproduction effectiveness. The two extreme values denote particular situations. For the case in which Trissolcus spp. are present, but no eggs parasitized by them are found in the field samples, we set $ \beta_T = 0 $. Note that if H. halys eggs were scarce, the presence of Trissolcus spp. could be inferred by sampling the adults with traps, beating sheets, or other methods. If instead all females of Trissolcus spp. parasitize all the available eggs, we set $ \beta_T = 1 $.

Anastatus bifasciatus behaves in a similar way on H. halys eggs. We can thus introduce corresponding functions and notations. However, like A. sinicus, it can also parasitize Trissolcus spp. This hyperparasitization must be described in the same way, considering hyperparasitization as the product of two different parasitization processes. Specifically, for A. bifasciatus it is necessary to distinguish between the parasitization rate $ r_A(A) $ on H. halys and the one on Trissolcus spp., denoted by $ h_A(A) $. In view of the previous remarks, we can thus write

with $ q_{T}, q_{{A, C}}, q_{{A, T}}, q_{I} > 0 $. Their reciprocals are the slopes at the origin of the parasitization or hyperparasitization rates. Note that different notations have been used for the parameters in the denominator: $ q_{A, C} $ and $ q_{A, T} $ stand for the parasitization and hyperparasitization due to A. bifasciatus, respectively. In addition to the ones mentioned above, the sex ratios also of these insects are known ^[21,25].

In summary, we have

Further, from (2.1) the reproduction rates $ r_X(X) $, $ X \in \{T, A \} $ and $ h_X(X) $, $ X \in \{ A, I \} $ must be nonnegative, so that the following inequalities must be satisfied,

which become

Let us denote by $ E_X $, $ X \in \{I, A, T, C \} $ the newly emerged offsprings of species $ X $ from a single egg mass. Let also $ p_X $ denote the respective rates. They are given by

so that

Since the rates $ p_X $ are known from available field data, we need to find further conditions on the rates $ r_X(X) $, $ X \in \{T, A \} $ and $ h_X(X) $, $ X \in \{ A, I \} $ so that they are feasible. To simplify the notation, for the rest of this section we drop the explicit dependence of these functions on the respective population sizes.

Now $ R_T h_I $ is the per capita hyperparasitization rate $ p_I $. Instead, $ r_A + r_T h_A $ is the sum of the direct per capita parasitization rate of $ A $ on $ C $, to which we add the hyperparasitization rate of $ A $ on $ T $, to get $ p_A $. Similarly, $ r_T (1 -h_A -h_I) $ represents the per capita net parasitization rate of $ T $ on $ C $, where we have discounted the hyperparasitizations of $ A $ and $ I $. It therefore represents $ p_T $. Also, $ 1- r_A -r_T $ represents the per capita net reproduction rate of $ C $, adjusted for the parasitizations of $ A $ and $ T $, and thus gives $ p_C $. These considerations lead to the following relationships

Since the rates must lie in the interval $ [0, 1] $, the following constraints must be satisfied:

where the second one is more restrictive than the first one. Ultimately, $ r_T $ must lie in the following interval

Note that this interval is nonempty; from (2.9) we have indeed $ p_{I} + p_{A} + p_{T} = 1 - p_{C} $ and since $ p_A \in [0, 1] $ we have $ p_I + p_T \le 1 - p_C $, the required result. In summary, the required feasibility conditions for the rates are

Now A. sinicus reproduces because it parasitizes the eggs of H. halys already parasitized by Trissolcus spp., ^[19], so that we can state

Instead, A. bifasciatus can parasitize the eggs of H. halys at rate $ s_C EC r_A $ and also those parasitized by Trissolcus spp. at rate $ s_C EC r_T h_A $, overall giving

Finally, Trissolcus spp. attack the eggs of H. halys

However, a further consideration should be made. Indeed, we have considered the reproduction process whereby insects emerge from the available H. halys eggs. It should be noted that from egg to adulthood, insects go through developmental stages that are different when heterometabolous, such as H. halys, and holometabolous, such as parasitoids and hyperparasitoid. This whole process is not at all considered in the modeling procedure: juvenile stages do not appear explicitly in the model. However, these stages are still affected by natural mortality, which reduces the eggs produced by factors $ \sigma_Y $, $ Y \in \{I, A, T, C\} $. These must therefore be included in the equation formulation.

Putting together the above considerations and (2.2), (2.14)–(2.16), the system to be studied is therefore

The parameters of the system (2.17) are listed in Table 1 together with their meanings.

3.   Simulation settings

The simulations were performed using our data collected in the field over the past five years.

A few caveats are necessary to describe the procedure used to overcome some shortcomings that might arise in the simulations.

Because the information on the egg masses did not cover the entire timespan, but had some gaps, a spline cubic interpolation on the two closest available data points was performed to obtain the values at times when they were missing. Furthermore, at the beginning and end of the season, the number of laid eggs was set to zero, through an interpolation procedure.

The beginning of the season, when H. halys females start oviposition, is assumed to be the 19-th week of the year, i.e., the second or third week of May ^[6]. The end before the onset of winter diapause is set at the 42-nd week, i.e., the third week of October ^[6]. Trap catch data before the 19-th week were discarded, as most individuals are still in diapause or have not yet started laying eggs.

Furthermore, most insect data other than those collected in the field, i.e., field collected eggs and trap catch counts, come from laboratory experiments, and therefore may differ from those occurring in the field ^{[23,24,27,28,29,30]} as specified below in detail in Subsection 3.1. Another limitation is that population data are just estimates on the actual numbers of H. halys in the environment, being calculated as an average of insects captured at various sites, which differ greatly in location and environmental conditions. A similar observation applies to parasitoids, which count an average number of those that emerge from field collected eggs. This entails that the differences between data and simulation values may sometimes be large.

The simulations ran starting from the year 2017, and iterated. In particular, note that all the populations with which the following year begins come from the corresponding values obtained at the end of the current year, in the fall, for which a fixed fraction is deducted that should account for their mortality during overwintering ^[6,26]. This is an important point, since each year the climatic conditions may change, and taking a constant value for winter mortality does not adequately mimic what happens in reality. However, little information is available and therefore this assumption attempts to surrogate the missing estimate. A similar observation can be made on intraspecific competition rates, which cannot be measured in the field.

3.1.   Developmental period and average female longevity

The data of Table 2 come from ^[27] for $ I $, ^[28] for $ A $, ^[23,29,30] for the two $ T $ species and ^[24] for $ C $.

Note that in Table 2 the hyperparasitoid $ I $ lays eggs within those of $ C $ that are already parasitized one week earlier by $ T $. It takes thus 3 more weeks to emerge. Further, the oviposition period of $ A $ is about 46 days, followed by a further life period of 17.8 days in which oviposition does not occur ^[28]. Thus, in the simulations the average lifetime is approximated to 14 weeks, see Table 2. We assume that hyperparasitization of $ A $ on $ C $ occurs within the first 3 days after oviposition.

Table 3 reports the temporal sequence of the various events within a single generation. Data of this table come from ^[27] for $ I $, from ^[28] for $ A $, from ^[23] for the two $ T $ species and from ^[24] for $ C $. Finally, note that in Table 3 new individuals are accounted for only when they become adult and thereby are able to reproduce.

3.2.   Egg mass data

Tables 4–8 contain the mean number of eggs per egg mass from which H. halys or one of its parasitoids emerged, considering all the egg masses collected in each week at sites in which at least two egg masses were present, from 2017 to 2021. Data of Table 4 come from field surveys in 2017, as it is the case for the following tables and the following years. Recall also that $ E $ represents healthy eggs, i.e., neither broken, nor preyed, nor parasitized by other species, while $ E_X $, $ X \in \{I, A, T, C\} $ represents the average number of each respective species emerged from a single egg mass.

3.3.   Trap data

Tables 9–12 contain the mean numbers of H. halys adults found per trap and per week at all sites from 2018 to 2021.

4.   Simulation results

Because the initial value of the H. halys population at the beginning of the year 2017 is not available, we assumed it to be of the same order of the one assessed by traps in the following years, of the order of 100. Since no $ T $ is found in the egg masses, but only $ A $ is present, and only a fraction of them parasitizes $ C $, the initial condition for the latter in the year 2017 is set to a smaller hypothetical value than the one for H. halys. We thus take

In these simulations, the intraspecific competition rate $ b_C $ is not known. For the years 2018–2021, it is estimated by a regression procedure based on the minimization of the discrepancy between the simulations results and the actual field data. For the year 2017 instead, the value has been assessed as the one that minimizes the difference between the final value at the end of the fall, discounted for the winter mortality, and the initial population in the following spring. Overwintering survival data in the literature are very variable depending on the temperature and many other factors, $ 14 $, $ 23 $ and $ 61\% $, respectively in ^[6,31,32]. We therefore assumed a mean data of $ 33\% $ of overwintering survival. The whole argument is repeated in the following years. Based on each insect average lifetime (Table 2), the various mortalities are set to

The value $ b_C $ is calculated for H. halys as the value that minimizes, in the sense of least squares, the discrepancy of the simulations results with the actual trap data for this species. Because no information on the intraspecific competition of the other populations is available, the values of the coefficients $ b_I $, $ b_A $ and $ b_T $ are set to the same value $ b_C $.

As discussed at the end of Subsection (2.3), we need to account for the natural mortality of the juvenile stages. We assume a weekly loss of 50%, which leads from the initial number of laid eggs to a lower number of adults. This implies for H. halys a reduction factor $ \sigma_C = 0.07 $ over the whole four week-period to reach the adult stage, and similarly a reduction factor $ \sigma_X = 0.25 $, $ X \in \{I, A, T\} $ for the parasitoids and hypeparasitoids, according to their average two week-developmental period. With $ n $ denoting the week in the year, the actual implementation of the model relies on using (2.3), (2.10) in (2.17) and thus ultimately on the following equations,

4.1.   H. halys simulations

In Figure 3, left frame, we show the population behavior for the H. halys at the start of the simulations, in the year 2017. After use of the Matlab minimization routine fminsearch, the value of the whole overwintering population is $ 550 $.

For the following years, the optimization procedure gives the results of Table 13.

4.2.   Simulations for all the populations

For the simulations in the following years the values of the intraspecific coefficients for the other insects are taken to be equal to those of $ b_C $ that can be read for each year in Table 13, thus in each case

The initial conditions for the year 2017 are given in (4.1). The results are shown in Figures 3–7, left frames.

4.3.   Simulations for the reproduction rates

In view of the fact that the reproduction rates (2.3) and (2.4) are implicitly time-dependent, because they depend on the respective population sizes, it is worth investigating also how they behave, when the populations evolve in time. Figures 3–7, right frames, contain the results of the simulations.

4.4.   Simulations discussion

The model simulations aim at a description of the H. halys invasion phenomenon. This species after its appearance, is monitored in the graphs starting from the year 2017 together with its indigenous parasitoid A. bifasciatus. In the following years the exotic parasitoids also appear and their joint action helps in keeping in check and finally curbing the H. halys population toward the end of the season. Indeed, in the first two years, the curve of the H. halys raises up, although not necessarily monotonically, from the spring to the fall.

In 2017, the A. bifasciatus experiences two peaks in the season, at the end of the spring or early summer, and toward the beginning of the fall.

In 2018, instead, it shows a declining behavior, compensated however by a raise in the Trissolcus spp. population. The two together help in a sharp decline of the stink bug around the 40th week of the simulation, followed, however, by a further rise at the end of the season.

In 2019, H. halys attains a small peak in the spring and a much higher one in the summer, which are immediately followed by corresponding maxima of A. bifasciatus. In the second part of the summer, Trissolcus spp. also raises up to replace the indigenous parasitoid as the most effective control measure. Two other smaller maxima for both the pest and A. bifasciatus appear before the end of the season, driving the stink bug to lower values. The maximum for H. halys is a bit reduced with respect to the maximal value attained in 2018, being respectively slightly below and above 600.

In 2020, the H. halys population raises up almost monotonically until the end of the summer, but with values that are much below those of the previous year. This is due to the joint action of A. bifasciatus and Trissolcus spp., which grow and exhibit interlaced maxima, finding their maximum values at the beginning of the fall. Note that the H. halys population maximum, about 250, is halved with respect to the same value in 2019.

In 2021, a similar trend is shown by the model, only in part mimicking the previous year. Indeed now the hyperparasitoid emerges at the end of the summer, and at the same time, a reduction in the maximum value of A. bifasciatus and an increase in Trissolcus spp. in its place can be observed. The latter is the most effective control on the stink bug at the end of the season. The joint action of the three parasitoids curbs the final value of H. halys to half the final value that it attains in 2020, namely roughly 100 versus 200, in spite of the fact that the stink bug has an overall maximum 300 in the whole season that is higher than the corresponding one observed in the previous year, i.e., 250.

As a general remark, we can conclude that the simultaneous action of the three biological control mechanisms appears to be able to keep the invaders population down at the end of the simulations and at the end of the season.

5.   System's equilibria

Here we summarize the results for which the mathematical details are provided in the Appendix B, both for the full model and in case of constant reproduction rates.

5.1.   The full model

For the full model (2.17) with population-dependent reproduction rates, (A.1), in addition to the origin $ O $ and coexistence $ X_6 $, the other equilibria are found as follows, where the notation $ X_k $ with $ X\in\{I, A, T\} $ emphasizes the value of the population $ X $ at the equilibrium $ E_k $, $ k = 1, \ldots, 5 $.

Some of these equilibria cannot be determined analytically. However, for $ X_2 $ and $ X_3 $ some sufficient conditions for their feasible existence can be assessed.

Proposition 1. The origin is always feasible. If $ m_{I}, m_{A}, m_{T} \neq 1 $, $ O $ is locally asymptotically stable for

Note that in general $ E $ represents the number of eggs in an egg mass from which individuals emerge. In fields data, generally it is found that $ E \ge 3 $, so that the origin is unstable in most of the cases.

Proposition 2. $ X_1 $ is feasible whenever

It is locally asymptotically stable if the following conditions are satisfied

Proposition 3. Sufficient conditions for the feasibility of $ X_2 $ are

Corollary If (5.4) holds, we also have the constraint for the $ C $ population:

Proposition 4. Letting

the stability conditions for $ X_2 $ are

Proposition 5. Sufficient conditions for the feasibility of $ X_3 $ are

Corollary Proposition 5 gives also the following constraint for the $ C $ population

Proposition 6. $ X_3 $ is locally asymptotically stable if

where

5.2.   A particular case

In the particular case of (2.17) with constant rates

equilibria are the origin, unconditionally feasible, and the coexistence point.

Proposition 7. Assuming (5.9), coexistence is given by

where

and for its feasibility we have the constraint

Proposition 8. Assuming (5.9), the origin is locally asymptotically stable for the following alternatives:

● Assuming that $ m_X \in [0, 1) $, $ X \in \{I, A, T \} $ and $ r_{A}+r_{T} < 1 $, $ O $ is asymptotically stable if and only if

● If $ m_{\widehat X} = 1 $, for some $ \widehat X \in \{I, A, T \} $, while $ m_X \in [0, 1) $ for $ X \in \{I, A, T \}-\{ \widehat X \} $, and (5.12) holds, $ O $ is stable, but not asymptotically.

Proposition 9. Assuming (5.9), using the feasibility condition, (5.11), and (5.10) local asymptotic stability is guaranteed by the following sets of inequalities, for $ X\in\{I, A, T\} $:

where, using (A.6)

6.   Conclusions

In this work, we modeled the parasitism and hyperparasitism on H. halys eggs in North Italy using both data collected during a five-year field survey and data available in the literature. The model presented here is of descriptive nature, although, as stated above, clearly based on a sound ecological basis. It cannot be taken as a tool for forecasts, because it is still in a rudimentary phase and therefore validation with real data at this stage is not considered. We plan in the future to refine and validate it accordingly.

As all models, the one considered here is subject to several limiting assumptions, listed below.

● In the modeling procedure juvenile stages do not appear explicitly; however insects experience developmental stages that differ for heterometabolous, (i.e., H. halys), and holometabolous, (i.e., parasitoids and hyperparasitoid) during their evolution from egg to adulthood.

● To fit the gaps on the egg masses data, an interpolation procedure was used in which eggs are forced to disappear at the start and end of each year.

● Unlike field insect data, i.e., field collected eggs and trap catch counts, biological parameters, such as longevity and sex ratio, came from laboratory experiments, which may differ from those occurring in the field.

● Population data are just estimates on the actual numbers of individuals in the environment; they are obtained as averages of insects captured at various sites, differing greatly for environmental conditions. This applies to H. halys as well as to parasitoids, counted as averages of those emerging from field collected eggs.

● All populations at the start of the following year come from the corresponding values at the end of the fall of the current year, discounted by a fixed fraction representing their mortality during overwintering, which is arbitrarily taken for the whole parasitoid populations. However, climatic conditions may change, so that the assumption of constant winter mortality could be refined.

● Intraspecific competition rates are not measurable in the field. Thus $ b_I $, $ b_A $ and $ b_T $ are set to the same value $ b_C $ that is instead calculated for H. halys through least squares regression, see Section 4.

● The average lifetime of the indigenous parasitoid is set to 14 weeks while $ A $ hyperparasitizes $ C $ within the first 3 days.

● Not having data at the start of 2017, the value of the H. halys is taken to be of the same order of the one assessed by traps in the following years, while for $ A $ we set a smaller hypothetical value than the one for H. halys, since only a fraction of $ A $ parasitizes $ C $ (4.1).

The model equilibria have been analytically assessed, when possible. Ecosystem collapse, represented by the origin, could occur in case of population-dependent reproduction rates if condition (5.1) holds. In general however, it does not, as the number of eggs in an egg mass usually exceeds the critical value 3.

H. halys alone can stably survive at equilibrium $ X_1 $, if feasibility (5.2) holds and conditions (5.3) are satisfied.

For both the points with H. halys and just one of the parasitoids $ T $ or $ A $ we have obtained sufficient conditions for their feasibility, (5.4) and (5.6). They are not stringent in the sense that even in case they are violated, these equilibria could nevertheless exist. Their local asymptotic stability conditions have instead completely assessed, respectively by (5.5) for $ X_2 $ and the equations (5.7) and (5.8) for $ X_3 $. An explicit interpretation of their meanings in terms of the model parameters appears however to be very difficult.

The coexistence point and the equilibrium with no hyperparasitoid $ I $ lead to nonlinear algebraic systems for which the analytic solution is not available. Similarly, the Jacobian evaluated at these points leads to a fourth order matrix, whose eigenvalues are impossible to calculate; formally, we could write the Routh-Hurwitz conditions for stability, but they would hardly shed any light on this issue. The recourse to numerical methods is therefore imperative.

In our simulations the populations of the indigenous and generalist parasitoid, A. bifasciatus, fluctuated over the five years, confirming that this species alone cannot significantly suppress H. halys populations, consistent with what was observed in previous field trials ^[9,33]. Examples of failed biological control exist in the literature. The most notable case concerns aphid species in open-air crops, both horticultural and fruit with the use of parasitoid species and the role played by hyperparasitoid species; both experimental ^[34] and by the use of mathematical models ^[35]. However, we are not observing a failure of biological control due to hyperparasitoid activity but merely describing the situation that, in our opinion, has not yet reached an equilibrium. Instead, populations of the exotic parasitoids T. japonicus and T. mitsukurii increased greatly from 2019 to 2021, after they first appeared in 2018 and 2016 respectively. This led to H. halys populations gradually decreasing, demonstrating that the exotic species can have a strong impact on their host. The hyperparasitoid A. sinicus, which in these surveys was detected for the first time in 2020, even if it had already been detected starting from 2016 in the study area, the Piedmont region ^[9], did not show as large an increase in the following years as the two Trissolcus species, thus demonstrating a minimal impact on parasitoids, without hampering their activity on bug populations, as modeled in ^[36]. Certainly, egg parasitoids are not the only natural enemies of H. halys. Indeed, eggs are also attacked by predators ^[33,37], and mobile stages can be affected by other parasitoids, predators, and entomopathogens ^[38,39]. Egg parasitoids clearly do not, by themselves, suppress H. halys populations to noneconomic levels, as already modeled in ^[36], but can play an important role in reducing H. halys populations, as seen in these simulations and also by ^[36]. These interactions between host, parasitoids, and hyperparasitoids tend to reach different equilibria over time, especially as the populations adapt to environmental pressures. In our model, this is reflected in the fluctuating dynamics of A. bifasciatus and the stabilizing effect of T. japonicus and T. mitsukurii on H. halys populations. The stability and biological significance of these equilibria depend on multiple factors, such as the reproductive rates of the species and their susceptibility to predation or parasitism, which our model attempts to approximate. More extensive field data could improve our understanding of these equilibria and the conditions that favor stability or instability in these populations. However, our simulations are based on partial field observations, as adults and eggs were not sampled at the same sites, and parameters from literature were obtained from laboratory trials. Furthermore, climate conditions, and climate change, were not considered, but they can affect populations of both host and parasitoids ^{[40,41,42,43,44,45]}. Incorporating these additional variables could further describe the stability of the modeled interactions and the long-term biological significance of these parasitoid-host dynamics. More accurate simulations could be made with additional collection of field data, and also by adding climatic data in the model.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare there is no conflict of interest.

Acknowledgments

The authors are very much indebted to the referees for their careful work that considerably helped in the improvement of the paper.

Appendix

A.   Mathematical appendix: Equilibria analysis of the full model

In this situation, (2.17) has population-dependent reproduction rates,

In addition to the origin $ O $ and coexistence $ X_6 $, the other equilibria are found as follows.

Some of these equilibria cannot be determined analytically. However, for $ X_2 $ and $ X_3 $ some sufficient conditions for their feasible existence can be assessed.

A.1.   Feasibility

A.1.1.   Equilibrium $ X_2 $

Proof of Proposition 3

For $ X_2 $, observing that $ C \neq 0 $, $ T \neq 0 $, the equilibrium equations of (2.17) to be considered are the last two. They can be rearranged as follows:

where $ \Pi(T) $ is a convex parabola in the $ T-C $ plane through the point on the vertical axis

where it has a positive slope and $ \Phi(T) $ is a hyperbola with intercept at the origin

and horizontal asymptote with height $ b_C^{-1} [\sigma_C s_C E (1-\beta_T)-m_C] $. Note that $ \Phi(T) $ is always decreasing, since

An intersection of $ \Pi(T) $ and $ \Phi(T) $ in the first quadrant is thus guaranteed if

so that the sufficient condition in this case turns out to be (5.4).

A.1.2.   Equilibrium $ X_3 $

Proof of Proposition 5

Here, we need to consider the second and fourth equilibrium equations of (2.17). Thus, we need to intersect the curves

Again $ \Psi(A) $ is a convex parabola and $ \Psi(A) $ is a hyperbola in the $ A-C $ plane, respectively through the points

At the origin, the slope of $ \Psi(A) $ is positive and the one of $ \Phi(A) $ is negative. Thus an intersection exists if (5.6) holds.

A.2.   Local Stability

In this section we recall the values of some important parameters, (4.2), that are used in the analysis that follows. System (2.17), in view now of the assumptions (A.1), has the following Jacobian $ J = J_{ik} $, $ i, k = 1, \ldots, 4 $, with $ J_{1, 2} = J_{2, 1} = J_{4, 1} = 0 $ and

A.2.1.   Origin

Proof of Proposition 1

Here the eigenvalues of (A.4) are all explicitly known,

thus yielding (5.1).

A.2.2.   Equilibrium $ X_1 $

Proof of Proposition 2

Feasibility follows by imposing the nonnegativity of the $ C $ population at equilibrium, $ C_1 $, giving (5.2).

For stability, again the four eigenvalues are explicitly found. For $ q_{A, C}, q_T \neq 0 $, we have

from which (5.3) follows.

Remark 1 For $ \beta_A = \beta_T = 0 $, the second and third eigenvalues would coincide with the corresponding ones of the origin, and the analysis would then be identical to the one of $ O $. The claim of Proposition 2 follows in view of the values of Table 1, $ -1 \le \lambda^{{X_1}}_{1} \le 0 $.

A.2.3.   Equilibrium $ X_2 $

Proof of Proposition 4

In this case two eigenvalues are known immediately, $ J_{11}^{X_2} $ and $ J_{22}^{X_2} $, because the Jacobian factorizes, providing the first two conditions (5.5). The remaining two are obtained from the roots of the quadratic equation

A.2.4.   Equilibrium $ X_3 $

Proof of Proposition 6

Here again the Jacobian factorizes giving two explicit eigenvalues $ J_{11}^{X_3} $ and $ J_{33}^{X_3} $, giving the first two stability conditions (5.7), while the other ones are the roots of the quadratic equation

which provide the last two stability conditions, (5.8).

A.3.   Analysis of a particular case

Proof of Proposition 7

We consider here the case where the primary parasitization rates $ r_A $ and $ r_T $, as well as the hyperparasitizations $ h_I $, $ h_A $, are assumed to be constant, (5.9).

The feasible equilibria of the system (2.17) are just the origin $ O $ and coexistence $ W $. The latter in principle is not unique, but only one instance can be accepted, (5.10).

Note that for feasibility of $ W $ we must impose that the $ C $ population is nonnegative, giving the constraint (5.11), with $ 1-r_{A}-r_{T} > 0 $ stemming from (2.10). Note that if (5.11) holds, $ I_- \le 0 $, $ A_- \le 0 $, $ T_- \le 0 $ and the other equilibria are not feasible. Since $ I_+ \ge 0 $, $ A_+ \ge 0 $, $ T_+ \ge 0 $, the only feasible equilibria are the origin and $ W $.

A.3.1.   Stability

For the stability, we need the Jacobian of (2.17),

where

Proof of Proposition 8

At the origin, the eigenvalues are easily determined, $ \mu^{O}_{1} = -m_{I} $, $ \mu^{O}_{2} = -m_{A} $, $ \mu^{O}_{3} = -m_{T} $, $ \mu^{O}_{4} = \sigma_C s_C E\left(1-r_{A}-r_{T}\right)-m_{C} $. While the first three lie in $ [-1, 0] $, for the fourth one there are the alternatives in the statement of Proposition 8. Note that if $ r_{A}+r_{T} = 1 $, then $ \mu^{O}_{4} = -m_{C} $ and similar considerations apply here as well. We omit the details.

Proof of Proposition 9

For the stability of $ W $, we have again four explicit eigenvalues for the Jacobian evaluated at this equilibrium:

From the feasibility of $ W $, (5.11), we find that $ \mu_4 < 0 $. For the asymptotic stability of the coexistence equilibrium, we need $ \mu_k^W \in (-1, 0) $, $ k = 1, \ldots, 4 $. If one of these inequalities attains the lower bound, only stability can be obtained. Once again, using (5.11) and (5.10) asymptotic stability is therefore guaranteed by (5.13) where

The above inequalities hold in view of the information of Table 1 on the various mortalities and from (2.6) for $ \gamma_T $. Further, note that $ \zeta_{X-} < 0 $ for all the populations $ X\in\{I, A, T\} $ and, therefore, this lower bound is indeed excluded from the conditions (5.13).