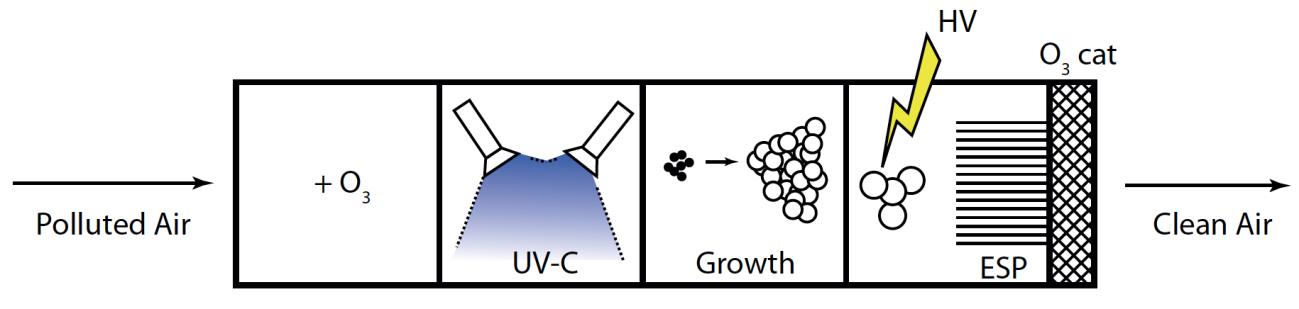
Gas-phase advanced oxidation (GPAO) is an emerging air cleaning technology based on the natural self-cleaning processes that occur in the Earth’s atmosphere. The technology uses ozone, UV-C lamps and water vapor to generate gas-phase hydroxyl radicals that initiate oxidation of a wide range of pollutants. In this study four types of GPAO systems are presented: a laboratory scale prototype, a shipping container prototype, a modular prototype, and commercial scale GPAO installations. The GPAO systems treat volatile organic compounds, reduced sulfur compounds, amines, ozone, nitrogen oxides, particles and odor. While the method covers a wide range of pollutants, effective treatment becomes difficult when temperature is outside the range of 0 to 80 °C, for anoxic gas streams and for pollution loads exceeding ca. 1000 ppm. Air residence time in the system and the rate of reaction of a given pollutant with hydroxyl radicals determine the removal efficiency of GPAO. For gas phase compounds and odors including VOCs (e.g. C6H6 and C3H8) and reduced sulfur compounds (e.g. H2S and CH3SH), removal efficiencies exceed 80%. The method is energy efficient relative to many established technologies and is applicable to pollutants emitted from diverse sources including food processing, foundries, water treatment, biofuel generation, and petrochemical industries.
1.
Introduction
Cardiac personalized modelling has been used for the non-invasive diagnosis and treatment of heart rhythm disorders, including risk classification of patients with heart attacks [1,2,3], prediction of the location of re-entry [4], and guidance for clinical ablation [5]. The key to the clinical application of heart models is the accurate creation of the personalized model, which is currently mostly segmented by experienced experts. Manual segmentation is subjective, irreproducible and time consuming, while model simulation takes a great deal of time and is time-critical in clinical practice, so how to minimize heart modeling time makes an automated segmentation method extremely important for the clinical application of personalized heart modelling.
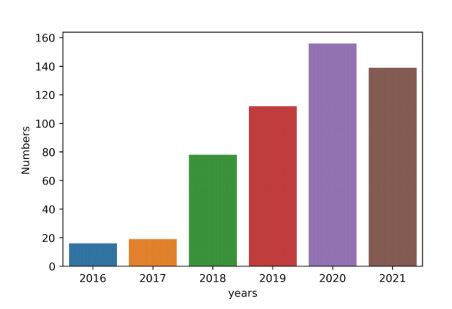
Before the rise of deep learning, classical medical image segmentation algorithms such as region-based, grayscale-based, and edge-based algorithms were well established for medical images [6,7,8,9], while traditional machine learning techniques such as model-based methods (e.g., active contour and deformable models) and atlas-based methods (e.g., single-atlas and multi-atlas) have achieved good performance [10,11,12,13]. Nevertheless, both classical image segmentation algorithms and machine learning techniques usually require some prior knowledge or feature annotation processing to achieve better results. In contrast, deep learning-based algorithms do not rely on these operations; it automatically discovers and learns complex features from the data for target segmentation and detection. These features are often learned directly from the data through generic learning procedures and end-to-end methods. This allows deep learning-based algorithms to be easily applied to other domains. Deep learning-based segmentation algorithms are gradually surpassing previously advanced traditional methods and are gaining popularity in research, not only because of developments and advances in computer hardware such as graphics processing units (GPU) and tensor processing units (TPU), but also because of the increase in publicly available datasets and open source code. This trend can be observed in Figure 1, where the number of deep learning-based cardiac image segmentation papers has grown considerably in the last few years, especially after year 2018. We searched the web of science database for the keywords cardiac image segmentation and deep learning, and all types of articles were counted.
Accurate localization and segmentation of medical images is a necessary prerequisite for diagnosis and treatment planning of cardiac diseases [14]. With the development of deep learning technology, various deep learning algorithms have been introduced into medical image processing and analysis with good results [15,16]. Convolutional neural networks (CNN) are one of the most common neural networks in medical image analysis, which are computationally fast and simple, and requiring no major adjustments to the network architecture [17]. CNN have been used with great success for medical image classification and segmentation, but a major drawback of this patch-based approach is that a separate network must be deployed for each patch at the time of inference, due to multiple overlapping in the image patches, which results in a large amount of redundancy and wasted resources. To solve this problem, fully convolutional networks [18] were created, which were designed to have an encoding-decoding structure that allows them to receive inputs of arbitrary size and produce outputs with the same size. However, this encoder-decoder structure also poses some limitations, such as the loss of some features, so there are many variants based on FCNs, but the most famous one is U-Net [19], which uses hopping connections to recover feature information in the down-sample paths to reduce the loss of spatial context information and thus obtain more accurate results. Subsequently U-Net gradually dominated in medical image processing, but it and its variants [20,21,22] also faced the lack of ability to build remotely correlated models. This is mainly due to the inherent limitations of the convolution operation [23].
On the other hand, the success of Transformer, which captures remote dependencies, has made possible the solution of the above problem in recent years. Transformer was designed for sequence modeling and transformation tasks, and it is known for its focus on modeling remote dependencies in data. Its great success in the language domain has motivated researchers to investigate its adaptability to computer vision, especially since it has achieved good results on some recent image classification and segmentation tasks [24,25,26]. ViT [25] first introduced transformer to computer vision tasks by segmenting an image into 16 non-overlapping patches, feeding them into standard transformer with positional embedding and comparing it with the CNN-based approach, ViT achieved a fairly good performance, which broke the monopoly of U-Net in computer vision. With the advent of VIT, more and more transformer-based image processing became popular, such as Swin-transformer [24] proposed a hierarchical transformer and a sliding window attention-based transformer, while the pyramidal visual transformer (PVT) [26] proposed a gradual shrinkage strategy to control the scale of feature maps and proposed a spatially reduced attention (SRA) layer to replace the traditional multiple head attention (MHA) layer in encoders, which were designed mainly to reduce the computational complexity. But these transformer-based networks have a limitation of unable extracting low-level features like convolutional operations [27], so some detailed features will be ignored.
To solve the above problem, we propose TF-Unet, a medical image segmentation framework that combines Transformer and U-Net. To fully utilize the advantages of both, we use two convolutional layers to learn high-resolution features and spatial location information in the learning feature phase, and use Transformer blocks to establish remote dependencies in the decoding phase. In terms of structure, inspired by the U-Net network structure, we divide the network into encoder-decoder blocks, and the self-attentive features of the coding blocks are combined with different high-resolution decoding features through hopping connections to reduce information loss. The results show that such a design allows our framework to maintain the advantages of both Convolution and Transformer, while facilitating the segmentation of medical images. Experimental results show that our proposed hybrid network has better performance and robustness compared to previous methods based on pure convolution and pure transformer.
2.
Materials and methods
2.1. Data description
The ACDC dataset: (1) Raw Nifti images of 100 patients were used as the training set, and clinical experts used the corresponding manual reference analysis of ED and ES time phases as segmentation criteria, where trabecular and papillary muscles were included in the ventricular blood pool; (2) raw Nifti images of another 50 patients were used as the test set, providing only basic patient information: height and weight, and ED and ES time phases. ACDC data were acquired using 1.5 T and 3.0 T MRI scanners with retrospective or prospective balanced steady-state free-feed sequences. The scan parameters were as follows: layer thickness of 5–8 mm, layer spacing of 5 mm, layer thickness and layer spacing combined were typically 5–10 mm, matrix size was 256 × 256, FOV was 300 × 330 mm2, and one complete cardiac cycle consisted of 28–40 time phases.
The Synapse dataset: (1) Raw Nifti images of 30 patients were used as training set; (2) Raw Nifti images of another 20 patients were used as test set, these 50 scans were taken at the portal venography stage with different volumes (512 × 512 × 85–512 × 512 × 198) and fields of view (approximately 280 × 280 × 280–500 × 500 × 650 mm3). The planar resolution varied from 0.54 × 0.54 to 0.98 × 0.98 mm2, while the slice thickness ranged from 2.5 to 5.0 mm.
2.2. Methodology overview
The general architecture of TF-Unet is shown in Figure 2, which maintains a U-shape similar to that of U-net [11] and consists of two main branches, i.e., encoder and decoder. Specifically, the encoder includes the feature extraction block, the transformer block, and the down-sampling block. The decoder branch includes the transformer block, the up-sampling block and the deconvolution block that finally maps the output. And, to recover the image details in the prediction, we add residual connections [28] between the corresponding feature pyramids of the encoder and decoder in a symmetric manner.
2.2.1. Feature extraction block
The feature extraction block is mainly responsible for converting each input image I into a high-dimensional tensor $ I\in {R}^{\frac{H}{4}\times \frac{W}{4}\times C} $, where H, W, C record the height, width, and sequence length of each input patch, respectively. Unlike Jieneng Chen et al. [24], who first flattened the input image directly and then preprocessed it in one dimension, we use a feature extraction layer which extracts low-level but high-resolution 3D features directly from the image and has more accurate spatial information at the pixel level.
We use two consecutive convolutional layers with a kernel size of 3 and step sizes of 2 and 1 and use LeakyReLU nonlinear activation functions and LayerNorm for each layer, which not only allows us to encode spatial information more accurately than the faceted position encoding used in the transformer, but also helps to reduce computational complexity while providing equally sized perceptual fields.
2.2.2. Transformer block
After the feature extraction block, we pass the high-dimensional tensor I to the Transformer block in two consecutive layers. The ability of the transformer to establish remote dependencies is fully exploited to establish the connection between the high-resolution features extracted in the upper layer and the multi-scale features obtained by convolutional downsampling in the next layer. Unlike the traditional multi-headed self-attentive module, this paper uses the Swin-Transformer module [24], who is constructed based on a sliding window. Since the window-based self-attentive module lacks cross-window connections, this limits its modeling capabilities. In order to introduce cross-window connectivity while maintaining efficient computation of non-overlapping windows, Ze Liu et al. [24] proposed a sliding window partitioning approach. In Figure 3, two consecutive transformer modules are given. Each Swin-Transformer block consists of a LayerNorm (LN) layer, a multi-headed self-attentive module, a skip connection, and an MLP (Multilayer Perceptron) with a LeakyReLU nonlinearity. The window-based multi-headed self-attention (W-MSA) module and the sliding window-based multi-headed self-attention (SW-MSA) module are applied in the two consecutive Transformer blocks, respectively. Based on this window division mechanism, the consecutive sliding Transformer blocks can be represented as Eqs (1)–(4).
where l is the index of the layer. W-MSA and SW-MSA denote the volume-based multi-headed self-attentive and its transfer version. where $ {y{'}}^{l} $ and $ {y}^{l} $ denotes the output of the W-MSA module and the MLP module of layer l, respectively. The computational complexity of SW-MSA on a volume of H × W × D patches is 4HWDC2 + 2SHSWSDHWDC, however, the computational complexity of naïve multi-headed self-attention (MSA) is 4HWDC2 + 2(HWD)2C. SH, SW, SD represent the height, width and depth of the sliding window respectively. SW-MSA greatly reduces the computational complexity of MSA, so our proposed algorithm is more efficient. The sliding window segmentation approach introduces connections between adjacent non-overlapping windows in the previous layer and has been found to be effective in image classification, object detection and semantic segmentation [23].
In calculating the self-attention, we refer to Han Hu et al. [29,30] and add the relative position bias, and the specific formula for calculating the self-attention is as follows:
where Q, K, V represent the query matrix, key matrix and value matrix, respectively. d is generally taken as the dimension of Q or K. $ B\in {R}^{\left(2H-1\right)\times \left(2W-1\right)} $ is the relative position encoding.
2.2.3. Convolutional down-sampling
Instead of completing the cascaded feature operations by using linear layers as in Swin-Unet [23], we directly use the convolution operation with stride size of 2. The reason for this is that the layered features generated by convolutional down-sampling help to model the target object at multiple scales. After such processing, the feature resolution is down-sampled by a factor of 2 and the feature dimension is increased to twice the original dimension.
2.2.4. Convolutional up-sampling
Corresponding to the Convolutional down-sampling, we also make changes in the up-sampling layer. We use stepwise deconvolution to up-sample the low-resolution feature map into a high-resolution feature map, i.e., by reconstructing the adjacent dimensional feature map into a higher-resolution feature map (2x up-sampling) and correspondingly reducing the feature dimension to half of the original dimension, and then by skip connecting, the features extracted from the encoder's down-sampling are combined with the decoder up-sampled features are merged. A deconvolution operation is also performed in the last patch extension block to produce the final result.
2.2.5. Skip connection
Similar to U-Net [19], skip connections are used to fuse multiscale features from the encoder with up-sample features from the decoder. We splice shallow and deep features together to reduce the loss of spatial information due to down-sample.
3.
Results
To fairly compare the experimental results, we test three times on the ACDC dataset to take the average, and to verify the robustness of our algorithm, we do the same test on the Synapse dataset.
3.1. Experimental details
We ran all experiments based on Python 3.6, pytorch 1.8.1 and Ubutun 20.04. All training programs were executed on an NVIDIA 2080 GPU with 11 GB of RAM. The initial learning rate was set to 0.01, and we used the "poly" decay strategy [31] by default. As described in Eq (6):
where $ max\_epoch $ represents the total number of training generations, default 1000, $ tem\_epoch $ represents the current training generations, γ is the hyperparameter, default take 0.9.
The default optimizer is stochastic gradient descent (SGD) and we set the momentum to 0.99. The weight decay is set to 3e-5. We use the weighted sum of the cross-entropy loss and the dice loss as the loss function. The training epochs is 1000 and each epoch contains 250 iterations.
3.2. Data pre-processing and data enhancement
All images in the same dataset are firstly resampled to the same target spacing and then cropped to the same size. Since there are not enough training samples, some data enhancement operations, such as rotation, scaling, Gaussian blur, Gaussian noise, brightness and contrast adjustment, are performed during the training process
3.3. Experimental result at ACDC
In conducting experiments on the ACDC dataset, we designed two experimental scenarios; one is to make full use of the dataset, we use all 100 training data as the training set and 50 test data as the test set. The other is to quantitatively evaluate our results, we divide the 100 labeled training data into 70 training sets, 10 validation sets and 20 test sets. The real labels of the 20 cases used for testing were not put into the training.
Figures 4 and 5 show the results of the first and second scenario, respectively. We randomly selected several patients' results for visualization [32].
The results of the second scenario are as follows, Table 1 shows the quantitative calculations and comparisons of RV, MYO and LV using the dice coefficients, and Figure 5 shows the raw plots of several randomly selected patient data, ground truth and predicted results. Due to the random nature of data partitioning, the results of the other methods in Table Ⅰ are taken from the results in the corresponding papers.
3.4. Experimental result at Synapse
For Synapse data, we only use the second scenario in ACDC, we chose a part of labeled training set for testing, with training sample: validation sample: test sample = 14:7:9. We used the mean dice similarity coefficient (DSC) for eight abdominal organs, namely the aorta, gall bladder, spleen, left kidney, right kidney, liver, pancreas and stomach, to evaluate the model performance. Figure 6 shows the results of the different layers of patients from the Synapse dataset, with different colors representing different organs, as shown in the legend in Figure 6.
3.5. Ablation study
In this section, we introduce the importance of learning rate strategies. In order to verify the effect of different learning rate strategies on the results, we did controlled experiments with four functions, inv, multistep, poly, step, and the results of the four methods are shown in Figure 7.
4.
Discussion
In this section, we discuss in detail the experimental results obtained by our algorithm and explore the impact of different factors on the model performance, which we have compared on the ACDC and Synapse datasets, respectively. Specifically, we discuss the effects of different learning rate strategies on network performance.
Analysis from a quantitative perspective. From Table 1, the best transformer-based model is Swin-Unet, which has an average dice coefficient of 90%. The best convolution-based model is R50-U-Net whose average dice coefficient is 87.55%, while our proposed TF-Unet is 1.72% higher than that of Swin-Unet and 4.17% higher than that of R50-U-Net. Considering that the current accuracy of these networks themselves is already very high, our proposed network improvement is still very effective, suggesting that our method can achieve better edge prediction. Analysis from a qualitative perspective. As can be seen in Figure 5, the middle represents the patient's true value and the rightmost represents our predicted value. By comparing layer by layer, the results obtained by our method are very close to the true value, and very good results are achieved even for the right ventricle, which is difficult to segment. In this work, we demonstrate that by combining Transformer with convolutional operations, better global and remote semantic information interactions can be learned, resulting in better segmentation results.
It is well known that most of the deep learning networks cannot predict the results well for the test set without labeled values, but the network model based on TF-Unet can get good results. Observing Figure 4, we can conclude that the results obtained with our method are generally quite accurate for the layers other than the root tip layer. However, in the lower right corner of Figure 4, i.e., the apical layer, our method does not segment it. On the one hand, the apical layer has less segmentation in the training set, which makes it difficult for the network to learn features in this region; on the other hand, the true areas of both RV and LV in the apical layer are small and easily confused with surrounding vessels or tissues, leading to difficulties in segmentation.
Figure 8 summarizes the learning process of our proposed network, it was observed that the training loss and validation loss decrease with the increase of iterations and reach a stable state at about 200 generations without overfitting. And the dice coefficient of the validation set increases with the number of iterations and reaches a steady state at 800 generations.
Quantitatively, as shown in Table 2, we performed experiments on Synapse and compared our TF-Unet with various transformer-based and Unet-based baselines. The main evaluation metric is the dice factor. the best performing transformer -based approach is Swin-Unet, which achieves an average score of 79.13. In contrast, DualNorm-UNet reports the best CNN-based results with an average of 80.37, slightly higher than Swin-Unet. our TF-Unet is able to outperform both Swin-Unet and DualNorm-UNet average performance by 6.33% and 5.09%, respectively, which is a considerable improvement on Synapse. Qualitatively, as can be seen in Figure 6, the middle column indicates the true value, and the rightmost column indicates the prediction result. For the segmentation of multiple organs, our proposed TF-Unet network still performs well, but there are some shortcomings for the stomach, as shown by the red boxes in the four lower right panels in Figure 6, one is that the prediction result is not smooth enough and there are many bursts, and the other is that it is difficult to segment to complex boundaries
Observing Figure 7 we can easily see that the results of all the functions are close except for the inv function. Through Figure 9 we speculate that this is because the learning rate of the inv function decreases too fast at the beginning of the iteration, and although it can speed up the search for the optimal solution, it is also easy to ignore the optimal solution and fall into the local optimal solution, leading to relatively poor results. The other three learning rates are all gradually decreasing, and although there is a big difference in the intermediate stages, the results do not differ much. These experiments show that the learning rate strategy has some influence on the experimental results, but it is generally enough to find the learning rate with the appropriate decreasing speed, and the different learning rate functions do not differ greatly.
5.
Conclusions
In this paper, we propose a new medical image segmentation network TF-Unet. TF-Unet is built on the intertwined backbone of convolution and self-attention, which makes good use of the underlying features of CNN to build hierarchical object concepts at multiple scales through U-shaped hybrid architectural design. In addition play Transformer's powerful self-attention mechanism that entangles long-term dependencies with convolutionally extracted features to capture the global context. Based on this hybrid structure, TF-Unet has made a great progress in previous Transformer-based segmentation methods. In the future, we hope that TF-Unet can replace manual segmentation operations for cardiac modeling, effectively improve the efficiency of personalized modeling, and accelerate the development of personalized cardiac models in clinical applications.
Acknowledgments
This study was supported by the Natural Science Foundation of China (NSFC) under grant number 62171408 and 81901841, the Key Research and Development Program of Zhejiang Province under grant number 2020C03016, the Major Scientific Project of Zhejiang Lab under grant number 2020ND8AD01, and Fundamental Research Funds for the Central Universities under grant number DUT21YG102.
Conflict of interest
The authors declare that there are no conflicts of interest.









 DownLoad:
DownLoad: