1. Introduction

Bacteriophage or virulent phage is a virus which can grow and replicate by infecting bacteria. Once residing in bacteria, phage grow quickly, which result in the infection of bacteria and drive the bacteria to die [17]. Thus, we can view them as bacteria predators and use them to cure the diseases induced by infecting bacteria [9,35]. Phage therapy has become a promising method because of the emergence of antibiotic resistant bacteria [12,9]. Indeed, as a treatment, phages have several advantages over antibiotics. Phages replicate and grow exponentially, while antibiotics are not [47]. Generally speaking, a kind of phages infect only particular classes of bacteria, and this limitation of their host is very beneficial to cure the diseases. Moreover, phages are non-toxic, and cannot infect human cells. Hence, there are fewer side effects as compared to antibiotics [12,35].

It is important to understand the interaction dynamics between bacteria and phage to design an optimal scheme of phage therapy. There have been a number of papers that study the mathematical models of bacteriophages (see, for example, [1,2,3,4,8,9,10,11,21,23,28,42] and the references cited therein). Campbell [11] proposed a deterministic mathematical model for bacteria and phage, which is a system of differential equations containing two state variables, susceptible bacteria $S$ and phage $P$, and incorporating a delay $\tau$ that represents the time period for phage replication in the bacteria. The model was developed by [28,32,36,40] to consider the effect of predation and competition with the limited resources. It was further studied by [3,4,21] to study the infections of marine bacteriophages, where bacteria populations from 5-6% up to 70% are infected by bacteriophages [38]. Smith and Thieme [42] formulate two models: a system of delay differential equations with infinite delay and a more general infection-age model that leads to a system of integro-differential equations to study the persistence of bacteria and phage.

It was observed that phage can exert pressure on bacteria to make them produce resistance through loss or modification of the receptor molecule to which a phage binds with an inferior competition ability for nutrient uptake [25]. More recently, biological evidences are found that there exists an adaptive immune system across bacteria, which is the Clustered regularly interspaced short palindromic repeats (CRISPRs) along with Cas proteins [6,14,13,18,26,27,31,41]. In this system, phage infection is memorized via a short invader sequence, called a proto-spacer, and added into the CRISPR locus of the host genome. And, the CRISPR/Cas system admits heritable immunity [14,13,18,26,31]. The replication of infecting phage in bacteria is aborted if their DNA matches the crRNAs (CRISPR RNAs) which contains these proto-spacer. On the other hand, if there is no perfect pairing between the proto-spacer and the foreign DNA (as in the case of a phage mutant), the CRISPR/Cas system is counteracted and replication of the phage DNA can occur [19,34,33,39]. Therefore, the CRISPR/Cas system participates in a constant evolutionary battle between phage and bacteria [7,13,27,47].

Mathematical models are powerful in understanding the population dynamics of bacteria and phages. Han and Smith [23] formulated a mathematical model that includes a phage-resistant bacteria, where the resistant bacteria is an inferior competitor for nutrient. Their analytical results provide a set of sufficient conditions for the phage-resistant bacteria to persist. Recently, mathematical models have been proposed to study the contributions of adaptive immune response from CRISPR/Cas in bacteria and phage coevolution [27,29]. In these papers, numerical simulations are used to find how the immune response affects the coexistence of sensitive strain and resistance strain of bacteria. In the present paper, we extend the model in [23] by incorporating the CRISPR/Cas immunity on phage dynamics. Following [23], we focus on five state variables: $R$, $S$, $M$, $I$ and $P$ which represent the concentrations of nutrient, sensitive bacteria and resistant bacteria, productively infected bacteria and phage in a chemostat. The following assumptions will be used in the formulation of mathematical model: $(i)$ all sensitive bacteria have the potential to get the acquired immunity; $(ii)$ only the resistance from the CRISPR/Cas immunity is considered, which is incomplete because phage can mutate under the pressure of CRISPR/Cas immunity; the resistant bacteria suffer the cost of competitive ability [28]; $(iii)$ the infected bacteria don't uptake nutrient, and cannot be infected again [23]; $(iv)$ the latent time for phage infection is omitted because it is small; $(v)$ the loss of phage due to multiple phage attachment to bacteria is omitted.

Let $k$ be the valid phage adsorption rate to both susceptible and resistant bacteria, which is reasonable because the CRISPR/Cas immunity does not interfere with phage adsorption. Following [23], we let the loss rates of phages due to adsorption to susceptible bacteria and resistant bacteria be described by $k S P$ and $k M P$ respectively, and the infection rate of sensitive bacteria be given by $k S P$. Note that the CRISPR/Cas immunity arises during the process of phage invasion. If $\varepsilon$ is the probability that the CRISPR/Cas immunity is successfully established in bacteria, then the transition rate of invaded bacteria to the resistance class is $\varepsilon kSP$ and the transition rate to the productively infected class is $(1-\varepsilon)k S P$. Moreover, we let $k'=\kappa k$ denote the infection coefficient of resistant bacteria where $0<\kappa\leq 1$ describes the mutant probability of phage to escape CRISPR/Cas suppression. Finally, by incorporating the terms discussed above to describe the effects of CRISPR/Cas immunity into the model in [23], we arrive at the following model:

$ $$\begin{split} &\dot{R}=D(R^0-R)-f(R)(S+\mu M), \\ &\dot{S}=-DS+f(R)S-kSP, \\ & \dot{M}=-DM+\mu f(R)M+\varepsilon kSP-k'MP, \\ &\dot{I}=-DI+(1-\varepsilon)kSP+k'MP-\delta I, \\ &\dot{P}=-D P-kSP-kMP+b\delta I, \end{split}$$ $

(1)

where a dot denotes the differentiation with respect to time $t$; $D$ and $R^0$ represent the dilution rate and nutrient supply concentration in the chemostat, respectively; $f(R)$ is the growth rate function which is taken to be Monod type: $f(R)=mR/(a+R)$, where $m$ is the maximal growth rate and $a$ is the half-saturation constant; parameter $\mu$ with $0<\mu<1$ is the cost of bacteria's resistance; parameter $b$ represents the total number of free virus particles released by each productively infected cell over its lifespan; parameter $\delta$ is the death rate of infected bacteria.

The paper is organized as follows. In the next section we present the mathematical analysis of the model that include the stability and bifurcation of equilibria. Numerical simulations are provided in Section $3$ to show the complicated dynamical behaviors of the model. A brief discussion concludes in Section $4$. The proofs of a few theorems are given in Appendix.

---

2. Mathematical analysis

In this section, we present the mathematical analysis for the stability and bifurcations of equilibria of (1). We start with the positivity and boundedness of solutions.

---

2.1. Positivity and boundedness of solutions

Proposition 1. All solutions of model (1) with nonnegative initial values are nonnegative. In particular, a solution $(R(t), S(t), M(t), I(t), P(t))$ of model (1) is positive for $t>0$ in the existence interval of the solution if $R(0)>0, S(0)>0, M(0)>0, I(0)>0, P(0)>0$.

Proof. We examine only the last conclusion of the proposition. First, we claim that $R(t)$ is positive for all $t>0$ in the existence interval of the solution. Suppose not. Then there is a time $t_1>0$ such that $R(t_1)=0$ and $R(t)>0$ for $t\in(0, ~t_1)$. Since $R(t_1)=0$, we have $\dot{R}(t_1)=DR^0>0$. Thus, there is a sufficiently small $\varepsilon>0$ such that $R(t)<0$ for all $t\in(t_1-\varepsilon, ~t_1)$, which is a contradiction. Hence, $R(t)$ is positive for $t>0$. It is evident that

$S(t)=S(0)e^{\int_0^t[-D-kP(\theta)+f(R(\theta))]d\theta}>0.$

In a similar way we can show the positivity of $M(t), I(t)$ and $P(t)$.

Proposition 2. All nonnegative solutions of model (1) are ultimately bounded.

Proof. Set

$L(t)=R(t)+S(t)+M(t)+I(t)+\frac{1}{b}P(t).$

Calculating the derivative of $L$ along the solution of (1), we obtain

$ $$\begin{eqnarray*} \dot{L}(t)&=DR^0-DR(t)-D S(t)-D M(t)-D I(t)-\frac{1}{b}DP(t)\\ &~~~-\frac{1}{b}k S(t)P(t)-\frac{1}{b}kM(t) P(t)\\ &\leq DR^0-DL(t). \end{eqnarray*}$$ $

It follows that the nonnegative solutions of $(1)$ exist on $[0, ~\infty)$ and

$ \label{upperlimit} \limsup\limits_{t\rightarrow\infty}L(t)\leq R^0. $

(2)

Therefore, the nonnegative solutions of model (1) are ultimately bounded.

---

2.2. Infection-free equilibria

$E_0=(R^0, 0, 0, 0, 0)$ is a trivial equilibrium. To find others, we assume

$ m>D, \;\;f(R^0)>D. $

(3)

Then $E_1=(\lambda_1, R^0-\lambda_1, 0, 0, 0)$ is an infection-free equilibrium, where $\lambda_1=D a/(m-D)$. Similarly, $E_2=(\lambda_2, 0, R^0-\lambda_2, 0, 0)$ is an infection-free equilibrium where $\lambda_2=D a/(\mu m-D)$ if

$ \mu m>D, \;\;\mu f(R^0)>D. $

(4)

It is easy to see that (3) and (4) imply

$\lambda_1<\mu\lambda_2<\lambda_2.$

Thus, the competitive exclusion in the absence of phage infection holds [24], and the boundary equilibrium $E_2$ is unstable. In what follows, we always assume that (3) and (4) are available.

The basic reproduction number $R_0$ of phage in the population of sensitive bacteria is computed through the matrix $F$ of new infection and the infective transition matrix $V$:

$F=\left( $$\begin{array}{cc} 0 & (1-\varepsilon)k (R^0-\lambda_1)\\ 0 & 0 \\ \end{array}$$ \right), $

and

$V=\left( $$\begin{array}{cc} D+\delta & 0 \\ -b\delta& D+k(R^0-\lambda_1) \\ \end{array}$$ \right), $

and is defined as the spectral radius of $FV^{-1}$ [16]. Hence,

$R_0=\sqrt\frac{b\delta(1-\varepsilon)k(R^0-\lambda_1)}{(D+\delta)[D+k(R^0-\lambda_1)]}.$

Analogously, the basic reproduction number $R^M_0$ of phage in the population of resistant bacteria is

$R^{M}_0=\sqrt\frac{b\delta\kappa(R^0-\lambda_2)}{(D+\delta)[D+k(R^0-\lambda_2)]}.$

Theorem 2.1. The infection-free equilibrium $E_1$ is locally asymptotically stable if $R_0<1$ and unstable if $R_0>1$.

The proof of Theorem 2.1 is postponed to Appendix.

Theorem 2.2. The infection-free equilibrium $E_1$ is globally asymptotically stable if $bk(R^0-\lambda_1)/D<1$.

Proof. Define a Lyapunov function by

$V(t)=R(t)-R_1-\int_{R_1}^R\frac{f(R_1)}{f(\xi)}d\xi+S(t)-S_1-S_1\ln\frac{S}{S_1}+M(t)+I(t)+\frac{1}{b}P(t), $

where $R_1=\lambda_1$ and $S_1=R^0-\lambda_1$. Calculating the derivative of $V$ along the solution of (1), we obtain

$ $$\begin{eqnarray*} \dot{V}(t)&=&\left(1-\frac{f(R_1)}{f(R)}\right)\dot{R}(t)+(1-\frac{S_1}{S})\dot{S}(t)+\dot{M}(t)+\dot{I}(t)+\frac{1}{b}\dot{P}(t)\\ &=&D(R^0-R)-\frac{D(R^0-R)f(R_1)}{f(R)}+(S+\mu M)f(R_1)+(D+kP-f(R))S_1 \\ &-&DS-DM-DI-\frac{D}{b}P-\frac{kSP+kMP}{b} \\ &=&D(R^0-R_1)(2-\frac{f(R_1)}{f(R)}-\frac{f(R)}{f(R_1)})-D(R-R_1)(1-\frac{f(R_1)}{f(R)})-D(1-\mu)M \\ &-&DI+(kS_1-\frac{D}{b})P-\frac{kSP+kMP}{b}.\nonumber \end{eqnarray*}$$ $

Since $bk(R^0-\lambda_1)/D<1$, it follows that $\dot{V}\leq 0$. Set

$ D_0=\{(R, S, M, I, P)\mid \dot{V}=0\}. $

It is easy to examine that the largest invariant set in $D_0$ is

$ \{(R, S, M, I, P)\mid R=\lambda_1, S=S_1, M=0, I=0, P=0\}. $

It follow from the LaSalle's invariance principle [22] that $E_1$ is globally stable.

---

2.3. Infection equilibria

In this subsection, we consider the infection equilibria of system (1) which satisfy

$ $$\begin{aligned} &D(R^0-R)-f(R)S-\mu f(R)M =0, &\\ &-D S+f(R)S-kS P =0, &\\ &-D M +\mu f(R )M +\varepsilon k S P -k'M P =0, &\\ &-DI +(1-\varepsilon)kS P +k'M P -\delta I =0, &\\ &-DP -kS P -kM P +b\delta I =0.& \end{aligned}$$ $

(5)

If $E_3=(R_3, 0, M_3, I_3, P_3)$ is an infection equilibrium dominated by the resistance strain, we have

$ $$\begin{aligned} &D(R^0-R_3)-\mu f(R_3)M_3=0, &\\ &-DM_3+\mu f(R_3)M_3-k'M_3P_3=0, &\\ &-DI_3+k'M_3P_3-\delta I_3=0, &\\ &-DP_3-kM_3P_3+b\delta I_3=0.& \end{aligned}$$ $

It follows that

$P_3=\frac{\mu f(R_3)-D}{k'}, \quad M_3=\frac{D(R^0-R_3)}{\mu f(R_3)}, \quad I_3=\frac{k'M_3P_3}{D+\delta}, $

and $R_3$ satisfies

$ $$\begin{aligned} -DP_3-kM_3P_3+b\delta I_3=P_3(kA_2M_3-D)=0, \end{aligned}$$ $

where $A_2=b\delta\kappa/(D+\delta)-1$. Substituting $M_3=D(R^0-R_3)/\mu f(R_3)$ and $f(R_3)=mR_3/(a+R_3)$ into it, we get

$ g(R_3):=R_3^2+(a+mA-R^0)R_3-R^0 a=0, $

(6)

where

$ A=\frac{\mu}{k}\frac{D+\delta}{b\delta\kappa-(D+\delta)}. $

By direct calculations, we obtain

$ g(R^0)=mAR^0>0, \\ g(\lambda_2)=(\lambda_2-R^0)(\lambda_2+a)+mA\lambda_2. $

Since $\mu f(R_2)>D=\mu f(\lambda_2)$, we have $\lambda_2<R_2$. Clearly, $g(\lambda_2)<0$ if

$A<\frac{(R^0-\lambda_2)(\lambda_2+a)}{m\lambda_2} =\frac{\mu(R^0-\lambda_2)}{D}, $

which is equivalent to $ R^{M}_0>1. $ Consequently, there exists a unique infection equilibrium $E_3$ when $R^{M}_0>1$, where $R_3$ lies between $\lambda_2$ and $R^0$, and $E_3$ does not exist when $R^{M}_0<1$. As a result, we can state the following theorem for the existence of $E_3$.

Theorem 2.3. The infection equilibrium $E_3$ exists if $R^{M}_0>1$ and does not exist if $R^{M}_0<1$.

To study the local stability of infection equilibria $E_3$, we set

$ $$\begin{eqnarray*} a_1&=&kM_3+3D+\delta+\mu M_3f^{'}(R_3), \\ a_2&=&kM_3(\mu M_3f^{'}(R_3)+2D-\mu f(R_3))\\ &&+D(2D+\delta)+(2D+\delta+\mu f(R_3))\mu M_3f^{'}(R_3), \\ a_3&=&DkM_3(\mu M_3f^{'}(R_3)+D-\mu f(R_3))+D(D+\delta)(\mu f(R_3)-D)\\ &&+\mu f(R_3)\mu M_3f^{'}(R_3)(2D+\delta), \\ a_4&=&kA_2(D+\delta)(\mu M_3f^{'}(R_3)+D)(\mu f(R_3)-D). \end{eqnarray*}$$ $

(7)

Moreover, for $\kappa<\mu$, we define

$ \label{L3} \lambda_3=f^{-1}(D(1-\kappa)/(\mu-\kappa)). $

(8)

Theorem 2.4. The infection-resistant equilibrium $E_3$ is asymptotically stable if

$ \kappa<\mu, \;\;R_3>\lambda_3, \;\;a_1a_2>a_3, \;\;(a_1a_2-a_3)a_3-a_4a_1^2>0, $

(9)

and is unstable when $\kappa>\mu$, or

$ \kappa<\mu, \;\;R_3<\lambda_3, \;\;a_1a_2>a_3, \;\;(a_1a_2-a_3)a_3-a_4a_1^2>0. $

(10)

The proof of Theorem 2.4 is given in Appendix.

Let us now consider the existence of coexistence equilibrium of (1). Denote such an equilibrium by $E_4=(R_4, S_4, M_4, I_4, P_4)$. By (5) we have

$ $$\begin{aligned} &P_4=\frac{f(R_4)-D}{k}, &\\ &M_4=\frac{\varepsilon D(R^0-R_4)(f(R_4)-D)}{[D-\mu f(R_4)+\mu \varepsilon(f(R_4)-D)+k'P_4]f(R_4)}, &\\ &S_4=\frac{D(R^0-R_4)[k'P_4+D-\mu f(R_4)]}{[D-\mu f(R_4)+\mu \varepsilon(f(R_4)-D)+k'P_4]f(R_4)}, &\\ &I_4=\frac{[(1-\varepsilon)kS_4+k'M_4]P_4}{D+\delta}.& \end{aligned}$$ $

(11)

Since $P_4>0, S_4>0, I_4>0$ and $M_4>0$, we need

$ \label{Positive} f(R_4)>D, \;\; k'P_4+D-\mu f(R_4)>0. $

(12)

Note that

$ $$\begin{aligned} F(R_4):=k'P_4+D-\mu f(R_4) =D(1-\kappa)+(\kappa-\mu)f(R_4), \end{aligned}$$ $

where $\kappa=k'/k$ is the phage mutant rate and the value of $\kappa$ can represents the relative resistance of bacteria for the CRISPR/Cas immune system. Though there is no definite relation between $\kappa$ and $\mu$ in biology, which is presented as fluctuating selection dynamics [7], in this paper we simply consider two ways for the CRISPR/Cas immune efficiency. First, we assume $\kappa\geq\mu$, which means that the mutant rate is great than the cost of bacteria's resistance. Secondly, we consider $\kappa<\mu$, which means that the mutant rate is inferior to the cost of bacteria's resistance.

Note that $R_4$ is the positive solution of the following equation:

$ -D+\left(\frac{b\delta\kappa}{D+\delta}-1\right)kM_4+\left(b\delta \frac{1-\varepsilon}{D+\delta}-1\right)kS_4=0. $

(13)

Set

$ A_1=b\delta(1-\varepsilon)/(D+\delta)-1, \quad A_2=b\delta\kappa/(D+\delta)-1. $

(14)

Using (11) and $f(R_4)=mR_4/(a+R_4)$, we see that (13) holds if and only if

$ G(R_4):=k(R^0-R_4)\left(e_1+e_2\frac{D}{f(R_4)}\right)-(e_3f(R_4)+e_4)=0, $

where

$ $$\begin{aligned} &e_1=\kappa A_1-\mu A_1+\varepsilon A_2, \;\; &&e_2=A_1-\kappa A_1-\varepsilon A_2, \\ &e_3=\mu\varepsilon-\mu+\kappa, &&e_4=(1-\mu\varepsilon-\kappa)D. \end{aligned}$$ $

Let $g_1(R_4)=k(R^0-R_4)(e_1+e_2D/f(R_4))$ and $g_2(R_4)=e_3f(R_4)+e_4$. It is easy to see that there are at most two intersection points for these two curves.

Evidently, $G(R^0)=-D<0$. When $R_4=\lambda_2$, we get $S_4=0$ and $M_4=R^0-\lambda_2$. As a result, we have

$ G(\lambda_2)=-D+kA_2(R^0-\lambda_2)=(D+k(R^0-\lambda_2))(R^{M}-1). $

Thus, $G(\lambda_2)>0$ if and only if $R^{M}_0>1$, where $R^{M}$ is the square of the basic reproduction number $R^{M}_0$. Similarly, we get

$ G(\lambda_1)=-D+kA_1(R^0-\lambda_1)=(D+k(R^0-\lambda_1))(R_0^2-1). $

Hence, $G(\lambda_1)>0$ if and only if $R_0>1$. From the above arguments, we conclude that system (1) has a unique positive equilibrium $E^{**}_4$ between $\lambda_2$ and $R^0$ when $R_0>1$ and $R^{M}_0>1$, has a unique positive equilibrium $E^{*}_4$ between $\lambda_1$ and $\lambda_2$ when $R_0>1$ and $R^{M}_0<1$, admits two positive equilibria $E^{**}_4$ and $E^{*}_4$ if $R_0<1$ and $R^{M}_0>1$, and has no positive equilibrium if $R_0<1$ and $R^{M}_0<1$.

For the case where $\kappa\geq\mu$, $F(R_4)$ are always positive. But for the case where $\kappa<\mu$, $F(R_4)$ may be negative at the equilibrium $E^{**}_4$. In view of the definition of $\lambda_3$ in (8), we see $F(\lambda_3)=0$. If $\lambda_3<R^0$, we have

$ $$\begin{aligned} G(\lambda_3)&=D(R^0-\lambda_3)(e_1+e_2\frac{D}{f(\lambda_3)})-(e_3f(\lambda_3)+e_4)&\\ &=D(R^0-\lambda_3)\frac{\varepsilon A_2(1-\mu)}{1-\kappa}-\frac{\mu\varepsilon D(1-\mu)}{\mu-\kappa}. &\nonumber \end{aligned}$$ $

Since $1-\kappa>\mu(\mu-\kappa)$, we see that $\lambda_3>\lambda_2$ and positive equilibrium $E^{**}_4$ exists when $G(\lambda_3)\leq 0$, and does not exist when $G(\lambda_3)>0$. It is easy to examine that $G(\lambda_3)\leq0$ is equivalent to

$ \lambda_3\geq R^0-\frac{\mu(1-\kappa)}{A_2(\mu-\kappa)}, $

(15)

and $G(\lambda_3)>0$ is equivalent to

$ \lambda_3<R^0-\frac{\mu(1-\kappa)}{A_2(\mu-\kappa)}. $

(16)

Solve $G(\lambda_3)=0$ in $b$ to obtain

$ $$\begin{aligned} b^{*}=\frac{D+\delta}{\delta}\left(\frac{(\mu-\kappa)(R^0-\lambda_3)}{(1-\kappa)\mu}+1\right). \nonumber \end{aligned}$$ $

Notice that $A_2$ increases as $b$ increases. Thus, $E_4^{**}$ does not exist as $b$ increases from $b^{*}$. In view of $F(\lambda_3)=0$, it follows that when $b=b^{*}$, we have $R_4=\lambda_3, S_4=0$ and

$ $$\begin{aligned} &P_4=\frac{f(\lambda_3)-D}{k}=\frac{D(1-\kappa)}{k(\mu-\kappa)}, &\\ &M_4=\frac{D(R^0-\lambda_3)(f(\lambda_3)-D)}{\mu f(\lambda_3)}, &\\ &I_4=\frac{k'M_4P_4}{D+\delta}.&\nonumber \end{aligned}$$ $

Set

$ $$\begin{aligned} R^{*}:=\frac{R_0}{R^{M}_0}=\sqrt{\frac{(D+k(R^0-\lambda_2))(1-\varepsilon)(R^0 -\lambda_1)}{\kappa(R^0-\lambda_2) (D+k(R^0-\lambda_1))}}. \end{aligned}$$ $

Solving $R^{*}=1$ in $\varepsilon$, we get

$ \varepsilon=\varepsilon^{*}:=1-\frac{\kappa(R^0-\lambda_2)(D+k(R^0-\lambda_1))}{(D+k(R^0-\lambda_2))(R^0-\lambda_1)}. $

Thus, $\varepsilon>\varepsilon^{*}(<\varepsilon^{*})$ is equivalent to $R^{*}<1(>1)$.

Let us consider three cases:

$(C1)$ $\kappa\geq\mu$, or $\kappa<\mu$ and $\lambda_3\geq R^0$.

$(C2)$ $\kappa<\mu$ and $b\leq b^{*}$ hold for $\lambda_3<R^0$.

$(C3)$ $\kappa<\mu$ and $b>b^{*}$ hold for $\lambda_3<R^0$.

The following Theorem states the existence of infection equilibria of (1) according to the above discussions.

Theorem 2.5. Let $(C1)$ or $(C2)$ hold. Then for $\varepsilon>\varepsilon^{*}$, we have:

$(i)$ If $0<R_0<R^{*}$, there is no infection equilibrium.

$(ii)$ If $R_0=R^{*}$, there exists one coexistence equilibrium $E^{*}_4$ of multiplicity $2$.

$(iii)$ If $R^{*}<R_0<1$, there exist two coexistence equilibria $E^{*}_4$ and $E^{**}_4$.

$(iv)$ If $1<R_0$, there is only one coexistence equilibrium $E^{**}_4$.

For $\varepsilon<\varepsilon^{*}$ we have:

$(i)$ If $0<R_0<1$, there is no infection equilibrium.

$(ii)$ If $1<R_0<R^{*}$, there is only one coexistence equilibrium $E^{*}_4$.

$(iii)$ If $R^{*}<R_0$, there is only one positive equilibrium $E_4^{**}$.

Proof. Note that $R_0=R^{M}_0$ when $\varepsilon=\varepsilon^{*}$, and the condition $\varepsilon>\varepsilon^{*}(<\varepsilon^{*})$ is equivalent to $R_0<R^{M}_0(>R^{M}_0)$. Furthermore, $0<R_0<R^{*}$ with $\varepsilon>\varepsilon^{*}$ is equivalent to $R_0<R^{M}_0<1$, $R^{*}<R_0<1$ is equivalent to $R_0<1<R^{M}_0$, and $R_0>1$ with $\varepsilon>\varepsilon^{*}$ is equivalent to $1<R_0<R^{M}_0$. For $\varepsilon<\varepsilon^{*}$, $0<R_0<1$ implies $R^{M}_0<R_0<1$, $1<R_0<R^{*}$ implies $R^{M}_0<1<R_0$, and $R_0>R^{*}$ implies $1<R^{M}_0<R_0$. Obviously, $F(R_4)>0$ always holds in case $(C1)$ or case $(C2)$. The conclusions of this theorem follow immediately from the preceding discussions.

This theorem indicates that the system (1) exhibits a backward bifurcation as $R_0$ crosses unity when $\varepsilon>\varepsilon^{*}$ for case $(C1)$ or case $(C2)$. Moreover, it admits a forward bifurcation when $\varepsilon<\varepsilon^{*}$.

Notice that the equilibrium $E^{**}_4$ does not exist for case $(C3)$. We can present another theorem for the existence of infection equilibria.

Theorem 2.6. Let $(C3)$ hold. The existence of infection equilibria is given as follows:

For $\varepsilon>\varepsilon^{*}$, we have

$(i)$ If $0<R_0<R^{*}$, there is no infection equilibrium;

$(ii)$ If $R^{*}<R_0<1$, there are two infection equilibria $E^{*}_4$ and $E_3$;

$(iii)$ If $R_0>1$, there is only one infection equilibrium $E_3$.

For $\varepsilon<\varepsilon^{*}$, we have

$(i)$ If $0<R_0<1$, there is no infection equilibrium;

$(ii)$ If $1<R_0<R^{*}$, there exists one infection equilibrium $E^{*}_4$;

$(iii)$ If $R_0>R^{*}$, there is only one infection equilibrium $E_3$.

The proof of this Theorem is omitted because it is similar to it for Theorem 2.5.

Theorem 2.6 presents the conditions for a forward bifurcation of the infection-free equilibrium and a transcritical bifurcation of the coexist equilibrium. Note that for $\lambda_3\geq R^0$, there is a backward bifurcation as $R_0$ crosses unity, but for $\lambda_3<R^0$, the existence of a backward bifurcation depends on the relation between $\kappa$ and $\mu$. More specifically, if $\kappa\geq\mu$, the backward bifurcation always exists and is independent of the size of $b$. But for $\kappa<\mu$, a critical value $b^{*}$ is needed to ensure the existence of backward bifurcation.

---

2.4. Global analysis for full CRISPR/Cas immunity

We now explore the persistence and extinction of phages in the case where $\kappa=0$, which leads to $k'=0$ and means that CRISPR/Cas immunity can fully suppress the invaded phages.

Theorem 2.7. Let $k'=0$. Then we have the following conclusions:

( $i$ ) The positive solutions of (1) satisfy

$ \lim\limits_{t\to\infty}(R(t), S(t), M(t), I(t), P(t))=(\lambda_1, R^0-\lambda_1, 0, 0, 0) $

if $R_0<1$.

( $ii$ ) If $R_0>1$, then bacteria populations and phage infection are uniformly persistent, i.e., there is a positive constant $\eta$ such that each positive solution of (1) satisfies

$ \liminf\limits_{t\to \infty} S(t)>\eta, \;\; \liminf\limits_{t\to \infty} M(t)>\eta, \;\; \liminf\limits_{t\to \infty} I(t)>\eta, \;\;\liminf\limits_{t\to \infty} P(t)>\eta. $

Proof. $(i)$ For a continuous function $f(t)$ which is bounded on $[0, \infty)$, we set

$ f^{\infty}=\limsup\limits_{t\to \infty}f(t), \;\;f_{\infty}=\liminf\limits_{t\to \infty}f(t). $

First, we claim that a positive solution of (1) admits $S^{\infty}\leq R^{0}-\lambda_1$. Indeed, by (2) we get

$ \dot{S}\leq -D S+f(R)S\leq -D S+f(R^{0}+\eta_0-S)S, \;\;\text{for all large } t, $

where $\eta_0>0$ is sufficiently small. Then by similar arguments to those in [42], we obtain $S^{\infty}\leq R^{0}-\lambda_1+\eta_0$. Taking $\eta_0\to 0$ leads to the conclusion as claimed. As a result of the claim, we see from the last two equations of (1) that for all large $t$:

$ \dot{I}\leq -DI+(1-\varepsilon)k(R^{0}-\lambda_1+\eta_1)P-\delta I, \\ \dot{P}\leq -D P-k(R^{0}-\lambda_1-\eta_1)P+b\delta I, $

(17)

where $\eta_1>0$ is sufficiently small. Let us consider a comparison system:

$ \dot{I}=-DI+(1-\varepsilon)k(R^{0}-\lambda_1+\eta_1)P-\delta I, \\ \dot{P}=-D P-k(R^{0}-\lambda_1-\eta_1)P+b\delta I. $

(18)

The Jacobian matrix of (18) is

$ J_1:=\left( $$\begin{array}{cc} -(D+\delta) & (1-\varepsilon)k(R^{0}-\lambda_1+\eta_1) \\ b\delta& -(D+k(R^0-\lambda_1-\eta_1) \\ \end{array}$$ \right). $

Since $R_0<1$, it is easy to examine that the eigenvalues of $J_1$ have negative real part for small $\eta_1>0$. Thus, the positive solutions of (18) approach to $(0, 0)$ as $t\to \infty$. It follows from (17) and the comparison principle that a positive solution of (1) exhibits that $(I(t), P(t))\to (0, 0)$ as $t\to \infty$. As a consequence, by the theory of an asymptotically autonomous system [43], it suffices to consider the asymptotic behaviors of the limiting system:

$ $$\begin{split} &\dot{R}=D(R^0-R)-f(R)(S+\mu M), \\ &\dot{S}=-DS+f(R)S, \\ & \dot{M}=-DM+\mu f(R)M. \end{split}$$ $

(19)

Since $\lambda_1<\lambda_2$, it follows from [24,25] that the positive solution of (1) exhibits that $(R(t), S(t), M(t))\to (\lambda_1, R^0-\lambda_1, 0)$ as $t\to \infty$.

$(ii)$ We first show that phage infection is uniformly persistent if $R_0>1$. Set

$ $$\begin{array}{l} X=\{(R, S, M, I, P): R\geq 0, S\geq 0, M\geq 0, I\geq 0, P\geq 0 \}, \\ X_0=\{(R, S, M, I, P)\in X: I>0, P>0\}, \\ \partial X_0=X\setminus X_0. \end{array}$$ $

We wish to show that (1) is uniformly persistent with respect to $(X_0, \partial X_0)$.

By Proposition 1, we see that both $X$ and $X_0$ are positively invariant for model (1). Evidently, $ \partial X_0$ is relatively closed in $X$. Moreover, Proposition 2 indicates that the nonnegative solutions of model (1) are point dissipative. Then we denote by $J_{\partial}$ the largest positively invariant set of (1) in $\partial X_0$. By similar discussions to those in [46], we see

$ J_{\partial}=\{(R, S, M, I, P)\in X: I=0, P=0\}. $

It is clear that there are three equilibria $E_0, E_1$ and $E_2$ in $J_{\partial}$. Since $\lambda_1<\lambda_2$, by [24,25] we see that $E_1$ is asymptotically stable in $J_{\partial}$ and the nonnegative solutions of (1) in $J_{\partial}$ except for $E_0$ and $E_2$ tend to $E_1$ as $t\to \infty$. Therefore, $E_0, E_1$ and $E_2$ are isolated invariant sets in $J_{\partial}$ and no subset of $\{E_0, E_1, E_2\}$ forms a cycle in $J_{\partial}$.

Note that (3) and (4) imply that a positive solution of (1) cannot approach $E_0$ as $t\to \infty$. We claim that this is also the case for $E_1$. Suppose not. Then there is a positive solution of (1) that satisfies $(R(t), S(t), M(t), I(t), P(t))\to (\lambda_1, R^0-\lambda_1, 0, 0, 0)$ as $t\to \infty$. It follows that for all large $t$, we have

$ \dot{I}\geq -DI+(1-\varepsilon)k(R^{0}-\lambda_1-\eta_2)P-\delta I, \\ \dot{P}\geq -D P-k(R^{0}-\lambda_1+\eta_2)P+b\delta I, $

(20)

where $\eta_2>0$ is sufficiently small. Let

$ J_2:=\left( $$\begin{array}{cc} -(D+\delta) & (1-\varepsilon)k(R^{0}-\lambda_1-\eta_2) \\ b\delta& -(D+k(R^0-\lambda_1+\eta_2) \\ \end{array}$$ \right). $

Since $R_0>1$, it is easy to examine that $J_2$ has a positive eigenvalue with a positive eigenvector for small $\eta_2>0$. It follows that the positive solutions of the following comparison system

$ \dot{I}=-DI+(1-\varepsilon)k(R^{0}-\lambda_1-\eta_2)P-\delta I, \\ \dot{P}=-D P-k(R^{0}-\lambda_1+\eta_2)P+b\delta I $

(21)

tend to infinity as $t\to \infty$. As a result, by (20) and the comparison principle we see that the positive solution of (1) satisfies $(I(t), P(t))\to (\infty, \infty)$ as $\to \infty$. We are led to a contradiction. Consequently, there is no positive solution of (1) that approaches $E_1$ as $t\to \infty$. In a similar way, we conclude that there is no positive solution of (1) that approaches $E_2$ as $t\to \infty$. Hence, $W^s(E_i)\cap X_0=\emptyset, i=0, 1, 2$. Finally, we claim that $E_0, E_1$ and $E_2$ are also isolated in $X_0$. Indeed, if $E_1$ is not isolated, then there exists a positive solution of (1) which is so close to $E_1$ for all time that (20) holds. Then repeating the above arguments leads to a contradiction. Similar discussions apply also to $E_0$ and $E_2$. Consequently, we conclude from [44,48] that phage infection is uniformly persistent.

By adopting the same techniques as above, we can show that the population $S$ of sensitive bacteria is uniformly persistent. From the third equation and (2), we obtain

$ \dot{M}\geq -D M+\varepsilon kSP. $

This, together with the uniform persistence of population $S$ and population $P$, implies that the population $M$ is uniformly persistent.

---

3. Numerical simulation

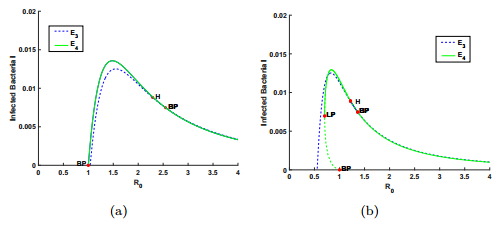
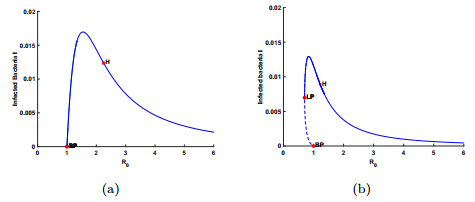
In this section, we implement numerical simulations to illustrate the theoretical results and explore more interesting solution patterns of model (1). Take the same parameter values as those in [23] where $D=0.2, ~m=0.7726$, $R^0=0.178212, ~ a=0.0727$ and $k'=0.15, ~\delta=0.4$. Then we choose $\mu=0.9$ so that $\mu f(R^0)>D$. First, we consider the case where $\kappa\geq \mu$. Let $k=0.15$ which means $\kappa=1>0.9=\mu$. If $\varepsilon=0.8>\varepsilon^{*}=0.023314$, there is a backward bifurcation, which is shown in panel (b) of Fig. 1. Furthermore, if $\varepsilon=0.01<\varepsilon^{*}=0.023314$, there is a forward bifurcation, which is shown in panel (a) of Fig. 1.

To demonstrate the second case where $\kappa<\mu$, we select $\mu=0.8$, $k=0.15, ~\kappa=0.6666$ and $b=110\leq b^{*}=135.618$. Then $(C2)$ holds. For $\varepsilon=0.3<\varepsilon^{*}=0.370362$, a forward bifurcation occurs, which is shown in panel (a) of Fig. 2. For $\varepsilon=0.8>\varepsilon^{*}$, we get a backward bifurcation shown in panel (b) of Fig. 2.

To show the case $(C3)$, we let $k=0.15, \kappa=0.8$, $b^{*}=46.802, \varepsilon^{*}=0.218651$ and $b=110>b^{*}$. Then $(C3)$ holds. For $\varepsilon=0.1<\varepsilon^{*}$, a transcritical bifurcation occurs at $E_4$ and a forward bifurcation emerges at $E_1$, which are shown in panel (a) of Fig. 3. For $\varepsilon=0.8>\varepsilon^{*}$, there are a backward bifurcation from $E_1$ and a transcritical bifurcation at $E_3$, which are shown in Fig. 3.

With the help of $\texttt{MatCont}$ package [15], we obtain more information for the dynamical behaviors of system (1), where the behaviors for $\kappa<\mu$ is more complicated than those for $\kappa\geq\mu$ when $\varepsilon$ and $R_0$ vary. As shown in Fig. 2 where case $(C2)$ holds, the coexistence equilibrium $E_4$ undergoes a Hopf bifurcation and a fold bifurcation. More specifically, the Hopf bifurcation point (H) occurs with $R_0=1.277977$, and a fold bifurcation point (LP) appears with $R_0=0.792644$. At the Hopf bifurcation point (H), the first Lyapunov coefficient is $-5.079166\times10^{-2}$, which means that the Hopf bifurcation is supercritical and the periodic solutions are born stable. The fold bifurcation leads to the existence of multiple infection equilibria with $0.792644<R_0<1$. Note that the simulation results indicate that the larger CRISPR/Cas immune efficiency $\varepsilon$ can induce backward bifurcations, which supports the results of our theoretical analysis.

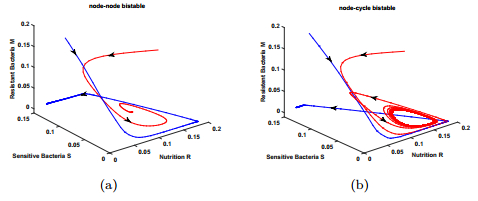
As discussed above, a bistable coexistence between the infection-free equilibrium and an infection equilibrium may occur when $\varepsilon>\varepsilon^{*}$. Panel (a) of Fig. 4 shows such a phenomenon. Interestingly, we find the bistable coexistence of the infection-free equilibria with a stable periodic solution, which is shown in panel (b) of Fig. 4.

---

4. Discussions

In this paper, we have developed a bacteriophage mathematical model based on CRISPR/Cas immune system. By combining theoretical analysis and numerical simulations, we have found that the model exhibits some new dynamical behaviors than the model without the immune responses in [23]. More specifically, the introduction of the CRISPR/Cas immune system induces a backward bifurcation from the infection-free equilibrium or a transcritical bifurcation from the coexist equilibrium, which means that although the basic infection reproduction number is below unity, the phage could coexist with bacteria. The coexistence of a stable infection-free equilibrium with a stable infection equilibrium(or stable coexist equilibrium), the bistable phenomenon of a stable infection-free equilibrium and a stable periodic solution are found, which are shown in panel (a) of Fig. 4 and panel (b) of Fig. 4. They provide reasonable explanations for the complexity of phage therapy [9,29] or bacteria-phages coevolution [13], and the coexistence of bacteria with phage in the biological experiments [20,29]. In contrast, there is no the backward bifurcation or bistable phenomena in the models of previous studies [23,42] where the immune response is ignored.

For case $(C3)$, the strain of sensitive bacteria may almost translated to resistent bacteria when the phage mutant rate (means as relative resistance) is inferior to the cost of bacteria's resistance for every values of $\varepsilon$, that is said, the CRISPR/Cas system have uninfluence on the bacteria and phages coexistence or the bacteria's diversity, which only influence by the released virus particles $b$ in this case. This analysis is consistent with [27]. The value of $b^{*}$ increases when $\mu$ increases or $\kappa$ decreases, while the effective of $\mu$ is greatly less than the change of $\kappa$. Thus, decreasing the values of phage mutant rate is contributed to sensitive bacteria survival when resistant bacteria have great bacteria's resistance cost value.

The mathematical analysis for the stability and bifurcation of equilibria of (1) in this paper present some insights into the underlying phage infection mechanisms by considering the CRISPR/Cas system in bacteria. It will be interesting to consider the analytical conditions for the Hopf bifurcation and the homoclinic bifurcation of the model and reveal how the immune response affect these bifurcations. It will be also interesting to consider the effect of latent period of infection like it in [23] or the nonlinear death rates like those in [29]. We leave these as future researches.

---

Acknowledgments

We are very grateful to the anonymous referees for careful reading and valuable comments which have led to important improvements of our original manuscript.

---

Appendix

Proof Theorem 2.1. Let $S_1=R^0-\lambda_1$. Evaluating the Jacobian matrix of system (1) at $E_1$ gives

$J(E_1)=\left( $$\begin{array}{cccccc} -D-S_1f^{'}(\lambda_1) & -D& -\mu D & 0 & 0 \\ S_1f^{'}(\lambda_1)& 0 & 0 & 0 & -kS_1 \\ 0 & 0 & -D+\mu D & 0 & \varepsilon k S_1 \\ 0 & 0 &0& -D-\delta & (1-\varepsilon)kS_1\\ 0 & 0 & 0 & b\delta & -D-kS_1 \\ \end{array}$$ \right), $

where $f^{'}$ denotes the differentiation of function $f$. The characteristic equation of $J(E_1)$ in $\omega$ is

$ (\omega+D)(\omega+S_1f^{'}(\lambda_1))[\omega^2+(2D+\delta+kS_1) \omega+f_0](\omega+D(1-\mu))=0, $

where

$ f_0=(D+kS_1)(D+\delta)(1-R_0^2). $

Since $0<\mu<1$, it is easy to see that all the roots of characteristic equation (A-1) have negative real parts if $R_0<1$, and the characteristic equation has one positive root if $R_0>1$. It follows from the Routh-Hurwitz criterion that $E_1$ is locally asymptotically stable. This completes the proof.

Proof Theorem 2.4. Evaluating the Jacobian of (1) at $E_3$ gives

$J(E_3)=\left( $$\begin{array}{cccccc} -D-\mu M_3f^{'}(R_3)& -f(R_3)& -\mu f(R_3) & 0 & 0 \\ 0& -D+f(R_3)-kP_3 & 0 & 0 & 0 \\ \mu M_3f^{'}(R_3) & \varepsilon kP_3 & 0 & 0 & -k'M_3 \\ 0 & (1-\varepsilon)kP_3 &k'P_3& -D-\delta & k'M_3\\ 0 & -kP_3 & -kP_3 & b\delta & -D-kM_3 \\ \end{array}$$ \right). $

Using $k'M_3(D+\delta-b\delta)=-D(D+\delta)$ and $k'P_3=\mu f(R_3)-D$, we get the characteristic equation in $\omega$:

$(\omega-f(R_3)+kP_3+D)(\omega^4+a_1\omega^3+a_2\omega^2+a_3\omega+a_4)=0, $

where $a_i$ (i=1, 2, 3, 4) are defined by (7). Set

$ F_1(\omega)=\omega-f(R_3)+kP_3+D, \;\;F_2(\omega)=\omega^4+a_1\omega^3+a_2\omega^2+a_3\omega+a_4. $

Note that $a_1>0$ and $a_4>0$. We see that the last two inequalities in (9) ensure that all the principal minors in the Routh-Hurwitz criteria are positive. Thus, the stability of $E_3$ is determined by the sign of $f(R_3)-kP_3-D$. Using $k'P_3=\mu f(R_3)-D$ and $f(R_3)=kA_2(R^0-R_3)/\mu$, we get

$ f(R_3)-kP_3-D=(1-\frac{\mu}{\kappa})f(R_3)+(\frac{1}{\kappa}-1)D:=F_0(\omega).\nonumber $

It is easy to see $F_0(R_3)$ is positive for any value if $\kappa\geq\mu$, which leads to the instability of $E_3$. Furthermore, if $\kappa<\mu$, $F_0(R_3)$ is negative when

$ f(R_3)>\frac{D(1-\kappa)}{\mu-\kappa}, \nonumber $

which is equivalent to $R_3>\lambda_3$. Consequently, $E_3$ is asymptotically stable if (9) holds, and is unstable if (10) is available. This completes the proof.

---