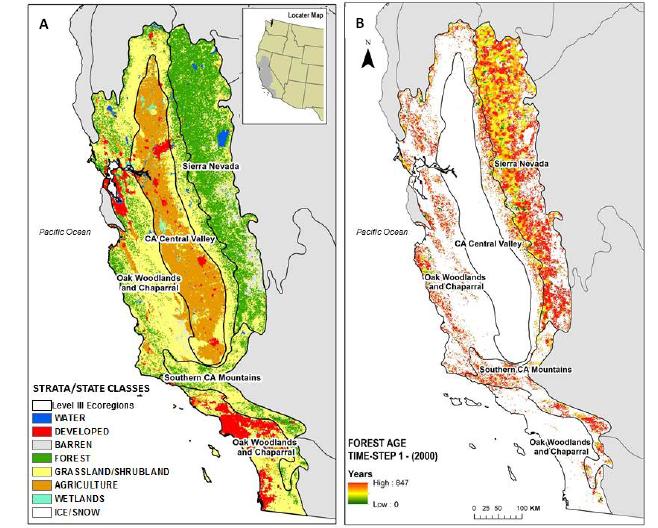
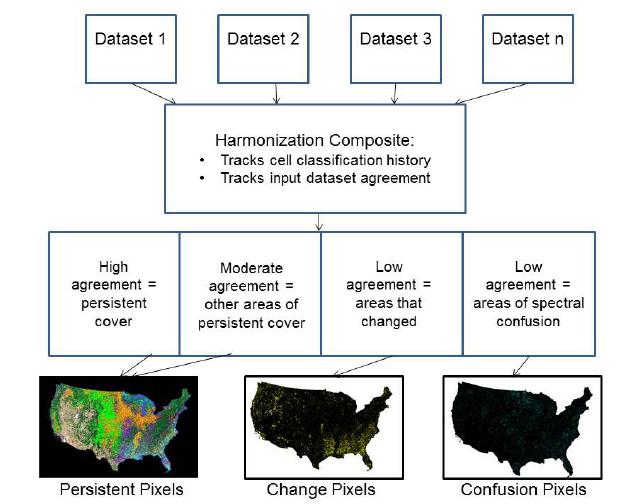
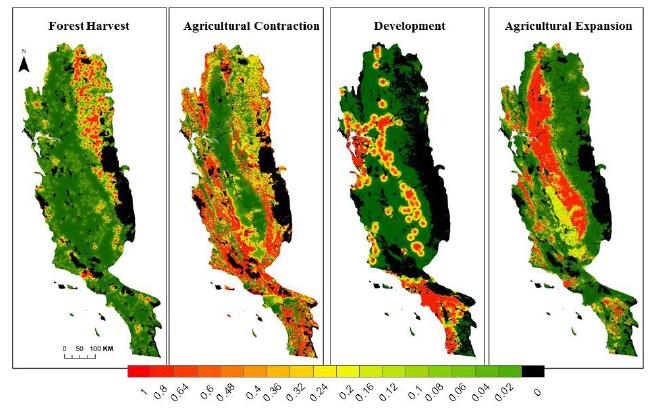
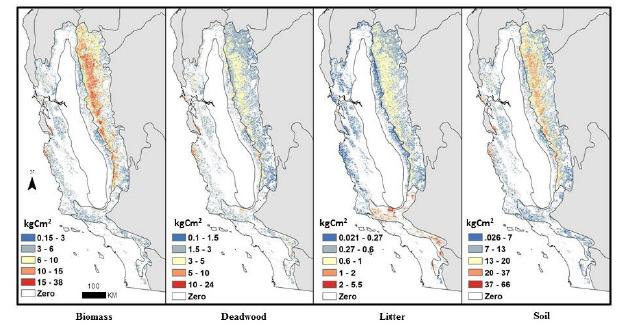
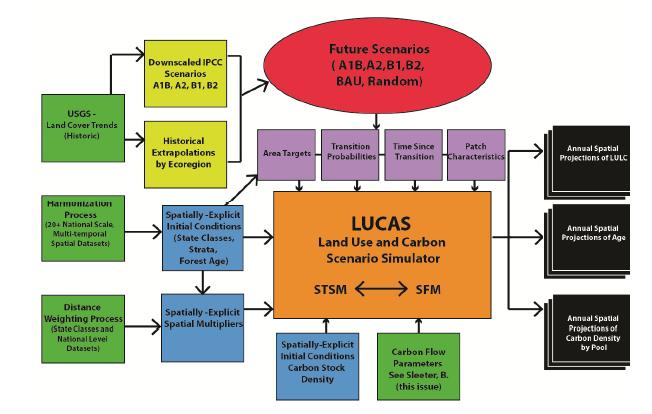
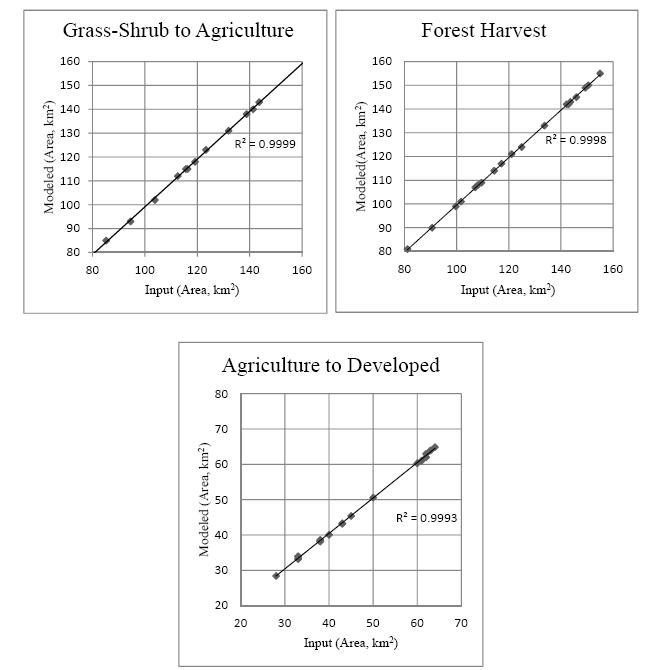
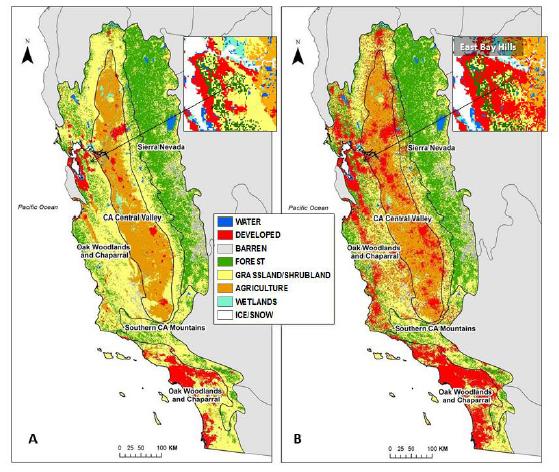
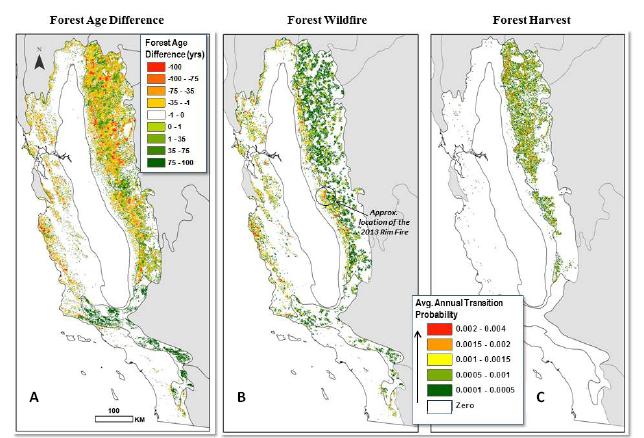
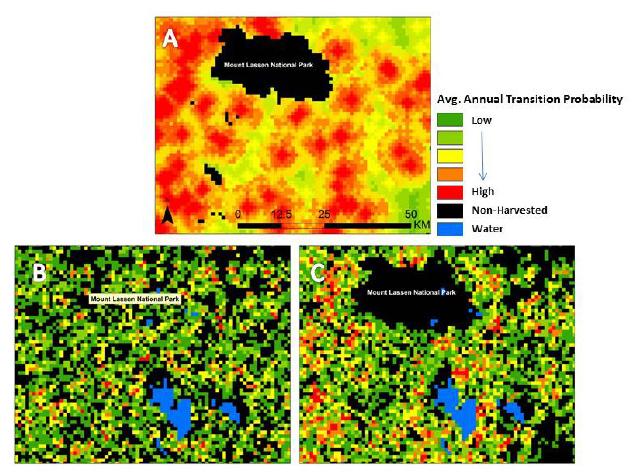
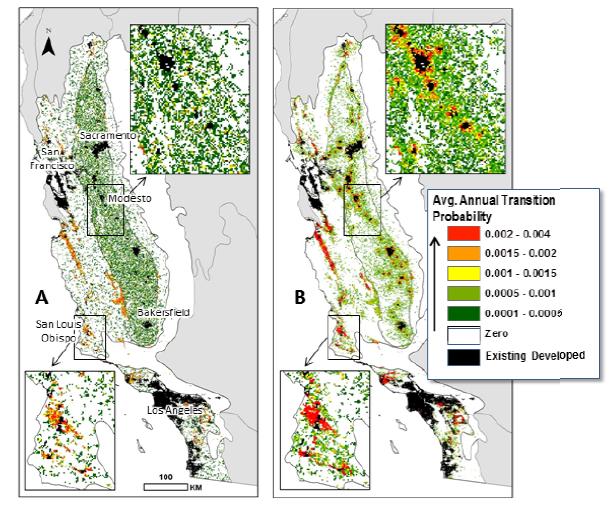
Spatially-explicit state-and-transition simulation models of land use and land cover (LULC) increase our ability to assess regional landscape characteristics and associated carbon dynamics across multiple scenarios. By characterizing appropriate spatial attributes such as forest age and land-use distribution, a state-and-transition model can more effectively simulate the pattern and spread of LULC changes. This manuscript describes the methods and input parameters of the Land Use and Carbon Scenario Simulator (LUCAS), a customized state-and-transition simulation model utilized to assess the relative impacts of LULC on carbon stocks for the conterminous U.S. The methods and input parameters are spatially explicit and describe initial conditions (strata, state classes and forest age), spatial multipliers, and carbon stock density. Initial conditions were derived from harmonization of multi-temporal data characterizing changes in land use as well as land cover. Harmonization combines numerous national-level datasets through a cell-based data fusion process to generate maps of primary LULC categories. Forest age was parameterized using data from the North American Carbon Program and spatially-explicit maps showing the locations of past disturbances (i.e. wildfire and harvest). Spatial multipliers were developed to spatially constrain the location of future LULC transitions. Based on distance-decay theory, maps were generated to guide the placement of changes related to forest harvest, agricultural intensification/extensification, and urbanization. We analyze the spatially-explicit input parameters with a sensitivity analysis, by showing how LUCAS responds to variations in the model input. This manuscript uses Mediterranean California as a regional subset to highlight local to regional aspects of land change, which demonstrates the utility of LUCAS at many scales and applications.
1.
Introduction
Oral health is a pivotal aspect of overall well-being, with dental ailments such as periodontal disease, cavities, and misalignments not only affecting masticatory function and aesthetics but also potentially correlating with systemic maladies like cardiovascular diseases and diabetes [1]. In the field of dental diagnostics, panoramic imaging, also known as orthopantomography, has become increasingly significant [2]. This technology provides a comprehensive view of the mouth, capturing images of all the teeth and the surrounding bone structure in a single shot. Unlike the traditional intraoral radiography, panoramic imaging offers a broad perspective, essential for a holistic assessment of dental health. It is particularly invaluable in identifying problems in areas such as tooth positioning, impacted teeth, and the development of tumors [3,4,5,6]. Moreover, in orthodontic treatments, tooth extractions, and pre-surgical planning, panoramic images offer clinicians a clear and detailed view, crucial for designing precise orthodontic appliances, assessing surgical risks, and formulating effective treatment plans, thereby significantly enhancing patient care [7,8]. Tooth segmentation not only significantly reduces diagnostic time and enhances diagnostic accuracy but also furnishes vital information for pathological analysis and personalized treatment planning [6]. For instance, accurate tooth segmentation can aid in evaluating the relationship between teeth and alveolar bone, determining the optimal position for dental implants, or assessing the outcomes of orthognathic surgery [9]. However, manual tooth segmentation in panoramic imaging interpretation, a task for radiologists and dental specialists, is time-consuming and costly, underscoring the urgent clinical need for automated segmentation technology to assist medical professionals in efficient and accurate diagnostics.
In recent years, the medical imaging field has witnessed a significant transformation with the rapid development of deep learning [10,11,12]. Unlike traditional methods that rely on manual feature extraction [13], deep learning can identify and categorize the complex and diverse features of both the 1D physilogical parameters and 2D medical images [15,16]. The capability of deep learning for automatic feature extraction in medical imaging leads to the creation of robust, quantifiable models with strong adaptability and generalizability, significantly aiding doctors in formulating precise and effective medical plans [17,18,19]. The advent of automatic tooth segmentation technologies [20], leveraging and computer vision techniques, has the potential to autonomously identify and segment dental structures [21,22].
Current approaches predominantly utilize U-shaped convolutional neural network architectures, with methods like Faster R-CNN [23] and Mask R-CNN [24] being widely applied in tooth segmentation and caries detection [25,26]. However, these are typically only suitable for downsampled Cone Beam Computed Tomography (CBCT) images. MSLPNet [27] employs a multi-scale structure to mitigate boundary prediction issues, subsequently utilizing a location-aware approach to pinpoint each dental pixel in panoramic images. Finally, an aggregation module is incorporated to diminish the semantic discrepancies across multiple branches. Two-stage segmentation methods [28,29] generally locate the approximate position of the teeth in the first phase, followed by precise segmentation in the second. In a similar vein, the model in [30] introduces a coarse-to-fine tooth segmentation strategy, pre-trained on large-scale, weakly supervised datasets to initially locate teeth, and then fine-tuned on smaller, meticulously annotated datasets. Beyond weak supervision, researchers often resort to semi-supervised learning strategies with limited annotated data, such as self-training and pseudo-label generation. A novel semi-supervised 3D dental arch segmentation pipeline is proposed by [31], utilizing k-means for self-supervised learning [32,33] and supervised learning on annotated data. The pipeline in [34] refines nnU-Net [35] architecture, training a preliminary nnU-Net model and then allowing medical professionals to supervise its performance on unannotated datasets, selectively updating the model. Undoubtedly, this semi-supervised approach is cost-intensive. Overall, while these methods have achieved commendable performance, convolution-based approaches are limited by their receptive field for relatively larger input images and rely on prior localization of teeth.
The long-range dependency capabilities of Transformer architectures [36,37,38,39] have inspired new paradigms in image processing. The sequence attention mechanism of vision Transformers aggregates different patches of the same image, allowing each patch to interact with others, a significant advantage over CNNs with their inductive bias priors. Transformers have similarly revolutionized medical imaging [40]. TransUNet [41] introduces a U-Net combined with Transformer architecture for medical segmentation, merging CNN's local focus with the Transformer's global feature extraction capabilities, significantly inspiring the medical segmentation field. BoTNet [42], blending Transformers with convolutions, proposes a lightweight instance segmentation backbone, replacing some of the final convolutional layers of ResNet with Transformers. Building on this, GT U-Net [43] introduces a Fourier loss leveraging dental prior knowledge, effectively segmenting dental roots. However, while these Transformer-based methods excel in capturing global interactions in the encoder, they often do not optimally leverage these encoded features due to limitations in their decoding mechanisms. This leads to certain deficiencies in current deep learning approaches to tooth segmentation, resulting in suboptimal performance.
To this end, we introduce STS-TransUNet, a model that merges a CNN-Transformer encoder—blending CNN's shallow local feature extraction with Transformer's deep global encoding [44] and a customized upsampling module as the decoder—aiming at prioritizing key information and filtering out the redundant. Specifically, we have innovated the decoder part of the architecture by incorporating channel and spatial attention mechanisms [45]. This enables the decoder to focus exclusively on pertinent information while disregarding redundant data. The use of deep supervision techniques allows for immediate feedback on each layer of the decoder, thereby accelerating the convergence rate. By integrating the input and output images, our method enhances the model's ability to directly associate and learn from the initial and desired final states of the images. This novel strategy overcomes some of the limitations observed in traditional segmentation methods, where a disconnect between input and processed images can lead to inefficiencies and inaccuracies. Furthermore, we employ a straightforward self-training semi-supervised strategy, effectively segmenting the MICCAI 2023 public challenge dataset (STS-2D) [46] and achieving a distinguished position in the competition. The primary contributions of this paper are threefold:
1). We propose the STS-TransUNet, a novel single-stage model tailored for precise and automated segmentation in clinical dentistry. This model is specifically devised for panoramic dental imaging and leverages advanced deep learning techniques to accurately identify and outline dental structures.
2). A decoder with spatial and channel attention mechanisms, combined with deep supervision techniques, effectively captures the irregularities in dental information, mitigates gradient vanishing, and accelerates convergence.
3). Extensive experiments conducted on the MICCAI STS-2D dataset demonstrate the exemplary performance of our approach.
2.
Related work
2.1. CNN-based methods in medical segmentation
Deep learning, particularly CNN-based approaches, has demonstrated exceptional performance across a broad spectrum of practical applications [47,48,49,50,51,52,53], including the domain of medical image segmentation. Diverging from traditional approaches in medical image segmentation [21,54,55,56], the advent of the U-Net [10] architecture has heralded a new era in this field, significantly enhancing the precision and efficiency of segmentation tasks. Its encoder-decoder structure was capable of extracting high-level features from input images and using them to generate fine segmentation results [35]. In [57], deep learning methods were first introduced into panoramic X-ray tooth segmentation. Specifically, they performed pre-training on the backbone using the Mask R-CNN on the MSCOCO dataset and fine-tune it on their own dataset. In [58], the influence of factors such as data augmentation, loss functions, and network ensembles on tooth segmentation based on U-Net was investigated, fully exploiting the performance of the U-Net. TSegNet [59] formulated the 3D tooth point cloud data segmentation task as the precise localization of each tooth's center based on distance perception and the segmentation task based on confidence perception. This task was accomplished through accurate positioning in the first stage and precise segmentation in the second stage. All the aforementioned methods employed supervised deep learning techniques. In the realm of semi-supervised learning, MLUA [60] adopted a teacher-student strategy, utilizing a single U-shaped network for both annotated and unannotated data. Considering the irregular shape and significant variability of teeth, this model introduced multi-level perturbations to train more robust systems. Similarly, the model proposed in [61] employed a comparable strategy, focusing on data augmentation in areas of carious lesions, resulting in a high-performing caries segmentation model. The proposal in [34] relied on the expertise of medical professionals to select data for semi-supervised segmentation. The success of these methods largely hinged on the profound impact of CNNs in image processing. However, CNNs inherently possess inductive bias limitations, particularly in their local feature extraction. In contrast to the aforementioned methods, our approach integrates CNN's capability for shallow local feature extraction with global Transformer encoding, thereby achieving comprehensive global capture of dependencies.
2.2. Transformer-based methods in medical segmentation
CNN-based methods inherently possess inductive biases and struggle to effectively learn global semantic interactions due to the locality of the convolution operation [62]. TransUNet [41] pioneered a new paradigm in medical segmentation by integrating the global encoding capabilities of Transformers with the upsampling features of U-Net. Following this, a multitude of methods based on the TransUNet framework have been custom-tailored and applied to various other domains of medical image segmentation [63,64], demonstrating its versatility and effectiveness. UNETR [65] took this further by transforming volumetric medical images into a sequence prediction problem, marking a significant application of Transformers in 3D medical imaging. Swin-Unet [66] merged the entire topological structure of Unet with the attention mechanisms of Swin Transformer. Its decoder used patch expanding for upsampling and showed remarkable performance on multi-organ CT and ACDC datasets. Similarly, the model in [67] developed a multi-task architecture based on Swin Transformer for segmenting and identifying teeth and dental pulp calcification. The Mask-Transformer-based architecture [68] has demonstrated impressive capabilities in tooth segmentation. It employed a dual-path design combined with a panoramic quality loss function to simplify the training process. While these methods leveraged the global dependency capabilities of Transformer encoders, they often overly focused on global feature extraction by the encoder. Moreover, few studies have explored combining Transformer methods with actual unannotated dental panoramic image data segmentation. Unlike methods based on pure Transformer encoder-decoder architectures, our encoder employs a CNN-Transformer architecture, maximizing the use of U-Net's skip connections. This design choice is informed by the inherent limitation of Transformer architectures in not effectively capturing global dependencies at shallower layers [44,69]. Our decoder focuses on relevant information without the need for prior tooth localization, employing a straightforward self-training method to generate pseudo-labels and iteratively update the model. This approach has demonstrated excellent performance on the MICCAI STS-2D dataset [46].
3.
Materials and methods
3.1. Materials
We utilize a high-quality MICCAI STS-2D dataset [46], including panoramic dental CT images of children aged 3–12 years, obtained from Hangzhou Dental Group, Hangzhou Qiantang Dental Hospital, Electronic Science and Technology University, and Queen Mary University of London. The dataset, serving as the official training set, comprises a total of 5000 images, including 2900 labeled and 2100 unlabeled images. All our experiments utilize this training set as the primary dataset. Our model's results on the official test set are detailed in Section 4.3.
3.2. Data partition and preprocessing
Data split: Fully supervised training data (random 2500 labeled images) are employed for fully supervised training. Semi-supervised training data (random 2000 labeled images and 2100 unlabeled images) are used for semi-supervised training. Test data (400 and 900 labeled images) are reserved for testing fully supervised and semi-supervised method, respectively.
Data preprocessing: The original images have a resolution of 640 × 320. To facilitate training, we resize them to 640 × 640, then further downsample them to 320 × 320 and 160 × 160. These smaller sizes are used for deep supervised training. During training, we apply data augmentation strategies, including random flips, rotations, and cropping, to enhance model robustness and performance.
3.3. Network architecture
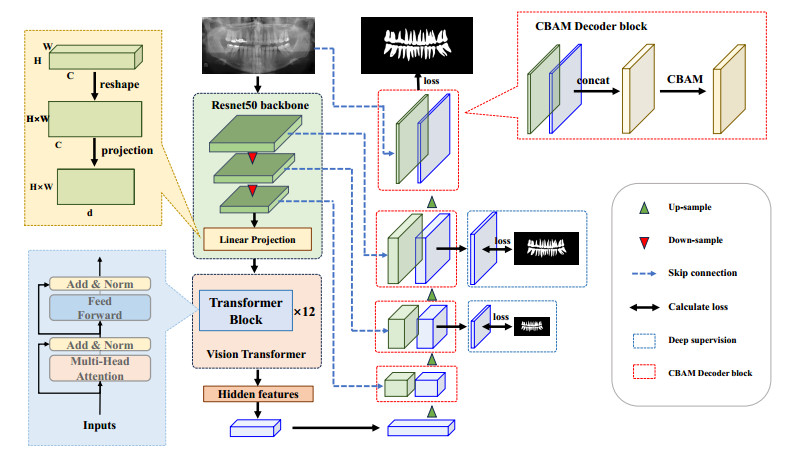
In our approach, we adopt the well-established Unet architecture, which comprises two fundamental components: An encoder and a decoder, as shown in Figure 1. The encoder plays a crucial role in extracting high-level features from the input images, while the decoder is responsible for generating the final segmented results. We represent our model with the following formulas:
where $ H $ denotes the hidden feature obtained from the CNN-Transformer hybrid encoder, and $ O_{1} $, $ O_{2} $, $ O_{3} $ represent the outputs from the last three layers of the CNN decoder, which are used for deep supervised training.
Recognizing the unique strengths of both convolutional neural networks (CNNs) and Transformers, we design a hybrid encoder structure. CNNs excel at capturing position-aware features, while Transformers are proficient at integrating long-range contextual information. By combining these two architectural elements, we harness their complementary advantages. This hybrid encoder structure enhances the model's ability to comprehend the underlying content within the images.
For the decoder, we employ a standalone CNN architecture. This choice aims to facilitate the model's effective learning of spatial and channel-related information. To further enhance performance, we introduce the Convolutional Block Attention Module (CBAM) [45].
CBAM is an attention mechanism employed in computer vision tasks with the primary objective of enhancing the performance of convolutional neural networks (CNNs). It enables better focus on important information in different channels and spatial locations when processing images. CBAM consists of two key components: Channel attention and spatial attention. Channel attention helps the model learn which channels are most crucial for tasks such as image classification, while spatial attention helps the model identify essential regions or positions in an image for the task. This adaptive weighting mechanism allows the model to adapt to various images and tasks. Moreover, CBAM has demonstrated significant performance improvements in computer vision tasks, including image classification, object detection, and semantic segmentation. Its main advantage lies in its ability to automatically learn which features are more important for a given task, thus enhancing the model's performance and robustness. CBAM has found wide application in deep learning, providing a potent tool for the field of computer vision.
where $ \otimes $ denotes element-wise multiplication. During multiplication, the attention values are broadcasted (copied) accordingly: channel attention values are broadcasted along the spatial dimension, and vice versa. $ F'' $ is the final refined output. Figure 2 depicts the computation process of each attention map. Following formulas describe the details of each attention module:
The CBAM module enhances proposed model's understanding of image content and assists it in prioritizing specific channels. To expedite the model's convergence during training and enhance its ability to generalize to different image scales, we implement a deep supervised training strategy. This strategy involves introducing supervised signals into the last three decoder layers, each corresponding to different image scales. It enables the model to better understand and adapt to various image scales effectively.
3.4. Training strategy
We train both fully supervised and semi-supervised models using a loss function that combines dice loss and IoU loss weighting. The formula of used total loss is as following:
where $ \hat{Y} $ and Y respectively represent the prediction and ground truth. We employ deep supervision by computing the loss at three different scales, the deep supervision loss are shown as following:
where $ \hat{Y}_{640}, \hat{Y}_{320}, \hat{Y}_{160} $ denote the outputs of the last three decoder layers, each with resolutions of 640,320, and 160, respectively. Similarly, $ Y_{640}, Y_{320}, Y_{160} $ represent the ground truth, resized to correspond to these resolutions. The following section details the specific two-stage training process.
3.4.1. First stage: Fully supervised training
In this stage, we implement a fully supervised training approach using samples with real labels, adopting a 5-fold cross-validation strategy to enhance model robustness. Instead of treating each fold's output as a separate model, we integrated these models from all five folds into a single ensemble model. This ensemble approach capitalizes on the strengths of each fold's training, resulting in a more robust and generalized model that effectively captures the diversity of the training data. The details of the first-stage training are as follows:
Learning rate initialization: We set the initial learning rate to 3e-4 to ensure a stable start to the training process.
Total training epochs: The training process encompasses a total of 200 epochs, providing the model with sufficient time to progressively enhance its performance. However, it is common for the initial few epochs to exhibit some instability.
Warm-up strategy: To mitigate the model's instability at the beginning of training, we implement a warm-up strategy. This involves gradually increasing the learning rate within the first 3 epochs, guiding the model towards a more stable training state.
Cosine curve strategy: Subsequent adjustments to the learning rate follow a cosine curve strategy. This strategy gradually reduces the learning rate, allowing for a more refined adjustment of model parameters until the learning rate decays to 0. This aids the model in better convergence during the later stages of training.
Fully supervised training is conducted to establish the foundational performance of the model, enabling it to learn feature extraction from labeled data and perform tasks. This training phase equips the model with a certain degree of predictive capability, laying the groundwork for subsequent semi-supervised learning.
3.4.2. Second stage: Semi-supervised training
In the second stage, we employ a semi-supervised training approach, capitalizing on the benefits it offers. Specifically, we adopt the self-training strategy [70] to generate pseudo-labels and facilitate model training. This phase harnesses unlabeled data effectively, maximizing the utility of available resources. The workflow of used self-training is shown as below:
Generating Pseudo-Labels: We initiate this phase by feeding 2100 unlabeled images into the model obtained from the first supervised training stage. The model, in response, produces outputs containing predicted class (foreground and background) probabilities for these images. These probabilities are then averaged across the entire set.
Pseudo-Label selection: To identify high-quality data points for training, we select the top 300 images based on the predicted probabilities. These images are paired with the corresponding high-quality pseudo-labels generated by the model.
Training with augmented data: The chosen images, along with their newly created pseudo-labels, are used to augment the training dataset. The training process initializes with an initial learning rate of 1e-4 and spanned three epochs. This helps the model adapt to the augmented dataset.
Iterative refinement: In pursuit of further model improvement, this process is repeated five times. In each iteration, a new model is employed, and the same steps are repeated. This iterative refinement strategy allows the model to learn progressively from the unlabeled data. This semi-supervised training strategy, specifically the self-training method, is valuable for harnessing the potential of unlabeled data, effectively expanding the training dataset, and improving the model's performance. It is a powerful tool for leveraging available resources and enhancing the robustness of the final model.
4.
Experiments and analysis
All our experiments are conducted on two 32 GB V100 GPUs. Our STS-TransUNet has a training duration of 12 hours, and we use Pytorch 1.12 as the experimental framework. Additionally, to ensure the reproducibility of our results, we have fixed the seed in all our experiments.
4.1. Comparative results
Quantitative analysis:After fully supervised and semi-supervised training, the results are presented in Table 1. We use Dice, IoU (Intersection over Union) and Hausdorff distance as our evaluation metrics. The formulas of them are shown as below,
where $ \hat{Y} $ and $ Y $ represent the prediction and the ground truth, respectively.
For the fully supervised training, models like UNet++ [71], UNet 3+ [72], and R2AU-Net [73], which rely solely on CNN, exhibits relatively weak perception of global information, resulting in less-than-ideal performance. Among the CNN-based models, R2AU-Net, which incorporates attention mechanisms, performed the best. While Transformer blocks are capable of capturing long-range information, they exhibit poorer position awareness inherently and require substantial training data to excel. As a result, the performance of Swin-Unet [66,74], DAE-Former [75] and SegFormer [76] are not on par with our model. In summary, the hybrid combination of CNN and Transformer in our model harnesses the strengths of both and delivered satisfying results. Even in the semi-supervised training phase, our model outperforms the other models. While all models experience a decrease in dice scores on the semi-supervised test set due to its larger size, our model retains its superior performance.
Qualitative analysis:Results from different models on randomly selected 4 samples are presented in Figure 4. Comparing models solely based on CNN with those incorporating attention mechanisms, the latter achieves clearer results. However, in comparison to Transformer-based models, the ability to segment the completeness of teeth remains a challenge, affirming the notion that Transformers possess stronger global modeling capabilities relative to CNN. Nevertheless, models based exclusively on Transformers often struggle with local information awareness compared to CNN. This is evident in Figure 4, where DAE-Former, while superior in overall results to CNN models, falls slightly short in fine details. Our model outperforms others in terms of texture and completeness.
4.2. Ablation study
To further validate the effectiveness of CBAM module and deep supervision strategy, we conduct extensive ablation experiments, as detailed in Table 2. Models a, b, c, d denote classical TransUNet, TransUNet$ + $CBAM, TransUNet$ + $CBAM+Concat, TransUNet$ + $Concat+DeepSupervision, TransUNet$ + $CBAM+Concat+DeepSupervision, respectively. The "Concat" means concat the input with the last output feature.
Effectiveness of CBAM: The comparison between models a and b, as well as models d and e, reveals that CBAM contributes to some improvement in the model's capabilities. Due to the ability of CBAM to dynamically adjust the importance of channels and spatial locations in the feature maps generated by CNNs. Through channel attention, it highlights crucial channels, emphasizing informative ones while downplaying less relevant ones. Furthermore, spatial attention allows the model to focus on significant regions within an image. This adaptive recalibration enhances feature representation, making CBAM effective in diverse computer vision tasks.
Effectiveness of deep supervision: According to the comparison between models c and e, deep supervision strategy plays an important role in our proposed STS-TransUNet. On the Dice metric, the adoption of the deep supervision strategy shows significant improvement in both full supervision and semi-supervised training. By introducing supervisory signals at multiple layers, deep supervision enables more effective learning of hierarchical features. In turn, this contributes to improved convergence during training and enhances the model's ability to capture intricate patterns in the data.
4.3. Competition results
We participated in MICCAI 2023 Challenges STS-2D Competition with STS-TransUNet and achieved top 3% rankings in both the fully supervised (first round) and semi-supervised (second round) tracks. The detailed results are as follows:
5.
Conclusions
We outline the methodology for both fully and semi-supervised learning with panoramic dental images, covering dataset, partitioning, preprocessing, network architecture, training, comparisons, and evaluation metrics.
We harness a high-quality dataset from various institutions and employ general data preprocessing techniques to ensure the performance and robustness of our model. Furthermore, we seamlessly merge fully supervised and semi-supervised learning, effectively harnessing both labeled and unlabeled data.
We employ a U-shape architecture and introduce a hybrid encoder merging CNN and Transformer strengths, enhancing positional awareness and long-range information fusion. Additionally, CBAM is incorporated to improve spatial and channel information management, contributing to exceptional performance. We train the model in two stages: First, with fully supervised training for a robust baseline, and then transition to semi-supervised training. The semi-supervised approach includes a 'self-training' strategy with pseudo-labels, data augmentation, and iterative model optimization, effectively improving performance with limited labeled data. For evaluation, we compare our model with others in the field. The results unequivocally show its superiority across various metrics, excelling in detail representation, tooth segmentation completeness, and global modeling capabilities. This reaffirms the soundness of our model's design.
Our research has limitations, such as the omission of prior clinical dental knowledge in the model construction. We have focused on the model's architectural priors, inadvertently overlooking the integration of valuable clinical insights. In our future work, we plan to adopt a more inclusive approach, incorporating a broader spectrum of clinical priors to infuse the model with greater real-world clinical relevance and accuracy.
In conclusion, our comprehensive methodology, diverse materials, and rigorous evaluation highlight the outstanding performance of our model in dental panoramic image segmentation. The innovative fusion of CNN and Transformer technologies, along with the implementation of semi-supervised training, establishes it as a front-runner in the field. This study not only provides valuable insights into deep learning applications in medical imaging but also underscores the potential of semi-supervised learning with unlabeled data. In the future, we aim to enhance the practical deployment of our model by integrating clinical information, ensuring that it not only excels in theoretical performance but also demonstrates greater real-world clinical efficacy and relevance.
Use of AI tools declaration
The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This work was supported by the Students' Innovation and Entrepreneurship Foundation of USTC (No. XY2023S007).
Conflict of interest
The authors declare that there are no conflicts of interest.









 DownLoad:
DownLoad: