Comparative analysis of apple and orange during forced convection cooling: experimental and numerical investigation

1.   Introduction

Dengue fever is a viral disease produced by a pathogenic agent and is spread through female Aedes aegypti mosquitoes. Specific temperature areas of the world are affected by dengue infection and are almost spread to 128 countries which brings much more losses in public health and economy ^[1]. The symptoms include, muscle pain, nausea, red eyes, high fever, joints pain, pain behind eyes, lower back pain, vomiting, severe fatigue and weakness, and mild bleeding etc. The carrier vector becomes infected when they bit an infected host and transmit four different serotypes of dengue to the host through their bites. Rare cases of vertical transmission in dengue infection are reported ^[2,3]. Due to the increased prominence of dengue viral infection in the past few decades, much effort has been made recently to develop a dengue vaccine. Yet, there is no fully effective vaccine although the partially effective vaccine is accessible in several states of the world ^[4,5]. Reduction of vector bites and environmental domain for vectors are other adopted control policies for dengue infection.

Epidemiological models are of great significance to gain insight into the comprehensive dynamics of infectious disease and to provide better control policies. To be more specific, analysis of these models predicts critical factors that play a central part in the prevention and spread of infection ^[6,7]. A number of the dynamical models have been established and approved to visualize the transmission of dengue infection ^[8,9,10,11]. The basic model of dengue infection was introduced by Lourdes Esteva and analyzed the stability of the model with variable human population ^[8,9]. Stability results for the equilibria of dengue infection model were established by in ^[10,11]. The role of vaccination on the transmission dynamics of dengue is examined in ^[12,13]. In dengue infection, asymptomatic carriers are frequently reported in ^[14,15] and are critical in the sense to increase the level of infection in endemic and non-endemic areas of the world.

It is eminent that vector-borne disease posses information about its previous stages and associative learning mechanism, to be more specific memory has a prominent role in the transmission dynamics of vector-borne disease. The memory in the host population associated to the individual awareness which reduces the contact rate between vector and hosts, while the mosquitoes use their prior experience about the human's location, blood selection, color, and the smell of humans sweat ^[16,17]. These types of phenomena can easily be captured by a fractional-order system in mathematical modeling of infectious diseases.

Fractional order system posses information about its previous and present stages to provide more realistic information about the dynamics of viral infections. Therefore, the dynamical behavior of epidemic diseases can be conceptualized and explore more accurately through non-integer order derivatives. A number of fractional-order models are introduced in the literature and successfully showed their positive role in different areas of physics, engineering, mathematics, and biology. For instant, a Maxwell model in fractional derivative is studied in ^[18]. Dengue dynamics in fractional derivative is considered in ^[19]. Application of fractional calculus to subdiffusion-reaction process is explored in ^[20]. An SIR model in fractional derivative is considered in ^[21]. The wave equation in a delay type fractional derivative is considered ^[22]. Recently, researchers proved that the fractional-order model can effectively handle the crossover behavior and complexity of communicable diseases, and offers a preferable fit for real data of the infection ^[23,24]. These properties make fractional-order systems more efficient than integer-order systems. For more related research on fractional order derivative and their applications to science and engineering problems, the authors investigated many piratical problems. For example, the author in ^[25] studied the fractional derivative and its applications to epidemic models. The corona virus model with lockdown is discussed through a mathematical model in ^[26]. The CoVID-19 and its impact on HIV and their future observation has been investigated in ^[27]. The corona virus model with fractional derivative is studied in ^[28], where the fractional operator is considered the Atangana-Baleanu type. The authors in ^[29] studded a corona virus model with nonlocal operator and using a power computational method. The M-fractional derivative and its applications to differential equations is discussed in ^[30]. An engineering problem with a new numerical results is studied in ^[31]. A fractional Schrodinger-Hirota equation and its optical solution is analyzed in ^[32]. The computer virus model in fractional derivative is considered in ^[33]. A review article that describing the harmonic wavelets and its fractal extension is studied in ^[34]. The solution of heat and diffusion equation with new technology is considered in ^[35]. A vector-host model with saturated treatment function and its optimal control analysis is discussed in ^[36]. The solution of Telegraph equation in new fractional operators is considered in ^[37]. The boundary value problems in fractional derivatives are studied in ^[38]. A fractional SEIR type model with treatment is studied in ^[39] while he dynamics of HIV with different transmission rates are analyzed in ^[40]. Therefore, motivated by these extraordinary properties, we analyze the dynamical behavior of dengue infection in the framework of the fractional-order derivative.

The article is structured as: In the second section, we put forward a brief summary of the basic concepts of fractional calculus. In the third section, we construct a fractional-order model for dengue infection with new assumptions, in addition, we proved basic results for our proposed fractional-order model. We established stability results for the steady-state in section four and carried out sensitivity analysis through the PRCC technique to point out the importance of input parameter on the output of $R_0$. We have shown the influence of different input factors on the basic reproduction number $R_0$, numerically. The fractional-order system is inspected numerically to observe the influence of $\vartheta$ on the dynamics of dengue in Section 5. In the last section of the article, ending remarks and conclusion of the overall analysis is presented.

2.   Basics of fractional calculus

Here, we will present a brief summary of the Caputo fractional derivative for further analysis of the dengue model. Caputo fractional derivative has the benefit of dealing with initial value problems and involves integration which posses information about the previous state of the system.

Definition 2.1. Let $\mathrm{g}:\mathbb{R}^+\rightarrow \mathbb{R}$, then the fractional integral of $\mathrm{g}$ is given by

where $\vartheta$ indicates the order of fractional integral and Gamma function is indicated by $\Gamma$.

Definition 2.2. The fractional derivative of order $\vartheta$ for a given function $g$ in the Caputo form is given by

where $n-1 < \vartheta < n, n\in N$.

Let $\eta_1, \eta_2$ be two positive numbers, then the Mittag-Leffler function is given by

Let $^{C}_0 D^{\vartheta}_t$ be the Caputo fractional derivative (CFD) of order $\vartheta$, then its laplace transform is define by

further, for the function $t^{\eta_2-1}E_{\eta_1, \eta_2}(\pm \omega t^{\vartheta})$, the laplace transform is given by

The following equation hold true by Mittage-Leffler function given in ^[41]:

Lemma 2.1. ^[42]. Consider a function $g:R^+ \times R^5 \rightarrow R^5$, which fulfills the conditions:

● The function $g(t, Y(t))$ is Lebesgue measurable in $R^+$ with respect to t;

● The function $g(t, Y(t))$ is continuous on $R^5$ with respect to $Y(t)$;

● The function $\frac{\partial g(t, Y(t))}{\partial Y}$ is continuous on $R^5$ with respect to $Y(t)$;

● and $\| g(t, Y(t)) \| \leq \aleph +\hbar \| Y \|, \forall t \in R^+, Y \in R^5,$ where $\aleph, \hbar$ are positive constants.

Then the fractional order system

where $0 < \vartheta\leq 1$, has a unique solution.

Lemma 2.2. ^[43]. Let a function $g(t) \in C(r, s]$ such that $^{C}_r D^{\vartheta}_t g(t) \in C[r, s]$ for $\vartheta \in (0, 1]$, then we have

Remark 1. Let a function $g \in C(r, s]$, such that $^{C}_r D^{\vartheta}_t g(t) \in C[r, s]$ for $\vartheta \in (0, 1]$. Then by Lemma (2.2) if $^{C}_r D^{\vartheta}_t g(t) \leq 0$, $\forall \; t \in (r, s)$, then $g(t)$ is non-increasing function for all $t \in [r, s]$, and if $^{C}_r D^{\vartheta}_t g(t) \geq 0$, $\forall \; t \in (r, s)$, then $g(t)$ is non-decreasing function for all $t \in [r, s]$.

3.   Formulation of the model

In construction of the model, we represent the mosquitoes and humans population by $N_v$ and $N_h$. The total mosquitoes size is divided into susceptible ($S_v$) and infected ($I_v$) compartments, while the total humans size is divided into susceptible ($S_h$), infected ($I_h$), carrier ($I_{hA}$), partially immune ($P$), and recovered ($R_h$) compartments.

We indicate the natural birth (or death) rate of mosquito and human by $\mu_v$ and $\mu_h$, respectively, and assumed that the disease-induced death rate to be negligible. Furthermore, we assumed that a fraction $\upsilon$ of susceptible hosts goes to partially immune class after implementation of vaccination and $\tau$ indicates treatment of infected host. The symptomatic fraction of infected class from susceptible and partially immune classes are indicated by $\psi$ and $\omega$, respectively. the parameter $\rho$ denotes the fraction of treated humans which join the partially immune class $P$ while remanning enter to recovered class $R_h$. Parameter $\gamma_h$ is used for recovery of symptomatic and asymptomatic humans while $\phi$ denotes the fraction of recovered humans which join the partially immune class $P$. The terms ($\frac{b \beta_1}{N_h} I_v$) and ($\frac{b \beta_2 }{N_h} I_v$) indicate the infection rate per susceptible host and partially immune host, respectively, while ($\frac{b \beta_3 }{N_h} I_h$) denotes the infection rate of per susceptible vector. In these terms $b$ accounts the bitting rate, $\beta_1$ and $\beta_2$ are the rates at which infected vectors transmit disease to susceptible and partially immune humans respectively, whereas $\beta_3$ represents the disease transmission rate from infected human to susceptible vector. The dynamics of dengue infection is given by

with the following initial condition

We denote the total human population size by $N_h$, and vector by $N_v$ so that, $N_h = S_h+I_h+I_{hA}+P+R_h$ and $N_v = S_v+I_v$. As the system (3.1) is independent of the state-variable $R_h$, thus, the proposed model (3.1) of dengue infection can be re-written in the following form without $R_h$:

further, assume that

then, we have $x_1+x_2+x_3+x_4 = 1$ and $x_5+x_6 = 1$. After replacing $x_6 = 1-x_5$ in the last equation of normalized system we obtained the following five dimensional reduced dengue model:

As fractional-order models describe the non-local behavior of biological systems and posses hereditary property, moreover, it provides information about its past and present state for the future, therefore, we represent the dynamical system (3.3) of dengue infection in the framework of fractional order Caputo's derivative to conceptualize the transmission of dengue fever in a more accurate way. Thus, the system consist of fractional derivatives is presented by

where $^{C}_0 D_t ^{\vartheta}$ indicates Caputo's fractional derivative of order $\vartheta$, the order $\vartheta$ indicates the index of memory in the system. In addition, the values

In Caputo's sense, the derivative of constant is equal to zero which is another advantage to make the system more reliable and flexible for analysis. Next, we will analyze the biologically feasible region of the fractional-order dengue model (3.4).

Theorem 3.1. The proposed fractional-order dengue infection system of equations (3.4) has a unique solution.

Proof. For the required result, we first prove that the fractional system (3.4) has a unique solution for all initial conditions in $R^5$. Clearly, the first three conditions of Lemma (2.1) are hold by the vector function $g$ of the system (3.4). Next, to prove the last condition of Lemma (2.1), we rewrite system (3.4) as

where

Symbolize the above

and taking norm, we get

Hence, the requirements of Lemma (2.1) are fulfilled, therefore the system of equations (3.4) has a unique solution.

Theorem 3.2. The closed set $\Omega = \{ (x_1, x_2, x_3, x_4, x_5) \in R^5_+: 0 \leq x_1+x_2+x_3+x_4 \leq M_1, 0 \leq x_5\leq M_2 \}$ is a positive invariant set for the proposed fractional order system (3.4).

Proof. To prove that the system of equations (3.4) has a non-negative solution, the system of equations (3.4) implies

Thus, the fractional system (3.4) has non-negative solutions. In the end, from the first four equations of the fractional system (3.4), we obtain

where $\mathcal{W} = min(\mu_h^\vartheta, ((1-\rho)\tau^\vartheta+(1-\phi)\gamma_h^\vartheta+\mu_h^\vartheta), ((1-\phi)\gamma_h^\vartheta+\mu_h^\vartheta), \mu_h^\vartheta)$. Solving the above inequality, we obtain

so by the asymptotic behavior of Mittag-Leffler function ^[44], we obtain

taking the same steps for the last equation of system (3.4), we get $x_5(t) \leq M_2$, where $M_2 = \frac{b^\vartheta e M_1}{b^\vartheta e M_1+\mu_v^\vartheta}$. Hence, the closed set $\Omega$ is a positive invariant region for the fractional-order dengue model (3.4).

4.   Reproduction number and stability analysis

The biological meaningful equilibria of fractional system (3.4) are DFE and EE, depending on infected classes in both the populations. To obtain the infection-free equilibrium, we set the fractional derivative $^{C}_0 D^{\vartheta}_t x_1, ^{C}_0 D^{\vartheta}_t x_2, ^{C}_0 D^{\vartheta}_t x_3, ^{C}_0 D^{\vartheta}_t x_4,$ and $^{C}_0 D^{\vartheta}_t x_5$ to zero of the fractional system (3.4) without infection, and get

The detailed concept of the basic reproduction number is presented in ^[45], and is normally denoted by $R_0$, and is calculated as

this is because of three infected comportment in the system, i.e., $m = 3$, which provides

which gives

The $R_0$ of the fractional-order dengue model (3.4) is obtained by using the next generation matrix as

Assume a fractional-order linear homogenous system of the following form

where $B\in M_{m\times m}(R)$ and $0 < \vartheta \leq 1$. The following theorems are on the stability of linear homogenous system (4.1).

Theorem 4.1. ^[46]. The origin of the fractional dynamical system (4.1) is asymptotically stable $\Leftrightarrow \mid arg(\lambda_i) \mid > \frac{\vartheta \pi}{2}$ is fulfilled for all eigenvalues $\lambda_i$ of matrix B.

Theorem 4.2. ^[47]. The steady state of fractional system (2.6) is locally asymptotically stable (LAS) if $\mid arg(\lambda_i) \mid > \frac{\vartheta \pi}{2}$ for all eigenvalues $\lambda_i$'s of $g(y)$ at steady state, otherwise unstable.

In order to prove the $LAS$ of infection-free steady state $E_0$ it is sufficient to confirm that all of the eigenvalues of the matrix of dynamics given by $J(E_0)$ lie outside the closed angular sector as shown in ^[46]. We state the following theorem for the desired result.

Theorem 4.3. The $DFE$ of the fractional-order system (3.4) is LAS if $R_0 < 1$ and $\mid arg(\lambda_i) \mid > \frac{\vartheta \pi}{2}$ for all eigenvalues $\lambda_i$'s of the Jacobian matrix $J(E_0)$ at steady state, otherwise it is unstable.

Proof. To obtain the demanded result for the fractional system (3.4), we take the Jacobian matrix of the system at infection-free equilibrium as

The characteristic equation in term of $\Lambda$ of the above matrix $J_{\mathcal{E}_0}$ which is given below:

where the associated coefficients are as follow:

, where $A = \psi b^\vartheta a x_1^0 + \omega b^\vartheta c x_4^0$ and $B = (1-\psi) b^\vartheta a x_1^0 + (1-\omega)b^\vartheta c x_4^0$. From (4.2) it is clear the argument of the first two eigenvalues $\lambda = -\mu_h^\vartheta$ and $\lambda = -(\mu_h^\vartheta+\upsilon^\vartheta)$ satisfy the necessary condition given (i.e., $\mid arg(\lambda_i) \mid > \frac{\vartheta \pi}{2}$ for all $\vartheta\in(0, 1)$). Furthermore, if $R_0 < 1,$ then all $a_i > 0$, for $i = 1, 2, 3,$ and it is easy to show that $a_1 a_2-a_3 > 0$ Thus, following ^[46], the arguments of all eigenvalues satisfy the necessary Matignon condition. Consequently, the infection-free steady-state is $LAS$.

Theorem 4.4. The infection-free steady state of the fractional-order system (3.4) is GAS without vaccination, if $R_0 < 1$.

Proof. Let $\upsilon = 0$, and $(x_1, x_2, x_3, x_4, x_5)$ be the solution of system (3.4) with suitable initial conditions $(x_1(0), x_2(0), x_3(0), x_4(0), x_5(0))$ in $\Omega$. Here, it is clear that the fractional system has only one equilibrium $E_0$ on the boundary of $\Omega$. Therefore, to achieve the target, it is enough to prove that the solution $(x_1, x_2, x_3, x_4, x_5)$ tends to the infection-free equilibrium as time tends to infinity. Since $x_i \leq x_i^0$, for $i = 1, 4$, then the system implies that

Taking the auxiliary system

this further implies

the coefficient matrix of the above fractional system is $F-V$, and if $R_0 = \rho(FV^{-1}) < 1$, then the eigenvalues of $F-V$ lies in the left half plane. Consequently, each positive solution of the fractional system (4.3) fulfills $\lim \limits_{t\rightarrow\infty}y_1 = 0$, $\lim \limits_{t\rightarrow\infty}y_2 = 0$ and $\lim \limits_{t\rightarrow\infty}y_3 = 0$ by Theorem 4.1. By the comparison theory of fractional differential equations ^[48], we have $\lim \limits_{t\rightarrow\infty}x_2 = 0$, $\lim \limits_{t\rightarrow\infty}x_3 = 0$ and $\lim \limits_{t\rightarrow\infty}x_5 = 0$. Then from system (3.4), we have

this can be further converted into

having the solution

taking the asymptotic behavior of Mittag-Leffler function ^[44] as

also the real parts of eigenvalues of $-B$ are negative, so it can be observed that $X(t) \rightarrow X^0$ as t tends to infinity. Hence, the infection-free steady-state of the system (3.4) is GAS without vaccination.

Next, we will demonstrate the persistence of infection in the fractional-order system. It describes the level of endemicity of infection in the system. Biologically speaking, the infection persists in the system if the level of infected fraction stays at a higher level for t large enough.

Theorem 4.5. In the fractional-order system (3.4), the dengue infection is uniformly persistent at $\vartheta = 1$ if $R_0 > 1$.

Proof. The threshold parameter $R_0$ is of high significance, which measures the level of infection in the system. If $R_0$ less than one then the asymptomatic stability of infection-free equilibrium$(E_0)$ prevent the system from the persistent of the infection. If $R_0$ greater than one then the sufficiently close solution of fractional system (3.4) to $E_0$ moves away from it due to its instability in the interior of $\Omega$ by Theorem (4.3). For uniform persistence of our system (3.4) at $\vartheta = 1$, we will prove that it fulfills the criteria of Theorem 4.3 in ^[49] for $R_0 > 1$. Select $X = R^5$ and $E = \Omega$. Here, the maximal invariant set on the boundary of $\Omega$ is the set $\{E_0\}$ and is isolated. So, the criteria of Theorem 4.3 in ^[49] satisfies for the system. Thus, the system (3.4) is uniformly persistent if $E_0$ is unstable for $R_0 > 1$.

4.1.   Sensitivity analysis and numerical results

In the section, we present the global sensitivity analysis in order to determine those model parameters which are most influential on the disease dynamics. The main goal of this analysis is to detect and measure the influence of input parameters on the output of the system. To be more specific, it is used to know how the input parameters and initial values contribute to the output of a system. Mostly, when there is a little uncertainty in initial conditions and input parameters partial derivative of output functions are computed with respect to the input factors around the base values. This method is named as the local sensitivity analysis and relies on the variations of parameters close to the base values. This technique is not most suitable for epidemiological models due to the uncertainty in the input of the system. Therefore, global sensitivity analysis is preferred to perform this analysis and to provide more accurate results.

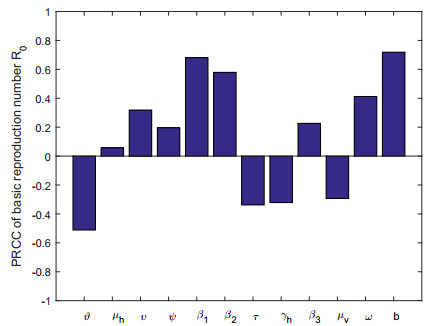
Here, we used the PRCC method ^[50] for sensitivity analysis to point out the input parameters that highly influence the results of $R_0$. It is an effective method and can successfully measure the monotonic, nonlinear relationship between input and output values of the system. PRCC analysis provides PRCC and p values for each factor involve therein, with which we can measure the contribution of each factor. More specifically, the input factors with sizeable PRCC and negligible p-values are considered to be highly effective factors in the system. In our analysis, we investigate all the parameter presented in Table 1 to know their contribution to the outcomes of $R_0$ and listed all the associated PRCC and p-values provided by the PRCC significance test. Figure 1 and Table 1 demonstrate that the parameter $b$ is highly influential with PRCC value 0.7022. After that, the parameter $\beta_1$, and $\vartheta$ are highly influential with PRCC values 0.6427, and -0.5112, respectively. Sensitivity analysis illustrated that $b, \beta_1$, and $\vartheta$ are critical parameters in $R_0$, which can remarkably influence the infection. Therefore by controlling these factors can greatly decrease and prevent the level of new dengue cases in the community.

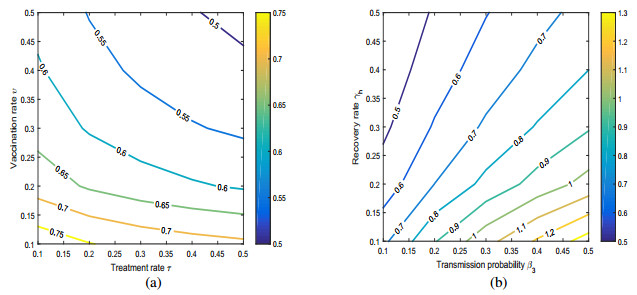
Next, we illustrate the influence of vaccination and treatment in on the threshold $R_0$ of the proposed system 2 (a). We noted that vaccination and treatment decrease the threshold parameter, moreover, we observed that vaccination reduces the susceptibility of host individuals in the system while the treatment reduces the infectivity of host individuals. In Figure 2 (b), we showed the influence of $\beta_3$ and $\gamma_h$ on the basic reproduction number $R_0$ of the proposed system of dengue fever.

5.   Numerical scheme for fractional model

We present in this section the solution of the model (3.4) by using the algorithm presented in ^[51]. To have a numerical scheme, we write the model (3.4) in the following form:

where $g = (x_1, x_2, x_3, x_4, x_5)\in \mathbb{R_+}^5$, $\mathcal{G}\Big(t, g(t)\Big)$ is used for a continuous real valued vector function, which additionally satisfies the Lipschitz condition and $g_0$ stands for initial state vector. Taking Caputo integral on both sides of (5.1) we get

In order to formulate an iterative scheme, we consider a uniform grid on $[0, \mathcal{T}]$ with $h = \frac{\mathcal{T}-0}{m}$ is the step size and $m\in \mathbb{N}$. Thus, the equation (5.2) gets the structure as follows after make use of the Euler method ^[52]

Thus, utilizing the above scheme (5.3), we deduced the following iterative formulae for the corresponding classes of the model (3.4)

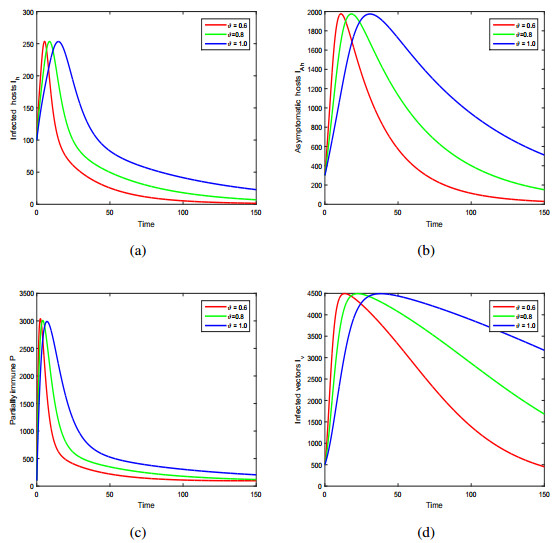
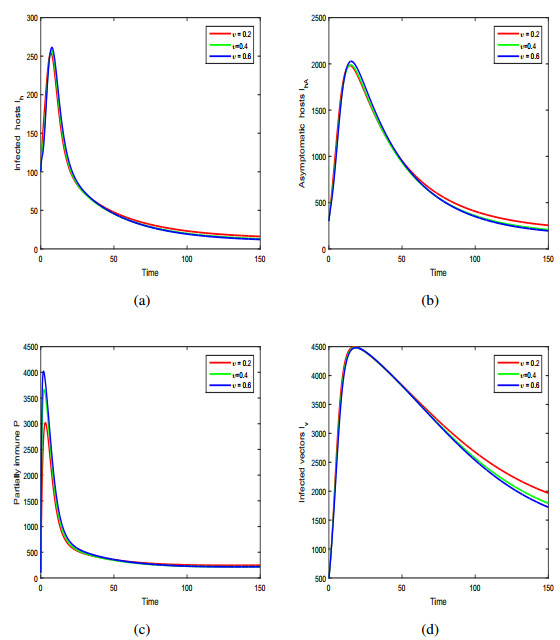
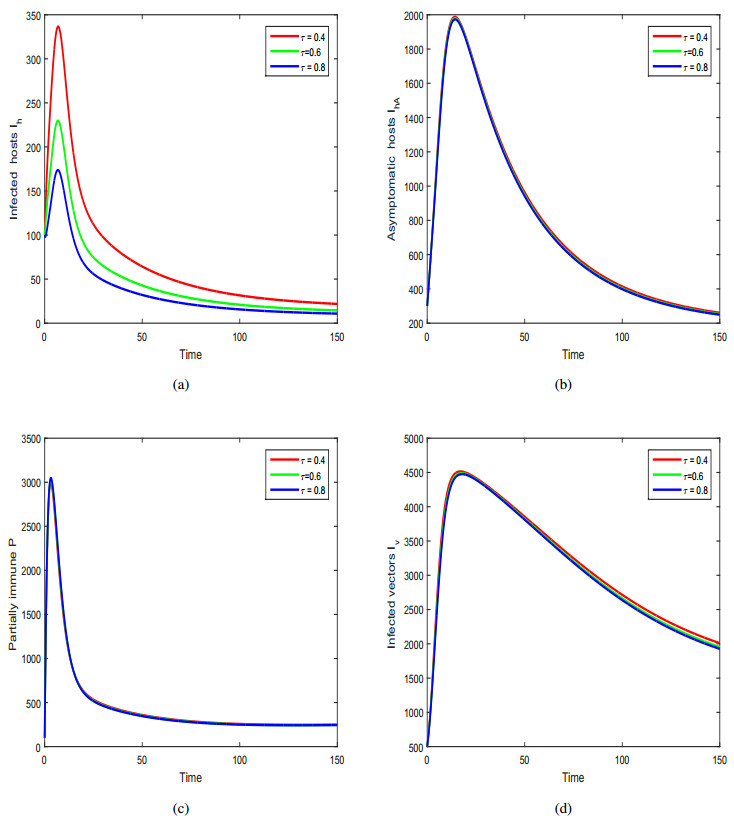
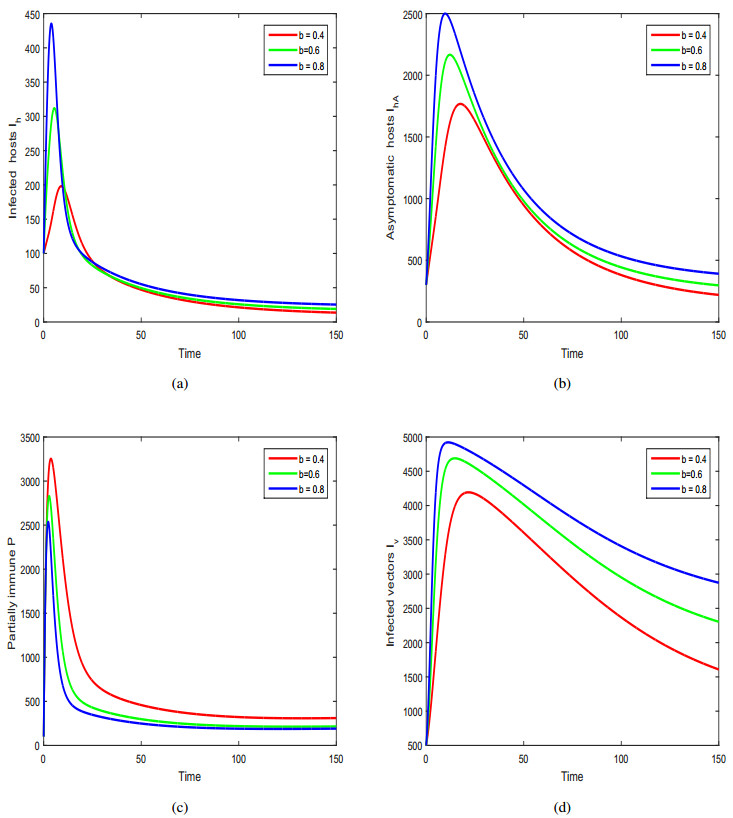
We used the above approximation for the solution of our fractional system. In Figure (3), we demonstrate the dynamics of infected host ($I_h$), asymptomatic host ($I_{hA}$), partially immune $(P)$ host and infected vector ($I_v$) with the variation of fractional-order $\vartheta$. We noticed that the variation of fractional-order $\vartheta$ has a great influence on the infection level of dengue in both the population. In other words, it can highly reduce the level of dengue fever in the community. In Figure (4) and Figure (5), we represent the dynamics of dengue fever with the variation of vaccination and treatment. In these simulations, we observed that vaccination and treatment decrease susceptibility and infectivity of the host population, and have a slight influence on the level of infection. We demonstrated the effect of biting rate $b$ of the mosquitoes on the dynamics of dengue and observed that the peak of infection can be greatly decreased by decreasing the biting rate $b$ in Figure (6). The mosquitoes biting and its generation further can be decreased by spraying or wasting the standing water around home or inside the home, which has great influence on population of mosquitoes that end up biting humans. Using bed-nets, avoid to visit areas prone to mosquitoes, using mosquito repellent, covering legs and arms by wearing long-sleeves and long pants are useful to prevent himself from the biting of mosquitoes. These scenarios predict that the infection can be controlled and prevented by decreasing the index of memory and biting rate of vectors in the community.

6.   Conclusion

In this article, we constructed a new epidemic model for the transmission of dengue infection with non-integer derivative. Basic results of the suggested fractional system are investigated through analytic skills. The basic reproduction number of the system is calculated through the next-generation method, indicated by $R_0$. We established stability results of infection-free steady-state of the system. Sensitivity analysis of $R_0$ is carried out in order to know the contribution of input factors in the results of $R_0$ and observed that $b, \mu_v$, and $\beta_3$ are the most critical parameters that highly contribute in the control and subsequent spread of dengue infection. We showed that the dengue infection is uniformly persistent in the system for $R_0 > 1$. We obtained feasible results for the dynamics of dengue infection with the variation of memory index $\vartheta$ and suggested that the index of memory has a dominant influence on the system. We concluded that the fractional-order model can explore more accurately the dengue epidemic disease transmission model rather than the integer-order derivative models. The numerical results for the suggested parameter can be considered useful for the possible eliminations of dengue infection in the community. We suggest that fractional-order(index of memory) $\vartheta$ and biting rate $b$ can remarkably control and greatly decrease the level of disease in the society.

Conflict of interest

No conflict of interest exists regarding the publications of this work.

Acknowledgements

The authors are thankful to the anonymous reviewers for the careful checking and suggestions that improved the presentation of the paper greatly. Fatmawati and Muhammad Altaf Khan are supported by Universitas Airlangga through Hibah Riset Mandat (No. 342/UN3.14/LT/2019). The funding of this paper was made from the project Universitas Airlangga through Hibah Riset Mandat (No. 342/UN3.14/LT/2019). Yasir Khan extends their appreciation to the Deanship of Scientific Research, University of Hafr Al Batin for funding this work through the research group project no.(G-108-2020).