1. Introduction
In the wake of the 2015 Paris Agreement, many countries are reconsidering which policies could drive deep reductions in carbon dioxide emissions (CO2). Carbon pricing is likely to feature prominently in this re-evaluation. In Japan, the government introduced a carbon tax in 2012 by adding a modest surcharge to current petroleum and coal tax schemes for crude oil, petroleum products, coal, liquefied petroleum gas and liquefied natural gas [1]. The tax revenue will then be recycled to help finance energy efficient and renewable energy technologies. The tax could also foreseeably motivate industries and consumers to save energy. But the current rates JPY289/tCO2 (USD 2.4/tCO2) are too low to induce these effects [2]. This raises an important question: what if tax rates were higher?
This paper examines this hypothetical “what if”. But rather than forecasting the effects of a higher carbon tax, the paper analyses historical fuel prices, subsidies, and investment data. This approach is taken because implementing a higher carbon tax would increase fuel prices and generate revenue that could subsidize investments in production upgrades, efficiency reforms, or technologies running on lower carbon fuels [3,4]. The consequent price gaps between conventional and lower carbon products may further influence consumer behavior [5,6]. Thus the paper will assess whether subsidy provisions and fuel price changes could improve energy and carbon intensity, thereby lowering CO2 emissions, and whether investments could lead to energy efficiency and carbon intensity improvements.
The study will focus on energy-intensive industries. At present, Japan’s industries account for 36% of the total CO2 emissions and 44% of total energy consumption. In the past, Japan succeeded in mitigating industrial-related CO2 emissions with reductions of 70MtCO2 between 1990 and 2014 [7]. However, these aggregate figures shed little light on what kinds of policy instruments affected energy and carbon-intensity in which industries. The paper hence concentrates on the iron & steel, chemical, and machinery industries for two reasons. The first is that they are significant contributors to CO2 emissions. The three selected industries account for 75% of CO2 emissions in Japan’s manufacturing sector (47.9% for iron & steel, 17.7% for chemical, 9.4% for machinery) [7]. They are also the top three contributors to the total domestic product in the manufacturing sector (11% in iron & steel, 16% in chemical and 42% in machinery industry) [8]. The second reason they are selected involves possible differences in their structure and responsiveness to varying policy changes. The paper will therefore also explore whether and to what extent the aforementioned fuel price changes and subsidy provisions had varying effects on investments that mitigate CO2 across different industries.
A time-series autoregressive moving average (ARMA) regression is used for these purposes. The regression results suggest the effects varied across industries. In the iron & steel industry, subsidies and price changes had negligible effects on energy or carbon intensity. This may be because existing iron & steel technologies have long lifetimes and sizable replacement costs [9,10]. It may also be because the industry is dominated by a few large companies that were relatively immune to policy changes 1. In the chemical industry, subsidies and fuel prices gave rise to investments that improved carbon and energy intensity. This may be because the industry has relatively higher operation costs that could be cut given financial incentives. In the cost structure of chemical industry, about 35 per cent of the total domestic production (gross outputs) is spent to purchase fuel products including coal, crude petroleum, natural gas, and oil and coal products 2. In the machinery industry, two of three fuel price changes (oil and gas), but not subsidy provisions, yielded improvements in carbon and energy intensity. This may reflect the heterogeneity of products that make up the industry 3 and other factors (such as a generally greater responsiveness to consumer demands and technology trends) 4. Overall, the study underlines that policymakers need to be cognizant of potentially varying effects of a carbon tax across different industries. This may require careful reflection on both the rate and the recycling of revenue in key industries.
1 A half of the total final energy consumption in iron and steel industry is by blast furnace manufacturing which is dominated by 15 entities in Japan. Data is available from METI (http://www.meti.go.jp/statistics/tyo/kougyo/result-2/h26/kakuho/sangyo/index.html and http://www.enecho.meti.go.jp/statistics/total_energy/results.html).
2 Ministry of Internal Affairs and Communications. Available from: http://www.soumu.go.jp/english/dgpp_ss/data/io/io11.htm
3 Machinery industry includes establishments such as electronic components and transportation equipment as well as production machinery. The number of business entities engaged in machinery industry accounts for about 78 per cent of the total establishments of manufacturing sector in Japan. (METI. Available from: http://www.meti.go.jp/statistics/tyo/kougyo/result-2/h26/kakuho/sangyo/index.html)
4 Machinery industry need to respond to fast changing consumer product demands and related technological trends. Therefore,energy consumption is likely to move with shifts in demands for products [64]. The industry also has comparatively high electricity demands [64] (also see METI. Available from: http://www.enecho.meti.go.jp/statistics/total_energy/results.html)
The remainder of the paper is divided into seven sections. The second section reviews literature to develop a simple conceptual model illustrating the links between key drivers of CO2 emission reductions. In the third section it describes the data and model based on the literature review. In the fourth and fifth sections results of a models are reported and discussed. The sixth section describes study limitations. A final section concludes with possible policy implications for a carbon tax in Japan.
2. Reducing CO2 Emissions
Cutting industrial-related CO2 emission often involves improving energy or carbon intensity. The former involves lowering energy per unit of production, while the latter entails lowering CO2 emitted per unit of energy [11,12]. Improving energy intensity requires altering energy consumption patterns or deploying energy efficient technologies [13,14,15,16,17]. Improving carbon intensity requires shifting to less-CO2 intensive energy sources or alternative fuels [12,18,19]. To lower energy use, fuel reductions, exhaust heat recovery and fuel swtching can be achieved through investments in improved technologies and equipment as well as operational efficiency gains. For energy efficiency improvements, the transformation of primary energy resources and economic structures can reduce energy demands [20]. On the other hand, fuel switching can curb energy use and improve CO2 emission intensity of industrial energy use [21,22]. For instance, Kagawa & Inamura (2001) demonstrate the main reduction of energy demand stems from structural changes to input factors.
In industries, renewable energy can replace conventional fossil fuels in non-utility generation; heat recovery and waste can also be reused for energy [24]. For example, the cement & ceramics and pulp & paper industries could reduce CO2 emissions by altering the fuel mix, using more biomass, improving efficiencies, and recycling energy from heat [25]. As suggested by these options, a combination of energy efficiency improvement and fuel switching is often needed to curb energy use and CO2 emissions.
Japan employed several of the above techniques to reduce its dependencies on imported oil and stabilise energy supplies throughout its modern history. Though initial efforts focused on shifting from oil to coal and improving coal efficiency in the 1980s [26], the approach concentrated more on shifting from coal to natural gas and nuclear by the 1990s into 2000s [27,28]. Following the Fukushima accident, renewable energy became a greater point of emphasis [29].
While the above options are well known, widespread implementation can be challenging. Gillingham et al. (2009) suggests a key reason for the challenge is market failure. Market failures stem from prices that do not reflect the true marginal social cost of energy consumption, thus curtailing incentives to adopt new technologies or otherwise improve production methods. Another hurdle is that decision makers are not always rational; hence they do not always minimise present value for energy service provisions even when a full accounting suggests the benefits outweigh the costs [30].
A carbon tax could be one of the tool to help overcome these barriers. By making fossil fuels more expensive and renewable energy more competitive, carbon pricing can incentivise industries to adopt technical measures such as fuel reduction, fuel switching and efficiency reforms. Since it puts a price on carbon, pricing can also send a signal to the market. If the price on carbon is high enough, it may also persuade consumers to reduce energy consumption [31,32,33]. This paper thus sets out to examine the effects of carbon tax on improving carbon and energy intensity. However, instead of looking at the impact of carbon tax, this paper focuses on a three key instruments that could improve carbon and energy intensity: 1) fuel price changes; 2) subsidy provisions; and 3) investments.
2.1. Subsidy provisions
One instrument that could improve energy and carbon intensity is subisdy provisions. Subsidies, including targeted grants and favourable loans, are a relatively straightforward approach to promoting new technologies or operational effiiciency reforms [34,35]. But while subsidies could help open or expand technology markets and encourage a range of supporting reforms, many maintain they are not cost-effective [25,36]. Rather often subsidies perform better when combined with tax policies [37,38,39]. More concretely, taxes on fuels can incentivise reductions in energy, while subsidies from tax revenue promote investments in energy efficient technologies. For instance, the Netherlands stimulated investments in clean automobiles with the subsidies that came from extra tax revenue from energy-intensitive cars [37]. In case of Japan, subsidies for measures of energy conservation and renewable energy are provided from the Special Account for measures to improve energy supply and demand structure of government budget. The financial sources of the Special Account include tax revenue from the petroleum and coal tax [40,41]. The subsidies includes fiscal incentives such as tax breaks as well as grants 5.
5 Tax break can improve the payback period by reducing the cost of energy-saving equipment through the reduction of tax payments [65].
2.2. Fuel price changes
Another possible instrument involves changing energy prices. Price changes incentivise energy use reductions. Estimating price elasticity has been used to assess regulatory policies and impacts of energy price shocks [42]. However, studies on energy price elasticity of energy demand show that price elasticity is much smaller than elasticities associated with GNP or energy efficiency improvements [20]. Price elasticity also tends to differ for particular fuel types and time-periods [43]. Moreover, there is a time lag between the price elasticity in the period of price rise and the period of price fall, and this cross-temporal variation is influenced by various factors such as technological changes, lifestyle changes, demographic changes [44]. Therefore, for the detailed of energy price elasticity of demand, each fuel type and individual industrial sector needs to consider price elasticity; these too vary significantly across fuel types and industries [43]. In the case of Japan, studies show that price elasticity of energy demand is significant only when the energy price reached the highest price levels in the long term although there are time lags in the price elasticity of energy demand and the elasticity varies by sectors [44].
2.3. Investment
Shifting investment from high to low energy intensity technologies or facilities is another approach to reducing CO2 emissions. Although Japan improved industrial energy efficiency, a shift to more energy efficiency technologies is required to reduce CO2 emissions. Technology innovation and technology installation to stimulate fuel switching, heat energy recycling and energy efficiency improvement can catalyse these reductions. Low-carbon research on Japan suggests that major investments in technologies offer cost-effective opportunities to improve energy efficiency as well as enhance international competitiveness [45]. Thus, stimulating investment is one of the factors that can promote the reductions of CO2 emissions in manufacturing industries. To facilitate technology investment, technology application and spill-over, policy and regulations play important roles by generating a market and securing investment in low-carbon technologies [46,47].
Investment in improving energy efficiency and replacing carbon intensive technologies can often be enhanced by a combination of subsidies. According to the IPCC (2007) 6, subsidies are frequently used to stimulate investment in energy-saving measures by reducing investment cost. Kimura & Ofuji (2013) analyses the effectiveness of subsidy programs for energy efficiency investment in Japan. The result implies that although a half of company questionnaire responses imply that, even though there was no subsidy, they were planned to implement energy efficiency investment, the subsidy programs were mostly cost-effective when compared to the avoided costs and carbon emission prices.
6 In IPCC (2007),subsidies to industrial sector include favourable loans and fiscal incentives,such as reduced taxes on energy-efficient equipment,accelerated depreciation,tax credits and tax deductions as well as grants.
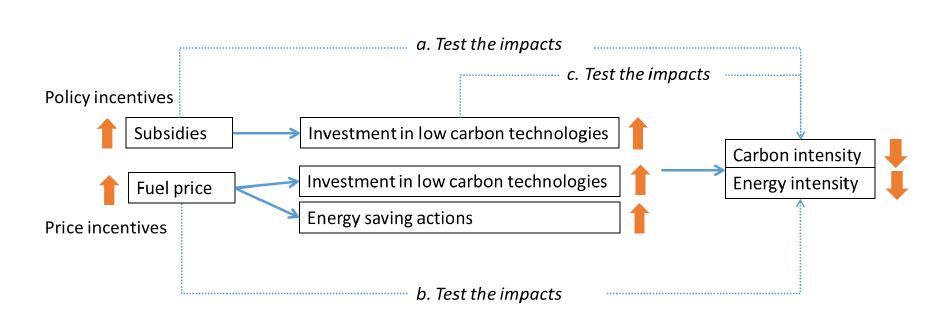
From here, the paper begins to employ econometric analysis to assess what types of instruments--subsidies, fuel prices and investments—reduce carbon and energy intensity in which sectors. The purpose of the modelling, as illustrated in Figure 1, is to understand:
a. the impacts of subsidies on carbon and energy intensity;
b. the impacts of fuel price changes on carbon and energy intensity; and
c. the impacts of investment on carbon and energy intensity.
This paper also reflects on possible differences across industries. In so doing, it hypothesizes that in industries that have high upfront capital cost such as iron & steel [50], policy instruments (subsidies) and price incentives (fuel prices) will not significantly reduce energy and carbon intensity. On the other hand, in industries with higher operational cost such as chemical industry [51], increasing subsidies for energy efficiency and renewable energy and fuel prices can create stronger incentives to transition to more efficient facilities. Thus, increasing subsidies of energy efficiency and renewable energy and fuel prices could have a more discernible impact on carbon and energy intensity. In industries that require high levels of electricity consumption such as the machinery industry 7, carbon and energy intensity could be affected by external factors such as energy mix of electricity companies, as well as by energy conservation and less emission measures implemented by the industry.
7 Approximately 69 per cent of the total energy consumptions is from electricity consumptions. METI. Available from: http://www.enecho.meti.go.jp/statistics/total_energy/results.html.
3. Methodology
A time-series analysis is used to assess the effects of these three policy instrument on carbon and energy intensity. Carbon intensity and energy intensity data from 1994 to 2013 is gathered for this analysis. A series of diagnostic tests are initially performed to determine: 1) whether serial correlations exist in the data; and 2) whether subsidies, fuel prices and investment variables have statistically and substantively significant effects on carbon and energy intensity in the three industrial sectors of interest.
3.1. Model specification
Temporal trends and complex error processes may affect time series data. There are numerous ways to analyze the time-series data where a variable is observed sequentially over time [52]. An ARMA model is one of such approach. An ARMA model is a time series model that identifies the data-generating process underlying the data (carbon and energy intensity in this paper). As a simplistic and univariate model, ARMA is particularly useful when data requirements are limited to the series of interest [53] 8 On the other hand, Autoregressive distributed lag models (ADL) observe structural relationships in historical data between dependent variable and different exogenous variables [54] 9, vector auto-regression model (VAR) considers endogenous variables to affect each other and is also used as a multiplier analysis with the exogenous variables [55]. Although ARMA and ADL models are similar model as both models can include exogenous variables, this paper uses ARMA with an exogenous variable because the model is relatively intuitive model that can help illustrate the effect of an explanatory variable on a dependent variable [53,54].
8 As examples using these models,ARMA model is used to assess the impact of exogenous shock on electricity demand [66]. ADL is used to analyze energy demand to respond differently (asymmetrically) to price increases and decreases [20, 67],and VAR is used to assess relationship between economic growth and energy consumption [68, 69, 70].
9 In ADL model,the current dependent variable is regressed on the values of the dependent variable with lags and the present and lagged values of one or more explanatory variables.
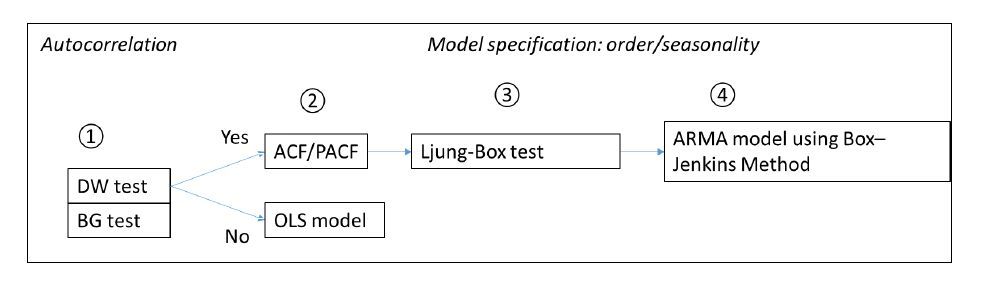
In the case of industrial energy intensity and carbon intensity, the unique properties of the industrial sector may affect the structure of the data. Therefore, to identify the methods for modeling a time series and variables observed at regular intervals annually, the time series carbon and energy intensity is disaggregated by sector. To identify the appropriate model for carbon and energy intensity data in the iron & steel, chemical and machinery industries, the below steps are followed (See Figure 2 for an illustration of these steps):
(1) A diagnostic test is performed to check if a simple static ordinary least squared (OLS) is appropriate for analyzing the data. A Durbin-Watson or Breusch-Godfrey is used to test for autocorrelation. These tests can assess the null hypothesis that there is no autocorrelation.
(2) If there is serial correlation, a set of diagnostics using the autocorrelation function (ACF) and partial autocorrelation function (PACF) to determine how current values in a series correlate with previous values to identify appropriate lag variables. It also helps isolate whether carbon and energy intensity data demonstrate trend and seasonal variations that would necessitate using an ARMA model.
(3) The Ljung-Box Q-test is then deployed to diagnose whether Box-Jenkins modeling process sufficiently filters the data. The test assesses the presence of autocorrelation in quantitative manner. That is, it tests for autocorrelation at multiple lags by measuring the accumulated autocorrelation of lags [52].
(4) The final step involves using the properly specified model to test which explanatory variables have a significant effect on carbon and energy intensity.
3.2. Data
The data and variables used in the analysis are as follows. The dependent variables are logged carbon intensity and logged energy intensity. Logged subsidies, logged fuel prices and logged investments are the explanatory variables (for the equation of ARMA model, please see Appendix 1).
Subsidies data is extracted from the breakdown of expenditure of subsidies for energy supply and demand measures (Special Accounts for Sophisticated Structure of Energy Supply and Demand budget) 10, which includes subsidies for energy efficiency and renewable energy technologies. The subsidy data is applied to the time series regression model.
10 Budget data is available from Ministry of Finance. Available from: https://www.mof.go.jp/budget/budger_workflow/budget/index.html
For fuel price data, price index of fuels (oil, coal and natural gas) published by the Institute of Electrical Engineers of Japan is used [56]. This analysis uses the price of oil, coal and liquefied natural gas as fuel variables. Depending on the type of fuels, the impact of the changes in fuel prices differ across industries. Therefore, the paper tests whether three fuel types fit the model: oil, coal and natural gas. To estimate the impacts of investment, capital investment flow data (installation basis) is extracted from the National Accounts of Japan database published by the Cabinet Office 11.
11 GDP data: Gross Capital Stock of Private Enterprises data is available from Cabinet Office,Government of Japan. Available from: http://www.esri.cao.go.jp/jp/sna/menu.html
The investment data is published by Ministry of Economy, Trade and Industry (METI) and includes total investment amount for newly installed facilities and equipment of industrial sectors. By using capital investment data of each industry and testing the variables for carbon and energy intensity, it is possible to determine whether new capital investment (installation base) improves carbon and energy intensity.
Data availability affects the time period for the analysis. Historical data on subsidies is available from 1990 to 2013, while investment flow data are available from 1994 to 2013. Thus, time-series regression analysis is applied for the 1994 to 2013 period.
4. Results
The time-series regression analysis of carbon and energy intensity suggest that for energy intensity, the non-seasonal ARMA (0, 1) model best fits the data (see Appendix 1for a review of the equation and Appendix 2 for the model identification). The ARMA (0, 1) means that the time lag of the impacts is influenced by the previous change in the residuals. The paper uses an ARMA (0, 1) model for carbon and energy intensity in each industry.
4.1. Subsidy provisions
4.1.1. Carbon intensity
As one of the factors influencing carbon intensity and energy intensity, the impact of subsidies is assessed using the ARMA (0, 1) model. The results indicate that subsidies for measures to enhance the energy supply-demand structure (including energy efficiency and renewable, and CO2 mitigation) improve carbon intensity in the chemical industry (Table 1). Since the z-ratio is more than |2.33|, it is statistically significant at the 0.01 level; there is only a 1% probability that the subsidies impact carbon intensity by random chance. However, the magnitude of the impact is small with an estimated effect of −0.0043. In case of iron & steel and machinery industry, values are not statistically discernible from zero—with z scores that are less than the standard |1.64| threshold.
Table 1.Carbon intensity
|
|
Iron & steel
|
Chemical
|
Machinery
|
|
|
SUB
|
SUB
|
SUB
|
|
|
Estimate
|
Standard error
|
z-ratio
|
|
Estimate
|
Standard error
|
z-ratio
|
|
Estimate
|
Standard error
|
z-ratio
|
|
| Intercept
|
0.838
|
0.005
|
40.267
|
***
|
0.877
|
0.036
|
24.594
|
***
|
0.700
|
0.077
|
9.101
|
***
|
| SUB
|
0.0000
|
0.0003
|
1.303
|
|
−0.004
|
0.002
|
−2.424
|
**
|
0.005
|
0.003
|
1.545
|
|
| MA(1)
|
0.667
|
0.155
|
4.790
|
***
|
0.183
|
0.539
|
0.340
|
|
0.767
|
0.147
|
5.207
|
***
|
|
Residual variance=0.0000009.
AIC=−215.99.
log-likelihood=110.99. Ljung-Box test for autocorrelation=12.068 (p=0.674).
|
Residual variance=0.0000021.
AIC=−198.26.
log-likelihood=102.13. Ljung-Box test for autocorrelation=12.459 (p=0.644).
|
Residual variance=0.0000113.
AIC=−164.13.
log-likelihood=85.06. Ljung-Box test for autocorrelation=13.210 (p=0.586).
|
OIL: logged oil price; COAL: logged coal price; GAS: logged gas price.
MA(1): First-order moving average
*: the alpha level of 0.05; **: the alpha level of 0.01; ***: the alpha level of 0.001
Notes: Estimates computed in R3.0.0. |
4.1.2. Energy intensity
The result also indicate that subsidies have impacts on energy intensity in the chemical industry (Table 2). The coefficient estimates suggest that the impact of the effect on energy intensity in the chemical industry is not only statistically significant but larger than carbon intensity in absolute terms (Table 3). Energy intensity improved by 4.3% (based on the coefficient of -0.043), on average, with increased subsidies. On the other hand, in the iron & steel and machinery industry, the results are similar to carbon intensity in that that there are no significant impacts on energy intensity with increasing subsidies.
Table 2.Energy intensity.
|
|
Iron & steel
|
Chemical
|
Machinery
|
|
|
SUB
|
SUB
|
SUB
|
|
|
Estimate
|
Standard error
|
z-ratio
|
|
Estimate
|
Standard error
|
z-ratio
|
|
Estimate
|
Standard error
|
z-ratio
|
|
| Intercept
|
1.924
|
0.798
|
2.412
|
**
|
4.363
|
0.237
|
18.425
|
***
|
3.854
|
1.248
|
3.087
|
***
|
| SUB
|
0.046
|
0.031
|
1.507
|
|
−0.043
|
0.009
|
−4.764
|
**
|
−0.039
|
0.048
|
−0.814
|
|
| MA(1)
|
0.852
|
0.238
|
3.580
|
***
|
0.361
|
0.198
|
1.823
|
*
|
0.703
|
0.222
|
3.165
|
***
|
|
|
Residual variance= 0.0000008.AIC=−77.58.log-likelihood=41.79. Ljung-Box test for autocorrelation=12.7516 (p=0.6215).
|
Residual variance= 0.00013.AIC=−116.24.log-likelihood=61.12. Ljung-Box test for autocorrelation=14.7107 (p=0.4724).
|
Residual variance= 0.0022.AIC=−58.93.log-likelihood=32.47. Ljung-Box test for autocorrelation=11.9376 (p=0.6837).
|
OIL: logged oil price; COAL: logged coal price; GAS: logged gas price.
MA(1): First-order moving average
*: the alpha level of 0.05; **: the alpha level of 0.01; ***: the alpha level of 0.001
Notes: Estimates computed in R3.0.0. |
4.2. Fuel prices
4.2.1. Carbon intensity
The results to the fuel price models indicate that there is a price elasticity of carbon intensity in the chemical industry. The results suggest that, though there is statistically significant effect on oil the price elasticity for carbon intensity, the expected improvement of carbon intensity was very small with estimated coefficients −0.0016 on a logged scale (Table 3). In the case of coal price and gas price, both price variables demonstrate a statistically significant effect on improving carbon intensity (coefficients estimates −0.0023). That is, there is an estimated 0.23% improvement in carbon intensity with each unit increases in fuel prices. On the other hand, the fuel price elasticity of carbon intensity is not statistically significant in the iron & steel industry. In machinery industry, the significance dependsupon the fuel type. Although there is statistically significance in oil and gas price, the impacts have a counter-intuitive worsening effect on carbon intensity with estimated coefficients of +0.0042 and +0.0052, respectively. Coal price does not show a significant effect on the machinery industry.
Table 3.Carbon intensity.
|
|
Iron & steel
|
Chemical
|
Machinery
|
|
|
Estimate
|
Standard error
|
z-ratio
|
|
Estimate
|
Standard error
|
z-ratio
|
|
Estimate
|
Standard error
|
z-ratio
|
z-ratio
|
| OIL
|
| Intercept
|
0.831
|
0.005
|
168.171
|
***
|
0.780
|
0.009
|
89.230
|
***
|
0.776
|
0.017
|
44.689
|
***
|
| OIL
|
0.0007
|
0.0005
|
1.305
|
|
−0.0016
|
0.0009
|
−1.774
|
*
|
0.0042
|
0.0017
|
2.457
|
**
|
| MA(1)
|
0.662
|
0.147
|
4.504
|
***
|
0.603
|
0.203
|
2.964
|
**
|
0.637
|
0.135
|
4.719
|
***
|
|
|
Residual variance= 0.0000008.AIC=−217.92.log-likelihood=111.96. Ljung-Box test for autocorrelation=12.068 (p=0.6351).
|
Residual variance= 0.000003.AIC=−193.88.log-likelihood=99.94. Ljung-Box test for autocorrelation=9.2392 (p=0.8647).
|
Residual variance= 0.00001.AIC=−167.03.log-likelihood=86.51. Ljung-Box test for autocorrelation=19.1849 (p=0.2055).
|
| COAL
|
| Intercept
|
0.840
|
0.006
|
135.345
|
***
|
0.784
|
0.012
|
67.351
|
***
|
0.797
|
0.024
|
128.842
|
***
|
| COAL
|
−0.0002
|
0.0007
|
−0.294
|
|
−0.0023
|
0.0013
|
−1.762
|
*
|
0.0024
|
0.0027
|
0.885
|
|
| MA(1)
|
0.676
|
0.155
|
4.358
|
***
|
0.738
|
0.260
|
2.834
|
***
|
0.645
|
0.141
|
4.101
|
***
|
|
|
Residual variance= 0.0000009.AIC=−216.07.log-likelihood=111.04. Ljung-Box test for autocorrelation=13.780 (p=0.5422).
|
Residual variance= 0.000003.AIC=−194.14.log-likelihood=100.07. Ljung-Box test for autocorrelation=7.862 (p=0.9292).
|
Residual variance= 0.00001.AIC=−162.58.log-likelihood=84.29. Ljung-Box test for autocorrelation=14.609 (p=0.4799).
|
| GAS
|
| Intercept
|
0.830
|
0.006
|
128.841
|
***
|
0.788
|
0.011
|
69.819
|
***
|
0.764
|
0.023
|
33.673
|
***
|
| GAS
|
0.0007
|
0.0006
|
1.166
|
|
−0.0023
|
0.0011
|
−2.111
|
*
|
0.0052
|
0.0022
|
2.409
|
**
|
| MA(1)
|
0.637
|
0.155
|
4.101
|
***
|
0.643
|
0.224
|
2.872
|
**
|
0.596
|
0.141
|
4.234
|
***
|
|
|
Residual variance=0.0000008.AIC=−217.38.log-likelihood=111.69. Ljung-Box test for autocorrelation=13.419 (p=0.5699).
|
Residual variance= 0.000003.AIC=−195.01.log-likelihood=100.51. Ljung-Box test for autocorrelation=9.448 (p=0.853).
|
Residual variance= 0.00001.AIC=−166.64.log-likelihood=86.32. Ljung-Box test for autocorrelation=20.65 (p=0.1484).
|
OIL: logged oil price; COAL: logged coal price; GAS: logged gas price.
MA(1): First-order moving average
*: the alpha level of 0.05; **: the alpha level of 0.01; ***: the alpha level of 0.001
Notes: Estimates computed in R3.0.0. |
4.2.2. Energy intensity
Price elasticity of energy demand often depends on the sectors and fuel types, thus it is reasonable to assume that the price elasticity of energy intensity varies with sectors and fuel types. Fuel prices for oil, coal and gas in the chemical industry appear to register significant effects on improving energy intensity with the coefficients −0.029, −0.027 and −0.035, respectively (Table 4). The impact of the increase in oil and gas prices in machinery industry statistically significant and is larger in absolute terms than the chemical industry with the coefficients −0.081 and −0.106. In the machinery industry, the share of energy consumptions of oil and oil products in the total energy uses fell from 20% in 1990 to 10% in 2013 while oil prices increased from 1990 to 2013. Fuel price elasticities of energy intensity do not seem significant in iron & steel industry, though coal and coal product accounts for 70.1% of the total energy use in the iron & steel industry (as of 2013).
Table 4.Energy intensity.
|
|
Iron & steel
|
Chemical
|
Machinery
|
|
|
Estimate
|
Standard error
|
z-ratio
|
|
Estimate
|
Standard error
|
z-ratio
|
|
Estimate
|
Standard error
|
z-ratio
|
z-ratio
|
| OIL
|
| Intercept
|
3.242
|
0.173
|
18.718
|
***
|
3.530
|
0.044
|
80.855
|
***
|
3.662
|
0.206
|
17.769
|
***
|
| OIL
|
−0.012
|
0.017
|
−0.676
|
|
−0.029
|
0.004
|
−6.776
|
***
|
−0.081
|
0.020
|
−4.012
|
***
|
| MA(1)
|
0.659
|
0.195
|
3.376
|
***
|
0.353
|
0.246
|
1.435
|
*
|
0.726
|
0.185
|
3.925
|
***
|
|
|
Residual variance= 0.001.AIC=−75.66.log-likelihood=40.83. Ljung-Box test for autocorrelation=13.5178 (p=0.5624).
|
Residual variance= 0.00009.AIC=−124.27.log-likelihood=65.13. Ljung-Box test for autocorrelation=24.1075 (p=0.06329).
|
Residual variance= 0.0013.AIC=−69.95.log-likelihood=37.98. Ljung-Box test for autocorrelation=13.4167 (p=0.5701).
|
| COAL
|
| Intercept
|
3.068
|
0.212
|
14.494
|
***
|
3.474
|
0.089
|
39.118
|
***
|
3.712
|
0.246
|
14.122
|
***
|
| COAL
|
0.007
|
0.024
|
0.274
|
|
−0.027
|
0.010
|
−2.694
|
**
|
−0.098
|
0.028
|
−0.973
|
|
| MA(1)
|
0.635
|
0.212
|
2.990
|
**
|
1.000
|
1.147
|
0.872
|
|
1.000
|
0.203
|
4.921
|
***
|
|
|
Residual variance= 0.0001.AIC=−75.28.log-likelihood=111.96. Ljung-Box test for autocorrelation=14.2754 (p=0.5048).
|
Residual variance= 0.00017.AIC=−107.94.log-likelihood=56.97. Ljung-Box test for autocorrelation=24.5917 (p=0.0557).
|
Residual variance= 0.0.0013.AIC=−67.19.log-likelihood=36.59. Ljung-Box test for autocorrelation=15.6845 (p=0.4033).
|
| GAS
|
| Intercept
|
3.209
|
0.233
|
13.748
|
***
|
3.596
|
0.069
|
51.954
|
***
|
3.946
|
0.288
|
13.684
|
***
|
| GAS
|
−0.008
|
0.022
|
−0.360
|
|
−0.035
|
0.007
|
−5.226
|
***
|
−0.106
|
0.028
|
−3.851
|
***
|
| MA(1)
|
0.669
|
0.203
|
3.300
|
***
|
0.451
|
0.234
|
1.929
|
*
|
0.876
|
0.180
|
4.868
|
***
|
|
|
Residual variance= 0.00097.AIC=−75.33.log-likelihood=40.67. Ljung-Box test for autocorrelation=14.0869 (p=0.5189).
|
Residual variance= 0.00011.AIC=−118.62.log-likelihood=62.3. Ljung-Box test for autocorrelation=24.98842 (p=0.0501).
|
Residual variance= 0.0012.AIC=−70.16.log-likelihood=38.08. Ljung-Box test for autocorrelation=10.3797 (p=0.7952).
|
OIL: logged oil price; COAL: logged coal price; GAS: logged gas price. MA(1): First-order moving average
*: the alpha level of 0.05; **: the alpha level of 0.01; ***: the alpha level of 0.001
Notes: Estimates computed in R3.0.0. |
4.3. Investment
4.3.1. Carbon intensity
As for investment, by using logged investment amount in industries it is possible to assess whether investments in new plants and equipment are devoted to improving energy efficiency or increasing alternative energy use (including renewable energies), which contribute to improving carbon and energy intensity. The results indicate that the impact of increasing investment in chemical and machinery industry is significant on carbon and energy intensity (Table 5). A one unit of increase in investment in chemical industry improves 0.28% of carbon intensity and a one unit of increase in investment in machinery industry improve carbon intensity by 4.8%.
Table 5.Carbon intensity.
|
|
Iron & steel
|
Chemical
|
Machinery
|
|
|
INV
|
INV
|
INV
|
|
|
Estimate
|
Standard error
|
z-ratio
|
|
Estimate
|
Standard error
|
z-ratio
|
|
Estimate
|
Standard error
|
z-ratio
|
|
| Intercept
|
0.496
|
2.795
|
0.177
|
|
8.193
|
1.281
|
6.393
|
***
|
11.813
|
2.624
|
4.502
|
***
|
| INV
|
0.153
|
0.163
|
0.941
|
|
−0.286
|
0.074
|
−3.870
|
***
|
−0.482
|
0.141
|
−3.421
|
***
|
| MA(1)
|
0.651
|
0.209
|
3.124
|
***
|
0.765
|
0.313
|
2.447
|
**
|
0.707
|
0.180
|
3.923
|
***
|
|
|
Residual variance= 0.00094.AIC=−76.07.log-likelihood=41.04. Ljung-Box test for autocorrelation=14.5235 (p=0.4863).
|
Residual variance= 0.00012.AIC=−116.8.log-likelihood=61.4. Ljung-Box test for autocorrelation=20.7272 (p=0.1458).
|
Residual variance= 0.00146.AIC=−67.15.log-likelihood=36.57. Ljung-Box test for autocorrelation=15.5819 (p=0.4104).
|
INV: logged investment (installed based) amount by sector
MA(1): First-order moving average
*: the alpha level of 0.05; **: the alpha level of 0.01; ***: the alpha level of 0.001
Notes: Estimates computed in R3.0.0. |
4.3.2. Energy intensity
The result of impact of investment on energy intensity suggests that in chemical industry, the variable of investment is statistically significant with a coefficient of −0.027 (Table 6). However, in other industries, the impacts of investment are not discernibly different from zero in terms of their effects on energy intensity.
Table 6.Energy intensity.
|
|
Iron & steel
|
Chemical
|
Machinery
|
|
|
INV
|
INV
|
INV
|
|
|
Estimate
|
Standard error
|
z-ratio
|
|
Estimate
|
Standard error
|
z-ratio
|
|
Estimate
|
Standard error
|
z-ratio
|
|
| Intercept
|
0.9368
|
0.0822
|
11.401169
|
***
|
1.2323
|
0.1168
|
10.548472
|
***
|
0.4952
|
0.2315
|
7.3278558
|
***
|
| INV
|
−0.0057
|
0.0048
|
−1.206176
|
|
−0.027
|
0.0067
|
−4.002377
|
***
|
0.0174
|
0.0124
|
−0.638437
|
|
| MA(1)
|
0.6475
|
0.1781
|
3.634986
|
***
|
0.4418
|
0.31
|
1.425193
|
*
|
0.6775
|
0.134
|
5.0488047
|
***
|
|
|
Residual variance= 0.0000008.AIC=−217.38.log-likelihood=111.69. Ljung-Box test for autocorrelation=10.5245 (p=0.7855).
|
Residual variance= 0.0000018.AIC=−201.31.log-likelihood=103.66. Ljung-Box test for autocorrelation=10.2885 (p=0.8012).
|
Residual variance= 0.000013.AIC=−162.58.log-likelihood=84.29. Ljung-Box test for autocorrelation=19.3235 (p=0.1994).
|
INV: logged investment (installed based) amount by sector
MA(1): First-order moving average
*: the alpha level of 0.05; **: the alpha level of 0.01; ***: the alpha level of 0.001
Notes: Estimates computed in R3.0.0. |
The individual results from the modelling are illuminating, but it may be difficult to see the bigger picture without an overall assessment. Such an assessment can be seen more easily in Table 7. That tables suggeststhat while in chemical industry the increase in subsidies, fuel prices and investments significantly improve both carbon and energy intensity, the same set of variables do not have significant effects on the carbon and energy intensity in iron & steel industry. Meanwhile, the machinery industry, the result depends on the variables (Table 7). While none of the variables improve carbon intensity, the increase in oil price, gas price and investment significantly improve energy intensity.
Table 7.Summary of results.
|
|
Subsidies
|
Fuel price
|
Investment
|
| Oil price
|
Coal price
|
Gas price
|
| Carbon intensity
|
Iron & steel
|
n.s
|
n.s
|
n.s
|
n.s
|
n.s
|
| Chemical
|
*
|
*
|
*
|
*
|
*
|
| Machinery
|
n.s
|
-
|
n.s
|
-
|
n.s
|
| Energy intensity
|
Iron & steel
|
n.s
|
n.s
|
n.s
|
n.s
|
n.s
|
| Chemical
|
*
|
*
|
*
|
*
|
*
|
| Machinery
|
n.s
|
*
|
n.s
|
*
|
*
|
* = significant to improve carbon/energy intensity (the value negatively impacts on the intensities)
- = significant to worsen carbon/energy intensity (the value positively impacts on the intensities)
n.g = not significant |
5. Discussion
This paper conducts a time-series regression analysis to assess the factors influencing CO2 emissions by assessing the degree of impacts of variables (subsidies, fuel prices and investment) on carbon and energy intensity. The result indicates that the impacts depends on industry.
In case of iron & steel industry, none of the variables have significant effects. A possible reason is that iron & steel industry require high upfront cost [50]. The physical life of the iron & steel facilities such as a blast furnace is long, and maintenance and repair fees are also expensive. Thus, the fixed costs, including initial investment and expenses, for maintenance and repair may make it difficult to transition to more efficient technologies or lower carbon production methods [57,58,59,60]. In addition, according to Keidanren (2014), high value added products and environmental regulations introduced after 1990 actually increased industrial energy consumption. For example, additional energy was required for the implementation of environmental measures such as recycling or preventing air and water pollution [61].
In the chemical industry, subsidy, fuel prices and investment improved carbon and energy intensity. This result makes sense in that the chemical industry has invested approximately 554.5 billion yen from 1997 to 2012 in global warming countermeasures [61]. Around 10-25 billion JPY was invested every year from 2006 to 2011 to improve the efficiencies of facilities and equipment, including cogeneration. Expenditures on research and development, as an R&D oriented industry, are also larger than other industries [62]. Another consideration is that chemical industry have relatively higher operation cost [51], making it beneficial to improve carbon and energy intensity.
In the machinery industry, although an increase in subsidies for energy supply and demand (including energy efficiency and renewable energy) could presumably reduce carbon and energy intensity, these effects are not found from the data. Nor does the analysis reveal that investment significantly improve energy intensity. Rather only oil and gas prices have the predicted effects on improving carbon and energy intensity.
6. Limitations of This Study
There are two notable limitations to the paper: 1) modelling and data; and 2) additional drivers of carbon and energy intensity.
In terms of the first set of limitations, although the time-series model is a useful for assessing the impact of explanatory variables, the time period 1994 to 2013 for carbon and energy intensity data is relatively short (with only 9 lags). A longer time period would arguably generate more robust results. In addition, this paper only uses one explanatory variable to assess and compare the impact of each variable; it did not assess a combination of variables that may also offer revealing insights into the additive effects of different instruments. As for the data, although subsidy data from Special Account is used, these figures include subsidies to promote energy efficiency and renewable energy for power, building, and transportation sectors not only industries. Thus, it does not always represent of subsidies for manufacturing sector.
In terms of the second set of limitations, there are other factors that may impact carbon and energy intensity besides fuel prices, subsidies and investment. For instance, the improvement of CO2 emission intensity from electricity may contribute to improvements in carbon intensity—though this depends on the share of electricity use to total energy used in industries. The CO2 emission intensity of electricity increased from 0.35 in 2010 to 0.487 ktCO2/kWh in 2012 following the Fukushima accident [63]. This is mainly due to the increased demands for natural gas in the electricity sector as an alternative to nuclear power. In line with the increase in the demands of natural gas, gas price went up in Japan from 2011, and the replacement of nuclear power generation to thermal power generation, including gas-fired power generation, resulted in an increase in electricity emission intensity. In consequence, carbon intensity increased in the machinery sector, especially after Fukushima. The effects could be large especially in machinery sector. Electricity accounts for a high proportion of total energy consumptions in the machinery industry of between 58% and 74% from 1990 to 2013 12. Therefore, increasing CO2 emitted from the electricity sector greatly affects carbon intensity. On the other hand, the chemical industry did not have a significant impact on carbon intensity although electricity emission intensity increased in 2011. This could be because electricity accounts for only 7% of the total energy consumption in the chemical industry. In the time-series analysis, while CO2 emission intensity from electricity apparently worsens carbon intensity in the iron & steel and machinery industries (with coefficients +0.014 and +0.081 (0.1% probability) respectively), the same variable is not significant in the chemical industry.
12 METI. Available from: http://www.enecho.meti.go.jp/statistics/total_energy/results.html.
7. Conclusion
From the findings in section 5, the conclusion returns to the initial discussion of the impact of carbon tax. Those findings suggest that although the fuel price elasticities of carbon intensity are dependent on fuel types and industry sectors, it is possible to increase the price elasticity of carbon and energy intensity, especially in chemical and machinery industry if fuel prices become higher. If a higher carbon tax is introduced from the current JPY289/tCO2, the impact could be greater and more significant on carbon and energy intensity. In the case of subsidies in the chemical industry, subsidies appear to reduce carbon intensity. The revenue from carbon tax could partly be used for subsidies on renewable energy, energy efficiency or CO2 emissions countermeasures. In terms of policy, this paper indicates that the deployment of subsidies could improve carbon intensity and lead to reductions in CO2 emissions in key sectors. But the results underline the need for careful analysis of the nature and extent to which subsidies affect changes within a sector. A closer analysis may help illustrate under which conditions subsidies promote improvements in carbon and energy intensity. They could also shed light on when the continuity of subsidies could prevent business sectors from making efforts to improve energy efficiency measures and promote CO2 emission reductions, perhaps creating barriers to the introduction of new policies such as carbon emission trading. In addition, as an alternative for other sources of tax revenue, a carbon tax could be used for the reduction of social security contributions for companies or individuals, while promoting the reduction of fossil fuel use.
The time-series analysis shows a clear trend toward improvements in carbon intensity in the chemical and machinery industries and improvements in the energy intensity in chemical industry. Thus, there is a possibility that raising fuel prices and subsidies through a carbon tax could increase the contribution to investment to improve carbon and energy intensity in these industries. On the other hand, for iron & steel industry, investment in R&D for new technologies for less energy use and less emissions or/and technology shift such as from blast furnace to electric furnace would be required.
For further reduction of CO2 emissions, a fuel mix for electricity with less carbon intensity and a fuel shift in each industrial sector is also required as well as a reduction in total energy use. The results further imply that a combination and harmonisation of various policies could be more effective than single policy in improving carbon and energy intensity. A carbon tax could help harmonize various instruments including energy price changes and investment. Policies to promote investment in less carbonintensive fuels and renewable energy as well as financial support to promote the replacement or installation of new facilities and equipment follow from a combination of policies and economic incentives may also follow. However, like the analysis offered here, more detailed industry specific policy analysis is required to understand these effects.
Conflict of Interest
All authors declare no conflicts of interest in this paper.
Appendix
Appendix 1. Equation of ARMA model
The equation of ARMA(p, q)(P, Q) h is:
|
(1−∅pB)(1−φPBh)yt=(1+θqB)(1−δQBh)ϵt
|
Where, yt is carbon or energy intensity at t year and ∈t is white noise of E[∈t]=0, Var (∈t)=σ2 at t year. B is the backward shift operator (a linear operator), which is a useful notational device when working with time series lags. ∅p is parameter when the current value of data has correlation only with p year before, the order expresses is one. θq can be expressed with partial autocorrelation coefficient. Each data is influenced by the random shock (historical errors). The parameter θq is stationary. Current value of data is influenced by the past errors. If the white noise has correlation with the data of one month before, the order becomes one. The combination of AR(p) and MA(q) with seasonal components of ARs (P) (Seasonal AR part of order P), φP and MAs (Q) (Seasonal MA part of order Q) is estimated.
Appendix 2. Model identification
For the model analysis, logged carbon intensity and energy intensity data from 1994 to 2013 is used. Using the methodology in section 3.1 and the equation in Appendix 1, the ARMA(0, 1) model is selected as the best fit model for carbon and energy intensity in iron & steel, chemical and machinery industry.
Iron & steel industry
Carbon intensity
In case of iron & steel industry, the ARMA(0, 1) model is selected for carbon intensity by comparing the result of the Akaike Information Criterion (AIC) as shown in Table A1 to Table A5. Although ARMA(0, 1) is not the best fit model for the model including oil fuel price variable, this analysis uses the same model for data covering carbon intensity in iron & steel industry.
Table A1.Model selection and test results: Carbon intensity: Subsidy
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
110.54
|
−215.08
|
13.389
|
0.5723
|
| ARMA(0, 1)
|
111.8
|
−217.59
|
12.068
|
0.6739
|
| ARMA(1, 1)
|
112.08
|
−216.17
|
10.136
|
0.8111
|
| ARMA(1, 0): AR1=s.e. NaN, ARMA(1, 1): AR1=s.e. NaN |
Table A2.Model selection and test results: Carbon intensity: Oil Fuel prices
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
112.15
|
−218.3
|
9.2269
|
0.8654
|
| ARMA(0, 1)
|
111.96
|
−217.92
|
12.575
|
0.6351
|
| ARMA(1, 1)
|
113.04
|
−218.08
|
7.2962
|
0.9489
|
Table A3.Model selection and test results: Carbon intensity: Coal Fuel prices
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
110.53
|
−215.06
|
11.942
|
0.6834
|
| ARMA(0, 1)
|
111.04
|
−216.07
|
13.781
|
0.5422
|
| ARMA(1, 1)
|
111.59
|
−215.19
|
11.641
|
0.7059
|
Table A4.Model selection and test results: Carbon intensity: Gas Fuel prices
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
111.42
|
−216.84
|
11.662
|
0.7044
|
| ARMA(0, 1)
|
111.69
|
−217.38
|
13.42
|
0.5699
|
| ARMA(1, 1)
|
112.2
|
−216.41
|
10.399
|
0.7939
|
Table A5.Model selection and test results: Carbon intensity: Investment
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
111.2
|
−216.39
|
9.2154
|
0.866
|
| ARMA(0, 1)
|
111.69
|
−217.38
|
10.524
|
0.7855
|
| ARMA(1, 1)
|
111.96
|
−215.91
|
9.9323
|
0.824
|
| ARMA(1, 0): AR1=s.e. NaN, ARMA(1, 1): AR1=s.e. NaN |
Energy intensity
ARMA(0, 1) model is selected for energy intensity in iron & steel industry by comparing the result of the AIC as shown in Table A6 to Table A10.
Table A6.Model selection and test results: Energy intensity: Subsidy
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
40.23
|
−74.46
|
18.456
|
0.2395
|
| ARMA(0, 1)
|
41.79
|
−77.58
|
12.752
|
0.6215
|
| ARMA(1, 1)
|
41.95
|
−75.89
|
12.568
|
0.6356
|
Table A7.Model selection and test results: Energy intensity: Oil Fuel prices
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
39.81
|
−73.63
|
16.077
|
0.377
|
| ARMA(0, 1)
|
40.83
|
−75.66
|
13.518
|
0.5624
|
| ARMA(1, 1)
|
40.91
|
−73.82
|
13.556
|
0.5594
|
Table A8.Model selection and test results: Energy intensity: Coal Fuel prices
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
39.68
|
−73.36
|
16.64
|
0.3408
|
| ARMA(0, 1)
|
40.64
|
−75.28
|
14.275
|
0.5048
|
| ARMA(1, 1)
|
40.77
|
−73.54
|
14.004
|
0.5252
|
Table A9.Model selection and test results: Energy intensity: Gas Fuel prices
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
39.57
|
−73.15
|
17.064
|
0.315
|
| ARMA(0, 1)
|
40.67
|
−75.33
|
14.087
|
0.5189
|
| ARMA(1, 1)
|
40.77
|
−73.55
|
14.044
|
0.5222
|
Table A10.Model selection and test results: Energy intensity: Investment
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
39.85
|
−73.69
|
17.475
|
0.2913
|
| ARMA(0, 1)
|
41.04
|
−76.07
|
14.524
|
0.4863
|
| ARMA(1, 1)
|
41.41
|
−74.82
|
12.78
|
0.6193
|
Chemical industry
Carbon intensity
In case of chemical industry, the ARMA(0, 1) model is selected for carbon intensity by comparing the result of the AIC as shown in Table A11 to Table A15. Although ARMA(0, 1) is not the best fit model for the model including oil fuel price variable, this analysis uses the same model for data covering carbon intensity in chemical industry.
Table A11.Model selection and test results: Carbon intensity: Subsidy
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
102.26
|
−198.52
|
11.361
|
0.7266
|
| ARMA(0, 1)
|
102.13
|
−198.26
|
12.459
|
0.644
|
| ARMA(1, 1)
|
102.26
|
−196.53
|
11.422
|
0.7221
|
| ARMA(1, 0): AR1=s.e. NaN |
Table A12.Model selection and test results: Carbon intensity: Oil Fuel prices
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
100.27
|
−194.53
|
9.5491
|
0.8471
|
| ARMA(0, 1)
|
99.94
|
−193.88
|
9.2392
|
0.8647
|
| ARMA(1, 1)
|
100.29
|
−192.58
|
9.7751
|
0.8336
|
Table A13.Model selection and test results: Carbon intensity: Coal Fuel prices
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
99.92
|
−193.84
|
13.701
|
0.5483
|
| ARMA(0, 1)
|
100.07
|
−194.14
|
14.609
|
0.4799
|
| ARMA(1, 1)
|
100.3
|
−192.61
|
8.286
|
0.9118
|
Table A14.Model selection and test results: Carbon intensity: Gas Fuel prices
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
99.73
|
−193.46
|
6.8141
|
0.9626
|
| ARMA(0, 1)
|
100.51
|
−195.01
|
9.4475
|
0.853
|
| ARMA(1, 1)
|
100.52
|
−193.05
|
9.122
|
0.8711
|
Table A15.Model selection and test results: Carbon intensity: Investment
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
103.18
|
−200.36
|
13.871
|
0.5354
|
| ARMA(0, 1)
|
103.66
|
−201.31
|
10.524
|
0.7855
|
| ARMA(1, 1)
|
103.67
|
−199.34
|
9.9323
|
0.824
|
Energy intensity
ARMA(0, 1) model is selected for energy intensity in chemical industry by comparing the result of the AIC as shown in Table A16 to Table A20. Although ARMA(0, 1) is not the best fit model for the model including oil, coal and gas variable, this analysis uses the same model for data covering energy intensity in chemical industry.
Table A16.Model selection and test results: Energy intensity: Subsidy
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
60.85
|
−115.69
|
16.477
|
0.3511
|
| ARMA(0, 1)
|
61.12
|
−116.24
|
14.711
|
0.4724
|
| ARMA(1, 1)
|
61.12
|
−114.25
|
15.09
|
0.445
|
Table A17.Model selection and test results: Energy intensity: Oil Fuel prices
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
65.15
|
−124.29
|
17.383
|
0.2965
|
| ARMA(0, 1)
|
65.13
|
−124.27
|
13.417
|
0.5701
|
| ARMA(1, 1)
|
65.3
|
−122.59
|
14.828
|
0.4639
|
Table A18.Model selection and test results: Energy intensity: Coal Fuel prices
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
58.56
|
−111.13
|
25.8
|
0.04018
|
| ARMA(0, 1)
|
56.97
|
−107.94
|
15.684
|
0.4033
|
| ARMA(1, 1)
|
58.38
|
−108.75
|
18.066
|
0.2592
|
Table A19.Model selection and test results: Energy intensity: Gas Fuel prices
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
62.32
|
−118.64
|
15.964
|
0.3845
|
| ARMA(0, 1)
|
62.31
|
−118.62
|
10.38
|
0.7952
|
| ARMA(1, 1)
|
62.32
|
−116.64
|
11.347
|
0.7276
|
Table A20.Model selection and test results: Energy intensity: Investment
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
61.26
|
−116.53
|
20.173
|
0.1654
|
| ARMA(0, 1)
|
61.4
|
−116.8
|
15.582
|
0.4104
|
| ARMA(1, 1)
|
61.72
|
−115.45
|
16.162
|
0.3714
|
Machinery industry
Carbon intensity
In case of machinery industry, the ARMA(0, 1) model is selected for carbon intensity by comparing the result of the AIC as shown in Table A21 to Table A25. Although ARMA(0, 1) is not the best fit model for the models including oil price variable, this analysis uses the same model for data covering carbon intensity in machinery industry.
Table A21.Model selection and test results: Carbon intensity: Subsidy
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
83.11
|
−160.22
|
11.073
|
0.7474
|
| ARMA(0, 1)
|
85.06
|
−164.13
|
14.44
|
0.4925
|
| ARMA(1, 1)
|
85.65
|
−163.29
|
10.155
|
0.8099
|
Table A22.Model selection and test results: Carbon intensity:Oil Fuel prices
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
85.61
|
−165.22
|
25.884
|
0.03926
|
| ARMA(0, 1)
|
86.51
|
−167.03
|
24.108
|
0.06329
|
| ARMA(1, 1)
|
87.5
|
−167
|
26.07
|
0.03729
|
Table A23.Model selection and test results: Carbon intensity:Coal Fuel prices
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
83.26
|
−160.51
|
32.08
|
0.006279
|
| ARMA(0, 1)
|
84.29
|
−162.58
|
24.592
|
0.0557
|
| ARMA(1, 1)
|
85.32
|
−162.65
|
33.455
|
0.004059
|
Table A24.Model selection and test results: Carbon intensity:Gas Fuel prices
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
85.65
|
−165.31
|
30.216
|
0.01117
|
| ARMA(0, 1)
|
86.32
|
−166.64
|
24.988
|
0.0501
|
| ARMA(1, 1)
|
87.09
|
−166.18
|
25.761
|
0.04061
|
Table A25.Model selection and test results: Carbon intensity: Investment
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
83.48
|
−160.95
|
28.167
|
0.02054
|
| ARMA(0, 1)
|
84.84
|
−163.69
|
20.727
|
0.1458
|
| ARMA(1, 1)
|
85.74
|
−163.49
|
24.003
|
0.06505
|
Energy intensity
The ARMA(0, 1) model is selected for energy intensity in machinery sector by comparing the result of the AIC as shown in Table A26 to Table A30.
Table A26.Model selection and test results: Energy intensity: Subsidy
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
31.55
|
−57.1
|
16.787
|
0.3317
|
| ARMA(0, 1)
|
32.47
|
−58.93
|
11.938
|
0.6837
|
| ARMA(1, 1)
|
32.48
|
−56.95
|
12.061
|
0.6744
|
Table A27.Model selection and test results: Energy intensity: Oil Fuel prices
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
36.47
|
−66.95
|
20.474
|
0.1545
|
| ARMA(0, 1)
|
37.98
|
−69.95
|
19.185
|
0.2055
|
| ARMA(1, 1)
|
38.08
|
−68.16
|
7.2962
|
0.9489
|
Table A28.Model selection and test results: Energy intensity: Coal Fuel prices
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
34.09
|
−62.19
|
13.701
|
0.5483
|
| ARMA(0, 1)
|
36.59
|
−67.19
|
14.609
|
0.4799
|
| ARMA(1, 1)
|
36.99
|
−65.98
|
8.286
|
0.9118
|
Table A29.Model selection and test results: Energy intensity: Gas Fuel prices
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
35.77
|
−65.55
|
21.538
|
0.1205
|
| ARMA(0, 1)
|
38.08
|
−70.16
|
20.65
|
0.1484
|
| ARMA(1, 1)
|
38.11
|
−68.22
|
16.339
|
0.3599
|
Table A30.Model selection and test results: Energy intensity: Investment
| ARMA
|
Log likelihood
|
AIC
|
X squared
|
p-Value
|
| ARMA(1, 0)
|
35.14
|
−64.27
|
17.433
|
0.2936
|
| ARMA(0, 1)
|
36.57
|
−67.15
|
19.324
|
0.1994
|
| ARMA(1, 1)
|
36.67
|
−65.33
|
12.649
|
0.6294
|









 DownLoad:
DownLoad: