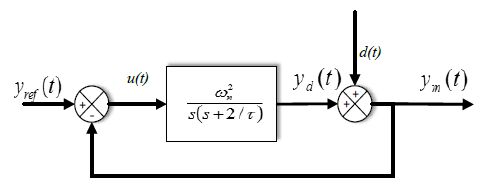
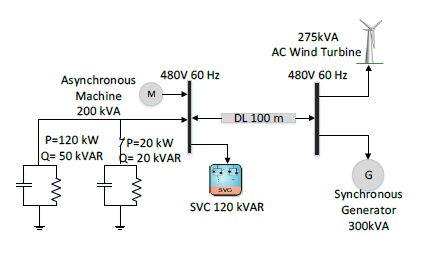
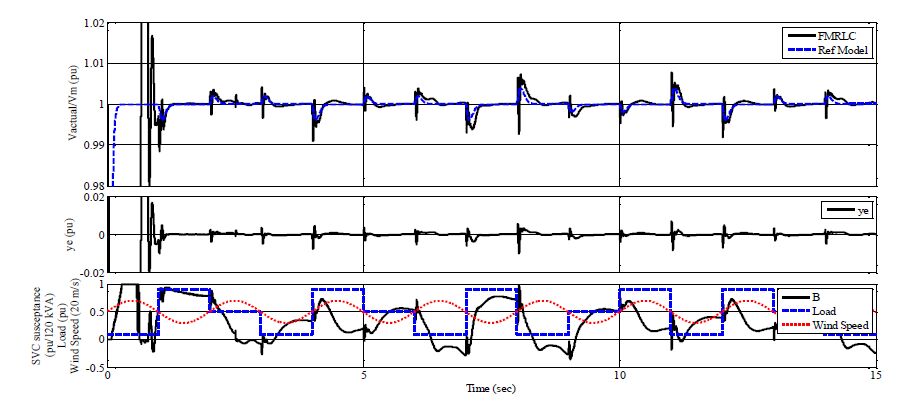
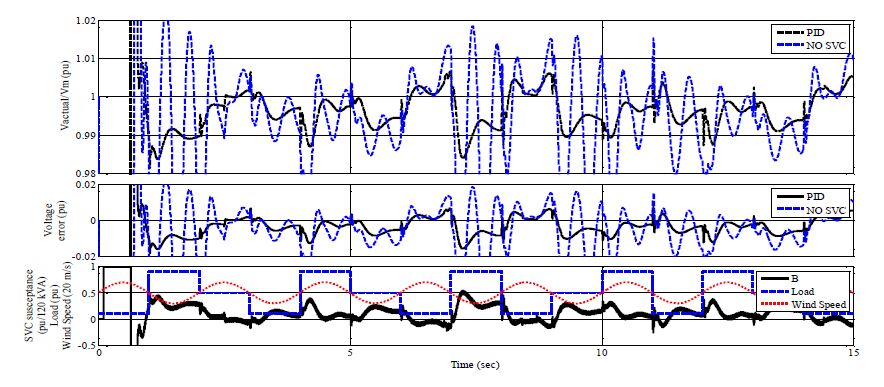
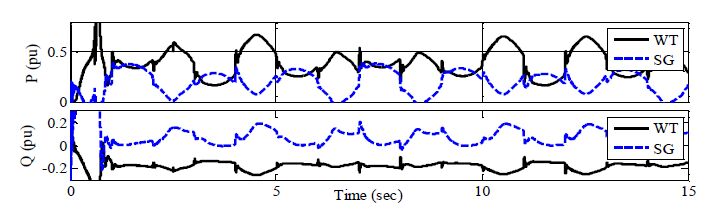
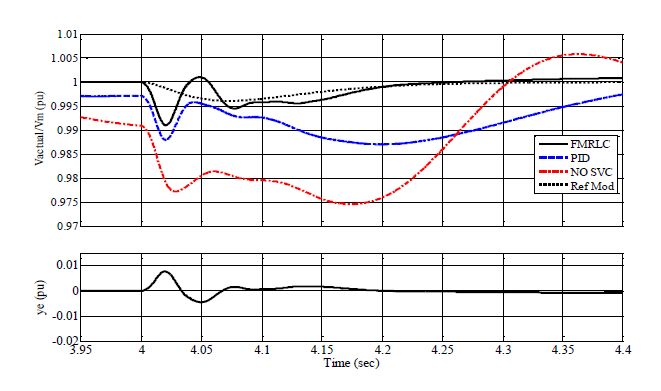
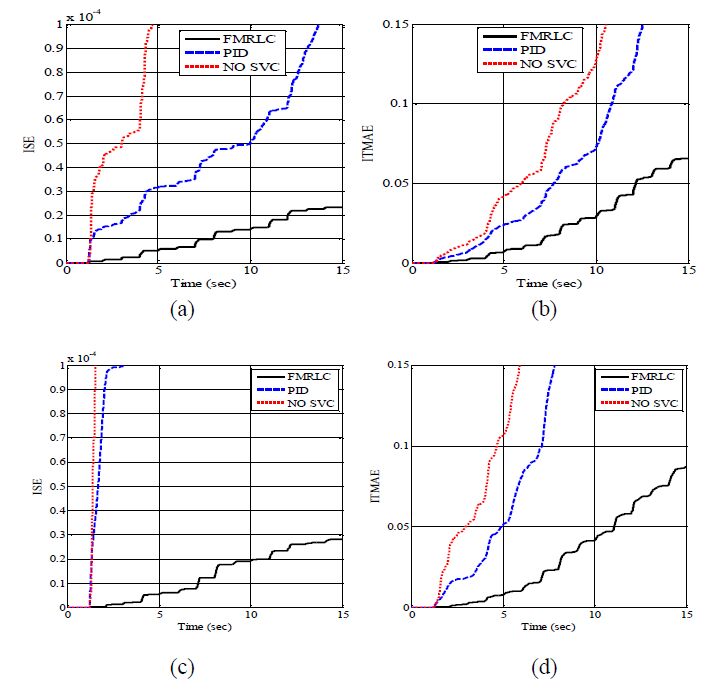
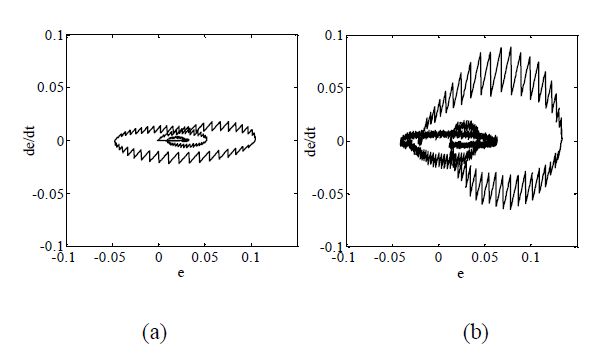
Maintaining voltage stability, within acceptable levels, for islanded Microgrids (MGs) is a challenge due to limited exchange power between generation and loads. This paper proposes an algorithm to enhance the dynamic performance of islanded MGs in presence of load disturbance using Static VAR Compensator (SVC) with Fuzzy Model Reference Learning Controller (FMRLC). The proposed algorithm compensates MG nonlinearity via fuzzy membership functions and inference mechanism imbedded in both controller and inverse model. Hence, MG keeps the desired performance as required at any operating condition. Furthermore, the self-learning capability of the proposed control algorithm compensates for grid parameter’s variation even with inadequate information about load dynamics. A reference model was designed to reject bus voltage disturbance with achievable performance by the proposed fuzzy controller. Three simulations scenarios have been presented to investigate effectiveness of proposed control algorithm in improving steady-state and transient performance of islanded MGs. The first scenario conducted without SVC, second conducted with SVC using PID controller and third conducted using FMRLC algorithm. A comparison for results shows ability of proposed control algorithm to enhance disturbance rejection due to learning process.
1.
Introduction
For many years the analysis of the time-varying behavior of financial assets has been the goal of extensive research. While it seems of course tempting to be able to forecast future price movements and returns, there is consensus that a monetarily profitable way of forecasting returns does not exist; see, e.g., Goetzmann and Jorion (1993); Nelson and Kim (1993); Kothari and Shanken (1997);
Stambaugh (1999); Torous et al. (2004); Campbell and Yogo (2006); Ang and Bekaert (2007), among others. On the other hand, however, it is a well known fact that the volatility of an asset's return series is very persistent and can be captured relatively well by several model types. The ability to estimate, at least approximately, the volatility of an asset's returns is interesting for a variety of practical reasons, most notably portfolio management and risk management. In particular, asset managers like pension funds or hedge funds usually profit from the ability to estimate volatility by being able to better adjust the risk-return tradeoff in their portfolios. Moreover, any institution holding financial assets, whether for speculation or hedging, is capable of better calculating the risks that are introduced to their balance sheets by specific assets if volatility estimates are available. An important practical application of this is, for example, the Value-at-risk, which is crucially dependent on accurate volatility estimates and forms a major part of the rules imposed by financial regulators on individual institutions.
One of the earliest and most influential of these models is the well known GARCH model introduced by Bollerslev (1986). Although countless extensions and adaptations have been suggested, it is very difficult to outperform the classic GARCH (1, 1) model in terms of forecasting quality (Hansen and Lunde, 2005).
In the last years, the focus of research on volatility has been extended beyond modeling volatility in general stochastic volatility (SV) or GARCH settings to the idea of computing accurate estimates of volatility using high-frequency data, introducing the notion of realized volatility; for more details, we refer to the seminal works of Andersen et al.(2001, 2003) or Barndorff-Nielsen and Shephard (2002), and for a more recent overview of the literature regarding realized volatility and its estimation to McAleer and Medeiros (2008). In order to capture long memory, one of the main stylized facts shown by assets' realized volatility time series, the time-varying dynamics of realized volatility are often modeled as an ARFIMA process; see, for example, Andersen et al. (2001). As an alternative, the most commonly used model for realized volatility is the heterogeneous autoregressive (HAR) model introduced by Corsi (2009). Although not formally belonging to the class of long memory models, the HAR model is able to closely mimic the behavior shown by realized volatility time series. Nowadays, the HAR model enjoys great popularity because of its very good out-of-sample forecasting performance and at the same time its computational simplicity. Similarly to the experience with the classic GARCH (1, 1) model, the standard HAR model has been extended along different directions in an attempt to improve its estimation and forecasting accuracy; see Corsi et al. (2012) for a recent survey.
The aim of this paper is to shed some light about the (possibly time-varying) lag structure driving realized volatility dynamics. Moreover, making use of the fact that the HAR model can be viewed as a (restricted) autoregressive (AR) process of daily realized volatility, we also analyze whether the lag structure and the maximal order lag implied by the HAR model, which is derived based on theoretical assumptions about the investor behavior, can be recovered purely by statistical means. %Making use of the fact that the HAR model can be viewed as an autoregressive process of daily realized volatility, we will analyze whether the implied lag structure, and in particular the maximal order lag, can be recovered based solely on statistical grounds. In order to do so, we will use the adaptive lasso introduced by Zou (2006), a refinement of the standard lasso technique due to Tibshirani (1996), as the estimation procedure and apply it to the set of past lags in an unrestricted AR model of a sufficiently large order. Additionally, we also see whether the lags that are significantly selected are in line with the HAR assumptions.*
*If the HAR model is the correct data generating process, applying the lasso we should expect to select lags up to order 22 in the active set, whereas the coefficients of the lags beyond 22 should be set to zero. Note that this is clearly different from testing the full HAR specification, as in this case the imposition of the equality restrictions across coefficients belonging to the same frequency (weekly, monthly) is necessary as well. This goal can be attained in the lasso context by considering, for example, the cluster group lasso (Bühlmann et al., 2013).
For the analysis, we will make use of the recently developed theory by Audrino and Camponovo (2015) who derived a conservative testing procedure for the coefficients estimated by the adaptive lasso. As shown in Leeb and Pötscher(2006, 2008) and Pötscher and Schneider (2009), among others, it is impossible to estimate the distribution of lasso estimators in the uniform sense (uniformity with respect to the underlying parameter of interest in a shrinking neighborhood of the origin). The conservative testing procedure introduced in Audrino and Camponovo (2015) aims to partially mitigate this problem. In particular, Audrino and Camponovo (2015) show that under appropriate conditions, their approach ensures uniform valid inference with respect to the selection of the adaptive lasso tuning parameter. While Zou (2006) was able to prove how to test hypotheses on the active set of parameters (the coefficients that are truly non-zero in the population), Audrino and Camponovo (2015) extended the theory to hypothesis testing on the passive set of variables (the coefficients that are truly identical to zero in the population), as well. This newly developed theory now makes it possible to test hypotheses regarding the coefficients and therefore to analyze which lags are significantly different from zero. For a comprehensive review of the literature regarding inference of the adaptive lasso, we refer to Audrino and Camponovo (2015).
Surprisingly, thus far there has been little research on the topic of analyzing the validity of the assumptions of the HAR model. While Craioveanu and Hillebr (2012) have shown that it is only of little importance what investment horizons are assumed for the different investor groups, that is which agammaegation frequencies are chosen in a HAR-like structure, Wang et al. (2013) show that an ARFIMA model subject to structural breaks in the mean and the memory parameters of the process can be approximated well by an AR model. They interpret this result as an indirect econometric explanation for the empirical success of the HAR model. Finally, Hwang and Shin (2014) develop an infinite-order extension of the HAR, called HAR ($\infty$), and show that in estimating it using a finite-order model HAR, the prediction error is mainly due to the estimation of the HAR coefficients rather than to errors made in approximating the HAR ($\infty$) process by the misspecified finite-order HAR model, thus providing a theoretical justification for the wide use of the standard HAR model.
The present paper goes in the same direction as the work by Audrino and Knaus (2016) who also analyze the optimal lag structure and maximal order lag of realized volatility dynamics in an unrestricted autoregressive setting. They adopt a similar approach and choose the lasso estimation procedure to recover the lags that seem most informative for predicting future realized volatility. In an out-of-sample analysis, the authors show that it is difficult to outperform the benchmark HAR model when applying a theoretically sound variable selection procedure in an unrestricted AR setting. This paper differs from Audrino and Knaus (2016) along several dimensions and, moreover, addresses the various open points mentioned in their concluding remarks section. First, Audrino and Knaus (2016) only analyze which lags are selected from the lasso but do not test formally for the presence of false positives. We extend the analysis by considering the adaptive lasso, a refinement of the lasso that should itself help reduce the number of false positives, and additionally perform a test on the significance of the coefficients in a statistically sound way. As we will show, the presence of false positives is pervasive in the analysis of the lag structure of realized volatility and, thus, must be taken seriously into account. Otherwise, we run the risk of drawing the wrong conclusions.
Second, we extend the data set cross-sectionally by considering more individual stocks belonging to the S & P 500. This allows us to better investigate the evolution of the structure of the selected lags over time. In contrast to Audrino and Knaus (2016) we can (ⅰ) verify whether there are common structural breaks affecting simultaneously the dynamics of (almost) all assets and (ⅱ) determine the factors, if any exist, that are able to explain the cross-sectional differences in how structural breaks influence the lag structure. Our results show that there are two main structural breaks in the period under investigation ranging from January 2001 to November 2010 that divide it into three different subperiods characterized by different market and realized volatility conditions: The first break corresponds to the end of the US stock market downturn in 2002 following the burst of the dot-com bubble, whereas the second break takes place with the onset of the financial crisis in 2008, located around the bankruptcy of Lehmann Brothers. Moreover, we show that the market sector and the beta of the individual assets are important factors in explaining the behavior cross-sectionally of the realized volatility lag structures: in fact, assets that belong to the same market sector or possess a similar beta with respect to the market index show very similar structures.
The content of this paper can be summarized as follows: Section 2 presents the theoretical foundations of both the HAR model and the adaptive lasso estimator and introduces the hypotheses of interest and the testing procedure. Section 3 illustrates the empirical results of the analysis by separately presenting them before and after testing. Section 4 concludes.
2.
Theoretical Considerations
This section will lay out the theoretical motivation of the empirical tests that follow. The idea is to estimate the optimal lag structure driving realized volatility dynamics and to test the validity of the lag structure and maximal order lag implied by the HAR model by employing the adaptive lasso as model selection device. The estimation results of the adaptive lasso will further be analyzed regarding statistical significance both individually and jointly. We will therefore first introduce the HAR model, then the estimation procedure via the adaptive lasso and the conditions under which inference can be conducted. Finally, the concept of multiple hypothesis testing will be briefly revisited.
2.1. The HAR model
In the past years, there has been a shift in the focus of the literature on modeling and forecasting volatility. For many years after the introduction of the GARCH model by Bollerslev (1986), the literature aimed at modeling the unobservable volatility of an asset. However, in recent years, the concept of realized volatility has gained popularity: in fact, by estimating the unobservable second moment more accurately using high-frequency data, volatility has been made somehow "observable". Let us briefly review the concept of realized volatility.
We assume that log-prices of an asset follow the stochastic process
where $W(t)$ is a standard Brownian motion and $\mu(t)$, $p(t)$ and $\sigma(t)$ satisfy the usual regularity conditions. Under this assumption, realized volatility is defined as the sample analogue to the quadratic variation $\sqrt{\int_{t-1d}^{t}{\sigma^2(s)ds}}$, where $d$ corresponds to the time interval of interest, usually one trading day.
As has been shown in previous research on quadratic variation by Andersen et al. (2003) and Barndorff-Nielsen and Shephard (2002), this theoretical quantity can be estimated consistently by means of the sum of squared log-returns, assuming the absence of microstructure noise and jumps. With appropriately chosen $\Delta$ and $M$, which reflect the length of the sampled time interval and the sampling frequency, one can therefore define realized volatility as
where $r_t$ are the asset's log-returns.
When it comes to modeling realized volatility dynamics over time, one of the most popularly used models for its simplicity and at the same time very high estimation and prediction accuracy, is the heterogeneous autoregressive model, henceforth the HAR model, introduced by Corsi (2009). The central idea of the HAR model is to predict future realized volatility dependent on past realized volatility in a linear setting.
The HAR model is stated under the key assumption that the market participants can be separated into three heterogeneous groups of traders according to their trading horizons, i.e. daily, weekly or monthly rebalancing. It further assumes that each of these groups create their own component of latent volatility and take into account their expectation of future volatility at a lower frequency. This cascade model of volatility can finally be written as the famous HAR equation. Furthermore, it is common to substitute realized volatility at different frequencies by the respective logarithms. This is done mainly for two reasons: First, the distribution of the logarithm of realized volatility more closely resembles the normal distribution than realized volatility in its level form. Second, by modeling the logarithm there is no need to impose restrictions on the parameters so that resulting estimates and forecasts are positive. After this transformation, we get:
Using the fact that the logarithms of weekly and monthly realized volatility, $\log RV_t^{(w)}$ and $\log RV_t^{(m)}$, are defined to be the averages of the logarithms of daily volatility over 5 and 22 days (the number of trading days in a week/month), respectively, this model can be rewritten as a constrained linear autoregressive (AR) process:
with the restrictions being
In inspecting the structural AR (22) specification implied by the HAR model, it is obvious that if the HAR model were the correct model for realized volatility, one would expect to observe in empirical data that indeed exactly the first 22 lags are relevant for forecasting tomorrow's realized volatility.†
†From the original assumptions it can be derived that all $\beta^{(\cdot)}$ are strictly positive, which rules out the scenario of any $\beta_i^{HAR}$ being $0$. This has been confirmed empirically.
It is now the goal to apply the adaptive lasso as a model selection device to the time series of realized volatility in an unrestricted AR model of a sufficiently large order. If the HAR model were the correct model, we would expect the adaptive lasso to select exactly the first 22 lags and set the remaining coefficients to zero. While this question was previously of interest for Audrino and Knaus (2016), our procedure differs in two ways: First, we will use the adaptive lasso, as opposed to the standard lasso, which was used by Audrino and Knaus (2016) in the main analysis. Second, we will additionally apply the newly derived theory by Audrino and Camponovo (2015) in order to check which of the lags that have been selected by the adaptive lasso are truly significant. In this way we will get rid of, or at least reduce the impact of, false positives (that is, variables that are selected to be active but are in reality inactive) that affect lasso-type approaches and can possibly lead to wrong conclusions.
2.2. The adaptive lasso
The adaptive lasso, as proposed by Zou (2006), is a generalized refinement of the lasso that was originally introduced by Tibshirani (1996). The lasso, an acronym for least absolute shrinkage and selection operator, can be viewed as a constrained least squares regression problem. Since the model to be tested is linearly autoregressive in the regressors, i.e.
where the $\epsilon_i$ are innovation variables with mean zero, we can consequently define the adaptive lasso estimator as
with $\lambda\ge0$ being a tuning parameter and $\lambda_j$ being individual weights for each of the coefficients. The special case of the classic lasso by Tibshirani (1996) corresponds to the setting where $\lambda_j = 1$ for $j = 1, ..., p$.
From this objective function it is obvious that setting $\lambda = 0$ will cause the lasso estimator to coincide with the ordinary least squares estimator, $\hat{\beta}_{OLS}$. Usually, this estimator will not set any of the coefficients equal to zero. However, by choosing a strictly positive $\lambda$, all coefficients that are not equal to zero will be penalized. Consequently, increasing $\lambda$ leads to more and more coefficients that will be set exactly to zero, therefore performing progressively stricter variable selection. Thus, assuming sparsity, we expect the adaptive lasso to select only the active set of regressors, i.e. the ones which are truly non-zero.
For the classical cross-sectional setting, assuming the innovation variables to be independent and identically distributed (iid), Zou (2006) showed that the adaptive lasso fulfills the so-called oracle properties, which means that it asymptotically both identifies the non-zero coefficients and estimates the coefficients of the truly active variables consistently and efficiently. This result is dependent on the fact that the individual weights $\lambda_j$ will be chosen data-dependent. Possible choices for the weights are, for example, the inverse of the absolute value of the coefficients estimated by either OLS (in the case that OLS can be performed) or the lasso (in the high-dimensional case where one has to deal with more regressors than observations).
However, for the specific question we are analyzing, the assumption of iid innovations is unrealistic. When it comes to linear time series processes, as is the case for the AR class of models we are dealing with in this paper, as shown in the previous section, it was further proved by Kock (2016) and Medeiros and Mendes (2016), among others, that the adaptive lasso satisfies the oracle properties as well.‡ The adaptive lasso is therefore a theoretically sound model selection device to investigate the time-varying behavior of the optimal lag structure in realized volatility dynamics and consequently to check the validity of the HAR lag structure assumption. Note, however, that although the adaptive lasso is able asymptotically to correctly identify the non-zero coefficients, it is not really designed to check the validity of the parameter restrictions implied by the HAR model (that is, the same value of the coefficients in the three different trading windows). For this purpose, alternatives to the adaptive lasso like the clustered lasso or the group lasso can be used (see, for example, Bühlmann et al., 2013).
‡Similar oracle properties have also been shown for multivariate VAR processes by Kock and Callot (2015) and Callot and Kock (2014).
2.3. Hypotheses of interest and testing procedure
In our application, we are interested in testing whether the estimated adaptive lasso coefficients in an unrestricted high-order AR model are significantly different than zero. In particular, there are two hypotheses of interest related to the validity of the HAR lag structure and maximum order lag assumptions on which we will focus: The first hypothesis the HAR model implies is that all lags up to the 22nd matter for prediction and are therefore non-zero. The first corresponding null hypothesis is therefore $H_0: \beta_i = 0, \forall i = 1, ..., 22$; a rejection of the null hypothesis is thus a confirmation of the HAR model. The second implication of the HAR model would be that lags beyond the 22nd should not matter for predicting future realized volatility, that is $H_0: \beta_j = 0$ for $j>22$, which would be rejected if the corresponding coefficient beyond the 22nd were found to be significantly different from zero, thus casting doubt on the correctness of the HAR dynamics. Given that we are not considering the parameter restrictions imposed by the HAR model, both tests are indirect tests for the validity of the HAR model. Constructing direct tests that consider under the alternative hypothesis the full HAR specification instead of an unrestricted AR model significantly complicates the testing procedure and is left for future research.
In order to test these hypotheses, the individual test statistics are constructed using the results of Audrino and Camponovo (2015). They recently developed a conservative inference procedure for the coefficients of the adaptive lasso. While this was previously only possible for the truly non-zero coefficients, this newly developed theory allows inference on all coefficients, thus allowing in particular to test for false positives. As we show empirically below, the presence of false positives cannot be neglected and may cause misleading interpretations of the results. Briefly, the inference procedure introduced in Audrino and Camponovo (2015) is motivated by the fact that the adaptive lasso coincides with OLS when $\lambda = 0$. The authors showed that the standard errors of the limiting distribution of the adaptive lasso estimators for each fixed value of $\lambda$ become smaller when $\lambda$ becomes greater than zero, which is why a conservative test for the adaptive lasso coefficients can be conducted by using the estimated OLS standard errors of the coefficients. Put formally, the individual significance of $\hat{\beta}_i$ can be found using the test statistic
with the OLS standard errors. Further details on the implementation and asymptotic properties of the testing procedure are given in the Appendix.
2.4. Multiple hypothesis testing
It is clear that the two hypotheses introduced above can be seen as joint tests. In particular, the second hypothesis can be rewritten as $H_0: \beta_{23} = \beta_{24} = ... = 0$ which would be rejected if one of the coefficients beyond 22 were found to be significantly different from zero, thus implying that the maximal order lag assumed under an HAR model specification were wrong. Practically, of course, only a finite number of lags can be tested but at the same time the order of the AR model should be chosen sufficiently large. For the sake of the exposition, let us assume that the first 100 lags will be considered (that is, $I = 100$ in (6)). In that case, the first hypothesis would be equivalent to a joint test of 78 individual hypotheses. This large number of hypotheses for the joint test justifies the use of a procedure that corrects for the fact that we are dealing with a multiple testing problem. Among those introduced in the literature§, we consider the procedure that controls the family-wise error rate, as suggested by Holm (1979) and Romano and Wolf (2005).
§See, as alternatives, Benjamini and Hochberg (1995) or Genovese et al. (2006).
The intuition behind this procedure is that for a large number of hypotheses one would expect to reject some test statistics in any case. The Holm procedure corrects for this fact by imposing a threshold on the probability $\alpha$ that one or more of the hypotheses are rejected. To state the exact procedure, we assume that the p-values of the individual $s$ statistics are sorted in ascending order, so that $\hat{p}_1 \le \hat{p}_2 \le...\le\hat{p}_s$. The step-wise procedure is then given by (Romano and Wolf, 2005):
1. If $\hat{p}_1 \ge \alpha/s$, accept $H_1, ...H_s$ and stop. If $\hat{p}_1 < \alpha/s$, reject $H_1$ and test the remaining $s-1$ hypotheses at level $\alpha/(s-1)$.
2. If $\hat{p}_1 < \alpha/s$ but $\hat{p}_2 \ge \alpha/(s-1)$, accept $H_2, ...H_s$ and stop. If $\hat{p}_1 < \alpha/s$ and $\hat{p}_2 < \alpha/(s-1)$, reject $H_2$ in addition to $H_1$ and test the remaining $s-2$ hypotheses at level $\alpha/(s-2)$.
3. And so on.
It needs to be stressed that this procedure is very conservative because for large numbers of hypotheses, the critical values will become very large. This would make the test tend to view the coefficients beyond the 22nd as not significantly different from zero jointly. Given that the individual test statistics are already conservative, this test could therefore be considered as too conservative in the case at hand.
3.
Empirical Analysis
3.1. Data set
We consider tick prices obtained from TickData consisting of intraday quotes of Alcoa, American Express, Baxter, Blackrock, Citigroup, Coca Cola, Dow, Exxon Mobil, Gilead, Goldman Sachs, Hasbro, Harley Davidson, Intel Corporation, Met, Microsoft, Nike, Pfizer, Verizon and Yahoo from January 2,2001 to November 15,2010, which corresponds to 2472 trading days after filtering.
The intraday quotes were used to compute daily realized variance measures based on the two-time scales estimator by Zhang et al. (2005), given its robustness in the presence of microstructure noise.¶ The two chosen scales were 2 and 20 ticks; however, the results are not sensitive to the grid size. In order to further mitigate the effect of microstructure noise, we also disregard the trades of the first and last 30 minutes of each trading day.
¶We found that our results do not change when using another estimator that is robust to microstructure noise, e.g. a realized kernel. In the presence of jumps, using the two-time scales estimator we end up focusing on the dynamics of total quadratic variation (that is, including the contribution of squared jumps). Instead, if the interest is on the continuous part of quadratic variation, estimators that are robust to jumps, like the MedRV estimator, can be considered.
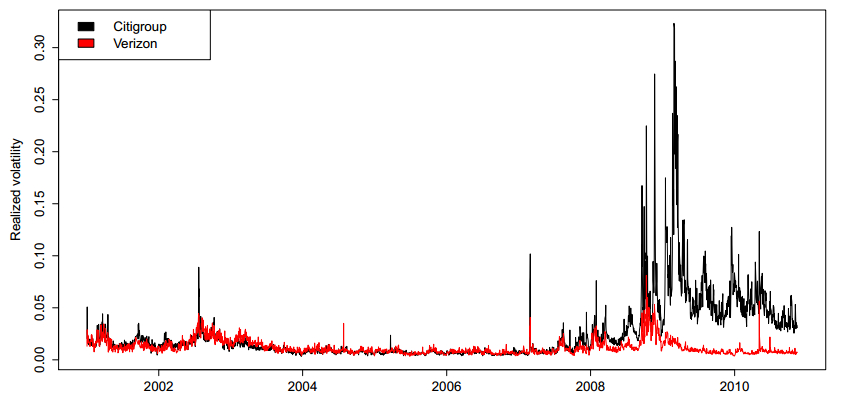
Figure 1 shows some illustrative examples of the computed realized volatility series for Citigroup and Verizon, belonging to the financial and technological sector, respectively.‖ It can be seen that, in general, realized volatility levels are higher for Citigroup than for Verizon. This is in line with expectations given the respective sectors. Summary statistics for the series under investigation are given in Table 1.
‖The sector classifications for all assets were adopted from Yahoo Finance.
Furthermore, in the considered time period we can identify two main events affecting realized volatility for all assets. The first is the period until roughly the fourth quarter of 2002, which corresponds to the aftermath of the burst of the tech bubble and the terrorist attacks on 9/11. In this period, realized volatility levels were higher than usual for all assets and more spikes can be observed. The subsequent period from 2003 to the end of 2007 can be viewed as relatively calm, with realized volatility levels remaining relatively constant with only a few spikes. The third period starts in 2008, with realized volatility reaching extremely high levels during the start of the financial crisis. It should be noted that in this period realized volatility returns to pre-crisis levels in 2009 for most non-financial assets, while Citigroup and other financial assets continue to have higher than usual levels of volatility. The mentioned properties can be observed across all assets, with only Citigroup being an exception with a persistently high realized volatility during the financial crisis.
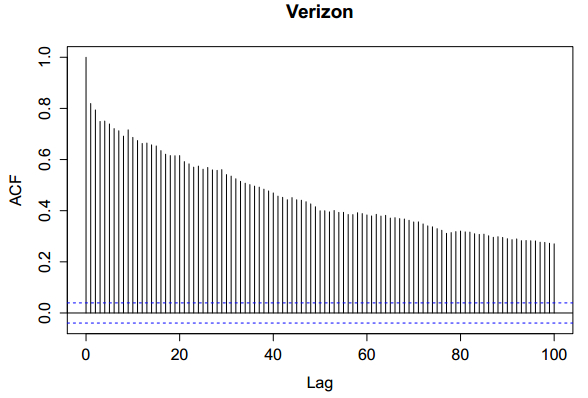
Figure 2 shows an example of the autocorrelation function for the time series of realized volatility of Verizon. This demonstrates that the autocorrelation function is very slowly decaying and confirms the well documented long-memory shown by realized volatility series. Moreover, it also provides clear evidence for the high correlation present among near lags of realized volatility. From an estimation point of view, this will lead to highly collinear regressors in our AR setting, which makes the isolation of the individual effects more difficult. This point must be carefully taken into account when discussing the results of the adaptive lasso analysis, in particular those related to the validity of the HAR lag structure when using the first testing hypothesis introduced in Section 2.3.
3.2. Rolling window analysis
The empirical analysis is conducted using a rolling window procedure to overcome problems related to the possible non-stationarity of the realized volatility series: see the discussion after Figure 1 and the extensive literature about structural breaks in realized volatility series such as Hillebrand and Medeiros (2016) and Bertram et al. (2013) and the references therein. The first step is the estimation of the adaptive weights $\lambda_i$. In this case, the OLS estimator is chosen in accordance with Audrino and Camponovo (2015), although theoretically any $\sqrt{n}$-consistent estimator would be a valid choice as well.**
**Empirically, it turns out that the choice of this first-step estimator is of very little importance and produces almost identical final results, as for example from using the standard lasso or other valid estimators.
Estimating the regression of the time series on its first $I = 100$ lags by OLS, the resulting coefficients are inverted in absolute value to obtain the weights:
These weights are then used to fit an adaptive lasso to the model, which of course still depends on the tuning parameter $\lambda$.
We choose $\lambda$ based on the one-standard-error rule via cross-validation. All estimations are conducted in R via the glmnet package: see Friedman et al.(2010)††
††Alternative ways of finding $\lambda$, for example based on the minimization of the BIC, have proved to be very similar after testing. Before testing, however, the adaptive lasso generally selects many more variables when minimizing the BIC than when applying the one-standard-error rule. We interpret this result as a signal that optimizing the shrinkage parameter using the BIC generally leads to many more false positives than when using cross-validation.
3.2.1. Adaptive lasso estimation
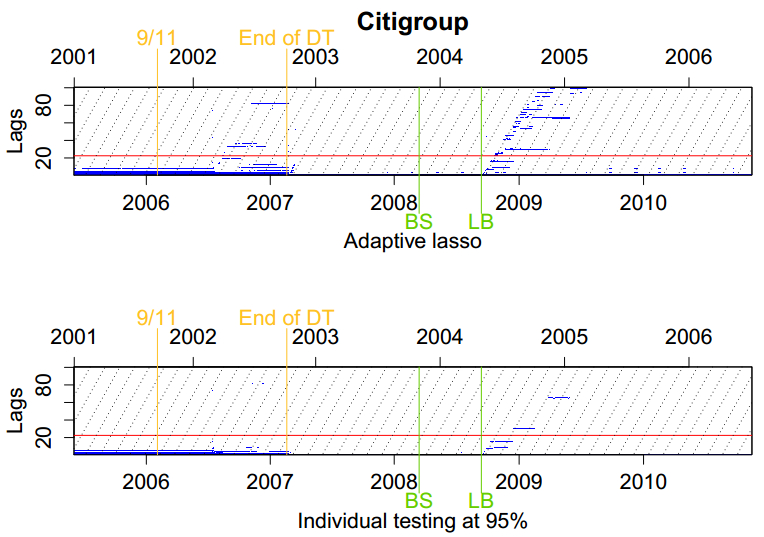
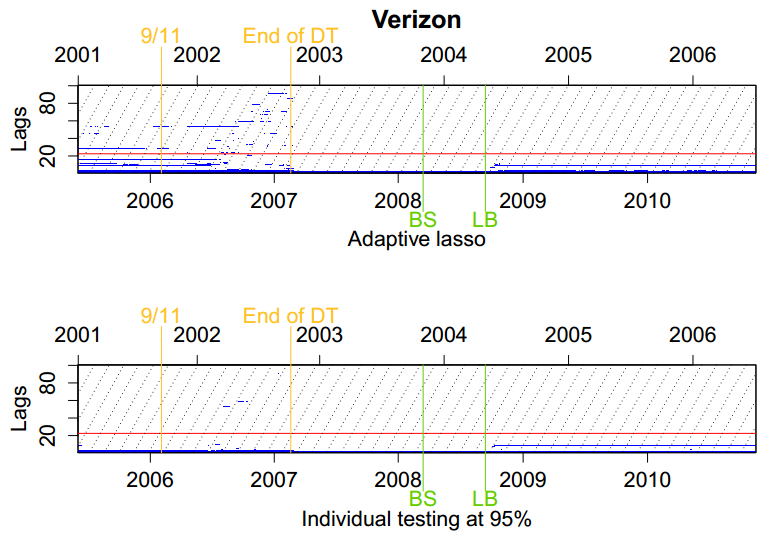
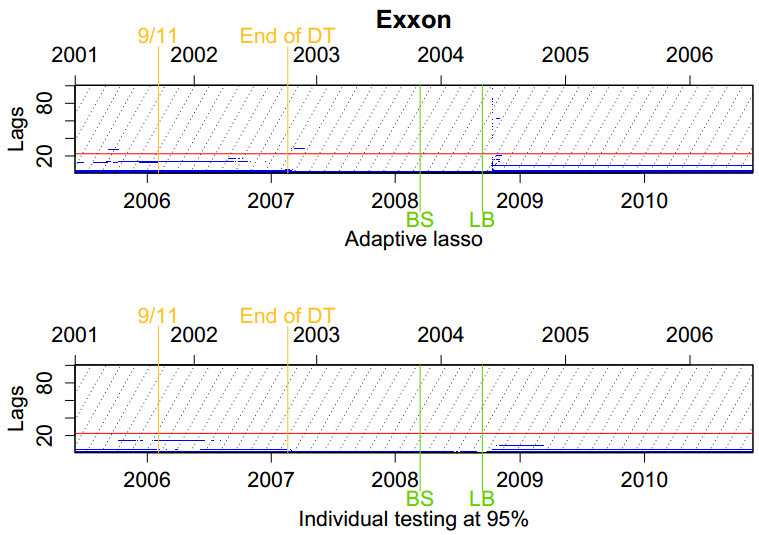
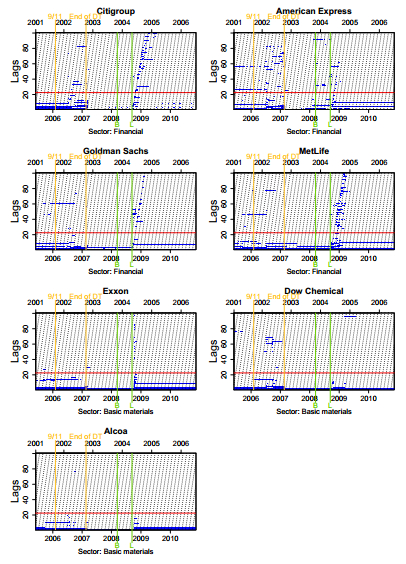
In a first step, we will analyze which lags are selected by employing the adaptive lasso. The above-mentioned procedure was conducted on a rolling window basis, with a window length of 1000 trading days (that is, about 4 years), rolled over day by day.‡‡The top panels in Figures 3 through 5 show the lags that are selected (blue rectangles) by the adaptive lasso for our illustrative examples, namely Citigroup, Verizon and Exxon Mobil. Results for the rest of the assets can be obtained from the authors upon request.
‡‡We find that choosing a different window length does not qualitatively alter the main results and conclusions.
Each column corresponds to the selected lags for one rolling window, with the start date and end date given at the top and bottom of the plot, respectively. Additionally, we mark four events in the timeline and the dates at which they left (entered) the rolling windows: 9/11, the end of the stock market downturn (we choose the day when the S & P 500 reached its lowest level), and the collapse of Bear Stearns (BS) and Lehman Brothers (LB). The diagonal dotted lines have slope one and help to illustrate how individual events propagate through the lag structure over time. The red line indicates the maximal order lag implied by the HAR model assumption.
Inspecting the plots of the results, we can make three key observations: First, we see that generally not all of the first 22 lags are selected by the adaptive lasso. This confirms the findings by Audrino and Knaus (2016). In fact, usually no more than 5 or 6 lags among the first 22 are selected by the adaptive lasso. Moreover, generally these active lags are among the first ten. This contradicts the implications of the HAR model. However, given the high multicollinearity of the lags of realized variance, it needs to be emphasized that this result should be viewed with caution: Since the lags are highly correlated and given that the adaptive lasso is not enforcing the parameter restrictions implied by the HAR model, it is to be expected that the estimation procedure will select only a few of these lags and that these will be highly significant. In other words, due to the penalization of any non-zero coefficient, it is not surprising that the adaptive lasso selects only a few of these lags that seem to have a highly similar informational content. Thus, the fact that the adaptive lasso does not select all the necessary lags should not be viewed as strong evidence against the validity of the HAR model.
Second, we see that the adaptive lasso selects many lags beyond the 22nd for many assets. In fact, it sometimes selects lags that are considerably far beyond the 22nd, for example for Citigroup and Verizon. These lags are not in line with the implications of the HAR model and furthermore appear to be relatively stable over long periods of time. This, as well, confirms the results by Audrino and Knaus (2016).
The third observation that can be made by inspecting the rolling window plots is that two structural breaks are clearly visible across almost all assets which divide the time period under investigation into three subperiods. It appears that the end of the stock market downturn and the collapse of Lehman Brothers mark two break points at which the lag structure selected by the adaptive lasso significantly changes. The effect of the collapse of Lehman Brothers is best visible by inspecting the lags selected for Citigroup in Figure 3: In the third period, right after the collapse and along the diagonal lines, the shocks to volatility propagate through the lag structure and remain for a short period. This pattern is, not surprisingly, also easily visible for the other financial titles.
The breakpoint dividing the first and the second subperiod appears to be the end of the stock market downturn during the final months of 2002. This is in line with the results of Hillebrand and Medeiros (2016) and Audrino and Knaus (2016) who also confirm the presence of a structural break in realized volatility around the end of 2002. In general, across many assets, it can be observed that larger lags tend to be selected as active variables by the adaptive lasso more often in the first and the third period than in the second. Throughout the second period there is very little variation in the lags selected, which is not surprising given that this period is characterized by calm market conditions. Furthermore, across assets the adaptive lasso selects only very few and very short lags in this period: for many assets, in fact, only up to the third lag. In other terms, it seems that during such a quiet period, characterized by low levels of realized volatility, very simple autoregressive processes perform best at predicting volatility. In fact, recalling the plot of realized volatility series during the 2003-2007 subperiod, we see that the persistence of the series is significantly lower than that observed in the preceding and following periods. The more quickly decreasing autocorrelation function in that period is therefore in line with the smaller order of the autoregressive process.
A plausible explanation for the fact that in this calm period only the shortest lags are selected is that there are far fewer spikes of volatility observable than in more hectic times, such as the first and the third period: The second period is characterized by a relatively constant level of volatility, which means that only very few events occur which affect volatility. Therefore, the time series of volatility is very smooth and given the lack of events with big impact, the preceding day's level of volatility is a high quality forecast. On the other hand, for the more hectic periods, there are many events that occur at a high frequency which lead to volatility spikes. Given the persistence of volatility in these periods, longer lags therefore have much greater forecasting power. With respect to the high number of volatility spikes, it is thus intuitively compelling that larger lags are also selected by the adaptive lasso, as compared to the calmer period.
Fourth, while this general pattern seems to hold across most of the assets in our sample, we also detect two other factors that have an impact on the lags selected by the adaptive lasso in the different subperiods: the market sector and the beta of the individual assets. Figure 6 shows how the adaptive lasso estimates for the financial stocks compare to those for the stocks of the basic materials sector. We can observe that generally many more large lags are selected for the financial assets than for the basic materials assets, across all periods. An intuitive explanation for this behavior is that compared to financial companies, basic materials companies are less subject to particular financial and/or economic events that have a big impact on volatility. Therefore, volatility progresses more smoothly and the shorter lags are much more valuable for forecasting than the large ones. On the other hand, the larger lags selected for the financial stocks, in particular those that propagate over the rolling windows, usually identify particular events yielding large spikes in realized volatility. For example, we see that the collapse of Lehman Brothers visibly propagates through the lag structure of the financial assets but does not have any effect on the basic materials assets.
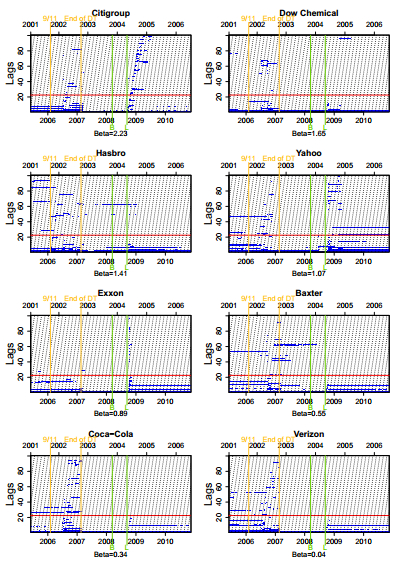
A second relevant factor impacting the lag structure selected by the adaptive lasso is the asset's beta. Figure 7 shows the grouped plots of the adaptive lasso estimates of the four assets with the highest betas (top) and the four assets with the lowest betas (bottom). In order to isolate the effect of beta from the effect of the sector, the plots show the assets with the highest and lowest betas from different sectors. We can see from these plots that the third period of the financial crisis is actually not only related to the sector but also to the beta. For the high beta assets we observe that lags beyond the 22nd are selected 1981 times in total in that period (in contrast to only 18 times for the low beta assets). This can again be explained by the fact that low beta assets are less influenced by market turbulence and therefore show fewer significant spikes of volatility in that period. While we can see that the sector and the beta have an influence on the lag structure that is selected by the adaptive lasso, we find that other factors such as liquidity and value do not seem to show visible effects.
3.2.2. Testing for false positives
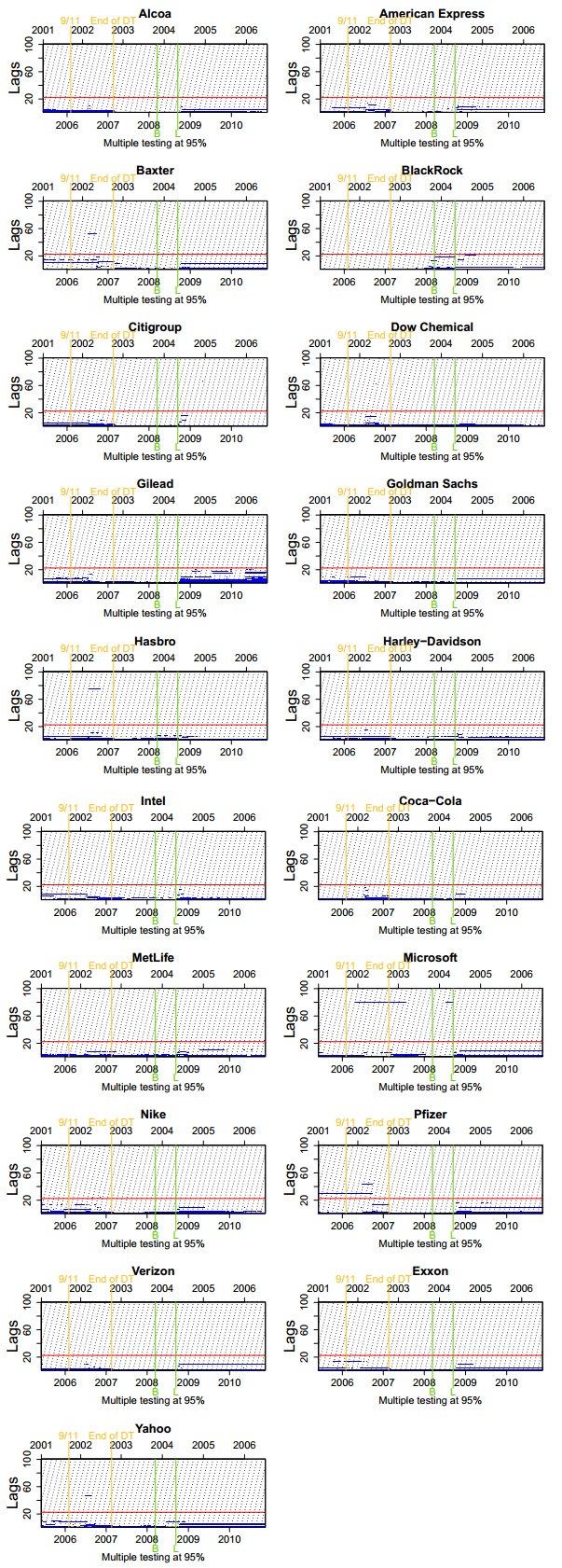
Having obtained the adaptive lasso estimates, we now test to see whether these estimates are indeed significantly different from zero or can be classified as false positives. We therefore test the two hypotheses of interest using the procedure described in section 2. This is done by dividing each estimate $\hat{\beta}_{AL, i}$ by its respective OLS standard error that was previously computed. The absolute value of the resulting quantity is then compared to the normal quantiles at the desired significance level; in our case we test at confidence level 95%. The plots reporting the significantly selected lags after testing are drawn in the bottom panels of Figures 3 through 5 for the three illustrative examples Citigroup, Verizon and Exxon Mobil, respectively.
Analyzing these plots, we can revisit the discussion of the previous subsection after controlling for false positives (although in a conservative way). To begin with, the first hypothesis is generally rejected because not all of the first 22 lags are selected by the adaptive lasso. We now see that most of these lags are also found to be significant, with some of the very short lags being the most significant. We can therefore conclude that much of the information contained in the lag structure is in fact due to the shorter lags. Nevertheless, similarly to what we discussed above, given that short lags are highly correlated, this result cannot be seen as strong evidence against the HAR model.
Second, while the adaptive lasso estimates seem to reject the second hypothesis, we now see that after testing we indeed fail to reject it at a significance level of 95% for most assets at most times. After testing, we observe that almost all lags that are selected beyond the 22nd are insignificant at the 95% level and can be generally interpreted as false positives. Except for a very few very short periods of time, the lags disappear completely, which therefore supports the validity of the HAR model. In fact we see that only four of the 19 assets retain a large lag that remains significant for a long period. On the other hand, however, given that we are using a conservative procedure favoring the null hypothesis of no active lags beyond 22, those exceptions can be interpreted as strong evidence against the lag structure and maximal order lag implied by the HAR model for the corresponding assets and subperiods.
Overall, the results regarding the significant lags provide a very good explanation as to why the HAR model performs so well in practice in the different forecasting applications: usually all the lags that are significantly selected by the adaptive lasso for forecasting tomorrow's realized variance are among the first 22 lags. The subset of lags that the HAR model focuses on therefore appears to contain all the relevant information. Due to the fact that these lags are highly correlated, it is also not as important which of these lags are used. Thus, it does not make a crucial difference that the HAR model, as opposed to the adaptive lasso, focuses on all of the first 22 lags. Since the HAR model imposes restrictions on the estimated parameters, it is nonetheless very parsimonious. This finding also explains the results found by Craioveanu and Hillebrand (2012) who show that the choice of the agammaegation frequencies does not make a significant difference for the performance of the HAR model.
Finally, we see that while most of the large lags are found to be insignificant, we still observe two breaks in structure among the significant ones. This is best seen by acknowledging the fact that the short lags that are significantly selected also usually change when the breaks occur.
3.2.3. Multiple testing
As mentioned in the theoretical section, the second hypothesis amounts to a joint test of 78 individual hypotheses. This would justify the procedure of controlling the family-wise error rate instead of the individual ones. We report the results for all assets for a significance level of 95% in Figure 8.
For the lags beyond the 22nd, the plots report the lags that are significant after multiple testing, while for the lags up to the 22nd, they report the ones that are significant after individual testing. Inspecting the figures, we see that after multiple testing all the lags beyond the 22nd are insignificant for most assets most of the time. One exception would be Microsoft, for example, for which a large lag is significantly selected throughout the first and second period. It is not surprising that generally most of the large lags turn out to be insignificant after testing multiply, given that the test procedure, as previously mentioned, is very conservative. Together with the already conservative way of estimating the standard errors, this amounts to a test which is too conservative in the sense that the critical values for the lags become extremely high.
4.
Conclusion
The goal of this paper was to estimate the optimal lag structure driving the behavior of the realized volatility dynamics in an autoregressive setting. Moreover, given that the HAR model assumptions are equivalent to stating that the dynamics of realized volatility follows a constrained AR (22) process, we also checked in an indirect way whether the structural assumptions that the HAR model implies can be recovered using solely statistical techniques.
For the empirical investigation, we employ the adaptive lasso as a selection device for the past lags that are most relevant for prediction. We make the observation that the lags selected for the 19 stocks under investigation generally do not corroborate the validity of the lag structure and maximal order lag implied by the HAR model: For most assets, lags far beyond the 22nd are selected and not all of the first 22 are selected either.
We further observe in the rolling window analysis that the lags selected are generally relatively stable over time. However, there appear to be two structural breaks, which significantly affect the lag structure across all assets, with the first one occurring at the end of the stock market downturn at the end of 2002 and the second one coinciding with the collapse of Lehman Brothers in 2008. We further see that for almost all assets, during the middle period, which is very calm in terms of realized volatility, only very short lags are selected by the adaptive lasso. This is in contrast to the more volatile periods in the beginning and the end in which for some assets very large lags are selected additionally. A likely explanation for this observation is that the larger lags are related to the frequency of spikes of volatility: In calm periods, a simple autoregressive process of small order is a very good predictor of the future behavior because volatility progresses very smoothly. For the more volatile periods in the beginning and in the end, large spikes of volatility cause the adaptive lasso to attribute predictive power even to very large lags.
Another observation that can be made is that the sector and the beta seem to have an effect on how the lag structure is affected by the structural breaks. Comparing the results of financial assets with basic materials assets, we see that for basic materials assets, significantly fewer large lags are generally selected. This can again be attributed to the fact that fewer spikes of volatility occur for these assets. Furthermore, for the financial titles, we see that the collapse of Lehman Brothers clearly propagates through the lag structure. In fact, the effect of the financial crisis is also closely linked to the size of the beta: We see that for low beta assets, in contrast to high beta assets, even across sectors virtually no large lags are selected in the final period.
Finally, we find that for almost all assets over all time windows, the large lags that are inconsistent with the HAR model are statistically insignificant. This explains the good empirical performance of the HAR model because it shows that the model focuses on the right subset of the lags that are significant for forecasting. The fact that not all of the first 22 lags are significant should not be overrated given that the HAR model puts constraints on the autoregressive process and the fact that the first lags are highly correlated. The HAR model therefore focuses in a parsimonious way on the subset of lags that contain the most important information.% for forecasting.
5.
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: