1. Introduction

While offshore installations are supposed to comprise the major element of wind energy penetration in the coming years, onshore installations will certainly continue to contribute to the overall growth of the wind energy market. For onshore wind energy development, since a lot of suitable sites in flat terrain have already been developed, more attention is going to be paid to sites in complex terrain. This is also due to the advantageous features of mountainous terrains. Mountainous terrains are characterized by richer wind resources in comparison to flat terrains, due to speed-up effects of hills. However, the increased wind turbulence, the higher fatigue loads and the increased costs for installation, maintenance and operation make onshore installations over complex terains a challenging task. Moreover, access to mountainous terrains may be difficult, at least when some infrastructures are not available, due to the steep terrain and the isolated location. Nevertheless, a specific location may still be appropriate to build a WF despite the infrastructure costs. In such cases, a design analysis has to be conducted prior to any investment, and one has to rely on remote sensing techniques for the terrain reconstruction as far as on site measurements are impossible.

Except for the terrain topography, wind turbines also affect wind flow. In a wind farm, the interaction of the flow with wind turbines results in lower power and higher loads at the area behind the turbine. Thus, wake losses should be taken into account during the wind park design. Computational Fluid Dynamics (CFD) wake models have been previously used to compute the wake effects caused by wind turbines [21]. Despite their increased accuracy in comparison to simpler linear approaches, the increased computational requirements render these methods impractical for use in an optimization framework, where wake losses have to be computed for many layouts. Therefore faster but less accurate wake models are used for layout optimization. Regarding wind turbine siting in onshore complex terrains, in [28,29,30] a particle tracking model is used to calculate the wake effects. Virtual particles were used to simulate the wake flow generated by a turbine. The motion of the particles is simulated based on the pre-calculated flow over the empty terrain and the speed wake effect is computed from the density of the particles. In [4] a simpler wake model is introduced. The model is an extension of the extensively used Jensen model.

A critical step during wind farm (WF) design is the WF layout optimization (WFLO), i.e. to identify the wind turbine positions that maximize energy production or minimize energy cost or both, while taking into account some physical constraints. Due to the inherent complexity, randomized optimization or heuristic techniques are usually employed. For an extensive review of the existing methods the reader is refered to [17]. Genetic algorithm (GA) is one of the most popular optimization methods that have been used for WFLO [19,7,18,10,34,27,16,6,5]. In most cases the terrain is discretized by applying rectangular [19,7] or equilateral-triangle [16] grids. A variable number of wind turbines can also be considered [18,10], optimizing at the same time the number of the wind turbines. Terrain constraints on the turbine placement can be introduced for more realistic scenarios, reducing this way the search space [27,6]. The main limitation of the, so-called, binary-coding GA approaches is that wind turbines can only be placed on the centers of the grid cells. To overcome this limitation real-coding genetic algorithms have also been proposed [34,18]. Particle swarm optimization (PSO) approaches [35,1,2,8] try to solve WFLO problem using a population of layouts that move around the search space according to a velocity. The velocity of each particle, layout in our case, depends on its best known position and the best positions of the other particles. Discrete and continuous space PSO approaches are available. Similarly to GA and PSO, Evolutionary algorithms (EA) are population-based metaheuristic optimization algorithm. Populations evolve stochastically according to a distribution that is defined based on the best solutions of each population. Evolutionary algorithms, and more specifically Covariance Matrix Adaptation Evolutionary Strategy (CMA-ES), have also been employed for the WFLO problem [32,24]. Except for population-based techniques, as the ones described before, single solution techniques have also been studied. For instance Simulated Annealing (SA) [23] has been used to solve the WFLO for offshore wind farms. The algorithm starts with a feasible solution and iteratively peturbs it to find better solutions. To avoid getting stuck in local optimal solutions the algorithm occasionally accepts worse solutions according to a probability. Finally, several studies [25,31,20] have proposed hybrid approaches that combine existing optimization strategies with the aim to overcome the disadvantages and exploit the advantages of each of the base methods. In [25] a solution is initially found using a greedy algorithm. In a second step an evolutionary algorithm is used to improve this solution. In [31] a stochastic optimization algorithm is used that had been previously developed by one of the authors and was applied on a biological problem [15,14]. The algorithm integrates GA and Markov Chain Monte Carlo (MCMC) algorithms. GA was repeatedly applied to find several optimal layouts on a grided space. The solutions from the GA were then used to construct the sampling distribution for the MCMC algorithm. During the second step a continuous search space was considered. In [20] a heuristic algorithm is used to generate an initial solution. Non-linear mathematical programming is then used to optimize the solution through local search.

The majority of the aforementioned studies are dedicated to offshore WFs. There are few studies focusing in onshore complex terrains. In [29,30] a terrain containing only a smooth hill with 120m height is considered, and in [4] an even simpler gaussian-shaped ridge was used. In the first case two different algorithms were used for WFLO the bionic optimization [29] and a greedy algorithm [30]. In bionic optimization each turbine is treated as an individual bion, intending to be relocated where its own power output can be increased. Starting from an empty layout turbines are positioned one by one, to the best locations until a pre-specified number of turbines is reached. While the later turbines will automatically avoid the wake flow from the former turbines, the wake flow generated by the later turbines can still affect the former turbines. For this reason a second step is taken during which turbines are removed and repositioned until convergence. To improve the bionic algorithm the authors presented a greedy algorithm [30]. In the new algorithm turbines are added to the terrain so as to bring maximum power increment to the wind farm, to avoid the wake flow of other turbines, and to avoid influencing existing turbines. In the second study [4] a random search algorithm in presented. The algorithm starts from an initial solution that may be an expert guess or the outcome of another optimization algorithm. At each iteration of the algorithm a WT is randomly selected and moved in a random direction with a random step. If the new layout is not feasible (e.g. due to distance constraints) the random move is repeated until a feasible solution is generated. The solution is then evaluated and if it is better than the previous one it is retained otherwise it is discarded and the wind turbine is moved towards the old direction with a random step. The number of WTs is again pre-defined.

While the terrains in [29,30,4] are more complex than flat terrains, they do not represent a typical mountainous area, which is characterized by steeper, higher and oftenly discontinuous areas. In this study we consider a real mountnainous area located in Southern Greece. The 3D representation of the terrain is reconstructed using high-resolution remote sensing data. We then use a well-known evolutionary optimization strategy, CMA-ES, to solve the WFLO problem. The aim of this study is to highlight the challenges of the problem and to investigate whether existing optimization algorithms that have been previously used for offshore layout optimization can be efficiently applied to complex terrains. The results highlight the increased problem complexity due to the higher terrain complexity, making clear that direct application of existing optimization algorithms provides far from optimal results. Another contribution of this work is the proposal of a pre-processing step that can in general be used with any optimization algorithm to guide the parameter space sampling. To the best of our knowledge, it is the first time that high-resolution remote sensing data are used in WF design, and WFLO problem is considered for a realistically complex terrain.

The remainder of the paper is organized as follows: in the Materials and Methods section a detailed description of the problem and the methods used is provided. More precisely, in section 2.2 the methodology for the reconstruction of the terrain representation is presented. In sections 2.3 and 2.4 we desribe the wind flow and wake models. A short description of the optimization algorithm is provided in section 2.5, followed by the presentation of the optimization function and the optimization constraints considered in the study. Section 3 summarizes our results.

2. Methodology

2.1. Problem Formulation

Let $\mathbf{WT}=\left\{(x_i, y_i, z_i)\right\}_{i=1}^{n}$ correspond to the 3D coordinates of the $n$ turbines. The aim of layout optimization is to find the layout $\mathbf{WT^{*}}$ that minimizes (maximizes) an optimization criterion $U$:

$$\mathbf{W}{{\mathbf{T}}^{*}}=\underset{\mathbf{WT}}{\mathop{\arg \min }}\,U(\mathbf{WT}).$$

(1)

The most commonly used objective functions are the Annual Energy Production (AEP) [35], the Cost of Energy (COE) [7,33,34,36], or the Profit [22]. In some studies combinations of the above criteria have been used. For instance in [19] a linear combination of AEP and COE was used. Clearly the aforementioned criteria depend on the wind speed $v$. In general the wind speed is a random variable with a Weibull distribution, whose parameters change with the direction of the wind $\theta$ (Section 2.3). Thus, the wind speed for a direction $\theta$ is described by a Weibull probability distribution $f(v,{{\lambda }_{\theta }},{{k}_{\theta }})={{k}_{\theta }}{{\lambda }_{\theta }}{{(v{{\lambda }_{\theta }})}^{{{k}_{\theta }}-1}}{{e}^{-{{(v{{\lambda }_{\theta }})}^{{{k}_{\theta }}}}}}$, where $\lambda_{\theta}$ and $k_{\theta}$ are the shape and scale parameters of the distribution. Moreover, wind flows from a certain direction with a probability $P(\theta)$. Given that $v$ is a random variable, $U$ is an expected value optimization criterion. If we consider a wind park consisting of a single turbine $i$, the optimization criterion is given by:

$$\begin{equation} U(WT_{i})=\int_{\theta}P(\theta)\int_{v} e_i(v) f(v;\lambda_{\theta}, k_{\theta})dv \end{equation}$$

(2)

where $e_i(v)$ can be, for instance, the power generated by wind turbine $i$ for a wind speed $v$ or the corresponding cost of energy. If we consider $n$ wind turbines the total optimization criterion is simply given by:

$$\begin{equation} U(\mathbf{WT}) = \sum_{i=1}^{n} U(WT_{i}) \end{equation}$$

(3)

2.2. Study area and terrain data

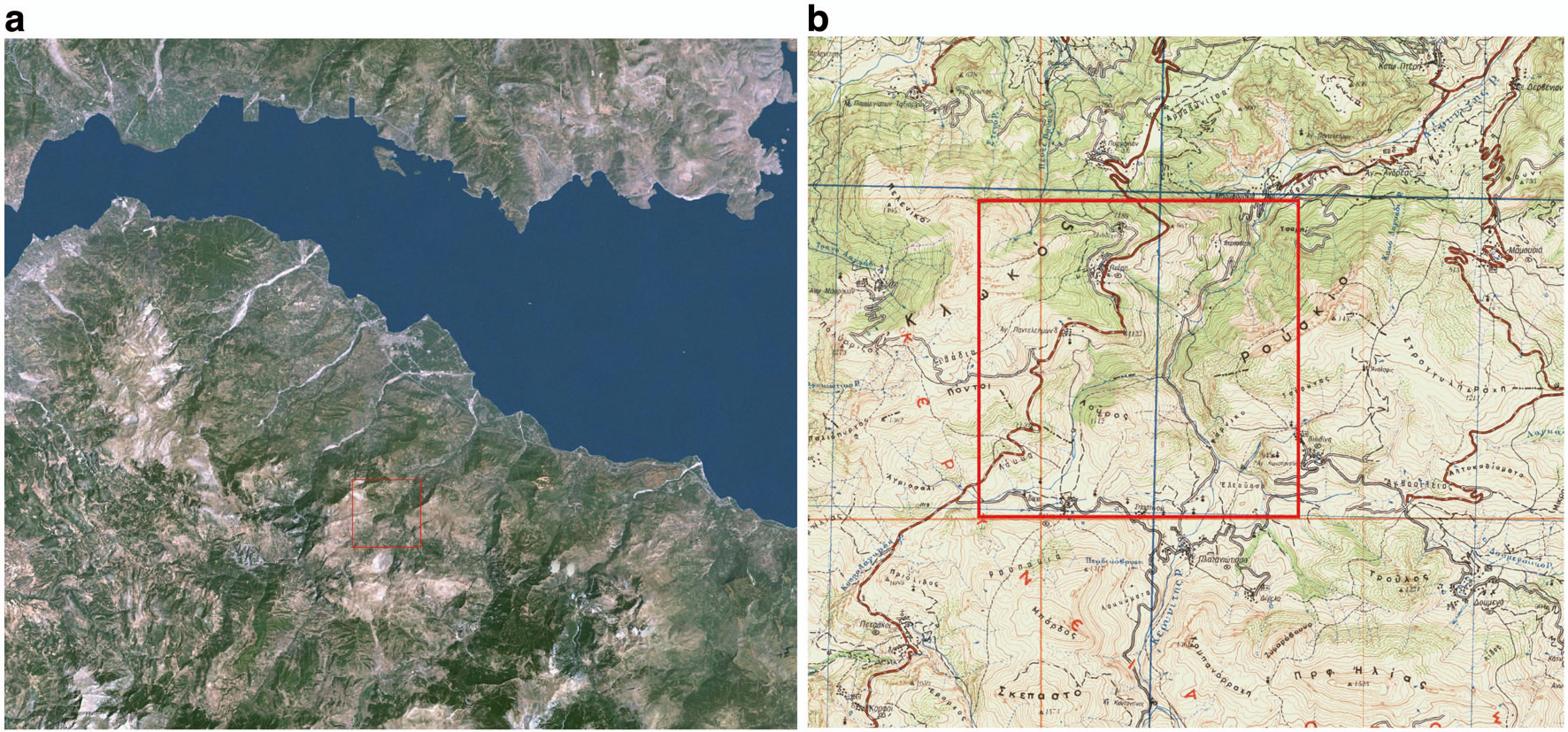
The area used in our study is a mountainous area located in Southern Greece. It is characterized by large mountain ranges with frequent changes in slope and land cover. A Landsat image of the wider study area is shown in Figure 1. In order to include the effect of complex terrain in wind flow estimations, a 3D representation of terrain's surface is needed. Therefore, Digital Elevation Models (DEMs) are used to describe the changes in terrain height. Except for the terrain shape, the types of land cover across the terrain are also essential for wind flow estimation. Land cover maps that describe the spatial distribution of the land cover types across a region are used for the computation of the terrain surface roughness, which is then used for wind flow estimations.

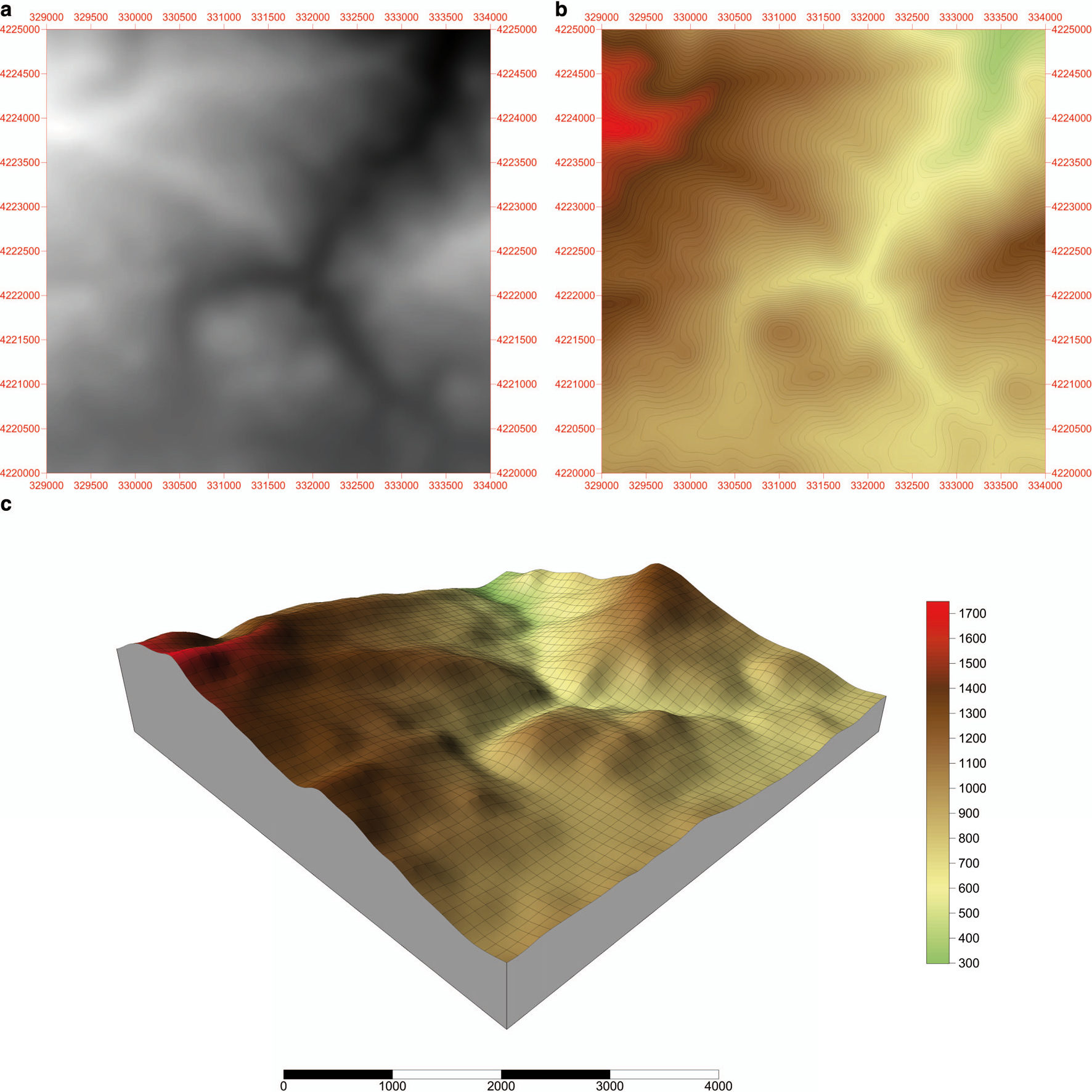
A high-resolution DEM of the study area was produced using a photogrammetric procedure based on the metric analog camera UMK-Zeiss of large format 13cm×18cm with focal length c=100mm. The conversion of aerial hard-copy photographs to digital images for photogrammetric purposes was done using Vexcel VX4000 photogrammetric scanner with scanning resolution of 3000dpi. The interior orientation process which defines how the images relate to the image plane of the camera is usually achieved by measuring the image positions of the camera fiducial marks. Relative orientation of images is based on the position of the images in a pair, relative to each other, determined by using tie points. In this work an automated image matching technique based on estimation of fundamental matrix F was used. For each stereo-pair a set of discrete points was extracted using an interest point detector. From the initial point sets, potential matches retrieved using normalized cross-correlation of the intensity values of the local neighborhood. The epipolar geometry was estimated from the set of potential matches containing outliers, using the RANdom Sampling Consesus (RANSAC) method. Once the epipolar geometry of the cameras has been fully determined, the matches can be reconstructed through triangulation. For every additional view a similar procedure is performed to update the camera position and reconstruct the view. The absolute orientation of the produced 3D model carried out using 25 ground control points widely distributed on the study area. The Digital Elevation Model and 3D terrain model derived from photogrammetric analysis are shown in Figure 2.

2.3. Wind flow computation over complex terrain

Wind conditions in the wind farm site were determined using a cup anemometer measurement campaign carried out for one year time period. The 30 m mast of the meteorological station was equiped with three cup anemometers and a wind vane in order to measure wind flow characteristics at a position about 2 km north of the wind farm site.

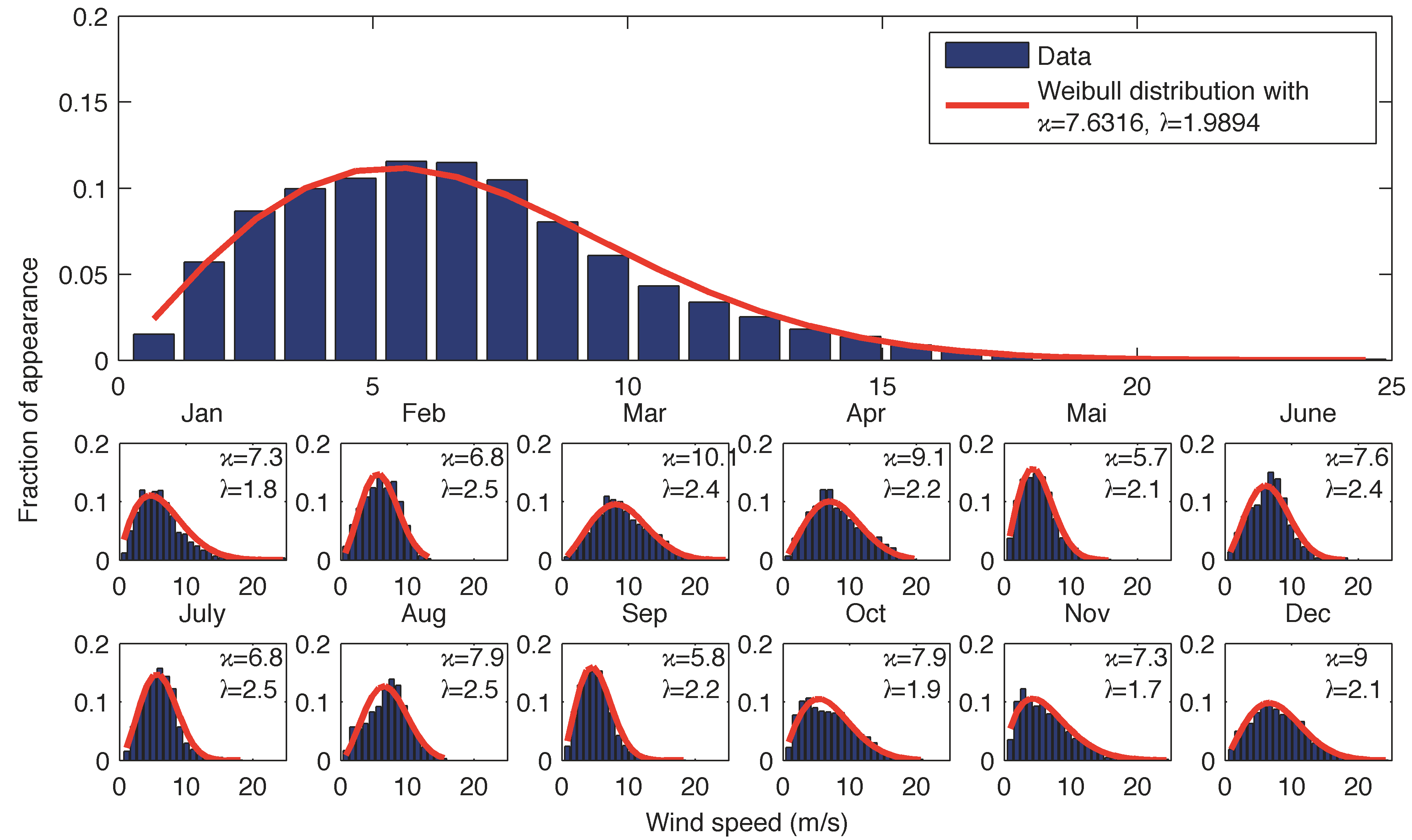
In the first level of analysis, we estimated the parameters of the Weibull distributions that best fit the data for the anemometer station and we overlaid the probability density functions with the histograms of the fraction of measurements falling within a given speed range (Figure 3). Except for the whole dataset, the above process was repeated for all monthly data. Although the 12-month measurements follow a Weibull distribution with a factor close to 2, this is not the case for the monthly data as in several cases the estimated Weibull distributions do not fit the data well.

The wind flow over the terrain was computed using a non-linear 3D Reynolds Averaged Navier-Stokes model in combination with a Re-Normalisation Group (RNG) $k$-$\epsilon$ model [37] to model the turbulence in the flow. Wind flow across the terrain was obtained by CFD simulations. More precisely, a gridded version of the wind farm site was considered, that was constructed after applying a 10m square mesh. Moreover, wind direction was discretized into 16 bins of equal width $\left\{0^{\circ}, 20^{\circ}, \ldots, 360^{\circ}\right\}$. Wind flow was computed for each direction. For each cell in the square mesh the average annual wind speed per direction is considered for the optimization step.

2.4. Wake modeling

One of the simplest and most efficient wake models is the one introduced by Jensen [13,12]. The model assumes that the wake behind a turbine has a diameter that spreads linearly as a function of the downwind distance, starting with a diameter equal to the turbine diameter. Formally, the diameter of the wake at distance $x$ from the turbine along the wind direction is given by

$$\begin{equation} D_x=D+2kx \end{equation}$$

(4)

where $k$ is the wake decay coefficient and $D$ the diameter of the turbine. The velocity inside the wake zone is assumed to be constant and at a distance $x$ from the turbine it is given by:

$$\begin{equation} v_x=v_0\left(1-\frac{1-\sqrt{1-C_t}}{\left(1+\frac{2kx}{D}\right)^2}\right)=v_0\left(1-\frac{1-\sqrt{1-C_t}}{\left(1+k\frac{x}{R}\right)^2}\right) \end{equation}$$

(5)

where $v_0$ is the wind speed at the turbine, $C_t$ is the thrust coefficient of the turbine, i.e. the amount of energy that the turbine extracts from the wind, and $R=\frac{D}{2}$ the radius of the turbine. To compute the wake effect of a turbine to another the overlap $A_o$ of the wake zone with the rotor swept area $A$ of the affected turbine should be calculated at the location of the latter. Assuming a flat terrain and turbines of the same height we can distinguish three cases depending on the relative locations of the turbines:

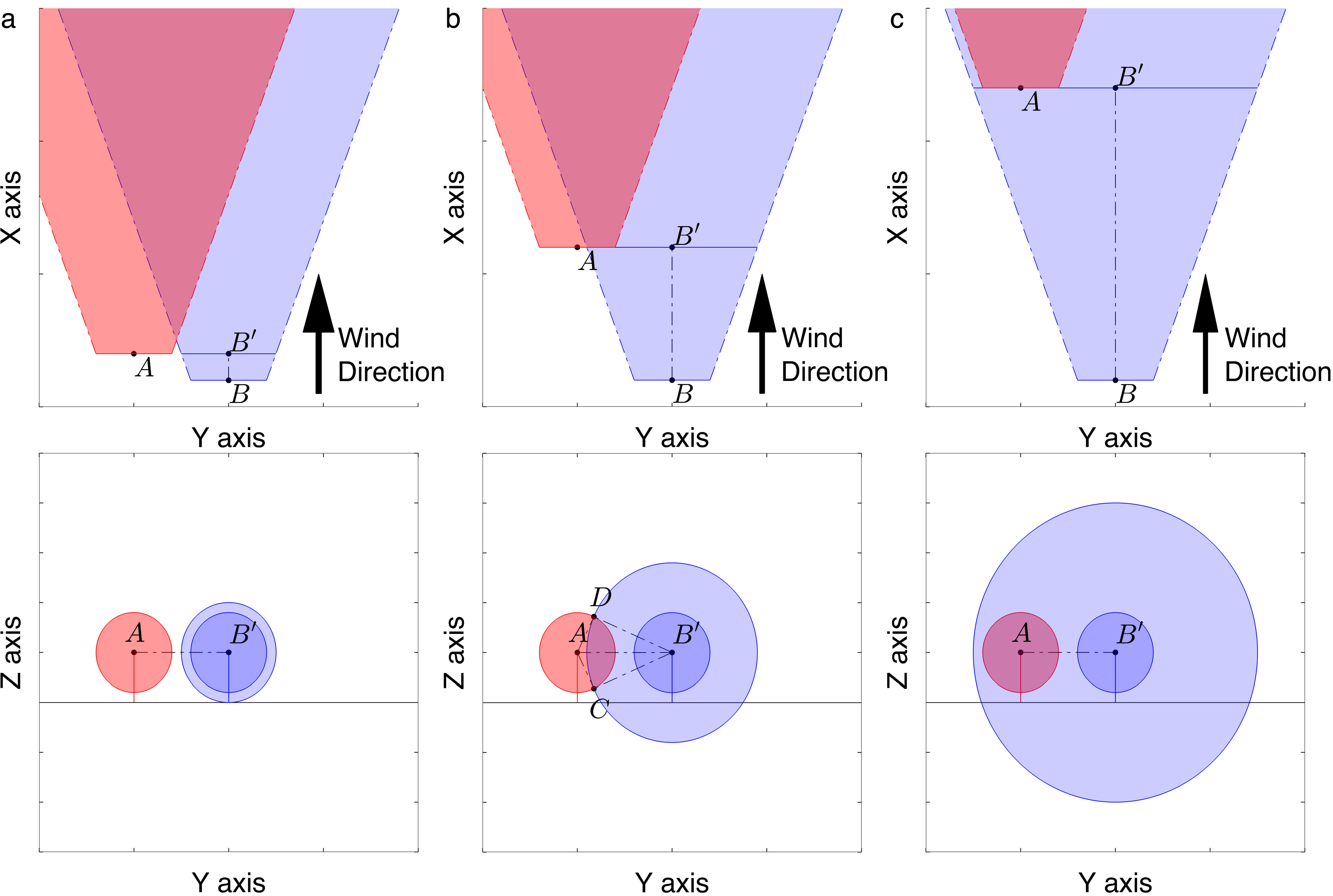
· No overlap or out of wake (Figure 4A). When the distance between the position of the turbine affected by the wake ($T_1$) and the projection of the position of the turbine causing the wake to the plane that is perpendicular to wind direction and passes from the point $T_1$ ($T_2^{\prime}$) is greater or equal to the sum $R+\frac{D_x}{2}$, there is no overlap between the rotor swept area $A$ and the wake zone area $B$. In this case $A_o=0$.

· Complete overlap or full wake (Figure 4C). If the distance between $T_1$ and $T_2^{\prime}$ is less or equal to the difference $\frac{D_x}{2}-R$, then the rotor swept area $A$ is completely covered by the wake zone area $B$. Clearly, in this case $A_o=\pi R^2$.

· Partial overlap or partial wake (Figure 4B). In the last case we have $\frac{D_x}{2}-R \leq d_{T_{1}T_{2}^{\prime}} \leq \frac{D_x}{2}+R$, and the two areas partially overlap. The overlap area is given by

$${{A}_{o}}={{A}_{\overset\frown{{{T}_{1}}DC}}}+{{A}_{\overset\frown{{{T}_{2}}DC}}}-{{A}_{\widehat{{{T}_{1}}C{{T}_{2}}}}}-{{A}_{\widehat{{{T}_{1}}D{{T}_{2}}}}}$$

(6)

where ${{A}_{\overset\frown{{{T}_{1}}DC}}}$ and ${{A}_{\overset\frown{{{T}_{2}}DC}}}$ are the areas of the circular sectors $T_1DC$ and $T_2DC$, while $A_{\widehat{T_1CT_2}}$ and $A_{\widehat{T_1DT_2}}$ are the areas of the two triangles $T_1CT_2$ and $T_1DT_2$. For more details about the calculations the reader is refered to [4].

Finally, the velocity deficit due to the wake effect is:

$$\delta {{v}_{x}}={{v}_{0}}(x)-{{v}^{\prime }}(x)=\frac{{{A}_{o}}}{\pi {{R}^{2}}}\left( {{v}_{0}}(x)-{{v}_{x}} \right)$$

(7)

where $v^{\prime}(x)$ is the effective wind speed at the affected turbine, and $v_0(x)$ is the wind speed at the affected turbine under free-stream conditions. In a wind farm with several wind turbines the wake effect at each turbine is computed based on the assumption that the kinetic energy deficit of several wakes is equal to the sum of the energy deficits for each wake [13], i.e:

$$\begin{align} & {{\left( {{v}_{0}}({{x}_{i}})-{{v}^{\prime }}({{x}_{i}}) \right)}^{2}}=\sum\limits_{j=1, j\ne i}^{n}{{{\left( {{v}_{0}}({{x}_{i}})-v_{j}^{\prime }({{x}_{i}}) \right)}^{2}}} \\ & =\sum\limits_{j=1, j\ne i}^{n}{{{\left( \frac{A_{o}^{j}}{\pi {{R}^{2}}}\left( {{v}_{0}}({{x}_{i}})-v_{{{x}_{i}}}^{j} \right) \right)}^{2}}}\Rightarrow \\ & {{v}^{\prime }}({{x}_{i}})={{v}_{0}}({{x}_{i}})-\sqrt{\sum\limits_{j=1, j\ne i}^{n}{{{\left( \frac{A_{o}^{j}}{\pi {{R}^{2}}}\left( {{v}_{0}}({{x}_{i}})-v_{{{x}_{i}}}^{j} \right) \right)}^{2}}}} \end{align}$$

(8)

In this study we used an adapted Jensen wake model, which has been previously proposed to model wake effects in complex terrains [4]. In the adapted model, it is assumed that the centerline of the wake zone follows the surface of the terrain along the wind directions, and the diameter of the wake zone and the speed deficit depend on the traveling distance of the wake, i.e. the curved distance between the wind turbines along the wind direction. In fact the main difference with the original model is in equation (4), which now becomes:

$$\begin{equation} D_x=D+2ks \end{equation}$$

(9)

where $s$ denotes the curved distance. In [4] a rather simple terrain was considered and only two wind directions were used. Regarding the terrain a gaussian-shaped ridge is used. The height of the surface depends only on the position along the x-axis. Moreover, both wind directions were along the x-axis ($0^{\circ}$ and $180^{\circ}$). The above mean that the centerlines of the wake effects and the wind turbines affected by the wake are at the same height and thus the distance between the wake centerline and the rotor center was computed along the y-axis only.

The present paper is focused on a more realistic scenario. First of all the area is considerably more complex than the one considered in [4]. Moreover, we considered $16$ wind directions instead of $2$. The higher number of wind directions and the terrain complexity introduce additional complexity to the wake effect computation. For each direction the terrain has to be rotated so as the x-axis to be parallel to the wind direction. Then, for each pair of wind turbines: (a) the upwind turbine is projected to the transversal plane passing from the downwind turbine, (b) the projection vector is rotated back to the unrotated terrain, and (c) the curved distance between the two wind turbines is computed using interpolation. It is important to note that in the current study the distance between the rotor center and the wake zone center is computed on the rotated y-z plane, as the centerlines of the wake effects and the wind turbines affected by the wake may not be at the same height. Given that the wind speeds and directions are computed for discrete bins, the integrals in equation 2 can be approximated by the Riemann sum.

It is important to note that while wake effects should be computed for each possible wind speed and direction, in this study only the average wind speeds per direction were considered. Moreover, we pre-computed the annual produced energy for each position in the terain using the power curve of the wind turbine (Section 3) and we computed the produced energy after the wake effects by taking into account that the power output is proportional to the cube of the wind speed:

$$\frac{{{E}^{\prime }}({{x}_{i}})}{{{E}_{0}}({{x}_{i}})}\propto \frac{{{v}^{\prime }}{{({{x}_{i}})}^{3}}}{{{v}_{0}}{{({{x}_{i}})}^{3}}} \begin{matrix} (8) \\ \Rightarrow \\ \end{matrix}\propto {{\left( 1-\sqrt{\sum\limits_{j=1, j\ne i}^{n}{{{\left( \frac{A_{o}^{j}}{\pi {{R}^{2}}}\left( 1-\frac{v_{{{x}_{i}}}^{j}}{{{v}_{0}}({{x}_{i}})} \right) \right)}^{2}}}} \right)}^{3}}$$

where $E_0(x_i)$ and $E^{\prime}(x_i)$ correspond to the energy produced in position $x_i$ before and after the wake effect respectively.

2.5. Optimization Algorithm

The layout optimization problem was solved using the CMA-ES algorithm [9]. CMA-ES is an evolutionary algorithm that creates populations of solutions using a multivariate normal distribution. The mean and the covariance matrix of the distribution are adapted at each iteration based on a subset of best performing, in terms of the objective function, solutions. The algorithm stops when some stopping criteria are met. More precisely, lets assume we want to find the vector $\hat{\mathbf{x}} \in \mathbb{R}^n$ that minimizes the obejctive function $f: \mathbb{R}^n \to \mathbb{R}$, i.e. $\widehat{\mathbf{x}}=\arg {{\min }_{\mathbf{x}\in {{\mathbb{R}}^{n}}}}f(\mathbf{x})$. In each iteration the algorithm samples $\lambda$ solutions from a multivariate normal distribution:

$$\begin{array}{*{35}{l}} \mathbf{x}_{(t)}^{i}\ & \tilde{\ }\ \mathcal{N}({{m}_{(t-1)}}, \sigma _{(t)}^{2}{{C}_{(t-1)}}) \\ {} & \tilde{\ }\ {{m}_{(t-1)}}+{{\sigma }_{(t-1)}}\mathcal{N}(0, {{C}_{(t-1)}})\qquad \text{for }i=1, \ldots , \lambda \\ \end{array}$$

(10)

where $m_{(t-1)}$ is the mean, $\sigma_{(t-1)}$ the step size, and $C_{(t-1)}$ the covariance matrix for iteration $t-1$. The objective function $f(\mathbf{x}_{(t)}^i)$ is then calculated for each randomly generated solution $i$ and the solutions are sorted according to their fitness.

$$\begin{equation} f\left(\mathbf{x}_{(t)}^{(i)}\right) < f\left(\mathbf{x}_{(t)}^{(j)}\right) \Leftrightarrow i < j \end{equation}$$

(11)

The new mean value $m_{(t+1)}$ is computed by a weighted sum of the $\mu$ best solutions

$$\begin{equation} m_{(t+1)}=\sum_{k=1}^{\mu} w_k \mathbf{x}_{(t)}^{(k)} \end{equation}$$

(12)

where $w_1 \geq w_2 \geq \ldots \geq w_{\mu} > 0$ and $\sum_{k=1}^{\mu} w_k = 1$. The covariance matrix $C_{(t+1)}$ and the step size $\sigma_{(t+1)}$ are updated using equations (13-16).

$${{p}_{{{\sigma }_{(t+1)}}}}=(1-{{c}_{\sigma }}){{p}_{{{\sigma }_{(t)}}}}+\sqrt{\left( {{c}_{\sigma }}(2-{{c}_{\sigma }}) \right){{\mu }_{eff}}}C_{(t)}^{-1/2}\frac{{{m}_{(t+1)}}-{{m}_{(t)}}}{{{\sigma }_{(t)}}}$$

(13)

$${{p}_{{{c}_{(t+1)}}}}=(1-{{c}_{c}}){{p}_{{{c}_{(t)}}}}+\sqrt{\left( {{c}_{c}}(2-{{c}_{c}}) \right){{\mu }_{eff}}}\frac{{{m}_{(t+1)}}-{{m}_{(t)}}}{{{\sigma }_{(t)}}}$$

(14)

$${{\sigma }_{(t+1)}}={{\sigma }_{(t)}}\exp \left( \frac{{{c}_{\sigma }}}{{{d}_{\sigma }}}\left( \frac{\|{{p}_{{{\sigma }_{(t+1)}}}}\|}{E\|\mathcal{N}(0, I)\|}-1 \right) \right)$$

(15)

$${{C}_{(t+1)}}=(1-{{c}_{cov}}){{C}_{(t)}}+\frac{{{c}_{cov}}}{{{\mu }_{cov}}}{{p}_{{{c}_{(t+1)}}}}p_{{{c}_{(t+1)}}}^{T}+{{c}_{cov}}\left( 1-\frac{1}{{{\mu }_{cov}}} \right)\sum\limits_{k=1}^{\mu }{{{w}_{k}}}\frac{\mathbf{x}_{(t)}^{(k)}-{{m}_{(t)}}}{{{\sigma }_{(t)}}}{{\left( \frac{\mathbf{x}_{(t)}^{(k)}-{{m}_{(t)}}}{{{\sigma }_{(t)}}} \right)}^{T}}$$

(16)

Equations (13, 14) correspond to two evolution paths that are used to capture the direction of the movement of the mean throughout the process. For more details on the algorithm and the default parameters, which were used it this study too, the reader is referred to [9]. It is important to note that stopping criteria should be defined to terminate the algorithm. The most common criteria are the number of interations, i.e. optimization stops after a pre-defined number of populations, the score threshold, i.e. optimization stops if the value of the objective function is below a pre-defined threshold, or fitness/variables stagnation, i.e. optimization stops when the changes in fitness function are very small or the step size becomes very small. In this study the latter ones were used.

2.6. Objective function

The objective function we consider falls into the class of profit functions. The objective of profit functions is to maximize net gains during turbine lifetime. The following profit function was proposed in [22]:

$$\begin{equation} p_e \cdot TEP - C_D - C_M - (C_f+C_g)\left(1+\left( \frac{r_l-r_i}{N_L}\right)\right)^{X\cdot N_l} \end{equation}$$

(17)

where $p_e$ is the energy price, $TEP$ the total energy produced during the wind turbines lifetime $X$, $C_D$ the degradation cost of the turbines, $C_M$ the maintenance costs, $C_f$ and $C_g$ the future value of the park and elctircal grid investments, $r_l$ and $r_i$ the inflation and interest rates, and $N_L$ the number of interests payments per year. Clearly the above function is very comprehensive but a significant number of parameters is required for its evaluation. We used a simplified version that considers only the total income from energy production and the costs of construction and maintenance. We assumed that the lifetime of a wind turbine is $X=20$ years, the price of energy is $p_e$=0.2$/kWh, the cost of a wind turbine is $C=3\cdot 10^6$$, and the annual maintenace cost per wind turbine is m=1.5% of the wind turbine cost. Therefore the objective function becomes:

$$\begin{equation} f(\mathbf{x})= C \cdot N_w +X\cdot N_w \cdot m \cdot C - p_e \cdot X \cdot AEP(\mathbf{x}) \end{equation}$$

(18)

where $N_w$ is the number of wind turbines, and AEP the annual energy production after taking into account the wake effects in kWh that depends on the location of the wind turbines.

2.7. Turbine Siting Constraints

WFLO is in general a constrained optimization problem. Constrains are introduced to avoid infeasible layouts due to improper positioning of the turbines. Here we consider the following constraints:

· Sampling space constraint: We consider a recangular farm. The length of each side is 5km. The turbine can be positioned in any point within the farm.

$$\begin{equation} \mathbf{x}_i \in [0, 5000] \end{equation}$$

(19)

In some cases we also consider a $10\times10$ square grid that divides the terrain in 100 possible turbine positions. In each grid cell we can place at most one turbine. The turbine can be positioned in any point within the cell. The locations of the borders of each cell define the upper and lower bounds for each variable. If we assume a search variable of the form $\left[x_1, y_1, x_2, y_2, \ldots, x_{100}, y_{100}\right]$ the constraint becomes:

$${{\mathbf{x}}_{i}}\in \left\{ \begin{matrix} \left[\left( i/2-1 \right)\cdot 500, i/2\cdot 500 \right] & \text{ }, \text{if} i is \text{even} \\ \left[\left( i/10-1 \right)\cdot 500, i/10\cdot 500 \right] & \text{ }, \text{if} i is \text{odd} \\ \end{matrix} \right.$$

(20)

· Turbine distance constraint: In most studies a minimum inter-turbine distance is defined. One of the main reasons for this proximity constraint is the high turbulence intensity in the near wake zone that can damage the turbine. For this reason the minimum allowed distance is usually set to 3 rotor diameters [3,26,38].

$$\begin{equation} \sqrt{((x_{2(i-1)+1}-x_{2(j-1)+1})^2+(x_{2i}-x_{2j})^2)} \geq 6R \qquad \forall i, j=1, \ldots, N_w \mbox{ and } i \neq j \end{equation}$$

(21)

· Terrain slope constraint: The slopes of the terrain in the study area range from $1.5^{\circ}$ to $44.5^{\circ}$. Such a big range of slopes is expected in mountainous terrains. Locations with a slope above $20^{\circ}$ are usually considered improper for wind turbine installation [11]. In [29,30,4] terrain slopes were not taken into consideration. Here we impose a terrain slope constraint.

Optimization constraints can be classified as either “hard” or “soft”. In the first case the conditions that correspond to the constraints have to be satisfied by the variables, while in the latter case variables that violate a constraint are penalized in the objective function. From the aforementioned constraints, turbine proximity could be considered as a “soft” constraint if one could estimate turbulence intensity. This is not the case here so all constraints are considered as “hard”. A way to model “hard” constraints in CMA-ES is by rejecting all solutions that violate them. Although, such an approach would guarantee that all solutions evaluated are feasible, it significantly affects the convergence of the algorithm as the majority of the sampled solutions would be rejected without evaluation. Thus the search space is explored very slowly. An alternative solution is to transform unfeasible solutions to feasible ones. For instance, one could map turbines that are placed outside the sampling space back into it or to completely remove them from the candidate solution considering only the remaining valid positions. An advantage of the latter case is that the number of turbines can vary and thus there is no need do define the exact number of wind tubines but a maximum number of them. Nevertheless, such an approach also affects the performance of the optimization algorithm as different candidate solutions may be assigned the same score if they are mapped to the same feasible solution. In the present study we used the aforementioned approach for the sampling space and terrain slope constraints, while the turbine distance constrained was treated as a hard constraint. More precisely, if in a candidate solution there are turbines positioned outside the sampling space or on a location with a high terrain slope then they are removed from the solution, which is then evaluated based on the remaining turbines. In the case that there are turbines that are positioned closer than 3 rotor diameters then the whole solution is discarded and a new one is generated.

3. Results

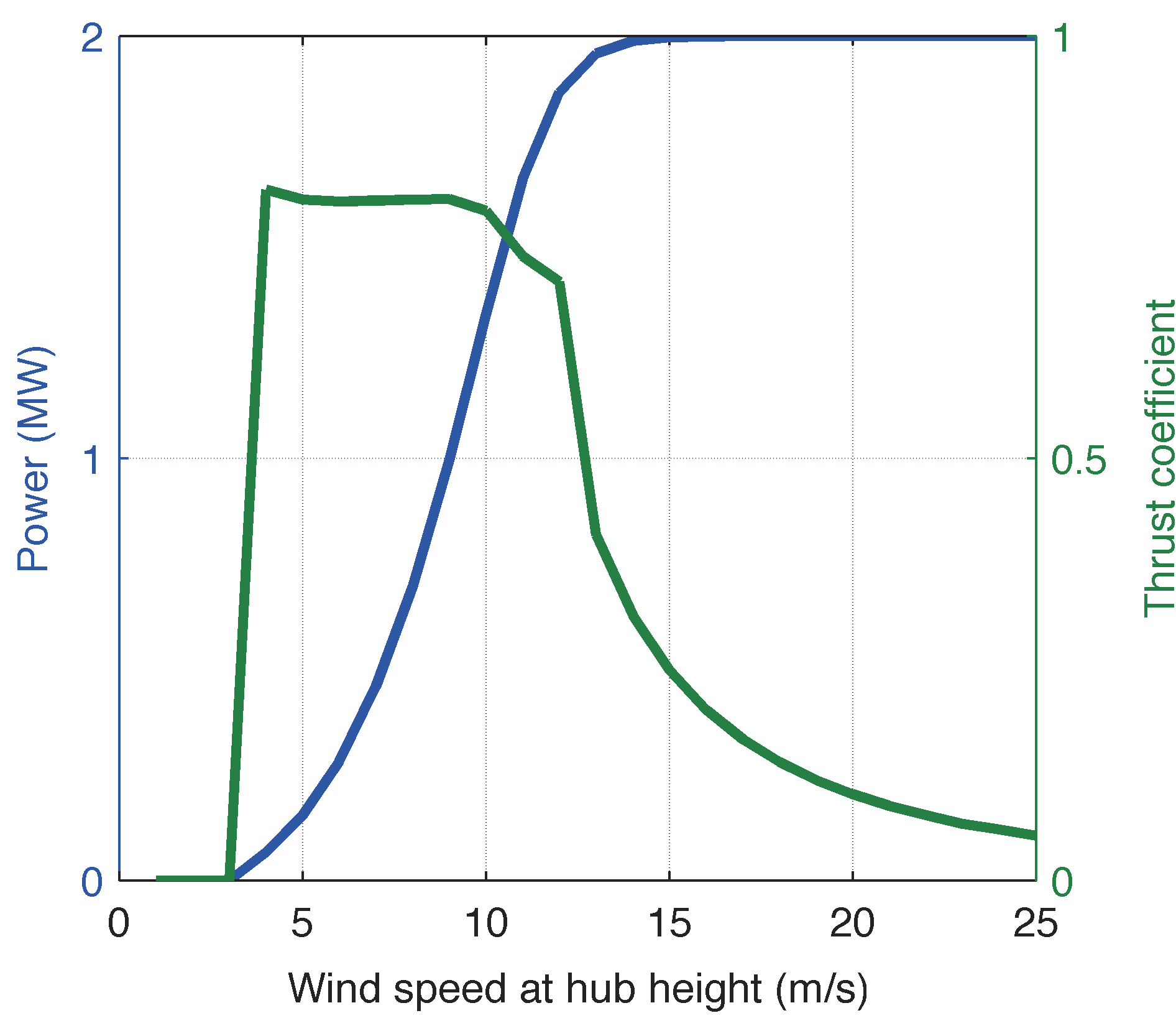
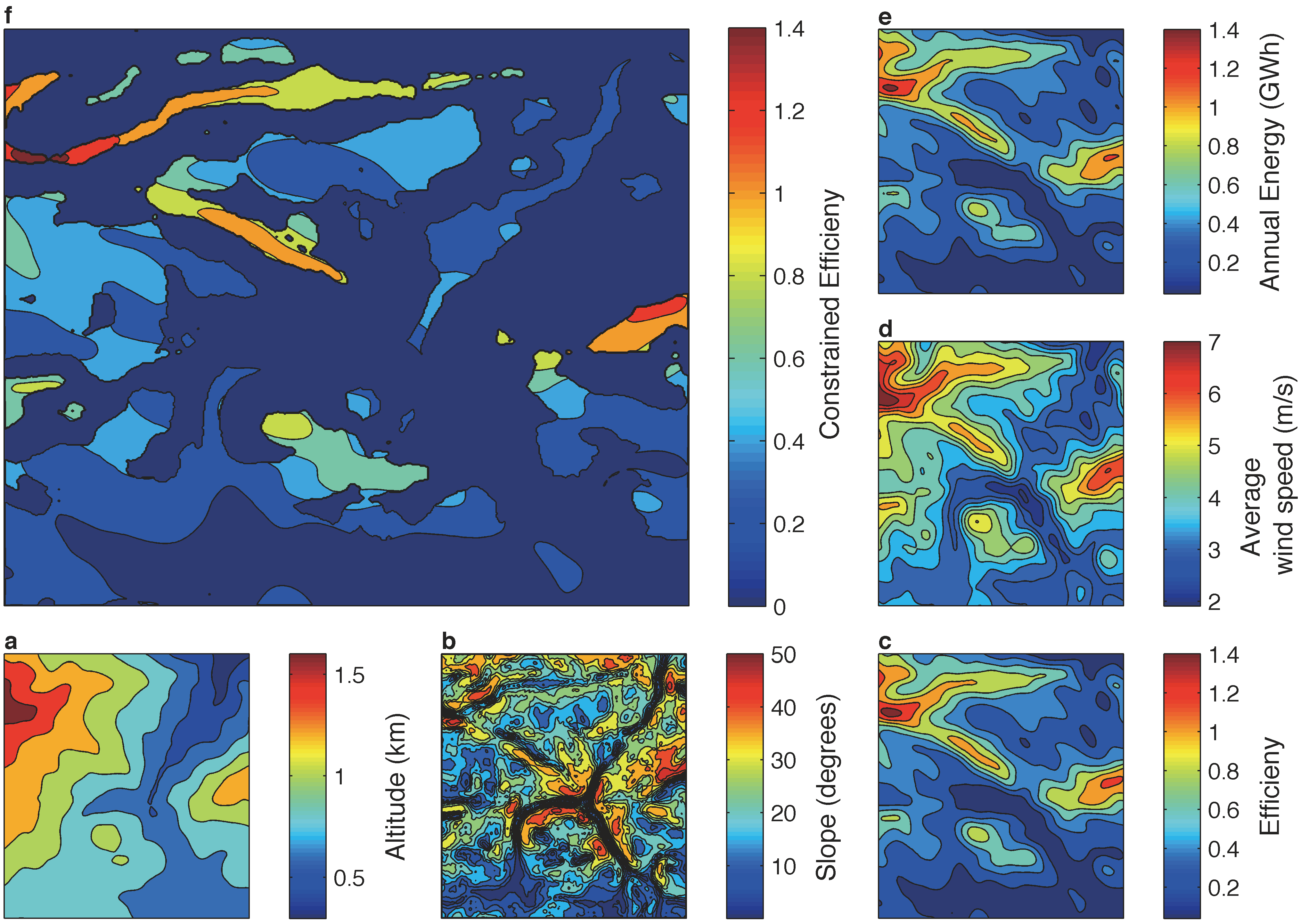
For our study the Vestas V80 wind turbines were used for the computation of the annual produced energy. These WT have a rated power of 2 MW, the diameter of the rotor is 80m and the cut-in and cut-off wind speeds 3 and 25 m/s respectively. In Figure 5 the power curve and the coefficient thrust of the WT are shown. Before optimizing the layout we aimed at evaluating the complexity of the problem by computing some important parameters across the terrain. One of the constraints that significantly affects the search space is the maximum terrain slope, which is $20^{\circ}$. While this is not a problem for smooth terrains in our case only 25% of the total area has a slope below $20^{\circ}$ (Figure 6b), considerably restricting the feasible search space. Moreover, a big part of the study area is characterized by low wind speeds (Figure 6d). Using the computed wind speeds we calculated for each position in the terrain the annual energy production using the power curve of the wind turbine (Figure 6e). Using the pre-computed annual energy production we calculated for each position in the terrain its efficiency, which is defined by:

$$\begin{equation} \mathrm{efficiency}(x, y)=\frac{p_e \cdot X \cdot AEP(x, y)}{C \cdot N_w +X\cdot N_w \cdot m \cdot C} \end{equation}$$

(22)

In Figure 6c a contour plot of the efficiency is shown. Clearly, the objective function (18) can be minimized by selecting locations with efficiency above 1. However, the 95% of the search area has an efficiency below 1. Finally, a constrained efficiency was computed by setting the efficiency of all positions with a slope above $20^{\circ}$ to 0. Only 2.5% of the study area has a constrained coefficient above 1 (Figure 6f). This preliminary analysis highlights the main difficulties of the WFLO problem for onshore complex terrains. In the following we investigate whether CMA-ES can find an optimal solution despite the inherent complexity of the problem.

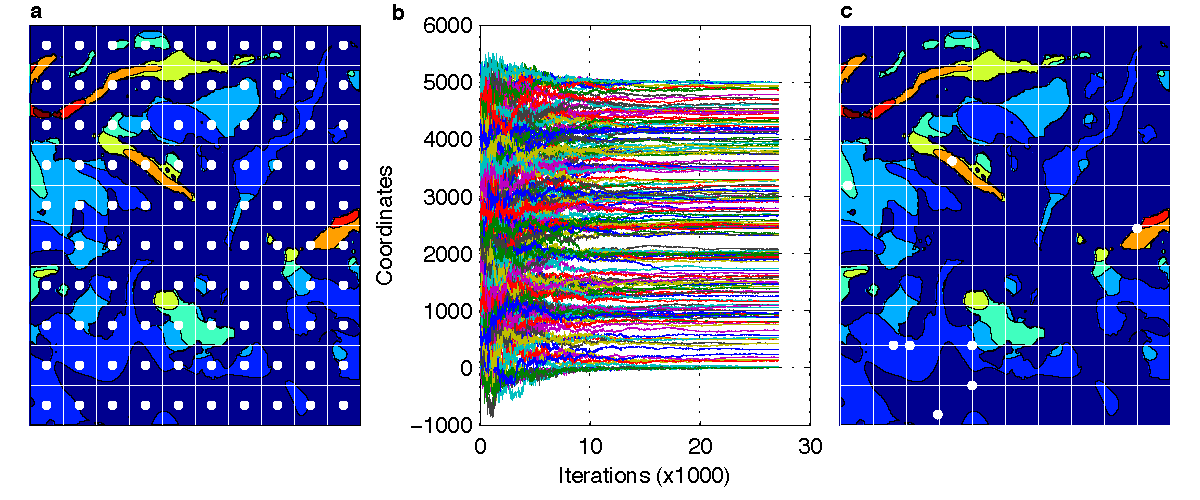
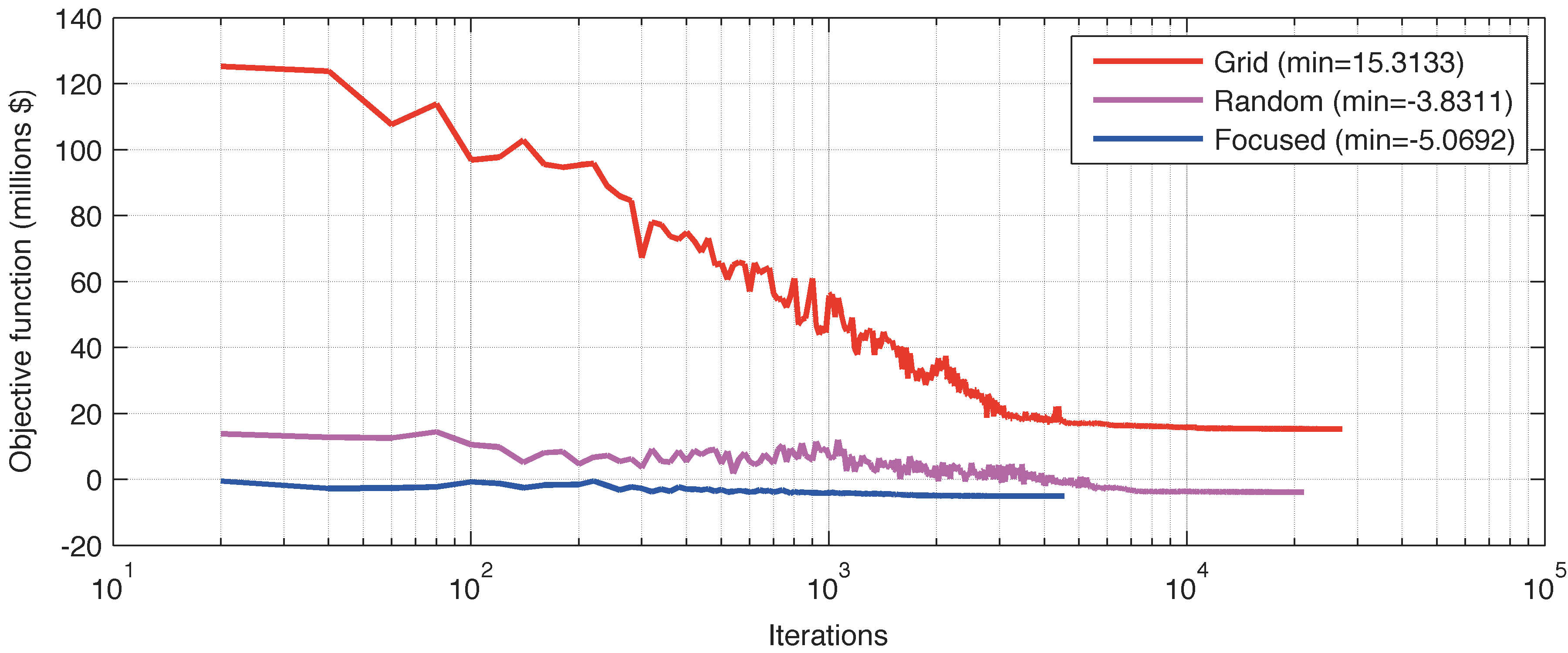
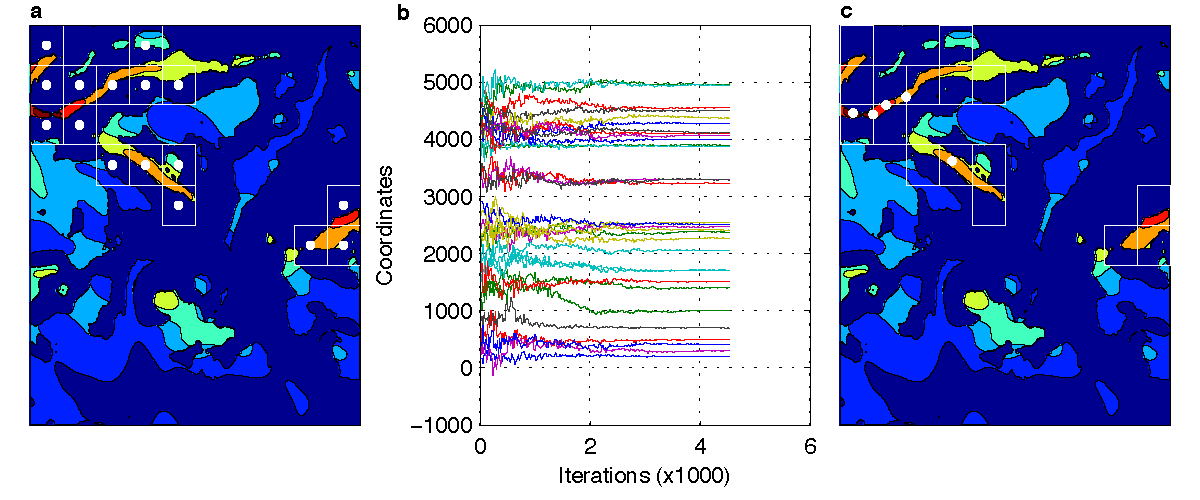
For the first iteration of CMA-ES algorithm, the mean and the standard deviation of the multivariate normal distribution have to be selected for the extraction of the first population of solutions. The selection of $m_{(0)}$ and $\sigma_{(0)}$ is not trivial. We investigated three different scenarios. In the first scenario, hereafter denoted as grid scenario, the search space was discretized by applying a $10 \times 10$ grid on the terrain. Each square cell has a width of 500m. The discretization of the search space is a common approach in the offshore WFLO. The size of the cell was selected based on the proximity constraint (6R=240m). When cells of smaller size were used many infeasible solutions were selected from the algorithm during the first iterations delaying convergence significantly. The coordinates of the center of each cell were selected as the initial mean $m_{(0)}$ (Figure 7a) and the initial standard deviations $\sigma_{(0)}$ where equal to one third of the cell width, i.e. $\frac{500}{3}$m. Therefore the maximum number of wind turbines is 100. Starting from this initial solution almost 30000 populations of size $\lambda=20$ are needed before convergence (Figure 7b). Despite the increased number of iterations several high efficiency locations were not included in the final solution (Figure 7c), which consists of 8 turbines. This is also evident from the final score (Figure 10). It is important to note that positive evaluations of the objective function correspond to layouts for which the investement is bigger than the income from the energy production.

In the second scenario, denoted as random scenario, we consider the whole search space without applying a grid. The maximum number of wind turbines is reduced to 30. Initially all turbines are placed on the center of the search space (Figure 8a) and for each coordinate a standard deviation of one third of the search space width is selected, i.e. $\frac{5000}{3}$m. The algorithm converges after around 20000 iterations (Figure 8b) providing a better solution (Figure 10) than the grid scenario. The number of wind turbines in the final solution is 4 (Figure 8c). A possible reason for the decreased number of iterations needed despite the improved prediction may be the smaller number of wind turbines in comparison with the grid scenario. However, at the same time the search space for each variable is 10 times bigger that the search space in the previous case. On the other side, in the grid approach wind turbines coordinates are limited into a specific cell, for which it is not guaranteed that an efficient position exists (i.e. with efficiency above 1). Although, a non feasible location could be selected the existence of such a location is not guaranteed too. Therefore, by enforcing each cell to be occupied by a WT we come across cases that a WT is “trapped” in a cell with no optimal or unfeasible solution available.

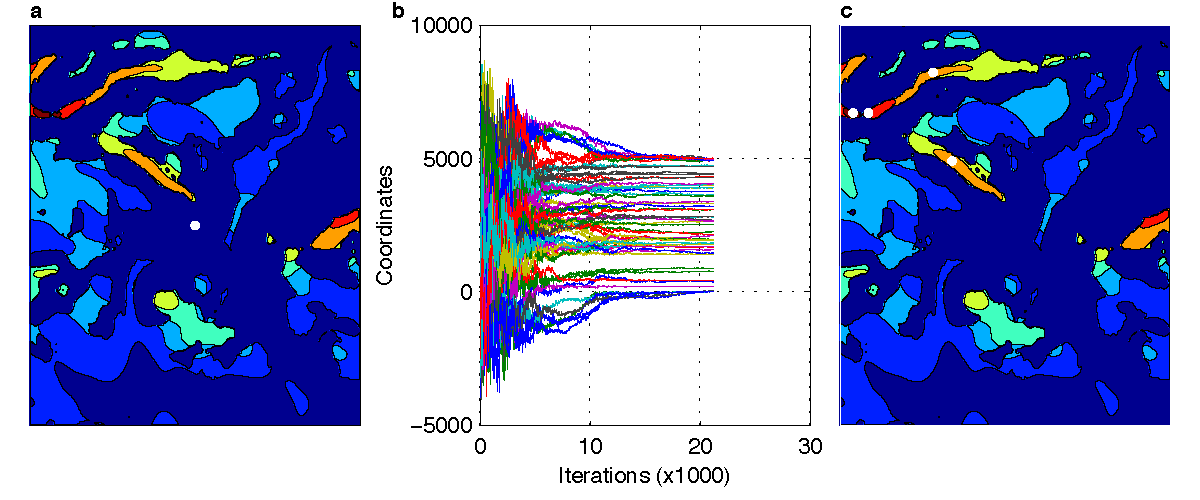
In the last case, that corresponds to a focused search scenario, we tried to overcome the above limitation of the grid approach exploiting a priori knowledge about the search space. The search space was again discretized but wind turbines could be positioned only in cells that contain areas with a constrained efficiency above 1. By focusing the search in these areas not only the size of the search space is considerably decreased but also for each wind turbine exists a location in its proximity for which the objective function is reduced, at least before taking into account the wake effects. The maximum number of wind turbines goes down to 16 and they are initially placed in the center of each cell (Figure 9a). The initial standard deviation is again one third of the size of each cell. After around 4000 iterations the algorithm converges to its final solution with only 5 out of the 16 turbines placed in a feasible location (Figure 9b,c). Both the convergence speed and the score of the final solution are improved in comparison to the previous approaches (Figure 10).

Increase of the population size has been previously reported to provide better results. Here this does not seem to be the case as repeating the random and focused search scenarios with a population size 60 did not improve the results. In both cases the best attained objective function was -3.72 and a higher number of iterations was needed, around 10000 and 40000 iterations for the random and focused scenario respectively.

4. Conclusions

We proposed a photogrammetric procedure to reconstruct high-resolution Digital Elevation Models from remote sensing data, e.g. aerial photographs. The procedure can be used to create 3D terrain models of areas for which on site measurements are not possible. We have applied the approach to design an onshore wind farm in a mountainous area in Southern Greece. Wind measurements were collected for a one-year period and wind flow was computed using a non-linear 3D RANS model. A linear model was used for the wake effects and an evolutionary optimization strategy, CMA-ES, for optimal wind turbine placement.

The use of a real mountainous area allowed us to highlight some of the difficulties with WFLO in onshore complex terrains. Most of these difficulties result from the high complexity of the terrain in combination with some restrictions in wind turbine installation. The above can render several optimization strategies that have efficiently been used for WFLO in offshore or flat terrain onshore areas inadequate for complex terrains. For instance, binary-coding GA approaches that place the turbines in the center of each grid cell would not be efficient due to the increased number of infeasible locations. To overcome these limitations, a priori information about the objective function and the search space can be used to improve the performance of the optimization algorithms. In the current case, the pre-computation of the annual energy production for each location of the terrain and its use to guide the search space exploration not only resulted in the identification of better layouts but also in a considerable reduction of the computational time. While this initial step is also computationally expensive, the calculations can be parallelized exploiting the capabilities of high-computing clusters that exist nowadays.

In the current study, the average value of the wind speed was used for each direction. In a more realistic scenario both wind speed and direction could be extracted from a wind rose, and an expected value criterion could be optimized instead. This would lead to more accurate estimation of the annual energy production and would improve the optimization output. Moreover, a more complicated wake model may provide better wake effect predictions. Nevertheless, we do not expect that our observations, regarding the challenges that complex terrains pose to optimization algorithms, will significantly change. Future work should consider more complicated wind scenarios, and investigate how other optimization algorithms like PSO or MCMC perform in complex terrains.

Acknowledgments

This work was supported by the Greek General Secretariat for Research and Technology (www.gsrt.gr) research program WiFoSAK.

Conflict of interest

All authors declare no conflicts of interest in this paper.