1. Introduction
Climate change is expected to exacerbate current stresses on water resources due to, for instance, population growth, land-use changes and urbanisation. Changes in precipitation and temperature lead to changes in runoff and water availability and hydrological models are extremely useful in predicting these changes [1]. However, one must account for the large uncertainties associated with forecasting discharge with such hydrological models. Hydrological models differ in their complexities. In a case study, Orth, et al.
[2] investigated model performance with respect to model complexity and concluded that added complexity does not necessarily lead to improvement in model performance, as performance can vary widely depending on the hydrological variables (e.g. runoff vs. soil moisture) or hydrological conditions (floods vs. droughts) investigated.
Hydrological models are used for a wide range of applications such as water management or flood forecasting [3]. These models use generally simple representations of physical processes within a catchment. A well calibrated hydrological model can give reasonable results for short-term forecasting, but is seldom accurate for forecasting of climate change impacts. There has been always a debate among the hydrological modelling community about the applicability of conceptual and physically based models for climate change studies. Michaud and Sorooshian [4] studied different factors including input data, initial conditions, model assumptions or parameter values, that can affect the accuracy of rainfall-runoff simulations. They found that results from a simple distributed model were just as acceptable as those from complex distributed models. However, when calibration is not performed, a complex model can perform better than a simple model. Ludwig et al.
[5] examined the level of uncertainty when hydrological models of different structure and complexity are driven by the same climatological boundary conditions and demonstrated that a physically-based model ought to be employed for climate change impact assessment. However, physically-based distributed models are difficult to apply because of high data demand, complex process descriptions and wide parameter spaces. To date several hydrological models have been widely used internationally as tools to assess climate change effects in the watersheds of interest. These range from simple conceptual lumped models to physically based distributed models. For example the HBV model [6,7,8,9,10,11,12], HYMOD ([13,14,15,16], Hydromad [17], TOPMODEL [14,16], SWAT [12,18,19], WaSiM-ETH [20,21,22], or TopNet [23,24,25].
For water resources agencies, the level of complexity of hydrological models may limit their applicability due to high data demand and computational cost. On the other hand, simple models may provide adequate results at reduced cost. Hence the choice of either a simple or a complex model should not only be based on sophistication, but also on purpose of utilisation and data availability. For example, physically based distributed models can be useful for detailed assessments of surface flow and other water balance applications, whereas for assessing climate change impacts, a conceptual model may be employed [26].
This study has two main objectives. Firstly, to investigate the consequences (uncertainty) of using simple versus complex hydrological models to predict discharge and to quantify the uncertainty of results owing to differences between such hydrological models. Secondly, to investigate the effects of using simple versus complex hydrological models in climate change studies. The complexity of each hydrological model is defined by (ⅰ) its input data requirements, (ⅱ) the number of parameters and (ⅲ) the level of description of the hydrological processes in the model. Model responses are compared for five hydrological models, ranging from conceptual-lumped to physically-based fully-distributed models, namely HYMOD, HBV, HydroMAD, TopNet and WaSiM-ETH, thereby using data from the Waiokura catchment in the North Island of New Zealand. All five hydrological models of different complexity are used to investigate the effects of climate on catchment hydrology. Three emission conditions (B1, A1B, and A1F1) based on the IPCC Ⅳ publication were studied. Discharges obtained from the hydrological models for the three scenarios were analysed for three different time periods: "current" (1980–1999), "2040 condition" (2030–2049) and "2090 condition" (2080–2099).
2. Study Area and Data
2.1. Study area
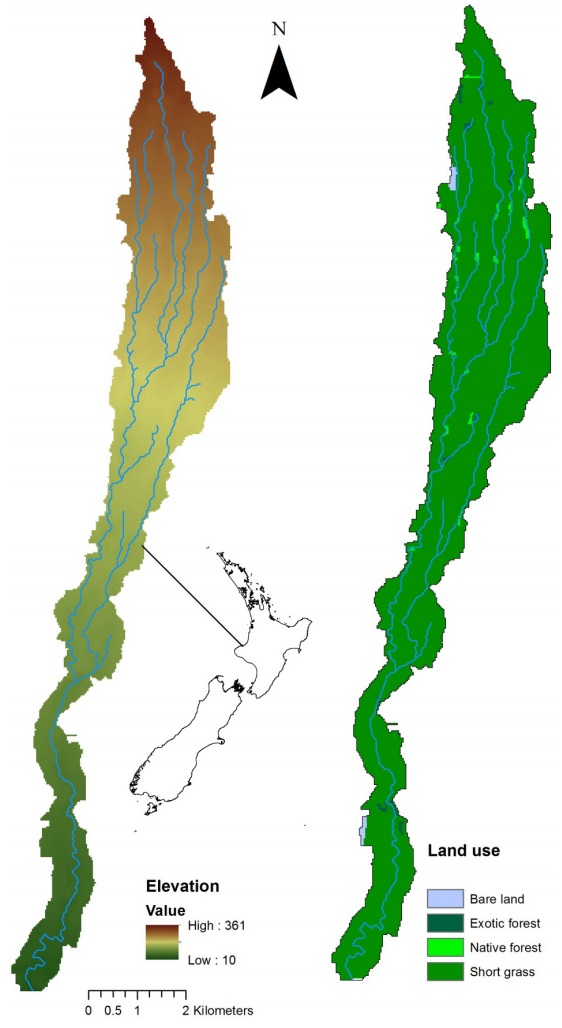
This study was carried out in the Waiokura catchmnet, located on the south-west coast of the North Island of New Zealand (Figure 1). The catchment is exposed to weather systems from the Tasman Sea, with high winds, but few climate extremes. Summer (December, January and February) has least extremes. Extreme events occur rather in winter (June, July and August). The region receives some 2000 hours of sunshine per year [27]. The upper (North) parts of the catchment receive as much as 50% more rainfall than the lower parts with 1800 mm in the headwaters and 1170 mm near the outlet. Annual precipitation is about 1250 mm with more rainfall in winter than summer. Mean temperature is between 21 ℃ and 26 ℃ in the summer and between 10 ℃ and 14 ℃ in the winter. The Waiokura catchment has a very distinct seasonal flow patterns: high in winter and low in summer. The headwaters of this catchment descend steeply from Mount Taranaki, before gradually levelling off towards the coastal plains. The Waiokura catchment is characterised by ephemeral streams and very high drainage density. The catchment has an area of 22.5 km2, and is divided into 31 sub-catchments, defined by first order streams according to the Strahler classification. Physical, climatic and hydrological characteristics of the study area are listed in Table 1.
Table 1. Physical, climatic and hydrological characteristics of the study area.
| Area (km2) |
22.5 |
| Mean elevation (m) |
183 |
| Range elevation (m) |
10–361 |
| Slope (%) |
1–20 |
| Dominant land use (% of wcatchmnet area) |
Grazed dairy pasture (99%) |
| Soil type |
Volcanic origin – Egmont brown loam |
| Prevailing wind direction |
Northwest |
| Monthly average rainfall (mm) |
Summer (Jan-Mar) |
100 |
| Winter (Jun-Aug) |
135 |
| Average air temperature (℃) |
Summer (Jan-Mar) |
21–26 |
| Winter (Jun-Aug) |
10–14 |
| Annual average sunshine (h) |
2000 |
| Rainfall (mm y-1) |
1250 |
| Flow range (m3/s) |
0.026–7.864 |
| Mean flow (m3/s) |
0.469 |
| Median flow (m3/s) |
0.391 |
| 95 percentile flow (m3/s) |
1.042 |
| Specific yield (mm km-2 y-1) |
31.4 |
2.2. Data
Data used in this study include daily rainfall, potential evapotranspiration, vapour pressure, maximum and minimum air temperature, soil temperature, relative humidity, solar radiation, wind speed and soil moisture. Data were obtained from the National Climate Database (CLIDB) and Virtual Climate Station Network (VCSN) of New Zealand. VCSN provides daily climate data interpolated on an approximately 5-km grid covering New Zealand. The interpolation method used is a thin-plate smoothing spline model and is based on data observations from climate stations [28]. The catchment characteristic data were obtained from the River Environment Classification (REC) [29]. REC provides physical characteristics, such as topography, geology and land cover for each New Zealand river network. REC information is available as Geographic Information System (GIS) layer. Geology data were obtained from the Land Resources Inventory, and land cover data from the 1997 version of the Land Cover Database [30].
2.3. Climate change data
General Circulation Model (GCM) simulations prepared by the IPCC Fourth assessment were used to prepare New Zealand climate change scenarios. Twelve global climate models of the IPCC report satisfactorily predict the climate in the New Zealand and South Pacific region. Model changes are statistically downscaled to provide spatial detail over New Zealand [31]. For statistical downscaling, historical observations are used to develop regression equations that relate local climate fluctuations to changes at the larger scale. These historical observations are then replaced by the model changes in the regression equations to produce fine-scale projections [31]. The resolution of the downscaled changes is approximately 5 km by 5 km (on a 0.05° grid) covering New Zealand.
Climate change datasets are related to the 1980–1999 period (1st January 1980 to 31st December 1999) which is abbreviated here as "1990". Climate change effects are investigated for two 20-year future periods: 2030–2049 (1st January 2030 to 31st December 2049), termed "2040" hereafter, and 2080–2099 (1st January 2080 to 31st December 2099), termed "2090" hereafter.
Statistical downscaling is applied to the projections obtained from 12 GCM simulations where emissions follow the A1B "middle-of-the-road" emissions scenario. The A1B scenario gives an intermediate level of warming by the end of the century and has more GCM output data available than any other scenario. Projections from the A1B scenario were rescaled using the known differences on the global scale between the A1B and other scenarios, to produce predictions for each individual emission scenario [31].
For the two future time periods studied here, three greenhouse gas emission scenarios were considered: B1 (low emission, 600 ppm eq-CO2), A1B (medium emission, 850 ppm eq-CO2) and A1F1 (high emission, 1550 ppm eq-CO2).
The A1 scenario assumes a very rapid economic growth, a peak of global population in mid-century and a rapid introduction of new and more efficient technologies. A1 is divided into three groups, where each represents an alternative direction of technological change. We choose just two scenarios of this main scenario: the A1FI scenario that assumes a fossil-fuel intensive future world and the A1B scenario, which assumes a balance across all sources. The B1 scenario assumes the same global population as A1, but describes a world which converges with more rapid changes in economic structures toward service and information economy [32].
For each emission scenario, an average dataset from the 12 GCM simulations was used for hydrological modelling. Each simulation with an emission scenario is then compared with the "1990" baseline simulation, in order to assess the resulting water discharge in the Waiokura catchment according to the chosen emission scenario choice.
3. Methodology
3.1. Hydrological models used
To demonstrate the influence of the choice of a certain hydrological model on forecast uncertainty different hydrological models, which have different representations of process description, parameter space and spatial representation, were employed. Specifically, these are a conceptual lumped model (HYMOD), a semi-distributed conceptual model (HBV), a conceptual lumped model (HydroMAD), a semi-distributed physically-based model (TopNet), and a physically-based distributed model (WaSiM-ETH). Appendix A lists the parameters of each hydrological model. A brief description of each model follows.
3.1.1. HYMOD
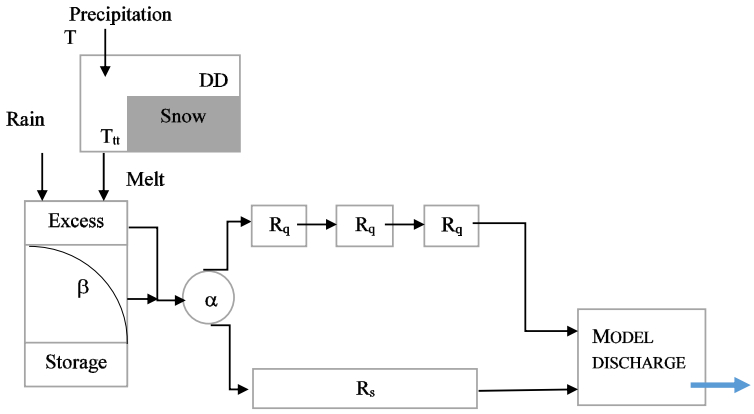
The HYdrologic MODel (HYMOD) is a lumped conceptual model. This model has two main components, rainfall excess and two series of linear tanks in parallel. A modified version of the model was used. A degree day based snow module was added to the model. This module depends on three parameters, which are the degree-day factor DD, precipitation/degree-day relation (Dew) and threshold temperature for snow melt initiation Ttt. Soil moisture content depends on the maximum storage capacity (Cmax) and the degree of spatial variability of soil moisture capacity within the catchment (β). Excess water from the soil zone flows into quick-flow tanks and groundwater, according to a partitioning factor which distributes the flow between a fast reservoir and slow reservoirs (α). The flow is distributed into three linear reservoirs in series which represent the fast runoff component and a slow-flow tank representing groundwater flow in parallel to the other flows. Reservoirs are characterised by their residence times Rs and Rq [13,33]. Figure 2 provides a schematic representation of this model.
3.1.2. HBV
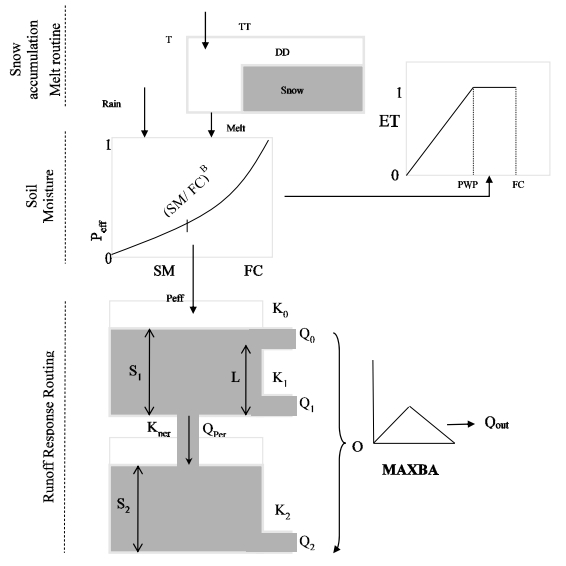
HBV (Hydrologiska Byråns Vattenbalansavdelning) [52] is a conceptual, semi-distributed model, which was developed by the Swedish Meteorological and Hydrological Institute (SMHI). This model has three main components: a snow accumulation and melt routine, a soil moisture accounting routine and a runoff response routine. The snowmelt routine is based on the degree-day method. Soil moisture accounting is achieved by computing an index of wetness of the entire catchment and takes account of interception and soil moisture storage. This routine is based on a modification of the bucket theory, which assumes a statistical distribution of storage capacities in a basin. This routine is controlled by two parameters, a shape coefficient which is the relative contribution to runoff or increase in soil moisture storage from a millimetre of rain or snowmelt and secondly the maximum soil storage in the basin. A model for evapotranspiration takes account of water loss and depends on LP, a parameter which is a soil moisture value above which evapotranspiration reaches its potential value. Runoff generation routing transforms the effective precipitation (i.e. excess water from the soil moisture zone and direct precipitation) to discharge. The runoff routine is based on two conceptual reservoirs, an upper non-linear and a lower linear reservoir, which represent quick runoff and slow runoff, respectively. Routing between sub-basins is calculated using the Muskingum method [34]. A schematic representation of this model is shown in Figure 3.
3.1.3. HydroMAD
The HYDROlogical Modelling Assessment and Development (HydroMAD) [35] is a modelling framework with a range of soil moisture accounting modules and routing functions. The HydroMAD R software package is used in this study. The class of hydrological models considered were spatially-aggregated conceptual models. There are two main components, a Soil Moisture Accounting (SMA) module and a routing or a unit hydrograph module. The SMA module converts rainfall and temperature into effective rainfall, which is converted into streamflow by the routing module (Figure 4).
The nine SMA models presented below, along with the exponential components transfer function as a routing model (EXPUH) [36], are used in this study.
CWI: The IHACRES Catchment Wetness Index (CWI) model uses a temperature-dependent drying rate to estimate a wetness index, which defines the runoff ratio.
CMD: The IHACRES Catchment Moisture Deficit (CMD) model calculates the effective rainfall by taking account of evapotranspiration and catchment moisture deficit. The effective rainfall is calculated from input rainfall by using a mass balance approach [37].
Sacramento model: The Sacramento model was developed by the US National Weather Service. It is the most complex model of the package. Two soil zones, upper and lower, are defined. The upper zone contains interception storage while the lower zone represents the bulk of the soil moisture and longer groundwater storage. In each soil zone, two moisture storages are represented, tension water and free water. A special aspect of the model lies in the representation process of the percolation from the upper zone to the lower zone. Evapotranspiration is computed using each part of the model according to a hierarchy of priorities. A mass balance approach is used to calculate the effective rainfall from lateral drainage that contributes from each of the soil zones [38].
GR4J: The Génie Rural à 4 paramètres Journalier (GR4J) model is a daily lumped four-parameter rainfall-runoff model. Firstly, the net rainfall and net potential evapotranspiration is determined and a production store is filled. The effective rainfall is divided into two flow components: 90% by a unit hydrograph and a non-linear routing store and 10% by a single unit hydrograph. A groundwater exchange is incorporated between the two components [39].
AWBM: The Australian Water Balance Model (AWBM) is a conceptual model. It is developed from concepts of saturation overland flow (i.e. excess rainfall after reaching the surface storage capacity of the catchment) and generation of runoff. Catchments are divided into three different areas with different storage. The effective rainfall is the sum of excess water in each area [40].
BUCKET model: The single-bucket (BUCKET) model takes account of interception, saturation excess runoff and subsurface flow [35].
SNOW: A degree-day snow (SNOW) model is essential in cold regions to estimate the snowmelt input to be used in streamflow forecasting. A daily snowmelt discharge series and an estimate of the water stored in the snow pack are produced in this model [41], which is coupled with the CMD soil moisture model.
Scalar model: The scalar model is a benchmark model which uses a constant runoff ratio. The mass balance with streamflow allows estimation of the constant fraction of rainfall which reaches the stream.
Intensity model: The intensity model uses a runoff ratio generated by raising rainfall to a power. It increases up to a full runoff level.
Runoff ratio model: The runoff ratio model scales the rainfall to a runoff coefficient, estimated by a moving average of the data.
dbm model: The dbm model is the typical initial model used in Data-Based Mechanistic modelling. The observed streamflow raised to a power defines an index of antecedent wetness. Rainfall is scaled by using this index [35].
The dbm and runoff ratio models cannot be used for prediction as the SMA module uses streamflow data. So, they were not used for climate change analysis.
Routing: Routing discharge is an exponential component, transfer function model. It is a linear transfer function which translates an input time series U into an output series X. The unit hydrograph is described by exponential decaying components. Each component is defined by its recession rate, α, and peak response, β. For the SMA models, two components are used, slow and quick components where these components are in a parallel configuration.
The total simulated flow is the sum of the quick and the slow components:
|
$
X\left( t \right) = {X_s}\left( t \right) + {X_q}\left( t \right)
$
|
(1)
|
Where, X is total simulated flow. t is time step. Xs and Xq are simulated quick and slow flow respectively.
The slow and quick flows are defined respectively by:
|
$
{X_s}\left( t \right) = { \propto _s}{X_s}\left( {t - 1} \right) + {\beta _s}U\left( t \right)
$
|
(2)
|
|
$
{X_q}\left( t \right) = { \propto _q}q\left( {t - 1} \right) + {\beta _q}U\left( t \right)
$
|
(3)
|
These parameters can be interpreted in terms of time constants τ and fractional volumes, v, and are defined as:
|
$
\tau = \frac{{ - 1}}{{{\rm{log}}\left( \alpha \right)}}
$
|
(4)
|
|
$
v = \frac{\beta }{{\left( {1 - \alpha } \right)}}
$
|
(5)
|
3.1.4. TopNet
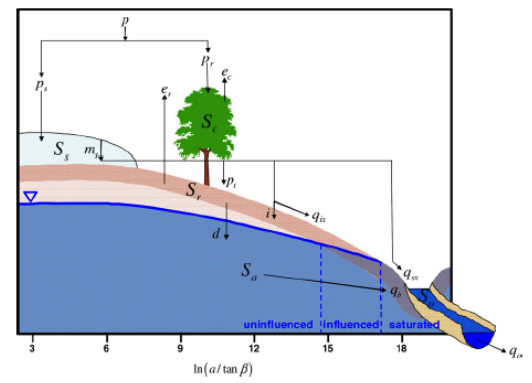
TopNet is a physically-based and semi-distributed model developed based on the TOPMODEL [42] concepts. It has two main components: a water balance for each sub-catchment and streamflow routing for each sub-catchment. The water balance model represents storages and fluxes of water in the canopy, snowpack, and unsaturated and saturated soil zones. A catchment is divided into sub-catchments linked by a river network. Then a kinematic wave is used to model the output discharge through the digital stream network. The routing component has three sources of runoff from each sub-catchment: saturation excess runoff from excess precipitation, infiltration excess runoff and base flow within the saturated zone. Saturation excess runoff occurs in the saturated portion of the catchment when soil water storage reaches its capacity. Infiltration runoff excess occurs in the uninfluenced and influenced portions of the catchment when the effective rainfall exceeds the infiltration rate.
TopNet uses TOPMODEL concepts for the representation of the soil moisture deficit using a topographic index to model the dynamics of variable source areas contributing to saturation excess runoff [43,44].
The input data are rainfall and temperature (minimal and maximal) at hourly time steps for each sub-basin, relative humidity, shortwave radiation, wind speed, and mean sea level pressure. A schematic representation of this model is shown in Figure 5.
3.1.5. WaSiM-ETH
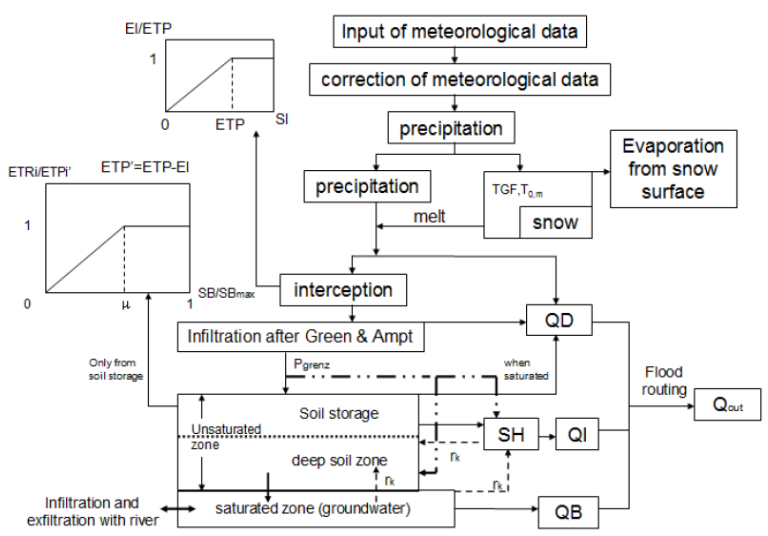
The Water Balance Simulation Model (WaSiM-ETH) is a physically-based distributed model developed at the Swiss Federal Institute of Technology in Zurich. It is used for runoff forecasting or modelling of substance transport.
Two versions of this model exist. Version 1 uses the conceptual TOPMODEL-approach in the soil model. This approach describes flow components between and within the saturated and unsaturated zone by fluxes to and out of several reservoirs. Several parameters have no physical meaning because it has a conceptual base. Version 2 uses the RICHARDS-equations for describing the water flow within the unsaturated soil [45]. Here, we use version 1.
WaSiM-ETH is able to simulate the water fluxes on a small scale for a large catchment. The spatial resolution is given by an input grid (30 m × 30 m in this study). Temporal resolution can range from one minute to a few days, depending on the time resolution of the meteorological data. The minimum input data are time series of temperature and precipitation, and grid information about topography, land use and soil type [46]. The Figure 6 shows the structure of the WaSiM-ETH model.
Several combinations of sub-models can be chosen individually depending on data availability and purpose of study. Several methods exist to perform the spatial interpolation of meteorological data. In this study, the inverse distance weighting interpolation is used. Then, to calculate the potential evaporation and transpiration different methods can be chosen for the evapotranspiration module. Data available are hourly data so the Penman-Monteith method is used. However, this method requires more detailed input data than other methods.
3.2. Complexity of models
Model complexity is defined in this work based on model type, number of parameters to be calibrated, input requirements, time needed to prepare and set up models and time needed to make a single run. Table 2 lists the different types of the models used in this study. Based on Table 2 WaSiM-ETH is the most complex model followed by TopNet. The simplest model of all is the runoff rainfall ratio model. HBV, HYMOD, TopNet were calibrated using the RObust Parameter Estimation (ROPE) algorithm [47]. WaSiM-ETH was calibrated using Shuffled Complex Evolution (SCE-UA) [48]. All the models of the HydroMAD package were calibrated using functions from the Bell Labs PORT library [35].
Table 2. Details for each hydrological model.
| Model name |
Model type |
No. of parameters that need to be calibrated |
Input requirements |
Output |
Time step |
NSE Calibration |
NSE Validation |
Time to calibrate |
Time taken for one run (for 6 years) |
Time to prepare inputs |
| Scalar |
Conceptual -Lumped |
4 |
Precipitation, temperature |
Discharge, intermediate state |
Daily |
0.47 |
0.58 |
< 1 hour |
3 min |
< 1 hour |
| Runoff ratio |
Conceptual -Lumped |
1 |
Precipitation, temperature, observed discharge |
Discharge |
Daily |
0.77 |
0.83 |
< 1 hour |
3 min |
< 1 hour |
| Australian Water Balance Model (AWBM) |
Conceptual -Lumped |
5 |
Precipitation, temperature |
Discharge, intermediate state |
Daily |
0.69 |
0.78 |
< 1 hour |
3 min |
< 1 hour |
| Intensity |
Conceptual -Lumped |
6 |
Precipitation, temperature |
Discharge, intermediate state |
Daily |
0.47 |
0.58 |
< 1 hour |
3 min |
< 1 hour |
| Data-Based Mechanistic (DBM) |
Conceptual -Lumped |
6 |
Precipitation, temperature, observed discharge |
Discharge, intermediate state |
Daily |
0.79 |
0.80 |
< 1 hour |
3 min |
< 1 hour |
| IHACRES Catchment Moisture Deficit (CMD) |
Conceptual -Lumped |
7 |
Precipitation, temperature |
Discharge, intermediate state |
Daily |
0.71 |
0.82 |
< 1 hour |
3 min |
< 1 hour |
| Génie Rural à 4 paramètres Journalier (GR4J) |
Empiric -Lumped |
4 |
Precipitation, temperature |
Discharge, intermediate state |
Daily |
0.78 |
0.19 |
< 1 hour |
3 min |
< 1 hour |
| Single-bucket |
Conceptual -Lumped |
8 |
Precipitation, temperature |
Discharge, intermediate state |
Daily |
0.72 |
0.82 |
< 1 hour |
3 min |
< 1 hour |
| IHACRES Catchment Wetness Index (CWI) |
Conceptual -Lumped |
9 |
Precipitation, temperature |
Discharge, intermediate state |
Daily |
0.78 |
0.62 |
< 1 hour |
3 min |
< 1 hour |
| Degree-day factor snowmelt |
Conceptual -Lumped |
13 |
Precipitation, temperature |
Discharge, intermediate state |
Daily |
0.73 |
0.72 |
< 1 hour |
3 min |
< 1 hour |
| Sacramento |
Deterministic -Lumped |
16 |
Precipitation, temperature |
Discharge, intermediate state |
Daily |
0.47 |
0.60 |
< 1 hour |
3 min |
< 1 hour |
| Hymod |
Conceptual-Lumped |
8 |
Precipitation, temperature, evapotranspiration |
Discharge |
daily |
0.74 |
0.80 |
3 hours |
< 5 min |
< 3 hours |
| Hydrologiska Byråns Vattenbalansavdelning (HBV) |
Conceptual-Semi -distributed |
10 |
Precipitation, temperature (daily and mean per month), potential of evaporation (daily and mean per month) |
Discharge |
daily |
0.74 |
0.8 |
3 hours |
< 5 min |
< 3 hours |
| TopNet |
Physically-based -Semi-distributed |
15 |
Precipitation, relative humidity, shortwave radiation, temperature min/max, wind speed, mean sea level pressure |
Discharge, snow water equivalent, canopy storage, soil moisture, depth to the water table, infiltration excess runoff, evaporation from soil… |
hourly |
0.73 |
0.85 |
2–3 days |
10 min (on Linux) |
> 3 days |
| Waterbalance Simulation Model (WaSiM-ETH) |
Physically-based -Distributed |
9 |
Precipitation, temperature, relative humidity, shortwave radiation, wind speed, land use, soil type, soil parameters, DEM |
Discharge, base flow, infiltration excess runoff, total runoff … |
hourly |
-0.11 |
-2.09 |
> 10 days |
2 -3 h |
> 7 days |
3.3. Evaluation criteria
To measure the performance of each model, an objective function, the Nash-Sutcliff Efficiency [49] was used for calibration and evaluation. This objective function gives the proportion of the variance of the data explained by the model [50]. Its value ranges from -∞ to 1:
|
$
NSE = 1 - \frac{{\mathop \sum \nolimits_{t = 1}^N {{\left( {{q_{obs}}\left( t \right) - {q_{sim}}\left( t \right)} \right)}^2}}}{{\mathop \sum \nolimits_{t = 1}^N {{\left( {{q_{obs}}\left( t \right) - \overline {{q_{obs}}} } \right)}^2}}}
$
|
(6)
|
where qobs(t) and qsim(t) are the observed and simulated discharge at time step t respectively, $\overline {{q_{obs}}} $ is the mean observed discharged over the entire simulation period of length N.
NSE compares the mean square error generated by a particular model simulation to the variance of the target output sequence. A value of NSE = 1 indicates perfect agreement between observed and modelled discharges, a value greater than 0 means than the simulated runoff gives a good estimate of the observed runoff and a NSE value < 0 means that the model doesn't represent the observed discharged well [51].
3.4. Data preparation
Daily input data from 2001 to 2011 were used to calibrate and validate the models. Firstly, the calibration was carried out for the period 11 May 2001 to 11 May 2006. Then, the validation was performed for the period, 12 May 2006 to 07 January 2011. For all conceptual models, daily data are used, whereas hourly data are used for physically-based models. For HydroMAD, both calibration and validation included a 3-month warm-up period. Data from this period are not used to assess model performance.
The hydrological models differ with respect to the time required to process input data to run these models. Input data for simple models such as HydroMAD are a time series of temperature, precipitation and observed discharge. Then the R package is used to run different SMA and the output data can be easily post-processed. Details about running the model are given by Andrews, et al. [35].
For hydrological models like HYMOD and HBV, a FORTRAN code is used to run them. Time series of temperature, precipitation and observed discharge in text file format is provided to the model.
For TopNet, input data are times series of precipitation, temperature, wind, solar radiation, relative humidity, potential evapotranspiration, mean sea level pressure and observed discharge. The input to the model is provided in netcdf file format. TopNet is widely used for hydrological modelling applications in New Zealand and uses nationally available data bases. Consequently, processing for this model is simple, as the study is carried out on a New Zealand catchment. However, to setup the model elsewhere it would take considerably longer.
It was most time consuming to process the input data for WaSiM-ETH and set up the model. Land use and soil cover, digital elevation model, catchment boundaries, sub-catchment boundaries must be provided and prepared using ArcGIS. Tanalys pre-process software was used to prepare the input files. To set-up a complex model like WaSiM-ETH requires a long time compared to other models in this study.
4. Results and Discussion
4.1. Comparison of model results in reproducing historical records
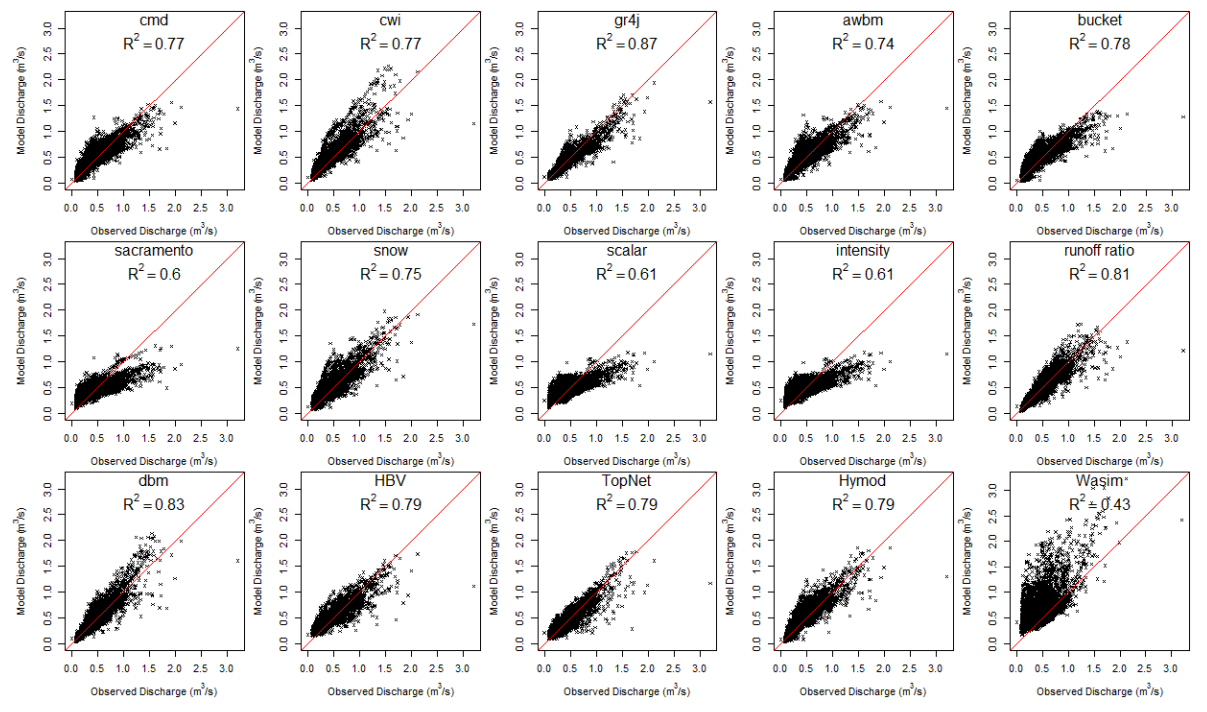
The performance of the hydrological models was evaluated by statistical and visual comparisons of observed and simulated discharges. Table 3 gives a summary of model performance for both the calibration and validation time periods. From Table 3, we see that, during calibration, except for the models Sacramento, Scalar, Intensity and WaSiM-ETH, all the models have acceptable NSE values. During validation, GR4J has the highest NSE value followed by TopNet, runoff ratio, bucket, cmd, dbm, HYMOD and HBV. However, the WaSiM-ETH performance was not acceptable as NSE is negative for both calibration and validation.
Table 3. Comparison of models regarding their capability to reproduce historical discharges in the Waiokura catchment.
|
Calibration |
Validation |
|
Mean daily flow (m3/s) |
Maximum daily flow (m3/s) |
NSE |
Mean daily flow (m3/s) |
Maximum daily flow (m3/s) |
NSE |
| observed |
0.48 |
3.20 |
|
0.44 |
2.12 |
|
| cmd |
0.46 |
1.56 |
0.71 |
0.46 |
1.52 |
0.82 |
| cwi |
0.48 |
1.42 |
0.78 |
0.57 |
2.27 |
0.62 |
| gr4j |
0.41 |
1.57 |
0.78 |
0.41 |
1.94 |
0.89 |
| awbm |
0.47 |
1.65 |
0.69 |
0.46 |
1.51 |
0.78 |
| bucket |
0.46 |
1.33 |
0.72 |
0.46 |
1.38 |
0.82 |
| sacramento |
0.46 |
1.30 |
0.47 |
0.42 |
0.97 |
0.60 |
| snow |
0.47 |
1.86 |
0.73 |
0.53 |
1.98 |
0.72 |
| scalar |
0.48 |
1.18 |
0.47 |
0.45 |
1.01 |
0.58 |
| intensity |
0.48 |
1.18 |
0.47 |
0.45 |
1.01 |
0.58 |
| runoff ratio |
0.48 |
1.47 |
0.77 |
0.45 |
1.72 |
0.83 |
| dbm |
0.48 |
1.99 |
0.79 |
0.47 |
2.13 |
0.8 |
| HBV |
0.49 |
1.43 |
0.74 |
0.49 |
1.73 |
0.8 |
| TopNet |
0.44 |
1.37 |
0.73 |
0.42 |
1.78 |
0.85 |
| Hymod |
0.50 |
1.47 |
0.74 |
0.48 |
1.86 |
0.80 |
| WaSiM-ETH |
0.67 |
2.42 |
-0.11 |
0.84 |
3.23 |
-2.09 |
Mean daily flow (Table 3) is well reproduced by all the models except snow and cwi, which give overestimated values for the validation time period. At the same time, a complex model like WaSiM-ETH gives a very high mean value for both the calibration and the validation period.
Values of maximum daily flow (Table 3) are underestimated during the calibration time period and validation time periods by most models except a few simple models like cwi, dbm and snow, which provide a maximum daily value close to the observed value.
Figure 7 compares measured daily runoff over the calibration period with model flow against the observed flow for all models. The scatter plot in Figure 7 supports the result that high flows are underestimated by all hydrological models. It can be seen that the peak flow of 3.2 m3/s is underestimated by most of the models except for WaSiM-ETH where the peak flow is closer to the observed value. However, the WaSiM-ETH model overestimates low flows. AWBM, bucket, runoff ratio, TopNet, HBV and HYMOD model outputs are best correlated with observed values.
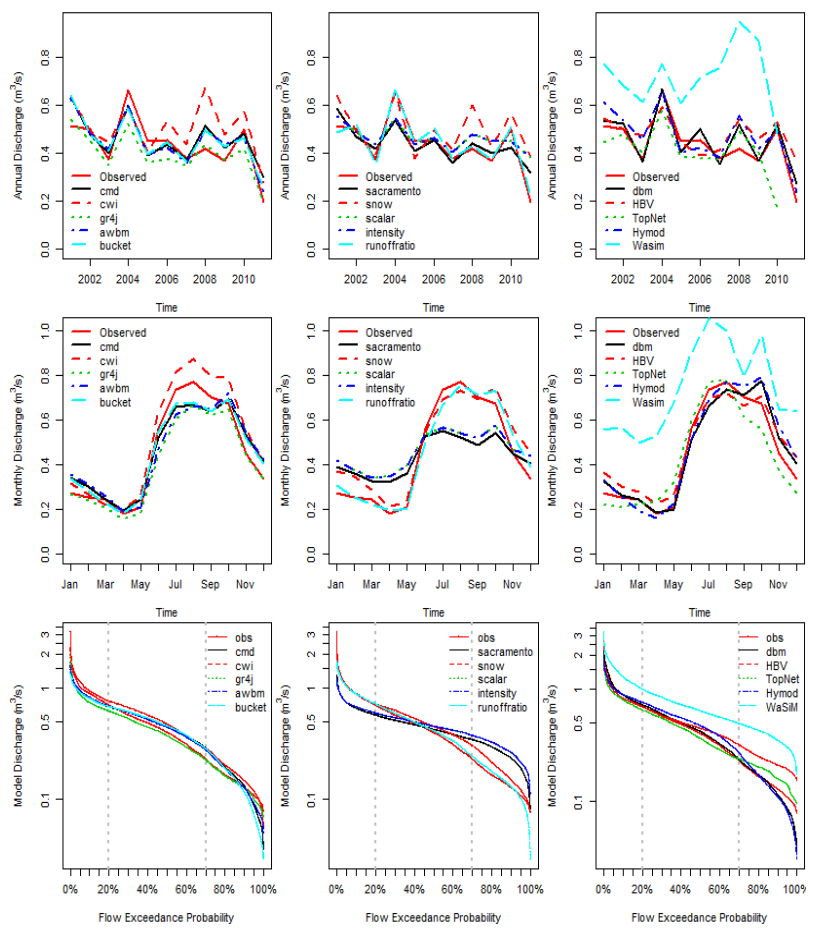
The model output comparison of mean annual streamflow, monthly streamflow and flow duration curves for the period from August 2001 to January 2011 is shown in Figure 8. It can be seen that mean annual and mean monthly streamflow patterns are well reproduced by all models except WaSiM-ETH, which overestimates observations. Sacramento, scalar and intensity models provide mean monthly flows that are less variable over time than the observed values. For the months of January to May, mean monthly flows are overestimated, and for the months from July to October they are underestimated. Snow, runoff ratio, HBV, HYMOD, dbm models reproduced the best mean monthly flows. Monthly streamflows from TopNet reproduced the patterns of observed runoff, but for the months of August to October they are underestimated.
Table 4 presents the values of rainfall-runoff ratio for each model. These models provide a similar rainfall-runoff ratio except WaSiM-ETH, which yields a rainfall-runoff ratio higher than the observed value. The values reflect the fact that land use cover of the catchment is pre-dominantly short grass (Figure). The soil is permeable and a great part of the rainfall is intercepted or infiltrated before it reaches the river. About 40% of the rainfall is converted into runoff. The runoff-ratio value of WaSiM-ETH reflects a soil with low permeability. The high rainfall runoff ratio probably results from an overestimation of flow by WaSiM-ETH model. This likely originated from the parameters provided to the model in the land use and soil table. The saturated conductivity and van-Genuchten parameters values were provided based on literature. Based on the results of the models, it can be concluded that, in a small catchment, a simple model can represent the catchment equally well as a complex model like WaSiM-ETH.
Table 4. Rainfall-runoff ratio for daily streamflow from August 2001 to January 2011.
| Observed |
0.43 |
Scalar |
0.44 |
| Cmd |
0.44 |
intensity |
0.44 |
| Cwi |
0.49 |
runoffratio |
0.44 |
| gr4j |
0.39 |
Dbm |
0.45 |
| Awbm |
0.44 |
HBV |
0.46 |
| Bucket |
0.43 |
TopNet |
0.41 |
| Sacramento |
0.42 |
Hymod |
0.46 |
| Snow |
0.47 |
WaSiM-ETH |
0.71 |
Overall, the results show that TopNet, HBV, runoff ratio, HYMOD and dbm reproduce historical runoff series satisfactorily. Simple to moderate complex models can model discharge with acceptable results. A Similar conclusion was reached by Orth, et al.
[2].
4.2. Comparison of model results in predicting hydrological response to changed climate
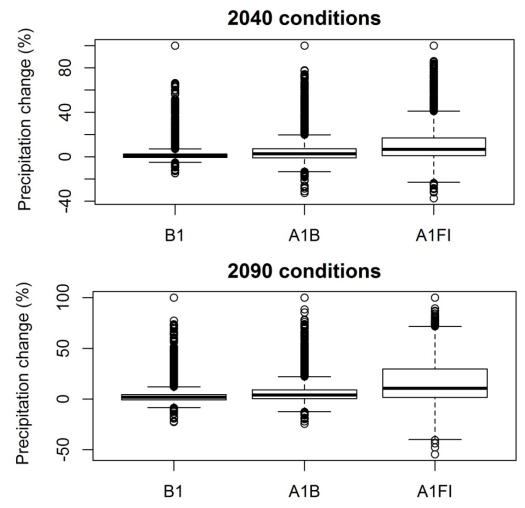
Table 5 presents the precipitation change over 1990 conditions for the various climate change scenarios in 2040 and 2090. The mean daily rainfall increases little under climate change scenarios for both 2040 and 2090 conditions. However, the maximum daily rainfall increases from a low to high emission scenario (from B1 to A1FI) and it is higher in 2090 conditions than 2040 conditions.
Table 5. Mean daily rainfall and maximum daily rainfall for the 1990 baseline and the B1, A1B and A1FI emission scenarios in 2040 and 2090.
|
1990 conditions |
2040 conditions |
2090 conditions |
|
B1 |
A1B |
A1FI |
B1 |
A1B |
A1FI |
| Mean daily rainfall [mm] |
3.0 |
3.1 |
3.1 |
3.1 |
3.1 |
3.1 |
3.1 |
| Maximum daily rainfall [mm] |
93.7 |
99.6 |
107.0 |
112.6 |
102.8 |
105.8 |
121.7 |
The mean daily temperature and maximum daily temperature over 1990 conditions for the different emission scenarios and future periods are presented in Table 6. It can be seen that the mean and maximum daily temperature increase from the lower to the higher emission scenarios and from the 2040 period to the 2090 period.
Table 6. Mean daily temperature and maximum daily temperature changes for the 1990 baseline and the B1, A1B and A1FI emission scenarios in 2040 and 2090.
|
1990 conditions |
2040 conditions |
2090 conditions |
|
B1 |
A1B |
A1FI |
B1 |
A1B |
A1FI |
| Mean daily temperature [℃] |
12.5 |
13.1 |
13.4 |
13.8 |
13.8 |
14.5 |
15.4 |
| Maximum daily temperature [℃] |
22.6 |
23.3 |
23.7 |
24.2 |
24.1 |
25.0 |
26.0 |
The precipitation change in 2040 and 2090 conditions over 1990 conditions are shown in Figure. Here the percentage change in the precipitation is less in the B1 scenario compared to the others. There is a slight increase in the percentage change from 2040 to 2090. For A1FI the percentage change in precipitation is very high for both time periods (2040,2090).
Table 7 presents mean daily flows for 1990,2040 and 2090 conditions for the three emission scenarios. It can be seen that there are two trends, one is evidenced by the cmd, cwi, awbm, bucket, snow and HYMOD models, which predict that mean flows decrease from the lower to the higher emission scenario as mean values for 2090 conditions are lower than mean values for 2040 conditions. The other trend is given by Sacramento, scalar and intensity, whereby the mean flow increases sin similar fashion for the 2040 conditions and 2090 conditions. The lower value corresponds to the lower emission scenario and the higher value to the higher emission scenario. The mean value for TopNet presents the two trends: for 2040 conditions, the mean value increases from lower to higher emission scenarios, and for 2090 conditions, the mean value decreases from lower to higher emission scenarios. WaSiM-ETH mean values are higher than the mean values of other hydrological models.
Table 7. Mean flows (m3/s) predicted by different hydrological models for various emission scenarios under climate change.
|
1990 conditions |
2040 conditions |
2090 conditions |
|
B1 |
A1B |
A1FI |
B1 |
A1B |
A1FI |
| cmd |
0.22 |
0.21 |
0.20 |
0.20 |
0.20 |
0.18 |
0.17 |
| cwi |
0.27 |
0.25 |
0.24 |
0.23 |
0.23 |
0.21 |
0.19 |
| awbm |
0.19 |
0.18 |
0.17 |
0.16 |
0.16 |
0.14 |
0.13 |
| bucket |
0.23 |
0.22 |
0.22 |
0.21 |
0.20 |
0.19 |
0.18 |
| sacramento |
0.27 |
0.28 |
0.28 |
0.29 |
0.28 |
0.28 |
0.29 |
| snow |
0.17 |
0.16 |
0.15 |
0.15 |
0.14 |
0.13 |
0.12 |
| scalar |
0.34 |
0.35 |
0.35 |
0.35 |
0.35 |
0.35 |
0.35 |
| intensity |
0.34 |
0.35 |
0.35 |
0.35 |
0.35 |
0.35 |
0.35 |
| HBV |
0.26 |
0.27 |
0.27 |
0.27 |
0.27 |
0.27 |
0.28 |
| TopNet |
0.41 |
0.41 |
0.41 |
0.41 |
0.41 |
0.40 |
0.40 |
| Hymod |
0.23 |
0.23 |
0.23 |
0.23 |
0.22 |
0.21 |
0.20 |
| Wasim |
1.00 |
0.99 |
0.99 |
1.00 |
1.00 |
1.00 |
1.00 |
Table 8 presents the maximum daily flow for each emission condition and scenarios. In general, all maximum daily flows increase from lower to higher emission scenarios, with the lower value for 2040 conditions and B1 emission scenario and the higher value for 2090 conditions and the A1FI emission scenario, except for the cwi model, where maximum daily flows decrease from lower to higher emission scenarios. If we exclude the results of WaSiM-ETH, we see that TopNet gives the highest maximum daily flow of all models. This again illustrates that if a single model (assuming more complex is good) like TopNet is used decision makers may not be provided with important indications about future flows.
Table 8. Maximum daily flows (m3/s) predicted by different hydrological models for various emission scenarios under climate change.
|
1990 conditions |
2040 conditions |
2090 conditions |
|
B1 |
A1B |
A1FI |
B1 |
A1B |
A1FI |
| cmd |
1.37 |
1.40 |
1.41 |
1.43 |
1.42 |
1.46 |
1.51 |
| cwi |
1.42 |
1.40 |
1.39 |
1.38 |
1.37 |
1.37 |
1.40 |
| awbm |
1.45 |
1.47 |
1.48 |
1.49 |
1.48 |
1.52 |
1.57 |
| bucket |
1.23 |
1.26 |
1.26 |
1.28 |
1.27 |
1.29 |
1.32 |
| sacramento |
1.01 |
1.05 |
1.07 |
1.10 |
1.09 |
1.13 |
1.19 |
| snow |
1.63 |
1.68 |
1.71 |
1.74 |
1.72 |
1.78 |
1.86 |
| scalar |
1.02 |
1.05 |
1.07 |
1.09 |
1.08 |
1.12 |
1.16 |
| intensity |
1.02 |
1.05 |
1.07 |
1.09 |
1.08 |
1.12 |
1.16 |
| HBV |
1.52 |
1.59 |
1.63 |
1.67 |
1.66 |
1.74 |
1.84 |
| TopNet |
2.16 |
2.22 |
2.22 |
2.18 |
2.21 |
2.19 |
2.23 |
| Hymod |
1.08 |
1.12 |
1.14 |
1.18 |
1.16 |
1.22 |
1.29 |
| Wasim |
5.37 |
5.21 |
6.04 |
5.43 |
5.37 |
5.37 |
5.53 |
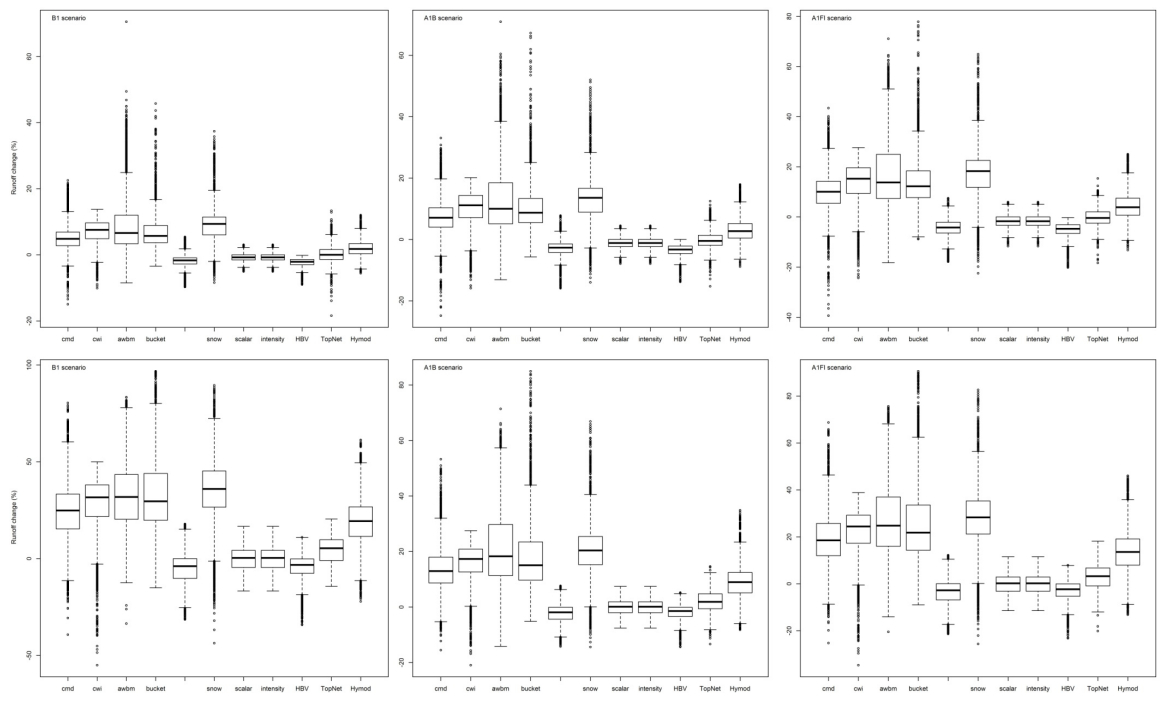
A comparison of daily runoff changes between runoff modelled for 2040 and 2090 conditions is shown in Figure. It is evident that Sacramento, scalar, intensity, HBV, TopNet and HYMOD are hydrological models that have less runoff change for 2040 conditions with the B1 scenario, and differences are higher with the A1FI scenario. The other models show a significant runoff difference, whereas the precipitation change for the B1 emission scenarios and 2040 conditions is small. For 2090 conditions, runoff changes of all models are higher, but always with models with less precipitation change. WaSiM-ETH distinguishes itself from other models by having runoff changes which decrease when emission scenarios increase. Runoff changes for WaSiM-ETH are almost non-existent for the A1FI scenario.
Sacramento, scalar, intensity, HBV, TopNet and HYMOD are models which provide simulated streamflow which follow patterns of precipitation change. The other models assessed her react more strongly to changing climate conditions. This shows that for climate change impact assessment those models with less complexity gives more reliable results than models with more complexity. These results are agree with those of Ludwig, et al.
[5].
Table 9 presents the rainfall-runoff ratio in 1990,2040 and 2090 conditions for each climate change scenario. The rainfall-runoff ratios for 1990 conditions for all models are lower than those estimated using historical records (i.e. 0.43 from observed records), except for the scalar and intensity models. Generally, the values of this coefficient decrease under climate change conditions. We have seen previously that mean daily rainfall is predicted to stay constant, so this trend indicates that less rainfall will become runoff under climate change conditions.
Table 9. Rainfall-runoff ratios for various emission scenarios under climate change.
|
1990 conditions |
2040 conditions |
2090 conditions |
|
B1 |
A1B |
A1FI |
B1 |
A1B |
A1FI |
| cmd |
0.27 |
0.26 |
0.25 |
0.25 |
0.24 |
0.23 |
0.22 |
| cwi |
0.34 |
0.31 |
0.30 |
0.29 |
0.28 |
0.26 |
0.24 |
| awbm |
0.24 |
0.22 |
0.21 |
0.20 |
0.20 |
0.18 |
0.16 |
| bucket |
0.30 |
0.28 |
0.27 |
0.26 |
0.26 |
0.24 |
0.22 |
| sacramento |
0.35 |
0.35 |
0.35 |
0.36 |
0.35 |
0.36 |
0.36 |
| snow |
0.22 |
0.20 |
0.19 |
0.18 |
0.18 |
0.17 |
0.15 |
| scalar |
0.44 |
0.44 |
0.43 |
0.44 |
0.43 |
0.44 |
0.44 |
| intensity |
0.44 |
0.44 |
0.43 |
0.44 |
0.43 |
0.44 |
0.44 |
| HBV |
0.33 |
0.34 |
0.34 |
0.34 |
0.33 |
0.34 |
0.35 |
| TopNet |
0.52 |
0.52 |
0.51 |
0.52 |
0.51 |
0.51 |
0.50 |
| Hymod |
0.29 |
0.29 |
0.28 |
0.28 |
0.27 |
0.26 |
0.25 |
| Wasim |
1.27 |
1.25 |
1.24 |
1.26 |
1.24 |
1.27 |
1.25 |
5. Conclusions
In this study, we investigated the impact of the choice of simple versus complex models with respect to reproducing historical discharge records and the effect of the model choice on hydrological climate change assessments. We studied several hydrological models with different level of complexity. Conceptual and lumped models (simple) yield equally good results in predicting catchment discharges as distributed and physically-based models (complex) in the Waiokura catchment. Those simple models reproduce historical records well and the prediction of hydrological response to climate change are consistent with meteorological data patterns. The main advantage of simple models is that they require fewer input data and are easier to set up and run as opposed to complex models such as WaSiM-ETH and TopNet. Furthermore, in the case of physically-based models, data are sometime not available and adoption of literature values may not be representative of the real state of the catchment. For example, in the Waiokura catchment, the calibrated value of WaSiM-ETH was very poor. For this model the time to fulfil all data requirements is rather extensive for an adequate representation of the basin. Additionally, calibration of parameters for complex models requires more time because of the number parameters that need calibration and there is more uncertainty owing to, for example, input errors, and parameterisation errors. TopNet, which is a moderately complex and physically-based model can give better results than a complex model. This occurred in the Waiokura for TopNet because readily accessible input data was available. However, too simple a model sometimes cannot be sufficient for the given purpose. For example, even if the runoff ratio model gives good results for historical events, we cannot use this model to predict streamflow under a climate change context, since observed discharge is required in this case. Models like HydroMAD, HBV and HYMOD give reliable results for historical records and sensible results for predictions of hydrological response to climate change in the Waiokura. Results from this study show that models should be chosen based on the purpose of the hydrological modelling work. Finally, we infer, based on our results from different scenarios, that a simple to moderately complex model is sufficient for predicting impacts of climate change. Ideally it would be better to use a multi-model ensemble, as this will reduce uncertainty due to model structure and complexity.
Acknowledgments
The author would like to thank George Griffiths and Markus Pahlow for their help in English editing of the paper. The authors would also like to thanks MS Srinivasan for providing some of the data used in this study. The author gratefully acknowledge the detailed and constractive comments made by the associated editor and two anonymous reviewers which greatly helped improve this article.
Conflict of Interest
The authors declare they have no conflicts of interest in this article.









 DownLoad:
DownLoad: