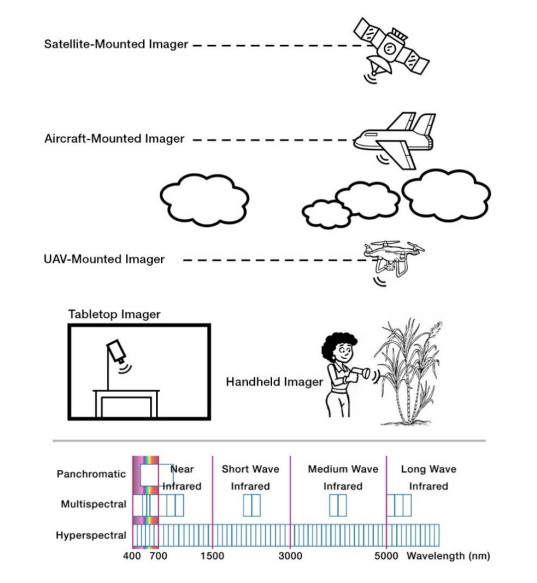
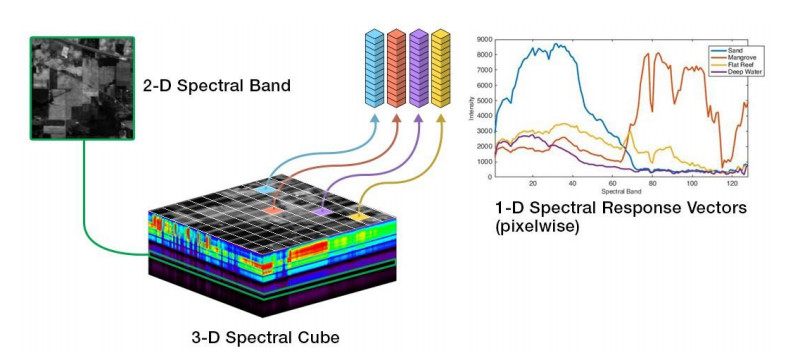
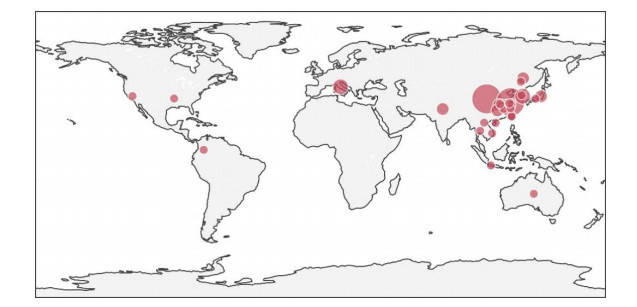
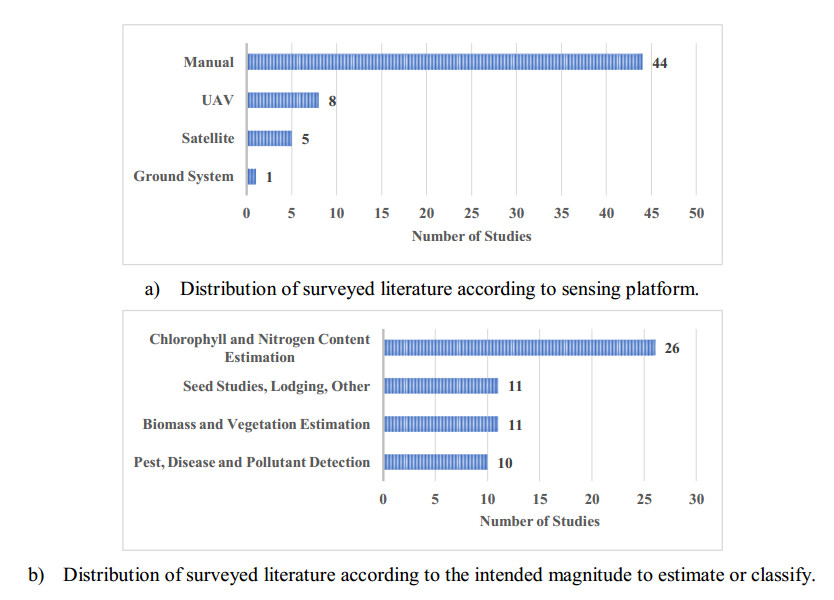
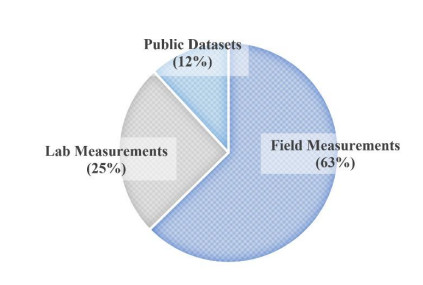
Hyperspectral imaging for rice cultivation: Applications, methods and challenges

1.   Introduction

Data from the World Heart Federation shows that the number of people with cardiovascular disease worldwide has exceeded 500 million. Known as the number one killer that threatens human health, cardiovascular disease is increasingly occurring in young people, including cardiac arrhythmia. An effective way to diagnose arrhythmia is to use electrocardiogram (ECG) signals, which contain important information for diagnosing the type of abnormal heart rhythm. But some information is less differentiated and an experienced physician is required. Therefore, automatic arrhythmia detection is particularly important.

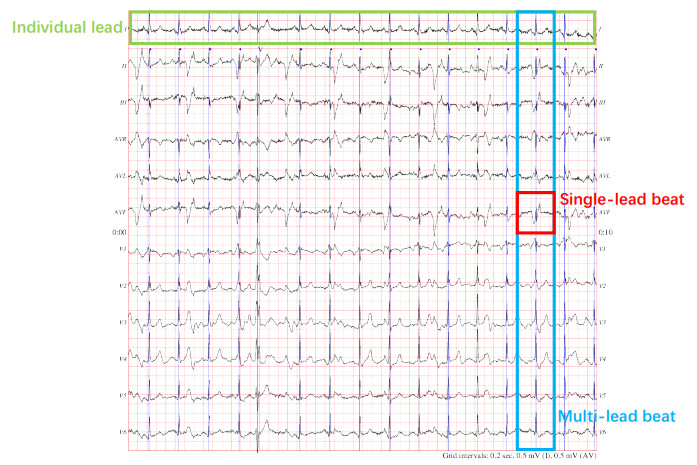
To date, there have been numerous studies on arrhythmia detection, including ECG signal preprocessing, feature extraction and classification models. In ECG signal preprocessing, noise reduction techniques are widely used to remove artifacts from baseline wander, powerline interference, electrode motion, muscle artifacts, etc. Feature extraction is crucial in ECG signal classification, but the classification results are heavily dependent on the complex feature extraction process, which cannot adapt to different application environments and may result in some important information loss. As deep learning techniques evolve, features will become automatically selectable and classification tasks will become processable end-to-end. Such techniques are also widely used in arrhythmia detection. However, plenty of studies focus on single lead information, and the interpretability is not strong. At the same time, multi-lead data requires analysis of the relationship between leads and the heartbeats within the lead as shown in Figure 1. In this figure, the ECG signals include 12 leads, i.e., Ⅰ, Ⅱ, Ⅲ, AVR, AVL, AVF, V1, V2, V3, V4, V5 and V6. Each lead (marked in green) contains information on multiple heartbeats, which are called single-lead beats (marked in red). Single-lead beats in the same time interval in multiple leads constitute one multi-lead beat (marked in blue). However, many studies have focused on the diagnosis of one-dimensional lead information or simple multi-lead information fusion, which cannot make good use of the comprehensive information in multi-lead signals, such as the relationship between the leads and heartbeats, or the relationship between multi-lead beats and single-lead beats.

Figure 1.  One record with multiple leads containing several premature ventricular contraction beats.

DownLoad: Full-Size Img PowerPoint

In summary, it is critical to simultaneously construct intra-lead and inter-lead correlations in the model for multi-lead arrhythmia detection. The instances (nodes) in the graph are associated with other nodes through complex correlations that are available to capture their interrelationships. Heterogeneous graphs take into account the rich interactions between multiple types of nodes and edges. Multi-lead ECG signals include different node types such as multi-lead beats, single-lead beats, and individual leads, meanwhile, they have complicated relationships among them. Therefore, in a study on arrhythmia detection using multi-lead ECG signals, heterogeneous graphs are suitable for modeling heartbeat data. The embedding of each node in the graph is jointly represented by the characteristics of the node and related nodes. In addition, interaction-related information is derived by means of information propagation between neighboring nodes in the graph.

To capture the rich interactions in multi-lead ECG signal data, an arrhythmia detection framework based on a heterogeneous graph attention network (MADHGAT) is developed in this work. A heterogeneous graph has been modeled for multi-lead ECG signals to integrate diverse data, which contains single-lead beats, multi-lead beats and multiple leads as nodes, additionally, intra-lead and inter-lead correlations are constructed. Heterogeneous graph attention networks (HGATs) are utilized for heterogeneous graph embedding to perform multi-lead beat classification as arrhythmia detection. Implementing a dual-level attention strategy in the HGAT allows for the learning of node-level and type-level contributions of adjacent nodes. The proposed framework does not need require any feature extraction for the ECG signals. We describe extensive experiments and show the effectiveness of the proposed model. The following key contributions of this work are summarized.

1) A heterogeneous graph has been modeled for multi-lead ECG signals to capture rich information, which can integrate diverse signal information and consider the inter-lead and intra-lead correlations at the same time.

2) An arrhythmia detection framework with HGATs is proposed for heterogeneous graph embedding and automatic cardiac arrhythmia classification. The implementation of a dual-level attention strategy in the HGAT permits the capture of the complex interactions between different heartbeat nodes and different node types.

3) To the best of our knowledge, this is the first time that multi-lead ECG signals have been modeled as a heterogeneous graph and HGATs have been employed for cardiac arrhythmia classification.

4) The results of extensive experiments indicate that the proposed model is able to well integrate the information of multiple leads, and results in significant improvements when applied to the INCART dataset without any feature extraction.

2.   Related works

Automatic arrhythmia detection algorithms for ECG signal data usually have three main tasks, which include data preprocessing, feature extraction and classification ^[1]. The preprocessing operations include data denoising ^[2] and heartbeat segmentation ^[3]. Feature extraction is crucial in ECG signal classification. Features can be extracted from the ECG signal's shape in the spatiotemporal domain, such as the QRS complex ^[4], R-peak ^[5], ST segment ^[6], Shannon entropy ^[7] and T duration ^[8]. Finally, signals are categorized into different types by machine learning methods, such as multilayer perceptrons (MLPs) ^[9], k-nearest neighbors ^[10], deep learning methods ^[11,12] and support vector machines ^[13]. However, the classification results heavily rely on a complex feature extraction process, which cannot be adapted to various environments. Additionally, missing important information may lead to misdiagnosis. Deep learning methods play an important role in automatic feature extraction, which are widely utilized for feature extraction ^[14,15,16] or arrhythmia detection ^[17,18,19] in an end-to-end mode without any handcrafted features. Deep learning methods reduce the amount of manual work and improve the detection performance. As shown in Figure 1, correlations among multi-lead ECG signals constitute important information for arrhythmia detection. However, most existing works regard beats as independent information, ignoring the intra-lead correlations among beats and the inter-lead correlations among leads.

ECG signals are shown as time-series data, so the intra-lead correlations among beats are mainly reflected in the temporal properties, which include statistical time features ^[20,21,22] and temporal dependency ^[23,24,25]. The temporal properties have been considered for both single-lead signals and multi-lead signals. Mahajan et al. ^[22] collected time-frequency data and linear and nonlinear features for single-lead ECG signal classification. Yao et al. ^[26] developed a time-incremental network based on an attention mechanism. It considered the spatial and temporal features of multi-lead ECG signals. Che et al. ^[27] developed a deep learning framework that integrated a transformer network into a convolutional neural network to capture the temporal features of multi-lead ECG signals. Compared to single-lead ECG signals, multi-lead signals contain more complex and abundant information on heartbeats, which is useful for achieving a more accurate cardiac disease diagnosis. However, some works only consider the temporal properties in ECG signals, ignoring the inter-lead correlations in multi-lead data as well as the correlations between multi lead beats and single-lead beats.

Various works have been proposed for automatic arrhythmia diagnosis based on multi-lead ECG signal data, such as studies focused on feature fusion ^[28,29,30] and inter-lead correlations ^[31,32,33]. Han and Shi ^[34] detected and located myocardial infarction through the use of a multi-lead residual neural network and feature fusion for 12-lead ECG signal data. Sepahvand and Abdali-Mohammadi ^[35] developed a multi-lead ECG personal recognition system, which calculated intra-correlations and cross-correlations among multi-lead signal data in the time-frequency domain to estimate functional dependencies. Different leads correspond to different aspects of heart activity. These works take multi-lead signals into consideration, thus improving the accuracy of arrhythmia diagnoses. However, feature fusion of multiple single-lead signals cannot systematically exploit the inter-lead signal correlations. Additionally, a majority of the aforementioned studies did not consider the intra-lead correlations between beats.

Graph neural networks include graph convolutional networks ^[36], graph attention networks ^[37], graph spatiotemporal networks ^[38], etc. They are applied successfully for many tasks, such as computer vision ^[39], traffic forecasting ^[38], protein interface prediction ^[40] and disease prediction ^[41]. However, there is no related work on automatic arrhythmia diagnosis with multi-lead ECG signals. Each element in a graph neural network is taken as a node while the relationships between elements are denoted by edges. The structure of homogeneous graphs ^[42,43], which only contain a single type of nodes and edges, is relatively simple. Therefore, graph neural networks for homogeneous graphs just need to aggregate a single type of neighbors to update the embedding of nodes. For example, a graph convolutional neural network was proposed to diagnose pneumonia caused by COVID-19 ^[44]. However, a majority of graphs in the real world should be constructed into heterogeneous graphs in consideration of the complex interactions among diverse nodes and edges, thus avoiding information loss. Compared to homogeneous graphs, the difference between neighbors in different relationships should be taken into consideration in heterogeneous graphs ^[45,46]. For example, a heterogeneous network with a variational graph auto-encoder is presented for miRNA-disease association prediction ^[47]. Therefore, in consideration of the various information types and relationships associated with multi-lead ECG signals, a heterogeneous graph can be constructed to capture the complex correlations within multi-lead ECG signal data for the task of automatic arrhythmia diagnosis, thereby improving diagnosis performance.

3.   Heterogeneous graph for multi-lead ECG signal data

We present an automatic arrhythmia detection framework based on an HGAT, which fully exploits both intra-lead correlations between beats and inter-lead correlations between leads based on the information spread along the graph. A flexible heterogeneous graph is presented first to model multi-lead ECG signal data and integrate abundant information as well as to capture the dependencies among multi-lead beats, single-lead beats and multiple leads, as shown in Figure 2. Then, we present a heterogeneous graph network with a dual-level attention strategy to embed the heterogeneous graph for arrhythmia detection. HGATs take into account information heterogeneity. Moreover, the attention strategy is able to learn the weights of different heartbeat nodes and node types.

Figure 2.  Constructed heterogeneous graph for multi-lead ECG signals.

DownLoad: Full-Size Img PowerPoint

Multi-lead beats were merely regarded as data objects for arrhythmia detection via multi-lead ECG signal data analysis in previous studies. Excluding for multi-lead beats, two types of additional information are considered, i.e., multiple leads and single-lead beats. As illustrated in Figure 2, the heterogeneous graph $G = (V, E)$ is constructed to model multiple leads $ML = \{ml_1, \ldots, ml_D\}$, multi-lead beats $MB = \{mb_1, \ldots, mb_N\}$ and single-lead beats $SB = \{sb_1, \ldots, sb_K\}$ as nodes, where $V = ML \bigcup MB \bigcup SB$. The collection of edges $E$ indicates their correlations and $K = D\times N$.

In detail, for the nodes of multiple leads, mean pooling is performed for the corresponding samples of all single-lead beats from the same lead, which realizes the embedding of every individual lead. For each multi-lead beat node, its representation is obtained by pooling the corresponding samples of all single-lead beats which constitute this multi-lead beat. For a better understanding of the constructed graph, an example is shown in Figure 3. Let us suppose that there are three multi-lead beats in the dataset, i.e., A1, A2 and A3. The whole graph contains 12 leads and each red box marks a single-lead beat. For each single-lead beat node, its feature is represented by its samples. Regarding each multi-lead heartbeat node–with A3 taken as an example, it is represented by pooling all single-lead beats comprising this multi-lead heartbeat. For the nodes of multiple leads, individual leads are represented by pooling the single-lead beats of A1, A2 and A3 in this lead.

Figure 3.  Example of node representation in the constructed heterogeneous graph.

DownLoad: Full-Size Img PowerPoint

So far, the maximum number of multiple leads for ECG signals is typically 12, so the maximum value of D is 12. We assign each multi-lead beat to these D leads. Therefore, the edge between one multi-lead beat and every individual lead has been built to enable analysis of the global significance of individual leads for arrhythmia detection and inter-lead correlations through the use of information propagation along the graph.

The beat segments in every lead are regarded as the nodes of single-lead beats. The embedding of one single-lead beat is the time series of samples and the embedding of one multi-lead beat is the mean pooling of multiple single-lead beats in this multi-lead beat. The edge between one multi-lead beat and one single-lead beat is built if one multi-lead beat contains this single-lead beat, providing information on the correlations between multi-lead beats and their corresponding single-lead beats, as well as the local significance of every single-lead beat for arrhythmia detection.

To further enhance multi-lead information and information propagation, the relationships between single-lead beats are considered. The edge between two single-lead beats is built if they belong to the same lead, which provides information on the inter-lead correlations. By incorporating multiple leads, single-lead beats and the correlations, the information of multi-lead beats is enriched, which greatly facilitates arrhythmia detection.

4.   Heterogeneous graph attention network for arrhythmia detection

The HGAT ^[48] is utilized for heterogeneous graph embedding and then arrhythmia detection, as shown in Figure 4. The HGAT considers the heterogeneity in the information on leads and beats via heterogeneous graph convolution. Furthermore, a dual-layer attention mechanism in the HGAT can capture and learn node-level and type-level importance between adjacent nodes in heterogeneous graphs. Finally, the labels of the multi-lead beats are predicted by a softmax layer.

Figure 4.  Framework of the proposed model MADHGAT for multi-lead arrhythmia detection.

DownLoad: Full-Size Img PowerPoint

4.1.   Heterogeneous graph convolution

For heterogeneous graph construction, three types of nodes have been modeled: multiple leads, multi-lead beats and single-lead beats. Though their feature space can be the same and a graph convolutional network can be adopted for heterogeneous graph embedding via the feature space concatenation of these three types of nodes $P = \{p_1, p_2, p_3\}$. Nevertheless, the performance will be degraded because the heterogeneity of distinct node types is not considered. To solve this problem, we adopt a heterogeneous graph convolutional network, which takes into account the distinction between different types of nodes and projects each of them with respective adjacency and transformation matrices into hidden space, as described by Eq (4.1).

where $\sigma$(·) is the activation function. $\tilde{A}_{p_i}\in \mathbb{R}^{|V| \times |V_{p_i}|}$ is the submatrix of the normalized adjacency matrix $\tilde{A}$ and is the adjacency matrix of each type $p_i$, whose rows and columns respectively denote all nodes and their adjacent nodes of the type $p_i$. The hidden embeddings of the nodes represented by $H^{(l+1)}\in \mathbb{R}^{|V|\times{q^{(l+1)}}}$ are learned by assembling information from their adjacent nodes of $H^{(l)}_{p_i}\in \mathbb{R}^{|V_{p_i}|\times{q^{(l)}}}$ with different types $p_i$ by using the corresponding transformation matrix $W^{(l)}_{p_i}\in \mathbb{R}^{q^{(l)}\times{q^{(l+1)}}}$. $q^{(l)}$ is the dimension of hidden embeddings in the $l^{th}$ layer. The transformation matrix $W^{(l)}_{p_i}$ considers the distinctiveness of different feature spaces that are projected into the hidden space $\mathbb{R}^{q^{(l+1)}}$.

4.2.   Dual-level attention mechanism

For a node in our graph, its adjacent nodes may include different types of nodes. In general, the information contained in different kinds of nodes has different contribution degrees. As we know, each lead in the ECG contributes differently to arrhythmia detection. Different weights are beneficial to better highlight important features in the ECG signal data. To capture more effective information about neighboring nodes, a dual-level attention strategy is applied to determine the different contributions at the node level and type level.

4.2.1.   Type-level attention

Type-level attention is used to capture the importance of different node types, such as multi-lead beats or single-lead beats. Specifically, given a node $v$, the sum of the adjacent node embeddings $h_{v'}$ with the type $p_i$ is used to express the embedding of type $p_i$ as $h_{p_i} = \sum_{v'\in N_v}\tilde{A}_{vv'}h_{v'}$. $\tilde{A}_{vv'}$ is one element of the normalized adjacency matrix $\tilde{A}$, where the row is $v$ and the column is $v'$. Then, the type-level attention score is computed by using the current node embedding $h_v$ and type embedding $h_{p_i}$ according to Eq (4.2):

where $\sigma(\cdot)$ is the activation function and $\|$ represents "concatenate". $\mu_{p_i}$ is the attention vector for type $p_i$, which is learned in the process of model training.

Finally, the attention score for each type is normalized by Eq (4.3) to obtain the attention weights at the type level.

4.2.2.   Node-level attention

Different neighbors also have different contributions. The node-level attention is developed to capture the weights of different neighbour nodes while reducing the importance of noisy nodes. This is a good way to minimize useless information in the ECG signal data. In detail, for a certain node $v$ of the type $p_i$ and its neighbor node $v'\in N_v$ of the type $p_j$, the node-level attention score for node $v'$ is calculated by using $h_v$, $h_{v'}$ and the type-level attention weight $\alpha_{p_j}$ according to Eq (4.4).

where $\nu_{p_j}$ is the node-level attention vector for the type $p_j$, and it is learned in the process of model training. Then, node-level attention score for each neighbour node is normalized by Eq (4.5).

In the end, the dual-level attention strategy with node-level and type-level attentions is integrated into the heterogeneous graph convolutional network by substituting the propagation rule in Eq (4.6) for that in Eq (4.1).

where $B_{p_i}$ denotes the attention matrix wherein every element is $\beta_{vv'}$ in Eq (4.5).

4.3.   Model training

The embeddings of nodes in the constructed graph are represented by the $L$-layer HGAT. So, the multi-lead beat nodes are supplemented by neighbor node information. Finally, multi-lead beat embeddings $H^{(L)}$ are input to the softmax layer for arrhythmia classification, as described by Eq (4.7). The cross-entropy loss with the L2-norm is adopted for model training, as described by Eq (4.8).

where $C$ represents the number of categories, $D_{train}$ is the training set of multi-lead beat data, $Y$ is the category matrix, $\Theta$ indicates the parameters of this model and $\eta$ is the regularization coefficient. At last, the gradient descent algorithm is applied for model parameter optimization.

5.   Experiments

5.1.   Experimental setup

5.1.1.   Dataset

We focus on multi-lead heartbeat classification. The ECG arrhythmia records used in this study are obtained from the St Petersburg INCART 12-lead arrhythmia database (INCART database) ^[49], which includes 75 annotated recordings collected from 32 patients under investigation for coronary artery disease. Every recording is 30 minutes long sampled at 257 Hz and consists of 12 standard leads, additionally each beat in the recording contains a beat annotation in the middle of QRS complex. Most features of the ECG signals are centered around the QRS complex. If the heartbeat is sampled over a long time interval, more noise information will be included, alternatively, a relatively short interval will lead to insufficient features. Therefore, 150 samples centered about the middle of the QRS complex are taken as the representation of each single-lead beat, which can cover the features of a QRS complex. To verify the proposed model, 1720 heartbeats from the INCART database with seven detailed categories are selected randomly. The statistics of the dataset are shown in Table 1.

Table 1.  Information about the dataset selected from the INCART database.

Type	Description	Quantity
N	Normal beat	500
V	Premature ventricular contraction	500
A	Atrial premature beat	200
F	Fusion of ventricular and normal beat	200
n	Supraventricular escape beat	30
R	Right bundle branch block beat	200
j	Nodal (junctional) escape beat	90
Total		1720

---

 | Show Table

DownLoad: CSV

5.1.2.   Evaluation metrics

Five-fold cross-validation is used for the experimental analysis. The heartbeats are sampled randomly in the dataset described above. In each experiment, one part is used as test data and the other four parts as training data. After five experiments, five confusion matrices are added together to obtain an overall confusion matrix, which is then used to compute the evaluation metrics in accordance with the corresponding formulas, including the overall accuracy (Ov.Acc), accuracy (Acc), sensitivity (Sen), precision (Ppv), specificity (Spe) and F1-score.

where TP, TN, FP and FN denote the true positive, true negative, false positive, and false negative rates, respectively. And, in Eq (5.1), $n$ means the number of arrhythmia categories, $(TPr)_i$ means the number of correct predictions in each category, and M means the number of all samples.

5.1.3.   Implementation details

Following previous studies, we choose 1, 2, 3 and 12 as respective values of D, which is the number of leads for experimental analysis. The ECG signals from Leads Ⅱ and V1 were found to have clear QRS and T waves, as well as large P waves. P waves can indicate potential changes in the atria and reflect atrial excitation. T waves reflect the depolarization process after ventricular excitation, and they have diagnostic significance. The ECG signals from Lead V5 are distinct with clear QRS waves. The R waves observed for Lead Ⅱ are always larger than the S waves. Lead V1 is dominated by negative waves, and Lead V5 is dominated by the R wave. Information fusion for these three leads can be applied to better detect different contents of QRS wave groups. Thus, the single leads, Lead Ⅱ, V1 and V5, are selected for experimental analysis, and their combination is used for multi-lead ECG classification.

For model training, the hidden dimension of the MADHGAT is set to be 512 and the number of layers is set as 2. The learning rate is set to be 0.003, while the dropout rate is 0.8 and the regularization coefficient $\eta$ is set to be 5 $\times 10^{-8}$. To avoid overfitting, the L2 regularization method is adopted.

5.2.   Baseline methods

Some baseline methods are described as follows, including the DL-CCANet ^[50], TL-CCANet ^[50], RandNet ^[50], PCANet ^[51], 1-D ResNet ^[52] and 1-D CCANet-SVD ^[52].

1) DL-CCANet is a model for two-lead arrhythmia detection, and TL-CCANet is used for three leads. Their main ideas are the same, and the core lies in the CCANet model, which includes two cascaded convolutional layers for the feature extraction of different leads, as well as an output layer. The difference between TL-CCANet and DL-CCANet is that TL-CCANet has an additional input channel.

2) RandNet is widely used in image learning. It is an unsupervised neural network with compressed inputs for deriving learning representations from compressed data to enable the accommodation of large amounts of data. RandNet was employed to process one-lead ECG signals for heartbeat classification.

3) PCANet uses principal component analysis (PCA), which is a linear subspace projection technique for downsampling high-dimensional datasets and minimizing reprojection errors. By applying PCA filtering for continuous convolution and iteration, the vector representations of the ECG signals were obtained and finally used for heartbeat classification.

4) 1-D ResNet is also widely used in image learning. The model has a deep residual learning framework, which includes residual representations and shortcut connections to solve the degradation problem in a deep learning environment and determine the accuracy gain of arrhythmia detection. Through the use of convolutional layers and residual blocks, two input channels can fuse the information of two leads.

5) 1-D CCANet-SVD is an improved variant of CCANet. For each set of two leads, three types of artificial features including the one-dimensional spectrogram, autoregressive model and time-domain features are applied as the input of CCANet-SVD for neural feature extraction. Then, neural features are fed to an SVM for heartbeat classification.

5.3.   Result analysis

5.3.1.   Single-lead ECG classification

Single-lead signals are a special case of multi-lead signal. We perform arrhythmia detection for three single-lead signals, i.e., Lead Ⅱ, V1 and V5. Tables 2–4 show their confusion matrices and performance results, which are obtained by applying our model for single-lead experiments. The overall accuracy is determined to be 0.9413, 0.9378 and 0.9378, respectively. Compared with PCANet and RandNet (Table 5), which do not incorporate any handcrafted features, our method improves the overall accuracy for all single leads by about 2% on average. And in the case of Lead V1, we improve the performance by 3% relative to RandNet, which shows that our method takes advantage of single lead data and the heterogeneous graph we constructed works. Since multi-lead beats are composed of their single-lead beats, the relationships between multi-lead beats and their corresponding single-lead beats are useless in the single-lead experiment. However, we still consider the relationship between heartbeats of the same lead as well as the relationship between the lead and the heartbeat, so that the model can still consider the global and local information. In the baseline model, PCANet and RandNet can only consider their own situation in the case of one lead, which reflects the advantages of our model.

Table 2.  Results for single-lead Ⅱ.

	Predicted							Acc	Sen	Ppv	Spe	F1-score
	N	V	A	F	n	R	j
N	487	4	5	3	1	0	0	0.9645	0.9740	0.9103	0.9607	0.9411
V	13	477	0	10	0	0	0	0.9715	0.9540	0.9483	0.9787	0.9511
A	20	1	176	1	0	1	1	0.9814	0.8800	0.9565	0.9947	0.9167
F	10	17	2	170	0	0	1	0.9738	0.8500	0.9189	0.9901	0.8831
n	3	0	1	0	26	0	0	0.9971	0.8667	0.9630	0.9994	0.9123
R	0	4	0	0	0	196	0	0.9971	0.9800	0.9949	0.9993	0.9874
j	2	0	0	1	0	0	87	0.9971	0.9667	0.9775	0.9988	0.9721
Average								0.9832	0.9245	0.9528	0.9888	0.9377
Overall accuracy												0.9413

---

 | Show Table

DownLoad: CSV

Table 3.  Results for single-lead V1.

	Predicted							Acc	Sen	Ppv	Spe	F1-score
	N	V	A	F	n	R	j
N	477	7	4	9	2	0	1	0.9657	0.9540	0.9298	0.9705	0.9418
V	4	483	2	11	0	0	0	0.9715	0.9660	0.9379	0.9738	0.9517
A	12	2	183	3	0	0	0	0.9860	0.9150	0.9632	0.9954	0.9385
F	17	21	1	157	0	2	2	0.9610	0.7850	0.8674	0.9842	0.8241
n	2	0	0	1	27	0	0	0.9971	0.9000	0.9310	0.9988	0.9153
R	0	1	0	0	0	199	0	0.9977	0.9950	0.9851	0.9980	0.9901
j	1	1	0	0	0	1	87	0.9965	0.9667	0.9667	0.9982	0.9667
Average								0.9822	0.9260	0.9402	0.9884	0.9326
Overall accuracy												0.9378

---

 | Show Table

DownLoad: CSV

Table 4.  Results for single-lead V5.

	Predicted							Acc	Sen	Ppv	Spe	F1-score
	N	V	A	F	n	R	j
N	488	6	3	1	0	0	2	0.9581	0.9760	0.8905	0.9508	0.9313
V	11	482	0	6	0	0	1	0.9733	0.9640	0.9451	0.9770	0.9545
A	25	5	169	1	0	0	0	0.9779	0.8450	0.9602	0.9954	0.8989
F	15	14	3	168	0	0	0	0.9767	0.8400	0.9545	0.9947	0.8936
n	2	0	0	0	28	0	0	0.9988	0.9333	1.0000	1.0000	0.9655
R	0	3	0	0	0	196	1	0.9977	0.9800	1.0000	1.0000	0.9899
j	7	0	1	0	0	0	82	0.9930	0.9111	0.9535	0.9975	0.9318
Average								0.9822	0.9213	0.9577	0.9879	0.9379
Overall accuracy												0.9378

---

 | Show Table

DownLoad: CSV

Table 5.  Results of applying various methods for single-lead analysis.

Method	Year	#Types	#Samples	Ov.ACC
PCANet (Ⅱ)	2018	7	1720	93.72%
PCANet (V1)	2018	7	1720	92.10%
PCANet (V5)	2018	7	1720	93.37%
RandNet (Ⅱ)	2019	7	1720	92.67%
RandNet (V1)	2019	7	1720	90.76%
RandNet (V5)	2019	7	1720	92.91%
MADHGAT (Ⅱ)	2022	7	1720	94.13%
MADHGAT (V1)	2022	7	1720	93.78%
MADHGAT (V5)	2022	7	1720	93.78%

---

 | Show Table

DownLoad: CSV

5.3.2.   Multi-lead ECG classification

The experimental results of multi-lead classification will be presented for two-lead, three-lead and 12-lead ECG signal data. Tables 6–8 show the confusion matrices and classification results for the MADHGAT model with two-lead signals. The overall accuracy is found to be 0.9494, 0.9523 and 0.9547, respectively. It is clear that the performance with two-lead signals is better than that with single-lead signals.

Table 6.  Results for two leads: Ⅱ and V1.

	Predicted							Acc	Sen	Ppv	Spe	F1-score
	N	V	A	F	n	R	j
N	484	7	2	5	2	0	0	0.9727	0.9680	0.9398	0.9746	0.9537
V	5	488	0	6	0	0	1	0.9767	0.9760	0.9457	0.9770	0.9606
A	13	1	181	4	0	1	0	0.9866	0.9050	0.9784	0.9974	0.9403
F	5	11	1	183	0	0	0	0.9797	0.9150	0.9104	0.9882	0.9127
n	3	0	0	1	25	1	0	0.9959	0.8333	0.9259	0.9988	0.8772
R	0	8	0	0	0	192	0	0.9936	0.9600	0.9846	0.9980	0.9722
j	5	1	1	2	0	1	80	0.9936	0.8889	0.9877	0.9994	0.9357
Average								0.9855	0.9209	0.9532	0.9905	0.9360
Overall accuracy												0.9494

---

 | Show Table

DownLoad: CSV

Table 7.  Results for two leads: Ⅱ and V5.

	Predicted							Acc	Sen	Ppv	Spe	F1-score
	N	V	A	F	n	R	j
N	484	8	1	6	1	0	0	0.9698	0.9680	0.9308	0.9705	0.9490
V	5	486	1	7	0	1	0	0.9785	0.9720	0.9548	0.9811	0.9633
A	14	2	181	3	0	0	0	0.9866	0.9050	0.9784	0.9974	0.9403
F	11	9	2	177	0	0	1	0.9773	0.8850	0.9171	0.9895	0.9008
n	3	0	0	0	27	0	0	0.9977	0.9000	0.9643	0.9994	0.9310
R	0	4	0	0	0	196	0	0.9971	0.9800	0.9949	0.9993	0.9874
j	3	0	0	0	0	0	87	0.9977	0.9667	0.9886	0.9994	0.9775
Average								0.9864	0.9395	0.9613	0.9909	0.9499
Overall accuracy												0.9523

---

 | Show Table

DownLoad: CSV

Table 8.  Results for two leads: V1 and V5.

	Predicted							Acc	Sen	Ppv	Spe	F1-score
	N	V	A	F	n	R	j
N	489	6	2	3	0	0	0	0.9750	0.9780	0.9386	0.9738	0.9579
V	4	489	0	7	0	0	0	0.9785	0.9780	0.9495	0.9787	0.9635
A	16	1	181	1	1	0	0	0.9866	0.9050	0.9784	0.9974	0.9403
F	7	16	1	175	0	1	0	0.9791	0.8750	0.9409	0.9928	0.9067
R	2	0	0	0	27	1	0	0.9971	0.9000	0.9310	0.9988	0.9153
j	0	3	0	0	1	195	1	0.9959	0.9750	0.9898	0.9987	0.9824
n	3	0	1	0	0	0	86	0.9971	0.9556	0.9885	0.9994	0.9718
Average								0.9870	0.9381	0.9595	0.9914	0.9483
Overall accuracy												0.9547

---

 | Show Table

DownLoad: CSV

Table 9 shows the confusion matrix and classification results for the MADHGAT model with three-lead signals. The overall accuracy is 0.9552. It can be noticed that the three-lead results are better than the two-lead results. However, we can find that the three-lead experiment yields similar results as the experiment with Leads V1 and V5. In this regard, we think that the key reason is limited sampled heartbeats, which has led slightly different experimental results. Table 10 shows the classification results for the MADHGAT model with 12-lead signals. The overall accuracy is 0.9721. It outperforms the three-lead experiment by almost 2%.

Table 9.  Results for three leads: Ⅱ, V1 and V5.

	Predicted							Acc	Sen	Ppv	Spe	F1-score
	N	V	A	F	n	R	j
N	489	6	2	3	0	0	0	0.9756	0.9780	0.9404	0.9746	0.9588
V	3	490	0	7	0	0	0	0.9791	0.9800	0.9496	0.9787	0.9646
A	16	1	181	1	1	0	0	0.9866	0.9050	0.9784	0.9974	0.9403
F	7	16	1	175	0	1	0	0.9791	0.8750	0.9409	0.9928	0.9067
n	2	0	0	0	27	1	0	0.9971	0.9000	0.9310	0.9988	0.9153
R	0	3	0	0	1	195	1	0.9959	0.9750	0.9898	0.9987	0.9824
j	3	0	1	0	0	0	86	0.9971	0.9556	0.9885	0.9994	0.9718
Average								0.9872	0.9384	0.9598	0.9915	0.9485
Overall accuracy												0.9552

---

 | Show Table

DownLoad: CSV

Table 10.  Results with 12 leads.

	Predicted							Acc	Sen	Ppv	Spe	F1-score
	N	V	A	F	n	R	j
N	484	2	9	4	0	0	1	0.9820	0.9680	0.9699	0.9877	0.9690
V	1	496	0	3	0	0	0	0.9907	0.9920	0.9764	0.9902	0.9841
A	8	0	191	0	0	0	1	0.9890	0.9550	0.9502	0.9934	0.9526
F	3	6	1	190	0	0	0	0.9901	0.9500	0.9645	0.9954	0.9572
n	1	0	0	0	29	0	0	0.9994	0.9667	1.0000	1.0000	0.9831
R	0	4	0	0	0	195	1	0.9965	0.9750	0.9949	0.9993	0.9848
j	2	0	0	0	0	1	87	0.9965	0.9667	0.9667	0.9982	0.9667
Average								0.9920	0.9676	0.9747	0.9949	0.9711
Overall accuracy												0.9721

---

 | Show Table

DownLoad: CSV

Figure 5 integrates our results above, and it can be clearly seen that as we apply more leads, the classification results gradually improved. This is because in the case of multiple leads, the heterogeneous graph we constructed can utilize the associations of leads so that the MADHGAT model can obtain more information on the multi-lead ECG signals to strengthen its learning ability and more accurately assign a multi-lead heartbeat to a certain category. It is proved that our model can consider the correlations between different leads and improve the performance of arrhythmia diagnosis.

Figure 5.  Results of our work with different leads.

DownLoad: Full-Size Img PowerPoint

Table 11 shows the results of comparing several models with multiple leads. DL-CCANet, TL-CCANet and MADHGAT are end-to-end models without any handcrafted features. The 1-D CCANet-SVD and 1-D ResNet models need handcrafted feature extraction. Our model with 12 leads achieves better performance than the others. Compared with DL-CCANet on the same leads, all three of our two-lead combinations outperform its results by approximately 1.3% on average. In the two-lead Ⅱ and V1, V1 and V5 combinations, the improvement is approximately 1.2% and 1.6%, respectively. Although DL-CCANet considers information fusion for two leads, it joins and reconstructs the signals of two leads separately to obtain features, which are then fed into CCANet to extract the fused features. However, it not only ignores the correlations between single-lead beats for the same lead, but also does not consider the associations between the overall leads and two-lead beats. It shows that our method can better utilize intra-lead and inter-lead correlations.

Table 11.  Results of applying various methods with multiple leads.

Method	Year	#Types	#Samples	Ov.ACC
DL-CCANet (Ⅱ and V1)	2019	7	1720	94.01%
DL-CCANet (Ⅱ and V5)	2019	7	1720	94.07%
DL-CCANet (V1 and V5)	2019	7	1720	93.90%
TL-CCANet (Ⅱ, V1 and V5)	2019	7	1720	95.52%
1-D ResNet (Ⅱ and V1)	2021	7	1720	86.25%
1-D CCANet-SVD (w/o SVD) (Ⅱ and V1)	2021	7	1720	93.60%
1-D CCANet-SVD (w/o ar) (Ⅱ and V1)	2021	7	1720	95.12%
1-D CCANet-SVD (w/o 1D-spec) (Ⅱ and V1)	2021	7	1720	94.77%
1-D CCANet-SVD (w/o time-domain feature) (Ⅱ and V1)	2021	7	1720	95.35%
1-D CCANet-SVD (w/o stack) (Ⅱ and V1)	2021	7	1720	94.83%
1-D CCANet-SVD (Ⅱ and V1)	2021	7	1720	95.70%
MADHGAT (Ⅱ and V1)	2022	7	1720	94.94%
MADHGAT (Ⅱ and V5)	2022	7	1720	95.23%
MADHGAT (V1 and V5)	2022	7	1720	95.47%
MADHGAT (Ⅱ, V1 and V5)	2022	7	1720	95.52%
MADHGAT (12 leads)	2022	7	1720	97.21%

---

 | Show Table

DownLoad: CSV

At the same time, the results for Leads Ⅱ and V1 indicate that our model still outperforms several variants of 1-D CCANet-SVD which need some artificial features. For example, 1-D CCANet-SVD without singular value decomposition (SVD) adds time-domain features, autoregressive modeling and a one-dimensional spectrogram, but lacks SVD assistance. Nonetheless, we can still achieve better arrhythmia diagnosis by obtaining information from the leads. In the case of 1-D CCANet-SVD, one-dimensional spectrogram features capture the frequency representation of the signal over time. Autoregressive modeling is applied to capture features that can fit their own time series. Time-domain features take into account the information from the previous heartbeat signal from the same lead, as well as include higher-order centroids and kurtosis. These manual features enable the capture of information about the previous heartbeat, the global frequency domain, etc. All of these features only consider each lead itself. Finally, the CCANet model was utilized to fuse the information of two leads for classification. However, this method aims to mine the content of each lead and heartbeat, missing the associations between different heartbeats of the same lead, as well as the associations between multi-lead heartbeats and single-lead heartbeats. Although 1-D CCANet-SVD achieved 95.70% with all of the handcrafted features, our overall accuracy of 97.21% with 12 leads, which is achieved without any feature extraction, is still higher by 1.51%. We have greatly improved the performance by taking into account inter-lead and intra-lead correlations. The performance of arrhythmia detection can still be excellent without cumbersome handcrafted feature extraction.

Overall, the MADHGAT model achieves the best results among all of the models for all different numbers of leads. Meanwhile, it is obvious that multiple leads are important for arrhythmia detection, as overall detection performance is improved significantly with more leads. This indicates the effectiveness of the proposed MADHGAT model to capture inter-lead and intra-lead information.

5.3.3.   Ablation experiment

For the constructed graph, we have defined three kinds of nodes. In this experiment, we decide to consider the importance of two kinds of nodes: multiple leads and single-lead beats. Three leads, i.e., Leads Ⅱ, V1 and V5 are applied in this experiment with seven categories. We eliminate the nodes of multiple leads and single-lead beats individually and in combination. The results in Table 12 indicate that the full graph with three types of nodes performs better than the graphs with missing nodes, proving the effectiveness of our graph structure.

Table 12.  Performance comparison with different graph nodes for three leads.

Graph	Ov.ACC	Avg-Acc	Avg-Sen	Avg-Ppv	Avg-Spe	Avg-F1
without multiple leads	0.9384	0.9824	0.9152	0.9345	0.9884	0.9243
without single-lead beats	0.8273	0.9507	0.7660	0.8507	0.9670	0.7975
only multi-lead beats	0.8070	0.9449	0.7070	0.8542	0.9623	0.7568
full graph	0.9552	0.9872	0.9384	0.9598	0.9915	0.9485

---

 | Show Table

DownLoad: CSV

We can find that the result of removing single-lead beat nodes is a deterioration for every metric relative to the full graph. The most obvious difference is in overall accuracy, which differs by about 13%. This reflects the importance of the relationship between single-lead beats and multi-lead beats, as well as the intra-lead correlations between single-lead beats, which are used to allow the MADHGAT model to capture the contribution of each single-lead beat.

When removing the nodes of multiple leads, relative to the results for the full graph, the overall accuracy is reduced by about 2%. At the same time, it is found that other indicators on average also decrease accordingly. The nodes of multiple leads consider the global information for all heartbeats from a certain lead and transmit the information to the multi-lead heartbeat nodes. Meanwhile, the inter-lead correlations between multiple leads are constructed, improving the performance of arrhythmia detection.

Finally, we remove the nodes of multiple leads and single-lead beats. Only multi-lead beat nodes remain in the heartbeat graph. The final result is the worst because it does not take into account any additional information. Compared to the other cases, it also proves the contributions of the inter-lead and intra-lead correlations.

5.3.4.   Impact of training set

The proposed MADHGAT model is based on an HGAT, which is transductive and therefore observes all of the data beforehand for classification. To evaluate the performance of MADHGAT with different training set proportions, experiments are conducted using Leads Ⅱ and V1 with different ratios of training data to test data, i.e., 1:2, 1:1, 2:1 and 3:1. The results have been compared with the five-fold results, as shown in Table 13. The experimental results of some baseline methods are also listed.

Table 13.  Impact of the training set with leads Ⅱ and V1.

Ratio of training set to test set	Method	Ov.ACC
4:1	DL-CCANet (Ⅱ and V1)	94.01%
4:1	1-D CCANet-SVD (w/o SVD) (Ⅱ and V1)	93.60%
4:1	1-D ResNet (Ⅱ and V1)	86.25%
4:1	MADHGAT	94.94%
3:1	MADHGAT	94.36%
2:1	MADHGAT	94.48%
1:1	MADHGAT	92.38%
1:2	MADHGAT	90.20%

---

 | Show Table

DownLoad: CSV

When the ratio of training set to test set is 1:2, our model is still able to achieve an overall accuracy of 90.20%, which is still better than the ResNet method. Meanwhile, when the ratio is greater than or equal to 2:1, the overall accuracy rate is above 94%. We find that after reducing the number of training sets, our results are still better than some methods. For example, in the case of a 2:1 ratio, our model achieves 94.48% which is higher than that for several methods listed in Table 13. Moreover, 1-D CCANet-SVD needs handcrafted features. Therefore, it is not difficult to conclude that MADHGAT can still achieve better results when the ratio of training data to test data is decreased. And it shows that our proposed MADHGAT framework can capture effective information, making the model more robust and generalizable.

6.   Conclusions

A novel multi-lead arrhythmia detection model based on an HGAT has been proposed in this paper. Multi-lead ECG signals are modeled as a heterogeneous graph to integrate rich information. Additionally, intra-lead and inter-lead correlations are constructed to capture intricate interactions among multi-lead signals. This work provides a reasonable and effective data model that utilizes a heterogeneous graph neural network with dual-level attention strategy to quantify the contributions of different types of information, thereby improving detection performance. At the same time, our model does not require any feature extraction process for ECG signal analysis, which avoids complex feature engineering.

Though the proposed model performs excellently for automatic arrhythmia detection, it is transductive. An extremely massive amount of memory is needed for the training process. In light of this problem, in the future, we will focus on developing an inductive learning model based on a graph neural network that can handle more data.

Acknowledgments

This work is supported by the Natural Science Foundation of Guangdong Province (No. 2021A1515012290), Guangdong Provincial Key Laboratory of Cyber-Physical Systems (No. 2020B1212060069) and National & Local Joint Engineering Research Center of Intelligent Manufacturing Cyber-Physical Systems.

Conflict of interest

The authors declare that there is no conflict of interest.