Citation: Etti G. Baranoff, Patrick Brockett, Thomas W. Sager, Bo Shi. Was the U.S. life insurance industry in danger of systemic risk by using derivative hedging prior to the 2008 financial crisis?[J]. Quantitative Finance and Economics, 2019, 3(1): 145-164. doi: 10.3934/QFE.2019.1.145
| [1] | Marco Tosato, Jianhong Wu . An application of PART to the Football Manager data for players clusters analyses to inform club team formation. Big Data and Information Analytics, 2018, 3(1): 43-54. doi: 10.3934/bdia.2018002 |
| [2] | Wenxue Huang, Qitian Qiu . Forward Supervised Discretization for Multivariate with Categorical Responses. Big Data and Information Analytics, 2016, 1(2): 217-225. doi: 10.3934/bdia.2016005 |
| [3] | Yiwen Tao, Zhenqiang Zhang, Bengbeng Wang, Jingli Ren . Motality prediction of ICU rheumatic heart disease with imbalanced data based on machine learning. Big Data and Information Analytics, 2024, 8(0): 43-64. doi: 10.3934/bdia.2024003 |
| [4] | Guojun Gan, Qiujun Lan, Shiyang Sima . Scalable Clustering by Truncated Fuzzy c-means. Big Data and Information Analytics, 2016, 1(2): 247-259. doi: 10.3934/bdia.2016007 |
| [5] | Jiaqi Ma, Hui Chang, Xiaoqing Zhong, Yueli Chen . Risk stratification of sepsis death based on machine learning algorithm. Big Data and Information Analytics, 2024, 8(0): 26-42. doi: 10.3934/bdia.2024002 |
| [6] | Sayed Mohsin Reza, Md Al Masum Bhuiyan, Nishat Tasnim . A convolution neural network with encoder-decoder applied to the study of Bengali letters classification. Big Data and Information Analytics, 2021, 6(0): 41-55. doi: 10.3934/bdia.2021004 |
| [7] | Cai-Tong Yue, Jing Liang, Bo-Fei Lang, Bo-Yang Qu . Two-hidden-layer extreme learning machine based wrist vein recognition system. Big Data and Information Analytics, 2017, 2(1): 59-68. doi: 10.3934/bdia.2017008 |
| [8] | Jinyuan Zhang, Aimin Zhou, Guixu Zhang, Hu Zhang . A clustering based mate selection for evolutionary optimization. Big Data and Information Analytics, 2017, 2(1): 77-85. doi: 10.3934/bdia.2017010 |
| [9] | M Supriya, AJ Deepa . Machine learning approach on healthcare big data: a review. Big Data and Information Analytics, 2020, 5(1): 58-75. doi: 10.3934/bdia.2020005 |
| [10] | Guojun Gan, Kun Chen . A Soft Subspace Clustering Algorithm with Log-Transformed Distances. Big Data and Information Analytics, 2016, 1(1): 93-109. doi: 10.3934/bdia.2016.1.93 |
Herbicides are regarded as a threat to the environment. These highly toxic compounds are resistant to biological and photochemical degradation, and as such, persist in the environment for extended periods of time, constituting a major risk to human health and to the ecosystem [1,2]. Herbicides are known as complex materials, characterized by high concentrations of organic (COD and TOC) and nitrogenous (TKN and NH4) compounds, inhibitory and non-biodegradable organic compounds, such as adsorbable organic halogens (AOX), and by high salinity. Conventional biological treatment processes are not always suitable for these types of contaminants.
The powdered activated carbon treatment (PACT) process, in which powdered activated carbon (PAC) is added directly into the aerobic reactor of an activated sludge system to concurrently provide biological oxidation and adsorption, was developed by Dupont in the 1970s [3]. It is advantageous to the conventional activated sludge (CAS) process in terms of (1) process stability; (2) removal of refractory organics; (3) increasing mixed liquor suspended solids (MLSS) concentration, with increased biological activity; and (4) enhanced nitrification due to adsorption of inhibitory compounds [4].
Membrane bioreactors (MBRs), which are increasingly used in the treatment of industrial wastewater, are capable of integrating nitrification and de-nitrification processes, as (1) they are operated at considerably high biomass concentrations; (2) have a long solids retention time (SRT) and a short hydraulic retention time (HRT); (3) they eliminate biomass settling problems (filamentous growth); and (4) produce high effluent quality: low levels of turbidity, total suspended solids (TSS), and bacteria [5]. Moreover, the long SRT results in reduced excess sludge removal requirements and reduces PAC makeup requirements (lower operating cost) [6].
The efficacy of the PACT process has been examined in numerous studies. Addition of PAC to a textile processing wastewater treatment plant resulted in a sharp increase of 87% in the AOX removal efficiency, however with no effect on COD removal [7]. Addition of PAC to a drug synthesis wastewater treatment plant was reported to significantly increase the removal rate of SCOD as well as increase the biomass oxygen uptake rate (OUR) due to increased adsorption of the inhibitory compounds [8].
The primary objective of this research was to investigate the effectiveness of modifying a dual-sludge membrane biological system (DSS-MBR) with PAC (DSS-MBR-PACT), thus increasing the removal efficiencies of nitrogen compounds, TOC, and AOX from the wastewater of an herbicides production plant.
The research, which was conducted in a dedicated pilot system, employed two consecutive, fully independent sludge systems: CAS for removal of readily biodegradable organic compounds, followed by a MBR for facilitating efficient nitrification and de-nitrification processes. PAC was added to the MBR system to improve nitrogen removal, as well as residual recalcitrant organic compounds. The removal efficiencies of the above mentioned compounds by the DSS-MBR and the DSS-MBR-PACT systems were compared. To the best of our knowledge, this is the first time in which applicability of PAC supplementation in the treatment of such wastewater has been addressed in the literature.
The wastewater of an herbicides production plant located in Israel is currently treated in a full-scale wastewater treatment plant that comprises two sequential systems—pretreatment in a physic-chemical system followed by the main biological treatment system, prior to effluent discharge into the sea. The pretreatment system is designed to decrease the load of the inhibitory compounds, suspended solids, and volatile organic compounds (VOCs) on the downstream biological treatment system in several consecutive process steps that include neutralization, coagulation and flocculation, clarification by gravitational settling and dissolved air floatation (DAF), and air stripping. The main biological treatment facility employs two consecutive systems—an aerobic CAS system followed by an aerobic and post-anoxic MBR system for nitrification and de-nitrification. In the present study, the research pilot plant was fed with wastewater from the physico-chemical system effluent tank.
Biological processes, particularly nitrification, are known to be very sensitive to high salinity wastewater. Therefore, the raw wastewater, with a high salinity of about 1.5% (w/w), is diluted with low salinity local well water to a ratio of 0.8 (volume of dilution well water/volume of raw wastewater) prior to being fed into the full-scale biological treatment plant. The characteristics of the raw wastewater after the physico-chemical pre-treatment are detailed in table 1.
| Parameter (Units) | Value |
| pH | 7.7 ± 0.34 |
| Alkalinity (meq/L) | 16.5 ± 5.0 |
| TSS (mg/L) | 59.3 ± 52.0 |
| Turbidity (NTU) | 73.2 ± 72.8 |
| Chlorides (g/L) | 5.23 ± 1.60 |
| TDS (g/L) | 14.2 ± 4.1 |
| NH3-N (mg/L as N) | 11.0 ± 6.80 |
| Norg-N (mg/L as N) | 219 ± 82.7 |
| TKN (mg/L as N) | 230 ± 84.9 |
| NO2-N (mg/L as N) | 0.37 ± 0.90 |
| NO3-N (mg/L as N) | 1.6 ± 2.50 |
| TN (mg/L as N) | 236 ± 71.0 |
| BOD (mg/L) | 3660 ± 1110 |
| tCOD (mg/L) | 6610 ± 1620 |
| sCOD (mg/L) | 5600 ± 1820 |
| TOC (mg/L) | 1720 ± 560 |
| AOX (mg/L) | 50.4 ± 25.4 |
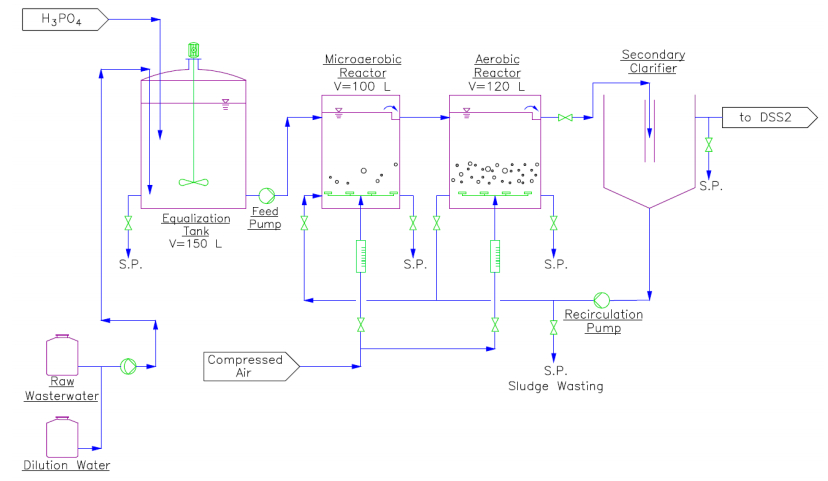
DownLoad: CSVThe study was conducted using a continuous dual sludge system (DSS) pilot plant that simulated the full-scale biological treatment plant. It employed two functional sludge systems. The first, a regular CAS system designated as DSS1 (Figure 1), consisted of a 100 L micro-aerobic reactor, a special eco-system in which aerobic and anaerobic bacteria can coexist. This eco-system was operated under O2 limited conditions with a Dissolved Oxygen (DO) of about 0.5 mg/L. Wastewater from herbicides manufacturing processes contains various compounds which are refractory under aerobic conditions and seem to be readily bio-transformed anaerobically. In turn, partially degraded products which resist anaerobic degradation can be completely mineralized by aerobic microorganisms. The combination of anaerobic and aerobic conditions has been shown to improve biodegradation and bio-detoxification [9,10]. This system was followed by 120 L aerobic reactor and a secondary gravitational clarifier for biomass separation. The micro-aerobic and aerobic reactors were equipped with air diffusers installed at the bottom of both tanks that maintained the Dissolved Oxygen (DO) concentrations at 0–1 mg/L and 3–5 mg/L, respectively. One magnetic dosing pump was used to ensure that wastewater from the 150 L equalization tank was continuously fed into the micro-aerobic reactor at a setpoint flow rate. On a daily basis, 5 cm3 of phosphoric acid solution (79% w/w) was added to the equalization tank to provide sufficient phosphorous nutrient for the biomass growth. At the beginning of each day, the equalization tank was filled with the wastewater at the correct dilution ratio. Effluent from the secondary clarifier overflowed to the second sludge system. Mixed liquor from the bottom of the clarifier was recirculated back and distributed evenly to the two reactors. A sludge age of 20–30 days was controlled via daily sludge wasting from the sampling ports (S.P. in figure 1 and 2).
Figure 1. Schematic diagram of the first (CAS) sludge system—DSS1.
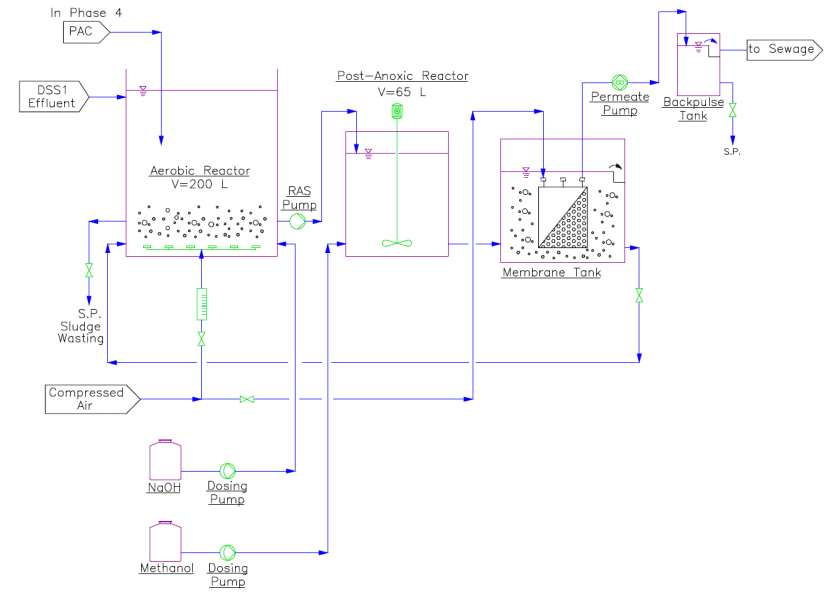
Figure 2. Schematic diagram of the second (MBR) sludge system—DSS2.The second sludge system, which is a MBR, designated as DSS2 (Figure 2), comprised a 200 L aerobic reactor followed by a 65 L post-anoxic reactor and a 36 L membrane tank for final biomass separation. The aerobic reactor was equipped with air diffusers that maintained a DO concentration of 4–4.5 mg/L. The mixed liquor from the aerobic reactor was pumped to the post-anoxic reactor by a 1/2" air-operated double diaphragm pump at a flow rate of approximately 3 m3/h. The post-anoxic reactor was continuously mixed by a top-mounted mixer to ensure that the mixed liquor remained in suspension. The mixed liquor from the post-anoxic reactor overflowed to the membrane tank through a bottom interconnecting pipe. The membrane tank employed a ZW-10 submerged hollow-fiber 0.04 µm ultrafiltration PVDF membrane module with a filtration area of 0.93 m2 (GE Water). The membrane system was operated on a repeating filtration cycle of two phases—5 min of permeation followed by 30 s of back-pulsing at a net flux of 3–4 L/(m2·h). The permeation/backwash cycles were commenced using a reversible gear pump (series GJ, model 150 by Micropump). Compressed air was introduced into the membrane module to provide the required air scouring for fouling control. Mixed liquor from the membrane tank recirculated back to the aerobic reactor by overflowing through a bottom interconnecting pipe. A sludge age of 90 days was controlled via daily sludge wasting from the aerobic reactor. Diluted methanol solution (0.3% v/v) was dosed to the post-anoxic reactor at a flow rate of 0.5 L/h to provide sufficient electron donors for the de-nitrification process.
The pilot plant was operated for about 400 days over the course of the study, which were divided into four consecutive phases (Table 2). The pilot system was initially seeded with biomass taken from the parallel sludge systems of the full-scale biological treatment plant, as it was already acclimated to this kind of wastewater.
| Phase | Dilution Ratio | Flow Rate (L/day) | PAC Conc. (mg/L) | Duration (days) |
| 1 | 0.8 | 100 | 0 | 93 |
| 2 | 0.5 | 80 | 0 | 112 |
| 3 | 0 | 80 | 0 | 111 |
| 4 | 0 | 80 | 2000 | 88 |
DownLoad: CSVDuring the first two phases, the raw wastewater dilution ratio decreased from 0.8 to 0.5, which brought about the reduction of the wastewater flow rate from 100 L/day to 80 L/day to sustain the same average contaminant load on the system, resulting in an increase of the overall HRT. The permeating net flux was thus decreased from 4.2 to 3.3 L/(m2–h). In the 3rd phase, the dilution ratio decreased to 0 (i.e., no dilution), but the flow rate was kept at 80 L/day to test the capability of the current system configuration to handle an increase of about 50% in the current organic load. In the 4th phase, 600 g of PAC was added to the second sludge system to reach an equilibrium concentration of 2000 mg/L. This PAC level was sustained by daily addition of 6.7 g (84 mg/L in DSS2 influent) to compensate for PAC loss in the wasted sludge, adjusted to maintain a sludge age of 90 days. As such, it was possible to accurately assess the contribution of PAC to system performance in terms of removal of the aforementioned compounds. System performance was evaluated based on the weekly average removal of ammoniacal nitrogen, organic nitrogen, total nitrogen, TOC, and AOX in the four research phases.
Activated carbon SX000X (Manufactured by Shanxi Sincere Industries Co. Ltd, China) was chosen to be the best adsorbent with this specific wastewater based on previous studies. The properties of this activated carbon are as follows: iodine number of 900, total surface area of 1400–1800 m2/g, apparent density of 210–370 kg/m3, ash content of 10%, and moisture level of 8%.
Samples were collected on a daily basis from three main sampling ports: equalization tank, DSS1 effluent, and final effluent. Two samples were taken from each of the first two ports, as one was filtered through 1.5 μm glass fiber filter paper (Grade 934-AH, Whatman). The DO, pH, and temperature of all reactors were monitored three times a day by field instruments.
The pH, alkalinity, TSS, VSS, turbidity, TDS, chlorides, nitrite, nitrate, total nitrogen, BOD, COD, TOC, and AOX were all measured according to the Standard Methods (APHA, 2012). Ammoniacal nitrogen was determined by salicylate titration using method 8155 by Hach (DR/2400 Spectrophotometer). AOX was analyzed by the Multi X 2500 system (Analytik Jena) conforming to Standard Method 5320 B (Adsorption-Pyrolysis-Titrimetric method).
The adsorption extent of AOX and TOC in DSS2 onto the PAC was examined in the lab by finding the best fit adsorption isotherms for both AOX and TOC. The adsorption isotherms can be used to estimate the required DSS2 PAC equilibrium concentration for the removal of AOX and TOC to below the sea discharge limits.
Adsorption tests were carried out in six 1 L glass flasks filled halfway with final (DSS2) effluent. PAC was added to five of the flasks (the sixth was a blank) at concentrations of 200,500,1000,5000 and 10 000 mg/L. All six flasks were mixed in a Jar Test system for 24 h at 120 RPM. A sample of 250 mL from each flask was filtered through 1.5 μm glass fiber filter paper into a plastic sampling jar for AOX and TOC analyses. These results were used to determine the best fit adsorption isotherms.
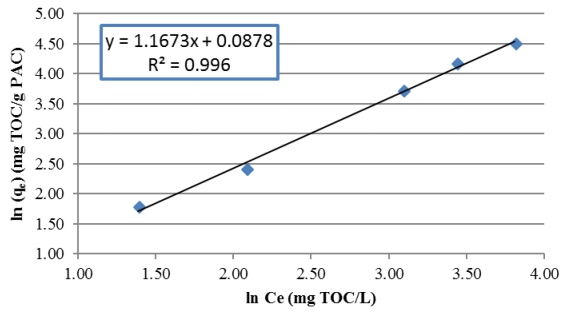
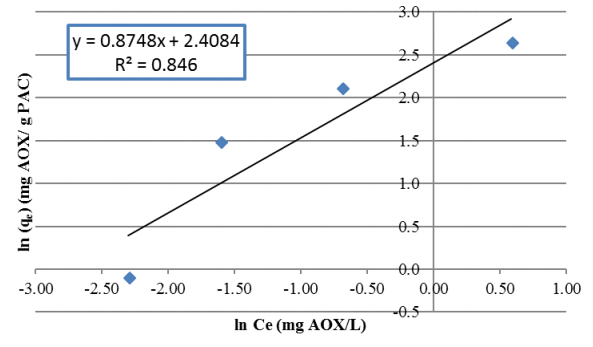
The TOC and AOX adsorption results show that the best fit to the experimental data was obtained using the Freundlich isotherm, with 99.6% and 84.6% fits, respectively (Figure 3 and 4). The Freundlich isotherm is described in equation 1:
| (1) |
Figure 3. Freundlich isotherm-fit for TOC adsorption onto PAC.
Figure 4. Freundlich isotherm-fit for AOX adsorption onto PAC.Where
qe: equilibrium adsorption capacity (mg adsorbate/g adsorbent).
Ce: equilibrium concentration of adsorbate (TOC or AOX) in solution after adsorption (mg/L).
Kf: Freundlich capacity factor (mg adsorbate/g activated carbon)(L water/mg adsorbate)1/n.
1/n: Freundlich intensity factor.
Inserting the derived adsorption constants for TOC adsorption onto PAC into the Freundlich equation results in equation 2:
| (2) |
Using equation 2, the maximum TOC adsorption capacity onto the PAC to ensure a maximum effluent TOC concentration of 100 mg/L, as required by environmental regulations, is 235 mg/g. Considering the DSS2 influent average TOC concentrations in phases 1, 2, and 3 of 170,450, and 480 mg/L respectively, the minimum equilibrium PAC concentrations in DSS2 that are in compliance with the TOC sea discharge limit should be 297,1490 and 1610 mg/L respectively.
Inserting the derived adsorption constants for AOX adsorption onto PAC into the Freundlich equation results in equation 3:
| (3) |
Using equation 3, the maximum AOX adsorption capacity onto the PAC to ensure a maximum effluent AOX concentration of 0.5 mg/L, as required by environmental regulations, is 6.04 mg/g. Considering the DSS2 influent average AOX concentrations in phases 1, 2, and 3 of 4.5, 11 and 17 mg/L respectively, the minimum equilibrium PAC concentrations in DSS2 that are in compliance with the AOX sea discharge limit should be 662,1740 and 2730 mg/L respectively.
The maximum required PAC adsorption capacity was much higher for the TOC than for the AOX, and therefore, the required equilibrium PAC concentration that is in compliance with the stringent discharge limits was much higher for the AOX than for the TOC, even though mass removal was higher for the TOC.
The 4th phase of the pilot operation involved an equilibrium concentration of 2000 mg/L, which represented the best tradeoff in terms of contaminant removal efficiency, economics (i.e., the elevated operational expenditure (OPEX) of the full-scale plant in terms of daily PAC make-up), and the potential for abrasion of the membrane fibers by the PAC particles, since a high concentration leads to stronger abrasion.
As required by environmental regulations, the sea discharge limits for ammoniacal nitrogen (NH3-N) and total nitrogen (TN) are 5 and 20 mg/L respectively. These two parameters and the organic nitrogen (Norg-N) content were therefore monitored on a daily basis throughout all four operation phases.
Figure 5 illustrates the influent nitrification potential of ammoniacal nitrogen, which represents the ammonia available for nitrification in DSS2, the effluent ammonia concentration with respect to the sea discharge limit of 5 mg/L, and the total ammonia removal efficiency during the pilot operation. Nitrification potential is defined as the influent TKN concentration minus the final effluent organic nitrogen concentration (considered as a non-biodegradable fraction). This term represents the "biodegradable" portion of the TKN that can potentially be removed by nitrification.
Figure 5. Ammoniacal nitrogen influent nitrification potentials and effluent concentrations and removal efficiencies.Table 3 details the average nitrification potential in each phase, the effluent average ammonia concentration, the average removal efficiency, the theoretical rise in effluent ammonia concentration (calculated based on the decrease of wastewater dilution only), and the actual rise in effluent ammonia concentration.
| Phase 1 | Phase 2 | Phase 3 | Phase 4 | |
| Nitrification Potential (mg N/L) | 68.8 ± 26.4 | 94.4 ± 57.6 | 205 ± 86.9 | 240 ± 105 |
| Effluent NH4-N (mg/L) | 2.26 ± 1.80 | 33.5 ± 32.7 | 64.6 ± 56.5 | 4.06 ± 7.46 |
| Removal | 95.6 ± 4.81 | 69.7 ± 26.1 | 73.7 ± 21.2 | 98.1 ± 1.50 |
| Theoretical Conc. Rise | 25% | 155% | 155% | |
| Actual Concentration Rise | 1380% | 2760% | 79% |
DownLoad: CSVThe effluent average ammonia concentration in phase 1 was far below the discharge limit (Table 3). As the dilution decreased to 0.5 and then to 0 in phases 2 and 3, respectively, the effluent average ammonia concentration rose sharply to almost 30 times the base concentration. At this stage, such an outcome was assumed to be due to a synergistic effect of the elevated salinity and the high concentration of inhibitory compounds in the raw wastewater as the dilution decreased, resulting in acute inhibition of the sensitive nitrifying bacteria. Therefore, the effluent ammonia concentration was far above the sea discharge limit.
The addition of PAC in the 4th phase resulted in a sharp decline in the effluent ammonia concentration to 4.06 mg/L, in spite of the high fluctuations in the plants' wastewater organic nitrogen content due to manufacturing variations during Phase 4. However, the low effluent ammonia concentration, which is below the sea discharge limit, indicates that the PAC addition sustained a very high and steady removal of the TKN. Furthermore, the observation that ammonia removal increased significantly to 98% with only minor fluctuations indicates a high-rate and stable removal. This can be attributed to the high capacity of the PAC, with its large specific surface area, to adsorb the toxic inhibitory compounds, thereby protecting the sensitive nitrifying bacteria, and allowing them to effectively oxidize the ammonia to nitrate. Additionally, the operation of phases 3 and 4 with equivalent mineral salinity levels meant that the acute inhibition of the nitrification process in this study, could be unequivocally determined to be the result only of the inhibitory compounds, which were adsorbed onto the PAC in phase 4. A comparison of the theoretical rise in effluent ammonia concentration and the actual rise in phase 4 showed that although the dilution decreased to 0 and the influent load increased by 50%, the actual rise (79%) was much lower than the theoretical increase (155%), which indicates a significant improvement in the nitrification process of the later phase compared to phase 1.
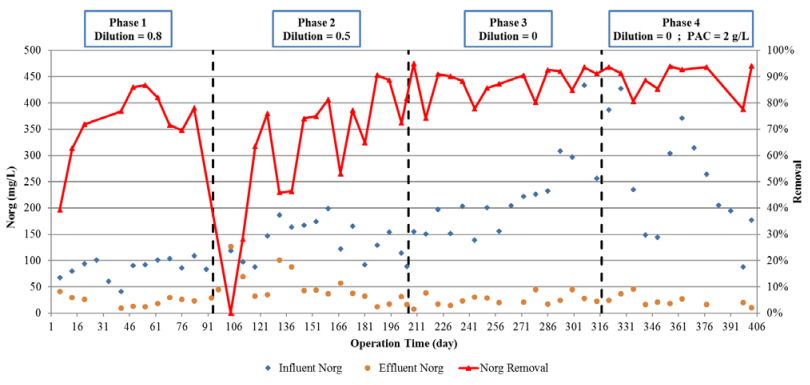
Figure 6 illustrates the influent and final effluent concentrations of organic nitrogen and its total removal efficiency in both sludge systems during the four operation phases.
Figure 6. Influent and effluent organic nitrogen concentrations and removal efficiencies.Table 4 details the average influent and final effluent concentrations of organic nitrogen, its removal efficiency in the first sludge system, and its total removal in both sludge systems.
| Phase 1 | Phase 2 | Phase 3 | Phase 4 | |
| Influent Norg (mg/L) | 85.2 ± 23.0 | 138 ± 45.4 | 210 ± 64.6 | 255 ± 106 |
| Effluent Norg (mg/L) | 23.0 ± 10.9 | 50.6 ± 34.1 | 25.7 ± 18.2 | 24.3 ± 13.2 |
| DSS1 Removal (%) | 62.2 ± 12.5 | 40.3 ± 22.5 | 61.6 ± 22.6 | 85.2 ± 8.85 |
| Total Removal (%) | 72.5 ± 13.8 | 65.5 ± 24.5 | 87.1 ± 5.94 | 89.2 ± 6.01 |
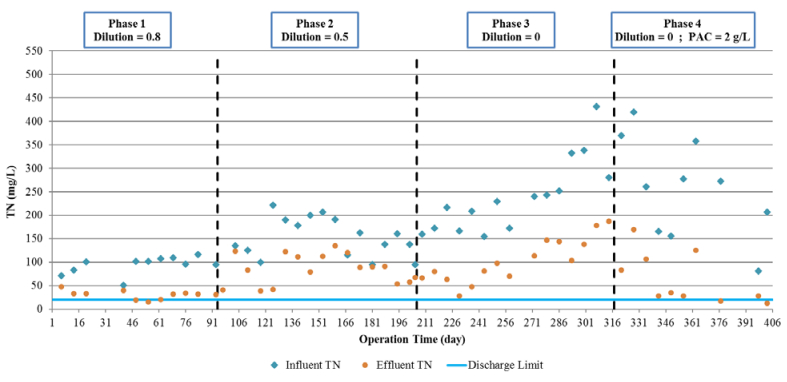
DownLoad: CSVFigure 7 illustrates the influent and final effluent total nitrogen concentrations with respect to the sea discharge limit of 20 mg/L in the four operation phases.
Figure 7. Influent and effluent total nitrogen concentrations.Considering phase 1, the effluent total nitrogen concentration is already above the sea discharge limit of 20 mg/L. The main reason for this was the presence of a certain non-biodegradable fraction of the wastewater organic nitrogen content (Table 4), constituting 71% of the effluent total nitrogen. Furthermore, as expected, most of the organic nitrogen was removed via ammonification in DSS1 in all four phases.
Reduction of the dilution ratio in the 2nd phase to 0.5 resulted in a sharp decline in the organic nitrogen removal efficiency (Figure 6) after severe inhibition of the heterotrophic bacteria in DSS1, which are also responsible for the ammonification process. It also resulted in DSS2 inhibition and in an increase in the ammonia effluent concentration to 33.5 mg/L, as some of the wastewater inhibitory compounds were not biodegraded in DSS1. Thus, the effluent total nitrogen concentration rose by 170% to 87.6 mg/L, a value far in excess of the sea discharge limit.
Following good acclimation of the DSS1 biomass to the ever increasing wastewater inhibitory compound load, further reduction of the dilution to 0 (phase 3) resulted in a steady improvement of the overall organic nitrogen removal (DSS1 + DSS2) to 87.1%. The effluent total nitrogen concentration, however, increased further to 106 mg/L following the aforementioned severe inhibition of the nitrifying bacteria in DSS2.
The steady improvement in organic nitrogen removal continued to phase 4, as the DSS1 removal efficiency increased to 85.2% with the steady acclimation of the ammonification bacteria. Thus, the addition of the PAC did not lead to any major improvement in the organic nitrogen removal in contrast to the improved ammoniacal nitrogen removal. However, the effluent total nitrogen concentration was still in excess of the sea discharge limit, mainly due to the organic nitrogen non-biodegradable fraction and the poor de-nitrification process control in the post-anoxic reactor. The methanol that was added as an electron donor to the post-anoxic reactor was not controlled by an oxidation-reduction potential (ORP) sensor. Instead, it was added manually and continuously on the basis of the average nitrification potential. Therefore, because it was not adjusted to the extreme fluctuations of the nitrification potential, the formed nitrate was not properly reduced, and hence, it contributed to the effluent total nitrogen concentration. Further treatment processes must be included upstream or downstream to greatly reduce the organic nitrogen non-biodegradable fraction and to ensure that compliance with the sea discharge limit is achieved. As to the elevated nitrate levels, proper electron donor controlled dosing must be implemented in the pilot plant.
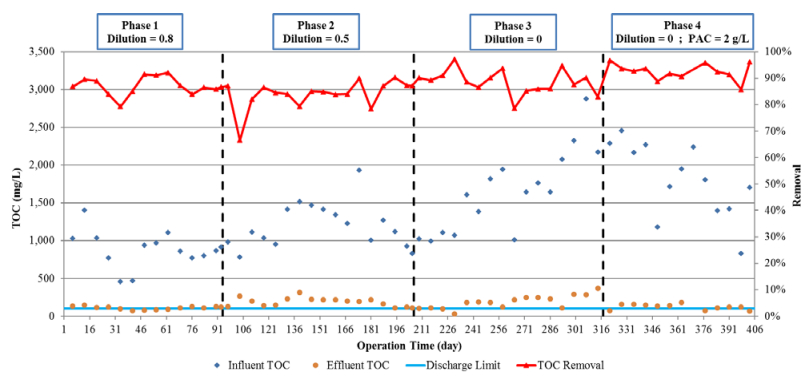
Figure 8 illustrates the influent and final effluent TOC concentrations with respect to the sea discharge limit of 100 mg/L and the total TOC removal efficiency during the four operation phases. Table 5 details the average influent and final effluent TOC concentrations, the removal efficiency in the first sludge system, and the total removal in both sludge systems. Furthermore, it details the theoretical rise in effluent TOC concentration (due to the decrease in the wastewater dilution) and the actual rise in effluent TOC concentration.
Figure 8. Influent and effluent TOC concentrations and removal efficiencies during the four operation phases.| Phase 1 | Phase 2 | Phase 3 | Phase 4 | |
| Influent TOC (mg/L) | 926 ± 258 | 1,215 ± 364 | 1,753 ± 535 | 1,852 ± 528 |
| Effluent TOC (mg/L) | 105 ± 23.0 | 189 ± 53.2 | 200 ± 95.5 | 124 ± 41.0 |
| DSS1 Removal (%) | 79.4 ± 6.50 | 63.4 ± 12.7 | 73.2 ± 9.70 | 79.7 ± 7.60 |
| Total Removal (%) | 87.0 ± 3.50 | 83.9 ± 5.50 | 88.6 ± 4.60 | 92.4 ± 3.17 |
| Theoretical Conc. Rise | 25% | 155% | 155% | |
| Actual Conc. Rise | 80% | 90.5% | 18% |
DownLoad: CSVThe effluent TOC concentration was already slightly above the sea discharge limit of 100 mg/L (Table 5). The main reason for that was the presence of a certain non-biodegradable fraction of the wastewater TOC content. As was the case with the organic nitrogen, most of the TOC, which includes many inhibitory compounds, was removed in the first sludge system throughout the entire pilot operation, in which DSS2 functioned for polishing purposes. Therefore, exposure of the downstream nitrifying bacteria to most of the toxic compounds was minimized, resulting in a highly efficient nitrification process.
Reduction of the dilution to 0.5 and to 0 in phases 2 and 3, respectively, did not result in any significant change in DSS1 TOC removal or in the total removal, as the removal was maintained in the range of 87–89%. Therefore, despite a rise in the influent TOC concentration and an increase of 50% in the influent loading, the heterotrophic bacteria in DSS1 sustained good TOC removal as a result of efficient bacteria acclimation. Although the total removal was stable, the final effluent TOC concentration was almost doubled relative to phase 1, due mainly to the non-biodegradable TOC fraction.
The addition of PAC to DSS2 did not improve the overall TOC removal, most of which occurred in DSS1 because of the ongoing acclimation of the heterotrophic biomass to the 0 dilution. As a result, the effluent TOC concentration dropped to 124 mg/L, which is still much higher than the sea discharge limit. Thus, a certain fraction of the raw wastewater TOC can be considered non-biodegradable and non-adsorbable onto PAC. This finding indicates the need for the inclusion of additional upstream or downstream treatment processes to achieve compliance with the TOC sea discharge limit.
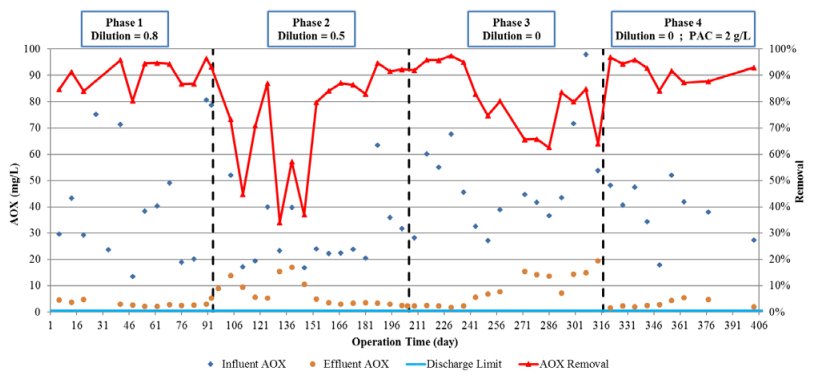
Figure 9 illustrates the influent and final effluent AOX concentrations with respect to the sea discharge limit of 0.5 mg/L and its total removal efficiency during the four operation phases.
Figure 9. Influent and effluent AOX concentrations and removal efficiencies during the four operation phases.Table 6 details the average influent and final effluent AOX concentrations, its removal efficiency in the first sludge system and its total removal in both sludge systems. Furthermore, it details the theoretical rise in effluent TOC concentration (due to the decrease in the wastewater dilution) and the actual rise in effluent AOX concentration.
| Phase 1 | Phase 2 | Phase 3 | Phase 4 | |
| Influent AOX (mg/L) | 43.7 ± 23.7 | 30.0 ± 17.1 | 50.4 ± 25.4 | 40.0 ± 26.2 |
| Effluent AOX (mg/L) | 3.20 ± 1.05 | 7.20 ± 6.50 | 9.24 ± 6.15 | 3.64 ± 2.37 |
| DSS1 Removal (%) | 85.4 ± 7.70 | 58.3 ± 18.7 | 66.5 ± 17.2 | 69.5 ± 14.9 |
| Total Removal (%) | 90.2 ± 5.50 | 73.5 ± 20.5 | 81.3 ± 12.5 | 91.5 ± 4.30 |
| Theoretical Conc. Rise | 25% | 155% | 155% | |
| Actual Conc. Rise | 125% | 189% | 14% |
DownLoad: CSVThe effluent AOX concentration in phase 1 was already much higher than the sea discharge limit of 0.5 mg/L. The main reason for this finding was the presence of a certain non-biodegradable fraction of wastewater AOX content. As in the cases of organic nitrogen and TOC, most of the AOX was removed in DSS1 over the entire course of pilot operation to protect the downstream nitrifying bacteria from the inhibitory compounds included in the influent AOX, and DSS2 acted as a polishing step for recalcitrant AOX removal.
The dilution reduction in phase 2 led to an acute inhibition of the heterotrophic bacteria in DSS1, as the removal efficiency dropped to only 58% and the final effluent concentration jumped by 125% to 7.2 mg/L. As a result, the nitrifying biomass in DSS2 was exposed to elevated concentrations of inhibitory compounds that markedly inhibited the nitrification process (Figure 5).
Further reduction of the dilution in phase 3 resulted in a minute improvement in the AOX removal efficiency, mainly in DSS1, while the total removal increased to 81%. However, the effluent AOX concentration continued to rise by 189% (with respect to phase 1) to 9.24 mg/L. This was the result of slow biomass acclimation in both sludge systems to the increasing concentration and load of inhibitors.
PAC addition in phase 4 led to a 7% increase in the DSS2 AOX removal, a 65% decrease in the total removal fluctuations, and a significant 64% decrease in the final effluent AOX concentration. This is attributed to the ability of the PAC to adsorb non-biodegradable AOX compounds, which remain in the system for the entire 90 days sludge age. The high sludge age facilitated the development of exotic bacteria, with a very low specific growth rate, capable of biodegrading these complex compounds. As a result of a certain fraction of the influent AOX that is non-biodegradable and non-adsorbable, the effluent AOX concentration was very high relative to the sea discharge limit. For this reason, additional upstream or downstream treatment processes must be included in the treatment system. Furthermore, as with the nitrification process, the operation of phases 3 and 4 with equivalent salinity levels meant that the acute inhibition of AOX removal in this study, could be unequivocally determined to be the result only of the inhibitory compounds that were adsorbed onto the PAC in phase 4. A comparison of the theoretical rise in effluent AOX concentration with the actual increase that occurred in phase 4 shows that although the dilution decreased to 0 and the influent load increased by 50%, the actual rise (14%) was much lower than the theoretical rise (155%), which indicates a significant improvement in the AOX removal process of the later phase relative to phase 1.
As demonstrated by Singh and Singh, many herbicides are highly toxic to natural bacteria and their biodegradation incorporates novel pathways, multispecies interactions, and community-level responses [2]. However, transformation of pure culture studies to full-scale reactor applications requires engineering modifications of the biological processes and inclusion of physico-chemical aiding technologies, as done in this study. For example, the combination of anaerobic and aerobic conditions has the potential to significantly improve the overall biodegradability of complex compounds and to reduce toxicity [9,10]. In this regard, the main conclusions of this study are:
• The ammonification and mainly nitrification processes were significantly inhibited by toxic compounds in the raw wastewater, particularly when the dilution ratio was decreased and the organic load was increased.
• The TOC and AOX adsorption onto the selected PAC showed best fits with the Freundlich isotherm.
• In the 4th phase of pilot operation, the PAC equilibrium concentration used was 2000 mg/L, which was considered the best tradeoff in terms of contaminant removal efficiency, economics (daily PAC makeup of 84 mg/L, based on a sludge age of 90 days and a flow rate of 80 L/day), and the increased possibility of MBR membrane fiber abrasion.
• The majority of the organic nitrogen, TOC, and AOX compounds were removed in the first sludge system, which protected the sensitive biomass in the second sludge system from high loads of toxic and inhibitory compounds.
• PAC addition to the second sludge system significantly increased ammoniacal nitrogen removal to 98% and decreased the removal fluctuations, resulting in an effluent concentration that was slightly below the 5 mg/L sea discharge limit. This outcome was the result of efficient PAC adsorption of the inhibitory compounds.
• The total nitrogen in the 4th phase was in excess of the 20 mg/L sea discharge limit. This was mainly due to the presence of a certain organic nitrogen fraction in the raw wastewater that is non-biodegradable and non-adsorbable onto the PAC, and residual nitrate as a result of poor post-denitrification process control.
• TOC removal was not affected by PAC addition, and its effluent concentration was slightly above the 100 mg/L sea discharge limit. This was attributed to the fact that most of the TOC was removed in the first sludge system and to the presence of a certain TOC fraction in the raw wastewater that is non-biodegradable and non-adsorbable onto the PAC.
• The PAC supplement in the 4th phase resulted in a 61% decrease in the effluent AOX concentration to 3.6 mg/L, which is still much higher than the sea discharge limit as defined by environmental regulations. This outcome was attributed mainly to the presence of a certain AOX fraction in the raw wastewater that is non-biodegradable and non-adsorbable onto the PAC.
• The synergistic effect of various toxic organic compounds, rather than the mineral salinity, was the major cause for the acute inhibitions of nitrification and AOX removal in this study.
The authors wish to thank the field staff of the wastewater treatment plant and are especially grateful to Mr. Eran Tzfati and Mr. Itsik Ariel from Environmental Protection Technologies (EPT), Israel, for assisting in the routine operation of the pilot plant over the course of the study. We also extend our gratitude to Mr. Aharon Glozshtein, who performed most of the laboratory analyses.
All authors declare no conflicts of interest in this paper.
| [1] | Acharya VV, Brownlees C, Engle R, et al. (2010) Measuring Systemic Risk, In Regulating Wall Street: The Dodd-Frank Act and the New Architecture of Global Finance, New York: John Wiley & Sons, 87–120. |
| [2] |
Acharya VV, Engle R, Richardson M (2012) Capital Shortfall: A New Approach to Ranking and Regulating Systemic Risks. Am Econ Rev 102: 59–64. doi: 10.1257/aer.102.3.59
|
| [3] |
Adrian T, Brunnermeier MK (2016) CoVaR. Am Econ Rev 106: 1705–1741. doi: 10.1257/aer.20120555
|
| [4] |
Baranoff EG, Sager TW (2002) The Relations among Asset Risk, Product Risk, and Capital in the Life Insurance Industry. J Bank Financ 26: 1181–1197. doi: 10.1016/S0378-4266(01)00166-2
|
| [5] |
Baranoff EG, Sager TW (2003) The Interrelationship among Organizational and Distribution Forms and Capital and Asset Risk Structures in the Life Insurance Industry. J Risk Insur 70: 375–400. doi: 10.1111/1539-6975.t01-1-00057
|
| [6] |
Baranoff EG, Sager TW, Papadopoulos S (2007) Capital and Risk Revisited: A Structural Equation Model Approach for Life Insurers. J Risk Insur 74: 653–681. doi: 10.1111/j.1539-6975.2007.00229.x
|
| [7] | Baranoff EG (2013) An Analysis of the AIG Case–Understanding Systemic Risk and its Relation to Insurance. J Insur Regul 31: 243. |
| [8] | Baranoff EG, Sager TW, Shi B (2013) Capital and Risk Interrelationships in the Life and Health Insurance Industries: Theories and Applications. Handb Insur, 889–915. |
| [9] | Baranoff EG, Sager TW, Shi B (2016) The Risk of Variable Annuity Guarantees and Life Insurer Capital. Asia-Pac J Risk Insur 10: 155–192. |
| [10] | Benoit SG, Hurlin CC, Pérignon C (2013) A Theoretical and Empirical Comparison of Systemic Risk Measures. Working Paper, University of Orléans, Orléans, France. |
| [11] |
Bernal O, Gnabo JY, Guilmin G (2014) Assessing the Contribution of Banks, Insurance and Other Financial Services to Systemic Risk. J Bank Financ 47: 270–287. doi: 10.1016/j.jbankfin.2014.05.030
|
| [12] |
Bierth C, Irresberger F, Weiß GN (2015) Systemic Risk of Insurers Around the Globe. J Bank Financ 55: 232–245. doi: 10.1016/j.jbankfin.2015.02.014
|
| [13] |
Billio M, Getmansky M, Lo AW, et al. (2012) Econometric Measures of Connectedness and Systemic Risk in the Finance and Insurance Sectors. J Financ Econ 104: 535–559. doi: 10.1016/j.jfineco.2011.12.010
|
| [14] | Bisias D, Flood M, Lo AW (2012) A Survey of Systemic Risk Analytics. Working Paper, MIT Operations Research Center. |
| [15] |
Black L, Correa R, Huang X, et al. (2016) The Systemic Risk of European Banks During the Financial and Sovereign Debt Crises. J Bank Financ 63: 107–125. doi: 10.1016/j.jbankfin.2015.09.007
|
| [16] |
Chen CY, Härdle WK, Okhrin Y (2019) Tail Event Driven Network of SIFIs. J Econom 208: 282–298. doi: 10.1016/j.jeconom.2018.09.016
|
| [17] |
Chen H, Cummins JD, Viswanathan KS (2014) Systemic Risk and the Interconnectedness between Banks and Insurers: An Econometric Analysis. J Risk Insur 81: 623–652. doi: 10.1111/j.1539-6975.2012.01503.x
|
| [18] |
Colquitt LL, Hoyt RE (1997) Determinants of Corporate Hedging Behavior: Evidence from the Life Insurance Industry. J Risk Insur 64: 649–671. doi: 10.2307/253890
|
| [19] |
Cummins JD, Phillip RD, Smith SD (2001) Derivatives and Corporate Risk Management Participation and Volume Decisions in the Insurance Industry. J Risk Insur 68: 51–90. doi: 10.2307/2678132
|
| [20] |
Cummins JD, Weiss MA (2014) Systemic Risk and the U.S. Insurance Sector. J Risk Insur 81: 489–527. doi: 10.1111/jori.12039
|
| [21] | Eling M, Pankoke DA (2016) Systemic Risk in the Insurance Sector: A Review and Directions for Future Research. Risk Manag Insur Rev 19: 249–284. |
| [22] | Geneva Association (2011) Variable Annuities with Guarantees and Use of Hedging. Available from: http://www.genevaassociation.org/PDF/Insurance_And_Finance/GA2011–I&FSC10.pdf. |
| [23] |
Glasserman P, Young HP (2015) How Likely is Contagion in Financial Networks? J Bank Financ 50: 383–399. doi: 10.1016/j.jbankfin.2014.02.006
|
| [24] |
Gouriéroux C, Héam JC, Monfort A (2012) Bilateral Exposures and Systemic Solvency Risk. Can J Econ 45: 1273–1309. doi: 10.1111/j.1540-5982.2012.01750.x
|
| [25] |
Härdle WK, Wanga W, Yu L (2016) TENET: Tail-Event driven NETwork risk. J Econ 192: 499–513. doi: 10.1016/j.jeconom.2016.02.013
|
| [26] |
Harrington SE (2009) The Financial Crisis, Systemic Risk, and the Future of Insurance Regulation. J Risk Insur 76: 785–819. doi: 10.1111/j.1539-6975.2009.01330.x
|
| [27] | Harrington SE (2013) The Dodd-Frank Act, Solvency II, and U.S. Insurance Regulation. J Financ Perspect 1: 1–12. |
| [28] |
Hoyt RE (1989) Use of Financial Futures by Life Insurers. J Risk Insur 56: 740–748. doi: 10.2307/253457
|
| [29] | Kessler D (2013) Why Re (insurance) Is Not Systemic. J Risk Insur 81: 477–488. |
| [30] |
Park SC, Xie X (2014) Reinsurance and Systemic Risk: The Impact of Reinsurer Downgrading on Property-Casualty Insurers. J Risk Insur 81: 587–622. doi: 10.1111/jori.12045
|
| [31] |
Pourkhanali A, Kim J, Tafakori L, et al. (2016) Measuring Systemic Risk Using Vine-Copula. Econom Model 53: 63–74. doi: 10.1016/j.econmod.2015.11.010
|
| [32] | Rauch J, Weiss MA, Wende S (2015) Default Risk and Contagion in the US Financial Sector: An Empirical Analysis of the Commercial and Investment Banking, and Insurance Sectors. Working Paper, University of Cologne, Cologne. |
| [33] | Weekly Special Report of the NAIC's Capital Markets Bureau (2010) Available from: http://www.naic.org/capital_markets_archive/110610.htm. |
| 1. | Kasra Ghaharian, Brett Abarbanel, Dylan Phung, Piyush Puranik, Shane Kraus, Alan Feldman, Bo Bernhard, Applications of data science for responsible gambling: a scoping review, 2022, 1445-9795, 1, 10.1080/14459795.2022.2135753 |
Etti G. Baranoff, Patrick Brockett, Thomas W. Sager, Bo Shi. Was the U.S. life insurance industry in danger of systemic risk by using derivative hedging prior to the 2008 financial crisis?[J]. Quantitative Finance and Economics, 2019, 3(1): 145-164. doi: 10.3934/QFE.2019.1.145
| Parameter (Units) | Value |
| pH | 7.7 ± 0.34 |
| Alkalinity (meq/L) | 16.5 ± 5.0 |
| TSS (mg/L) | 59.3 ± 52.0 |
| Turbidity (NTU) | 73.2 ± 72.8 |
| Chlorides (g/L) | 5.23 ± 1.60 |
| TDS (g/L) | 14.2 ± 4.1 |
| NH3-N (mg/L as N) | 11.0 ± 6.80 |
| Norg-N (mg/L as N) | 219 ± 82.7 |
| TKN (mg/L as N) | 230 ± 84.9 |
| NO2-N (mg/L as N) | 0.37 ± 0.90 |
| NO3-N (mg/L as N) | 1.6 ± 2.50 |
| TN (mg/L as N) | 236 ± 71.0 |
| BOD (mg/L) | 3660 ± 1110 |
| tCOD (mg/L) | 6610 ± 1620 |
| sCOD (mg/L) | 5600 ± 1820 |
| TOC (mg/L) | 1720 ± 560 |
| AOX (mg/L) | 50.4 ± 25.4 |
DownLoad: CSV| Phase | Dilution Ratio | Flow Rate (L/day) | PAC Conc. (mg/L) | Duration (days) |
| 1 | 0.8 | 100 | 0 | 93 |
| 2 | 0.5 | 80 | 0 | 112 |
| 3 | 0 | 80 | 0 | 111 |
| 4 | 0 | 80 | 2000 | 88 |
DownLoad: CSV| Phase 1 | Phase 2 | Phase 3 | Phase 4 | |
| Nitrification Potential (mg N/L) | 68.8 ± 26.4 | 94.4 ± 57.6 | 205 ± 86.9 | 240 ± 105 |
| Effluent NH4-N (mg/L) | 2.26 ± 1.80 | 33.5 ± 32.7 | 64.6 ± 56.5 | 4.06 ± 7.46 |
| Removal | 95.6 ± 4.81 | 69.7 ± 26.1 | 73.7 ± 21.2 | 98.1 ± 1.50 |
| Theoretical Conc. Rise | 25% | 155% | 155% | |
| Actual Concentration Rise | 1380% | 2760% | 79% |
DownLoad: CSV| Phase 1 | Phase 2 | Phase 3 | Phase 4 | |
| Influent Norg (mg/L) | 85.2 ± 23.0 | 138 ± 45.4 | 210 ± 64.6 | 255 ± 106 |
| Effluent Norg (mg/L) | 23.0 ± 10.9 | 50.6 ± 34.1 | 25.7 ± 18.2 | 24.3 ± 13.2 |
| DSS1 Removal (%) | 62.2 ± 12.5 | 40.3 ± 22.5 | 61.6 ± 22.6 | 85.2 ± 8.85 |
| Total Removal (%) | 72.5 ± 13.8 | 65.5 ± 24.5 | 87.1 ± 5.94 | 89.2 ± 6.01 |
DownLoad: CSV| Phase 1 | Phase 2 | Phase 3 | Phase 4 | |
| Influent TOC (mg/L) | 926 ± 258 | 1,215 ± 364 | 1,753 ± 535 | 1,852 ± 528 |
| Effluent TOC (mg/L) | 105 ± 23.0 | 189 ± 53.2 | 200 ± 95.5 | 124 ± 41.0 |
| DSS1 Removal (%) | 79.4 ± 6.50 | 63.4 ± 12.7 | 73.2 ± 9.70 | 79.7 ± 7.60 |
| Total Removal (%) | 87.0 ± 3.50 | 83.9 ± 5.50 | 88.6 ± 4.60 | 92.4 ± 3.17 |
| Theoretical Conc. Rise | 25% | 155% | 155% | |
| Actual Conc. Rise | 80% | 90.5% | 18% |
DownLoad: CSV| Phase 1 | Phase 2 | Phase 3 | Phase 4 | |
| Influent AOX (mg/L) | 43.7 ± 23.7 | 30.0 ± 17.1 | 50.4 ± 25.4 | 40.0 ± 26.2 |
| Effluent AOX (mg/L) | 3.20 ± 1.05 | 7.20 ± 6.50 | 9.24 ± 6.15 | 3.64 ± 2.37 |
| DSS1 Removal (%) | 85.4 ± 7.70 | 58.3 ± 18.7 | 66.5 ± 17.2 | 69.5 ± 14.9 |
| Total Removal (%) | 90.2 ± 5.50 | 73.5 ± 20.5 | 81.3 ± 12.5 | 91.5 ± 4.30 |
| Theoretical Conc. Rise | 25% | 155% | 155% | |
| Actual Conc. Rise | 125% | 189% | 14% |
DownLoad: CSV| Parameter (Units) | Value |
| pH | 7.7 ± 0.34 |
| Alkalinity (meq/L) | 16.5 ± 5.0 |
| TSS (mg/L) | 59.3 ± 52.0 |
| Turbidity (NTU) | 73.2 ± 72.8 |
| Chlorides (g/L) | 5.23 ± 1.60 |
| TDS (g/L) | 14.2 ± 4.1 |
| NH3-N (mg/L as N) | 11.0 ± 6.80 |
| Norg-N (mg/L as N) | 219 ± 82.7 |
| TKN (mg/L as N) | 230 ± 84.9 |
| NO2-N (mg/L as N) | 0.37 ± 0.90 |
| NO3-N (mg/L as N) | 1.6 ± 2.50 |
| TN (mg/L as N) | 236 ± 71.0 |
| BOD (mg/L) | 3660 ± 1110 |
| tCOD (mg/L) | 6610 ± 1620 |
| sCOD (mg/L) | 5600 ± 1820 |
| TOC (mg/L) | 1720 ± 560 |
| AOX (mg/L) | 50.4 ± 25.4 |
| Phase | Dilution Ratio | Flow Rate (L/day) | PAC Conc. (mg/L) | Duration (days) |
| 1 | 0.8 | 100 | 0 | 93 |
| 2 | 0.5 | 80 | 0 | 112 |
| 3 | 0 | 80 | 0 | 111 |
| 4 | 0 | 80 | 2000 | 88 |
| Phase 1 | Phase 2 | Phase 3 | Phase 4 | |
| Nitrification Potential (mg N/L) | 68.8 ± 26.4 | 94.4 ± 57.6 | 205 ± 86.9 | 240 ± 105 |
| Effluent NH4-N (mg/L) | 2.26 ± 1.80 | 33.5 ± 32.7 | 64.6 ± 56.5 | 4.06 ± 7.46 |
| Removal | 95.6 ± 4.81 | 69.7 ± 26.1 | 73.7 ± 21.2 | 98.1 ± 1.50 |
| Theoretical Conc. Rise | 25% | 155% | 155% | |
| Actual Concentration Rise | 1380% | 2760% | 79% |
| Phase 1 | Phase 2 | Phase 3 | Phase 4 | |
| Influent Norg (mg/L) | 85.2 ± 23.0 | 138 ± 45.4 | 210 ± 64.6 | 255 ± 106 |
| Effluent Norg (mg/L) | 23.0 ± 10.9 | 50.6 ± 34.1 | 25.7 ± 18.2 | 24.3 ± 13.2 |
| DSS1 Removal (%) | 62.2 ± 12.5 | 40.3 ± 22.5 | 61.6 ± 22.6 | 85.2 ± 8.85 |
| Total Removal (%) | 72.5 ± 13.8 | 65.5 ± 24.5 | 87.1 ± 5.94 | 89.2 ± 6.01 |
| Phase 1 | Phase 2 | Phase 3 | Phase 4 | |
| Influent TOC (mg/L) | 926 ± 258 | 1,215 ± 364 | 1,753 ± 535 | 1,852 ± 528 |
| Effluent TOC (mg/L) | 105 ± 23.0 | 189 ± 53.2 | 200 ± 95.5 | 124 ± 41.0 |
| DSS1 Removal (%) | 79.4 ± 6.50 | 63.4 ± 12.7 | 73.2 ± 9.70 | 79.7 ± 7.60 |
| Total Removal (%) | 87.0 ± 3.50 | 83.9 ± 5.50 | 88.6 ± 4.60 | 92.4 ± 3.17 |
| Theoretical Conc. Rise | 25% | 155% | 155% | |
| Actual Conc. Rise | 80% | 90.5% | 18% |
| Phase 1 | Phase 2 | Phase 3 | Phase 4 | |
| Influent AOX (mg/L) | 43.7 ± 23.7 | 30.0 ± 17.1 | 50.4 ± 25.4 | 40.0 ± 26.2 |
| Effluent AOX (mg/L) | 3.20 ± 1.05 | 7.20 ± 6.50 | 9.24 ± 6.15 | 3.64 ± 2.37 |
| DSS1 Removal (%) | 85.4 ± 7.70 | 58.3 ± 18.7 | 66.5 ± 17.2 | 69.5 ± 14.9 |
| Total Removal (%) | 90.2 ± 5.50 | 73.5 ± 20.5 | 81.3 ± 12.5 | 91.5 ± 4.30 |
| Theoretical Conc. Rise | 25% | 155% | 155% | |
| Actual Conc. Rise | 125% | 189% | 14% |
