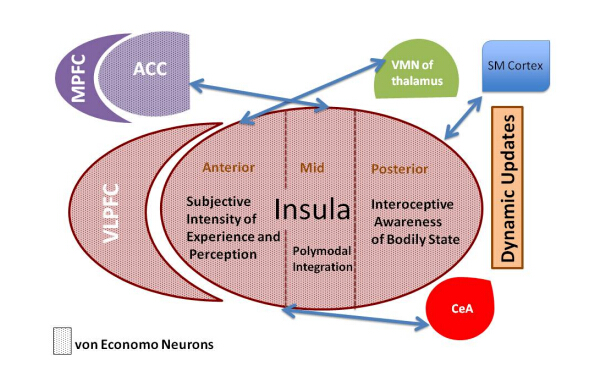
Background: The insula is instrumental in integrating the emotional, cognitive, and sensory-motor systems. This manuscript lays a foundational framework for understanding the insula’s mechanistic role in moderating brain networks in illness and wellness. Methods: Reviewed here is the select literature on the brain anatomy and function relevant to the insula’s role in psychiatrically ill and normative populations. Results: The insula is a hub for moderating social cognition, empathy, reward-driven decision-making, arousal, reactivity to emotional stimuli, and somatic pain processing. Findings indicate a spectrum of increasing complexity in insular function – from receiving and interpreting sensorimotor sensations in the posterior insula to subjective perception of emotions in the anterior insula. The insula plays a key role at the interface of cognitive and emotional domains, functioning in concert with other brain regions that share common cytoarchitecture, such as the ventrolateral prefrontal cortex and the anterior cingulate cortex. Pharmacotherapy and mindfulness-based interventions can alter insular activation. Conclusion: The insula serves as a receiver and interpreter of emotions in the context of cognitive and sensory-motor information. Therefore, insular function and connectivity may potentially be utilized as a biomarker for treatment selection and outcome.
1.
Introduction
In water resource planning, to quantify the flow requirements in space and time that are necessary to sustain desired ecosystem services [8,40] is referred to as instream flow need (IFN) assessment [3]. Ecologists, mathematicians and environment managers have paid increasing attention to the investigation of spatial population dynamics and invasions of stream or river species, which suggests solutions to IFNs and provides evidence on the influence of flows on ecosystems.
River ecologists are interested in the "drift paradox" problem, which asks how river organisms can persist in a river with unidirectional water flow [34,35]. Population persistence over large spatial and temporal scales is an important component of instream flow need assessment studies [3]. Krkosěk and Lewis [25] proposed three measures for population persistence that relate to lifetime reproductive output of a species in a spatially variable environment and they previously have been applied to river population models [20,31]. These measures are connected through the next-generation operator, which maps the population forward in time from one generation to the next. The first measure, $ R_{loc}(x) $, describes the fundamental niche of the species. It represents the local persistence at any location $ x $ in the absence of dispersal, depending only on reproduction and survival at the location $ x $. The second measure, $ R_\delta(x) $, describes the realized niche. It is the lifetime reproductive output of an individual, initially introduced at $ x $, undergoing survival, reproduction, and dispersal, and hence, its value, larger than one or less than one, also determines the source and sink regions in the habitat. The third measure is the net reproductive rate $ R_0 $. It represents the average number of offspring produced by a single individual over its lifetime where the spatial distribution of the individual is given by the dominant eigenfunction of the linearized next-generation operator; see theories for $ R_0 $ in e.g., [9,47]. The net reproductive rate has a long history as measures for population persistence/extinction in ecological modeling. Intuitively, if $ R_0 > 1 $ the population will grow, but if $ R_0 < 1 $ the population will likely become extinct. While this has the potential to make $ R_0 $ a powerful tool for studying population persistence, further mathematical work is required if $ R_0 $ is to be linked rigorously to behavior of the associated nonlinear model. Existing studies of the three measures for river species have revealed the influence of hydrodynamics on long term behaviors of river populations, especially of the net reproductive rate $ R_0 $, but it is only for idealized spatially homogeneous or one-dimensional (longitudinal) varying rivers (see e.g., [20,31]). Therefore, it is necessary and important to establish persistence theories in more realistic two or three-dimensional rivers.
Most population models in river ecology have been investigated under simple assumptions for hydrodynamics, such as a constant water depth or a constant flow velocity throughout the river (see e.g., [19,29,38,39,41]). A few have taken into account spatial or temporal variations in riverbed structure or the flow regime, but only for simplified and essentially one-dimensional structures (see e.g., [20,23,24,28]). The results from these models are interesting but only provide limited information about the influence of realistic hydrodynamics on spatial population dynamics. There also have been methodologies relying on habitat suitability models and physical habitat availability as a proxy for population status (see e.g., [3,14,21,26,40]). They link flow regimes with ecology qualitatively, but lack a mechanistic foundation, and hence they can well predict habitat quality rather than species long term behavior in the habitat. Thus, direct integration of ecological systems into water flow dynamics and quantitative analysis of the impact of flows on ecology are still rare but in urgent need. A hybrid modeling approach was proposed to simulate the spatial dynamics of macroinvertebrates in a section of the Merced River in central California in [2]. The hydrodynamic model in MIKE 21 Flow Model FM [11] was used to characterize the two dimensional flow field in the longitudinal and lateral directions through the Robinson Reach of this river. The hydraulic prediction from the two dimensional model was then coupled with a particle tracking algorithm [12] to compute the drift dispersal. While the work focused on the effect of hydraulic flow on population dispersal in a two dimensional river, the main work of integration of hydraulic dynamics and ecology was simplified to the study of the steady state of a one dimensional representation model. In [22], a hybrid physical-biological modeling approach was presented to directly link river hydrology with river population models. A governing equation for the gradually varied flow was first coupled to a single population equation in one-dimensional rivers and then in two-dimensional rivers. Moreover, population spread and invasion ratchet phenomenon were studied for these models.
By coupling hydrodynamics and ecological dynamics, one can explicitly investigate the influence of physical factors and hydraulic conditions on spatiotemporal dynamics of a population in a river, which strengthens the ecological component of environmental flow assessments that is currently still lacking. By using the hybrid physical-biological modeling approach coupled to River2D [22], one can observe the evolution of the density of a single stage drifting population in a two-dimensional river. While such calculation can certainly predict the long-term dynamics of persistence or extinction of a population in a specific river, the calculation itself is expensive and the transient running time may be long. Therefore it is advantageous to develop qualitative and quantitative methods that can directly determine population persistence in a two dimensional river.
In this paper, we are interested in species living both in the flowing water and on the benthos of a river (see e.g., [1,13,20,28,38]). We extend the results of persistence measures ($ R_{\text{loc}} $, $ R_{\delta} $ and $ R_0 $) for a benthic-drift population [20] in a one-dimensional river to a benthic-drift model in a two-dimensional depth-averaged river environment, in order to see how different factors, especially hydraulic factors, influence population persistence, and to distinguish how the sedentary stage helps populations persist in a two dimensional river. Our hybrid biological-physical modeling approach, coupled to the River2D program, provides a method to analyze the impact of river morphology on population persistence in a realistic river. It can be used to calculate not only the benthic and drift population densities but also the net reproductive rate of a specific species and its source/sink regions in any depth-averaged river model, given the river morphologic information and population demographic information. To our knowledge, this is the first study that quantitatively describes population persistence in a two-dimensional river environment based on the explicit bio-physical coupling of hydrology and benthic and drift compartments. It is expected that this work could provide an important methodology for ecologists or environment managers to determine population dynamics of a specific species in a specific river.
This paper is organized as follows. In Section 2, we introduce a benthic-drift model for a population in a two-dimensional depth-averaged model of a river. In Section 3, we define the next generating operator for the linearized system and derive three measures of persistence, $ R_{\text{loc}}(x, y) $, $ R_{\delta}(x, y) $, and $ R_0 $. We show that $ R_0 $ can be used as a threshold to determine global population persistence or extinction for the nonlinear model. In Section 4, we present a numerical method to calculate $ R_0 $ and $ R_{\delta} $ when coupling the population model and hydrodynamic model in River2D. In Section 5, we choose two typical rivers and investigate how the water flow, birth rate, transfer rates, diffusion rate, river bottom slope, and river bottom roughness influence population persistence via numerical simulations for $ R_0 $ and $ R_{\delta} $ under different conditions. Finally, a short section of discussion completes the paper.
2.
Model
Denote the two dimensional river region by a bounded and smooth domain $ \Omega $ in $ \mathbb{R}^2 $ with boundary $ \partial \Omega $. Consider the following two dimensional benthic-drift population model, a derivation of which is provided in Appendix A:
where $ N_d(x, y, t) $ is the population density in the drifting water (unit: 1/volume) at location $ (x, y) $ and time $ t $, $ N_b(x, y, t) $ is the population density on the benthos (unit: 1/area) at location $ (x, y) $ and time $ t $, $ N_d^{0} $ and $ N_b^{0} $ are initial population densities, $ f $ is the reproduction rate of the population (unit: 1/time), $ m_d(x, y) $ is the mortality rate of the drift population at location $ (x, y) $ (unit: 1/time), $ m_b(x, y) $ is the mortality rate of the benthic population at location $ (x, y) $ (unit: 1/time), $ D(x, y) $ is the diffusion rate (unit: area/time), $ \mu(x, y) $ is the per capita rate at which individuals on the benthos enter the drift (unit: 1/time), $ \sigma(x, y) $ is the per capita rate at which individuals return to the benthos from the drift (unit: 1/time), $ h(x, y) $ is the river depth at location $ (x, y) $ (unit: length), $ v(x, y) = (v_1(x, y), v_2(x, y)) $ is the depth-averaged flow velocity at location $ (x, y) $ with $ v_1(x, y) $ the flow velocity (unit: length/time) in the $ x $ direction and $ v_2(x, y) $ the flow velocity (unit: length/time) in the $ y $ direction, $ \triangledown = \left(\partial/\partial x, \partial/\partial y\right) $, $ \vec{n} $ is the unit outward normal vector on the boundary, and $ a(x, y) $ and $ b(x, y) $ are nonnegative bounded functions on $ \partial \Omega $ satisfying $ a^2+b^2\neq 0 $. For each $ t\geq 0 $, the solutions $ N_b(\cdot, \cdot, t) $ and $ N_d(\cdot, \cdot, t) $ are in the function space $ X $, which is the continuous function space $ C(\bar{\Omega}, \mathbb{R}) $ or the subspace of $ C(\bar{\Omega}, \mathbb{R}) $ consisting of continuously differentiable functions vanishing on the boundary if Dirichlet conditions are applied to some part of the boundary.
The boundary conditions of (2.1) can be Dirichlet, Neumann or Robin conditions. The following typical conditions could be assumed in different portions of the boundary of a river.
(BI) At the river inflow (upstream boundary condition): zero-flux or zero density.
(ⅰ) Zero-flux (individuals cannot enter or leave at the source). The condition is
$ a(x, y) N_d+b(x, y)\frac{\partial N_d}{\partial\vec{n}} = 0 $ with $ a(x, y) = -v(x, y)\cdot\vec{n} > 0 $ since $ v $ and $ \vec{n} $ have opposite directions and $ b(x, y) = D(x, y) $.
(ⅱ) Zero density (hostile condition) (e.g., the living condition at the upstream end is extremely bad so that individuals die whenever they reach there): $ N_d = 0. $
(BB) Along the bank: zero-flux $ a(x, y) N_d+b(x, y)\frac{\partial N_d}{\partial\vec{n}} = 0 $ with $ a(x, y) = -v(x, y)\cdot\vec{n} $ and $ b(x, y) = D(x, y) $.
(ⅰ) If no discharge flows into the river through the bank, then $ v $ and $ \vec{n} $ are perpendicular along the bank, hence $ a = 0. $ Thus, the boundary condition becomes $ \frac{\partial N_d}{\partial\vec{n}} = 0. $
(ⅱ) If water flows into the river from the bank of the river (e.g., small streams or tributaries or groundwater flow entering the larger main river), then we have $ a(x, y) N_d+b(x, y)\frac{\partial N_d}{\partial\vec{n}} = 0 $ with $ a\geq 0 $ since $ v $ and $ \vec{n} $ have opposite directions.
(BO) At the river outflow (downstream boundary condition): free-flux or zero density.
(ⅰ) Free-flux (Danckwert's condition): $ \frac{\partial N_d}{\partial\vec{n}} = 0. $ Individuals can freely leave the river with water flow.
(ⅱ) Zero density (hostile condition) (e.g., all individuals die at the downstream boundary): $ N_d = 0. $
We make the following assumptions throughout this paper.
(H1) $ D, h, v_1, v_2, \in C^2(\bar{\Omega}, (0, \infty)). $
(H2) $ \mu, \sigma, m_d, m_b $ are positive continuous functions in $ \Omega $.
(H3) The function $ f(x, y, N_b) $ is Lipschitz continuous with respect to $ N_b $ with Lipschitz constant $ c $, $ f(x, y, 0)-m_b(x, y) < \infty $, $ f(x, y, N_b) $ is monotonically decreasing in $ N_b $ and for each $ (x, y) $ there exists a unique value $ K(x, y) > 0 $ such that $ f(x, y, K(x, y))-m_b(x, y) = 0 $, $ f(x, y, 0)-m_b(x, y)-\mu(x, y)\leq 0 $ on $ \Omega $.
(H4) $ \mu, \sigma, m_d, m_b $, $ D $, $ f $, $ a $ and $ b $ do not depend on the vertical height of the location in the river.
3.
River metrics for population persistence
In this section, we extend the theories of persistence measures for a one-dimensional benthic-drift model in [20] to obtain three river metrics for population persistence based on the linearized system of (2.1) at the trivial solution $ (0, 0) $. To this end, we first introduce the next generation operator.
3.1. The next generation operator
Linearizing system (2.1) at the trivial steady state $ (N^\ast_d, N^\ast_b) \equiv (0, 0) $ yields
where $ \mathcal{L} $ is the linear partial differential operator defined as
for any $ N_d\in C^2(\Omega, \mathbb{R}) $.
Remark 1. If $ f(x, y, 0)-m_b(x, y)-\mu(x, y) > 0 $ on $ \Omega $, then
which implies that $ N_b $ grows exponentially as $ t\rightarrow \infty $ and $ (0, 0) $ is unstable for (3.1). Hence, population persists for (2.1) regardless of other conditions. For this reason, we impose the last condition in (H3) in the rest of the paper for interesting results.
Suppose that a population is introduced into the river environment $ \bar{\Omega} $ with initial distribution $ (\psi_d^{0}, \psi_b^{0})\in X\times X $. The individuals in this population then experience dispersal, transfer between mobile and stationary classes and reproduction until they die, so the distribution of these initially introduced individuals at time $ t $, denoted by $ (\psi_d(x, y, t), \psi_b(x, y, t)) $, is governed by the following system
Then $ f(x, y, 0)\psi_b(x, y, t) $ is the rate of reproduction by the initially introduced individuals at location $ (x, y) $ at time $ t $, and therefore the total reproduction by the initially introduced individuals during their lifetime at $ (x, y) $ is given by $ \int_0^{\infty}f(x, y, 0)\psi_b(x, y, t)dt $. Noting that offsprings are reproduced only on the benthos, we have the following definition.
Definition 2. The next generation operator $ \Gamma: X\times X\rightarrow \{0\}\times X $ associated with (3.1) is defined by
where $ (\psi_d(x, y, t), \psi_b(x, y, t)) $, the distribution of the initially introduced individuals in the river at time $ t $, is the solution of (3.2).
This next generation operator $ \Gamma $ maps an initial population distribution to its "next generation" (offspring) distribution.
3.2. River metrics
Now we define three river metrics for population persistence as those in [20,31].
River metric 1: Fundamental niche $ R_{\text{loc}}(x, y) $ – a local persistence metric that describes the full range of environmental conditions and resources (biological and physical) that the organism can possibly occupy and use, especially when limiting factors are absent.
Assume that an individual only experiences birth and death after being introduced into the river but does not disperse during its lifetime. Define $ R_{\text{loc}}(x, y) $ as the number of offspring produced over its lifetime by an individual introduced at location $ (x, y) $ in the benthic zone. For $ (x, y)\in\Omega $,
where $ n_b(x, y, t) = e^{-m_b(x, y)t}dt $ is the solution of
Then $ R_{\text{loc}}(x, y) > 1 $ implies that an individual introduced at $ (x, y) $ will produce more than one offspring at $ (x, y) $ in the next generation, hence the population size at $ (x, y) $ will increase over generations. Therefore, locations with $ R_{\text{loc}}(x, y) > 1 $ correspond to the fundamental niche of the species.
River metric 2: Source-sink distribution $ R_{\delta}(x, y) $ – a local persistence metric that determines source and sink regions in the river.
Assume that an individual undergoes birth, death and dispersal after being introduced into the river and we use $ R_{\delta}(x, y) $ to describe the number of offspring produced over its lifetime by an individual introduced at location $ (x, y) $ in the benthic zone.
Note that the next generation distribution from a single individual introduced at location $ (x_0, y_0) $ is defined by
where $ (\psi_d(x, y, t), \psi_b(x, y, t)) $ is the solution of (3.2) with initial conditions $ \psi_d(x, y, 0) = 0 $, $ \psi_b(x, y, 0) = \delta(x-x_0)\delta(y-y_0) $ and $ \delta(\cdot) $ is the Dirac delta distribution. Then $ R_\delta(x_0, y_0) $ is defined as
If $ R_\delta(x_0, y_0) > 1 $, then an individual introduced at location $ (x_0, y_0) $ will produce more than one offspring in the whole river, we call location $ (x_0, y_0) $ a source. If $ R_\delta(x_0, y_0) < 1 $, then an individual introduced at location $ (x_0, y_0) $ will produce less than one offspring in the whole river, we call location $ (x_0, y_0) $ a sink.
River metric 3: Net reproductive rate $ R_0 $ – a global persistence metric that determines population persistence or extinction in the whole river.
For any nonnegative initial distribution $ (N_d^0(x, y), N_b^0(x, y)) $ of the model (3.1), the associated next generation distribution is
where $ (N_d(x, y, t), N_b(x, y, t)) $ solves (3.2) with initial condition $ (N_d^0, N_b^0) $.
Define
where $ r(\Gamma) $ is the spectral radius of the linear operator $ \Gamma $ on $ X\times X $. Then $ R_0 $ represents the average number of offspring an individual may produce during its lifetime. We call $ R_0 $ the net reproductive rate. Similarly as we did in [20], we can show the following result. A sketch of the proof is given in Appendix B.
Theorem 3. Assume (H1)–(H4) for (2.1). The following statements are valid:
(i) If $ R_0 < 1 $, then the extinction equilibrium $ (0, 0) $ is asymptotically stable for (2.1) for all nonnegative initial value conditions.
(ii) If $ R_0 > 1 $, then there exists $ \epsilon_0 > 0 $ such that any nonnegative solution $ (N_d(x, y, t), N_b(x, y, t)) $ of (2.1) with $ (N_d^0, N_b^0)\geq, \not\equiv 0 $ satisfies
Remark 4. Theorem 3 implies that $ R_0 $ is a threshold for global dynamics of the population in the whole river. Population persists in the river in the sense that the inequality (3.9) is valid if $ R_0 > 1 $; population will be extinct in the river if $ R_0 < 1 $.
4.
Numerical methods for computing $ R_0 $ and $ R_{\delta} $ in River2D
River2D is a hydrodynamic and fish habitat model developed specifically for use in natural streams and rivers. We implemented the population model into River2D to calculate river metrics $ R_0 $ and $ R_\delta $ for a species in a river with two dimensional depth-averaged velocities. Starting with creating a preliminary bed topography file from the raw river field data, we edited and refined the data, developed a computational discretization of the river, and then solved for the water depths and velocities throughout the discretization under given inflow and outflow conditions. To obtain steady river flow conditions the River2D model is run from an initial set of conditions with constant inflow and outflow conditions until a steady state of the river is obtained. We then implemented the two dimensional population model equations into the steady river flow in River2D to calculate $ R_0 $ (see (3.8)) as well the next generation distribution and $ R_\delta $ (see (3.6)). River2D is a finite element model, based on a conservative Petrov-Galerkin upwinding formulation (see e.g., [7]). The hydrodynamic component of the River2D model is based on the two-dimensional, depth averaged Saint Venant Equations expressed in conservative form. See [15,16,43] for more details about River2D.
In what follows, we present the methods to calculate $ R_\delta $ and $ R_0 $ for a benthic-drift model in a spatially two-dimensional (longitudinal-lateral) river in River2D.
For numerical calculation convenience, we introduce a new variable $ N_v $ for the offspring that the initially introduced individuals reproduce and consider the following system based on the linearization of model (2.1):
Note that individuals can stay on the benthos or drift in water but the recruitment only occurs when they stay on the benthos. Here $ N_b $ and $ N_d $ are densities of benthic population and drift population of the first generation (i.e., initially introduced population), respectively; $ N_v $ is the population density of the second generation (i.e., offspring of the first generation population). Individuals are only introduced on the benthos. The boundary condition along the river bank is chosen as the no-flux condition and the conditions at the upstream and downstream ends can be chosen as any from boundary assumptions (BI) and (BO) in Section 2. In numerical simulations in the next section, we use the following hostile upstream and Dankwert's downstream conditions,
or zero flux upstream and Dankwert's downstream conditions,
For a well-defined river, we first run the river in River2D to the steady flow to obtain $ v(x, y) $ and $ h(x, y) $. Then we implement the above population model into the steady flow to calculate river metrics. The algorithms for computing $ R_\delta $ and $ R_0 $ are given as below.
4.1. Calculation of $ R_\delta $
Note that $ N_v(x, y, \infty) $ is the total number of new offspring produced at location $ (x, y) $ and $ \int_\Omega N_v(x, y, \infty)dxdy $ is the total number of offspring produced by initially introduced individuals in their lifetime in the whole river. If a single individual is introduced at location $ (x_0, y_0)\in \Omega $, then
where $ N_v(x, y, \infty) $ is the third compartment of the solution to system (4.1) as $ t\rightarrow \infty $, with initial distribution $ N_b(x_0, y_0, 0) = N^0_b(x, y) = \delta(x-x_0, y-y_0) = \delta(x-x_0)\cdot\delta(y-y_0) $, where $ \delta $ is the Dirac delta function. Numerically, in River2D, (4.4) is approximated by
where $ N_v(x_i, y_j, \infty) $ is approximated by $ N_v(x_i, y_j, t_1) $ for sufficiently large $ t_1 $ and $ \{(x_i, y_j)_{i\in I, j\in J}\} $ is a division of the river region $ \bar{\Omega} $ in the simulation.
4.2. Calculation of $ R_0 $ and the next generation function
Consider system (4.1). For any initially introduced population distribution $ (0, N_b^0, 0) $ with $ \int_\Omega N_b^0(\xi, \eta)d\xi d\eta = 1 $, define
where $ N_v^{(l)}(x, y, \infty) $ is the third compartment of the solution to system (4.1) with the normalized initial condition $ (0, N_b^l, 0) $ as $ t\rightarrow \infty $. Note that the total population size of $ N_b^l $ is $ 1 $ since $ \int_\Omega N_b^l(\xi, \eta)d\xi d\eta = 1 $. Equations in (4.6) indicate that $ N_v^{(l)}(\cdot, \cdot, \infty) $ is the final distribution of offspring of the initial population $ N_b^l $ of total size $ 1 $.
In the numerical program in River2D, we approximate $ R_0 $ by
and the next generation function by
for sufficiently large positive integer $ l $, where $ \{(x_i, y_j)_{i\in I, j\in J}\} $ is a division of the river region $ \bar{\Omega} $ in simulation. Intuitively, the above approximations in (4.7) and (4.8) illustrate that $ R_0 $ represents the average number of offspring a single individual produces in the whole river in its lifetime and that the distribution of all offspring of a single individual is $ \phi_n^\ast(x, y) $. Mathematically, the reason why the net reproductive rate $ R_0 $ defined in (3.8) can be approximated by (4.7) is given in Appendix C.
Remark 5. The approximations (4.5), (4.7) and (4.8) for $ R_\delta $, $ R_0 $ and the eigenfunction are derived for the general model (4.1); nevertheless, our current numerical program in River2D only assumes constant parameters for (4.1).
5.
Applications
5.1. Population persistence in a river with an island
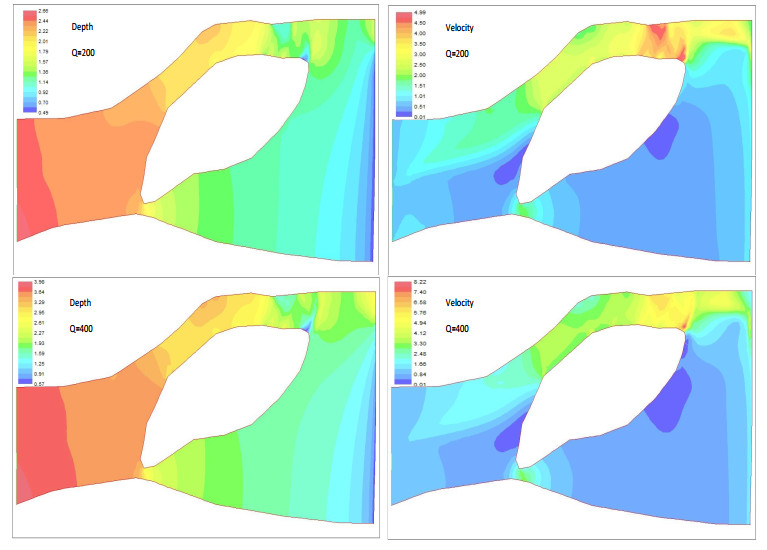
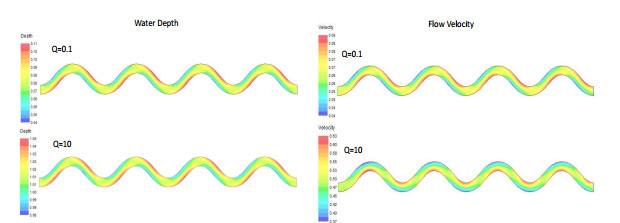
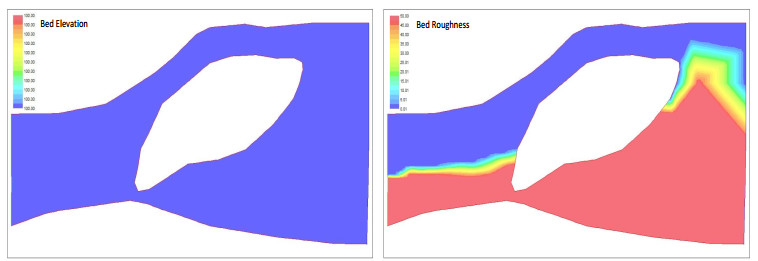
We consider a river with an island (see Figure 1) and find persistence metrics of a population in the river. The river is in a region with dimensions $ 458 $ m by $ 247 $ m (unit: m). The bed elevation and effective bed roughness height are defined as in Figure 1. We consider two flow cases: the instream flow of $ 200 $ m$ ^3 $/s and the outflow water depth of $ 0.5 $ m; the instream flow of $ 400 $ m$ ^3 $/s and the outflow water depth of $ 0.5 $ m. Under such flow boundary conditions, the steady flow conditions can be calculated in River2D and the plan view distributions of the water depth and flow velocity are shown in Figure 2.
We then introduce a population into the river and calculate $R_\delta$ and $R_0$ as well as the corresponding next generation function under these two different flow conditions.
The zero-flux condition is chosen along the bank and hostile conditions (4.2) are chosen at the upstream and downstream ends.
We choose the following model parameters: $D(x,y)\equiv $1 m$^2/$s,
$\sigma(x,y)\equiv 0.75/$s, $\mu(x,y)\equiv 1.8/$s, $m_b(x,y)\equiv m_d(x,y)\equiv 0.1/$s, and $f(x,y,0)\equiv
r=0.5$ or $0.322/$s.
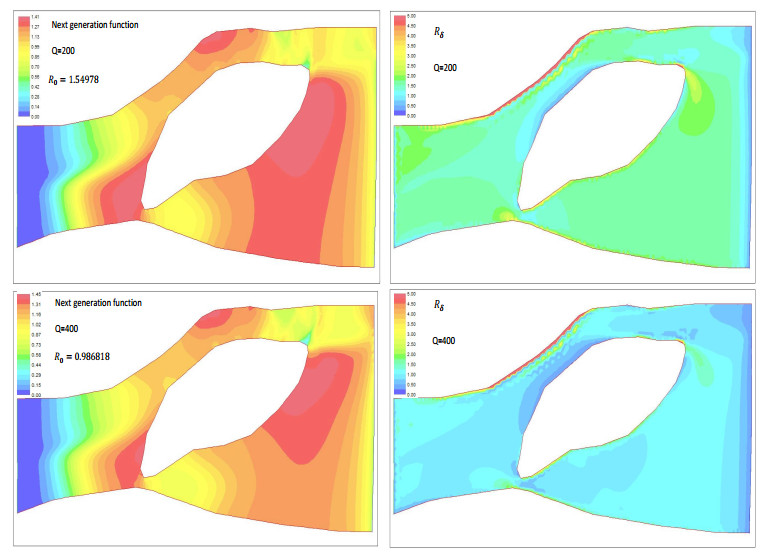
Two different cases are considered. Case 1: $ Q = 200 $ m$ ^3/ $s and $ r = 0.5/ $s; case 2: $ Q = 400 $ m$ ^3/ $s and $ r = 0.322/ $s. We obtain that $ R_0 = 1.54978 $ in case 1 and $ R_0 = 0.986818 $ in case 2. The $ R_\delta $ distribution and the next generation function are shown in Figure 3, respectively. It follows from Theorem 3 that the population persists in the river in case 1 (when $ Q = 200 $ m$ ^3/ $s) and will be extinct in case 2 (when $ Q = 400 $ m$ ^3/ $s). When the flow discharge is low (i.e., in case 1), the $ R_\delta $ distribution shows that most parts of the river are source regions ($ R_\delta (x, y) > 1 $) that are suitable to introduce the population if it is expected to grow in the river. The next generation function distribution shows that the next generation offspring will not be distributed near the upstream end. They occupy other parts of the river, especially in the middle parts, and this ensures the persistence of the population in the whole river. However, when the flow discharge is large (i.e., in case 2), the population will go extinct even though there are some source regions in the river. Note that we choose different birth rate $ r(x, y) $ in the examples here to easily illustrate the phenomenon of persistence and extinction. In fact, even with the same birth rate, the population may persist under low flow but will be extinct under high flow.
5.2. Population persistence in a periodic meandering river
We consider a two dimensional periodic meandering river and study the influence of ecological factors and flow characteristics on population persistence metrics in such a river.
5.2.1. A periodic meandering river
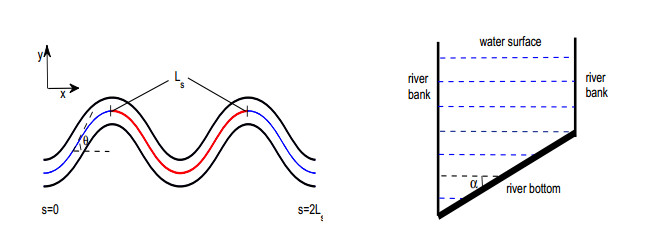
The channel of a meandering river is represented by a sine generated curve $ \theta = \theta_m \sin{\left(2 \pi s/L_s\right)} $ (see Figure 4), where $ \theta $ represents the angle between the channel and the longitudinal line with the maximum $ \theta_m $, $ s $ is the distance from the upstream end of the river, $ L_s $ is the length of one period of the channel, and the lateral bed slope is $ \tan \alpha $ where $ \alpha = \alpha_m \sin{\left(2\pi s/L_s\right)} $ with maximum $ |\alpha_m| $. See also, e.g., [27]. We selected the following parameter values to build the meandering river profile for input to the River2D environment: the river length $ L = 800 $m, the channel period $ L_s = 200 $ m, the width $ 20 $ m, the longitudinal slope of the river bottom $ S_0 = 0.0002 $, $ \theta_m = \pi/4 $, $ \alpha_m = -\pi/1000 $, the bottom roughness $ n = 0.1 $m. See Figure 5. In particular, most nodal points inside the numerical domain are uniformly distributed with a $ 5 $ m spacing, but nodes near the boundary are slightly shifted and the space discretization on the boundary is smaller than $ 5 $m, for better numerical results.
With a specific constant flow discharge at the upstream boundary, River2D can simulate the steady state flow for this river, where the water depths and flow velocities vary periodically. See Figure 6 for the steady flow when $ Q = 0.1 $m$ ^3/ $s and $ Q = 10 $m$ ^3/ $s.
5.2.2. Effects of biological, physical and hydraulic factors on population persistence
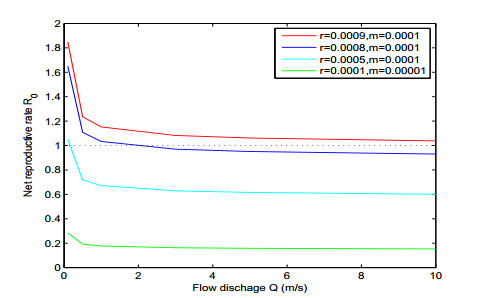
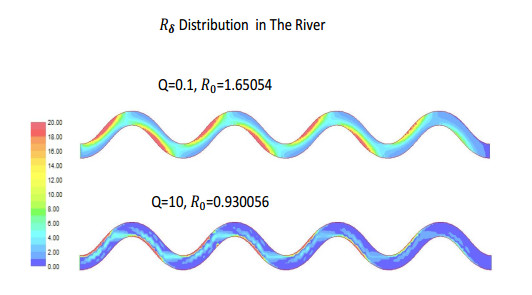
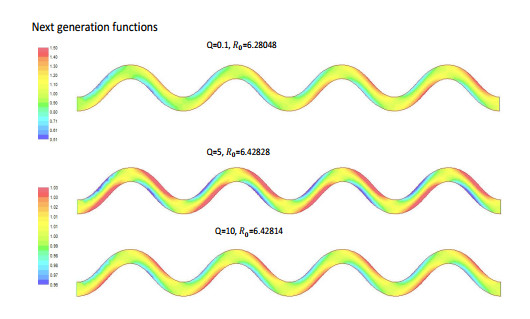
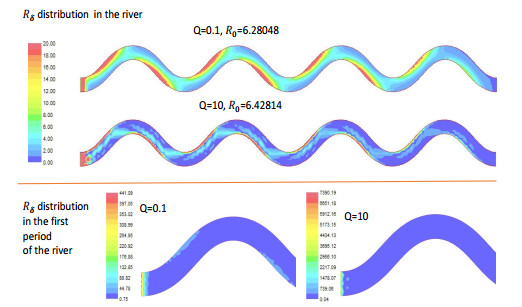
1. The co-influence of the flow discharge and the population growth rate. Consider model (2.1) in the meandering river with boundary conditions (4.2). We calculate the net reproductive rate $ R_0 $ and obtain the next generation function as well as the source/sink distribution $ R_\delta $ under conditions of different birth rates, death rates, and flow discharges. Figure 7 shows the relationship between $ R_0 $ and the flow discharge $ Q $ under different growth rate conditions. $ R_0 $ decreases as the flow increases, but increases as the birth rate increases. When the flow only carries organisms to the downstream but does not help them grow, it has only a negative effect on population persistence in the river; a higher growth rate clearly helps population persistence. This coincides with the analysis and simulations for persistence conditions for single population models and benthic-drift population models; see [20,31,38]. Figures 8 and 9 show the next generation function distribution and the distribution of $ R_\delta $ under different flow conditions. While the next generation function values are almost zero in the first three periods of the river, Figures 8 only shows the next generation function distribution in the last period of the river. Note that the next generation function corresponds to the steady distribution of offspring. This indicates that if the upstream boundary condition is hostile, then in a long run, the next generation concentrates near the downstream end, especially in the region with low flow velocity at the downstream end. Figure 9 shows that the source regions are located in the shallow areas with relatively low flow velocities and are more likely in the upstream. When the flow discharge becomes larger, the downstream contains more sink regions and hence becomes a worse environment for the population to live. Note that here we assume that the flow only has a negative effect on the population. In some rivers, the flow may help persistence by bringing nutrients to organisms; see [19] for drift feeders. In our simulations, the birth rate is assumed to be constant. If the birth rate increases in the downstream direction, then the increased flow plays a trade-off role (see [31] and [20] for models in one-dimensional rivers). Moreover, higher flow rate may be associated with changes in dissolved oxygen [50], hence it would be interesting to investigate how the flow rate affects the concentration of dissolved oxygen in a river, and thus affects the population survival.
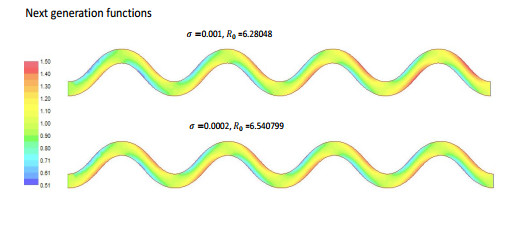
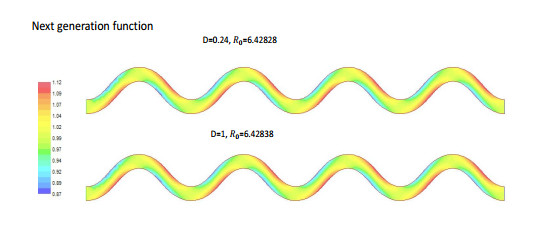
2. The effect of the transmission rates. We consider the influence of individuals' transfer rates between the benthos and the water column on population persistence. Figure 10 shows the net reproductive rate and corresponding next generation function under boundary conditions (4.3) for different transfer rates. We choose the ratio between $ \sigma $ (the transfer rate from benthos to water column) and $ \mu $ (the transfer rate from water column to benthos) to be $ 1/4 $. It shows that the smaller the transfer rate is, the larger the net reproductive rate is, which coincides with the result from the benthic-drift model in a one-dimensional river (see Figure 5 in [20]). Therefore, when the ratio between transfer rates is fixed, more frequent transfer between the benthos and the water column does not help population persistence in the whole river. Note that Remark 1 implies that if $ f(x, y, 0)\equiv r > \mu(x, y)+m_b(x, y) $, then population persistence is guaranteed. In our situation, this means that if $ \sigma(x, y) < (f(x, y, 0)-m_b(x, y))/4 $, then there is unconditional persistence, regardless of the flow rate or other parameter conditions. This is consistent with the result for the benthic-drift model in a one-dimensional river in [38] and again indicates that the lower the transfer is, the better it would be for population persistence.
3. The effect of the diffusion rate. The net reproductive rate and corresponding next generation function with boundary conditions (4.3) for different diffusion rates are shown in Figure 11. The net reproductive rate slightly increases with the diffusion rate here. Hence, under the flow condition given in the example, diffusion in the water column helps population persistence in the river. This is because in a river with low flow more random movement of the population increases the chance of individuals' upstream dispersal and hence helps persistence since the upstream end is not lethal. This is consistent with the results from the one-dimensional models; see e.g., Figure 3.2 in [23].
4. The effect of the river bottom roughness height. The net reproductive rate and next generation function with boundary conditions (4.2) corresponding to different river bottom roughness heights are shown in Figure 12. The net reproductive rate increases with the bottom roughness height $ n $ of the river. As the bottom roughness indicates the living condition on the benthos, this implies that a river with a rough bottom (e.g., a river with rocks or stones on the bottom) is better for a population to live and persist than a river with smooth bottom (e.g. sand). It has been shown in [22] (see Figure 3(d) in [22]) that the river bottom roughness increases the upstream speed of a population in a one-dimensional river. Since the conditions for positive upstream speed in an infinitely long river and that for population persistence in a bounded river have been proved to be the same in many literatures (see e.g., [23,24,29]), our result that the river bottom roughness helps population persistence in a two-dimensional river is essentially consistent with that in [22].
5. The effect of the river bottom slope. The net reproductive rate and next generation function with boundary conditions (4.2) corresponding to different river bottom slopes are shown in Figure 13. The net reproductive rate decreases as the river bottom slope increases. Therefore, it is easier for the population to persist in a river with flatter bottom than in a river with steeper bottom. This is also consistent with the result in [22] that the river bottom slope decreases the upstream speed of a population in a one-dimensional river. In a previous work [20] for a one-dimensional benthic-drift model, we observed that when deep pools are close to the upstream, more offspring are produced and live upstream to avoid being washed out and hence deep pools close to upstream help population persistence. In a meandering river constructed as in our examples, deep pools and shallow regions may appear on the same cross section, so the effect of pools on persistence may not be as clear as in the one-dimensional case.
6. The effect of boundary conditions. We use boundary conditions (4.2) (with hostile upstream boundary condition) and (4.3) (with zero-flux upstream boundary conditions) in above simulations. It can been seen from Figures 8 to 15 that boundary conditions greatly influence the value of the net reproductive rate and the next generation function distribution as well as the source/sink regions. When a hostile boundary condition is applied at the upstream end, the upstream part of the river becomes a poor region for the distribution of the next generation function; the offspring occupy only the region near the downstream end and the density near the downstream end becomes high. See Figures 8, 12, and 13. By way of contrast, when the zero-flux boundary condition is applied at the upstream end, the entire river becomes a more suitable region for the next generation distribution, and hence, the next generation offspring are more evenly distributed in the river, although the population density is higher in deep water than in shallow water. See Figures 10, 11, and 14. Moreover, the zero-flux boundary condition at the upstream end yields a much larger net reproductive rate than a hostile boundary condition does. The source/sink regions in the river are also very different under the two different boundary conditions. Under the hostile boundary condition at the upstream, the upstream end is the sink region and the source regions are concentrated in the shallow areas in the river (see Figure 9). However, under the zero-flux condition at the upstream, $ R_\delta $ attains its maximum at the upstream end and the upstream end becomes the most important source region for the population; see Figure 15. The different scales in the lower part of Figure 15 also illustrate why $ R_0 $ is higher when $ Q = 10 $ than when $ Q = 0.1 $; $ R_\delta $ is an order of magnitude larger when $ Q = 10 $ compared to when it is $ Q = 0.1 $. We also see a strange phenomenon, unlike in Figure 7, about the next generation function distribution for system (4.1) under the zero-flux upstream boundary condition (4.3), when varying the flow discharge; see Figure 14. When the flow discharge increases, the net reproductive rate first increases and then decreases. This seems to be hard to understand. When the water discharge increases, the water depth and flow velocity increase throughout the river. It is hard to see which parameter causes the drop of the net reproductive rate when the discharge increases from 5 to 10.
6.
Discussion
Understanding hydrodynamics and ecological dynamics is crucial in stream and river management. While there is a need to integrate hydraulic and biological features to discover how river morphology and water flows affect the ecological status of rivers [8,40], a reasonable and efficient method for such integration becomes critical. Based on the fruitful development of habitat models in river habitat assessment, most existing methods (e.g., the physical habitat simulation model (PHABSIM), ecological limits of hydrologic alteration (ELOHA) framework, Software for Assisted Habitat Modeling (SAHM), etc.) link habitat suitability index of river species (e.g., fish) to physical conditions, focusing primarily on habitat suitability and availability; see e.g., [4,32,33,36,40,43,44,46,48].
A few works have attempted to incorporate ecological factors explicitly into hydrodynamic modeling analysis; see e.g., [2,6,18,22,30]. The modelling framework in this paper extends the approach in [22]. The results therein have made it possible to directly analyze how river morphology influences short and long term behaviors of a population in a river. In the current work, by analyses and calculations for the coupled hydrodynamics and population models in partial differential equations, we are able to determine the source/sink regions and global dynamics of a specific population in a two-dimensional depth-averaged river model. Hydraulic, physical and demographic features are explicitly incorporated into the model and their effects on suitable habitat or population persistence/extinction can be numerically analyzed.
Our results showed that the increase of the growth rate and the diffusion rate yields larger net reproductive rate and helps population persistence while larger transfer rate decreases the net reproductive rate and drives population to be extinct. Moreover, higher river bottom roughness height helps population persist but higher bottom slope leads to population extinction more quickly, which might be due to the fact that changes to these parameters change the flow velocity, to a lower level in the former case and to a higher level in the latter case. When the upstream end is imposed with hostile boundary condition, the offspring concentrate in the downstream region and the source regions are in the shallow areas throughout the river. When the upstream end is imposed with the zero-flux boundary condition, the offspring concentrate in deep water regions and the source regions are mainly in the shallow water regions with the most significant source at the upstream end. We also saw a challenging phenomenon which is very hard to understand: When the upstream end is imposed with the zero-flux conditions, when the flow discharge increases, the net reproductive rate may increase first and then decrease.
In order to use the River2D program to calculate $ R_\delta $ and $ R_0 $ for a population in a river, the following data need to be collected by ecologists and river managers: Biological data including the birth rate, the death rate, the diffusion rate, transfer rates between the benthos and the drifting water, and population boundary conditions; river bed topography data including bed location ($ x $-coordinate, $ y $-coordinate), bed elevation, bed roughness height, and boundary type; and flow data such as the upstream inflow and the downstream water surface level. It is our hope that this work would be a useful tool for ecologists to predict or control long term behaviors of river and stream species and for water resources managers in identifying more accurately the targets for flow regulation.
In the current River2D program, the biological parameters (birth, death, diffusion, and transfer rates) are assumed to be constants. We will further incorporate spatial heterogeneities of these parameters in the program so that it can be widely used to investigate population persistence and source-sink dynamics in more realistic scenarios. Moreover, since the living conditions for aquatic species in rivers can vary seasonally, the theory developed in this work could be extended to more general situations by incorporating temporal variations in population demography features and flow regime. As a future work, we may consider dynamics of interacting species models coupled with hydrodynamic equations and hence provide better river ecology management strategies.
Acknowledgements
The authors thank Peter M. Steffler for valuable discussions and comments. The authors also wish to thank Lewis Lab for fruitful discussions. Y. J. gratefully acknowledges an AMS-Simons Travel grant and NSF Grant (DMS 1411703). Q. H. gratefully acknowledges support from NSF of China (11871060), the Fundamental Research Funds for the Central Universities (XDJK2018B031), and the faculty startup fund from Southwest University (20710948). M. A. L. also gratefully acknowledges a Canada Research Chair, NSERC Discovery and Acceleration grants, and a Killam Research Fellowship.
Conflict of interest
The authors declare no conflict of interest.
Appendix
A. Derivation of model (2.1)
We first develop a single-compartment model, and then extend it to a benthic-drift model by dividing the river channel into two zones and the population into two corresponding groups.
Let $ N(x, y, t) $ be the population density (unit: quantity/volume) at location $ (x, y) $ and time $ t $. Let $ h(x, y) $ be the water depth (unit: length) at location $ (x, y) $ and $ v(x, y) = (v_1(x, y), v_2(x, y)) $ be the depth averaged flow velocity (unit: length/time) at $ (x, y) $ with $ v_1 $ and $ v_2 $ being the flow velocities in the $ x $ and $ y $ directions, respectively.
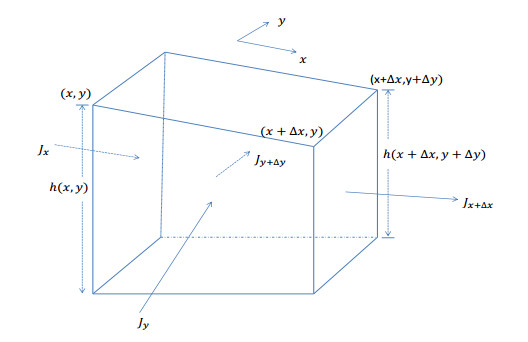
Consider a water flow box containing the cross-section through $ (x, y) $ with the volume estimated by $ \Delta V = \Delta x\Delta y h(x, y) $ (see Figure 16). We want to understand how the population density in the box changes over time due to flows of population into and out of the box. In the $ x $-direction, the population enters the box with a flux $ J_x $ and leaves the box with a flux $ J_{x+\Delta x} $. In the $ y $-direction, the population enters the box with a flux $ J_y $ and leaves the box with a flux $ J_{y+\Delta y} $. The flux expresses the density of population that passes a unit area per unit of time. It has dimension density/(area$ \cdot $time). The population density that flows into or out of the box in the $ x $ direction per unit time can be estimated by the product of the flux in the $ x $ direction and the area of the surface over which the flux occurs, $ J_x\cdot A_x $, or $ J_{x+\Delta x}\cdot A_{x+\Delta x} $. Similar formulas apply for the population inflow and outflow in the $ y $ direction. We then have the balance equation:
Letting $ \Delta x, \Delta y\rightarrow 0, $ we have
Microscopically, the flux due to advection can be written as
The flux due to dispersion can be written as
where $ D > 0 $ is the diffusion coefficient. Moreover, $ J_x = J_x|_{advection}+J_x|_{dispersion} $ and $ J_y = J_y|_{advection}+J_y|_{dispersion} $.
By combining the flux divergence formula (A.2) with the microscopic formula for advection (A.3) and dispersive flux (A.4) and also considering a reproduction or decay process of the population, we obtain the following general 2-dimensional model for a population that only lives in the drifting water.
where $ g(x, y, N) $ is the population growth rate.
Hydrologically, the presence of free-flowing water zones on the top and transient storage zones along the bottom in rivers is an important hydraulic characteristics in the ecology of streams. In the storage zones, water movement can be approximated as zero flow [5,10]. Ecologically, many aquatic organisms reside mainly in the storage zone but occasionally jump into the free-flowing zone and drifting downstream until they settle down on the benthos again [1]. Motivated by these facts, we extend the single-compartment model (A.5) to the following benthic-drift model by partitioning the river into two zones, drift zone and benthic zone, and dividing the population into two interacting compartments, individuals residing on the benthos and individuals dispersing in the drift zone:
where $ N_d $ and $ N_b $ represent the population density in the drifting water and the population density on the benthos, respectively, $ f $ is the reproduction rate of the population $ m_d $ and $ m_b $ are the mortality rates of individuals in the drift and individuals on the benthos, respectively, and $ \triangledown = \left(\partial/\partial x, \partial/\partial y\right) $.
B. Proof of Theorem 3
Theorem 3 can be proved by following the same process as in Section 3.3 in [20]. Substituting $ N_d(x, y, t) = e^{\lambda t}\phi_1(x, y) $ and $ N_b(x, y, t) = e^{\lambda t}\phi_2(x, y) $ into (3.1), we obtain the associated eigenvalue problem
By applying similar arguments as in Theorem 3 and Lemma 4 in [20], we can prove the following results.
Lemma 6. (a) The eigenvalue problem (B.1) has a simple principal eigenvalue $ \lambda^{\ast} $ with a positive eigenfunction if $ f(x, y, 0)-m_b(x, y)-\mu(x, y) < 0 $.
(b) $ R_0-1 $ and $ \lambda^\ast $ have the same sign, where $ \lambda^\ast $ is the principal eigenvalue of (B.1).
Then by using similar arguments as in the proof of Theorem 5 in [20], we can obtain the following results.
(ⅰ) If $ \lambda^\ast < 0, $ then the extinction equilibrium $ (0, 0) $ is asymptotically stable for (2.1) for all nonnegative initial value conditions.
(ⅱ) If $ \lambda^\ast > 0, $ then there exists $ \epsilon_0 > 0 $ such that any positive solution of (2.1) satisfies
These results together with Lemma B.1 complete the proof of Theorem 3.
C. Approximating $ R_0 $ by (4.7)
Let $ (N_d(x, y, t), N_b(x, y, t), N_v(x, y, t)) $ be the solution of system (4.1) with initially introduced population distribution $ (0, N_b^0, 0) $. Denote the final distribution of offsprings by $ N_v^1 $, i.e.,
Let $ \bar{\Gamma}:X\rightarrow X $ be defined as
By using similar derivation as in Appendix A.5 in [20], we can obtain the formula of the operator $ \bar{\Gamma} $:
for any $ \varphi \in X $, where $ k(x, y, \xi, \eta) $ is the solution of the ordinary boundary value problem
for a fixed point $ (\xi, \eta)\in \Omega $. Note that the solution to (C.3) is a Green's function (see (2–11) in Chapter 7 in [17], (2.9) in Chapter 3 in [42], or Appendix B in [31]). Furthermore, we obtain the following result.
Proposition 7. The spectral radius of $ \Gamma $ is equal to the spectral radius of $ \bar{\Gamma} $, i.e.,
Proof. Define an operator $ \hat{\Gamma}:X\rightarrow X $ as
for all $ \varphi\in X $, where $ k(x, y, \xi, \eta) $ is the solution of the ordinary boundary value problem (C.3). By similar proof as for Theorem 6 in [20], we obtain that the spectral radius of $ \Gamma $ is equal to the spectral radius of $ \hat{\Gamma} $, i.e.,
Define two operators $ T_1, T_2: X\rightarrow X $:
for all $ \varphi\in X $, where $ k $ is defined in (C.3). Then both $ T_1 $ and $ T_2 $ are bounded and linear, and we further have $ \hat{\Gamma} = T_2 \circ T_1 $, $ \bar{\Gamma} = T_1\circ T_2 $. This yields the result that the spectral radii of these two operators are the same, i.e.,
Hence, we obtain
To numerically approximate $ \bar{\Gamma} $, we can discretize (C.2) in the river region $ \bar{\Omega} $. Divide $ \bar{\Omega} $ into a grid (uniform except in the area near the boundary). Let $ \{(x_i, y_j)_{i\in I, j\in J}\} $ represent all the nodes of the grid. Let $ n $ be the total number of the nodes and rearrange all nodes such that they are represented by a sequence of points $ \{P_h, 1\leq h\leq n\} $. By applying a numerical quadrature (e.g., Newton-Cotes, Gauss, Simpson, etc.) to (C.2), we can approximate (C.2) by
where $ \eta_{h, s} > 0 $ depends on parameter functions in (4.1) and the numerical quadrature (see e.g., [37,45]). Let
Then we can approximate the operator $ \bar{\Gamma} $ by the positive matrix operator $ \bar{\Gamma}_n $ and hence approximate $ r(\bar{\Gamma}) $ by $ r(\bar{\Gamma}_n) $, i.e.,
for large positive integer $ n $.
The Perron-Frobenius Theorem implies that $ \bar{\Gamma}_n $ admits a positive principal eigenvalue $ \lambda_n^\ast $ which is equal to $ r(\bar{\Gamma}_n) $ and is associated with a positive eigenvector $ \phi_n^\ast $. Since $ \bar{\Gamma}_n $ is a positive matrix, we can use the power method to numerically calculate $ \lambda_n^\ast $. For any nonnegative function $ N_b^0 $ with $ \sum_{h = 1}^n N_b^0(P_h) = 1 $, let
We then have
Note that we use $ \bar{\Gamma}_n $ to approximate $ \bar{\Gamma} $. The definition of $ \bar{\Gamma} $ in (C.1) implies that $ \bar{\Gamma}_n N_b^{l-1} $ approximates the offspring distribution of system (4.1) with the initial population $ N_b^{l-1} $. Denote
(C.9) implies that
and
Following this idea, we do not directly find $ \bar{\Gamma}_n $ to estimate $ \lambda_n^\ast $ (and hence $ R_0 $) in our River2D simulations. Instead, we solve (4.1) numerically for any nonnegative function $ N_b^0 $ satisfying $ \sum\limits_{(x_i, y_j)\in \bar{\Omega}}N_b^0(x_i, y_j) = 1 $, and define the following sequence by following the idea as in (C.1) and (C.8):
where $ N_v^{(l)}(x_i, y_j, \infty) $ is the offspring compartment of the numerical solution to system (4.1) with the normalized initial condition $ (0, N_b^l, 0) $ as $ t\rightarrow \infty $. Then by (C.4), (C.7), (C.10) and (C.11), we approximate $ R_0 $ by
and the next generation function by
for sufficiently large positive integer $ l $.









 DownLoad:
DownLoad: