On the Caginalp phase-field system based on the Cattaneo law with nonlinear coupling

1.   Introduction

Intelligent optimization algorithms are increasingly popular in the field of intelligent computing and are widely applied in various other fields, including engineering, medicine, ecology and environment, marine engineering, and so forth. Classical intelligent optimization algorithms include: Particle swarm algorithm (PSO)^[1], genetic algorithm (GA)^[2], simulated annealing (SA)^[3], etc. PSO refers to a swarm intelligence optimization algorithm that simulating bird predation, in which each bird is treated as a particle and the particles follow the current optimal particle to find the optimal solution in the solution space. GA is a computational model based on Darwin's theory of evolution and Mendelian genetics to simulate biological evolution. Genetic algorithms obtain the optimal solutions through three basic operations: chromosomal self-selection, crossover and mutation. SA marks the first natural algorithm proposed to simulate the high-temperature annealing process of metallic materials. When SA is heated at high temperatures and then slowly cooled, the particles eventually reach a state of equilibrium and solidify into crystals of minimal energy. Many scholars have also developed many bionic intelligence optimization algorithms based on classical intelligence algorithms, such as Sine Cosine Algorithm (SCA) ^[4], the Artificial swarm algorithm (ABC) ^[5], the Bat algorithm(BA) ^[6], the Bee Evolutionary Genetic Algorithm (BEGA) ^[7], the Squirrel Search Algorithm (SSA) ^[8], the Atomic Search optimisation (ASO) Algorithm ^[9], etc.

The Atomic Search Optimisation (ASO) algorithm is a new intelligent optimisation algorithm based on molecular dynamics derivatives that was proposed in 2019. ASO is composed of geometric binding force and the interaction force between atoms, following the laws of classical mechanics ^[10,11]. Geometric binding forces are the interaction between the Lennard-Jones(LJ) potential ^[12,13] and the co-borrowing bonds among atoms. In ASO, atoms represent solutions in the search space. The larger the atomic mass, the better the solution, and vice versa. Compared to traditional intelligent system algorithms, ASO requires fewer physical parameters and can achieve better performance. As a result, it has been widely used in various fields, Zhang et al. applied ASO to hydrogeological parameters estimation ^[9] and groundwater dispersion coefficients calculation ^[14]. Ahmed et al. utilized ASO in fuel cell modeling and successfully built an accurate model. Simulations showed that it was as good as commercial proton exchange membrane(PEM) fuel cells ^[15], Mohammed et al. used ASO to reduce the peak sidelobe level of the beam pattern ^[16], Saeid combined the ASO with the Tree Seeding Algorithm (TSA) to enhance its performance in exploration ^[17]. Ghosh et al. proposed an improved Atomic Search Algorithm(ASO) based on binary variables and combined it with Simulated Annealing (SA) technique ^[18]. Elaziz et al. proposed an automatic clustering algorithm combining the ASO and the SCA algorithm to automatically find the best prime numbers and the corresponding positions ^[19]. Sun et al. applied improved ASO to engineering design ^[20].

Since ASO is prone to finding only locally optimal solutions with low accuracy, an Improved Atom Search Algorithm(IASO) algorithm based on particle velocity updating is proposed in this paper. The IASO algorithm has the same principle as the ASO algorithm, but IASO is optimized for speed iterative updates to improve the convergence speed of the algorithm, avoid finding local optimal solutions, and allow a more extensive search for optimal solutions. IASO adopts the idea of particle update speed in PSO and introduces inertia weights $ w $ to improve the performance of ASO. In addition, the learning factors $ c_{1} $ and $ c_{2} $ are added into IASO, which not only ensure the convergence performance of the algorithm, but also accelerate the convergence speed, effectively solving the problem that the original ASO tends to find only the local optimal solution.

Array signal processing is one of the important research directions of signal processing, which has been developing rapidly in recent years. DOA estimation of signals is an ongoing research hotspot in the field of array signal processing. It has great potential for hydrophone applications. Hydrophones are generally divided into scalar hydrophones and vector hydrophones. Due to the scalar hydrophones can only test scalar parameters in the sound field, many scholars have turned to the study of vector hydrophones. Xu et al. used alternating iterative weighted least squares to deal with the off-grid problem of sparsity-based ^[21], DOA of an array of acoustic vector water-modulated microphones. Amiri designed a micro-electro-mechanical system (MEMS) bionic vector hydrophone with a piezoelectric gated metal oxide semiconductor field-effect transistor (MOSFET) ^[22]. More and more scholars have been doing research in the direction of vector array. Song et al. studied the measurement results of an acoustic vector sensor array and proposed a new method to obtain better DOA estimation performance in noisy and coherent environments ^[23], using the time-frequency spatial information of the vector sensor array signal, Gao et al. combined elevation, azimuth and polarization for the estimation of electromagnetic vector sensor arrays based on nested tensor modeling ^[24], Baron et al. optimised, conceptualised and evaluated a hydrophone array for deep-sea mining sound source localisation validation ^[25], and Wand et al. proposed an iterative sparse covariance matrix fitting direction estimation method based on a vector hydrophone array ^[26]. In recent years, Some scholars applied compressed sensing to signal DOA estimation. Keyvan et al., proposed the Three Dimensional Orthogonal Matching Pursuit(3D-FOMP) algorithm and the Three Dimensional Focused Orthogonal Matching Pursuit (3D-FOMP) algorithm to obtain better estimation performance in low signal-to-noise ratio and multi-source environments, and to solve the problem that conventional DOA estimation algorithms cannot distinguish between two adjacent sources ^[27]. Keyvan et al, designed a new hybrid nonuniform linear array consisting of two uniform linear subarrays and proposed a new DOA estimation method based on the OMP algorithm. This algorithm has lower computational complexity and higher accuracy compared with the FOMP algorithm. It can distinguish adjacent signal sources more accurately and solve the phase ambiguity problem ^[28].

With the development of vector hydrophone, the direction of arrival estimation of the vector hydrophones signal has an increasingly wide application, which is of great importance for the functional extension of sonar devices ^[29]. Many useful estimation methods, multiple signal classification (MUSIC)^[30], estimated signal parameters via rotational invariance technique (ESPRIT) ^[31] and maximum likelihood (ML) ^[32] etc. have been proposed by many scholars.

In 1988, Ziskind and Max added ML estimation to DOA and achieved ideal results ^[33]. compared with MISIC and Espirit, the ML estimation method is more effective and stable, especially in the case of low signal-to-noise ratios (SNR) or small snapshots.However, in MLDOA estimation, the solving problem of the likelihood function is a multidimensional nonlinear polar problem that requires a multidimensional search for global extrema, which increases the computational burden.

Many scholars have used various methods in combination with ML to improve the estimation performance of DOA. Zhang, C.Y. et al. proposed a sparse iterative covariance-based estimation method and combined it with ML to improve its performance. However, its resolution and stability ^[34] are not high, and Hu et al. proposed a multi-source DOA estimation based on the ML in the spherical harmonic domain ^[35], Ji analyzed the asymptotic performance of ML DOA estimation ^[36], Selva proposed an effective method to calculate ML DOA estimation in the case of unknown sensor noise power ^[37], Yoon et al. optimized the sequence and branching length of taxa in phylogenetic trees by using the maximum likelihood method ^[38], Vishnu proposed a line propagation function (LSF)-based sinusoidal frequency estimation algorithm to improve the performance of ML DOA ^[39].

In response to the complexity of the ML DOA estimation problem, some scholars have used intelligent optimization algorithms to optimize MLDOA and achieved better performance. Li et al. applied the bionic algorithm genetic algorithm to MLDOA estimation for the first time, but the genetic algorithm is prone to problems such as premature convergence ^[40]. Sharma et al. applied the PSO algorithm to MLDOA estimation, but there are still some drawbacks in the estimation of multi-directional angles because the PSO algorithm converges slowly and tends to fall into local optimal solutions ^[41], Zhang et al. combined artificial colony bees with ML DOA estimation to reduce the computational complexity in calculating ML functions ^[5], Feng et al. combining bat algorithms with ML to optimize the multidimensional nonlinear estimation of spectral functions ^[6], Fan et al. applied the Improved Bee Evolutionary Genetic Algorithm (IBEGA) to MLDOA estimation ^[7], Wang et al. used an improved squirrel search algorithm (ISSA) in MLDOA estimation, which reduced computational complexity and enhanced the simulation effect ^[42], and Li et al. proposed a search space that limits the search space for particle swarm optimization ^[43].

As calculating the likelihood function for maximum likelihood DOA estimation is a multi-dimensional non-linear polar problem, a multi-dimensional search for global extremes is required, which requires extensive computation. To solve this problem, the proposed IASO is applied to MLDOA estimation. Simulation results show that the combination of IASO and MLDOA estimation significantly reduces the computational complexity of multidimensional nonlinear optimization of ML estimation.

The main structure of this article is as follows: Section2 presented the improved ASO and compared the convergence performance of ASO and IASO on 23 benchmark functions; Section3 gives the data model and ML estimation; Section4 combines IASO with ML DOA, providing the simulation results to validate the convergence performance and statistical performance of IASO ML estimation and compareing it with ASO, PSO, GA and SCA combined with ML DOA estimation separately. Section 5 concludes the paper.

2.   Improved atom search algorithm (IASO)

The Atomic Search Algorithm (ASO) was proposed by Zhao et al. in 2018. It is a physics-inspired algorithm developed by molecular dynamics. The algorithm is simple to implement, featured with few parameters and good convergence performance and thus it has been used to solve a variety of optimization problems.

The ASO algorithm is based on the interaction forces between atoms and geometric constraints, and the position of each atom in the search space can be measured by its mass. This means that the heavier the atoms, the better the solution. The search and optimisation process is based on the mutual repulsion or attraction of atoms depending on the distance between them. The lighter atoms flow at an accelerated speed to the larger atoms, which widens the search area and performs a large search. The acceleration of heavier atoms is smaller, making it more concentrated to find better solutions. Suppose that a group of atoms has $ N $ atoms, the position of the $ i^{th} $ atom is $ X_i = [ x_{i}^1, x_{i}^2, \cdots, x_{i}^d], $ according to Newton's second law

where $ F_{i} $ is the total force of the interaction force on the atom $ i $, $ G_{i} $ is the geometric binding force on the atom $ i $, and $ m_{i} $ is the mass of the atom $ i $.

2.1.   Random initialization

The general unconstrained optimization problem can be defined as

where $ x^d(d = 1, 2, \cdots.D) $ is the $ d $ components in the search space, $ Lb $ is the lower limit, $ Ub $ is the upper limit, and $ D $ is the dimension of the search space.

2.2.   Fitness evaluation

The fitness value $ Fit_{i}(t) $ of the position of each atom is calculated according to the fitness function defined by the user. The mass of each atom is Eq (2.3) and Eq (2.4), which can be derived from its fitness.

where $ Fit_{best}(t) $ and $ Fit_{worst}(t) $ refer to the best fitness value and worst fitness value of the atom in $ i^{th} $ iterations, $ Fit_{i}(t) $ is the fitness value of atom $ i $ at the $ i^{th} $ iteration, and the expressions of $ Fit_{best}(t) $ and $ Fit_{worst}(t) $ are as follows

2.3.   Interaction

The interaction force between atoms is obtained from the literature ^[9,11], after optimizated by the LJ potential energy

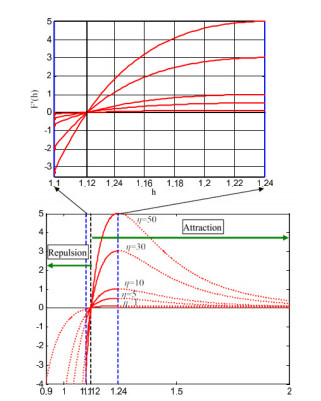
where $ \eta(t) $ is the depth function that adjusts the repulsion and attractive force, $ \alpha $ is the depth weight, $ T $ is the maximum number of iterations, and $ t $ is the current number of iterations. Figure 1 shows the functional behavior of function $ F $, the $ \eta(t) $ corresponding to different $ h $ ranges from 0.9 to 2. It can be seen that when $ h $ is from 0.9 to 1.12, it is repulsion; when $ h $ is from 1.12 to 2, it is gravity; and when $ h = 1.12 $, it reaches a state of equilibrium. Therefore, in order to improve the exploration in ASO, the lower limit of the repulsive force with a smaller function value is $ h = 1.1 $, and the upper limit of the gravitational force is 1.24.

where $ h_{ij}(t) $ is the distance function, $ h_{min} = 1.1 $ and $ h_{max} = 1.24 $ represent the lower and upper limits of $ h $, $ r_{ij} $ is the Euclidean distance between atom $ i $ and atom $ j $, and $ \sigma(t) $ is defined as follows

where $ x_{ij} $ is the position component of atom $ i^{th} $ in the $ j^{th} $ dimensional search space, $ \|\cdot\|_{2} $ stands for two norm and KBest is a subset of the atom group, which is composed of the first $ K $ atoms with the best function fitness value.

where $ g_{0} $ is a drift factor, which can shift the algorithm from exploration to development

Therefore, the atom $ i^{th} $ acting on other atoms can be considered as a total force, expressed as

2.4.   Geometric binding

The geometric binding force also plays an important role in ASO. Assume that each atom has a covalent bond with each atom in KBest, and that each atom is bound by KBest, Figure 2 shows the effect of atomic interactions. $ A_{1}, A_{2}, A_{3} $ and $ A_{4} $ are the atoms with the best fitness value, called KBest.In KBest, $ A_{1}, A_{2}, A_{3} $ and $ A_{4} $ attract or repel each other, and $ A_{5}, A_{6}, A_{7} $ attract or repel each other for every atom. Each atom in the population is bound by the optimal atom $ A_{1} $($ X_{best} $), the binding force of the atom $ i^{th} $ is

where $ x_{best}^d(t) $ is the atom which is in the best position in the $ i^{th} $ iteration, $ \beta $ is the multiplier weight, and $ \lambda(t) $ is the Lagrange multiplier.

2.5.   Acceleration

Under the action of geometric constraint force and interaction force, the acceleration of atom $ i^{th} $ atom at time $ t $ is

2.6.   Speed, location update

In the original ASO, the algorithm was found to be prone to local optima. As a result, changes were made in the iterative update process of the speed, allowing the algorithm to go beyond the local optimum, search and optimise more broadly. The particle update velocity from PSO is used in ASO and the inertial weight $ w $ is introduced in the original ASO velocity update.The algorithm is not prone to local optima at the start of the algorithm and improves the performance of the IASO algorithm. The addition of learning factors $ c_{1} $ and $ c_{2} $ not only ensures convergence performance, but also speeds up convergence, effectively solving the problem that the original ASO tends to fall into local optimality.

At the $ (t+1)^{th} $ iteration, the position updating of the $ i^{th} $ atom can be expressed as

2.7.   Stopping criterion

The maximum number of iterations, convergence normalisation, maximum running time and accuracy of the fitness function value are commonly used convergence criteria.In this paper, the maximum number of iterations and convergence normalisation are used as criteria for stopping the iterations.The maximum number of iterations is 200 and the convergence normalisation results are as follows

where $ Fit_i $ is the fitness value of $ i^{th} $ squirrel and $ \overline{Fit} $ is the average fitness value of the population, the accuracy $ \varepsilon $ is often taken as $ 1E-6 $.

2.8.   Pseudocode of IASO

Thus, by iterating over the above operations several times, we can eventually find the optimal solution exactly. Table 1 shows the main steps of the IASO algorithm.

The pseudocode of IASO is present in Algorithm 1.

2.9.   The performance comparison between IASO and ASO after improvement

To test the performance of the IASO algorithm, 23 known benchmark functions were used. These benchmark functions are described in Tables 1, 2, 3, $ F1-F7 $ is unimodal function, and each unimodal function has no local optimization, only one global optimum. Therefore, the convergence speed of the algorithm can be verified. $ F8-F13 $ are multimodal functions with many local optimizations. While $ F14-F23 $ is a low dimensional function, each function has less local optimal value. Therefore, multimodal function and low dimensional function are very suitable for local optimal test avoidance and algorithm exploration ability.

In this experiment, the population size for IASO and ASO was $ 50 $ and the maximum number of iterations was $ 100 $. There are three performance evaluation indexes for comparing IASO and ASO: the average, minimum and standard deviation of the optimal solution. The smaller the average value of the optimal solution, the less likely it is that the algorithm will enter a local optimum and the easier it is to find the global optimum; The smaller the standard deviation of the optimal solution, the more stable the algorithm will be; the smaller the minimum value, the more accurate it will be. Tables 3–5 shows the comparison of optimization results of different types of functions, and the corresponding convergence curve is shown in Figures 3–5. Table 4 and Figure 6 are the optimization results and convergence curves of unimodal function $ F_1(x)-F_7(x) $. It can be seen that IASO algorithm has better performance than ASO algorithm and its convergence speed is faster. Table 5 and Figure 7 are the optimization results and convergence curves of multimodal function $ F_8(x)-F_{13}(x) $. It can be seen that the overall performance of IASO is better than that of ASO. Table 6 and Figure 8 are the optimization results and convergence curves of low dimensional function $ F_{14}(x)- F_{23}(x) $. The convergence curve shows that ASO converges faster, but IASO is more accurate. By comparing IASO with ASO, it can be seen that the improved IASO converges much faster and is more stable than ASO It is also less likely to enter the local optimum.

3.   Signal model and ML estimation

3.1.   Model establishment

Assume that $ N $ far-field narrowband signal sources are incident on the hydrophone array of the $ M(M > N) $ vector sensor. The incident angle is $ { \bf{\Theta} } = [\Theta_1, \Theta_2, \cdots, \Theta_N]^T $, where $ \Theta_n = (\theta_n, \alpha_n)^T $, $ (\cdot)^T $ is the transposition, $ \theta_n $ is the horizontal azimuth angle of the $ n^{\rm{th}} $ incident signal, $ \alpha_n $ is the elevation angle of the $ n^{\rm{th}} $ incident signal, respectively, the incident wavelength is $ \lambda $, and the distance between adjacent arrays is $ d $. Then the signal received by the array can be expressed in vector form as

Among them, $ { \bf{Z} }(t) $ is the $ 4M\times 1 $ dimensional received signal vector, and ${ \bf{N} }(t) $ is the array $ 4M\times 1 $ dimensional gaussian noise vector. It is assumed that the noise is gaussian white noise, which are independent of each other in time and space. $ { \bf{S} }(t)$ is the $ M\times 1 $ dimensional signal source vector. $ {\bf{A}}({\bf{\Theta }}) $ is the signal direction matrix of the vector hydrophone array

where $ \otimes $ is the Kronecker product, $ { \bf{a} }_n(\Theta_n) = [1, e^{-j\beta_n}, e^{-j2\beta_n}, \cdots, e^{-j(M-1)\beta_n}]^T $ is the sound pressure corresponding to $ n^{\rm{th}} $ signal, $ { \bf{u} }_n = [1, \cos\theta_n \sin \alpha_n, \sin\theta_n \sin \alpha_n, \cos \alpha_n]^T $ is the direction vector of the $ n^{\rm{th}} $ signal source, and $ \beta_n = \frac{2\pi}{\lambda}d\cos \theta_n \sin \alpha_n $. Then the array covariance matrix of the received signal is

where $ { \bf{R} }_s $ is the signal covariance matrix, $ \sigma^2 $ is Gaussian white noise, $ { \bf{I} } $ is the identity matrix, $ (\cdot)^H $ is the conjugate transpose of matrix $ (\cdot) $, Assume that the signal and the array are on the same plane, that is, $ \alpha_n = \frac{\pi}{2} $, so only $ \theta_n $ is considered in this paper. In actual calculations, the received data is limited, so the array covariance matrix is

where $ K $ represents the number of snapshots.

3.2.   Maximum likelihood estimation

By uniformly and independently sampling the received signal, the joint probability density function of the sampled data can be obtained as follows

where $ {\rm{det}}(\cdot) $ represents the determinant of the matrix $ (\cdot) $, $ \tilde{\theta} $ is the unknown signal orientation estimation, $ P(\cdot) $ is a multidimensional nonlinear function of unknown parameters $ \tilde{\theta}, \sigma^2 $ and $ { \bf{S} } $. Take the logarithm of Eq (3.5)

In Eq (3.6), Take the partial derivative of $ \sigma^2 $, set it to 0, get $ \sigma^2 = \frac{1}{4M}{\rm{tr}}\left\{{{\bf{P_A}}^\perp \hat{{ \bf{R} }}}\right\} $, where $ {\rm{tr}}\{\cdot\} $ is the trace of matrix $ (\cdot) $, $ {\bf{P_A}}^\perp $ is the orthogonal projection matrix of matrix $ {\bf{A}} $, $ \hat{{ \bf{S} }} = {\bf{A}}^{+}{ \bf{Z} } $ and $ {\bf{A}}^{+} = ({\bf{A}}^H{\bf{A}})^{-1}{\bf{A}}^H $ are the pseudo-inverse of matrix $ {\bf{A}} $, substitute $ \sigma^2 $ and $ \hat{{ \bf{S} }} $, into Eq (3.6), then

where $ g(\tilde{\theta}) $ is the likelihood function, which can be expressed as

$ \hat{\theta} $ is the estimated DOA angle of the estimated signal. Seeking the maximum value of the likelihood function $ g(\tilde{\theta}) $ can get a set of solutions corresponding to this value, which is the estimated angle sought.In order to compare the convergence of different methods, the following equation is defined as the fitness function

where $ \theta $ is the known signal in Eq (3.1), $ g(\theta) = {\rm{tr}} \left\{\left[{\bf{A}}(\theta)({\bf{A}}^H(\theta){\bf{A}}(\theta))^{-1}{\bf{A}}^H(\theta)\right]\hat{{ \bf{R} }}\right\} $, Eq (3.7) can thus be expressed as

when $ f(\tilde{\theta}) $ is close to 0, it means that the estimated angle is more accurate.

4.   Simulation experiment and discussion of the combination of IASO and ML-DOA

The initial position is expressed as $ \theta_i = [ \theta_{i}^1, \theta_{i}^2, \cdots, \theta_{i}^d] $. Taking Eq (3.9) in ML DOA as the fitness function $ Fit_{i}(t) $ in IASO, then the fitness function $ Fit_{i}(t) $ of Eq (2.3) in Section 2 is changed to $ f(\tilde{\theta}) $. Then the geometric binding force of Eq (2.15) can be expressed as $ x_{i}^d(t+1) = x_{i}^d(t)+v_{i}^d(t+1) $; The acceleration is changed from Eq (2.17) to

The speed update is changed from Eq (2.18) to

the location update is changed from Eq (2.19) to

In this part, we demonstrated the simulation results of the iterative process and convergence performance of the IASO. Then, we compared the ML DOA estimation performance between the IASO and ASO, SCA, GA, and PSO. In the experiment, the receiving array should be a uniform linear array composed of 10 acoustic vector sensors, the number of snapshots is 300, and the added noise is Gaussian white noise.

4.1.   Convergence performance

In the simulation experiment, in $ 100 $ independent Monte Carlo experiments, the population number is $ 30 $, the maximum number of iterations is $ 200 $, the signal-to-noise ratio is $ 10 $dB, and the search range is $ [0,180] $. Taking one source $ \theta = [30^\circ] $, two sources $ \theta = [30^\circ, 60^{\circ}] $, respectively, the minimum process curve of fitness value is obtained. Compared with IASO, ASO, SCA, GA and PSO, Table 7 shows the parameters of the five algorithmsan and Figure 9 shows the fitness convergence curve.

Figure 9 shows the fitness variation curves of the ML DOA estimators of the IASO, ASO, SCA, GA and PSO in the case of 1, 2, 3 signal source and 200 iterations. As can be seen from the picture. Regardless of the number of signal sources is 1, 2, or 3, IASO has the fastest convergence speed. When the number of signal sources is 1, IASO converges fastest, followed by ASO, In comparsion PSO, SCA and GA have large convergence range, and their fitness values are high, which indicates that they can easily to fall into local optimum, when the number of signal sources is 2, IASO has better convergence effect. When the signal source is 3, IASO still remained the best, followed by ASO. But SCA, GA and PSO not only converge rather slowly but can also easily fall into local optimum. Even after 200 iterations, the fitness function cannot converge to 0.

4.2.   Statistical performance

In order to compare the statistical performance of different algorithms and their relationship with Cramér–Rao Bound(CRB), we performed a comparison and estimated the mean-variance of the algorithm based on the root mean square error (RMSE). The overall size is 30 iterations and the maximum number of iterations is 200.

where $ L $ is the number of experiments, $ \theta_i $ is the DOA of the $ i^{th} $ signal, $ N $ is the number of signals, and $ \hat{\theta}_i(j) $ denotes the estimate of the $ i^{th} $ DOA achieved in the $ j^{th} $ experiment.

Figure 10 shows the RMSE of the ML DOA estimator for the five algorithms of IASO, ASO, SCA, GA and PSO when the number of signal sources is 1, 2 and 3, changing the signal-to-noise ratio ranges from -20dB to 20dB. It can be seen that the performance of IASO is more stable regardless of the source and more closer to CRB. When the number of signal sources is 3, the estimation performance of several algorithms decreases, but the DOA estimation performance based on IASO algorithm is still closer to CRB, followed by ASO, GA, PSO and SCA.The SCA performs well at low signal-to-noise ratios, but poorly at high signal-to-noise ratios. However, the MLDOA estimation performance of PSO and GA is poor, and their fitness functions have difficulty converging to the global optimum solution. Even after 200 iterations, a large RMSE is still generated.

4.3.   Population size

Population size marks the most important parameter in biological evolutionary algorithms. In general, the estimation accuracy of intelligent algorithms improves as the population size increases. However, when the population increases, the computational load on the algorithm also increases. For ML DOA problems, the population size determines the number of likelihood functions calculated in each iteration. Therefore, this highlights the need for an algorithm with a small population size and high estimation accuracy.

Figure 11 shows the RMSE curves of the ML DOA estimators of IASO, ASO, SCA, GA and PSO when the population size ranges from 10 to 100. As can be seen from the figure, the IASO can maintain low RMSE, high estimation accuracy and closer to CRB regardless of the number of signal sources. When there is one signal source, the RMSE of IASO, ASO, SCA and PSO is similar, while the GA algorithm keeps a relatively high RMSE when the population is less than 50. When there are two signal sources, the RMSE of IASO algorithm maintains a lower RMSE, while the ASO algorithm is somewhat unstable, and the PSO and GA still keep a higher RMSE. When the signal source is three, only IASO algorithm has lower RMSE, ASO, PSO, SCA and GA, and they have higher RMSE. This shows the population size is 100, GA and PSO algorithms only need a large population number size, bue also they also need a large number of iterations. For ML DOA estimation, when the number of signal source are 1, 2, 3, IASO algorithm can accurately estimate DOA with a smaller population number requiring less computational effort.

4.4.   Computational complexity

In addition to the convergence and statistical performance described above, the quality of an algorithm can also be judged by its computational complexity. The computational complexity is independent of the number of signal sources. Rather it is related to the maximum number of iterations, the population size and the maximum number of spatial variations. The following figure illustrates the average number of iterations calculated by stopping the standard formula 30 in the case of two signal sources: $ 1e-6 $.

Figure 12 shows the average iteration time curves of the different algorithms for 100 independent Monte Carlo experiments. It can be seen that the IASO algorithm has the smallest number of iterations when the signal-to-noise ratio range from -20dB to 20dB and the number of iterations is $ 200 $, followed by the ASO, PSO, GA and SCA algorithms, which require at least 100 iterations. When the number of IASO iterations was significantly lower than the other groups, the number of iterations was significantly lower than the other algorithms. In general, the IASO algorithm has the smallest number of iterations on the mean curve of signal-to-noise ratio and overall size. For ASO, SCA, GA and PSO, more iterations are still needed to find the optimal solution under signal-to-noise ratio and overall transformation. As a result, IASO has the lowest computational load.

5.   Conclusions

This paper proposes an improved ASO, employing 23 test functions to test IASO and ASO and finds that it overcomes the shortcomings of ASO that it can easily to fall into local optimality and poor convergence performance. ML DOA estimation is a high-resolution optimization method in theory, but the huge computational burden hinders its practical applications. In this paper, IASO is used in ML DOA estimation, and simulation experiments are carried out. The results show that, compared with ASO, SCA, GA and PSO methods, the ML DOA estimator of IASO proposed in this paper has faster convergence speed, lower RMSE and lower computational complexity.

Acknowledgment

This research was funded by National Natural Science Foundation of China (Grant No. 61774137, 51875535 and 61927807), Key Research and Development Foundation of Shanxi Province(Grant No. 201903D121156), and Shanxi Scholarship Council of China (Grant No. 2020-104 and 2021-108). The authors express their sincere thanks to the anonymous referee for many valuable comments and suggestions.

Conflict of interest

The authors declare that they have no conflict of interest.