Corporate social responsibility toward employees and green innovation: Exploring the link in the tourism sector

1.   Introduction

Fractional calculus have recently become a fascinating field of study due to its vast applications in various aspects of modern life. It has been observed that many physical phenomena can be modeled successfully by means of fractional order differential equations, where the integer-order differential equations fails in modeling certain issues ^[1]. Compared to integer order derivatives some properties of the non-integer order derivatives are very tedious to deal with. Thus, it becomes of great importance to establish more results for fractional calculus. Recently lots of researchers have proposed new and efficient analytical and numerical schemes to approximate the solutions of numerous fractional order problems. In this connection one can find efficient work done by researchers such as the analysis of fractional Drinfeld-Sokolov-Wilson model with exponential memory ^[2], a homotopy perturbation sumudu transform method (HPSTM) for solving fractional equal width (EW) equation ^[3]. The ternary-fractional differential transform method, that extends its applicability to encompass initial value problems in the fractal 3D space ^[1]. The local fractional homotopy perturbation Sumudu transform scheme and the local fractional reduced differential transform method for a fractal vehicular traffic flow problem ^[4]. The authors in ^[5] have proposed a numerical algorithm based on homotopic technique to examine the fractional vibration equation in Atangana-Baleanu sense. The authors in ^[6] have presented the efficiency of the Atangana-Baleanu (AB) derivative over Caputo-Fabrizio (CF) to some nonlinear partial differential equations. The authors in ^[7] have done a comparative analysis of exothermic reactions model having constant heat source in the porous media via Caputo, Caputo Fabrizio and Atangana-Baleanu theories. In ^[8] a hybrid numerical scheme based on the homotopy analysis transform method (HATM) to examine the fractional model of nonlinear wave-like equations having variable coefficients is presented. The Klein-Gordon is one of the most important mathematical model which finds its applications in numerous phenomenon in science and engineering. It has been applied to non linear optics, quantum field theory, Plasma physics, fluid dynamics, chemical kinetics and solid state physics ^[9,10,11]. In literature a lot of work has been done on solving the Klein-Gordon equation analytically some of them are the $\tanh$ and the sine-cosine methods ^[12], the differential transform method ^[13], Modified Kudryashov method ^[14,15], ansatz method ^[16], Exp$(-\phi(\epsilon))$-expansion method ^[17], and the variational iteration method ^[18]. The residual power series method for linear time fractional Klein-Gordon equation ^[19], homotopy analysis method ^[20,21], local fractional series expansion method ^[10], homotopy perturbation method ^[22], and the fractional Riccati expansion method ^[23]. In ^[24] a hybrid method based on local fractional Sumudu transform method and homotopy perturbation technique is employed to find the non differentiable solution of Klein-Gordon equation on Cantor sets. Since Most of the problems cannot be solved analytically so one must use numerical methods. Despite the fact that, numerical approximation of these equations are rare, in literature some excellent work is available, such as Mohebi et al utilized the Compact finite difference method ^[25] and the implicit RBF meshless method ^[26] for the approximation of linear time fractional Klein-Gordon equations. M. M. Khader ^[27] applied an efficient method based on the generalized laguerre polynomials for approximating the linear time fractional Klein-Gordon equations. In ^[28] the authors used the wavelet method for approximating a class of fractional Klein-Gordon equations. The authors in ^[29] proposed a numerical algorithm based on the applications of the operational matrices of the Legendre scaling functions for the approximation of fractional Klein-Gordon equation. The authors in ^[30] applied a high order compact finite difference scheme to two dimensional fractional Klein-Gordon equations. Dehghan et al ^[31] used radial basis functions to approximate the solution of non linear Klein-Gordon equations. However in these time stepping schemes the computations may be very expansive because each new iteration is dependent on the previous time step. An alternative way is to use the Laplace transform coupled with these numerical methods. In literature one can find numerous research work on the coupling of other numerical methods and Laplace transform. The Laplace transform was first coupled with the boundary integral method by Rizzo and Shippey ^[32]. Moridis and Reddell coupled Laplace transform with finite difference, boundary element and finite element methods ^[33,34,35]. In ^[36] the authors coupled the Galerkin method with Laplace transform. Moridis and Kansa ^[37] coupled multiquadric method and Laplace transform for the approximation of PDEs. In ^[38] the author studied RBF method coupled with Laplace transform on unit sphere. Similarly the coupling of Laplace transform with other numerical methods such as spectral method, finite difference method, boundary particle method, RBF method, and the finite element method can be found in ^{[39,40,41,42,43,44]} and the references therein. In this work we apply the idea of ^[45,46], the Laplace transform is coupled with local RBF method to approximate linear time-fractional Klein-Gordon equation. The Laplace transform is used to avoid the stability restrictions, which are commonly encountered in time-stepping procedure. The local radial basis function method is used to resolve the issue of ill-conditioning of the differentiation matrices and the sensitivity of shape parameter in global radial basis functions method. The main idea of the local radial basis function method is the collocation on overlapping sub-domains of the whole domain. The overlapping sub-domains remarkably reduce the size of collocation matrix by solving many small size matrices. Each small matrix has the same size as the number of nodes in the domain of influence of each node. In order to validate our method we consider linear time-fractional Klein-Gordon equation of the form ^[25]

with initial and boundary conditions given in (1.2) and (1.3),

Here $\mathcal{L}$ and $\mathcal{B}$ are the governing and boundary differential operators, and $\frac{\partial^{\alpha}}{\partial t^{\alpha}}$ is the Caputo fractional derivative of order $\alpha$ defined by ^[47]:

Let the Laplace transform of $\chi(t)$ be denoted and defined by

and the Laplace transform of the Caputo derivative is defined by

2.   Proposed scheme

Here we construct a local RBF method coupled with Laplace transform for the approximation of the solution of the linear time-fractional Klein-Gordon equations. In order to avoid the time stepping procedure the Laplace transform is used to eliminate the time variable. Then the local RBF method is utilized to approximate the time independent linear PDE.

Applying the Laplace transform to Eqs (1.1) and (1.3), we get

thus we have the following linear system

where

In the following section the local RBF method is used to approximate the differential operator $\mathcal{L}$ and $\mathcal{B}$ in order to solve the problem (2.2)–(2.3) in Laplace space.

2.1.   Local RBF method

In local RBF method the approximation of the function $\hat{\chi}({\bf{x}})$, for a given set of data points $\{\hat{\chi}({\bf{x}}_i):i = 1, ..., N\}$, where $\{{\bf{x}}_{i}:i = 1, ..., N\}\subset \Omega\subset \mathcal{R}^{d}, \; d\geq 1$ takes the form

where ${\mathit{\boldsymbol{\lambda}}}^{i} = \{\lambda^{i}_{j}:j = 1, ..., n\}$ is the vector of expansion coefficients, $\phi(r), \; r \geq 0$ is radial kernel and the distance between the centers ${\bf{x}}_{i}$ and ${\bf{x}}_{j}$ is $r = \|{\bf{x}}_{i}-{\bf{x}}_{j}\|$, and $\Omega_{i}$ is a sub domain of $\Omega$ containing ${\bf{x}}_i$, and around ${\bf{x}}_i$ it contains $n$ neighboring centers. So we have $N$ number of $n \times n$ linear systems given by

the elements of the interpolation matrix $\Phi^i$ are $b^{i}_{kj} = \phi(\|{\bf{x}}_k-{\bf{x}}_j\|), \text{where} \; {\bf{x}}_k, {\bf{x}}_j \in \Omega_{i}$, each $n\times n$ system is then solved for the unknowns ${\mathit{\boldsymbol{\lambda}}}^{i} = \{\lambda^{i}_{j}:j = 1, ..., n\}$. Next the operator $\mathcal{L}\hat{\chi}({\bf{x}})$, is approximated by

the above Eq (2.6) can be expressed as

where ${\mathit{\boldsymbol{\nu}}}^i$ is of order $1\times n$ and ${\mathit{\boldsymbol{\lambda}}}^{i}$ of order $n\times 1$, the entries of ${\mathit{\boldsymbol{\nu}}}^i$ are shown in the following equation

using Eq (2.5), the coefficients ${\mathit{\boldsymbol{\lambda}}}^{i}$ can be eliminated as,

using the values of ${\mathit{\boldsymbol{\lambda}}}^{i}$ from (2.9) in (2.7) we get,

where,

Hence the linear differential $\mathcal{L}$ is approximated using the local RBF method for each center ${\bf{x}}_i$ as

The matrix ${\bf{D}}$ is sparse differentiation matrix which approximates the linear differential operator $\mathcal{L}$. The matrix ${\bf{D}}$ has order $N\times N$ which contains $n$ non-zero and $N-n$ zero entries, where $n$ is the number of centers in the sub domain $\Omega_{i}.$ The same procedure can be applied to the boundary operator $\mathcal{B}$.

2.2.   Selecting good value of shape parameter

In literature a large number of radial kernels are available. In this article we have selected the multi-quadrics $\phi(r) = \sqrt{1+(r c)^2}$ for our numerical approximation. The accuracy of the numerical solution greatly depends on the parameter $c$. The researchers always search for that value of $c$ which gives an optimal solution. In this regard a large amount of work has been done such as ^[48,49,50] and references therein. Here we utilize the uncertainty principle ^[51] for optimal shape parameter $c$.

Algorithm:

● The interval $10^{12} < Cond < 10^{16}$ is selected for the condition number (Cond) of the system matrices of the given problem.

● Using SVD, the interpolation matrix is decomposed as ${\bf{R, P, Q}} = svd(\Phi^i)$. The order of $\Phi^i$ is $n \times n$ (n is the number of centers in each $\Omega_{i}$), and the $n$ singular values of the matrix $\Phi^i$ lies on the diagonal of the matrix ${\bf{P}}$ (${\bf{P}}$ is a diagonal matrix), and the condition number of $\Phi^i$ is $Cond = \|\Phi^i\|\|(\Phi^i)^{-1}\| = \frac{\mbox{max}({\bf{P}})}{\mbox{min}({\bf{P}})}$.

● The $c$ is searched until the condition $10^{12} < Cond < 10^{16}$ is satisfied, the algorithm is given as

Step 1: set $Cond = 1$

Step 2: select $10^{12} < Cond < 10^{16}$

Step 3: $\mbox{while}\; Cond > Cond_{max} \; \mbox{and}\; Cond < Cond_{min}$

Step 4: ${\bf{R, P, Q}} = svd(\Phi^i)$

Step 5: $Cond = \frac {\mbox{max}({\bf{P}})}{\mbox{min}({\bf{P}})}$

Step 6: $\mbox{if}\; Cond < Cond_{min}, \; c = c-\delta c$

Step 7: $\mbox{if}\; Cond > Cond_{max}, \; c = c+\delta c$

$c\; {(\mbox{optimal})} = c$.

Optimal value of the parameter $c$ is obtained, when the above condition is satisfied, and then we can compute the inverse using $({\Phi^i})^{-1} = {\bf{(RPQ^{T}})}^{-1} = {\bf{Q}}{\bf{P}}^{-1}{\bf{R}}^{T}$ ^[52]. Hence ${\bf{w}}^i$ in (2.11) can be computed.

Following the discretization by local RBF method of the linear differential and boundary operators $\mathcal{L}$ and $\mathcal{B}$ respectively, the system (2.2)–(2.3) is solved for each point $s$. Finally the solution of the problem (1.1)–(1.3) is obtained using the inverse of Laplace transform

In applying the Laplace transform method the calculation of inverse Laplace transform is the main difficulty. In many cases it is difficult to find the inverse Laplace transform analytically so numerical methods must be used. A large number of methods for the numerical inversion of Laplace transform have been developed. In this work we use the idea of ^[39,42] in which the integration is performed over a parabolic or hyperbolic path $\Gamma,$ so the integral in equation (2.13) can be written as

where $\Gamma$ is a path of integration joining $\sigma-i\infty$ to $\sigma+i\infty$ and

using (2.15) in (2.14), we find the following expression

Finally the trapezoidal rule with uniform step size $k$ is used to approximate (2.16), as

3.   Error analysis

The approximate solution of the proposed scheme is defined by Eq (2.17). The accuracy of (2.17) greatly depends on the path of the integration $\Gamma$. There are various contours available in the literature. Recently the hyperbolic ^[41] and parabolic ^[42] contours are used to approximate the integer and fractional order PDEs. In our computations the hyperbolic path due to ^[41] is used.

where $\eta \geq 0$, $\gamma > 0$, $\frac{1}{2}\pi < \beta < \pi$, and $0 < \delta < \beta - \frac{1}{2}\pi$. In fact, when we choose $Im \; \omega = \lambda$, the Eq (3.1) is reduced to the left branch of the hyperbola

transforming the strip $Z_{r} = \{\omega: Im \; \omega \leq r, r > 0\}$ into the hyperbola $\Omega_{r} = \{s: \omega \in Z_{r}\}\supset \Gamma.$ Suppose $\Sigma_{\phi} = \{s \neq 0 :|arg s|\leq\phi \} \cup 0, \; 0 < \phi < \frac{(1-\alpha)\phi}{2},$ and let $\Sigma^{\eta}_{\beta} = \eta+\Sigma_{\beta}, \Gamma\subset \Omega_{r}\subset \Sigma^{\eta}_{\beta}.$ The following theorem gives the error estimate of the scheme for the contour $\Gamma$.

Theorem 3.1 (^[41], Theorem 2.1) let the solution of (1.1) be $\chi({\bf{x}}, t)$, with $\hat{f}({\bf{x}}, t)$ analyitc in $\Sigma^{\eta}_{\beta}.$ Let $\Gamma\subset \Omega_{r}\subset \Sigma^{\eta}_{\beta},$ and $b > 0$ be defined by $b = cosh^{-1}(\frac{1}{\theta \tau \sin(\delta)})$, where $\tau = \frac{t_0}{T}$, $0 < \theta < 1$, $0 < t_0 < T$, and let $\gamma = \frac{\theta \overline{r}M}{bT}.$ Then for the approximate solution defined by (2.17), with $k = \frac{b}{M}\leq \frac{\overline{r}}{log 2}, \; |\chi({\bf{x}}, t)-\chi_{k}({\bf{x}}, t)|\leq \left(\|\chi_{0}\|+\|\hat{f}({\bf{x}}, t)\|_{\Sigma^{\eta}_{\beta}}\right)CQe^{\eta \tau}g(\rho_{r}M)e^{-\mu M},$ for $\mu = \frac{\overline{r}(1-\theta)}{b}$, $\rho_r = \frac{\theta \overline{r} \tau \sin(\delta-r)}{b}$, $g(x) = \mbox{max}(1, log(\frac{1}{x}))$, $\overline{r} = 2\pi r$, $r > 0$, $C = C_{\delta, r, \beta}$, and $t_0\leq t \leq T.$ Thus the corresponding error estimate is of the order

4.   Stability analysis

In order to investigate the systems (2.2)–(2.3) stability, we represent the system in discrete form as

where $Y$ is the sparse differentiation matrix of order $N \times N$ obtained using local RBF method. For the system (4.1) the constant of stability is given by

where C is finite using any discrete norm $\|.\|$ on $R^{N}$. From (4.2) we may write

Similarly for the pseudoinverse $Y^{†}$ of $Y$, we can write

Thus we have

We can see that Eqs (4.3) and (4.5) confirms the bounds for the stability constant $C$. Calculating the pseudoinverse for approximating the system (4.1) numerically may be very expansive computationally, but it ensures the stability. The MATLAB's function condest can be used to estimate $\|Y^{-1}\|_{\infty}$ in case of square systems, thus we have

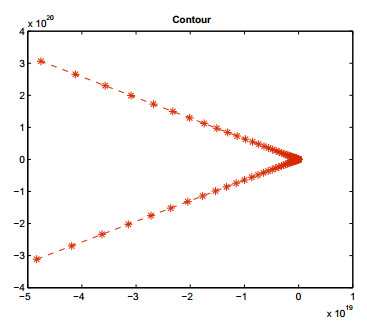
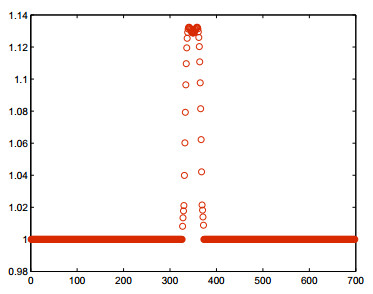
This work well with less number of computations for our sparse differentiation matrix $Y$. Figures 1 and 2 show the bounds for the constant $C$ of our system (2.2)–(2.3) for Problem 3. Selecting $N = 50$, $M = 80$, $n = 15$, and $\alpha = 0.8$ at $t = 1$, we have $1 \leq C \leq 1.1620.$ It is observed that the stability constant is bounded by very small numbers, which guarantees the stability of the proposed local RBF scheme.

5.   Numerical results

This section is devoted to the numerical experiments. The proposed method is tested here for 1-D time fractional order Klein-Gordon equations. The multi-quadrics radial kernels $\phi (r)$ = $(1+(r c)^2)^{1/2}$ are used in all our numerical experiments. The Uncertainty principle ^[51] is used to optimize the shape parameter $c$. The accuracy of the method is measured using $L_{\infty}$ error defined by

is used. Here $\chi_{k}$ and $\chi$ are the numerical and exact solutions respectively.

5.1.   Problem 1

If we use $\beta = 1$, $\kappa = 1$, and $\eta = 0,$ Eq (1.1) takes the form

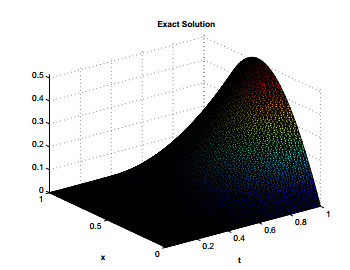
where $\; 1\leq \alpha \leq2, \; t\geq 0, \; 0\leq x\leq1,$ with zero boundary and initial conditions. The domain $[0, 1]$ is selected for the problem with exact solution

and non homogeneous term

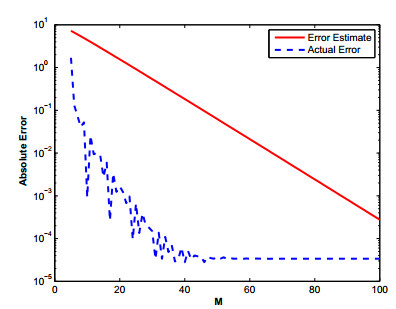
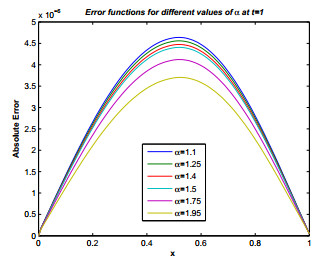
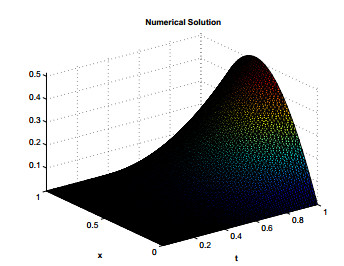
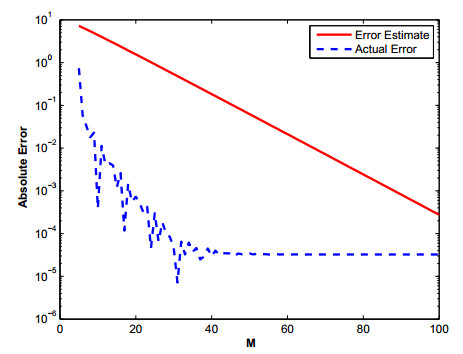
The MATLAB's command $\omega = -M:k:M$ is used to generate the quadrature points along the path of integration $\Gamma$. The parameters used in our computations are $\alpha = 1.75, \eta = 2, \tau = \frac{t0}{T}, r = 0.1387, \theta = 0.1, \delta = 0.1541, t_0 = 0.5 \; \mbox{and}\; T = 5.$ Using Eq (3.1) the remaining optimal parameters can be found for the hyperbolic path $\Gamma$. In our computations $n = 6$ in the sub domain $\Omega_{i}$ and $N = 40$ in the global domain $\Omega$ are selected. The error estimates and $L_{\infty}$ errors are shown in Tables 1 and 2. The efficiency of the method can be seen in the results. The actual error and error estimates are shown in Figure 3 and the absolute errors for different values of $\alpha$ are shown in Figure 4. The numerical and the exact solutions are shown in Figures 5 and 6 respectively.

5.2.   Problem 2

If we use $\beta = 1$, $\kappa = 1$, and $\eta = 1,$ Eq (1.1) takes the form

where $\; 1\leq \alpha \leq2, \; t\geq 0, \; 0\leq x\leq1,$ with zero initial and boundary conditions, the exact solution of the problem is

and non homogeneous term is

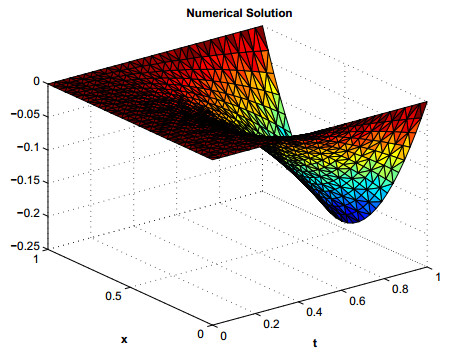
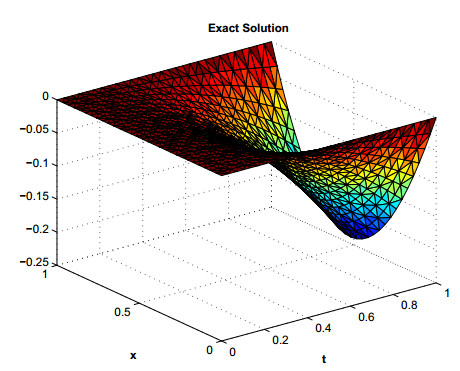
The MATLAB's command $\omega = -M:k:M$ is used to generate the quadrature points along the path of integration $\Gamma$. The parameters used in our computations are $\alpha = 1.75, r = 0.1387, \delta = 0.1541, \theta = 0.1, \tau = \frac{t0}{T}, \eta = 2, t_0 = 0.5 \; \mbox{and}\; T = 5.$ Using Eq (3.1) the remaining optimal parameters can be found for the hyperbolic path $\Gamma$. In our computations $n = 7$ centers in the sub domain $\Omega_{i}$ and $N = 50$ in the global domain $\Omega$ are selected. The error estimates and $L_{\infty}$ errors are shown in Tables 3 and 4. Also the maximum absolute errors for different values of $\alpha$ are shown in Table 5, which shows the efficiency of the proposed method. The numerical and exact solutions of this problem are shown in Figures 7 and 8 respectively and plot of Actual error and Error Estimate corresponding to problem 2 are shown in Figure 9.

5.3.   Problem 3

Here we consider the 1-D linear Klein-Gordon equation of the form ^[19]

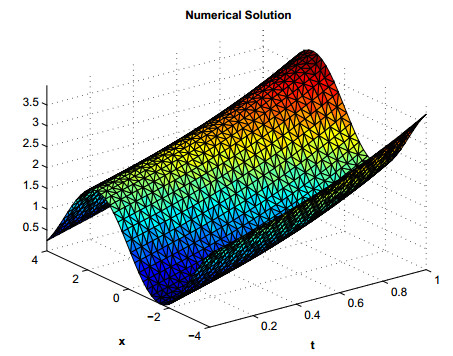
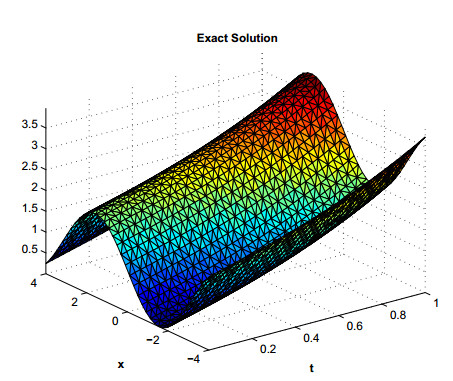
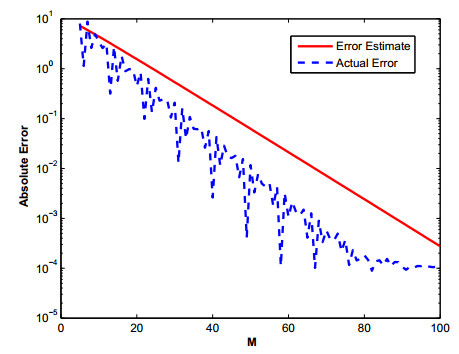
with initial condition $\chi(x, 0) = 1+\sin(x)$ and exact solution $\chi(x, t) = \sin(x)+E_{\alpha}(t^{\alpha})$, where $E_{\alpha}(t) = \sum^{\infty}_{m = 0}\frac{t^{m}}{\Gamma(\alpha m+1)}.$ The domain $[-4, 4]$ is selected for the given problem. The quadrature points are generated using the MATLAB's command $\omega = -M:k:M$ along the path of integration $\Gamma$. The parameters used in our computations are $\alpha = 0.8, r = 0.1387, \eta = 2, \tau = \frac{t0}{T}, \theta = 0.1, \delta = 0.1541, t_0 = 0.5 \; \mbox{and}\; T = 5.$ Using Eq (3.1) the remaining optimal parameters can be found for the hyperbolic path $\Gamma$. In our computations we select $n = 6$ centers in the sub domain $\Omega_{i}$ and $N = 40$ in the global domain $\Omega$ are selected. The error estimates and $L_{\infty}$ errors are shown in Tables 6 and 7. Similar behavior is observed as in the previous examples. The numerical and exact solutions for problem 3 are shown in Figures 10 and 11 and plot of Actual error and Error Estimate corresponding to problem 3 are shown in Figure 12.

6.   Conclusion

In this article, we constructed a local RBF method based on Laplace transform proposed for the approximation of the solution of the linear time fractional Klein-Gordon equations. In time stepping procedure usually the time instability is encountered and for accuracy we need a very small time step size. Global RBF methods are efficient and accurate only for small amount of nodes. They become inefficient and the differentiation matrix becomes ill-conditioned for large amount of nodes. The main advantage of this method is that it avoids the time stepping procedure with the help of Laplace transform, and the local RBF method has been used to resolve the issue of ill-conditioning. The numerical results confirmed the stability and convergence of the method. The comparison of the results with other methods led us to conclude that the proposed local RBF method coupled with Laplace transform is an efficient method for approximation of the solution of the linear time fractional Klein-Gordon equations.

Acknowledgments

The authors wish to thank the referees for their careful reading of the manuscript and valuable suggestions.This work was supported in part by the National Key Research and Development Program under Grant 2018YFB0904205, in part by the Key Laboratory of Pattern Recognition and Intelligent Information Processing, Institutions of Higher Education of Sichuan Province under Grant MSSB-2020-12.

Conflict of interest

The authors declare that no competing interests exist.