Collecting silences: creating value by assetizing carbon emission mitigations and energy demand reductions

1.   Introduction

Soliton theory is a branch of nonlinear science and is widely used in various fields of physical science. Over the past decades, with the rapid development of soliton theory, the use of numerical analysis and scientific computing in mathematical physics has attracted considerable attention, especially for solving real-world problems ^{[1,2,3,4,5,6]}. Accordingly, interest in studies related to exact solutions is likely to increase in the field of nonlinear mathematics, where extracted solutions are of considerable significance for furthering our understanding of nonlinear wave dynamics in applications such as optical fibers ^[3,4], magneto-electro-elastic circular rod ^[5] and multifaceted bathymetry ^[6]. Inelastic interactions of traveling waves play an important role in various complex physical phenomena. It is known that related physical phenomena could be simulated using nonlinear evolution equations (NLEEs) under certain constraints. Furthermore, the inelastic interactions can be represented by resonant multi-soliton solutions. The findings are expected to contribute to a better understanding of wave propagation in fields such as optics, plasmas and fluid mechanics ^{[7,8,9,10,11,12,13,14,15,16,17,18,19]}. Although various reliable approaches have been proposed, obtaining exact resonant soliton solutions and identifying inelastic interactions remains a major challenge for researchers in the field of soliton theory. Past studies have focused on finding exact solutions in mathematical physics to better explain and understand mechanisms underlying physical phenomena. Fortunately, two state-of-the-art approaches, namely the simplified linear superposition principle (LSP) ^{[9,10,11,12,13,14,15,16,17,18,19]} and velocity resonance (VR) ^{[20,21,22,23,24,25,26,27,28,29]}, have been developed to deal with inelastic interactions based on two resonant mechanisms. Importantly, two recent studies have detailed the special connection between a resonant multi-soliton solution and a soliton molecule ^[15,29]. The results obtained in these studies provided new information about different types of wave solutions, and the studies showed that the obtained solutions were accurate.

Very recently, Ma ^[7] developed a new fourth-order nonlinear model, which is as follows:

where $\alpha, \beta\ {\mathrm{a}\mathrm{n}\mathrm{d}\ \delta }_{j}(j = \mathrm{1, 2}, \mathrm{3, 4}, 5)$ are variable coefficients. Notably, the study of the formulation of new NLEEs and the simultaneous determination of their exact wave solutions has attracted considerable attention, and newly constructed equations and solutions are helpful for simulating the propagation of traveling waves. Moreover, the obtained results could help unravel the nature of nonlinearity in various sciences ^{[30,31,32,33,34,35,36,37,38,39,40,41,42,43]}; examples of such studies are those of Wazwaz ^[42] and Ma ^[43]. Resonant multi-soliton solutions are mainly used to simulate inelastic collisions of multi-wave solutions, which are relevant to real-world problems. To the best of our knowledge, there are few studies on the model in Eq (1.1). By determining the specific values of the free coefficients, we can reduce the model in Eq (1.1) to a variety of well-known NLEEs used in shallow-water wave theory and Jimbo–Miwa (JM) classification ^{[16,19,30,32,40,41,43]}, such as the Hirota–Satsuma–Ito (HSI) ^[19,43], Calogero–Bogoyavlenskii–Schiff (CBS) ^[30,32], JM equations ^[16,41] and the references therein. However, a variety of models that are likely to be useful in mathematical physics and that have hitherto been unreported can be derived from Eq (1.1). For determining the mechanism of the resonant wave and for constructing new NLEEs, this study derived several models from Eq (1.1). Furthermore, in order to determine the exact resonant multi-soliton solutions for different cases, we employed the simplified LSP and VR to examine the extended equations.

The objectives of this work were twofold. First, we identified specific conditions of Eq (1.1) and used them along with the simplified LSP to determine the existence of resonant multi-soliton solutions. Second, the extracted new equations and solutions were examined using VR, and the particular conditions for displaying the soliton molecules were formally confirmed.

2.   Methodology

The LSP is an effective tool for obtaining resonant N-wave solutions with the aid of the Hirota bilinear form ^[9,10,11,12]. The constraint guaranteeing the existence of resonant solutions is that wave numbers should satisfy the related bilinear equation.

Solving Eq (2.1) is considerably difficult for highly nonlinear partial equations, (i.e., high-dimensional high-order equations), and it involves a considerable amount of tedious calculations. In order to reduce the complex calculations and simultaneously increase the accuracy of the extracted results, we present the simplified version of the LSP. Detailed algorithms can be found in recent works ^{[13,14,15,16,17,18,19,29]}. Herein, we briefly illustrate the main steps of the simplified LSP.

Step 1. Extract the dispersion relation of the examined equation as

where $k, l, m\ \mathrm{a}\mathrm{n}\mathrm{d}\ \omega$ are wave numbers, and $\eta = kx+ly+mz+\dots +\omega t$.

Step 2. From the formula form of the dispersion relation, we can intuitively conjecture the corresponding wave numbers to be

where $\lambda \ \mathrm{a}\mathrm{n}\mathrm{d}\ \mu$ are powers of ${k}_{i}$, and $a\ \mathrm{a}\mathrm{n}\mathrm{d}\ b$ are real constants to be determined later. Importantly, $\mu$ should be consistent with the one obtained by substituting ${k}_{i} = {k}_{i}{\ \mathrm{a}\mathrm{n}\mathrm{d}\ l}_{i} = a{k}_{i}^{\lambda }$ into Eq (2.2).

Substituting Eq (2.3) into Eq (2.1) and solving the equation yields the values of $\lambda, \mu, a\ \mathrm{a}\mathrm{n}\mathrm{d}\ b$, and the resonant N-wave solutions can be directly constructed.

3.   Constrained equations and resonant multi-soliton solutions

3.1.   Application of simplified LSP

In ^[4], the expression $u = 2{\left(\mathit{ln}f\right)}_{x}$ was used to transform Eq (1.1) into the bilinear form

After applying the algorithms mentioned in Section 2, we thoroughly investigated Eq (3.1) and divided the constraints into two cases, which guarantees the existence of resonant multi-soliton solutions to the corresponding equations.

Case 1.

and

Using Eq (2.1) and substituting Eqs (3.2) and (3.3) into Eq (3.1), we obtain

We solve this equation and obtain

and

Then, the corresponding equation and resonant multi-soliton solution can be constructed as

Specifying $\alpha = {\delta }_{1} = {\delta }_{2} = 1$ in Eq (3.7) gives the HSI equation, and the results are consistent with our report in ^[19].

Case 2.

and

Using Eqs (3.9) and (3.10) and proceeding as before, we obtain

Clearly, from this equation, we can obtain

where the free coefficients $\alpha \ \mathrm{a}\mathrm{n}\mathrm{d}\ b$ can be determined by specifying values for ${\delta }_{2}, {\delta }_{4}{\ \mathrm{a}\mathrm{n}\mathrm{d}\ \delta }_{5}$ in Eq (3.9). For example, specifying ${\delta }_{2} = {\delta }_{5} = 1{\ \mathrm{a}\mathrm{n}\mathrm{d}\ \delta }_{4} = 2$ yields

Thus, the corresponding equation and resonant multi-soliton solution can be constructed as

where

Equations (3.6) and (3.16) are constructed with distinct physical structures. In other words, they represent different traveling waves. Hence, the corresponding nonlinear wave equations (3.7) and (3.14) describe different physical phenomena, respectively.

3.2.   Velocity resonance behavior

We recall that in ^[15,29], the VR conditions (${k}_{i}\ne {k}_{j}, {l}_{i}\ne {l}_{j}$) were

Using the related dispersion relation of Eq (3.7) ^[15,29], we obtain

Equation (3.17) can be used to solve Eq (3.18), and the wave numbers can then be obtained as

Thus, VR is successfully used to extract the wave numbers in Eq (3.19) to soliton molecules. In what follows, we show that the solutions (3.3) and (3.5) are consistent with the VR conditions (3.17) and (3.19).

Specifying $\alpha = {\delta }_{1} = {\delta }_{2} = 1$ and substituting Eqs (3.3) and (3.5) into (3.19) yields

Apparently, the result (3.20) reveals that the results (3.3), (3.5) and (3.19) are perfect because of the relationship

In other words, by choosing the appropriate values for the free parameters ${k}_{i}, {l}_{i}{\ \mathrm{a}\mathrm{n}\mathrm{d}\ \omega }_{i}$, the two approaches give the same results. Equation (3.19) can be used to simulate the dynamics of soliton molecules, and Eq (3.21) revealed that the special connection between resonant multi-soliton and soliton molecule is considered as one kink wave

Case 1 guarantees the existence of resonant multi-soliton solutions by using the simplified LSP and VR. Moreover, the derived Eq (3.7) with variable coefficients provides many more versions of mathematical models than the constant-coefficient equation ^[19]. Notably, VR cannot be used for Case 2 since for the special conditions in (3.9), the corresponding dispersion relation is obtained as $\alpha {\omega }_{i} = \beta {l}_{i}$; similar cases were reported in ^[15].

3.3.   Discussions

In this work, a novel fourth-order (2+1)-dimensional nonlinear wave equation was investigated using the LSP and VR. The following results were obtained.

(ⅰ) Equation (3.1) was examined in detail by using the simplified LSP, and it was confirmed that the two reduced equations (3.7) and (3.14) guarantee the existence of a resonant multi-soliton solution. The results were double checked by using VR. Moreover, compared to the methods reported in the critical references ^[44,45], the simplified LSP is found to be much easier to use to generate the exact resonant multi-soliton solutions without resorting to computational software. In other words, by applying the simplified LSP with the dispersion relationship, researchers can handle the examined nonlinear NLEEs directly. Furthermore, the accuracy of exact multi-soliton solutions can be checked by substituting the wave numbers into the phase shift term and making the phase shift term vanish, and detailed explanations can be found in the literature ^{[16,17,18,19]}.

(ⅱ) Compared with the existing HSI equation ^[19], Eq (3.7) in Case 1 can be considered as a general form of the HSI equation. Furthermore, we found that Case 2 cannot be solved using VR because its dispersion relation is $\alpha {\omega }_{i} = \beta {l}_{i}$, which is consistent with the work reported in ^[15]. Importantly, a literature survey showed that Eq (3.14) is new, and it may be of great help in studying real-world nonlinear wave problems.

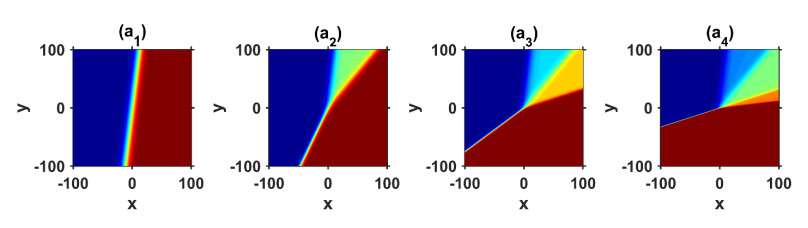
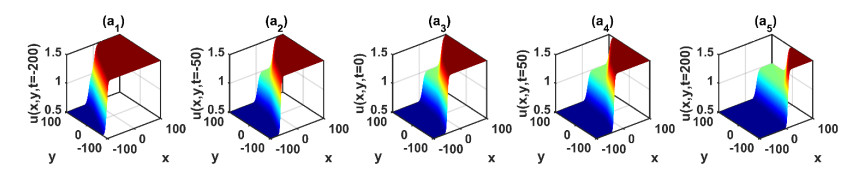
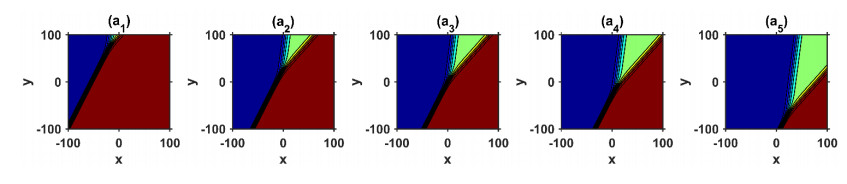
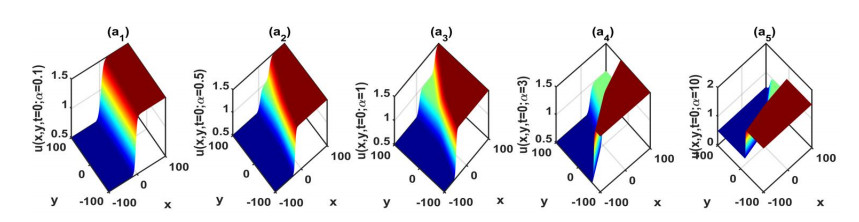
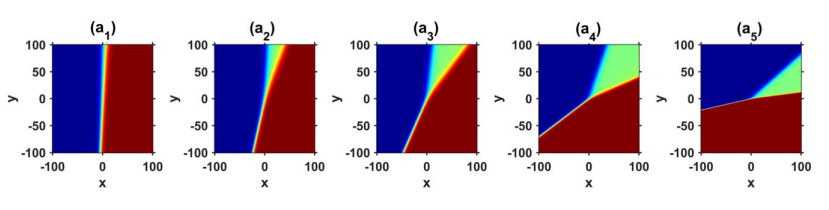
(ⅲ) By assigning specific values to the free parameters in solutions (3.6), (3.8), (3.15) and (3.16), we can simulate a variety of inelastic interactions of Y-type multi-soliton waves by using the mathematical software MATLAB. Moreover, the dynamic characteristics of the obtained solution (3.8) can be determined by considering the distinct values of free parameters presented in Figures 1–4. Figure 1(a₁)–(a₄) shows 3D plots of the solution (3.8) in the (x, y)-plane for $N = 2, N = 3, N = 4\mathrm{ }\ \mathrm{a}\mathrm{n}\mathrm{d}\ N = 5$ and correspondingly gives one kink, 2-kink, 3-kink and 4-kink waves, respectively. Figure 2(a₁)–(a₄) shows the contour plots corresponding to Figure 1(a₁)–(a₄). It is apparent from Figures 1 and 2 that when $N\ge 3$, the solution (3.8) signifies a multi-kink wave. From the above observations, we found that the number of stripes increased with $N$ at $\mathrm{t} = 0$. Figure 3 presents the splitting propagation of a traveling 2-kink wave at different times in solution (3.8) for $N = 3$. In Figures 3 and 4, 3D plots and their corresponding contour graphs for different times, namely, $\mathrm{t} = -200, \mathrm{ }-50, \mathrm{ }0, \mathrm{ }50\mathrm{ }\ \mathrm{a}\mathrm{n}\mathrm{d}\ \mathrm{ }200$, are displayed. It is remarkable that the graphs and plots show the fission behavior when time ($\mathrm{t}$) increases. In particular, the ${k}_{i}$ value affects the amplitude and speed of the traveling wave. Accordingly, the kink wave is split into two waves that travel at different speeds. The upward kink wave moves faster than the other one. Furthermore, in Figures 5 and 6, 3D plots and their corresponding contour graphs with $\alpha = 0.1, \alpha = 0.5, \alpha = 1, \alpha = 3, \alpha = 10$ are displayed, where the nonlinear term $\alpha$ influences the traveling wave speed and the initiation time of splitting. The result is consistent with Eq (3.6). Similar results can be obtained for $N = 4$ and $N = 5$.

(ⅳ) Other equations derived from Eq (1.1) may provide multi-soliton, lump and rogue wave solutions, but they should be free from resonant multi-soliton solutions, such as the CBS and JM equations ^[30,31,32]. The main reason for this is that the related wave numbers are constructed as ${k}_{i}\pm {k}_{j} = 0$; the related works can be found in ^[1,15,19,30].

4.   Conclusions

In summary, this study investigated resonant Y-type multi-soliton solutions and the soliton molecules for the fourth-order nonlinear wave equation (1.1) by using the simplified LSP and VR. The results of multi-soliton solutions and the soliton molecule for the generated equations (3.7) and (3.14) are discussed. In case 1, under the specified constraints, Eq (3.7) provides resonant Y-type multi-soliton solutions and the soliton molecule. On the basis of past studies, Eq (3.7) can be considered as a general variable-coefficient HSI equation. In case 2, Eq (3.14) can be considered as a novel nonlinear wave model. However, under certain constraints, Eq (3.14) provides only resonant multi-soliton solutions, without any soliton molecule, because of the corresponding dispersion relation constructed as $\alpha {\omega }_{i} = \beta {l}_{i}$. Notably, the results demonstrate the fact that the ${k}_{i}$ value affects the amplitude and the speed of the traveling wave; furthermore, the nonlinear term $\alpha$ influences the traveling wave speed and the initiation time of splitting.

To the best of our knowledge, the presented resonant Y-type waves and equations are new and have not been reported before. This study presents comprehensive results and contributes significantly to existing knowledge in nonlinear wave dynamics. The presented simplified LSP and VR are direct, concise and effective mathematical tools for generating resonant multi-soliton solutions and soliton molecules. Finally, the newly formulated equations (3.7) and (3.14) will boost the study of resonant multi-wave solutions. The soliton molecule is a special kind of N-soliton solution, and the dynamic characteristics of nonlinear traveling waves play an important role in studying real-world problems. Therefore, investigating the dynamical behaviors of soliton molecules, lump waves, and rogue waves associated with these equations are worth further exploring in future studies.

Acknowledgments

This work was supported by the Ministry of National Defense, Taiwan, and the Ministry of Science and Technology, Taiwan, under grant number MOST 111-2221-E-013-002.

Conflict of interest

The authors declare that they have no conflict of interest.