1. Introduction
Portfolio selection aims at either maximizing the return or minimizing the risk. In 1952, Markowitz (1952) suggests to select the portfolio by minimizing the standard deviation at a given expected return under the assumption that asset returns are normally distributed. This means that standard deviation is chosen as the risk measure. Markowitz's work laid down the cornerstone for modern portfolio selection theory framework.
Risk measures and probability distributions are two important constituents of the portfolio selection theory. Traditional Markowitz's model (Markowitz, 1952) is established based on normality assumption and standard deviation is chosen as the risk measure.
One disadvantage of taking standard deviation (StD) as a risk measure is that the loss in the extreme cases tends to be underestimated. To overcome such a difficulty, the idea of Value at Risk (VaR) is also widely used in practice.
Artzner et al. (1999) suggests that desirable risk measure should be "coherent". However, VaR does not fulfill the subadditivity condition as required by the definition of "coherence".
Yiu (2004) proposed an optimal portfolio selection under Value-at-Risk. On the other hand, Expected Shortfall (ES) is coherent as a popular risk measure for portfolio selection that aims at averaging the tail uncertainties.
It is well-known that financial data cannot be described satisfactorily by normal distribution. The normality assumption is restrictive and is generally violated due to financial market uncertainties and managers' risk aversion. As Behr and Ptter (2009) pointed out, alternatives for multivariate normal distribution are necessary for portfolio selection. A desirable alternative model should be able to explain tail heaviness, skewness, and excess kurtosis. Various heavy tailed distributions have been applied to portfolio selection problems. Among these, Mandelbrot (1997) concluded that the daily rate of return of stock price data exhibit heavy tailed distributions;
Hu and Kercheval (2010) apply multivariate skewed t and student t distribution for efficient frontier analysis; Generalized hyperbolic distribution is extensively studied in (Behr and Ptter, 2009; Eberlein, 2001; Hellmich and Kassberger, 2011; Hu and Kercheval, 2007; Surya and Kurniawan, 2014; Socgnia and Wilcox, 2014), with special cases including hyperbolic distribution (Bingham and Kiesel, 2001; Eberlein and Keller, 1995), Variance Gamma distribution (Seneta, 2004), Normal Inverse Gaussian distribution (Barndor-Nielsen, 1995), etc.
Recently, Asymmetric Laplace distribution has received various attention in the literature, to name a few, (Ayebo and Kozubowski, 2003; Kollo and Srivastava, 2005; Kozubowski and Podgrski, 1999; Kozubowski and Podgrski, 2001; Punathumparambath, 2012). Compared to Normal distribution, the Asymmetric Laplace distribution describes asymmetry, steep peak, and tail heaviness better. Portfolio selection models are extensively studied under Asymmetric Laplace framework.
Zhu (2007), Kozubowski and Podgrski (2001) apply Asymmetric Laplace distribution to financial data. By assuming that the asset data is generated from autoregressive moving average (ARMA) time series models with Asymmetric Laplace noise, Zhu (2007) establish the asymptotic inference theory under very mild conditions and present methods of computing conditional Value at Risk (CVaR).
Zhao et al. (2015) further propose a so-called mean-CVaR-skewness portfolio selection strategy under Asymmetric Laplace distribution, this model can be further transformed to quadratic programming problem with explicit solutions.
In this paper, we extended Hu's work (Hu, 2010) to Asymmetric Laplace framework. We first derived the equivalence of mean-VaR/ES/Std-skewness-kurtosis models, and show that these models can be reduced to quadratic programming problem. Since Zhao et al. (2015) utilized moment estimation for parameter estimation of Asymmetric Laplace distribution which less efficient compare to maximum likelihood estimation. Taken into consideration of the normal mean-variance mixture of Asymmetric Laplace distribution, followed by Expectation-Maximization algorithm for multivariate Laplace distribution in Arslan (2010), we derived the EM algorithm for Asymmetric Laplace Distributions that outperforms moment estimation in Zhao et al. (2015). The advantage of the proposed EM algorithm is to alleviate the complicated calculation of Bessel function. This improves many existing methods of estimating Asymmetric Laplace distributions, for example, Hrlimann (2013), Kollo and Srivastava (2005) and Visk (2009). Extensive simulation studies and efficient frontier analysis are complemented to confirm that our algorithm performs better than moment estimation for parameter estimation.
The rest of the article is organized as follows. In Section 2, properties of Asymmetric Laplace distributions and coherent risk measures are summarized. In Section 3, portfolio selection under Asymmetric Laplace framework are derived, complement with Expectation-Maximization (EM) algorithm for parameter estimation of Asymmetric Laplace distributions. In Section 4, simulation studies are provided to show the efficiency of the Expectation-Maximization procedure. Section 5 presents real data analysis of Asymmetric Laplace Distributions based portfolio selection models, followed by conclusive remarks in Section 6.
2. Preliminary knowledge
2.1. Asymmetric Laplace distribution
Kotz et al. (2001) proposed the Asymmetric Laplace Distribution with density function
|
f(x)=2ex′Σ−1μ(2π)n/2|Σ|1/2(x′Σ−1x2+μ′Σ−1μ)v/2Kv(√(2+μ′Σ−1μ)(x′Σ−1x)),
|
(2.1)
|
denoted as X∼ALn(μ,Σ). Here, n is the dimension of random vector X, v=(2−n)/2 and Kv(u) is the modified Bessel function of the third kind with the following two popular representations:
|
Kv(u)=12(u2)v∫∞0t−v−1exp{−t−u24t}dt,u>0,
|
(2.2)
|
|
Kv(u)=(u/2)vΓ(1/2)Γ(v+1/2)∫∞1e−ut(t2−1)v−1/2dt,u>0,v≥−1/2.
|
(2.3)
|
When μ=0n, we can obtain Symmetric Laplace distribution SL(Σ) with density
|
f(x)=2(2π)−n/2|Σ|−1/2(x′Σ−1x/2)ν/2Kν(√2x′Σ−1x).
|
When n=1, we have Σ=σ11=σ. In such cases, (2.1) becomes the univariate Laplace distribution AL1(μ,σ) distribution with parameters μ and σ. The corresponding density function is
|
f(x)=1γexp{−|x|σ2[γ−μ⋅sign(x)]} with γ=√μ2+2σ2.
|
(2.4)
|
The symmetric case (μ=0) leads to the univariate Laplace distribution SL1(0,σ).
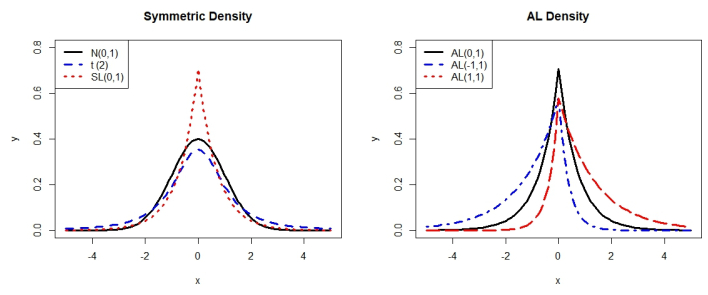
Figure 1 displays plot of symmetric densities and AL densities. Symmetric densities including standard normal distribution, student t distribution with 2 degrees of freedom, and univariate symmetric Laplace distribution, denoted as N(0,1),t(2),SL1(0,1). The student t distribution possesses heavier tail than normal distribution, whereas SL1(0,1) distribution imposes greater peakedness and heavier tail than normal case. As for plots of AL densities, when μ>0, the density skews to the right. On the other hand, when μ<0, the density skews to the left.
Important results of univariate and multivariate asymptotic Laplace distributions that will be used later on are presented below.
Proposition 2.1. (See Kotz, 2001)
(1). If X=(X1,⋯,Xn) follows multivariate Asymmetric Laplace distribution, i.e., X∼ALn(μ,Σ), n is the number of securities. The linear combination w′X=w1X1+⋯+wnXn follows univariate Asymmetric Laplace distribution, i.e. w′X∼AL1(μ,σ), with μ=w′μ,σ=√w′Σw,w=(w1,⋯,wn)′.
(2). Assume that univariate random variable Y∼AL1(μ,σ). To measure the asymmetry and peakedness of the distribution, define the skewness (Skew[Y]) and kurtosis (Kurt[Y]) as the third and fourth standardized moment of a random variable Y. Then,
|
Skew[Y]=E(Y−EY)3[E(Y−EY)2]3/2=2μ3+3μσ2(μ2+σ2)3/2,Kurt[Y]=E(Y−EY)4[Var(Y)]2=9μ4+6σ4+18μ2σ2(μ2+σ2)2.
|
(3). Let X=(X1,X2,⋯,Xn)∼ALn(μ,Σ). Then the first and second order moments of X are
(4). The Asymmetric Laplace distribution can be represented as a mixture of normal vector and a standard exponential variable, i.e., X∼ALn(μ,Σ) can be represented as
where Y∼Nn(0,Σ),Z∼Exp(1). This indicate that we can simulate multivariate Asymmetric Laplace random vector X∼ALn(μ,Σ) as follows:
1. Generate a multivariate normal variable Y∼Nn(0,Σ);
2. Generate a standard exponential variable Z∼Exp(1);
3. Construct Asymmetric Laplace random vector as X=μZ+Z1/2Y.
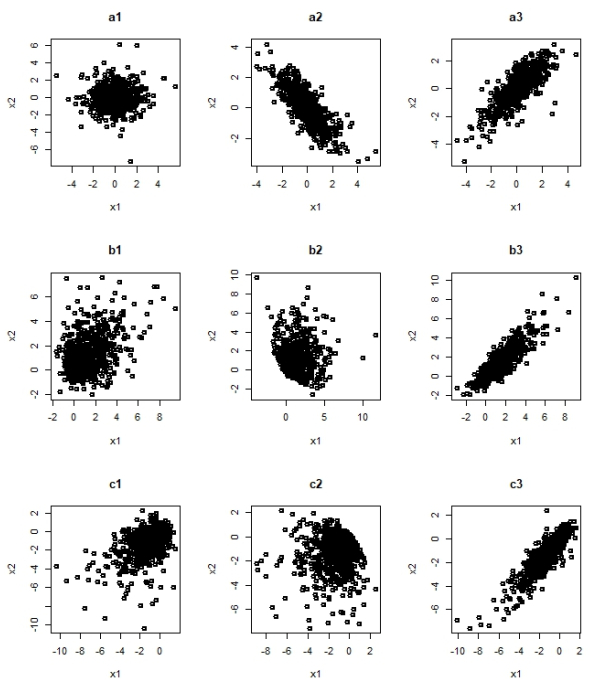
Figure 2 displays several realizations of bivariate Asymmetric Laplace distribution with different levels of asymmetry and peakedness.
2.2. Risk measures
Since mean and covariance matrix cannot be used to characterize non-Gaussian distribution, alternative risk measures are necessary for portfolio selection problems. Artzner et al. (1999) suggests that a desirable risk measure should be defined fulfilling certain properties and such a risk measure is said to be coherent.
A risk measure ϕ that maps a random variable to a real number is coherent if it satisfies the following conditions:
1). Translation invariance: ϕ(l+h)=ϕ(l)+h, for all random losses l and all h∈R;
2). Subadditivity: ϕ(l+h)≤ϕ(l)+ϕ(h), for all random losses l,h;
3). Positive homogeneity: ϕ(λl)=λϕ(l) for all random losses l and all λ>0;
4). Monotonicity: ϕ(l1)≤ϕ(l2) for all random losses l1,l2 with l1≤l2 almost surely.
Standard deviation is not coherent in general excepting the Gaussian cases. VaR is coherent when the underlying distribution is elliptically distributed. Expected Shortfall, or the so-called conditional value at risk (CVaR) is a coherent risk measure since it always satisfies subadditivity, monotonicity, positive homogeneity, and convexity. For any fixed α∈(0,1), α-VaR is the α-quantile loss while α-ES is the average of all β-VaR for β∈(α,1). Both VaR and CVaR measure the potential maximal loss. VaR and ES can be written as
|
VaRα=F−1(α)andESα=E[L|L≤-VaRα]=−1α∫−VaRα−∞VaRβdβ,
|
where F(⋅) is the cumulative distribution function of loss L and ESα is the expected loss above VaRα. Thus, the estimation process are
|
∫−VaRα−∞fX(x)dx=αandESα=−1α∫−VaRα−∞xf(x)dx.
|
(2.5)
|
Under normality assumption, VaRα and ESα are
|
VaRα=μ+σΦ−1(1−α),ESα=μ+σψ(Φ−1(1−α))α.
|
where ψ(⋅) as the normal density distribution, and Φ−1(⋅) is the quantile distribution.
As shown in Hu et al. (2010), portfolio selected by minimizing standard deviation, VaRα, and ESα are the equivalent under elliptical distribution assumption.
It is well-documented that asset securities are not normally distributed. As an alternative to Gaussian distribution, Asymmetric Laplace distribution exhibits tail-heaviness, skewness, and peakedness.
3. Portfolio selection under ALD framework
Let X=(X1,X2,⋯,Xn)∼ALn(μP,ΣP) be the return vectors of n securities, and w=(w1,w2,⋯,wn)′ is the allocation weight vector. Then, the portfolio is defined as
According to Proposition 2.1 (2), P(w)∼AL1(μ,σ) with μ=w′μ,σ=√w′Σw.
From Theorem 3.1–3.2 below, in order to select a portfolio under Asymmetric Laplace distribution, it suffices to obtain the unknown parameters μP and ΣP. Thus portfolio selection models under Asymmetric Laplace distribution lead to parameter estimation for ALn(μP,ΣP).
Zhao et al. (2015) proposed the multi-objective portfolio selection model under Asymmetric Laplace framework and derived the simplified model that can be reformulated as quadratic programming problem. However, to estimate the unknown parameters, the authors adopt a moment estimation method that is less efficient compared to maximum likelihood method. Since Asymmetric Laplace distribution can be represented as a mixture of exponential distribution and multivariate normal distribution, we derived the Expectation-Maximization algorithm for parameter estimation of Asymmetric Laplace distribution. The algorithm for estimating these unknown parameters is discussed in Section 3.2.
3.1. Portfolio selection theorems
Theorem 3.1. Let X=(X1,⋯,Xn)∼ALn(μP,ΣP) be a n-dimensional random vector that follow multivariate Asymmetric Laplace distribution, each element (Xi,i=1,2,⋯,n) represent a stock. Let w be the weight vector and P(w)=w′X=∑ni=1wiXi be the portfolio. Then, under Asymmetric Laplace framework, risk measures of StD, VaRα, and ESα at α∈(0,1) level formulated as
|
Standard Deviation: StD(P(w))=σ√2;Value at Risk: VaRα(P(w))=−σ2γ+μlnαγ(γ+μ)σ2;Expected Shortfall: ESα(P(w))=σ2γ+μ−σ2γ+μlnαγ(γ+μ)σ2.
|
Here, μ=w′μP=mean(P(w)),σ=√w′ΣPw=std(P(w)) and γ=√μ2+2σ2.
Proof. Let μP=(μ1,⋯,μn) be the mean return vector of the securities (X1,⋯,Xn) and ΣP=(σP)pi,j=1 be the scale matrix of (X1,⋯,Xn). Denote the allocation vector by w=(w1,⋯,wn)′. Then, the portfolio P(w)=∑ni=1wiXi follows univariate Asymmetric Laplace distribution with
|
P(w)=n∑i=1wiXi∼AL1(μ,σ) with μ=n∑i=1μiwi,σ=(n∑i=1n∑j=1σPijwiwj)1/2.
|
If μ=0n, the univariate symmetric Asymmetric Laplace distribution becomes AL1(0,σ) with density
|
g(x)=1γexp{−|x|σ2γ} with γ=√2σ.
|
Thus, standard deviation (StD) of portfolio P(w)=w′X is
|
StD(P(w))=∫+∞−∞1γ|x|exp{−γσ2|x|}dx=2∫+∞0xγexp{−γσ2x}dx=2σ4γ3=σ√2.
|
According to the definition of VaRα and ESα as defined in (2.5) and univariate Asymmetric Laplace density (2.4), we have
|
−∫−VaRα−∞1γexp{−|x|σ2[γ−μ⋅sgn(x)]}dx=α,σ2γ(γ+μ)exp{−γ+μσ2VaRα}=α.
|
Thus, VaRα and ESα are
|
VaRα(P(w))=−σ2√μ2+2σ2+μlnα(μ2+2σ2+μ√μ2+2σ2)σ2=−σ2γ+μlnαγ(γ+μ)σ2;ESα(P(w))=−1α∫−VaRα−∞xfX(x)dx=−1α∫−VaRα−∞x1γexp{−|x|σ2[γ−μ⋅sgn(x)]}dx=σ2μ+√μ2+2σ2−σ2μ+√μ2+2σ2ln{2α+α(μ2+μ√μ2+2σ2)σ2}=σ2γ+μ−σ2γ+μlnαγ(γ+μ)σ2.
|
Then we have the following theorem.
Theorem 3.2. Let X∼ALn(μP,ΣP). Then, portfolio P(w)=w′X with following models based on ESα, VaRα, and StD (as defined in Theorem 3.1)
|
minwESα(P(w)) or minwVaRα(P(w)) or minwStD(P(w))maxwSkew[P(w)]=2μ3+3μσ2(μ2+σ2)3/2maxwKurt[P(w)]=9μ4+6σ4+18μ2σ2(μ2+σ2)2s.t.w′μ=r0,w′1=1.
|
are equivalent. Here, μ=w′μP=mean[P(w)],σ=√w′ΣPw=std[P(w)],w=(w1,w2,⋯,wn)′.
Proof. Let g(μ,σ)=σ2μ+√μ2+2σ2. Then, ESα[P(w)] and VaRα[P(w)] are
|
VaRα[P(w)]=−g(μ,σ)ln(2α+αμg(μ,σ))=−g(μ,σ)[lnα+ln(2+μg(μ,σ))],ESα[P(w)]=g(μ,σ)−g(μ,σ)ln(2α+αμg(μ,σ))=(1−lnα)g(μ,σ)−g(μ,σ)ln(2+μg(μ,σ)).
|
Differentiating the above expressions with respect to σ, we have
|
∂VaRα[P(w)]∂σ=∂g(μ,σ)∂σ[−lnα−ln(2+μg(μ,σ))+μg(μ,σ)2+μg(μ,σ)]>0,∂ESα[P(w)]∂σ=∂g(μ,σ)∂σ[1−lnα−ln(2+μg(μ,σ))+μg(μ,σ)2+μ2+g(μ,σ)]>0,
|
where
|
∂g(μ,σ)∂σ=∂[σ2μ+√μ2+2σ2]∂σ=2σμ+μ2+σ2√μ2+2σ2(μ2+√μ2+2σ2)2>0.
|
The derivative of skewness measure with respect to σ is
|
∂Skew[P(w)]∂σ=∂[2μ3+3μσ2(μ2+σ2)3/2]∂σ=−3μσ3(μ2+σ2)5/2<0.
|
The derivative of kurtosis measure with respect to σ is
|
∂Kurt[P(w)]∂σ=9μ4+6σ4+18μ2σ2(μ2+σ2)2∂σ=−12μ4σ3−12μ2σ5(μ2+σ2)4<0.
|
The monotonicity of VaRα[P(w)], ESα[P(w)], Skew[P(w)], and Kurt[P(w)] with respect to σ indicate that the portfolio selection problems based on these risk measures are equivalent. This means that minimizing VaRα[P(w)], ESα[P(w)], StD[P(w)] are equivalent to minimizing w′ΣPw.
3.2. Parameter estimation of Asymmetric Laplace distribution
Assume X=(X1,X2,⋯,Xn)∼ALn(μ,Σ). Let x1,x2,⋯,xT∈Rn be the T observations. We aim at fitting a multivariate Asymmetric Laplace distribution ALn(μ,Σ) with unknown parameters μ,Σ.
Hrlimann (2013), Kollo and Srivastava (2005), Visk (2009) consider moment matching methods that is less efficient than maximum likelihood estimation. Kotz et al. (2002) and Kotz et al. (2001) presented the maximum likelihood estimators for parameter estimation of Asymmetric Laplace distributions. However, maximum likelihood estimation require computation of complicated Bessel function. Thus we derived the expectation-maximization algorithm for parameter estimation of Asymmetric Laplace distribution.
3.2.1. Moment estimation
As Zhao et al. (2015) pointed out, according to Proposition 2.1 (3), Asymmetric Laplace distribution can be estimated via moment method (Moment-AL) with
where ˉx=1n∑ni=1xi,Cov(X)=∑ni=1(xi−ˉx)T(xi−ˉx).
3.2.2. Maximum likelihood estimation
Consider sample points x1,x2,⋯,xn and density function of Asymmetric Laplace distribution as defined in (2.1). Taken logarithm with respect to likelihood function, the log-likelihood is
|
ℓ(μ,Σ)=lnL(μ,Σ)=T∑t=1lnf(xt;μ,Σ)=T∑t=1xtΣ−1μ+Tln2−Tn2ln(2π)−T2ln(|Σ|)+ν2T∑t=1ln(x′tΣ−1xt)−νT2ln(2+μ′Σ−1μ)+T∑t=1lnKv{√(2+μ′Σ−1μ)(x′tΣ−1xt)}.
|
Generally, we can directly maximize the log-likelihood function ℓ(μ,Σ) with respect to parameters μ,Σ and thus obtain the maximum likelihood estimator. Unfortunately, the density function involves modified Bessel function of the third kind with density (2.2), (2.3) that are too complex and complicated for numerical maximization. However, Gaussian-Exponential mixture representation of the Asymmetric Laplace distribution allows us to employ the expectation-maximization algorithm without involving modified Bessel functions.
3.2.3. Expectation-maximization algorithm
Then we derive the Expectation-Maximization algorithm for parameter estimation of multivariate Asymmetric Laplace Distribution (mALD), we follow the EM derivation for Multivariate Skew Laplace distribution in Arslan (2010).
Let X=(X1,X2,⋯,Xn) be Asymmetric Laplace distributed random vector. Proposition 2.1 suggests that X can be generated from a latent random variable Z=z through multivariate Gaussian distribution with zμ,zΣ, i.e. X|Z=z∼Nn(zμ,zΣ),Z∼Exp(1) with density
|
fX|Z(x,z)=1(2π)n/2|zΣ|1/2exp{−12(x−zμ)′(zΣ)−1(x−zμ)},fZ(z)=e−z1{z≥0}.
|
Thus the joint density function of X and Z is
|
fX,Z(x,z)=fX|Z(x,z)fZ(z)=1(2π)n2zn2|Σ|12exp{−12zx′Σ−1x+x′Σ−1μ−z2μ′Σ−1μ−z1{z≥0}}.
|
Suppose that there are T observations X1,…,XT generated from the latent random variables z1,z2,⋯,zT respectively. The complete data is defined as {(xt,zt)},t=1,2,⋯,T. In the EM algorithm, xt and zt are the observed and missing data respectively. The log-likelihood up to an additive constant can be written as
|
˜L(μ,Σ)=T∑t=1lnfX,Z(xt,zt)=−T2ln|Σ|−12T∑t=11ztx′tΣ−1xt+T∑t=1x′tΣ−1μ−12μ′Σ−1μT∑t=1zt−T∑t=1zt1{zt≥0}.
|
Note that the last term of the above equation does not contain any unknown parameters and thus is negligible. Then, the E-step becomes
|
E(˜L(μ,Σ)|xt,ˆμ,ˆΣ)∝−T2ln|Σ|+T∑t=1x′tΣ−1μ−12T∑t=1E(z−1t|xt,ˆμ,ˆΣ)x′tΣ−1xt−12μ′Σ−1μT∑t=1E(zt|xt,ˆμ,ˆΣ).
|
where E(zt|x,ˆμ,ˆΣ) and E(z−1t|x,ˆμ,ˆΣ) are the conditional expectations of zt and z−1t given xt and the current estimates ˆμ,ˆΣ.
To evaluate conditional expectations E(z−1t|xt,ˆμ,ˆΣ) and E(zt|xt,ˆμ,ˆΣ), we need the conditional density of Z given X, fZ|X. After some straightforward algebra, the conditional distribution of Z given X is an inverse Gaussian distribution with density function
|
fZ|X(z|x,μ,Σ)=fX,Z(x,z)fX(x)=1(2π)n2zn2|Σ|12exp{−12zx′Σ−1x+x′Σ−1μ−z2μ′Σ−1μ−z1{z≥0}}2ex′Σ−1μ(2π)n/2|Σ|1/2(x′Σ−1x2+μ′Σ−1μ)v/2Kv(√(2+μ′Σ−1μ)(x′Σ−1x))=(2+μ′Σ−1μx′Σ−1x)v/2z−n/2exp{−12[z−1x′Σ−1x+z(μ′Σ−1μ+z1{z≥0})]}2Kv(√(2+μ′Σ−1μ)(x′Σ−1x)).
|
(3.1)
|
Lemma 3.1. (GIG (Stacy, 1962)) A random variable X follows Generalized Inverse Gaussian distribution(denoted as X∼N−(λ,χ,ψ)) if its density function could be represented as
|
f(x)=χ−λ(√χψ)λ2Kλ(√χψ)xλ−1exp{−12(χx−1+ψx)},x>0.
|
where Kλ denotes the third kind modified Bessel function, and the parameters satisfy
|
{χ>0,ψ≥0,ifλ<0;χ>0,ψ>0,ifλ=0;χ≥0,ψ>0,ifλ>0.
|
After some algebraic manipulations, it is easy to show that Z|X follows Generalized Inverse Gaussian distribution:
|
Z|X∼N−(2−n2,x′Σ−1x,2+μ′Σ−1μ).
|
If χ>0,ψ>0, the moments could be calculated through the following formulas:
|
E(Xα)=(χψ)α/2Kλ+α(√χψ)Kλ(√χψ),α∈R,E(lnX)=dE(Xα)dα|α=0.
|
Denote χ=x′Σ−1x,ψ=2+μ′Σ−1μ. Then, Z|X∼N−(2−n2,χ,ψ). From the conditional density function of (3.1), we can obtain the conditional expectations with the following moment properties:
|
at=E(zt|xt,ˆμ,ˆΣ)=√χtψKn2−2(√χtψ)Kn2−1(√χtψ),t=1,2,⋯,T;bt=E(z−1t|xt,ˆμ,ˆΣ)=√ψχtKn2(√χtψ)Kn2−1(√χtψ),t=1,2,⋯,T.
|
where χt=x′tΣ−1xt, R(λ)=Kλ+1(x)Kλ(x) is strictly decreasing in x with limx→∞Rλ(x)=1 and limx→0+Rλ(x)=∞. Thus, at>0,bt>0,t=1,2,⋯,T.
Finally, if the conditional expectation E(zt|xt,ˆμ,ˆΣ) and E(z−1t|xt,ˆμ,ˆΣ) are replaced by at and bt respectively, the objective function becomes
|
Q(μ,Σ|xt,ˆμ,ˆΣ)=−T2ln|Σ|+T∑t=1x′tΣ−1μ−12T∑t=1btx′tΣ−1xt−12μ′Σ−1μT∑t=1at.
|
(3.2)
|
Denote S=Σ−1. The objective function (3.2) becomes
|
Q(μ,Σ|xt,ˆμ,ˆS)=T2ln|S|+T∑t=1x′tSμ−12T∑t=1btx′tSxt−12μ′SμT∑t=1at.
|
(3.3)
|
Taking derivative of objective function (3.3) with respect to μ,S, we obtain
|
∂Q∂μ=T∑t=1x′tS−T∑t=1atμ′S=0,∂Q∂S=T2S−1−12T∑t=1btx′txt+T∑t=1x′tμ−12T∑t=1atμ′μ=0.
|
Substituting S by Σ and setting these derivatives to zero yield
|
T∑t=1x′tΣ−1−T∑t=1atμ′Σ−1=0,T2Σ−12T∑t=1btx′txt+T∑t=1x′tμ−12T∑t=1atμ′μ=0.
|
Thus, maximization of the objective function Q(μ,Σ|xt,ˆμ,ˆΣ) can be achieved by the following iterative updating formulas:
|
ˆμ=ˉxˉa;ˆΣ=¯btx′txt−ˉx′ˉxˉa.
|
where ˉa,ˉb stand for the average of {at}Tt=1 and {bt}Tt=1 respectively and ˉx is the average of {xt}Tt=1. In what follows, we present the iterative reweighted Expectation-Maximization algorithm for parameter estimation of Asymmetric Laplace distribution.
| Algorithm 1 Iterative reweighting algorithm |
1. Set iteration number k=1 and select initial estimates for parameters μ(0),Σ(0).
2. (E-Step) At k-th iteration with current estimates μ(k),Σ(k), define the corresponding log-likelihood as
l(k)=logT∑t=1f(xt|μ(k),Σ(k)),k=1,2,⋯.
With notations χt=x′tΣ−1xt,ψ=2+μ′Σ−1μ, we can obtain iterative weights
at=E(zt|xt,ˆμ,ˆΣ)=√χtψK2−n2(√χtψ)K1−n2(√χtψ),t=1,2,⋯,T;
bt=E(z−1t|xt,ˆμ,ˆΣ)=√ψχtK−n2(√χtψ)K1−n2(√χtψ),t=1,2,⋯,T.
3. (M-Step) Employ the following iteration formulas to calculate the new estimates μ(k+1),Σ(k+1) at (k+1)-th iteration:
μ(k+1)=ˉxˉa,Σ(k+1)=¯btx′txt−ˉx′ˉxˉa.(3.4)
The log-likelihood at (k+1)-th iteration becomes
l(k+1)=logT∑t=1f(xt|μ(k+1),Σ(k+1)).
4. Repeat these iteration steps until convergence with criterion l(k+1)−l(k)<ε, where ε>0 is a small number that control the convergence precision, for convenience, we take ε=1e−16. |
4. Simulation studies
To evaluate the performance of portfolio selection models and parameter estimation methods in Section 3, we generate 100 datasets from Gaussian distribution and Asymmetric Laplace distribution respectively. Each dataset consists of T=200 observations with the following parameter settings: Case (1): n=3,μ=(0.03,0.06,0.09); Case (2): n=5,μ=(0.01,0.02,0.06,0.08,0.09); Case (3): n=10,μ=(0.01,0.02,0.03,⋯,0.10). For each case, we set Σ=diag(μ/10). All the simulation studies are carried out on a PC with Intel Core i7 3.6 GHz processor under R platform.
Each dataset are estimated under both multivariate Gaussian and Asymmetric Laplace distribution. ALD (EM-AL) is estimated using the EM algorithm described in Section 3.2. We evaluate the estimation performance using Bias measure, defined as Bias=‖. The mean log-likelihood and mean bias of the simulated 200 datasets are reported in Table 1.
Table 1. Model fitting results of Gaussian data and Asymmetric Laplace data using Gauss Model and EM-AL Model.
| Gaussian Data |
|
Log-Likelihood |
Bias |
|
Gauss |
EM-AL |
Gauss |
Moment-AL |
EM-AL |
| Case (1) |
709.6159 |
641.2472 |
0.0153 |
0.0451 |
0.0183 |
| Case (2) |
1363.0231 |
1260.3676 |
0.0280 |
0.0886 |
0.0319 |
| Case (3) |
2593.1151 |
2432.2192 |
0.0672 |
0.3309 |
0.0766 |
| Asymmetric Laplace Data |
|
Log-Likelihood |
Bias |
|
Gauss |
EM-AL |
Gauss |
Moment-AL |
EM-AL |
| Case (1) |
619.1798 |
735.0847 |
0.0542 |
0.0252 |
0.0226 |
| Case (2) |
1250.7110 |
1463.9149 |
0.0870 |
0.0376 |
0.0302 |
| Case (3) |
2432.3401 |
2919.9878 |
0.3750 |
0.1304 |
0.0832 |
Table 1 indicate that if the model is correctly specified, the estimation performance is always the best in terms of bias. If the data is generated from Gaussian distribution, the estimation from Gaussian model is the best, so does Asymmetric Laplace distribution. If data is generated from Gaussian distribution, then the estimation log-likelihood of Gaussian model is larger than Asymmetric Laplace distribution, this is true for Asymmetric Laplace data as well.
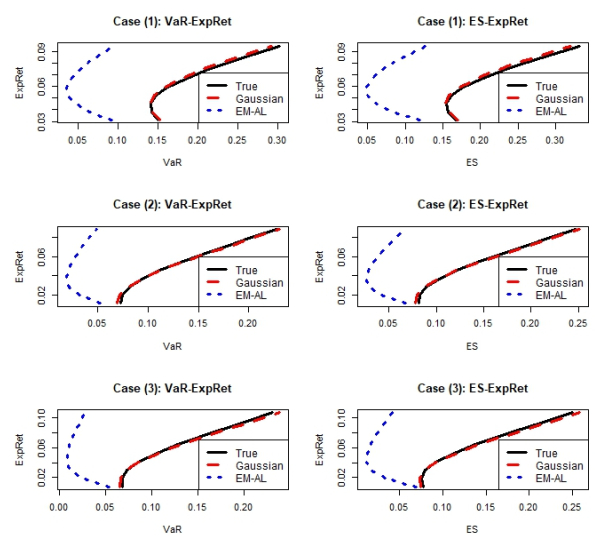
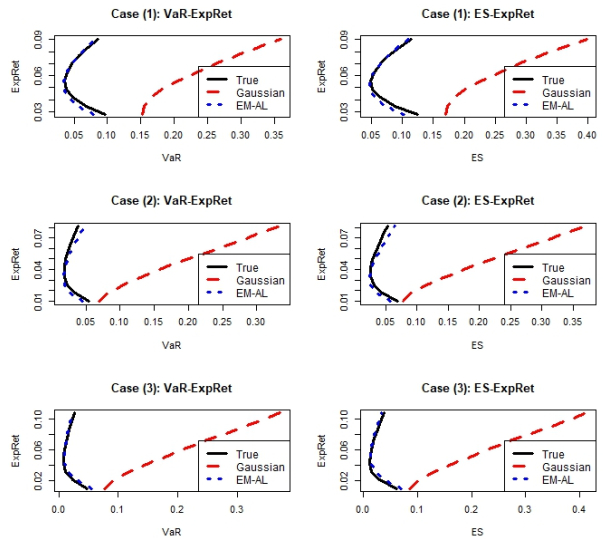
Figure 3 show that for Gaussian data, since Gaussian data fit the model better, efficient frontiers under Gaussian data are more close to Gaussian models; Figure 4 indicate that for generated Asymmetric Laplace data, efficient frontiers nearly equivalent to true Asymmetric Laplace data. Figure 3–4 suggest that we can first modeling data using Gaussian and Asymmetric Laplace distribution, and use the fitted log-likelihood to determine the distribution, then we evaluate the performance with the corresponding efficient frontier analysis.
5. Real data analysis
In this section, we apply our proposed methodology to two real financial datasets, Hang Seng Index and Nasdaq Index, both datasets are downloaded from Bloomberg, with daily data range from January 4, 2011, to December 29, 2017. The variable of interest is the rate of returns multiplied by the annualized ratio \sqrt{252}, formulated as
|
\text{LogRet}\, (t) = \sqrt{252} \Big\{ \log\big(\text{price}[t+1]\big)-\log\big(\text{price}[t]\big) \Big\}, \quad t = 1, 2, \cdots, 1721.
|
These two datasets are analyzed through efficient frontier analysis under ALD framework on \texttt{R} platform. Theorem 3.1–3.2 indicate that portfolio selection models under ALD framework can be reduced to the following quadratic programming problem:
|
\min\limits_{{\boldsymbol{w}}} \sigma^2 = {\boldsymbol{w}}' {\bf{\Sigma}} {\boldsymbol{w}} \quad \text{ s.t. } \quad {\boldsymbol{w}}'{\boldsymbol{\mu}} = r_0\, , {\boldsymbol{w}}'{\boldsymbol{1}} = 1.
|
with explicit solution (see Lai and Xing, 2008) as follows:
|
\hat{{\boldsymbol{w}}} = \frac{D-r_0B}{AD-B^2}{\bf{\Sigma}}^{-1}{\boldsymbol{1}} + \frac{r_0A-B}{AD-B^2}{\bf{\Sigma}}^{-1}{\boldsymbol{\mu}}.
|
(5.1)
|
Here, A = {\bf{1}}'{\bf{\Sigma}}^{-1}{\bf{1}}, B = {\bf{1}}'{\bf{\Sigma}}^{-1}{\boldsymbol{\mu}} and D = {\boldsymbol{\mu}}'{\bf{\Sigma}}^{-1}{\boldsymbol{\mu}}.
5.1. Example 1: Hang seng index
In the first example, we construct a portfolio consisting of 8 Hang Seng indexes: HK1, HK175, HK2007, HK2318, HK4, HK6, HK66. The summary descriptive statistics are reported in Table 2. It is clear that the all stock returns exhibit larger skewness and kurtosis. The median of these stocks are close to zero, the log-likelihood of Asymmetric Laplace distribution is larger than gaussian distribution, indicating that Asymmetric Laplace distribution would be a good fit than gaussian distribution.
Table 2. Hang Seng data statistics.
| Descriptive Statistics |
|
StD |
Mean |
Median |
Skewness |
Kurtosis |
Jarq.Test |
Jarq.Prob |
| HK1 |
19.7819 |
0.2370 |
0.0000 |
3.9601 |
71.8163 |
375244.7434 |
0.0000 |
| HK175 |
3.7101 |
0.2183 |
0.0000 |
1.1510 |
28.6192 |
59264.8528 |
0.0000 |
| HK2007 |
2.1968 |
0.1115 |
0.0000 |
0.5928 |
16.5623 |
19825.4392 |
0.0000 |
| HK2318 |
12.6007 |
0.3431 |
0.0000 |
0.6174 |
6.2371 |
2908.6947 |
0.0000 |
| HK4 |
5.8690 |
0.0409 |
0.0000 |
0.4894 |
7.6362 |
4263.7750 |
0.0000 |
| HK6 |
13.0712 |
0.1517 |
0.0000 |
-1.1430 |
20.3112 |
30037.3385 |
0.0000 |
| HK66 |
5.8708 |
0.1545 |
0.0000 |
-1.7941 |
19.9392 |
29510.3684 |
0.0000 |
|
Gaussian |
EM-AL |
| Log-likelihood |
-39707.45 |
-37865.83 |
| Parameter Estimation |
|
HK1 |
HK175 |
HK2007 |
HK2318 |
HK4 |
HK6 |
HK66 |
| \mu |
0.2370 |
0.2183 |
0.1115 |
0.3431 |
0.0409 |
0.1517 |
0.1545 |
| \Sigma |
HK1 |
HK175 |
HK2007 |
HK2318 |
HK4 |
HK6 |
HK66 |
| HK1 |
406.4426 |
12.8089 |
11.4547 |
130.0934 |
68.3857 |
94.4069 |
60.3087 |
| HK175 |
12.8089 |
7.3656 |
1.6330 |
12.0356 |
4.7467 |
4.8725 |
3.6070 |
| HK2007 |
11.4547 |
1.6330 |
3.8506 |
9.9261 |
4.6830 |
3.9055 |
2.4395 |
| HK2318 |
130.0934 |
12.0356 |
9.9261 |
174.0423 |
42.1879 |
48.2877 |
35.0499 |
| HK4 |
68.3857 |
4.7467 |
4.6830 |
42.1879 |
44.6336 |
26.5314 |
17.6232 |
| HK6 |
94.4069 |
4.8725 |
3.9055 |
48.2877 |
26.5314 |
205.1471 |
32.5570 |
| HK66 |
60.3087 |
3.6070 |
2.4395 |
35.0499 |
17.6232 |
32.5570 |
41.6153 |
Then we fit the data to Asymmetric Laplace distribution through EM algorithm as described in Section 3.2. Parameter estimation results are displayed in Table 2, we construct portfolios under Asymmetric Laplace framework at different levels of expected return. Consider increasing target expected return values
|
r_0 = 0.040\, , 0.0745\, , 0.1081\, , 0.1417\, , 0.1753\, , 0.2088\, , 0.2424\, , 0.2760\, , 0.3096\, , 0.3431\, .
|
Portfolio selection results are summarized in Table 3, with kurtosis, skewness, sharpe ratio, VaR and ES results at \alpha = 0.01, 0.05, 0.10 levels.
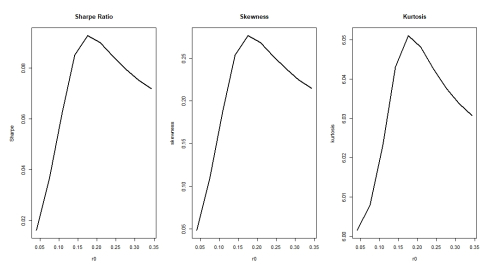
Table 3. Efficient frontier results of Hang Seng data.
|
r |
\mu |
\sigma |
Skew |
Kurt |
Sharpe |
VaR_{0.01} |
ES_{0.01} |
VaR_{0.05} |
ES_{0.05} |
VaR_{0.10} |
ES_{0.10} |
| 1 |
0.0409 |
0.0409 |
2.5461 |
0.0482 |
6.0016 |
0.0161 |
6.9429 |
8.7229 |
4.0782 |
5.8582 |
2.8444 |
4.6244 |
| 2 |
0.0745 |
0.0745 |
2.0565 |
0.1086 |
6.0079 |
0.0362 |
5.5080 |
6.9254 |
3.2268 |
4.6442 |
2.2444 |
3.6618 |
| 3 |
0.1081 |
0.1081 |
1.7299 |
0.1869 |
6.0233 |
0.0625 |
4.5256 |
5.6960 |
2.6420 |
3.8124 |
1.8308 |
3.0011 |
| 4 |
0.1417 |
0.1417 |
1.6650 |
0.2537 |
6.0430 |
0.0851 |
4.2684 |
5.3771 |
2.4841 |
3.5928 |
1.7156 |
2.8243 |
| 5 |
0.1753 |
0.1753 |
1.8891 |
0.2763 |
6.0510 |
0.0928 |
4.8095 |
6.0606 |
2.7960 |
4.0471 |
1.9288 |
3.1799 |
| 6 |
0.2088 |
0.2088 |
2.3199 |
0.2682 |
6.0480 |
0.0900 |
5.9208 |
7.4601 |
3.4434 |
4.9827 |
2.3764 |
3.9157 |
| 7 |
0.2424 |
0.2424 |
2.8656 |
0.2523 |
6.0425 |
0.0846 |
7.3493 |
9.2579 |
4.2774 |
6.1861 |
2.9544 |
4.8631 |
| 8 |
0.2760 |
0.2760 |
3.4724 |
0.2372 |
6.0375 |
0.0795 |
8.9467 |
11.2679 |
5.2108 |
7.5321 |
3.6018 |
5.9231 |
| 9 |
0.3096 |
0.3096 |
4.1134 |
0.2247 |
6.0337 |
0.0753 |
10.6386 |
13.3966 |
6.1999 |
8.9578 |
4.2882 |
7.0462 |
| 10 |
0.3431 |
0.3431 |
4.7749 |
0.2147 |
6.0307 |
0.0719 |
12.3871 |
15.5962 |
7.2222 |
10.4313 |
4.9978 |
8.2069 |
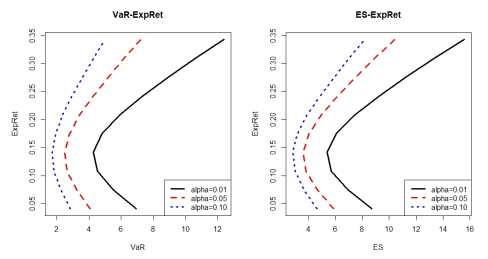
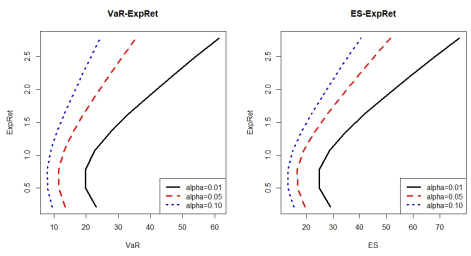
The efficient frontier tendencies are displayed in Figure 5. It is suggested that aggressive investors should impose higher confidence levels and conservative investors may choose smaller confidence levels. Figure 6 depicts the kurtosis, skewness, and sharpe ratio tendency of portfolio selection models. Results show that Sharpe Ratio, Skewness and Kurtosis increase fast and decreases slowly down as the target expected returns increases.
5.2. Example 2: Nasdaq index
In the second example, we consider Nasdaq index, including CTRP, MNST, NFLX, NTES, NVDA, TTWO, and report the descriptive statistics in Table 4. All the indexes exhibit significant skewness and kurtosis. Jarq.Test results indicate that this dataset deviates from normality significantly. We fit the log returns data to Gaussian and Asymmetric Laplace distributions. Since Asymmetric Laplace model achieve higher log-likelihood results compared to Gaussian model, we choose EM-AL model for data fitting. Parameter estimation results are displayed in Table 4.
Table 4. Nasdaq data statistics.
| Descriptive Statistics |
|
StD |
Mean |
Median |
Skewness |
Kurtosis |
Jarq.Test |
Jarq.Prob |
| CTRP |
12.5853 |
0.2100 |
0.0000 |
1.5907 |
16.5100 |
20786.4126 |
0.0000 |
| MNST |
10.0679 |
0.4904 |
0.1587 |
1.9632 |
25.7988 |
50065.6119 |
0.0000 |
| NFLX |
32.9311 |
1.5015 |
-0.0079 |
1.0314 |
20.0251 |
29796.6074 |
0.0000 |
| NTES |
58.0910 |
2.7817 |
1.2700 |
1.2457 |
26.0418 |
50315.0307 |
0.0000 |
| NVDA |
25.2360 |
1.6024 |
0.3175 |
1.7413 |
40.3981 |
120864.0386 |
0.0000 |
| TTWO |
12.2826 |
0.8786 |
0.1587 |
2.1392 |
52.3926 |
203127.9368 |
0.0000 |
|
Gaussian |
EM-AL |
| Log-Likelihood |
-46400.25 |
-42798.03 |
| Parameter Estimation |
|
CTRP |
MNST |
NFLX |
NTES |
NVDA |
TTWO |
| \mu |
0.2100 |
0.4904 |
1.5015 |
2.7817 |
1.6024 |
0.8786 |
| \Sigma |
CTRP |
MNST |
NFLX |
NTES |
NVDA |
TTWO |
| CTRP |
187.1236 |
25.4281 |
129.9104 |
246.6268 |
46.1539 |
40.0369 |
| MNST |
25.4281 |
116.7107 |
51.2572 |
82.0634 |
26.2438 |
23.5405 |
| NFLX |
129.9104 |
51.2572 |
900.1261 |
327.6980 |
122.5361 |
83.8650 |
| NTES |
246.6268 |
82.0634 |
327.6980 |
2380.8894 |
213.1414 |
121.1493 |
| NVDA |
46.1539 |
26.2438 |
122.5361 |
213.1414 |
259.7019 |
53.8530 |
| TTWO |
40.0369 |
23.5405 |
83.8650 |
121.1493 |
53.8530 |
111.0020 |
Then we consider increasing target expected returns
|
r_0 = 0.2100, 0.4958, 0.7815, 1.0673, 1.3530, 1.6388, 1.9245, 2.2102, 2.4960, 2.7817.
|
Results of skewness, kurtosis, sharpe ratio and VaR, ES results are summarized in Table 5.
Figure 7 displays the efficient frontiers at confidence level \alpha = 0.01, 0.05, 0.10. These results show that the portfolio capture higher risk at higher \alpha levels.
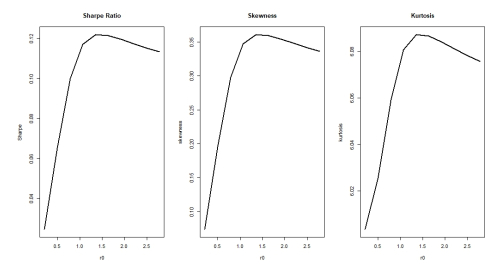
Figure 8 displays the skewness, kurtosis, and Sharpe Ratio Tendency. The optimal portfolios can be obtained from (5.1) with the corresponding VaR, ES, skewness, kurtosis and Sharpe Ratio.
Table 5. Efficient frontier analysis of Nasdaq data.
|
r |
\mu |
\sigma |
Skew |
Kurt |
Sharpe |
VaR_{0.01} |
ES_{0.01} |
VaR_{0.05} |
ES_{0.05} |
VaR_{0.10} |
ES_{0.10} |
| 1 |
0.2100 |
0.2100 |
8.5237 |
0.0739 |
6.0036 |
0.0246 |
23.0672 |
28.9903 |
13.5344 |
19.4575 |
9.4288 |
15.3519 |
| 2 |
0.4958 |
0.4958 |
7.5957 |
0.1951 |
6.0254 |
0.0653 |
19.8220 |
24.9509 |
11.5675 |
16.6963 |
8.0125 |
13.1413 |
| 3 |
0.7815 |
0.7815 |
7.8219 |
0.2973 |
6.0590 |
0.0999 |
19.7857 |
24.9397 |
11.4907 |
16.6447 |
7.9183 |
13.0723 |
| 4 |
1.0673 |
1.0673 |
9.1167 |
0.3472 |
6.0806 |
0.1171 |
22.7065 |
28.6414 |
13.1547 |
19.0896 |
9.0409 |
14.9758 |
| 5 |
1.3530 |
1.3530 |
11.1127 |
0.3608 |
6.0870 |
0.1218 |
27.5608 |
34.7713 |
15.9560 |
23.1665 |
10.9581 |
18.1686 |
| 6 |
1.6388 |
1.6388 |
13.5025 |
0.3597 |
6.0865 |
0.1214 |
33.4993 |
42.2627 |
19.3952 |
28.1586 |
13.3208 |
22.0843 |
| 7 |
1.9245 |
1.9245 |
16.1117 |
0.3541 |
6.0838 |
0.1194 |
40.0422 |
50.5132 |
23.1898 |
33.6608 |
15.9318 |
26.4028 |
| 8 |
2.2102 |
2.2102 |
18.8494 |
0.3478 |
6.0808 |
0.1173 |
46.9392 |
59.2083 |
27.1927 |
39.4619 |
18.6883 |
30.9575 |
| 9 |
2.4960 |
2.4960 |
21.6671 |
0.3418 |
6.0781 |
0.1152 |
54.0563 |
68.1800 |
31.3251 |
45.4488 |
21.5353 |
35.6590 |
| 10 |
2.7817 |
2.7817 |
24.5371 |
0.3365 |
6.0757 |
0.1134 |
61.3178 |
77.3329 |
35.5424 |
51.5576 |
24.4416 |
40.4567 |
Table 5 and Figure 7 suggests that as r_0 increases, all ES (ES_{0.01}, ES_{0.05}, ES_{0.10}) increases, indicating that higher return is derived from higher risk. It is interesting that under the ALD assumption, as r_0 increases, Sharpe ratio and skewness first decreases then increases accordingly. As \alpha increases, VaR and ES measures decreases. Thus, conservative investors can choose larger \alpha levels and aggressive investors would select smaller \alpha levels.
6. Conclusion and prospects
In this paper, we derive several equivalent portfolio selection models under ALD framework, these models can be transformed to quadratic programming problem with explicit solutions. The Expectation-Maximization algorithm for parameter estimation of Asymmetric Laplace distribution is obtained and outperforms moment estimation.
There are several advantages of Asymmetric Laplace distribution based models. First, the equivalence of risk measures such as VaR, ES and StD at maximization of skewness and minimization of kurtosis faciliate portfolio selection models significantly. Second, confidence levels of these models offer investors various portfolio selection choices. Conservative investors can choose larger \alpha levels and aggressive investors can select smaller \alpha levels. Finally, ALD model is able to explain skewness and kurtosis in financial data. Therefore, the Asymmetric Laplace distribution can be widely applied to handle real financial datasets.
We may further extend the Asymmetric Laplace based portfolio selection model to cases of mixture Asymmetric Laplace distributions. Another direction is to combine clustering techniques (see Dias et al., 2015; Iorio et al., 2018) with Asymmetric Laplace distribution for portfolio selection of time series models.
Acknowledgments
Chi Tim, Ng's work is supported by the 2016 Chonnam National University Research Program grant (No. 2016–2762).
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad: