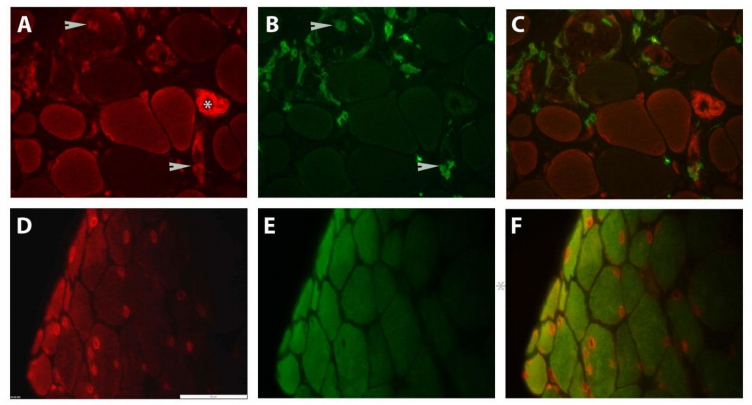
Nuclear factor κB (NF-κB) is a well-known pro-inflammatory transcription factor that regulates the expression of the tissue’s immune-active components, which include cytokines, chemokines and adhesion molecules. In addition, the versatile nuclear factor of activated T-cells (NFAT) family of transcription factors plays a crucial role in the development and function of the immune system, integrating calcium signaling with other signaling pathways. NF-κB and NFAT share many structural and functional characteristics and likely regulate gene expression through shared enhancer elements. This review describes recent research data that has led to new insights into the involvement of NFκB- and NFAT-mediated pathways in the different idiopathic inflammatory myopathies. The general activation of NF-κB p65 in blood vessel endothelium, seems to flag down inflammatory cells that subsequently accumulate mostly at perimysial sites in dermatomyositis. The joint activation of p65 and NFAT5 in myofibers specifically at perifascicular areas reflects the characteristic tissue damage pattern observed in that particular subgroup of patients. In immune cells actively invading nonnecrotic muscle fibers in polymyositis and sporadic inclusion body myositis on the other hand, p65 activation is an important aspect of their cytotoxic and chemoattactant properties. In addition, both transcription factor families are generally upregulated in regenerating muscle fibers as components of the differentiation process. It can be concluded that the two transcription factor families function in close relationship with each other, representing two-edged swords for muscle disease: on the one hand promoting cell growth and regeneration, while on the other hand actively participating in inflammatory cell damage. In this respect, cytokines function as important go-betweens at the crossroads of the pathways. Beyond NF-κB and NFAT, many fascinating winding roads relevant to inflammatory myopathy disease management still lie ready for the exploring.
1.
Introduction
The inequalities discovered by C. Hermite and J. Hadamard for convex functions are considerable significant in the literature (see, e.g., [9], [18], [27,p.137]). These inequalities state that if f:I→R is a convex function on the interval I of real numbers and a,b∈I with a<b, then
Both inequalities hold in the reversed direction if f is concave.
The Hermite-Hadamard inequality, which is the first fundamental result for convex mappings with a natural geometrical interpretation and many applications, has drawn attention much interest in elementary mathematics. A number of mathematicians have devoted their efforts.
The most well-known inequalities related to the integral mean of a convex function are the Hermite Hadamard inequalities or its weighted versions, the so-called Hermite-Hadamard-Fejér inequalities. In [17], Fejer gave a weighted generalization of the inequalities (1.1) as the following:
Theorem 1. f:[a,b]→R, be a convex function, then the inequality
holds, where g:[a,b]→R is nonnegative, integrable, and symmetric about x=a+b2 (i.e. g(x)=g(a+b−x)).
In this paper we will establish some new Fejér type inequalities for the new concept of co-ordinated hyperbolic ρ-convex functions.
The overall structure of the paper takes the form of four sections including introduction. The paper is organized as follows: we first give the definition of co-ordinated convex functions, the definition of fractional integrals and related Hermite-Hadamard inequality in Section 1. We also recall the concept of hyperbolic ρ-convex functions and co-ordinated hyperbolic ρ-convex functions introduced by Özçelik et. al in [23]. Moreover, we give a lemma and a theorem which will be frequently used in the next section. Some Hermite-Hadamard-Fejer type inequalities for co-ordinated hyperbolic ρ-convex functions are obtained and some special cases of the results are also given in Section 2. Then, we also apply the inequalities obtained in Section 2 to establish some fractional Fejer type inequalities in Section 3. Finally, in Section 4, some conclusions and further directions of research are discussed.
A formal definition for co-ordinated convex function may be stated as follows:
Definition 1. A function f:Δ:=[a,b]×[c,d]→R is called co-ordinated convex on Δ, for all (x,u),(y,v)∈Δ and t,s∈[0,1], if it satisfies the following inequality:
The mapping f is a co-ordinated concave on Δ if the inequality (1.3) holds in reversed direction for all t,s∈[0,1] and (x,u),(y,v)∈Δ.
In [11], Dragomir proved the following inequalities which is Hermite-Hadamard type inequalities for co-ordinated convex functions on the rectangle from the plane R2.
Theorem 2. Suppose that f:Δ:=[a,b]×[c,d]→R is co-ordinated convex, then we have the following inequalities:
The above inequalities are sharp. The inequalities in (1.4) hold in reverse direction if the mapping f is a co-ordinated concave mapping.
Over the years, the numerous studies have focused on to establish generalization of the inequality (1.1) and (1.4). For some of them, please see ([1,2,3,4,5,6,7,8], [19,20,21,22,23,24,25,26], [28,29,30,31,32,33,34,35,36]).
Definition 2. [29] Let f∈L1(Δ).The Riemann-Lioville integrals Jα,βa+,c+,Jα,βa+,d−,+Jα,βb−,c+ and Jα,βb−,d−of order α,β>0 with a,c≥0 are defined by
respectively. Here, Γ is the Gamma funtion,
and
First, we give the definition of hyperbolic ρ-convex functions and some related inequalities. Then we define the co-ordinated hyperbolic ρ
-convex functions.
Definition 3. [10] A function f:I→R is said to be hyperbolic ρ-convex, if for any arbitrary closed subinterval [a,b] of I such that we have
for all x∈[a,b]. If we take x=(1−t)a+tb, t∈[0,1] in (1.5), then the condition (1.5) becomes
If the inequality (1.5) holds with "≥", then the function will be called hyperbolic ρ-concave on I.
The following Hermite-Hadamard inequality for hyperbolic ρ-convex function is proved by Dragomir in [10].
Theorem 3. Suppose that f:I→R is hyperbolic ρ-convex on I. Then for any a,b∈I, we have
Moreover in [12], Dragomir prove the following Hermite Hadamard-Fejer type inequalities for hyperbolic ρ-convex functions.
Theorem 4. Assume that the function f:I→R is hyperbolic ρ-convex on I and a,b∈I. Assume also that p:[a,b]⟶R is a positive, symmetric and integrable function on [a,b], then we have
For the other inequalities for hyperbolic ρ-convex functions, please refer to ([12,13,14,15]).
Now we give the definition of co-ordinated hyperbolic ρ-convex functions.
Definition 4. [23] A function f:Δ→R is said to co-ordinated hyperbolic ρ-convex on Δ, if the inequality
holds.
If the inequality (1.9) holds with "≥", then the function will be called co-ordinated hyperbolic ρ-concave on Δ.
If we take x=(1−t)a+tb and y=(1−s)c+sd for t,s,∈[0,1], then the inequality (1.9) can be written as
Now we give the following useful lemma:
Lemma 1. [23] If f:Δ=[a,b]×[c,d]→R is co-ordinated ρ-convex function on Δ, then we have the following inequality
for all (x,y)∈Δ.
2.
Fejer type inequalities for co-ordinated hyperbolic ρ-convex functions
Theorem 5. Let p:Δ→R be a positive, integrable and symmetric about a+b2 and c+d2. Let, f:Δ→R be a co-ordinated hyperbolic ρ-convex functions on Δ. We have the following Hermite-Hadamard-Fejer type inequalities:
Proof. Multiplying the inequality (1.1) by p(x,y)>0 and then integrating with respect to (x,y) on Δ, we obtain
Since p is symmetric about a+b2 and c+d2, one can show that
This completes the proof.
Remark 1. If we choose p(x,y)=1 in Theorem 5, then we have the following the inequality
which is proved by Özçelik et. al in [23].
Corollary 1. Suppose that all assumptions of Theorem 5 are satisfied. Then we have the following inequality,
Proof. Let us define the function p(x,y) by
Clearly, w(x.y) is a a positive, integrable and symmetric about a+b2 and c+d2. If we apply Theorem 5 for the function w(x,y) then we establish the desired inequality (2.3).
Remark 2. If we choose w(x,y)=1 for all (x,y)ϵΔ in Corollary 1, then we have the following the inequality
which is proved by Özçelik et. al in [23].
Theorem 6. Let p:Δ→R be a positive, integrable and symmetric about a+b2 and c+d2. Let f:Δ→R be a co-ordinated hyperbolic ρ-convex on Δ, then we have the following Hermite-Hadamard-Fejer type inequalities
Proof. Since f is co-ordinated hyperbolic ρ-convex on Δ, if we define the mappings fx:[c,d]→R, fx(y)=f(x,y) and px:[c,d]→R, px(y)=p(x,y), then fx(y) is hyperbolic ρ-convex on [c,d] and px(y) is positive, integrable and symmetric about c+d2 for all x∈[a,b]. If we apply the inequality (1.8) for the hyperbolic ρ-convex function fx(y), then we have
That is,
Integrating the inequality (2.7) with respect to x from a to b, we obtain
Similarly, as f is co-ordinated hyperbolic ρ-convex on Δ, if we define the mappings fy:[a,b]→R, fy(x)=f(x,y) and py:[a,b]→R, py(x)=p(x,y), then fy(x) is hyperbolic ρ-convex on [a,b] and py(x) is positive, integrable and symmetric about a+b2 for all y∈[c,d]. Utilizing the inequality (1.8) for the hyperbolic ρ-convex function fy(x), then we obtain the inequality
i.e.
Integrating the inequality (2.10) with respect to y on [c,d], we get
Summing the inequalities (2.8) and (2.11), we obtain the second and third inequalities in (2.5).
Since f(a+b2,y) is hyperbolic ρ-convex on [c,d] and px(y) is positive, integrable and symmetric about c+d2, using the first inequality in (1.8), we have
Multiplying the inequality (2.12) by cosh[ρ1(x−a+b2)] and integrating resulting inequality with respect to x on [a,b], we get
Since f(x,c+d2) is hyperbolic ρ-convex on [a,b] and py(x) is positive, integrable and symmetric about a+b2, utilizing the first inequality in (1.8), we have the following inequality
Multiplying the inequality (2.14) by cosh[ρ2(y−c+d2)] and integrating resulting inequality with respect to y on [c,d], we get
From the inequalities (2.13) and (2.15), we obtain the first inequality in (2.5).
For the proof of last inequality in (2.5), using the second inequality in (1.8) for the hyperbolic ρ-convex functions f(x,c) and f(x,d) on [a,b] and for the symmetric function py(x), we obtain the inequalities
and
If we multiply the inequalities (2.16) and (2.17) by sech[ρ2(d−c)2]cosh[ρ2(y−c+d2)] and integrating the resulting inequalities on [c,d], then we have
and
Similarly, applying the second inequality in (1.8) for the hyperbolic ρ-convex functions f(a,y) and f(b,y) on [c,d] and for the symmetric function px(y), we have
and
Multiplying the inequalities (2.20) and (2.21) by sech[ρ1(b−a)2]cosh[ρ1(x−a+b2)] and integrating the resulting inequalities on [a,b], then we have
and
Summing the inequalities (2.18), (2.19), (2.22) and (2.23), we establish the last inequality in (2.5). This completes the proof.
Remark 3. If we choose p(x,y)=1 in Theorem 6, then we have
which is proved by Özçelik et. al in [23].
Remark 4. Choosing ρ1=ρ2=0 in Theorem 6, we obtain
which is proved by Budak and Sarikaya in [5].
Corollary 2. Let g1:[a,b]→R and g1:[c,d]→R be two positive, integrable and symmetric about a+b2 and c+d2, respectively. If we choose p(x,y)=g1(x)g2(y)G1G2 for all (x,y)∈Δ in Theorem 6, then we have
where
Remark 5. If we choose ρ1=ρ2=0 in Corollary 2, then we have
which is proved by Farid et al. in [16].
3.
Fractional inequalities for co-ordinated hyperbolic ρ-convex functions
In this section we obtain some fractional Hermite-Hadamard an Fejer type inequalities for co-ordinated hyperbolic ρ-convex functions.
Theorem 7. If f:Δ→R is a co-ordinated hyperbolic ρ-convex functions on Δ, then we have the following Hermite-Hadamard and Fejer type inequalities,
where
Proof. If we apply Theorem 5 for the symmetric function
then we get the following inequality
From the definition of the double fractional integrals we have
which completes the proof.
Remark 6. If we choose ρ1=ρ2=0 in Theorem 7, then we have the following fractional Hermite-Hadamard inequality,
which was proved by Sarikaya in [29,Theorem 4].
Remark 7. If we choose α =β=1 in Theorem 7, then we have
Thus, we get the following Hermite-Hadamard inequality,
which is proved by Özçelik et al. in [23].
Theorem 8. Let p:Δ→R be a positive, integrable and symmetric about a+b2 and c+d2. If f:Δ→R is a co-ordinated hyperbolic ρ-convex functions on Δ, then we have the following Hermite-Hadamard-Fejer type inequalities,
where
Proof. Let us define the function k(x,y) by
Clearly, k(x.y) is a a positive, integrable and symmetric about a+b2 and c+d2. If we apply Theorem 5 for the function k(x,y) then we obtain,
From the definition of the double fractional integrals we have
This completes the proof.
Remark 8. If we choose ρ1=ρ2=0 in Theorem 3, then we have the following fractional Hermite-Hadamard inequality,
which is proved by Yaldız et all in [34].
Remark 9. If we choose α =β=1 in Theorem 3, then we have Theorem 1.3 reduces to Theorem 5.
Theorem 9. If f:Δ→R is a co-ordinated hyperbolic ρ-convex functions on Δ. Then we have the following Hermite-Hadamard type inequalities for fractional integrals,
where
and
Proof. If we apply Theorem 6 for the symmetric function
then we get the following inequality
This completes the proof.
Remark 10. Under assumptions of Theorem 9 with α=β=1, the inequalities (3.1) reduce to inequalities (2.5) proved by Özçelik et. al in [23].
Remark 11. Under assumptions of Theorem 9 with ρ1=ρ2=0, the inequalities (3.1) reduce to inequalities proved by Sarikaya in [29,Theorem 4]
4.
Conclusions
In this paper, we establish some Fejer type inequalities for co-ordinated hyperbolic ρ-convex functions. By using these inequalities we present some inequalities for Riemann-Liouville fractional integrals. In the future works, authors can prove similar inequalities for other fractional integrals.
Conflict of interest
All authors declare no conflicts of interest.













 DownLoad:
DownLoad: