1. Low K+-induced cerebellar granule neurons (CGN) death as a model for neuronal apoptosis
The apoptosis of CGN explanted at 7th-8th postnatal day, cultured and matured in vitro is widely accepted as a good model for the apoptotic death of neurons during in vivo development and in response to stress and neurotoxic insults. Furthermore, as noted by Contestabile [1] our present understanding of mechanisms related to neuronal apoptosis during developmental stages and in response to stress and toxicity comes, to a relevant extent, from studies carried out on dissociated cultures of CGN derived from neonatal rat or mouse cerebellum.
Chronic partially depolarizing conditions produced by 25 mM KCl in the culture medium is a survival requirement for CGN in culture [2,3]. Changing the KCl concentration of the medium to 5 mM (low potassium conditions) results in extensive CGN cell death by apoptosis both during the maturation process and after the neurons have acquired the morphological characteristics of mature neurons after >8 days in vitro [2,3,4,5,6,7]. As the physiological potassium concentration in the cerebrospinal fluid is 5 mM, raising KCl concentration up to 25 mM can be seen as a simple and efficient in vitro approach to mimic granule neurons maintaining an active network of synaptic connections in vivo in the cerebellum. It is to be recalled that neurons with low level of functional synaptic connections die through apoptosis during brain development. Thus, the apoptosis of CGN in low-potassium conditions in vitro has become a simple and elegant model for neuronal apoptosis during cerebellum maturation in vivo.
Low potassium-induced apoptosis of mature CGN in serum-free medium leads to approximately 50% neuronal death after 24 hours of the change to 5 mM KCl medium [1,8,9]. This is a time scale that is very useful for the temporal dissection of cellular signaling during the apoptotic process, as well as for the critical evaluation of potential neuroprotection agents against neuronal death through apoptosis. A major conclusion derived from the temporal analysis was the finding that the critical no-return point of the low potassium-induced apoptosis of mature CGN in culture in serum-free medium is delayed several hours from switching the extracellular medium of CGN, i.e. approximately 4 hours [9,10,11]. This defined a time period quite useful for development of novel and better treatments aimed to prevent neurodegeneration through apoptosis, as well as to gain a deeper knowledge of pro-apoptotic cell signaling events in the early stages of this complex process.
The characteristic irreversible process of the apoptosis of CGN is the activation of caspases, both in vivo and low potassium-induced apoptosis in vitro, more specifically caspase-3 activation downstream of other caspases, like caspase-6 and 8 [12,13,14,15]. However, it is to be noted that in vitro this takes place only several hours after the critical no-return point of this apoptotic process, as caspases activation begins to be noticed around 6-8 hours after the change to 5 mM KCl medium [9,16]. This is consistent with the proposal that caspases activation play an essential role in accelerating, but not in being the initial agent of CGN apoptosis in vitro [1,17]. Chromatin fragmentation and nuclear condensation are also events in low K+-induced CGN apoptosis that are observed after the entry in the irreversible phase of this process [9,10]. Indeed, mitochondrial depolarization clearly precedes caspase-3 activation in low potassium-induced CGN apoptosis in vitro, as the loss of the mitochondrial membrane potential takes place between 4 and 8 hours after the change to 5 mM KCl medium, although it begins approximately 1-2 hours after the critical no-return point of this apoptosis [16,18,19]. The release of cytochrome c precedes mitochondrial membrane potential loss in low potassium-induced CGN apoptosis in vitro and peaks around 3-4 hours after the change to 5 mM KCl medium [18,19,20], and has been suggested to be a consequence of previous Bax translocation into the mitochondria [21]. A critical role of Bax in the signaling pathway leading to CGN apoptosis was suggested by the decreased susceptibility to cell death in pro-apoptotic conditions of CGN prepared from Bax-knockout mice [22,23]. Consistently, CGN from mice deficient in the anti-apoptotic gene Bcl-2 were more prone to apoptotic death than those prepared from wild-type mice [24]. However, no significant changes of the expression levels of Bax and Bcl-2 seem to occur during the temporal period before the critical no-return point of low potassium-induced CGN apoptosis [25].
cAMP, through activation of protein kinase A (PKA), and some neurotrophins, like bFGF, BDNF and IGF-1, protects against low potassium-induced CGN apoptosis [4,26,27,28,29,30]. Inhibitors of NF-kappaB activity counteract the protection afforded by cAMP and IGF-1 against CGN death elicited by potassium deprivation in the extracellular medium [31], and this suggests that the activation of the transcription factor is mediating the cell signaling pathway to reach the critical no-return point of this apoptotic process. In addition, the activation of PI-3 kinase and of the Akt/PKB kinase downstream to it have been also shown to mediate the protection afforded by IGF-1and also BDNF [30,32,33,34,35,36]. In addition, BDNF antagonizes c-Jun N-terminal kinase [34,36], thereby inhibiting induction of Fas ligand, which is a downstream effector of the apoptotic action mediated by c-Jun phosphorylation [37]. Noteworthy, the raise of cytosolic calcium of CGN in a depolarizing medium induces the production of the endogenous peptide PACAP, which acts as a neurotrophic factor for CGN during in vivo development of the cerebellum [38] and also elicits CGN survival in low potassium medium through increase of cAMP and downstream activation of PKA and mitogen-activated protein kinase (MAPK) [28,29,39,40,41].
2. L-type calcium channels (LTCC) inactivation is the primary pro-apoptotic signal in low K+-induced CGN death
As pointed out above, mature CGN in culture undergo a slow apoptosis when the extracellular concentration of KCl in the medium is lowered from 25 to 5 mM. The sustained decrease of the KCl concentration in the extracellular medium is a sufficient signal for triggering CGN apoptosis, as the CGN death through apoptosis can be blocked by simply raising the extracellular KCl concentration up to 25 mM up to 3-4 hours after the change of CGN to a 5 mM KCl medium [9,10]. Since these changes of KCl concentration elicit rapid changes of the plasma membrane potential, this pointed out to voltage-operated channels as the primary effector targets in this pro-apoptotic signaling pathway. The study of putative voltage-operated channels involved in low-K+ induced CGN apoptosis revealed that LTCC inactivation play the leading role in this apoptotic process [42,43]. Indeed, it has been shown that blockade of LTCC with nifedipine or nimodipine can also elicit CGN apoptosis in a medium with 25 mM KCl and that addition of LTCC activators like Bay K-8644 to the low-K+ medium resulted in a large delay or blockade of CGN-death through apoptosis [42,43].
The primary consequence of the inactivation of LTCC in low-K+ pro-apoptotic conditions is the sustained drop of cytosolic calcium, because of the major contribution of these calcium channels to maintain cytosolic calcium homeostasis in mature CGN in culture [42,43,44]. As a result, the cytosolic calcium concentration rapidly falls (in less than 1-2 min) below the critical level needed to maintain the neuronal activity that allows for neuronal survival, and the cells begin the development of the complex signaling pathway leading to apoptosis. As indicated above, the entry in the irreversible phase of this apoptotic process is delayed several hours, as CGN can be rescued from apoptotic death restoring the activity of LTCC by partial depolarization of the plasma membrane with 25 mM KCl up to 3-4 hours in low-K+ medium, e.g. restoring the cytosolic calcium concentration within the range allowing for neuronal survival in culture.
An alternate way of raising the steady-state cytosolic calcium concentration of mature CGN in culture is the chronic stimulation of N-methyl-D-aspartate (NMDA) receptors or another ionotropic or metabotropic receptors of glutamate, or muscarinic acetylcholine receptors, which are expressed in mature CGN. For example, stimulation of metabotropic glutamate receptors increase the survival of CGN in moderately low 10 mM KCl medium [5,45] and elevated mGluR4 expression or the activation of this receptor promotes CGN survival [46]. However, it is to be noted that the contribution of NMDA receptors activity to the cytosolic calcium concentration homeostasis in mature CGN in culture is negligible, both in pro-apoptotic low-K+ (5 mM KCl) and in survival high-K+ (25 mM KCl) medium [44,47]. This is due to the low release of L-glutamate to the extracellular medium observed in mature CGN in culture, unless specifically stimulated, and the low concentration of L-glutamate attained in the extracellular medium of these cultures [47], insufficient to elicit an activation of glutamate receptors affording a significant contribution to raise the steady-state cytosolic calcium up to the survival range of concentration. Consistently CGN can be rescued from apoptotic death in low-K+ medium by supplementation of the media with agonists leading to stimulation of NMDA receptors [48,49] or, to a variable degree, to stimulation of other ionotropic and metabotropic glutamate synaptic receptors [5,45,49,50] as well as of muscarinic acetylcholine receptors [51]. Indeed, protection by NMDA receptors stimulation correlated with a decreased expression of caspase 3 in low-K+ medium [35].
These findings have physiological correlations because both NMDA receptor activation and membrane depolarization increase the cytosolic calcium concentration in neuronal survival and plasticity during brain development [52]. Thus, the partial depolarization of the plasma membrane required for CGN survival in culture can be seen as an experimental way to mimic in vivo conditions for survival of CGN forming active excitatory synapses with mossy fibers in the development of cerebellar cortex, as the apoptotic elimination of post-migratory neurons closely matches the temporal pattern of mossy fiber development in the internal granular layer [53,54]. Moreover, pharmacological blockade of the NMDA receptor leads to an increase of apoptotic death of post-migratory neurons in the internal granular layer [6,55].
It is probable that, at least in part, cytosolic calcium protects against CGN apoptosis in vivo through the activation of calmodulin-dependent protein kinases (CaMKs). Studies with low-K+ induced apoptosis of mature CGN in culture have shown the neuroprotective effect of activation of CaMKs [56], and in particular of CaMK-IV [57]. See et al. [57] has proposed that high cytosolic calcium prevents caspase 3-dependent proteolysis of CaMK-IV, maintaining the level of CREB-dependent gene expression needed for CGN survival.
3. Reactive oxygen species (ROS) production precedes and triggers the entry of CGN in the irreversible stages of low K+-induced apoptosis
An overshot of ROS production by CGN can be observed just before the entry in the irreversible phase of low K+-induced apoptosis of mature CGN in culture [8,9,16]. Superoxide anion is a major and critical component of this ROS overshot, as addition of extracellular superoxide dismutase (SOD) not only largely attenuated this ROS overshot but also blocks the apoptotic process [8,9]. In addition, addition of several antioxidants to the low K+ medium like some flavonoids [58] and N-acetyl-L-cysteine [59] or ROS scavengers like mannitol or dimethylsulfoxide [16] largely delays or counteract low K+ apoptosis, as experimentally assessed by strong decreases of cell death, phosphatidylserine translocation, chromatin condensation and of the activation of executor caspases 3 and 8.
Despite that mitochondrial energy metabolism is impaired in early phases of low K+-induced apoptosis of CGN [60], the release of cytochrome c and the sustained drop of mitochondrial membrane potential are temporal events that have been noticed soon after the ROS overshot [19]. However, a major drop of cellular NADH, but not of NADPH nor of NAD+, is an event that takes place well before the ROS overshot, i.e. within 30-60 min after changing CGN to a low K+ medium [9], meaning an overstimulation of cellular NADH oxidases. Noteworthy, Schulz et al. [59] concluded that ROS production in potassium deprivation-induced apoptosis of CGN is blocked by inhibitors of mRNA and protein synthesis, and that ROS act downstream of interleukin-1β converting enzyme (ICE)-like proteases. The bcl-2 gene is a mammalian homolog of the C. elegans ced-9 gene, which is a potent suppressor of cell death and regulates antioxidant pathways to prevent apoptosis in lymphocytes [61,62]. Thus, the ROS overshoot observed in CGN apoptosis before entry in the irreversible phase of this process is likely a signaling mechanism for irreversible commitment to cellular suicide once defense mechanisms to restore an impaired energy metabolism are exhausted.
A large part of the ROS overshot that plays a signaling role in low K+-induced CGN apoptosis is extracellularly oriented [58]. Moreover, the fact that extracellular SOD is an efficient scavenger of this ROS overshot not only pointed out to superoxide anion as a major component of this overshot, but also suggested that it is largely produced by redox systems located at or near the neuronal plasma membrane, because of the low permeability of lipid bilayers to superoxide anion [63]. In previous works we have concluded that deregulation of the NADH oxidase activity of the redox system cytochrome b5 reductase (Cb5R)/cytochrome b5 is largely responsible for this ROS overshot [19,64]. Cb5R is a redox system that has been shown to be associated with several subcellular membranes of mammalian cells [64,65,66]. In the plasma membrane, Cb5R is part of the “so-called” plasma membrane redox chain, where it displays NADH oxidase, ascorbate free radical reductase and coenzyme Q reductase activities [67,68,69]. Our results have pointed out that within 1 and 3 hours after changing CGN to a low-K+ medium the mRNA levels of both Cb5R and of cytochrome b5 increased nearly 3-fold and this is accompanied by an enhanced translocation of Cb5R to the neuronal plasma membrane [19]. Noteworthy, the redox enzyme system Cb5R/cytochrome b5 plays a pleiotropic role in cell biology, for a recent review in this topic see [70]. Both, the time course and extent of this enhanced expression and translocation of this redox system to the plasma membrane accounted well for the observed 3 to 4-fold increase of superoxide anion production after 3 hours of the change of CGN to a pro-apoptotic low K+ medium. Furthermore, as the cellular levels of cytochrome b5 are not saturating for this redox system the increase of the expression of cytochrome b5 can account for the stimulation of the NADH activity of the plasma membrane of CGN in this time window after switching CGN to the low K+ medium [9]. This increase of activity results in a deregulation of the NADH oxidase activity of the plasma membrane of CGN which closely correlates with the temporal course of superoxide anion overshot observed in the early phase of apoptosis, well before other well accepted markers of the apoptotic process can be detected, like phosphatidylserine externalization, release of cytochrome c from mitochondria, mitochondrial depolarization, chromatin condensation and caspases activation.
Recently, we have shown that Cb5R and cytochrome b5 are heavily expressed in CGN of the cerebellum cortex of adult rat brain, but also in other neurons present in the brain neocortex and in the cerebellum, such as Purkinje cells and pyramidal neurons, and in neuronal motor nuclei of the brain stem [71]. Owing to the recognized role of oxidative stress due to excess ROS production in the apoptosis of other neuronal types, such as cortical and dopaminergic neurons, a major contribution of this signaling pathway to the commitment to apoptosis is likely playing a widespread role in brain degeneration through neuronal apoptosis, and not only restricted to CGN apoptosis. Indeed, there have been described more than 40 naturally occurring mutations of the human Cb5R, and more than 50% of them produce recessive congenital methemoglobinemia of type II, an inherited disease where mild cyanosis is accompanied by severe neurological impairment and reduced life expectancy [72,73,74]. In this rare disease, individuals show developmental delay, progressive microcephaly, generalized dystonia, movement disorders, failure to thrive, and cortical and subcortical atrophy [72,73,74,75,76], including cerebellar atrophy [77].
4. Clustering of LTCC and ROS producing enzymes in plasma membrane lipid rafts in CGN
It has been experimentally demonstrated that the calcium transport systems of the neuronal plasma membrane more relevant for the control of cytosolic calcium homeostasis are clustered within focalized nanodomains of a diameter size lower or equal to few hundreds of nanometers [78,79]. Lipid rafts of the plasma membrane are dynamic nanodomains of a dimension between 10 and 200 nm [80], which define cellular sub-microdomains of the plasma membrane anchoring caveolins, see e.g. [81], and it has been suggested that caveolin-rich nanodomains associated with neuronal plasma membrane lacking the morphological appearance of “caveola invaginations” can serve to focalize signal transduction in neurons [82]. Lipid rafts are enriched in cholesterol and sphingolipids [80], including gangliosides, a lipid family particularly enriched in the plasma membrane of neurons. Wu et al. [83] reported that survival of CGN in culture was significantly improved in the presence of cholera toxin B subunit, a ligand which binds to GM1 with specificity and high affinity, an effect that is mediated by an enhanced calcium influx through LTCC. Moreover, cerebellar neurons lacking complex gangliosides degenerate in the presence of depolarizing levels of potassium [84]. In this study, it was shown that a mice knockout for the enzyme GM2/GD2 synthase, an enzyme responsible for the synthesis of complex neuronal gangliosides, displayed impaired motor coordination. Moreover, CGN explanted in vitro from these mice survived under physiological potassium concentration and degenerated under high potassium concentration, which is opposite to the behavior of the neurons from wild-type mice.
In previous works, we have demonstrated LTCC association with lipid rafts nanodomains in mature primary cultures of CGN using fluorescence resonance energy transfer (FRET) microscopy imaging [85]. The association of LTCC with lipid rafts nanodomains has a major functional relevance for the regulation by protein kinases of the calcium influx through these channels in neurons, see e.g. [79]. First, within the brain the α1c subunit of LTCC forms a complex with PKA [86] and Razani et al. [87] have demonstrated the co-localization and direct interaction between the scaffolding domain of caveolin-1 and the catalytic subunit of PKA in vivo and in vitro, respectively. Second, experimental data have suggested the possibility of direct association of CaMKII with lipid rafts [88], which is consistent with the reported co-localization of CaV1.2, the predominant LTCC subtype in the brain, and CaMKII [89]. On the other hand, our studies have led to the conclusion that LTCC and NMDA receptors are vicinal proteins within lipid rafts nanodomains of mature CGN in culture [78]. Moreover, the major calcium transport systems for calcium extrusion from the cytosol, i.e. PMCA and sodium/calcium exchanger, are also present in these lipid rafts nanodomains [78].
Therefore, lipid rafts nanodomains of the plasma membrane of mature CGN can be seen as microchip-like structures for the fine coupling and control of systems playing a major role in the maintenance of a cytosolic calcium homeostasis within the range that allows for survival and normal functionality of neurons [79]. Because of the relevance of oxidative stress in low K+-induced apoptosis of CGN in culture, it is of utmost importance to note that two enzymatic sources of reactive oxygen and nitrogen species (ROS/RNS) are also associated with these lipid rafts nanodomains of mature CGN in culture, namely, neuronal nitric oxide synthase (nNOS) and Cb5R [19,64,78,85,90,91,92,93]. Sato et al. [94] showed that two domains of the nNOS, the oxygenase and the reductase domains, interact with the scaffolding domain of caveolin-1. More recently, using FRET microscopy imaging our group has shown that nNOS is associated with lipid rafts nanodomains enriched in NMDA receptors and LTCC in mature CGN in culture, and these three proteins are vicinal proteins in these nanodomains [93]. In addition, previous works of our laboratory have shown that the Cb5R, whose deregulation at the onset of neuronal apoptosis generates a burst of superoxide anion that stimulates the entry in the irreversible phase characterized by caspases activation [9,19,58,64], is also associated with lipid rafts nanodomains enriched in LTCC and NMDA receptors in mature CGN in culture [19,64,85]. Thus, the association with these lipid rafts nanodomains of a source of nitric oxide (nNOS) and of a source of superoxide anion (Cb5R) point out that these nanodomains may play also a major role in the focalized generation of the harmful oxidant peroxynitrite in focalized points of the plasma membrane when CGN are exposed to sustained cellular stress conditions.
In previous works, we have presented experimental evidences which point out that there is a large mesh/network of lipid rafts-associated nanodomains in the plasma membrane of the soma of mature CGN in culture, being particularly enriched in neuron/neuron contact areas [64]. Microscopy images have also shown a distribution map that closely overlap with the distribution map of flavoproteins bound to the plasma membrane [64,95], consistent with the association of the flavoproteins nNOS and Cb5R with these nanodomains. Because of the strong impairment of the activity of calcium transport systems present in these nanodomains by many ROS/RNS that can be generated in the neuronal cytoplasm under a variety of cellular stress conditions, it should be expected that even exposure of neurons to a relatively mild oxidative stress should elicit a partial and sustained failure of the control of calcium homeostasis and calcium signaling pathways within these neurons.
5. Lipid rafts nanodomains are fast response calcium/nitric oxide transducers of the switch of CGN to the pro-apoptotic low K+ medium
Neuronal survival is extremely dependent of the fine tuning of cytosolic calcium homeostasis, because cytosolic calcium concentration has to be maintained between 70 and 200 nM for survival of CGN in culture [44,47]. A large amount of experimental data reported by many investigators show sustained deviations of cytosolic calcium concentration out of this narrow window lead to neuronal cell death, see e.g. [79]. Protein compartmentation within sub-microdomains allows for a more efficient and rapid functional coupling between influx and efflux calcium transport systems, and this is particularly relevant for neuronal activity because neurons have to deliver fast responses to many repetitive and simultaneous extracellular stimuli coming from different neighbor cells. As we have shown recently [78] and also we have analyzed in more detail elsewhere [79], the calcium transport systems of the plasma membrane more relevant for the control of cytosolic calcium homeostasis in CGN, i.e. LTCC, NMDA receptors, PMCA and sodium/calcium exchangers, are associated with lipid rafts sub-microdomains or nanodomains. The functional properties of all these systems are highly sensitive to their exposure to ROS/RNS [79,96]. LTCC are the most relevant calcium channels in the fine tuning of the steady state level of cytosolic calcium concentration in the neuronal soma of mature CGN in culture and, thus, in the fine tuning of threshold neuronal excitability [97,98,99]. This gives a special relevance to our experimental results showing that caveolin-rich lipid rafts where these calcium transport systems are largely clustered in mature CGN also contain redox proteins such as nNOS and Cb5R, and the latter releases superoxide anion and hydrogen peroxide [64,100]. Owing to their close spatial proximity, these calcium transport systems are primary targets for the ROS overshot observed in the early stage of low K+-induced apoptosis of mature CGN in culture, as well as in other oxidative stress-induced or mediated forms of neuronal death [79,96,101].
Despite that LTCC are highly prone to ROS/RNS-induced oxidative chemical modifications which modulate their activity, reviewed in detail in [79,96], it is to be noted that only reversible oxidative modifications of LTCC take place before the entry in the irreversible phase of CGN apoptosis, at least up to three-four hours after changing CGN to a pro-apoptotic low K+ medium. This is pointed out by the rapid full recovery of the steady-state cytosolic calcium concentrations after raising extracellular calcium concentration to 25 mM and parallel blockade of the entry in the irreversible phase of CGN apoptosis. Indeed, no increase of protein nitrotyrosines, a good marker of irreversible oxidative modifications of proteins exposed to a combined ROS/RNS insult [102], can be observed in this early period of the CGN apoptosis [Marques-da-Silva D and Gutierrez-Merino C, unpublished data].
As we have noted in previous publications [78,79,93], these lipid rafts nanodomains play a key role as calcium/nitric oxide signaling transducers in mature CGN neurons. This assertion is based on the following experimental facts: the calcium concentration for half-the-maximum activity of nNOS is ca. 0.2-0.4 µM [103], and cytosolic calcium higher than 0.4 µM elicits a rapid CGN death [44,47,78], but the calcium concentration reaches values in the micromolar range upon activation of LTCC and NMDA receptors in small volume elements close to the cytosolic side of their calcium channel structures [104,105,106]. Due to the rapid diffusion of calcium ions in the aqueous space of the cytoplasm, the calcium entry through the high conductance LTCC and NMDA receptors channels will raise in less than 1 microsecond the calcium concentration up to the micromolar range within lipid rafts nanodomains of a size lower than 200 nm [78]. The high concentration of calcium attained within the nanodomains associated with lipid rafts allows for a stronger and faster selective stimulation of the pool of nNOS localized therein. Because of the rapid diffusion coefficient of nitric oxide, these nanodomains can be seen as the most relevant plasma membrane points for focalized nitric oxide generation in neurons and, therefore, define the sub-microcompartments of neurons where higher transient concentrations of nitric oxide are attained upon nNOS stimulation. Let us recall here that nitric oxide has been reported to induce activation of LTCC in hippocampal neurons by plasma membrane depolarization [107]. Therefore, changing of mature CGN to a low-K+ pro-apoptotic medium rapidly switch-off this focalized nitric oxide production, as the changes of the steady-state cytosolic calcium concentration produced by changes of extracellular K+ concentration takes place with a half time lower than 1 min [44,78,108], transducing the inactivation of LTCC by plasma membrane polarization into inactivation of nitric oxide signaling pathways. Noteworthy, it has been shown that nitric oxide has a major role as a neuronal survival factor, reviewed in [109,110]. Thus, the rapid switch-off of nitric oxide production after changing CGN to a low K+ pro-apoptotic medium is a very early and relevant event in the signaling pathway of this apoptotic process.
Owing to the major role of kinases signaling in the early phases of low K+ apoptosis, briefly commented above, we shall now analyze the consequences for protein kinases associated with these lipid rafts nanodomains derived from the switch-off of nitric oxide signaling in CGN immediately after extracellular K+ deprivation. The major signaling protein kinases that have been reported to be associated with the protein components present in the lipid rafts of mature CGN in culture, see above, are: CaMKII, PKA and Akt/PKB, reviewed in [79]. Besides PKA direct interaction with brain isoforms of LTCC [86], PKA also interacts with caveolin-1 [87], and CaMKII binds to LTCC subunit β2a and with NMDA receptors subunit NR2B [89,111]. In addition, it is also well known that PI-3 kinase and Akt/PKB kinase also associate with lipid rafts [112,113] and that the activity of the PI-3 kinase Akt/PKB pathway is activated by the basal levels of cytosolic calcium in neurons [114]. First, a direct consequence of the steep calcium concentration gradient generated by calcium entry through lipid rafts associated LTCC and NMDA receptors is the stronger selective activation of the pool of CaMKII and of Akt/PKB that lies in their vicinity over other pools of these kinases present in neurons. In turn, this will selectively potentiate phosphorylation of CaMKII substrates present in lipid rafts associated nanodomains. Regarding the cytosolic calcium homeostasis in mature CGN in culture, it bears a special relevance the activation of LTCC upon phosphorylation by CaMKII [111,115,116], which serves to potentiate the increase of the local gradient of calcium concentration within these nanodomains, leading to a longer lasting increase of the concentration of cytosolic calcium with the concomitant increase in nitric oxide production by co-localized nNOS. Second, nitric oxide produces a more sustained activation of the CaMKII because it induces calcium-independent activity of this enzyme through S-nitrosylation [117,118]. Third, nitric oxide may also afford an indirect activation of PKA via cGMP [119], and PKA phosphorylation also activates LTCC [120,121,122,123]. Therefore, the change of CGN to a pro-apoptotic low K+ medium elicits a rapid fall of the steady-state calcium concentration followed by switch-off of focalized nitric oxide production in lipid rafts nanodomains, resulting in downregulation of cellular signaling pathways dependent on CaMKII, PKA and PI-3 kinase-Akt/PKB kinase. As signaling pathways dependent on these kinases have been shown to play a relevant role for survival of mature CGN in culture, as briefly summarized in section 1 of this review, the functional switch of lipid rafts nanodomains after changing CGN to a low K+ medium can be seen as the earliest cellular signaling event in the reversible phase of CGN apoptosis.
6. Conclusions
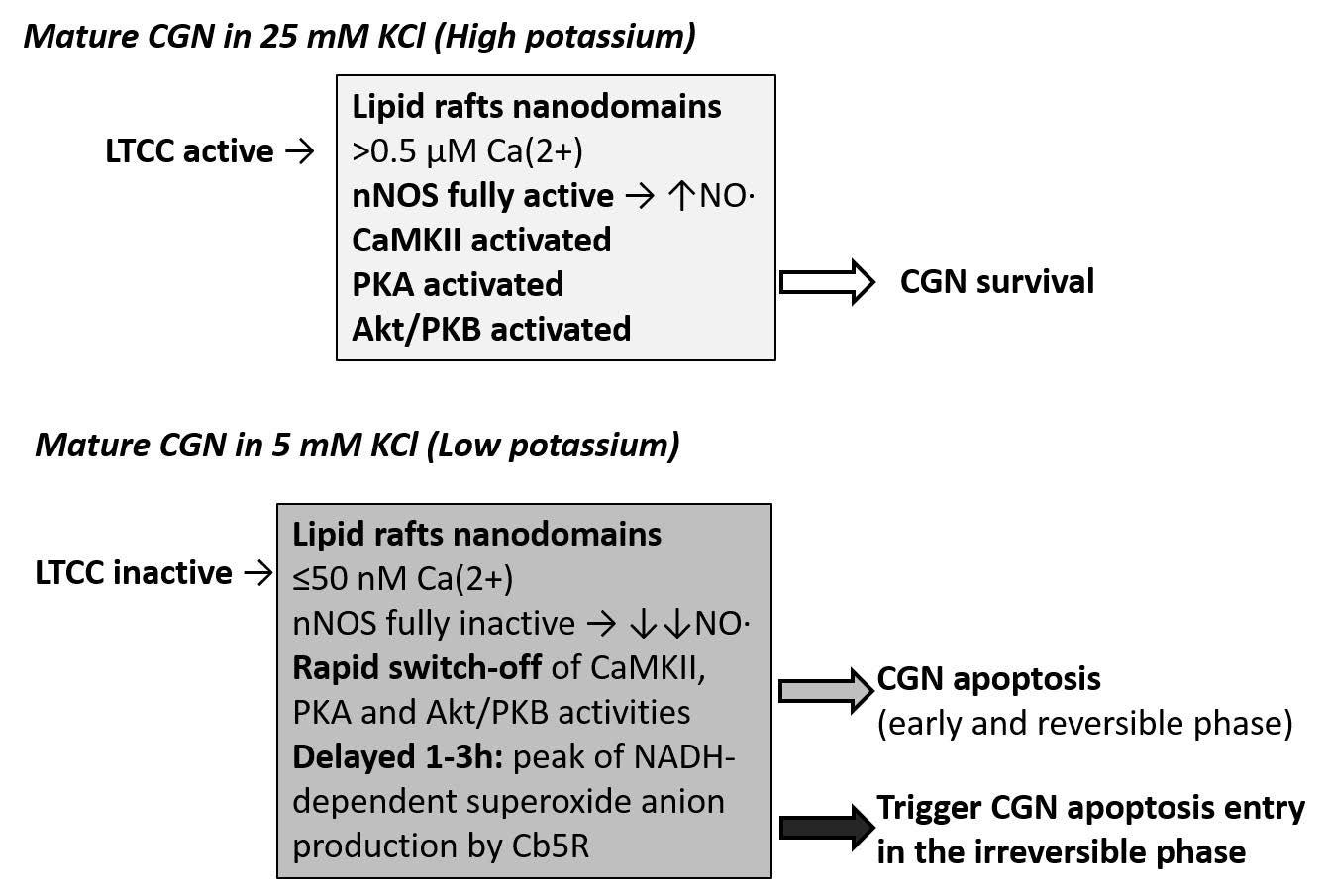
The rapid inactivation of LTCC after changing CGN matured in vitro to a low K+ extracellular medium initiates the execution of neuronal apoptosis. This apoptosis can be split into two major and sequential cellular signaling phases: one reversible phase and an irreversible later phase. The reversible phase lasts 3-4 hours after the change of CGN to a low K+ medium and this phase sets the temporal window to rescue neurons from death through experimental or pharmacological interventions. A ROS overshot, largely of superoxide anion, plays a major role in triggering the entry in the later irreversible phase, where characteristic cell signaling events are sequentially ordered as follows: proteolytic degradation of cytochrome c released from mitochondria, sustained depolarization of mitochondria, phosphatidylserine externalization, caspases activation, chromatin fragmentation and nuclear condensation, and finally cell death. Deregulation of the pool of Cb5R associated to plasma membrane-lipid rafts, at least in part due to overexpression of cytochrome b5, can account for the critical superoxide anion overshot which triggers the entry in the irreversible phase of low K+ apoptosis of CGN.
Lipid rafts of mature CGN also provide a unique platform for transduction of calcium signaling into ROS/RNS signaling and play a major role in the onset of the cellular signaling pathways of the reversible phase of this apoptosis. In mature CGN, these lipid rafts serve to clustering the major proteins responsible for cytosolic calcium homeostasis (LTTC, NMDA receptors, PMCA and sodium/calcium exchangers) and also nNOS and Cb5R within signaling nanodomains focalized in the plasma membrane. CaMKII, PKA and Akt/PKB are protein kinases whose activity is critical for survival of CGN in culture that binds to one or several of these calcium transport and redox systems. As a result, LTCC inactivation upon changing CGN to a low K+ medium is rapidly transduced into a large drop of cytosolic calcium, a switch-off of nitric oxide production and subsequent inactivation of survival signaling pathways dependent on the activity of CaMKII, PKA and Akt/PKB kinases.
Finally, we wish to note that the major molecular components of the cellular signaling pathway of low K+-induced CGN apoptosis outlined herein and schematically shown in the Figure 1 are widely present in many types of brain neurons. Thus, it is likely that the major features of this signaling pathway will be a common feature in oxidative stress-induced or in oxidative stress-mediated neuronal apoptosis observed in brain neurodegeneration. On these grounds, the key role of specific components of lipid rafts nanodomains in neuronal apoptosis unraveled during last years should help to the design of new drugs for improved therapies of neurodegenerative diseases.
Acknowledgements
This work has been supported by Grants BFU2011-30178 and BFU2014-53641-P of the Spanish Plan Nacional de I+D+I and by Grant GR15139 of the Junta de Extremadura to the Research Group BBB008 “Estrés oxidativo y bioenergética en neuronas y cerebro”, both with co-financing by the European Funds for Structural Development (FEDER). Sofia Fortalezas has been supported by a predoctoral fellowship of the Portuguese Fundação para a Ciência e a Tecnologia (FCT). Alejandro K. Samhan-Arias is supported by a Post-doctoral Fellowship SFRH/BPD/100069/2014 of the Fundação para a Ciência e Tecnologia, Portugal.
Conflicts of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: 



