1. Introduction
Nursing is considered an Angel of Mercy profession, but it is also one of the most stressful jobs compared to other health care sectors. During their routine work, nurses interact more with children, families and people which creates more stressful situations. Previous studies have provided evidence that they have stress and mild mental problems, especially those in critical care areas [1,2].
Nurses must be well adjusted to work stressors that they may encounter during their duties. Evidence shows that when nurses work in a satisfied setting, they will provide high quality nursing care. This will improve the standards of the provided nursing care [2].
The adaptive response to stressors may be effective in the short-term, but prolonged stress leads to physical and psychological disturbances [3]. Symptoms of unsatisfied work include physical burden, as well as mild psychiatric symptoms [4,5,6]. In the work environment, the symptoms may also lead to fatigue, irritability, anger, carelessness, behavior changes, or work absenteeism which will decrease the quality of the provided nursing care [7,8].
It has been reported that there are higher levels of anxiety among emergency nurses compared with other nursing care settings [9], This is attributed to the work burden and the tension in critical settings [10,11]. Furthermore, the prolonged stress not only has significant effects on nurses’ quality of life, but also may decrease the quality of emergency nursing care and diminish productivity. Despite that, a limited number of studies have examined the rate of work related anxiety among nurses in the critical care settings.
The ministry of health in Saudi Arabia mainly depends on a non-Saudi female nursing workforce. Furthermore, the Saudi nursing graduates are insufficient in meeting the demands of the increasing healthcare services. Moreover, Saudi nurses in health sectors represent less than 30% of the overall nursing workforce over the Kingdom [12]. This descriptive study aimed to determine the anxiety levels and related symptoms among critical care nurses in Albaha governmental hospitals.
2. Methods
This is a descriptive cross-sectional study. It was conducted in Albaha at four governmental hospitals (King Fahad Hospital, Buljurashi Hospital, Almandaj Hospital, and Algara Hospital) in the period from January to March 2015.
Sixty nurses from critical care settings (intensive care units, emergency room, and operating room) were selected by convenience sampling from the four hospitals. Sample distribution included King Fahad Hospital n = 20, Buljurashi Hospital n = 18, Almandaj Hospital n = 17, and Algara Hospital n = 5. The nurses included were multinationals and have experiences in critical care settings.
The study was approved by the Faculty of Applied Medical Sciences at Albaha University (attached). Targeted nurses received a cover letter explaining the purpose and outcomes of the study an assuring them that their participation is voluntary with the right to withdraw at any time without any penalty. Furthermore, nurses were assured that all information will be kept confidential by which the researcher only have the right to review. Nurses who agreed to participate signed a written consent form.
The data were collected by questionnaire which consisted of two parts: the first part was for demographic variables and the second part was an anxiety level questionnaire, derived from the Hamilton Anxiety Rating Scale. Data analysis was performed using Statistical Package for Social Sciences (SPSS version 20). The descriptive analysis was performed then the chi square test was done to identify the relationship between the demographic characteristics compared to the anxiety levels. The p-value less than 0.05 was considered significant.
3. Results Summary
As shown in Table 1, 60 nurses working in critical care settings (ICU, ER, or OR) at four hospitals in Albaha participated in this study. The majority had bachelor's degree (75%), followed by diploma (23.3%) and only one had master's degree (1.7%). They are about 33 ± 9 years old and have worked as a nurse about 11 ± 8 years.
Table 1. Demographic characteristics of nurses under study in Albaha Hospitals, 2015. (n = 60).
| Parameters | Items | Freq | Percent |
| Hospitals | King Fahad Hospital | 20 | 33.3 |
| Buljurashi Hospital | 18 | 30.0 |
| Almandaj Hospital | 17 | 28.3 |
| Algara Hospital | 5 | 8.3 |
| Nurses' qualification | Diploma | 14 | 23.3 |
| Bachelor | 45 | 75.0 |
| Master | 1 | 1.7 |
| Work area | ICU | 22 | 36.7 |
| ER | 23 | 38.3 |
| OR | 15 | 25.0 |
| Nurse: patient ratio | 1:1 | 11 | 18.3 |
| 1:2 | 29 | 48.3 |
| 1:3 | 19 | 31.7 |
| 1:4 | 1 | 1.7 |
| Age | Mean | 33 | |
| SD | 9 | |
| Years of experience | Mean | 11 | |
| SD | 8 | |
| ICU = Intensive Care Unit; ER = Emergency Room; OR = Operating Room; SD = Standard Deviation |
As shown in Table 2, the nurses participating in this study expressed a low level of anxiety; the score of anxiety level was mainly mild < 17 in 58.3% of nurses in Albaha hospitals. All respondents considered the fourteen items as a low stressor (the mean was 1.1). The symptoms of anxiety reported by nurses ranged from 0.60 to 1.52 (Table 2 and Table 3).
Table 2. Levels of anxiety for nurses in Albaha hospitals 2015, (n = 60).
| Cluster | Mean | SD |
| Anxious mood | 1.52 | 1.0 |
| Tension | 1.43 | 1.0 |
| Fears | 1.31 | 1.1 |
| Insomnia | 1.03 | 1.0 |
| Intellectual (cognitive) | 0.78 | 0.9 |
| Depressed mood | 0.97 | 1.0 |
| Somatic (muscular) | 1.33 | 1.1 |
| Somatic (sensory) | 0.67 | 0.7 |
| Cardiovascular Symptoms | 0.68 | 0.9 |
| Respiratory Symptoms | 0.60 | 0.8 |
| Gastrointestinal Symptoms | 0.75 | 0.9 |
| Genitourinary Symptoms | 0.75 | 0.9 |
| Autonomic Symptoms | 0.78 | 0.8 |
| Behavior at Interview | 0.70 | 0.9 |
| Average anxiety level | 1.01 | 0.6 |
| SD = Standard Deviation |
Table 3. A score level of anxiety among nurses in Albaha hospitals 2015, (n = 60).
| Level of anxiety | Freq. (%) |
| Mild anxiety (< 17) | 35 (58.3) |
| Mild to moderate anxiety (18-24) | 21 (35) |
| Moderate to severe anxiety (25-30) | 4 (6.7) |
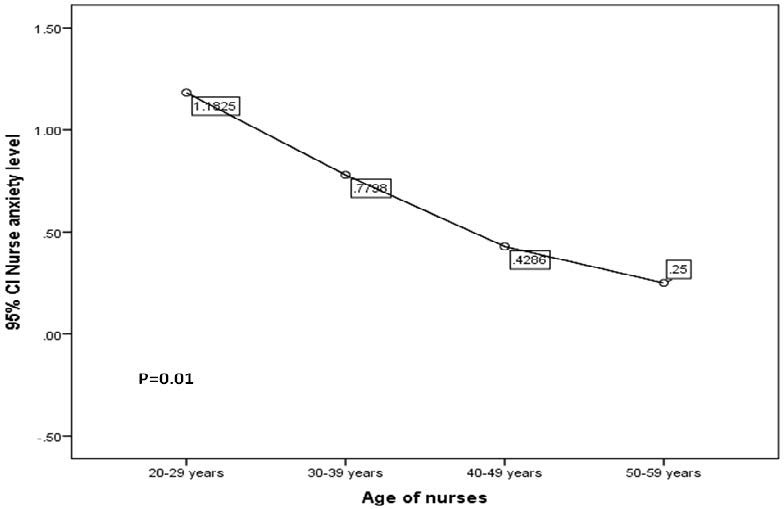
Figure 1 shows decrease in anxiety level with increasing age of surveyed nurses. The relationship between nurses' age and anxiety level was reached significance (p = 0.01).
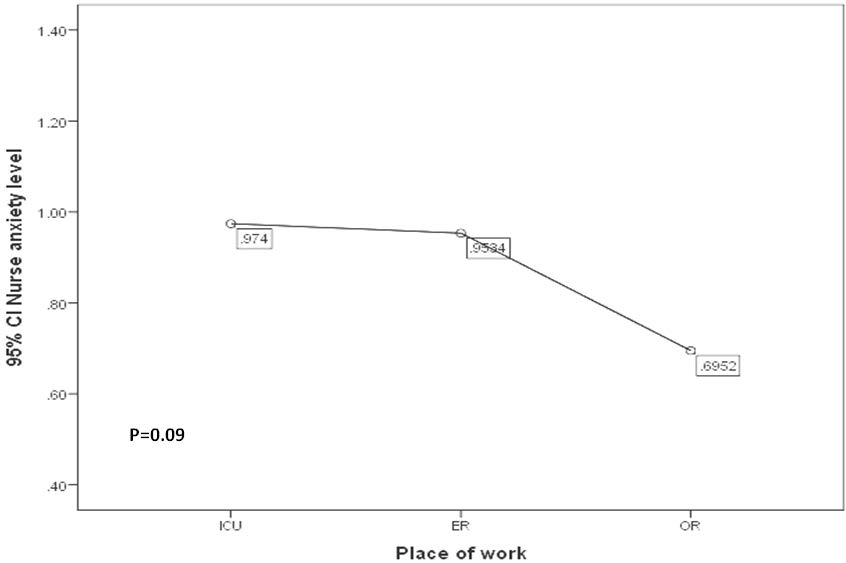
Figure 2 showed the relationship between place of work and anxiety level. A higher anxiety level was observed among ICU and ER workers, but this did not reach significant (p = 0.09).
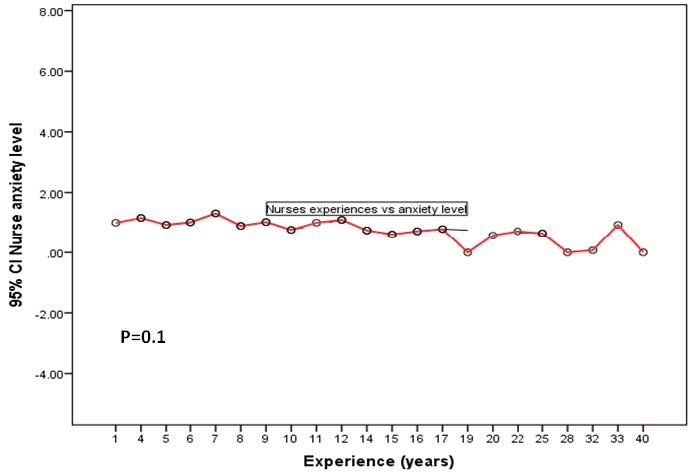
Figure 3 shows the relationship between duration of work and anxiety level. No changes in anxiety level were observed with different years of experience (p = 0.10).
4. Discussion
This study was conducted among nurses in four governmental hospitals in Albaha. Sixty nurses from critical care settings (ICU, ER, or OR) at four governmental hospitals in Albaha participated in this study. They were about 33 ± 9 years old and have worked for 11 ± 8 years, and most of them had bachelor qualifications.
The nurses in this study have mild level of anxiety (mean = 1.1) which ranged from 0.60 to 1.52. Thus, level of anxiety may be beneficial for nurses working in critical care settings. This study showed that 58.3% of nurses in critical care units Albaha hospitals have mild anxiety (< 17). These findings are higher than findings from a study conducted on the anxiety and depression on nurses at King Fahad Medical City, Kingdom of Saudi Arabia which showed that 47% of nursing staff had anxiety symptoms (HAD Average Score ≥ 8). Of those (47% of nursing staff), 20% were probable clinical cases (mild to moderate or moderate to severe anxiety) (HAD Score ≥ 11) [13]. This study figures are also higher than the prevalence reported by Schmidt D et al. in a study conducted in Brazil and found that the prevalence of anxiety (HAD Score ≥ 8) was 31.3% among nursing professionals working at surgical units [14]. These variations could be justified by the nurses working in the critical care settings are more vulnerable for anxiety than those working in the other nursing units. The critical care settings in Albaha Hospitals are the local where the nurses suffer a lot, they are involved in End-of-Life decisions and the work is very stressful. The nurses in critical care settings provide total care and highly competent skills which creates stress and anxiety.
The findings of this study reflect a statistically significant inverse correlation between anxiety levels and the age of critical care nurses. Based on these findings we recommend setting policy measures such as a periodic rotation, for nursing staff in the more stressful environments in hospitals.
The findings from this study were similar to the findings of a study conducted in Greece among emergency nurses. That study showed that emergency nurses have mild anxiety [2]. Our findings were also comparable with the findings of a study conducted in Dubai, United Arab Emirates. In this study, investigators found that the anxiety level of the staff nurses in Albaha hospitals was similar to the anxiety level of medical staff in Dubai city. The Dubai study showed that, about 2.2% of medical staff in Dubai exhibited anxiety [15].
On the other hand this study found that anxiety level among critical care nurses was mild which is lower than the level of anxiety reported in a study for nurses in Hawler city. They were suffering from mild to moderate anxiety while 3.1% were complained from severe anxiety disorders [16].
The major strength of this study are the study distributed to four hospitals with good representation of nursing anxiety symptoms from three highly stressful environmentsand using the Hamilton Anxiety Rating Scale, a widely used and well-validated tool for measuring anxiety levels. The major weakness of the study is the sample, which represents a limited geographical area thus reducing its generalizability.
5. Conclusion
The anxiety level of the critical care nurses in Albaha hospitals is mild. The most frequently reported symptoms of anxiety include anxious mood, tension, insomnia, somatic symptoms and fear.
Recommendations
It is recommended that further studies to be conducted to investigate the main causes of anxiety for critical care nurses. Experimental studies are needed to identify the most effective ways for minimizing the high levels of unproductive anxiety. Finally, the rotation may prevent escalation of anxiety symptoms which would be detrimental to nurses in high stress work environments.









 DownLoad:
DownLoad: