1.
Introduction
In recent years, adversarial differential games have provided a framework to analyze the conflicting scenarios of opposing teams in fields such as aerospace and robotics [1,2]. The problem is theoretically interesting since the method of solving the optimal strategy of each player should take into account the player's own state information, as well as the potential strategies of opponents [3]. Due to the complex interactions between different players and differences in velocity, capture radii and goals, it is challenging to analyze the pursuit-evasion (PE) and reach-avoid (RA) problems, which include optimal decision-making, path planning, resource allocation, winning regions, accessibility, etc. [4,5,6]. In addition, the uncertainties of players' behaviors and decision-making have a large impact on the outcome of games [7].
In adversarial differential games, the PE problem is a basic scenario since the only goal of attackers (evaders) is to avoid the interception of defenders (pursuers) [8]. While in the RA games, in addition to avoiding interception, attackers need to reach the target region as well [9]. Another kind of game, called capture-the-flag (CTF) games, has the most complicated setting among the adversarial differential games [10]. In CTF games, there is one more goal for the attacker, which is required to capture the flag and return to the specified region [11]. Notice that there is an upgrade in the complexity of the attackers' tasks in these three types of games. In general, players need to make reasonable decisions according to their strategy sets. However, in some cases, there are unexpected opponent actions that are inconsistent with a limited strategy set [12]. Therefore, the key problem of the adversarial differential games is adopting the saddle-point strategy, which is the optimal strategy of both attackers and defenders. Note that, no matter what strategies the opponent team actually adopts, the saddle-point equilibrium can guarantee its own payoffs [13]. For example, if the attackers do not play optimally, the defenders can guarantee the payoffs by updating the obtained optimal state-feedback strategies. Conversely, attackers can implement saddle-point strategies to reduce their cost when defenders do not adopt optimal strategies [8].
At present, there are few relevant surveys about adversarial differential games [14,15], and no analysis from the perspective of players' goals. The contribution of this paper is to compare and analyze the solutions of the differential games mentioned above. Different from [13] and [15], which mainly studied the PE games or modeled the PE problem as zero-sum differential games, this paper is focused on analyzing RA games and CTF games in terms of analytical and geometric methods as well. In the low-dimensional situations, the analytical methods can describe the player's optimal strategy clearly and accurately through the use of Hamilton-Jacobi-Isaacs (HJI) equations. However, in multi-player and high-dimensional situations, the use of analytical methods brings about greater computational complexity. To solve the problem, geometric methods can help players determine the winning regions. The surface that separates the players' winning areas is called a barrier. If the barrier can be determined by geometric methods, the players will choose strategies according to the area in which they are located. Nevertheless, it is still complicated to obtain the barrier when considering the capture radii and different velocities of the players. In the end, this paper introduces corresponding prospects for these three different types of games under the conditions of an open environment, imperfect information, multi-objective regions, heterogeneity and large-scale networks; applications are also discussed.
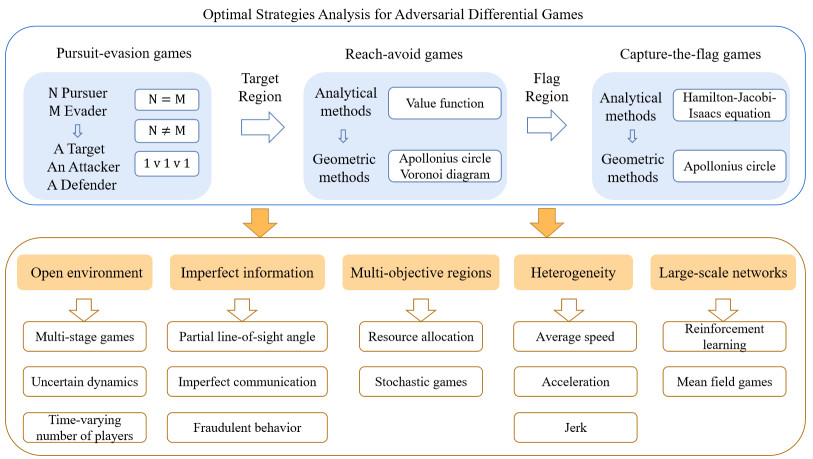
The remainder of this paper is organized as follows. In Section Ⅱ, the literature comparison results for PE games are introduced from the perspective of different players' numbers, and a special type of target-attacker-defender (TAD) game is introduced. In Sections Ⅲ and Ⅳ, RA games and CTF games are compared in terms of the analytical and geometrical methods, respectively. In the last section, future research directions for adversarial differential games are put forward. The overall structure of this analysis is reflected in Figure 1. Morever, as seen in Table 1, this paper compares PE games, TAD games, RA games and CTF games in terms of the of methods and applications. In Table 1, A and G represent the analytical method and geometric method, respectively. The velocities of the attacker, defender and target are vA, vD and vT, respectively. α is the speed ratio for the attacker and defender, and β is the speed ratio for the target and attacker.
2.
Pursuit-evasion games
In the classic PE problem, there are two opposing groups of players, one group acting as pursuers and the other group acting as evaders. The basic configuration of PE games is shown in Figure 2(a). The core problem of PE differential games is finding the saddle-point equilibrium strategy, that is, obtaining the minimax value of the payoff function. No matter what strategies the opponents adopt, the saddle-point strategies can guarantee the players' optimal payoffs [13]. Supposed that there are two opposing teams in PE games with N pursuers and M evaders; we will discuss relevant works in three different cases, i.e., N=M, N≠M and N=M=1, as below.
2.1. N Pursuers, M Evaders (N=M)
The premise of PE games begins with a conflict between two opposing teams with a common performance function. For example, we take the distance between the pursuer and the evader as the payoff function, i.e., J=√(xP−xE)2+(yP−yE)2, where xP=(xP,yP) is the position of the pursuer and xE=(xE,yE) is the position of evader. The evader wants to maximize the distance and the pursuer wants to minimize it. We first analyze the case in which the number of pursuers and evaders are the same. In adversarial differential games, the entire state space is divided into the pursuers' dominant region and evaders' dominant region. The surface that separates these two dominant areas is a barrier. In PE games, considering a defender and a spy in a circular area [16], the barriers and optimal strategies of the players were obtained via geometric methods. When the state of the system was in the winning region of the defender, the strategy designed in [16] could not guarantee the defender's payoff. Then, a semi-permeable barrier surface was proposed in [3] to solve this problem. The above works were aimed at the situation in which the defender is faster. When the attacker has a faster velocity, the defender's optimal strategy can be found by using variational methods [17]. Although the previous works considered the case of one pursuer and one evader, the assumption can be extended to the case of N pursuers and M evaders, which satisfies N=M. For the multi-player PE situation, the optimal strategies were obtained via value function methods; consequently, the curse of dimensionality was overcome [8,18].
Furthermore, in order to allocate and capture evaders in multi-player games, the binary variable σij was defined in [8]. If σij=1, then Pursuer i (i=1,...,N) captures Evader j (j=1,...,M), and if σij=0, then Pursuer i is not assigned to capture j. A pursuer is assigned a task only once, that is, it can only capture one evader; then, ∑Mj=1σij≤1. For pursuers, the condition for game termination is:
where xPi and xEj represent the positions of Pursuer i and Evader j, respectively. For N<M, due to the large number of evaders, there is no guarantee that each evader will be assigned to a pursuer. If the termination condition is that all evaders are caught, there must be some tasks that will be reassigned to the pursuers. Therefore, the set (2.1) is suitable for the case in which the number of pursuers and evaders satisfies N=M or N>M.
2.2. N Pursuers, M Evaders (N≠M)
In the case of multi-player PE games, the N-pursuers-M-evaders (N≠M) problem has been well analyzed in [19]. For example, a scalable polynomial-time allocation algorithm based on a new decomposition method was proposed in [20]; it outperformed some defense strategies. However, the traditional analytical methods for differential games were not easily applied to analyze the situation of N≠M due to the computational complexity. In these situations, the analytical methods were replaced with geometric methods [21] based on Voronoi diagrams [22], resulting in open-loop saddle-point equilibrium strategies.
The previous solutions have been for the slower evaders, but the problem is more challenging when the attackers are faster. In this case, faster evaders are more difficult to capture for pursuers, and their optimal strategies are complicated to analyze. A new Cartesian ellipse analytical method was proposed to obtain the players' winning regions when the pursuers had a positive capture radius in [23]. Evaders and pursuers with different velocities were considered in [24], the PE problem was modeled as zero-sum differential games. The state-feedback optimal strategies of the players were derived analytically in the attack and retreat stages. Regarding the multi-player PE differential games with malicious pursuers, the problem was modeled as non-zero-sum games [25], and the Nash equilibrium was analyzed. In a game process, if any player chooses the optimal strategy when the strategies of other players are determined, the combination is a Nash equilibrium. More specifically, any player who unilaterally changes his/her strategy under the combination will not increase his/her own payoffs. Furthermore, for pursuers with limited observations, the Nash equilibrium based on the best achievable performance metrics can be employed within a limited time horizon [26]. Moreover, a special class of PE games with a moving target is an interesting problem. In the following subsection, we mainly discuss the particular type, i.e., TAD games.
2.3. One target, one attacker, one defender
The TAD differential game is a kind of PE game with three players, i.e., target, attacker and defender. The attacker's goal is to capture the target [27], and the target's goal is to evade and avoid being captured by the attacker, as illustrated in Figure 2(b). In addition, the defender can cooperate with the target, who pursues and attempts to intercept the attacker before the attacker captures the target [28].
In TAD differential games composed of an arbitrary number of attackers and defenders, optimal control methods and the assignment of attacker-defender pairs were analyzed in [29]. The performance of attackers and defenders can be guaranteed by their saddle-point state-feedback strategies [30]. In general, the attacker/defender team tried to minimize/maximize the distance between the target and the attacker. Regarding differential games in high-dimensional state spaces, through the use of a continuously differentiable value function, the complete closed-form solution and state-feedback optimization strategies were analyzed in [31]. In addition, the TAD problem was modeled as zero-sum differential games as well in [32]. In the case of zero-sum TAD games [33], they are worth studying to determine the region of space wherein the attacker wins. When the state space was in the attacker's winning region, given the attacker's optimal strategy, the target can still be captured despite the defender's best efforts [34]. In other situations, if the velocity of the attacker and the defender is the same but the velocity of the target is lower, the optimal strategies of the players can be determined by calculating the barrier. Furthermore, the hyperbola divided the Cartesian plane into two regions of the barrier surface, as shown in Figure 3.
In the case of TAD games[35], the situation of the attacker being faster than both the target and the defender is complicated. There is a greater threat to the target and defender, making it harder to determine their optimal strategies. Cooperation between the target and the defender will better help the defender catch the attacker. For example, when the attacker is faster, the target can lure the attacker into the defender's capture route through its movement. By taking full advantage of their cooperative strategies, the target can be protected [36]. In addition, the active target defense differential games [37] was extended in [38]. The target needs to find an optimal heading and control the energy [39]. Therefore, the problem can be modeled as linear-quadratic differential games to be solved. In addition, explicit strategies and geometric analysis methods can be used to study the winning regions of players [40].
3.
Reach-avoid games
As shown in Figure 4(a), compared with that of PE games, the mechanism of RA games is slightly more complicated. In RA games, there are not only two opposing teams, i.e., the attacker team and the defender team, but there is also the target area. The attacker team's goal is to reach the target area without being captured, while the defender team attempts to delay or prevent the attacker team from entering the target area by capturing attackers [41].
3.1. Analytical methods
In past works, the methods to solve the RA problem included mixed-integer linear programming methods, nonlinear model predictive control methods [42] and approximate dynamic programming methods [1,43]. In some special situations, HJI reachability [44] is a powerful tool for low-dimensional RA differential games. However, since defenders and attackers have conflicting and asymmetric goals, there may be complicated cooperation within each team. Therefore, it is challenging to obtain optimal solutions directly.
For RA games, the main problem is to construct a barrier that divides the entire state space into two disjoint parts, i.e., the defender's dominant region and the attacker's dominant region [45,46]. The RA set, which was divided by the barrier, was computed by solving the HJI partial differential equation in the player's state space[47]. Moreover, the HJI method can be applied to a wide variety of player dynamics.
In order to combine the time-varying dynamics, objectives and constraints, a modified HJI equation in the form of a two-barrier variational inequality was proposed in [48]. Through this equation, it is simple to determine the winning regions and the optimal strategies for the time-varying games. In general, HJI partial differential equations can be solved by the numerical approximation of the value function on a continuous state-space grid [47,48] and the characteristic line method [31]. However, the dimension of the system state will increase exponentially with the number of players, leading to a high computational cost as a result of directly solving the corresponding high-dimensional HJI equation. This is the main reason why the approach cannot be applied to multi-player differential games [9,49]. The maximum matching method of graph theory was shown to be less computationally expensive than the HJI partial differential equation method when applied to multi-player RA games [49]. In addition, Q-learning was shown to be a feasible method for high-dimensional optimal control tasks [50,51], as a strategy was obtained to maximize the accumulated payoff at each time step. The extended conservative Q-learning method with less computation costs can learn the value functions of games to determine the optimal strategies for players, as shown in [52]. Importantly, the RA Q-learning algorithm resulting from the reinforcement learning formulation converges under similar conditions in the traditional Lagrangian-type problems [53].
Since the HJI method cannot solve high-dimensional problems, some researchers derived state-feedback strategies to obtain a continuously differentiable value function; they proved that it was a solution to the HJI equation [2,12,54]. The game's value function is
where J is the terminal cost/payoff function, x0 is the initial state of the system and uA and uD are the attacker and defender teams' state-feedback strategies, respectively [9]. A new perspective on solving HJI equations was studied in [55], where the associated HJI equations can be solved by convex programming [56] for a special subgame. Furthermore, if RA problems were modeled as linear-quadratic differential games, a closed-form solution of the zero-sum games would be obtained. Players can exploit the opponent's non-optimal strategies to win by carrying out closed-loop state-feedback strategies [57]. In this case, by implementing the strategies, players can transfer the value of the game to themselves.
3.2. Geometric methods
For RA games, geometric methods play an important role in solving players' optimal strategies. Voronoi diagrams, which divide the plane into different regions based on a set of specific points, have been widely used for situations in which defenders and attackers possessed equal velocities [58,59]. In general, an attacker can be seen as a specific point in a small Voronoi cell. The defenders in the cell are closer to a specific attacker than other attackers. Especially, in the case of the group tracking of single or multiple evaders, Voronoi diagram methods can provide constructive cooperative strategies, such as minimizing the area of the generalized Voronoi partitions of evaders [60,61] or tracking evaders in a relay way [62].
However, the velocities of attackers and defenders are not equal in some situations [63]. When the velocities of defenders are faster than those of attackers, the Apollonius circle first proposed by Isaacs can be used to analyze the multi-player RA games, as shown in Figure 5. What is more, the Apollonius circle has been used to construct a barrier between the attackers and the defenders in a convex domain [1]. To ensure that the largest number of evaders are intercepted, the task assignment can be performed by solving simplified 0-1 integer programming, which can greatly reduce the computational complexity. For the case of only one defender and multiple attackers, there is a time difference between the pursuit and escape of the defender and the second attacker. The δ-Apollonius circle has been used to handle the pursuit of the second attacker [64]. Moreover, the potential barrier and two winning regions were constructed to analyze the optimal strategies of the players.
4.
Capture-the-flag games
With multiple potential objectives, the CTF problem is considered as a complex type of adversarial games. The multi-stage interaction between different players makes CTF games more challenging than PE games and RA games. In the case of CTF games, opposing defender and attacker teams control their own area and protect their flag. There are two phases as illustrated in Figure 4(b), which are the CTF phase and the safe return phase [10,11]. A team wins by dispatching the players to enter the opposing team's area, capturing the flag and returning to their own safety region. In addition, the team's flag cannot be possessed by the opposing team during this process. In order to solve the problem of optimal strategies in CTF games, many scholars have made various assumptions regarding players' behaviors, such as modeling a player as a point with no capture radius [63]. Two kinds of methods, i.e., analytical methods and geometric methods, are compared below.
4.1. Analytical methods
The multi-stage characters of the CTF problem make the analysis complicated; this is because each player must choose the appropriate control at each stage to ensure the viability of their respective winning goals in the next phase [65]. A two-team CTF game can be modeled as a zero-sum differential game [10], and an upper limit of the player's velocity can be assumed. The corresponding winning strategies have been derived by applying analytical solutions of the HJI equation. In addition, the solution in [10] was for one-on-one CTF games.
Consider the augmented input ˜u of Player Ⅰ, the general system dynamics and the augmented system dynamics, respectively, as follows:
where u is the control input of Player Ⅰ, u_ is the freezing input, ˜U is the set of finite horizon controls, x is the game state, d is the control input of Player Ⅱ, ˜x is the trajectory of the augmented system and x0 is the initial condition [66]. The player's goal can be expressed as the following constrained terminal cost problem:
where T⊂Rn(K⊂Rn) is the target (undesired) set, ϕ is the function Rn→R, [0,T] is a finite time horizon and ˉJT is the supremum of the value.
The upper value (4.4) of this problem is calculated by using the viscosity solution of the HJI equation:
where H(⋅,⋅) is the Hamiltonian. The players' optimal strategies can be accurately determined by solving the HJI equation. Moreover, two-stage joint optimization strategies were determined by modeling the game as a constrained nonlinear optimization problem and solving it with a sequential quadratic programming algorithm [11,18]. However, as the number of continuous states increase, the curse of dimensionality will occur, which will lead to increasing computational complexity.
4.2. Geometric methods
In addition to the methods above, there are heuristics to analyze CTF games, and they have often relied on geometric methods like vertical bisectors [67], Apollonius circles [11,68] and Cartesian ovals, as shown in Figure 6. Different from [10], two different terminal costs/payoffs were proposed in [67]. In the first stage, when the defender captured the attacker, the distance between the attacker and the flag was the terminal costs/payoffs. Moreover, the distance between the attacker and the safe region at the last moment was used in the second stage. In each stage of the differential games, the optimal state-feedback strategies of each player were determined via the correlation calculation for the value function. Moreover, if two players have the same velocity, the vertical bisector between them plays an important role in the analysis of the optimal strategy [33].
As with PE games and RA games, the idea of CTF games is to obtain the barriers that separate the players' winning regions. A composite boundary for the fixed position of the defender was constructed in [68]. Based on the winning region, each player could evaluate the analytical construction of the barrier surface to determine the corresponding optimal strategies. The Apollonius circle shows the benefits of analyzing the winning region for players with unequal velocity. Therefore, optimization strategies and winning regions were analyzed in [11].
In addition to the optimal strategies and winning regions of players, there are still some open issues that are worth considering further. For players, the outcome and actual payoffs are important. The actual payoffs of a player should be deducted from the cost. In a realistic situation, the optimization goal is to consider cost in addition to winning the game. Therefore, the problem can be transformed into multi-objective optimization.
5.
Future research directions
In the adversarial differential games, the analysis of players' optimal strategies is based on some ideal conditional assumptions, such as point capture [63], instantaneous heading [8] and full information state [1]. Therefore, there are still some interesting and challenging problems in differential games that are worthy of further exploration, such as open environments, imperfect information, multi-objective regions and kinetic heterogeneity.
5.1. Open environment
Due to the unpredictability of players' circulation behaviors in actual tasks [9], uncertain dynamics of games [69] and multi-stage modeling in an open environment can be considered. Among them, the Markov process can be used to describe more practical, memoryless circulation behavior in the uncertainty dynamics, and the proposed state transition process will be described by a Markov chain. After the end of each stage, the design of the supplementary mechanism for both teams will have an impact on the final results. Therefore, if the number of players is time-varying, it is worth considering the order in which players are allocated between the two teams.
In addition, the situation of modeling multiple stages in a time-varying open environment also exists in practical tasks. For example, we suppose that there are N defenders and M attackers in RA differential games [1]. At each stage, some players from both teams enter the game; then, the remaining players will be supplemented according to the results of the previous stage. That is, if the attackers reach the target region or all attackers are captured by the defenders in the i-th stage, the game ends. As a result, it is worth analyzing what strategies should be adopted by both teams to maximize their payoffs.
5.2. Imperfect information
Adversarial differential games can be used to model real-world situations in robotics, aircraft control, safety and other domains [16]. Regarding these previous works, most of them relied on the full-state information model [33,55]. However, each player may not obtain full-information feedbacks in more practical situations [70,71]. In the cases in which one or more players lack partial information about the games, it is a kind of differential game with imperfect information [72,73]. What is more, there may be imperfect communication between different players during actual tasks (e.g., information about opponents or teammates is sometimes not available) [74,75]. Therefore, if there is cooperation within the team, it is worth analyzing what strategies the players should choose to maximize their payoffs in the adversarial differential games with imperfect information [76].
It is common for defenders or attackers to possess a partial line-of-sight angle [28], that is, the players can only know information about opponents or teammates in their sight. If there is a certain degree of error in the opponent's information, the opposing team may engage in fraudulent behavior [77]. To deal with this situation, the cooperation between teammates and opponents' matchings are challenging problems. Moreover, in a large-scale gaming region, each player cannot know the status information of other players in real time [73]. The mean field games [78] and algorithms can provide a research direction for this situation with imperfect information.
5.3. Multi-objective regions
In the current research on adversarial differential games, there is only one target area [46,49]. In many practical applications, multiple target regions are distributed across the play region [79]. However, the total number of defenders and attackers in each team is limited. It is significant to allocate resources reasonably in each target region to achieve the victory of the game. At the same time, for the attacker or the defender team, the strategy for choosing the local or global victory is different, as it can be transformed into 0–1 integer programming or mixed integer programming for analysis. In addition, there is a certain probability that the attackers will capture the target or reach the target area [80]. Therefore, random games can be chosen to determine the optimal strategy of the attacker in the future.
5.4. Heterogeneity
Some ideal assumptions of velocities have been proposed in the literature [3,8]. For instance, defenders are faster, or all players have the same velocity in multi-player games [16,21]. It is worth mentioning that the velocity of each player is limited by upper and lower bounds in a more practical situation. A general case is to use the average velocity to characterize a player's velocity, not a constant. Furthermore, considering the heterogeneity in system dynamics, such as acceleration and jerk constraints, players could be prevented from changing directions instantaneously in adversarial differential games. If the velocity constraint is applied to players in differential games, the analysis of optimal strategies and winning regions will be an interesting research direction.
5.5. Large-scale networks
Regarding large-scale networks, the network system needs to process massive amounts of real-time data. Therefore, there is competition or cooperation between different network nodes. This problem can be modeled as an adversarial differential game and solved by a mean-field reinforcement learning algorithm. Moreover, in a large-scale gaming region, the state information of all nodes cannot be obtained in real time. The mean field games and algorithms [78] are feasible research directions for this situation with imperfect information.
5.6. Applications
Regarding artificial intelligence, machine learning and deep learning have not been successful enough to solve imperfect information games, such as Texas Hold'em poker. Some scholars have tried to use deep learning and deep reinforcement learning to solve the problem, but the effect has not been satisfactory. However, it can be modeled as an adversarial game to assist decision-making. Artificial intelligence-based analytical methods for differential games can provide a good solution for adversarial problems [52].
Acknowledgments
This work was supported by the Key Project of Science and Technology Innovation 2030 (2018 AAA 0101302), National Natural Science Foundation of China (Key Program: 62136003), the Program of Shanghai Academic Research Leader, China (No. 20 XD 1401300), the China Postdoctoral Science Foundation (Grant 2021 TQ 0107) and Shanghai AI Lab.
Conflict of interest
The authors declare that there is no conflict of interest.









 DownLoad:
DownLoad: