1.
Introduction
Human–computer interaction (HCI) is an interdisciplinary and integrated field of various areas such as service design, computer science, behavioral science, and artificial intelligence (AI). This implies that the focal point of HCI lies in examining and understanding the interaction between people and machines for more usable and reliable systems, as well as functionality of these interactions [1].
In the last two decades, the concept of HCI has been transformed through the sensational impact of data science and artificial intelligence [2]. In line with this trend, numerous researchers in AI, data science, humanities, and biology collaborate with each other. This is not surprising, given that scientific collaboration leverages the intellectual and material resources from different parts of the academic domain [3], which naturally improves the quality, efficiency, and visibility of scientific research outcomes [4].
As mentioned earlier HCI is a field which is interdisciplinary and integrated into various areas. In this sense, we can take an in-depth look into the HCI field and do more productive research using collaborative analysis. Moreover, unlike other single domain research analyzing collaboration within the domain, it is helpful to see core researchers using CNA as HCI has a wide range of applications and domains [5].
Thus, several researchers have attempted to explore collaboration networks of researchers in specific areas [6]. This is because collaboration network analysis (CNA) can be designated as one of the most efficient methods to reveal overall research trends, popular collaboration areas, and key researchers within different clusters [7] and to elucidate the evolution of the collaboration and the mechanisms underlying large-scale real-world networks among researchers [8]. Thus, collaboration networks have been studied extensively, in diverse approaches and from different perspectives, worldwide. Through this method, it is helpful for the development of research to look at core researchers that were not known before.
After the emergence of web and mobile environments in the mid-2000s, HCI such as ubiquitous, virtual reality and haptic became an important research topic also in Korea. Furthermore, HCI has grown with the development of many companies and industries. According to Lee [9], there were only five Korean researchers in the international HCI conference CHI '99. However, in 2014, there were 200 Korean participants ranked fifth among 47 countries. Like this, Korean HCI research is improving now. However, in Korea, few studies have analyzed current trends and collaboration networks of Korean HCI researchers [10]. Thus, this study aimed to analyze the collaboration networks of HCI researchers in Korea, in order to investigate the academic trends and cooperation structures among the HCI researchers. In addition, we suggest the potential future directions of HCI research. The research questions (RQs) considered are as follows:
● RQ1. What is the research trend in HCI publications in Korea?
● RQ2. How extensive is the structure of the collaboration network among HCI researchers in Korea?
By addressing the given RQs, we believe that our study will contribute to
● Administering the first comprehensive and focused study of the scientific collaboration network in the HCI field of Korea;
● Providing insights into the distinct collaboration patterns and the trends of HCI research, based on 243 researchers in 7,155 publications, collected from the SciVal* and HCI Korea Research Directory†; and
*https://www.scival.com/
†http://labs.hcikorea.org/html/interview.html
● Providing the dataset publicly available‡.
‡https://github.com/merry555/ProfNetwork
The remainder of the study is organized as follows. Section 1 provides an overview of the trends and history of HCI research, followed by an examination of previous research on CNA. Section 2 outlines the data collection and methodology used in our CNA. Section 3 discusses the results and limitations of the study. Finally, in Section 4, we present the implications of this study and the scope for future research.
2.
Literature review
2.1. History and trend of global HCI research
The field of HCI originated from "intertwined roots in computer science, cognitive computer graphics, operating systems, human factors, ergonomics, industrial engineering, cognitive psychology, and the systems part of computer science" [11]. HCI has a relatively short history as compared to other areas within human factors; it was only in the late 1970s and the early 1980s that specialists began to consider a professional field of usability and HCI [12]. At the time, the popular topics of HCI research included interactive system development, interface building, user-centered design, and usability testing for computer applications [12]. In 1989, following the introduction of the internet, the main topic areas in HCI evolved into designing for web usability, cost-justifying usability, and computer-supported cooperative work [12]. With the advances in ubiquitous computing in 1999, the main HCI topic areas have been focused on designing for user control and context-sensitive transparency of systems anywhere, anytime model of computing, as well as addressing the challenges inherent in the design and evaluation of such systems [12].
2.2. History and trend of Korean HCI research
South Korea has a relatively short history of HCI research as compared with other advanced countries (e.g., the United States and European countries). However, with the development of information and communication technology, HCI research has developed significantly in both quantity and quality [9].
HCI research in Korea has been conducted mainly through a series of annual conferences held by HCI Korea [13]. HCI Korea is one of the special topic/research groups of the Korean Information Science Society (KISS). The HCI Research Group of the KISS commenced in 1990 as a research group affiliated with the Korea Advanced Institute of Science and Technology (KAIST) AI Research Center. At the time, scholars from various fields (e.g., computer science, cognitive psychology, design, linguistics, industrial engineering, and philosophy), who were interested in graphical user interface (GUI) and multimedia participated in the group. Since the HCI Research Group of the KISS held a symposium in 1991 and began its official activities, the significance of the group has gradually increased. In 2005, the HCI Research Group was officially registered as a corporation and established as HCI Korea [14]. Since then, HCI Korea has held an annual academic conference to promote academic development and interaction among members in the HCI field. It has played the role of a venue to make joint research more active among researchers in various fields [10].
The trend of topics in the HCI Korea conference emerged and accelerated the development of ICT technologies [9]. In the early and the mid-1990s, with the growth of the computer industry, GUI was considered to be one of the most popular research areas, while visual programming, human factors, and information searching were ascertained to be the top research keywords. From the mid-1990s to the mid-2000s, web and mobile environments emerged as important research topics, while Internet-based content, multimedia interaction, and mobile/IPTV appeared as important research keywords. In the mid-2000s, user experience emerged as an important research topic, while major research keywords were ubiquitous, physiological/emotional interface, virtual reality/space, and haptic/touch [14]. In the 2010s, smartphones, augmented reality, and social network services appeared as prominent research keywords. However, in recent years, the Internet of Things, crowd computing, and human computation have emerged as leading research keywords [10].
Subsequently, HCI research has become remarkably and consistently associated with other domains. Comprehending the emergence and influence of HCI research through keywords and topics did not pose a challenge [10]. To this end, the importance of collaborations among researchers from different domains in HCI has been emphasized more than ever [15].
2.3. Collaboration network analysis (CNA)
CNA is a meaningful measurement for exploration of the status and emergence of research collaborations [4]. Hence, CNA was employed to understand the overall research trends, popular collaboration areas, and key researchers within different clusters [7]. Moreover, it was used to explain the evolution of collaboration, and the mechanisms underlying large-scale real-world networks among researchers [8]. Because of this advantage, collaboration networks have been extensively used in various ways for multiple purposes. For example, Lee [16] examined the network of research collaboration based on the resumes and survey results of 443 scholars from a university research center in the United States to examine the impact of collaboration on the outcomes. Cheng [4] examined the collaboration network of Library Hi Tech to identify key researchers and trends in collaboration publications. Larrosa [8] examined the structure of the collaboration network of Argentine economists during 1964 to 2014, to identify key researchers and universities of collaboration. Simultaneously, Higaki [17] explored a collaborative research network set during 2009–2019 in cardiovascular medicine using machine intelligence to identify key researchers.
As aforementioned, there are several studies that investigated collaboration networks with consideration of diverse countries and fields. However, few studies conducted network analyses on Korean HCI researchers. Thus, this study addressed the aforementioned research questions with a network analysis to efficiently examine the collaboration evolution among researchers and to determine the overall trend of Korean HCI research.
3.
Data collection
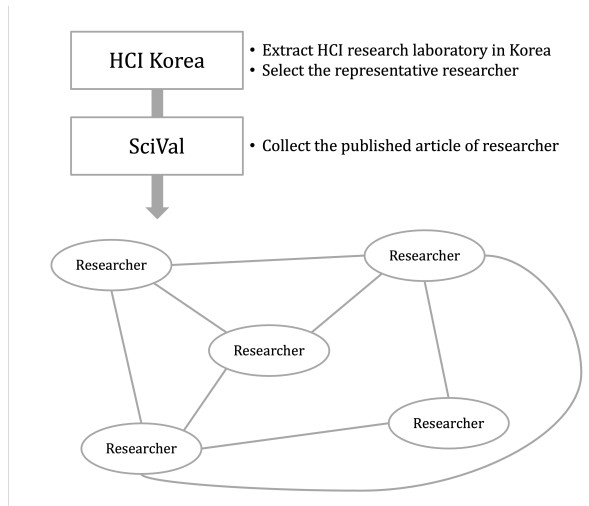
To investigate the collaboration network among HCI researchers in Korea, we identified researchers who are members of HCI Korea. Further, we assimilated the publication information of each researcher in SciVal, a website that provides comprehensive access to the research performance of over 20,000 research institutions, and their associated researchers from 230 countries worldwide. Specifically, we listed the Korean representative HCI laboratories and professors and among them, we sampled the research lists from each researcher. To collect the data of researchers, we had to know the affiliation of each researcher. Also, by obtaining the affiliation information, we can analyze the main affiliation which actively conducts HCI research and its detailed information about the key researchers.
As a result, we obtained the information of a total of 243 HCI Korea members and their corresponding publications (7,155; Category: articles) in the set duration of 2010 to 2019.
When building our collaboration network, nodes represent researchers and the edges represent the number of co-associative relationships between two specific researchers. The example of data collection and network building is on Figure 1.
4.
Methods
Centrality analysis is one of the most important approaches for identifying key researchers in collaboration networks [4]. Centrality measures typically include degree centrality, closeness centrality, betweenness centrality and PageRank. Thus, we used the centrality approach to conduct an analysis of our collaboration network of HCI Korea researchers.
4.1. Degree centrality
Degree centrality is defined as "the number of edges incident upon a node" [18]. It is amongst the most rudimentary centrality measurements. It is evaluated using the number of edges connected to a node in a graph structure. In a weighted graph, degree centrality is calculated as the sum of the weights associated with the nodes. A node obtains a higher degree centrality when it has a greater number of edges connected to the other nodes in the network. Equation 4.1 is as follows:
where n is the number of nodes in the network, and i and j are nodes that are directly linked [19]. In collaboration networks, degree centrality indicates significant researchers who are connected with other researchers. The higher degree centrality indicates the greater productivity of researcher and higher connectivity with other researchers.
4.2. Closeness centrality
Closeness centrality, introduced by Bavelas [20], measures the importance of a node based on its proximity to other nodes in the network. Closeness centrality is calculated using the total length of the paths between a node and all other nodes in a network. A node obtains a higher closeness centrality, if the total length between itself and all other nodes in the network is shorter than the length of the other nodes. (Equation 4.2), Cc(ni) is the closeness centrality and d(ni,nj) is the distance between two nodes in the network: (Equation 4.2):
Distance d is defined as the shortest path which is the path with minimum number of edges. In social networks, closeness centrality is used to understand the importance of a specific researcher and to measure their influence on the entire collaboration network [21].
Thus, a specific researcher with a higher closeness centrality can be considered to have a broader range of influence over the entire collaboration network.
4.3. Betweenness centrality
Betweenness centrality measures the importance of a specific node, based on how much a given node is in-between other nodes in the network [22]. A node with a greater betweenness centrality has a considerable influence within a network as it controls the passing of information between other nodes. This metric is assessed by the number of shortest paths that pass through a node [8]. The metric is calculated as follows: (Equation 4.3):
where gjik is all geodesics linking node j and node k, which passes through node i, and gjk is the geodesic distance between nodes j and k. Here, geodesic distance indicates the number of edges between the two nodes.
In collaboration networks, the betweenness centrality of a specific researcher shows their impact in bridging two separate research groups in the network. This implies that researchers with a greater level of betweenness centrality can manage and initiate collaborations among researchers in different research fields [23]. Thus, the greater betweenness centrality was explained by greater interdisciplinary collaborations of researchers [4].
4.4. PageRank
The term PageRank was first introduced by Page and Brin, who attempted to explain the level of authority a particular page holds, through the topological structure of a web [24]. PageRank treated the web as a graph, with pages as vertices, and links between the pages as edges. The ranks of the pages were determined by the sum of the ranks of their backlinked pages. Hence, nodes with a higher total of significant (direct) neighbors had a higher PageRank. This metric is determined as follows: (Equation 4.4):
Here, N is the total number of pages on the web, d is the damping factor, C(pi) is the out link of pi, and pi is the number of in-links of p. It is iterated until all vertices are assigned stable PageRank values.
In our collaboration network, researchers and the number of collaborations between two specific researchers were denoted by vertices and edges, respectively. A researcher was awarded a greater PageRank when they collaborated with a greater number of influential researchers. Through PageRank, the importance of a researcher can be calculated based on the number of their influential collaborators [4].
4.5. Interpretation of measures
We applied different types of network measure to find the main researchers from various points, while each measure indicates unique characteristics of researchers. Rather than simply comparing the number of documents, we can learn the academic characteristics of researchers through the network analysis measures. Among the 4 different measures, degree centrality and closeness centrality mainly indicates the individual researcher's academic productivity and influence in the HCI. betweenness centrality and pagerank mainly focus on the researcher's academic collaboration and significant relationship with other researchers.
4.6. Network analysis
We conducted two-stage analyses. First, the trends in HCI publications were observed. Specifically, we considered the number of annual publications of the members of HCI Korea across the years, based on affiliations and keywords. Second, a CNA using the employed centralities—PageRank, degree, closeness, and betweenness centralities—was performed.
5.
Results
5.1. Overall trends of HCI in Korea
5.1.1. Distribution of publications
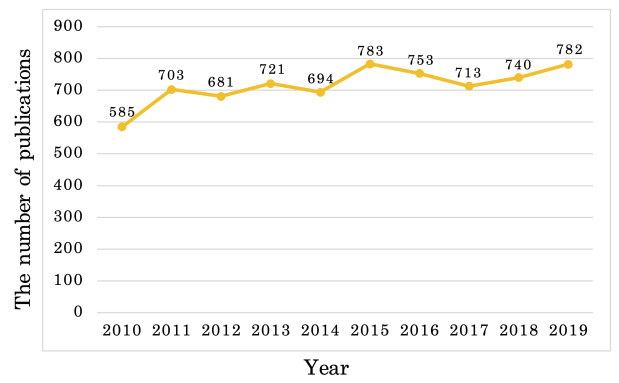
We conducted a descriptive analysis of 7,155 publications, retrieved from SciVal over the last decade (2010–2019). As shown in Figure 2, the highest number of publications (783) were published in 2015, while the annual average number of publications was 715.50 (SD = 57.60).
We also analyzed the researchers' affiliations (Table 1). The results indicated that the KAIST was the most productive affiliation, with 1,189 publications (16.61%) in the decade considered, followed by Sungkyunkwan University (SKKU; 673, 9.40%) and Seoul National University (SNU; 526, 7.35%).
Table 2 shows the top 30 productive researchers, based on the number of publications. Professor Joonki Paik, who is affiliated with Chung-Ang University (CAU), ranked first (218 publications). His research area generally focuses on cultural content, graphics, game and human–robot interaction. Professor Sukhan Lee of robotics, affiliated with SKKU, ranked second (162 publications). His major research interests were user robotics, computer vision, human–robot interaction and AI. Professor Kyujin Cho of mechanical engineering at SNU, ranked third (152 publications). His research is focused on haptics, tangible display, and soft robotics.
5.1.2. Trend of keywords
Table 3 displays the major keywords and their frequencies. The results show the keywords with high frequencies including 'haptics', 'augmented reality', and 'touch'. Early researchers in HCI Korea leaned towards 'multi-touch' interaction in diverse environments. After 2015, other emerging topics, such as 'gesture', 'text entry', or 'object detection', were considered. Moreover, several studies on 'augmented reality', 'object detection', and 'convolutional neural network' (CNN) were recently conducted.
5.2. Network of collaboration
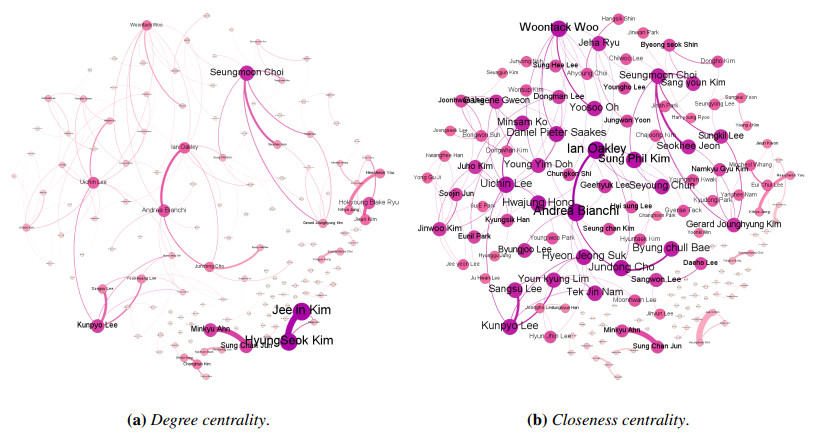
Table 4 lists the top 30 researchers as per the results of degree centrality (DC) analysis. The results indicated that Professor Jeein Kim and Professor HyungSeok Kim (DC: 36), who are with Konkuk University (KKU), have the highest degree centrality. The main areas of their research were wearable device/cognitive computing/communication, and augmented reality/virtual reality/3D modeling, respectively. Professor Seungmoon Choi of computer science (DC: 27), who is affiliated with Pohang University of Science and Technology (POSTECH), ranked third. His research interests were haptics, virtual reality, and tactile perceptions.
Table 5 presents the summary of the closeness centrality (CC) analysis. Professor Ian Oakley of human factors and ergonomics at Ulsan National Institute of Science and Technology (UNIST; CC: 282.416 * 10−3) has the highest closeness centrality. It indicates that he can be largely influential to other researchers and his research areas are wearable, haptics, and tangible user interfaces [25,26]. Professor Andrea Bianchi (279.674 * 10−3), who is affiliated with KAIST, ranked second. His major research interests were wearable, haptics, and augmented reality [27,28]. Professor Sungphil Kim (259.573 * 10−3), who is affiliated with UNIST ranked third. His research focuses on haptics, cognitive engineering, and voice.
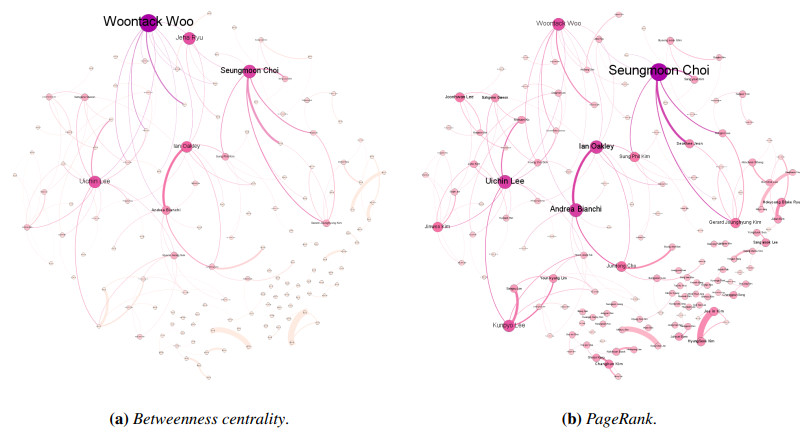
In the case of betweenness centrality (BC), as shown in Table 6, Professor Woontack Woo (BC: 17.82 * 10−2), affiliated with KAIST, has the highest betweenness centrality. He is academically cooperative researcher and his main research interests include augmented reality, interaction design, and wearables [29]. Professor Uichin Lee at KAIST ranks second (13.60 * 10−2). His research focuses on user experience and interactive computing. Professor Seungmoon Choi at POSTECH whose main research interests include haptics [30], ranks third (12.48 * 10−2).
In the case of PageRank (Table 7), Professor Seungmoon Choi (2.728*10−2) shows the highest values, while Professors Andrea Bianchi (2.253*10−2) and Ian Oakley (2.178*10−2) are also considered. It can be said that Professor Seungmoon Choi was collaborative with influential researchers.
6.
Discussion and conclusion
The current study aimed to analyze the collaboration networks of HCI researchers in Korea from 2010 to 2019, to gain an insight into the academic trends and structure of cooperation in South Korean HCI society. First, we determined the trends of research topics in HCI through an analysis of the distribution of HCI publications in the last ten years (2010–2019). Second, we studied the network structure of researchers in HCI Korea by identifying key researchers through a network analysis. We employed a dataset extracted using SciVal for this purpose. The dataset included 243 researchers and 7,155 publications from 2010 to 2019.
We organized the dataset into a collaboration network comprising 163 edges and 143 nodes. Further, we computed the degree centrality, closeness centrality, betweenness centrality, and PageRank, using this network, and identified the top 30 researchers.
With regards to the first research question, we discovered that the number of HCI publications has increased over the past 10 years. In terms of numbers, KAIST was the most productive affiliation, while Professor Joonki Park from CAU, was the most productive researcher.
In addition, as a result of the keyword analysis, we identified keywords related to 'haptic', and 'touch', such as 'touch', 'tactile display', 'touch screens', and 'multi-touch', to be the popular research topics over the years. Starting from 2019, 'CNN' and 'object detection' emerged as new major topics.
Similarly, with regards to the second research question (Figure 3 and Figure 4), we discovered that Professors Jeein Kim and HyungSeok Kim (CAU) ranked first in terms of degree centrality, followed by Professor Seungmoon Choi (POSTECH, Figure 3a). In the case of closeness centrality, Professor Ian Oakley (UNIST) ranked first, followed by Professors Andrea Bianchi (KAIST) and Sungphil Kim (UNIST, Figure 3b). In terms of betweenness centrality, Professor Woontack Woo (KAIST) ranked first, followed by Professors Uichin Lee (KAIST) and Seungmoon Choi (POSTECH, Figure 4a). In the case of PageRank, Professor Seungmoon Choi (POSTECH) ranked the first, followed by Professor Andrea Bianchi (KAIST) and Ian Oakley (UNIST, Figure 4b).
Although several researchers were not listed among the most productive researchers (Table 2), such as Professors Andrea Bianchi, Jeein Kim, and HyungSeok Kim (KKU), they were included in the lists of other network analyses.
The findings of this study have several implications. First, as previously stated in the introduction, only a few studies have analyzed the current trends and collaboration networks of Korean HCI researchers with domestic publications [10]. In contrast, this study contributes to the trends and collaborations with HCI Korea researchers by considering their international publications. Second, one of the notable findings of this study was the identification of key researchers made possible using the CNA, which were otherwise not evident from the results of the most productive researchers.
One of the main findings is that we identified the latest trends in South Korean HCI research. Through our findings, future researchers will be able to conduct follow-up HCI research that reflects trends by referring to our research results. This could eventually contribute to the latest HCI technology advancements. According to our research results, HCI research has undergone the following evolutionary process: In research that encompasses one-dimensional simple device operation including keywords such as haptic and touch, the scope of human interaction has been expanded including keywords such as gesture. In recent years, application of machine learning and deep learning technologies have been shown in the field of HCI.
Although the current study afforded several pertinent findings, several limitations remain. Primarily, we only considered researchers who were registered as members of HCI Korea for our CNA. There may be other researchers who have conducted active research in the field of HCI but were not registered as members of HCI Korea. Thus, future studies should consider these limitations to extend the findings of the current study. Despite these limitations, it is obvious that our study has made a methodological contribution to domain-specific regional collaboration network analysis. Our data analysis approach can be used in other domains or regions that our analysis framework would become an interesting contribution that can help researchers gain insights in different research areas.
Acknowledgements
This study was supported by the Research Program funded by the SeoulTech (Seoul National University of Science and Technology).
Conflict of interest
The authors declare there is no conflict of interest.
Appendices









 DownLoad:
DownLoad: