1. Introduction
Vehicles powered by hydrogen fuel cells are slowly finding their way to market; the Toyota Mirai and Honda Clarity are available for lease in several locales. This is an encouraging sign that hydrogen may be primed to play an increasingly important role in satisfying our energy needs. Owing to its flammability, vital to any use of hydrogen as a fuel is its safe storage. Among the various methods for the safe storage of hydrogen that hold potential viability, absorption of hydrogen in transition metals or alloys has received a great deal of attention. Studies of the absorption and desorption of hydrogen by transition metals and alloys date back over a hundred years [1,2]. The ability of certain transition metals and alloys to absorb large amounts of hydrogen has led to realized energy-related applications, such as the use of metals and alloys as hydrogen purification membranes [3], and potential energy-related applications, such as the aforementioned use of the metal or alloy as a fuel storage medium in vehicle applications [4].
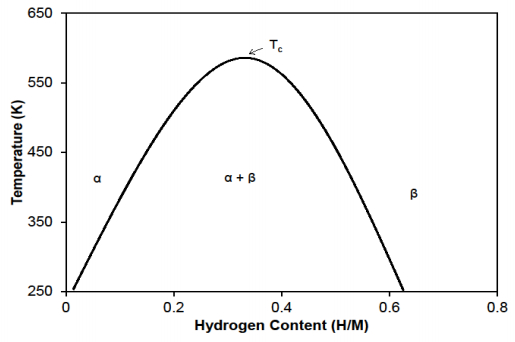
One feature of many of the transition metals and alloys that have a large capacity to absorb hydrogen is that they undergo a transition from a dilute solution of hydrogen to a dense solution of hydrogen upon absorbing hydrogen. This transition is thermodynamically reversible upon desorption of hydrogen. The dense solution of hydrogen in the metal matrix is often referred to as a hydride phase. Depending on the temperature at which hydrogen absorption/desorption occurs, the transition between dilute solution and hydride can be continuous or discontinuous, though above Tc the dense solution is often referred to as the αphase to emphasize the continuous nature of the hydrogen absorption/desorption process. This is nicely illustrated by the palladium-hydrogen (Pd-H) system, the phase diagram for which is shown in Figure 1.
In the Pd-H system, the α phase is the dilute solution while the β phase is the hydride. Tc is the critical temperature of the (α + β) two-phase coexistence region. If the α ➔ β and/or β ➔ α transition occurs above Tc, the transitions occur in a continuous fashion with no abrupt volume change in the Pd matrix. If, however, hydrogen absorption/desorption occurs below Tc, the transitions are discontinuous owing to the abrupt volume change in the Pd matrix that occurs as the two-phase region is traversed. For example, the volume difference between the α phase and the β phase at 298 K is ~11% [5].
The abrupt volume change that occurs when a two-phase coexistence region is traversed in a metal-hydrogen (M-H) system often results in cold working of the metal matrix [6]. Along with an increase in the strength and hardness of the metal, the cold work results in varying degrees of embrittlement [6]. The Pd-H system is particularly susceptible to hydrogen embrittlement. Several authors of the current study have carried out a thorough characterization of the hydrogen embrittlement in Pd [7]. In that study, the generation of dislocations during the discontinuous transitions between the α and β phases was identified as the primary factor leading to pronounced embrittlement. In most, if not all, applications of M-H systems, the occurrence of hydrogen embrittlement is detrimental to the long-term use of these materials. Significant effort has been brought to bear on identifying metallic systems that are resistant to hydrogen embrittlement, such as the palladium-silver alloy system [8].
Though Pd suffers significantly from the effects of hydrogen embrittlement, the metal can be returned to a near defect-free state by appropriate thermal treatment that facilitates recrystallization and recovery. Recrystallization and recovery of a plastically deformed metal involves conditions (annealing temperature, annealing duration, annealing environment) that allow a significant reduction in the dislocations in the metal matrix [9]. The ability to effectively and efficiently reverse the effects of hydrogen embrittlement is, in many ways, an exercise in recycling valuable (and often expensive) materials that are important not only in the field of hydrogen energy but also in many other areas of science and technology where hydrogen plays a role.
Given the fact that hydrogen causes embrittlement in Pd and other metals, it may seem counterintuitive that the presence of hydrogen during annealing of a cold-worked metal may accelerate recovery to a less brittle state. However, several studies have found that the presence of hydrogen can enhance thermal recovery of cold-worked palladium. Goltsov et al. have shown that the presence of hydrogen during annealing results in perceptible enhancement of the recovery of mechanically deformed Pd [10]. In another interesting investigation, Gol'tsova and Zhirov showed that the presence of hydrogen during annealing of β-phase Pd (see Figure 1) results in the material having greater ductility (less embrittlement) than annealed Pd that was never exposed to hydrogen [11]. These results certainly provide strong preliminary evidence that hydrogen is effective in aiding in the recovery of cold-worked Pd. The present study nicely complements the previous work and reports the results of the recovery of palladium that was cold-worked by passage through the two-phase region of the Pd-H system. The present study uses an interesting combination of techniques to investigate the hydrogen-assisted recovery of cold-worked Pd-mechanical property measurements and hydrogen solubility measurements.
2. Materials and Methods
Palladium (99.9% total purity) foil (Alfa-Aesar, Ward Hill, MA, USA) of 0.25 mm thickness was used in this study. These foils were unidirectionally cut into 38.1-mm-long by 6.4-mm-wide specimens. A reduced section of 3.2-mm width was machined into each specimen that was used for tensile testing. Specimens were lightly abraded with fine emery paper, then chemically polished in a 2:2:1 volume mixture of H2SO4:HNO3:H2O, followed by liberal rinsing, in an ultrasonic cleaner, with distilled water and then acetone. All specimens were then stress relieved in vacuo at 723 K for 48 h, followed by a 24 h annealing in vacuo at 823 K. These annealing temperatures were high enough to allow recovery of each specimen to a nearly defect-free state, as evidenced by hydrogen solubility measurements. Several of the fully annealed specimens were set aside for use in the subsequent solubility and mechanical test investigations.
The remaining fully annealed Pd specimens were cold-worked by dosing to saturation with the protium isotope (1H) of hydrogen at 323 K (i.e. complete traversal of the (α
+ β) two-phase coexistence region). Upon reaching hydrogen saturation, specimens were evacuated at 323 K for 24 h to remove the absorbed hydrogen. Several of the fully cold-worked specimens were set aside for use in subsequent solubility and mechanical test investigations.
For Pd specimens that were used to measure the dilute phase solubility of hydrogen, pressure-composition isotherms were determined using an all-stainless steel system of calibrated volumes. The temperature of the specimen chamber of the system was maintained by either a regulated water bath or computer-controlled furnace. Hydrogen gas pressures were measured with MKS diaphragm gauges with a tolerance of +/– 0.001 torr. The hydrogen content (expressed as the H/Pd ratio) of the specimens was determined by means of the Ideal Gas Law from changes in the hydrogen gas pressure. More specifics details of the solubility measurements are given in the Results and Discussion section.
For specimens intended for tensile and microhardness testing, respective samples of fully cold-worked Pd specimens were subject to 24 h annealing at 50 K increments from 523 K to 673 K; one regime of annealing was carried out in vacuo, another regime under a hydrogen pressure of 1.33 × 104 Pa (100 torr), and yet another regime under a hydrogen pressure of 6.67 × 104 Pa (500 torr). In the case of the annealing treatments done under a hydrogen pressure, the hydrogen was not introduced until the annealing temperature was reached and, after 24 hs at the annealing temperature, the hydrogen was evacuated at the annealing temperature for two hs followed by cooling to room temperature. All hydrogen exposure treatments were carried out in the above-mentioned all-stainless steel system of calibrated volumes. The temperature of the specimen chamber of the system was maintained by either a regulated water bath or computer-controlled furnace. Hydrogen gas pressures were measured with MKS diaphragm gauges. The evacuation of hydrogen was carried out via a vacuum system composed of a HyVac two-stage pump (HyVac Products, Pottstown, PA, USA). Following each annealing treatment, respective specimens underwent tensile testing using an Instron Series Ⅸ Automated Materials Testing System (Instron Corporation, Norwood, MA, USA) using a constant elongation rate of 1.27 mm/min. Specimens used for microhardness testing were subjected to a series of polishings culminating in a 0.05 micron alumina polishing. Vickers microhardness tests were performed on a LECO Microhardness Tester (LECO Corporation, St. Joseph, MI, USA) using a load of 100 g.
3. Results and Discussion
3.1. Solubility results
Hydrogen solubility was measured at 323 K to monitor the recovery of Pd that had been previously cycled through the α ➔ β and β ➔ α phase changes (i.e. fully cold-worked) at 323 K. As indicated in the experimental section, hydrogen solubility is measured via pressure-composition isotherms. These isotherms are determined by carrying out a series of hydrogen doses of progressively increasing pressure and, during each dose, allowing the Pd to absorb hydrogen until equilibrium is reached. The amount of absorbed hydrogen is determined from the difference between the hydrogen dosing pressure and the hydrogen equilibrium pressure. The hydrogen content is then plotted versus the square root of the equilibrium hydrogen pressure. The square root of the equilibrium hydrogen pressure is used owing to the fact that the diatomic H2 molecules dissociate to atomic hydrogen during the absorption into the Pd matrix.
Respective samples of Pd specimens were annealed in vacuo or in the presence of 500 torr hydrogen at 523 K for 24 h. At 523 K, the pressure of hydrogen employed during annealing was less than that which would result in formation of the hydride (β) phase. For those specimens annealed under hydrogen, all hydrogen was removed at 523 K followed by cooling to room temperature. These treatments were followed by determination of the aforementioned 323 K pressure-composition isotherms.
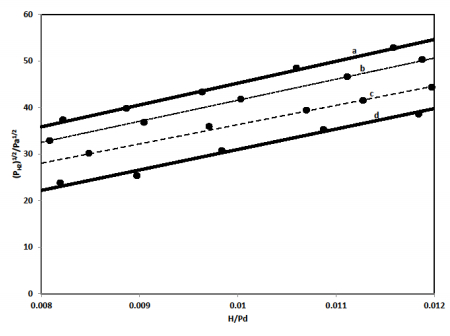
A portion of a representative set of 323 K pressure-composition isotherms is shown in Figure 2 where the H content (the H/Pd ratio) is plotted versus the PH21/2 (square root of the equilibrium hydrogen pressure). As can be seen in Figure 2, there is a perceptible difference in dilute-phase hydrogen solubility between the vacuum-annealed Pd (curve c) and Pd annealed in the presence of hydrogen (curve b). As is clear from Figure 2, at a given equilibrium hydrogen pressure the solubility is lower in the Pd annealed in hydrogen versus that annealed in vacuo. For example, the solubility corresponding to an equilibrium PH21/2 of 35 Pa1/2 is ~0.0092 (H/Pd) for hydrogen-annealed Pd and ~0.0097 (H/Pd) for vacuum-annealed Pd. For comparison, pressure-composition isotherms are shown for fully annealed Pd (curve a) and fully cold-worked Pd (curve d).
It has been shown that hydrogen solubility can be a sensitive probe for many changes that occur to the metal matrix of metal-hydrogen systems. Changes in hydrogen solubility have been used to detect such phenomena as order-disorder transitions and metal atom segregation in metal-hydrogen systems [12,13]. Hydrogen solubility has also been shown to be a sensitive probe for the dislocation stress fields which can be introduced into palladium as a result of cold-work, including that due to the α ➔ β and/or β ➔ α hydride phase changes. This is because hydrogen dissolves reproducibly but to different degrees in well-annealed and fully cold-worked Pd [14,15]. Studies have shown that dilute-phase (i.e. α phase) solubility increases as the dislocation density increases due to hydrogen trapping in the dislocation stress fields and thus the solubility of cold-worked Pd is greater than the solubility in defect-free Pd [16]. This is certainly shown in Figure 2 when the solubility of fully annealed Pd is compared to that of fully cold-worked Pd.
So a tell-tale sign that recovery is occurring in Pd should be a decrease in dilute phase solubility due to the elimination of dislocations during annealing. The present results bear this out. As mentioned earlier, included in Figure 2 are the dilute phase solubility of fully annealed Pd and Pd fully cold-worked (i.e. cycled through the (α + β) coexistence region with no further annealing treatment). As can be seen, annealing in vacuo and in 500 torr hydrogen at 523 K both result in a measure of recovery. The solubility of both annealed samples are less than the solubility of fully cold-worked Pd. The figure also shows that the degree of recovery is not equal to that resulting from full annealing as described in the experimental section. When comparing the solubility of cold-worked Pd that has been annealed in vacuo to that annealed in the presence of an appropriate pressure of hydrogen (a pressure that does not cause the Pd to enter the (α +
β) coexistence region), our results show that annealing in the presence of hydrogen appears to facilitate a greater degree of recovery than annealing in vacuo.
It can be concluded that there is a small amount of recovery of cold-worked Pd by annealing for 24 h at 523K, as monitored by hydrogen solubility. The degree of this modest recovery appears greater in hydrogen-annealed Pd than in vacuum-annealed Pd. The effect is small and could not be detected by TEM since the samples annealed under both conditions have very large dislocation densities. This would not be the first time that hydrogen solubility is a more sensitive probe than other techniques. In studies on order-disorder transitions in palladium-manganese alloys, hydrogen solubility measurements showed evidence of the transitions under conditions where the more traditional techniques of electron diffraction and electrical resistivity measurements did not [12].
3.2. Strength and hardness results
Encouraged by the hydrogen solubility results, a more rigorous investigation was carried out utilizing changes in the mechanical properties of palladium. Stress-strain tests and Vickers microhardness tests were carried out on fully-annealed and fully cold-worked specimens of Pd to establish the extremes of mechanical properties. In addition, these tests were carried out on fully cold-worked Pd specimens exposed to recovery annealing treatments as described in the Experimental section. In particular, fully cold-worked Pd specimens were subjected to 24 h annealings at 523 K, 573 K, 623 K, and 673 K. One set of anneals was done under vacuum, one under 100 torr hydrogen, and one under 500 torr hydrogen. From the stress-strain tests, the ultimate strength, yield strength, and total elongation (i.e. elongation at failure) of each specimens was determined.
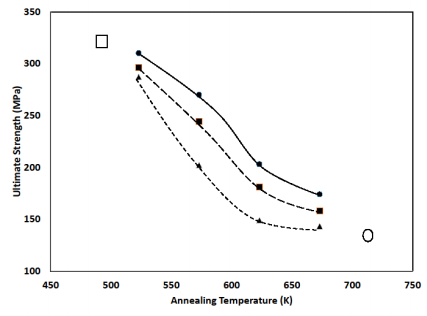
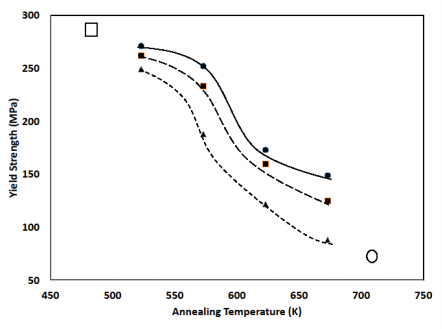
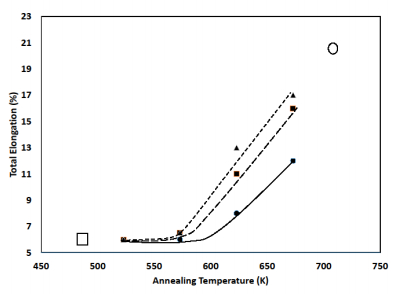
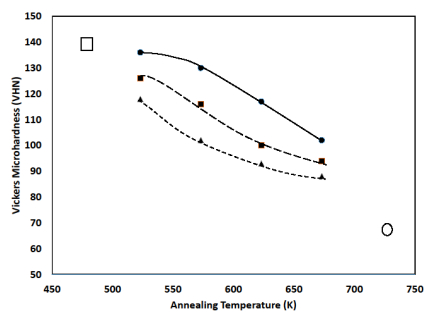
Figures 3–6 show the ultimate strength, tensile strength, total elongation, and Vickers microhardness, respectively, as a function of annealing temperature. For comparison, the values of these mechanical properties for fully-annealed and fully cold-worked Pd are included in each figure. Several features stand out in these figures.
First, under all annealing environments a measure of recovery takes place. As can be seen in the figures, the values of strength and microhardness are lower than the corresponding values of fully cold-worked Pd. As expected, the higher the annealing temperature, the higher the degree of recovery; the strength and microhardness values steadily decrease toward the value for fully-annealed Pd as the annealing temperature increases. Initially elongation appears to be less sensitive to annealing environment than strength and hardness but eventually the elongation increases toward the value for fully annealed Pd as the annealing temperature increases.
Second, the results make clear that the presence of hydrogen during annealing does affect the degree of recovery experienced by cold-worked Pd. With the exception of elongation values at 523 K, at each annealing temperature the degree of recovery under 500 torr hydrogen is greater than the degree of recovery under 100 torr hydrogen, which in turn is greater than the degree of recovery in vacuo. The results indicate that there is little, if any, discernable synergistic effect between annealing temperature and hydrogen pressure.
Finally, the results show that the conditions covered in the present study do not result in a recovery back to a fully annealed state. It would be interesting in any future studies to extend the temperature range covered during annealing, along with altering the annealing time, to optimize the conditions required to return cold-worked Pd to its fully annealed state in the presence of hydrogen.
The current results are consistent with the findings of Goltsov et al. that hydrogen can be an effective agent in enhancing the recovery of cold worked palladium [10]. Hydrogen's ability to aid in the recovery of cold worked palladium may provide a more effective and efficient way, as compared to annealing in vacuo, to extend the usefulness of palladium in applications where the Pd experiences the deleterious effects of embrittlement that accompany cold working. Also, it would be interesting to see if hydrogen has a similar effect on other transition metals and alloys that suffer hydrogen embrittlement.
What may be causing the observed results? Hydrogen has been found to cause metal atom mobility under conditions where such mobility is effectively absent under identical conditions in vacuo. Such hydrogen-induced metal atom mobility has been observed in several palladium-based alloy systems such as palladium-manganese alloys [12] and palladium-rhodium alloys [13]. Examples of hydrogen's ability to affect the mobility of dislocations in nickel and iron have been known for some time now [17,18]. Deutges et al. have shown that hydrogen has a measurable effect on the dislocation density in cold-worked palladium, though their study involved cold-rolling of palladium specimens while containing dissolved hydrogen [19]. In the cases of palladium-manganese and palladium-rhodium, it is thought that the expansion of the metal matrix that results from the absorption of hydrogen contributes to the enhancement of the mobility of metal atoms allowing them to diffuse to their thermodynamically stable positions more rapidly than in the absence of hydrogen [20]. Fukai has found that the generation of large amounts of palladium vacancies during hydrogen exposure at temperatures and hydrogen pressures much higher than the present study enhances palladium mobility [21]. Whether the generation of lattice vacancies plays a role under the conditions of the present study was not investigated. Through the mechanism of lattice expansion and the weakening of the distance-dependent London Dispersion Forces between the palladium atoms, crystal defects, such as dislocations, which affect the mechanical properties of the metal may be eliminated and the changes in mechanical properties, such as embrittlement in the case of Pd, due to these defects can be reversed. In the case of the Pd-H system, the presence of small amounts of hydrogen during annealing and the accompanying slight expansion of the palladium matrix may provide enough of a thermodynamic driving force for a degree of dislocation annihilation via enhanced Pd mobility that is lacking in the absence of hydrogen during annealing. It is crucial that the presence of hydrogen during annealing of Pd not cause the Pd-H system to enter the (α + β) two-phase coexistence region so that the volume expansion due to hydrogen absorption does not occur discontinuously. If the system does enter the (α + β) two-phase coexistence region any hydrogen-enhanced recovery would be more than offset by embrittlement due to the dislocations generated by the discontinuous volume change from the dilute solution α phase to the dense β hydride phase. Even at temperatures above the critical temperature (Tc) of the (α + β) two-phase coexistence region care should be taken with regard to the amount of hydrogen present during annealing in attempts to enhance recovery of Pd. Several authors of the present study have shown that absorption of significant amounts of hydrogen by Pd above Tc will result in hydrogen embrittlement, though not nearly as pronounced as the embrittlement that results at temperatures below Tc [7].
4. Conclusion
We have provided evidence that the changes in the mechanical properties of palladium caused by the cold-work that occurs when there is a discontinuous conversion between the α and β phases of the palladium-hydrogen system can be reversed by annealing at temperatures greater than 523 K. By varying the annealing environment to include modest pressures of hydrogen, the degree of recovery of cold-worked palladium can be enhanced compared to annealing in vacuum. The hydrogen-enhanced recovery increases as the hydrogen pressure during annealing increases, though care must be taken to avoid hydrogen pressures that would cause the palladium matrix to incur the formation of the β hydride phase during annealing. Dilute phase hydrogen solubility has been shown to be an effective, albeit indirect, probe for detecting the thermal recovery in cold-worked palladium and can distinguish the presence of hydrogen-enhanced recovery. More directly, the determination of strength, elongation and hardness of recovered palladium has shown quantitatively that hydrogen during annealing does allow for greater thermal recovery of cold-worked palladium. The problem of hydrogen embrittlement has been a bane to the effective use of metals and alloys in many areas of science and technology. The current results are encouraging in that they provide compelling evidence that the very same hydrogen that causes embrittlement may provide an effective tool in more efficiently recycling embrittled metals and alloys.
Acknowledgements
The authors wish to thank the Petroleum Research Fund of the American Chemical Society for financial support of this research.
Conflict of Interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: