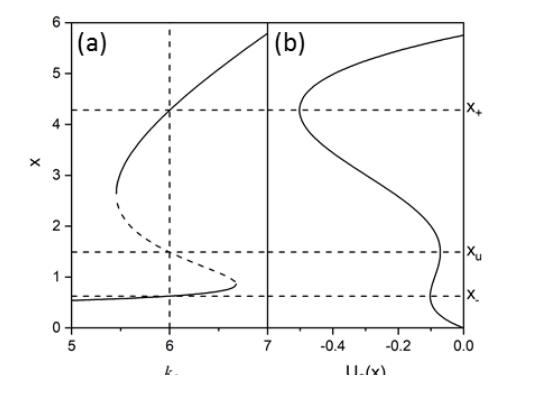
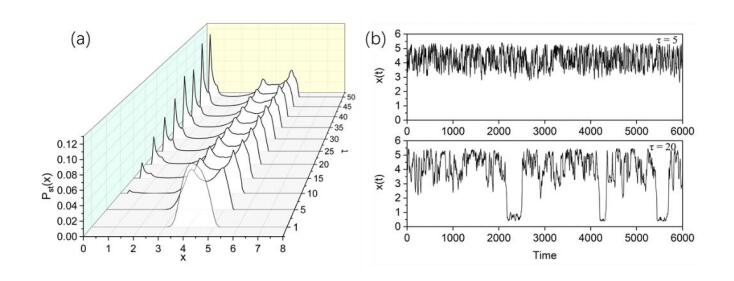
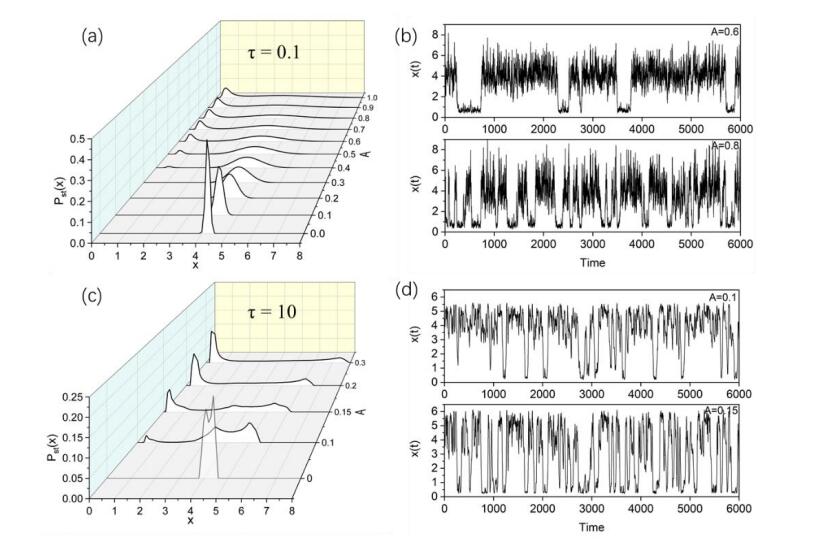
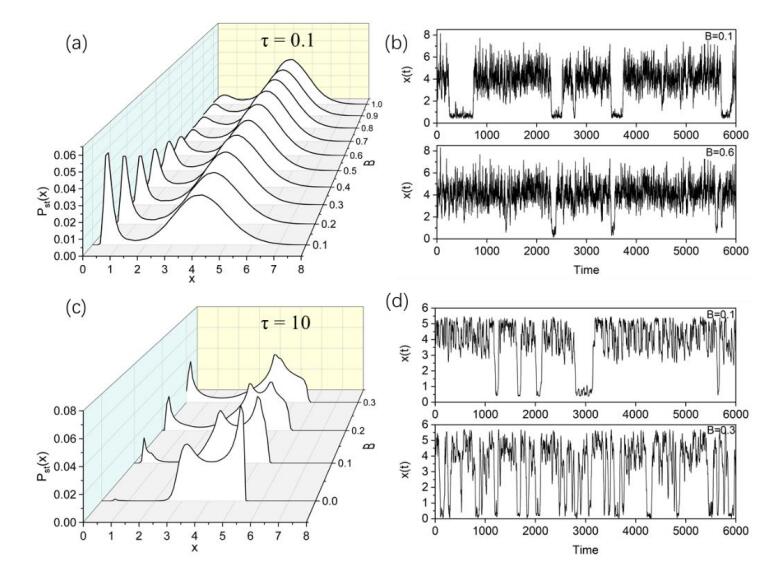
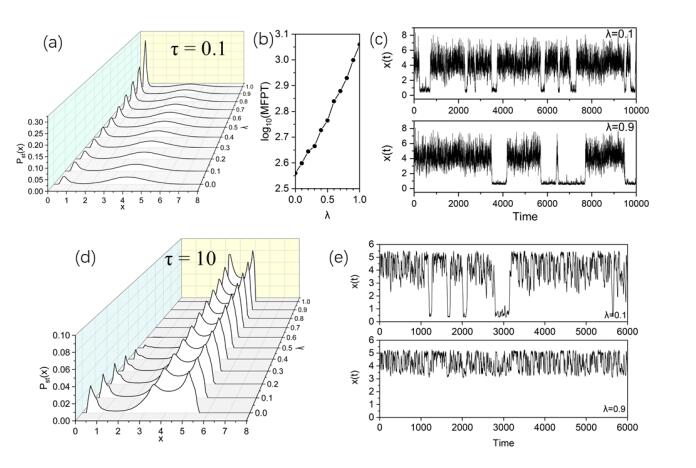
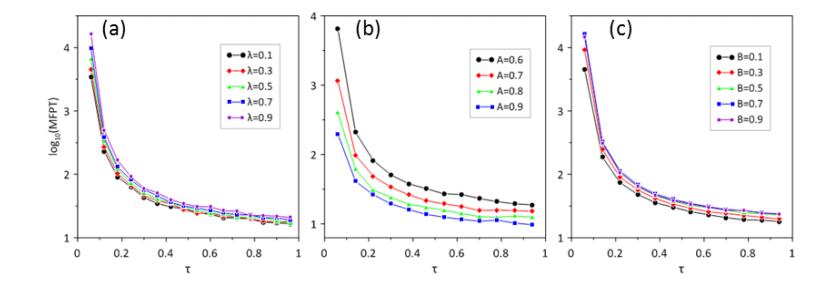
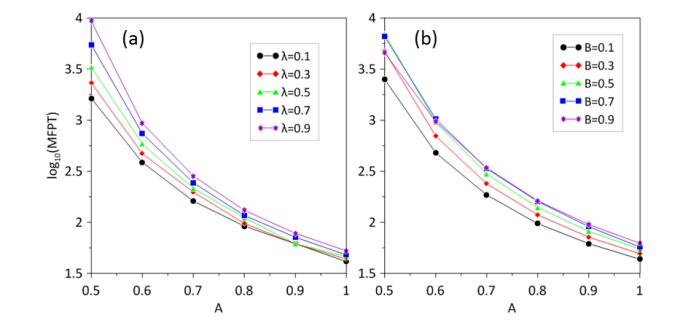
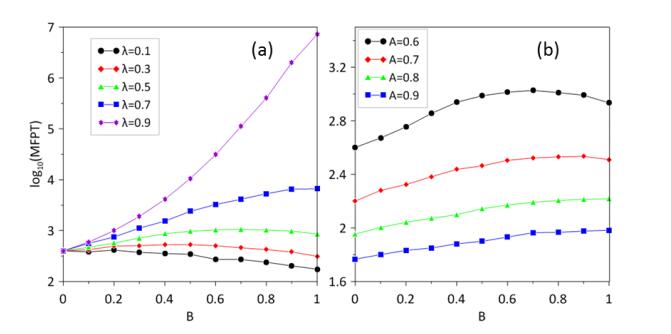
We studied fluctuation-induced switching processes in the gene transcriptional regulatory system under cross-correlated sine-Wiener (CCSW) noises. It is numerically demonstrated that the increase of the multiplicative noise intensity A and cross-correlation time τ in CCSW noises can reduce the concentration of the TF-A monomer and switch to an "off" state. In addition, when the cross-correlation time τ is small, the increase of the additive noise intensity B leads to a switch of the process from "off"→"on". Simultaneously, the increase of the cross-correlation intensity λ of CCSW noises contributes to maintaining the current state. When the cross-correlation time is large, the high concentration state has two peaks and the stationary probability distribution presents a three-peak structure.
1.
Introduction
Highly sensitive marine clays, termed quick clays, pose a serious threat for large landslides causing huge material damages, costs, and in worst case, loss of lives. The brittle behavior of quick clays causes these landslides to develop fast and expand very far. In the last decade construction work has caused several quick-clay landslides in Norway, such as the landslide leading to the collapse of the Skjeggestad bridge in 2015, and the landslide at Sørum in 2016 where three people were killed. The most densely populated areas and best farmland in Norway are situated on thick marine deposits in the Eastern part and Mid-Norway where the largest quick-clay deposits are found. Great emphasis is made on inhibiting quick-clay landslides from being triggered by human actions or natural causes.
Quick clays are found in Scandinavia, Canada, Alaska and northern Russia, and are sometimes referred to by Canadian authors as Leda and Champlain clays. In Norway, quick clays are defined by a remolded shear strength (su, remc) of less than 0.5 kPa [1]. Understanding its behavior is crucial when designing infrastructure development and landslide mitigation measures. An estimated cost for landslide mitigation in quick-clay areas in Norway is of the order of 2.5 billion NOK [2]. With a high pressure on property development and infrastructure projects in these areas, cost effective and sustainable methods to inhibit quick-clay landslides from being triggered is needed. Clays are electrochemically very active. Increased knowledge on the impact of geochemistry on quick-clay behavior may aid in developing new and effective ground improvement methods in general and methods for quick-clay landslide mitigation in particular. This paper presents the mineralogy, geochemical and geotechnical properties of the quick clay at the research site Dragvoll in Trondheim, Norway.
2.
Research site Dragvoll
2.1. Geological history
Norwegian soils are young, deposited during the Pleistocene-Holocene transition. Norway was completely covered by the ice cap during the Weichsel era, with the exception of a few islands. During the ablation, the ocean followed the regressing glacier front. Consequently, grinded bedrock flour was deposited in seawater. Glacio-marine deposits cover the mainland of Norway up to the altitude of the marine limit. The marine limit is defined as the maximum sea level after the last ice age related to todays' altitude. Along the coastline, the marine limit is some tens of meters above present sea level, with increasing altitude towards the maximum of the ice thickness, which was in Bottenviken, Sweden. Oslo has the highest marine limit in Norway at 222 m.a.s.l., and in Trondheim, the marine limit is found at 175–180 m.a.s.l. [3,4].
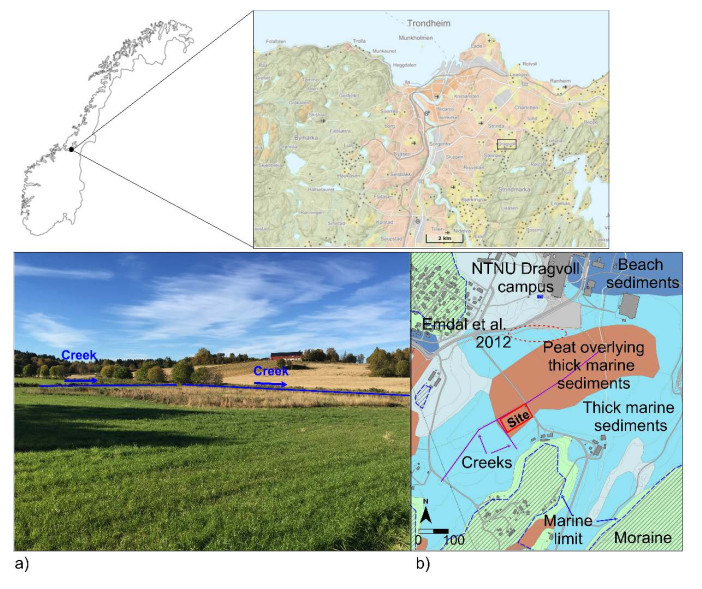
The research site Dragvoll is located in a relatively flat area at around 156 m.a.s.l., which is slightly below the marine limit (Figure 1). At the time of deglaciation (ca. 11,500–10,500 years before present (BP)), the fjord coveredmost of the area, and the glacier front was located approximately 1 km east of the Norwegian University of Science and Technology (NTNU) Dragvoll campus [7]. The fjord 10,500 years BP was at the level which now is 160 m.a.s.l. Beach sediments were accumulated at the NTNU Dragvoll campus area and west of the site (dark blue area in Figure 1b). At this time, the location of the research site Dragvoll was covered with brackish water, where tides from the fjord were flowing in and out of the area from the north. Because of the rapid deglaciation following the Younger Dryas era, the rate of the isostatic uplift increased, and the shoreline elevation was lowered by an average 6 cm per year over the next millennium. For several centuries, the area was covered by a fresh-water lake within the thresholds in north and west. The lake drained towards north, through the sand and gravel deposits and in the period 8900–8400 years BP, the area turned into a swamp. Some 5000 years BP the bog or peat stage started. Traces of cultivation are dated back to around 2500 years BP.
Today, the area is used as farmland, and the topsoil is drained to small creeks next to the site to the north and west side (Figure 1a). Peat was not found on the site, but wet areas (peat) are still present in the eastern part of the marked brown area in Figure 1b, and directly west of the site. Today, the glaciomarine sediments are around 50 m thick [7] located in between outcropping bedrock at distance in the small hills on the northwest and southeast side of the site. A previous study, [5], characterizes the clay at a site (red dashed-lined ellipse in Figure 1b) in a distance of about 300 m south-east of the research site described herein (red rectangle in Figure 1b).
2.2. Source of material
The glacial and post-glacial clays of Scandinavia, eastern part of Canada, Alaska and northern Russia are mostly physical weathering products (also chemical weathering products may be present) from when the glacier grinded the bedrock during the last ice age [8]. Therefore, marine glacial and post-glacial clays normally have small amounts of clay minerals. Detrital primary minerals dominate Norwegian clayey soils.
The clay mineralogy in Norwegian clays mainly consist of low-active (non-swelling) illite and chlorite [9,10,11,12]. Illites and chlorites are net negatively charged because of isomorphous substitution. Isomorphous substitution means that the cations in the tetrahedral and octahedral sheets are replaced by metal ions of lower valence [13 amongst others]. The surplus net negative charge is balanced by adsorbing positively charged ions (cations) to the mineral surface. Due to the electrochemical activity of clay minerals, the chemistry in the depositional and post-depositional environment greatly affects the geotechnical properties.
2.3. Depositional environment and post-depositional processes
The Norwegian glacial and post-glacial clays were accumulated in a marine environment with a salt content of 30–35 g/L [14,15]. Due to the high salt content, the clay minerals flocculated in an open structure accommodating high water content and entrapped seawater in the large voids [16]. Isostatic uplift elevated the clay deposits above sea level, and the clays were exposed to leaching by meteoric groundwater flow.
Clay minerals are net negatively charged, and the surface charge is compensated for by accumulating an equivalent amount of cations from the pore fluid to reduce the surface charge to a minimum [17]. The adsorbed cations are often referred to as counter-ions. The negative surface charge and the counter-ions together with water form the electric diffuse double layer (DDL) around the particles. Clay particles surrounded by pore water of low ionic strength have thicker DDLs than clays with pore water of high ionic strength. The larger DDL thickness, the larger repulsion between the clay particles, and the easier the clays are to remold.
The electrical potential is at its highest at the mineral surface, decaying from the surface to the free pore water [17]. The DDL thickness is considered as the distance from the clay mineral surface to the center of gravity of the decaying electric potential. Electrolyte concentration and composition affects the size of the electrical potential, thus also the DDL thickness. Clays with low salt content (low electrolyte concentration) in their pore water have higher electric potential at the surface and a slower decay of potential with distance to the surface than clays with high salt contents in their pore water. Hence, low-saline clays have larger DDL thicknesses and are easier to remold than high-saline clays.
Valence and hydrated radius of the cations also affects the DDL thickness at low salt contents. If the same type of clay is suspended into two different electrolytes of the same concentration, but with cations of different valence, the clay suspended in a monovalent solution will have a larger DDL thickness than clays suspended in a divalent solution [17]. This is a result of higher ionic strength. Potassium (K+) having a smaller hydrated radius than sodium, allows it to approach the negatively charged mineral surface closer than Na+, thus suppressing the DDL further than Na+.
After leaching has diluted the salt content in a glaciomarine clay deposit, the DDL thickness increases. As a consequence the electrostatic repulsion between the clay particles increases, causing the clays to liquefy when remolded [18]. Quick clays normally have salt contents of less than 2 g/L [19,20], and at salt contents of less than 1 g/L they may even behave as a liquid when remolded, depending on the ion composition in the pore water [8,14,18,21].
The major cations, sodium (Na+), potassium (K+), magnesium (Mg2+) and calcium (Ca2+), are the most commonly found cations in the pore water in marine clays. As sodium is the abundant cation in seawater, sodium is normally the abundant cation in the pore water and on the clay mineral surfaces in marine clays not heavily leached. In groundwater, calcium (Ca2+) and magnesium (Mg2+) are normally the abundant cations [15]. Leaching groundwater dilutes the salt content and feeds the clay-water system with Ca2+ and Mg2+, which both have higher affinity than Na+. Thus, the clay mineral surfaces adsorb Ca2+ and Mg2+, and release Na+ from the clay mineral surfaces into the pore water. This ongoing ion exchange taking place between the continuously changing pore water and the clay mineral surfaces, is the reason why Na+ is still the abundant cation in the pore water in quick clays [14].
After several thousands of years, of unceasing leaching, a strange feature may be seen. A quick clay may with time cease to be quick. This happens when leaching almost totally depletes Na+ in the clay-water system. As Na+ being practically removed from the clay-water system, the concentration of cations of greater impact on suppressing the diffuse double layer increases in the pore water and the clays cease to be quick [14,21,22,23]. When the KMgCa-ratio (equation given in Table 1) exceeds as little as 20% (all concentrations in equivalents), the repulsive forces between the clay particles decreases so that the clays render non-quick with a remolded shear strength above 1 kPa [24].
To find the ion composition in the pore water in the Dragvoll quick-clay (Table 1), clay samples were centrifuged and pore water extracted and filtered. The ion composition was determined from ion chromatography. The Dragvoll clay is heavily leached with a salt content in the pore water of only 0.6–0.7 g/L. Sodium (Na+) and chloride (Cl-) are the abundant ions in seawater [15]. Very little chloride (Cl-) remains in the Dragvoll clay from the seawater at time of sedimentation; 0.3 meq/L compared to about 566 meq/L in seawater [15]. Sodium is still the abundant cation (85–92%) in the electrolyte remaining from the time of deposition, while as a result of leaching freshwater, bicarbonate (HCO3-) is the abundant anion.
2.4. Distribution of quick clay over the site
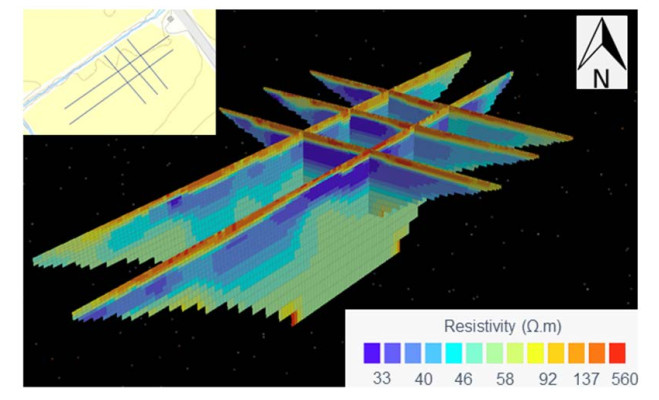
Mapping of the quick-clay extent over the site was done by electrical resistivity tomography (ERT) profiling. Conductivity, the reciprocal of electrical resistivity, and pore-water salinity are closely related. Marine clays with high salt content are more conductive than low-saline quick clays. Therefore, ERT is considered useful as part of landslide risk assessments in quick-clay areas [25,26]. Resistivity values in the range of 10–100 Ωm (conductivity 10–100 mS/m) may indicate quick-clay deposits [27].
Three 40 m and two 80 m long ERT profiles with electrode spacing of 0.5 m and 1.0 m were conducted at Dragvoll [28] with penetration depths of 7.2 and 15.6 m respectively (Figure 2). The surveys were carried out using a 12-channel Terrameter LS recording unit [29], with the multiple gradient array acquisition protocol [30]. The model resistivity distribution was obtained by inverting the raw data with the software RES2DINV [31].
Resistivity cone penetration tests (RCPTU) were conducted to correlate with the ERT vertical sections, and for interpreting the geotechnical properties on the site. A resistivity module, with slightly larger diameter than the probe, connected behind the conventional CPTU, allows collecting conventional CPTU data as well as providing resistivity data with depth. The resistivity module consists of four ring electrodes with 5 cm spacing and measures resistivity as an average over 20 cm (Wenner-α array [32]).
The ERT resistivity corresponds well with the resistivity measured with RCPTU. Underneath a thin weathered top layer (dry crust) of about 1 m thickness, the resistivity decreases to around 50 Ωm, typical for leached clays, and this layer may therefore be interpreted as quick clay. The clay within the measured profiles seem to be homogenous, extending deeper than the penetration depth of 15 m (Figure 2).
3.
Composition, mineralogy and fabric
3.1. Composition and mineralogy
Clays in Mid-Norway are normally silty. At the Dragvoll site, shells and shell fragments, and gravel, are commonly found in the upper 4 m, and are also occasionally found at greater depths. Quick clay is encountered at around 3.5 m depth. The clay deposit is interbedded with millimeter thick silt and sand layers found with a few centimeters spacing. These closely spaced silt/sand layers increase to a thickness of 1–2 cm at around 7.5–8.0 m depth. The clay content (<2 µm) determined from hydrometer tests is of the order of 34–41%. The X-ray diffraction analysis (XRD) showed a bulk mineralogy dominated by the non-clay minerals quartz and albite [33]. In the clay-size fraction, the clay mineralogy is dominated by illite (Table 2). In contrast to the mineralogy of the clay-sized fraction, the amount of illite and chlorite in the bulk mineralogy is quite similar with slightly larger fractions of illite. This may be caused by higher fractions of chlorite in the silt and sand fraction.
The size of the surface charge is reflected by the cation exchange capacity (CEC) in meq/100 g dry soil. Non-swelling minerals such as illites have smaller CEC than swelling minerals such as vermiculites, which have exchangeable hydrated ions in their interlayer positions. The degree of crushing and weathering, bedrock origin, depositional and present physio-chemical environment, present isomorphous substitutions, amongst others, all affects the CEC. Therefore, CEC is presented in wide ranges in several textbooks, i.e. [34]. Glaciomarine clays of low activity (non-swelling), commonly found in Scandinavia, have small specific surface areas, thus low CECs [35]. Therefore, the specific surface area and CEC, may be small [8,35] compared to reported ranges for clay minerals of diagenetic origin as reported in Grim [34]. For three Norwegian very sensitive illitic-chloritic clays, CEC is reported in the range of 9–11 meq/100 g dry soil at clay contents of 42–44% [36], and for Quebec chloritic-illitic clays, CEC is reported in the range of 6–17 meq/100 g dry soil in clays with clay contents of 30–83% [37].
Analysing the CEC for the Dragvoll clay caused some challenges. For illites, [34] report specific surface areas in the range of 65–100 m2/g when the CEC is in the range of 10–40 meq/100 g dry soil. At Dragvoll, the specific surface area of the clay minerals, determined by the nitrogen (N2) adsorption analysis (BET), is much lower, in the range of 18.3–27.8 m2/g. In [24] CEC was determined by fully saturating clay specimens with strontium prior to running X-ray fluorescence (XRF) analysis of both major and trace elements. Larger CECs than expected for Scandinavian detrital clastic clays were found; around 25 meq/100 g dry soil, most probably due to the calcite present. In the fall of 2018, a new attempt to determine the CEC was carried out by first saturating clay specimens with NaOAc-NaCl, which replace the adsorbed ions on the mineral surface with Na+. After that Na+ was replaced by Mg2+ by extracting the specimens with Mg(NO3)2 [38,39]. Applying this procedure, the CEC for the Dragvoll clay was determined to be in the order of 6.3–7.7 meq/100 g dry soil.
3.2. Fabric
Clay minerals flocculated in a marine environment orient themselves in a complex edge-to-edge and edge-to-face lattice. The agglomerates of flocculated particles with large water-filled voids form a "house-of-cards" like fabric with both clay and silt particles in the matrix [16,40]. At high salt contents, the repulsive forces between the clay particles in the "house-of-cards"—like fabric are small, and the structure is strong. Leaching dilutes the salt content, increases the repulsion between the clay particles and the "house-of-cards" easily collapses when disturbed. In remolded quick clay, the large repulsion between the clay particles cause the particles to be dispersed in the low-saline expelled pore water.
Undisturbed, quick clays have large pores. However, in clays the pore spaces may not necessarily be well hydrodynamically interconnected. Clays have low permeability inhibiting advective transport. Nevertheless, entrapped pores may be available for molecular diffusion [41,42,43], which may aid transport of chemical agents improving geotechnical properties in the clay volume. In saturated clays, the entire volumetric porosity may be considered available for diffusion, often referred to as the water-filled effective porosity (εw). The geometry of the pores influences the velocity of molecular diffusion, and must be determined to be able to calculate the effective diffusion coefficient for the soil matrix.
The geometry of the pores may be described by the formation factor. The formation factor (F) is defined as the ratio between the electrical pore-water conductivity (σw) and the electrical soil conductivity (σt) as the electrical current travels along the same path as the pore-fluid. This is, however, not the case in clays as their surfaces are charged, and F in clays is therefore not so easily determined. Archie's law [44] may also be applied for determining F (Eq 1).
Archie's law is valid for spherical particles. Clay particles are, however, more like plates. The higher values of exponent m, the less spherical are the grains. A rather high m (2.5–5.4) may account for the plate shaped particles [45,46,47,48]. In the Dragvoll clay with an average volumetric porosity (equivalent to εw) of 0.51, an exponent m of 2.6 and F of 5.6 were estimated from PHREEQC [49] simulations of solute transport [50].
4.
Geotechnical properties
4.1. Index properties
High quality mini-block samples were extracted from the quick clay from 4 m to 8 m depth. Mini-block samples are downsized Sherbrooke block samples with a diameter of approximately 16 cm and a height of 25–30 cm. For further description of the mini-block sampler, see [51]. Water content (w), density (ρ), Atterberg limits, fall-cone undrained (su) and remolded shear strength (su, rem) [52] were determined on samples from 4.0–4.3 m, 4.7–5.0 m, 5.7–6.0 m and 7.7–8.0 m depth within 24 hours after extraction from the ground to delimit storage effects.
Quick clay is encountered at around 3.5 m depth at the site. The quick clay is very soft and highly sensitive, with a fall-cone undrained shear strength (su) of 8–16 kPa. The remolded shear strength (su, rem) is of 0.5 kPa at 4 m depth, and decreases to less than 0.1 kPa at 5 m depth (Table 3). From 4 m depth to 8 m depth, the plastic limit (wP) decreases from 18% to 15%. The liquid limit (wL) of 21–24%, also decreases with depth and is much lower than the natural water content, which is typical in highly sensitive quick clays. The quick clay is of low plasticity with a plasticity index (IP) of 4.4–6.3%, and the liquidity index (IL) is in the range 3.4–4.3.
4.2. Engineering properties
The pore pressure and hydraulic conductivity were measured in BAT standard filter tips [54] installed at 6 m depth. The weathered top soil (dry crust) responds relatively quickly on precipitation. Open boreholes and the wells installed at the site showed that the ground water table fluctuates between 0.5 m and 1.0 m depth below the terrain depending on the amount of precipitation. Based on the measurements, the pore pressure is assumed to be hydrostatic over the site.
Inflow tests were executed in the installed BAT filters, and the in-situ hydraulic conductivity (k) was determined by Hvorslev's equation [54]. The k is measured over a screen of height 3.5 cm, with contribution from both horizontal and vertical flow. In the quick clay at 6 m depth, the in-situ k is of about 2.3 × 10-10 m/s. The in-situ k was smaller than the vertical hydraulic conductivity (kv) determined from the CRS tests. At in-situ overburden effective stresses, kv is in the range of about 1.4 × 10-9 m/s. Interpreting kv from CRS tests carried out on small specimens, may however not be representative. Natural variations in the soil may also cause this difference as the installation depth of the filter tip and the CRS tests do not coincide. In addition, installing the BAT filter may remold the clay surrounding the filter tip. Consequently, in-situ k may have been measured on reconsolidated clay with slightly lower permeability, thus lower hydraulic conductivity.
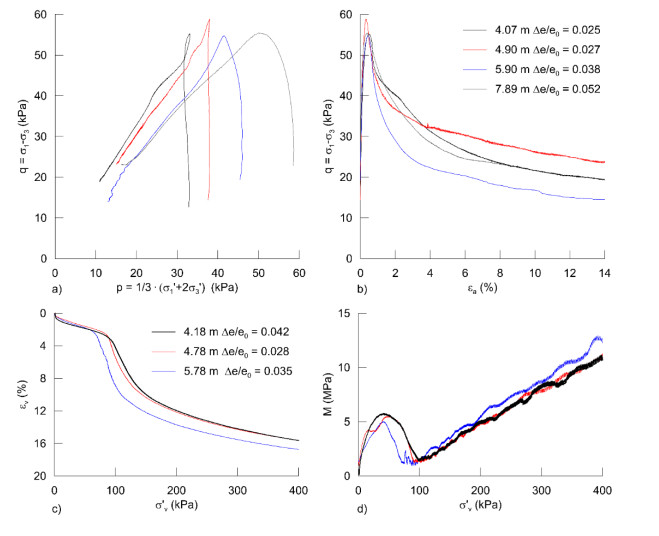
Constant rate of strain oedometer tests (CRS) and anisotropically consolidated, undrained compression triaxial tests (CAUC) were conducted on all samples. The CRS tests were conducted with a strain rate of 0.75%/hr. The CAUC samples were anisotropically consolidated to the best estimate of their overburden stresses applying a coefficient of earth pressure at rest (K0) of 0.7 at all depths regardless of OCR. Such high K0 was chosen to avoid the imposition of higher shear stresses than foun in-situ during consolidation. The samples were consolidated for approximately 16 hrs before applying a backpressure of 250 kPa, and left to rest prior to shearing at a strain rate of 1.5%/hr. The quality assessment of the tests is based on the difference in void ratio from the start of the test (e0) to the void ratio at an in situ effective overburden stress (Δe/e0)
[53]. The quality of the CAUC and CRS tests were all of "very good to excellent quality" (Δe/e0 < 0.04 at OCR 1–2), except from the CAUC from 7.89 m depth and the CRS from 4.18 m depth, which were of "good to fair quality".
The triaxial tests (CAUC) show that the quick clay has a contractive and very brittle behavior (Figure 3), typical for highly sensitive low-plastic quick clays. During loading the stress path increases until peak-shear strength (suC). At further loading, the strength decreases rapidly. This post-peak strength is lower than suC. In the Dragvoll quick clay, the suC is in the range of 28–30 kPa, reaching the suC at strains (εa) of 0.3–0.5% (Table 3). The angle of friction is in the range of 26–35o, and the attraction 1–6 kPa, which are common values in Norwegian medium soft clays.
The site is located close to the marine limit. Even so, the clay is slightly overconsolidated with an overconsolidation ratio (OCR) of 2.2 at 4.2 m depth, decreasing to 1.2 at 5.8 m depth. The apparent preconsolidation stress (σ'p) is interpreted based on [55]. At loads exceeding the σ'p, the deformations increases rapidly. This rapid collapse of the structure is similar to the one seen in the CAUC tests. The oedometer modulus (MOC) in the overconsolidated range is slightly higher in the top than deeper down in the investigated profile; 5.5 MPa and 5.0 MPa respectively (Figure 3). Normalized M/suC is in the range of 179–196, within common values for Norwegian clays of 100–200. The coefficient of consolidation at in-situ sress is in the range of 13–23 m2/yr, which are typical for medium soft clays.
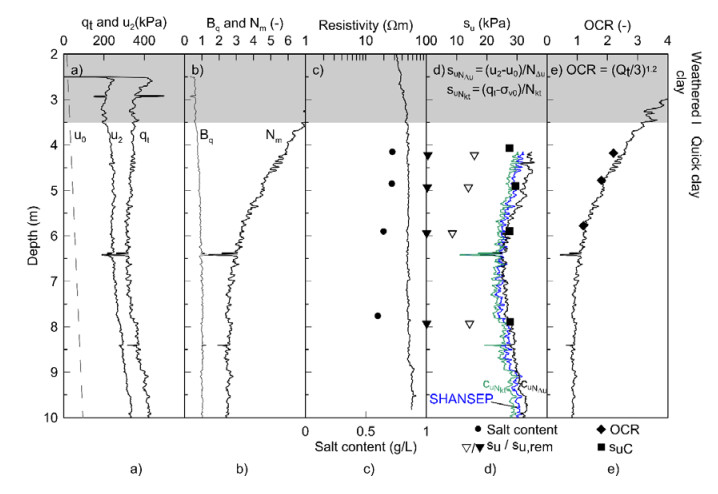
CPTUs are commonly used in Norway for interpreting engineering properties in clays. The RCPTU in the Dragvoll quick clay was carried out with a 5 tons GeoTech CPTU Nova probe with a tip area of 10 cm2 [56] measuring the uncorrected tip resistance (qc), uncorrected sleeve friction (fs), pore pressure behind the cone (u2) and the conductivity of the soil (σt). Several interpretation models may be used for interpreting engineering properties from CPTU data. In Figure 4 the correlations made for Norwegian clays [57] are applied (Eqs 2–11):
where α is the area factor of the cone, qt is the corrected cone resistance, qn is the net tip resistance, a is the attraction, Bq is the pore-pressure parameter, Nm is the normalised tip resistance, N∆u is the bearing factor for excess pore-water pressure, Nkt is the bearing factor for net tip resistance, Qt is the cone factor, and su, N∆ and su, Nkt are the shear strength based on bearing factors N∆u and Nkt.
The Bq is around 1 in the quick clay, and the Nm decreases, commonly seen in highly-sensitive quick clays [58]. The shear strength and OCR profiles correspond well with the laboratory determined properties, as well do the SHANSEP su profile (Eq 12).
The interpreted OCR from the RCPTU data was applied (Eq 8). At 7.89 m depth, the OCR is assumed to be 1, and the α = suC/σ'v0 = 0.38. By applying a constant m of 0.75, there is a reasonable fit between the suC determined from the CAUC tests and su, SHANSEP (Figure 4d). For further details, see [59].
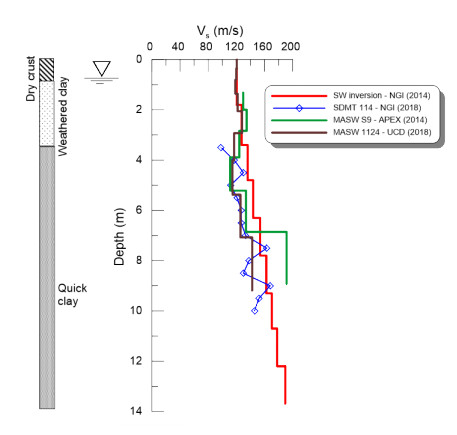
Characterization of the stress-strain behavior of soils is an integral part of many geotechnical design applications, including site characterization, settlement analysis, seismic hazard analysis, site response analysis and soil-structure interaction. The shear modulus (G) of geomaterials is highly dependent upon strain level. The small-strain shear modulus (Gmax) is typically associated with strains in the order of 10-3% or less. With information of Gmax, the shear response at various level of strain can be estimated using published modulus reduction curves (i.e. G/Gmax). According to elastic theory, Gmax may be calculated from the shear wave velocity multiplying the density of the soil (ρ) with the shear wave velocity squared (vs2). In situ vs profiles have been measured by MASW at the Dragvoll site by [60,61], and repeated in 2018 by University College Dublin (UCD). In addition, a seismic dilatometer test (SDMT) was carried out by NGI on the site fall 2018. The SDMT vs determination is a true interval test as there are two receivers spaced at 0.5 m above the DMT blade. When a shear wave is generated at surface, it reaches first the upper receiver, then, after a delay, the lower receiver. The delay between the two seismograms acquired by the two receivers is determined. vs is obtained as the ratio between the difference in distance between the source and the two receivers and the delay from the first to the second receiver [62]. All four profiles give more or less identical results of vs (Figure 5). L'Heureux et al. [61] summarized vs profiles measured on clay sites in the Trondheim area. The Dragvoll profiles falls at the lower boundary of the test results, suggesting that the Dragvoll clays are amongst the softest in the region.
5.
Engineering solutions for building in quick-clay areas
Norway is a country with mountains and fjords. The agricultural land is along the fjords, below the marine limit. This is where most people live. This is where cities, roads and railways are built, and also where the quick clays may be found. The most serious risk when doing construction in such areas is related to large, progressive landslides. Historically a majority of such slides are unfortunately initiated by construction activity. The costs of necessary actions to ensure safe solutions and safe construction may be enormous. In some cases favorable projects for the society are not considered cost-beneficial and must be cancelled.
Terrain levelling are commonly used landslide-mitigation measures in quick-clay slopes with marginal safety. Height differences are reduced to improve the stability. Unfortunately this is tremendously expensive and reshapes the natural terrain dramatically. Ground improvement by lime cement columns may serve as an alternative avoiding large interventions to the terrain. The lime-/cement increases both the strength and stiffness, and the method is commonly used for improving soft clays such as quick clays. But the installation method may induce excess pore pressures, which may temporarily reduce the slope stability, and they are costly. Therefore, lime-/cement piles are not ideal for improving slope stability in natural quick-clay slopes. Moreover, the production of lime and cement cause large climate-gas emissions. As part of the Norwegian commitment to the Paris agreement, Norway is required to reduce the climate gas emissions substantially during the next decade.
A third alternative for reducing the risk of having large quick-clay landslides may be using salt wells. The idea is simply to remedy the effect of leaching and get the salt back into the clay. The purpose is to make the quick clay not quick again. In order to use such a method effectively, it is important to understand the diffusion process, the geochemistry with cation exchanges and the corresponding change in strength and stiffness of the clay. During the 1960s and 1970s, several studies were carried out to increase the knowledge on how geochemistry affected the geotechnical properties in Norwegian quick clays. For decades nothing more was done until recently, e.g. [24]. This study aims to contribute the understanding of how changed pore-water chemistry affects the geotechnical properties in quick clays. Salt wells filled with potassium chloride were installed at the quick-clay research site Dragvoll. The ultimate goal of the research was to investigate whether installation of wells filled with potassium chloride would serve as an effective landslide-mitigation measure or not. The study concluded that retrogressive landslides may be inhibited, and the risk for progressive landslides may be reduced treating quick clays with potassium chloride. The effect is considered permanent in an engineering time-scale. To realize the salt-well method, a new research project "Stabilising quick clays using salt (SAK)" (2018–2019) has been initiated on NGTS Flotten—Tiller, Trondheim to find careful installation procedures to avoid excess pore pressures. The feasibility of four different installation procedures will be evaluated based on monitored pore pressures during and after installation, cost-benefit analysis and calculations of climate-gas emissions.
6.
Summarizing comments
Low plastic, highly sensitive quick clays are found in Scandinavia, Canada, Alaska and northern Russia. Quick clays are very brittle, collapsing at loads exceeding peak-shear strength with a significantly reduced post-peak strength. Clays are electrochemically very active. Changing their pore-water chemistry entails changed geotechnical properties. Therefore, understanding the chemical impact on clays behavior aids developing new ground improvement methods that may also serve as landslide mitigation measures. This paper present geochemical, mineralogical and geotechnical data of a Norwegian quick-clay site, aiming to provide valuable data necessary for developing efficient new ground-improvement methods for highly sensitive quick clays. In broad terms knowledge from Dragvoll can be added to knowledge from other sites when it comes to typical features of clay chemistry and characteristics of Norwegian quick clays.
Acknowledgments
Site investigations and laboratory work was carried out as part of the head authors PhD study at Norwegian University of Science and Technology (NTNU). Professor Emeritus J.K. Torrance (Carleton University), associate professor A. Emdal (NTNU) and V. Thakur (NTNU) are acknowledged for their valuable discussions and advice on the study. The authors express their sincere gratitude to all colleagues and personnel involved in the work at the site and in the laboratories at NTNU, University of Oslo, Norwegian Public Roads Administration, Norwegian Geotechnical Institute and Norwegian Geological Survey. Anders Lindgård (NGI) is acknowledged for carrying out the SDMT and Andrew Trafford (UCD) for carrying out the MASW fall 2018. Financial support from the research program "Natural hazards: infrastructure for floods and landslides (NIFS)" made this study possible.
Conflict of interest
All authors declare no conflicts of interest in this paper.









 DownLoad:
DownLoad: