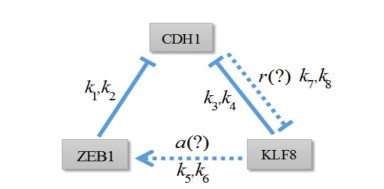
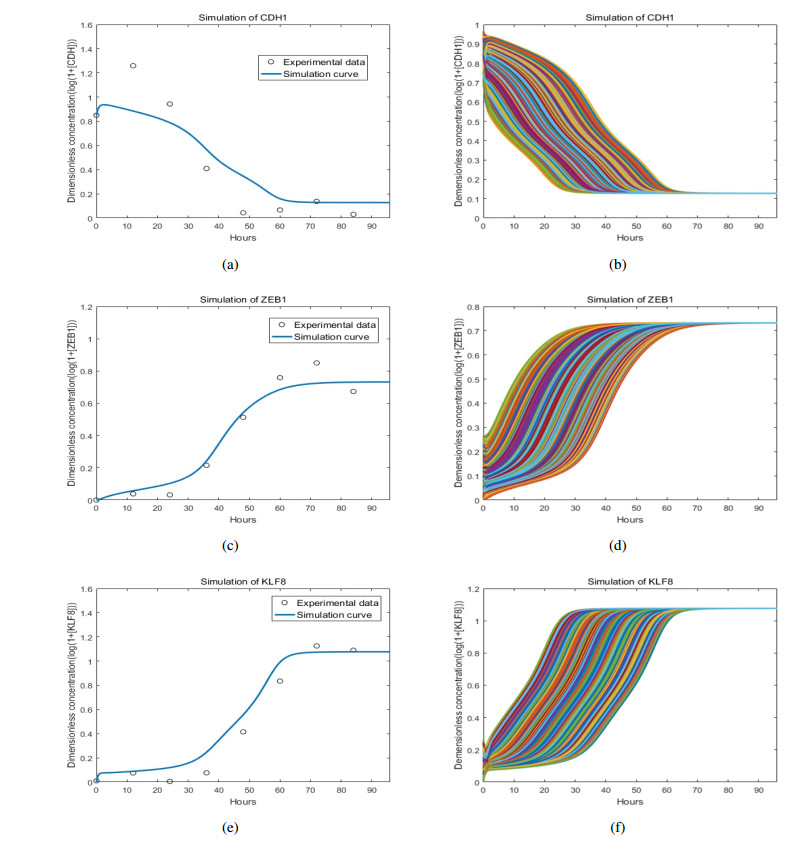
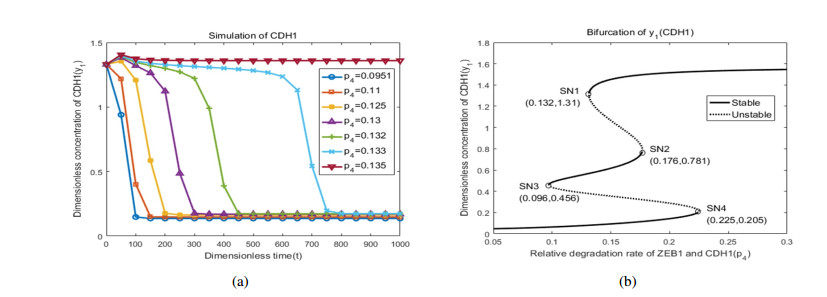
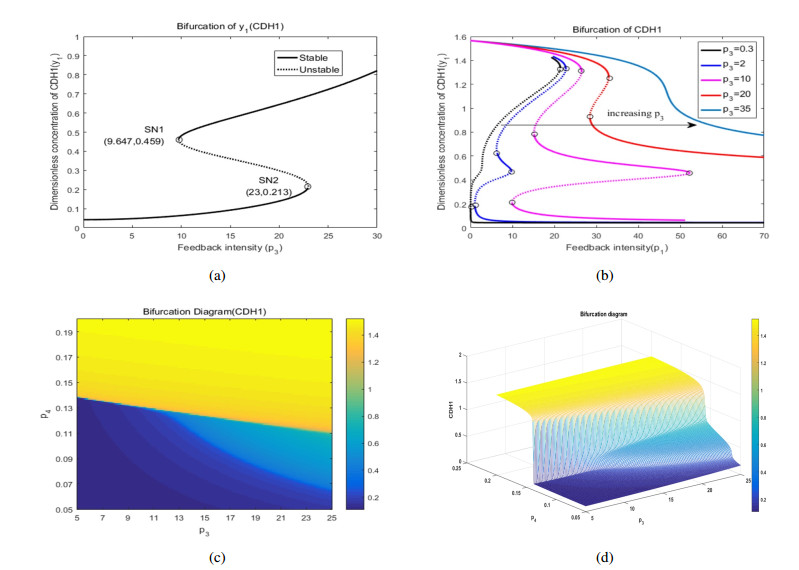
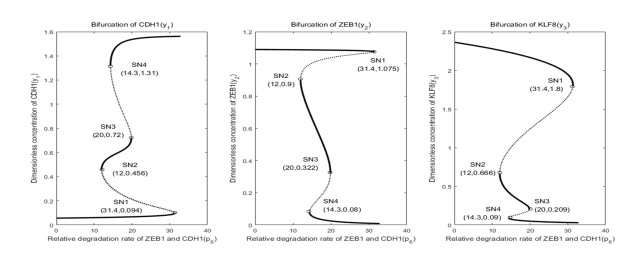
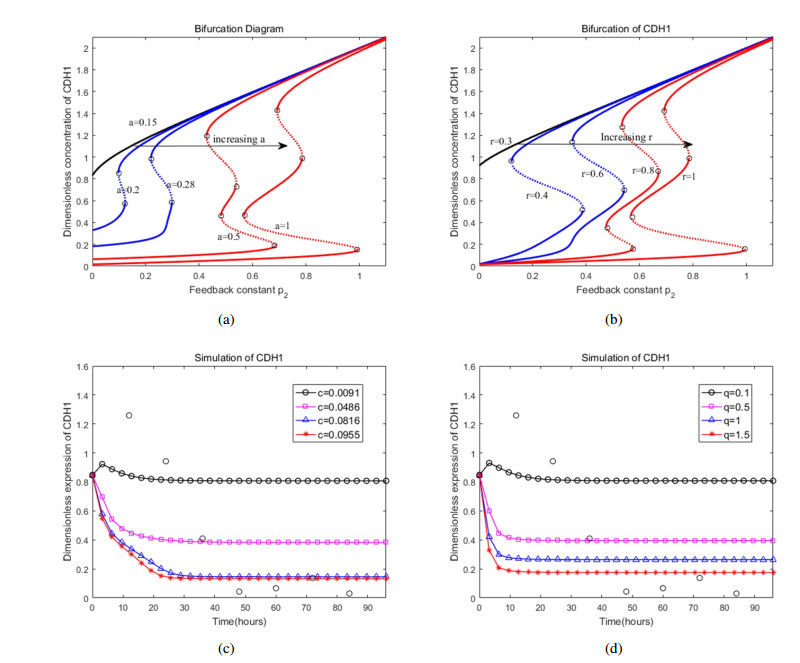
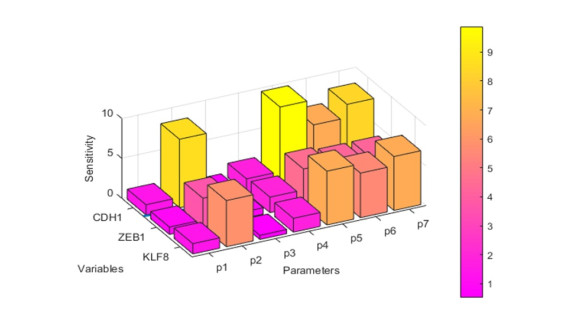
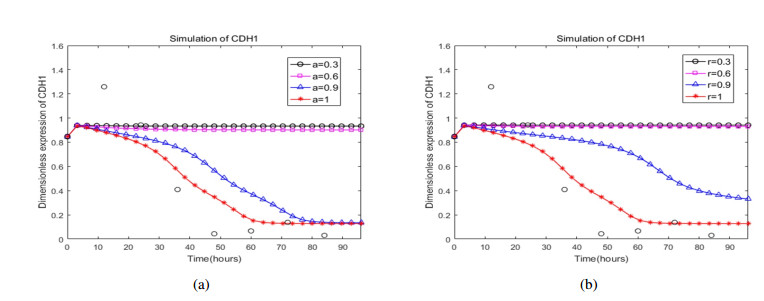
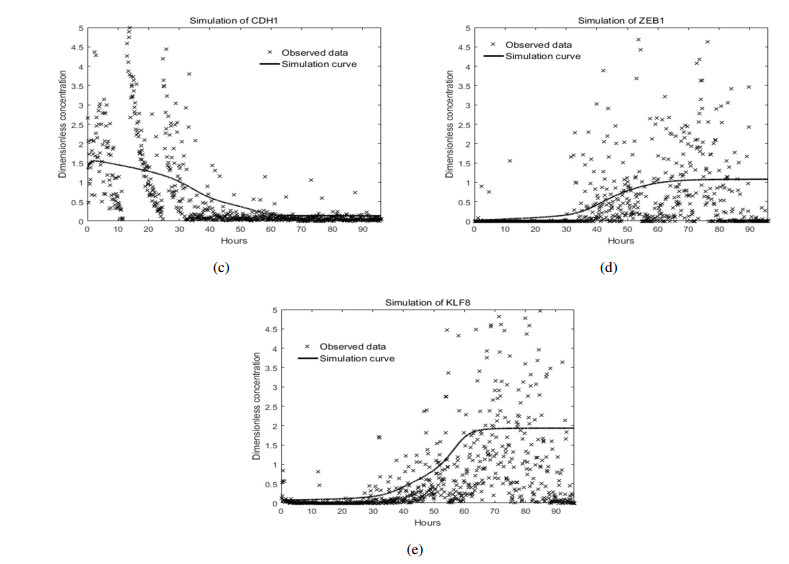
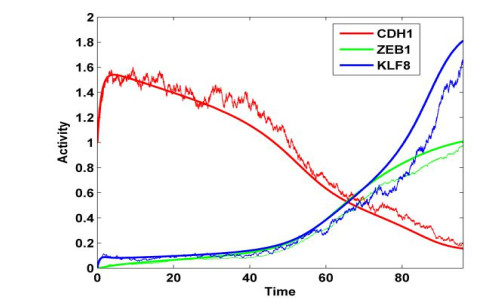
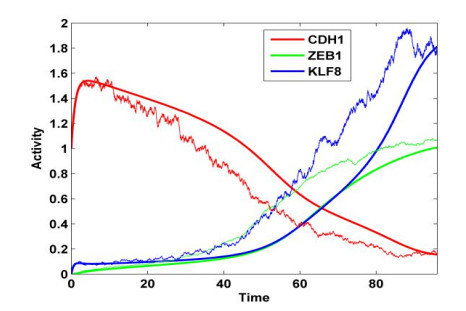
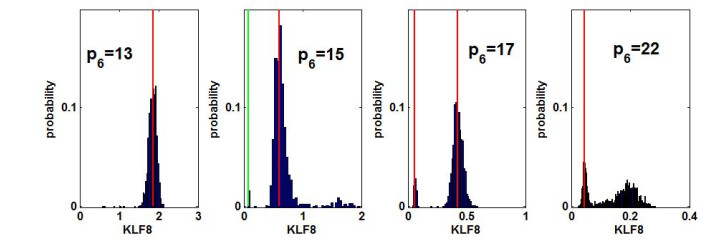
Embryonic development is widely studied due to its application in disease treatment. The published literature demonstrated that Krüppel-like factor 8(KLF8) plays an important role in modulating mesendoderm to definitive endoderm (DE) differentiation. However, it is not clear how KLF8 interacts with other key genes and affects the differentiation process. To qualitatively and quantitatively explore the molecular mechanisms of KLF8 during the differentiation of human embryonic stem cells (hESCs) in detail, we developed a mathematical model to describe the dynamics between KLF8 and two other significant genes, E-cadherin(CDH1) and Zinc-finger E-box-binding homeobox1(ZEB1). Based on the single-cell RNA-seq data, the model structure and parameters were obtained using particle swarm optimization (PSO). The bifurcation analysis and simulation results reveal that the system can exhibit a complex tristable transition, which corresponds to the three states of embryonic development at the single-cell level. We further predict that the novel important gene KLF8 promotes the formation of DE cells by reciprocal inhibition between CDH1 and KLF8 and promotion of the expression of ZEB1. These results may help to shed light on the biological mechanism in the differentiation process of hESCs.
1.
Introduction and statement of the results
Cloaking using transformation optics (changes of variables) was introduced by Pendry, Schurig and Smith [30] for the Maxwell system and by Leonhardt [16] in the geometric optics setting. These authors used a singular change of variables, which blows up a point into a cloaked region. The same transformation had been used to establish (singular) non-uniqueness in Calderon's problem in [10]. To avoid using the singular structure, various regularized schemes have been proposed. One of them was suggested by Kohn, Shen, Vogelius and Weinstein [11], where instead of a point, a small ball of radius ε is blown up to the cloaked region. Approximate cloaking for acoustic waves has been studied in the quasistatic regime [11,26], the time harmonic regime [12,19,27,20], and the time regime [28,29], and approximate cloaking for electromagnetic waves has been studied in the time harmonic regime [4,14,24], see also the references therein. Finite energy solutions for the singular scheme have been studied extensively [9,32,33]. There are also other ways to achieve cloaking effects, such as the use of plasmonic coating [2], active exterior sources [31], complementary media [13,22], or via localized resonance [23] (see also [17,21]).
The goal of this paper is to investigate approximate cloaking for the heat equation using transformation optics. Thermal cloaking via transformation optics was initiated by Guenneau, Amra and Venante [8]. Craster, Guenneau, Hutridurga and Pavliotis [6] investigate the approximate cloaking for the heat equation using the approximate scheme in the spirit of [11]. They show that for the time large enough, the largeness depends on ε, the degree of visibility is of the order εd (d=2,3) for sources that are independent of time. Their analysis is first based on the fact that as time goes to infinity, the solutions converge to the stationary states and then uses known results on approximate cloaking in the quasistatic regime [11,26].
In this paper, we show that approximate cloaking is achieved at any positive time and established the degree of invisibility of order ε in three dimensions and |lnε|−1 in two dimensions. Our results hold for a general source that depends on both time and space variables, and our estimates depend only on the range of the materials inside the cloaked region. The degree of visibility obtained herein is optimal due to the fact that a finite time interval is considered (compare with [6]). The analysis in this paper is of frequency type via Fourier transform with respect to time. This approach is robust and can be used in different context. A technical issue is on the blow up of the fundamental solution of the Helmholtz type equations in two dimensions in the low frequency regime. We emphasize that even though our setting is in a bounded domain, we employs Fourier transform in time instead of eigenmodes decomposition. This has the advantage that one can put the non-perturbed system and the cloaking system in the same context.
We next describe the problem in more detail and state the main result. Our starting point is the regularization scheme [11] in which a transformation blows up a small ball Bε (0<ε<1/2) instead of a point into the cloaked region B1 in Rd (d=2,3). Here and in what follows, for r>0, Br denotes the ball centered at the origin and of radius r in Rd. Our assumption on the geometry of the cloaked region is mainly to simplify the notations. Concerning the transformation, we consider the map Fε:Rd→Rd defined by
In what follows, we use the standard notations
for the "pushforward" of a symmetric, matrix-valued function A, and a scalar function ρ, by the diffeomorphism F, and I denotes the identity matrix. The cloaking device in the region B2∖B1 constructed from the transformation technique is given by
a pair of a matrix-valued function and a function that characterize the material properties in B2∖B1. Physically, this is the pair of the thermal diffusivity and the mass density of the material.
Let Ω with B2⋐Ω⊂Rd (d=2,3)* be a bounded region for which the heat flow is considered. Suppose that the medium outside B2 (the cloaking device and the cloaked region) is homogeneous so that it is characterized by the pair (I,1), and the cloaked region B1 is characterized by a pair (aO,ρO) where aO is a matrix-valued function and ρO is a real function, both defined in B1. The medium in Ω is then given by
*The notation D⋐Ω means that the closure of D is a subset of Ω.
In what follows, we make the usual assumption that aO is symmetric and uniformly elliptic and ρO is a positive function bounded above and below by positive constants, i.e., for a.e. x∈B1,
and
for some Λ≥1. Given a function f∈L1((0,+∞),L2(Ω)) and an initial condition u0∈L2(Ω), in the medium characterzied by (Ac,ρc), one obtains a unique weak solution uc∈L2((0,∞);H1(Ω)) ∩C([0,+∞);L2(Ω)) of the system
and in the homogeneneous medium characterized by (I,1), one gets a unique weak solution u∈L2((0,∞);H1(Ω))∩C([0,+∞);L2(Ω)) of the system
The approximate cloaking meaning of the scheme (1.4) is given in the following result:
Theorem 1.1. Let u0∈L2(Ω) and f∈L1((0,+∞);L2(Ω)) be such that suppu0,suppf(t,⋅)⊂Ω∖B2 for t>0. Assume that uc and u are the solution of (1.7) and (1.8) respectively. Then, for 0<ε<1/2,
for some positive constant C depending on Λ but independent of f, u0, and ε, where
As a consequence of Theorem 1.1, limε→0uc(t,⋅)=u(t,⋅) in (0,+∞)×(Ω∖B2) for all f with compact support outside (0,+∞)×B2 and for all u0 with compact support outside B2. One therefore cannot detect the difference between (Ac,ρc) and (I,1) as ε→0 by observation of uc outside B2: Cloaking is achieved for observers outside B2 in the limit as ε→0.
We now briefly describe the idea of the proof. The starting point of the analysis is the invariance of the heat equations under a change of variables which we now state.
Lemma 1.1. Let d≥2, T>0, Ω be a bounded open subset of Rd of class C1, and let A be an elliptic symmetric matrix-valued function, and ρ be a bounded, measurable function defined on Ω bounded above and below by positive constants. Let F:Ω↦Ω be bijective such that F and F−1 are Lipschitz, det∇F>c for a.e. x∈Ω for some c>0, and F(x)=x near ∂Ω. Let f∈L1((0,T);L2(Ω)) and u0∈L2(Ω). Then u∈L2((0,T);H10(Ω))∩C([0,T);L2(Ω)) is the weak solution of
if and only if v(t,⋅):=u(t,⋅)∘F−1∈L2((0,T);H10(Ω))∩C([0,T);L2(Ω)) is the weak solution of
Recall that F∗ is defined in (1.2). In this paper, we use the following standard definition of weak solutions:
Definition 1.1. Let d≥2 and T>0. We say a function
is a weak solution to (1.9) if u(0,⋅)=u0 in Ω and u satisfies
in the distributional sense for all φ∈H10(Ω).
The existence and uniqueness of weak solutions are standard, see, e.g., [1] (in fact, in [1], f is assumed in L2((0,T);L2(Ω)), however, the conclusion holds also for f∈L1((0,T);L2(Ω)) with a similar proof, see, e.g., [25]). The proof of Lemma 1.1 is similar to that of the Helmholtz equation, see, e.g., [12] (see also [6] for a parabolic version).
We now return to the idea of the proof of Theorem 1.1. Set
Then uε is the unique solution of the system
where
Moreover,
In comparing the coefficients of the systems verified by u and uε, the analysis can be derived from the study of the effect of a small inclusion Bε. The case in which finite isotropic materials contain inside the small inclusion was investigated in [3] (see also [5] for a related context). The analysis in [3] partly involved the polarization tensor information and took the advantage of the fact that the coefficients inside the small inclusion are finite. In the cloaking context, Craster et al. [6] derived an estimate of the order εd for a time larger than a threshold one. Their analysis is based on long time behavior of solutions to parabolic equations and estimates for the degree of visibility of the conducting problem, see [11,26], hence the threshold time goes to infinity as ε→0.
In this paper, to overcome the blow up of the coefficients inside the small inclusion and to achieve the cloaking effect at any positive time, we follow the approach of Nguyen and Vogelius in [28]. The idea is to derive appropriate estimates for the effect of small inclusions in the time domain from the ones in the frequency domain using the Fourier transform with respect to time. Due to the dissipative nature of the heat equation, the problem in the frequency for the heat equation is more stable than the one corresponding to the acoustic waves, see, e.g., [27,28], and the analysis is somehow easier to handle in the high frequency regime. After using a standard blow-up argument, a technical point in the analysis is to obtain an estimate for the solutions of the equation Δv+iωε2v=0 in Rd∖B1 (ω>0) at the distance of the order 1/ε in which the dependence on ε and ω are explicit (see Lemma 2.2). Due to the blow up of the fundamental solution in two dimensions, the analysis requires new ideas. We emphasize that even though our setting is in a bounded domain with zero Dirichlet boundary condition, we employs Fourier transform in time instead of eigenmodes decomposition as in [6] to put both systems of uε and u in the same context.
2.
Proof of the main result
To implement the analysis in the frequency domain, let us introduce the Fourier transform with respect to time t:
for φ∈L2((−∞,+∞),L2(Rd)). Extending u,uc, uρ and f by 0 for t<0, and considering the Fourier with respect to time at the frequency ω>0, we obtain
and
where
The main ingredient in the proof of Theorem 1.1 is the following:
Proposition 2.1. Let ω>0, 0<ε<1/2, and let g∈L2(Ω) with suppg⊂Ω∖B2. Assume that v,vε∈H1(Ω) are respectively the unique solution of the systems
and
We have
for some positive constant C independent of ε, ω and g. Here
and
The rest of this section is divided into three subsections. In the first subsection, we present several lemmas used in the proof of Proposition 2.1. The proofs of Proposition 2.1 and Theorem 1.1 are then given in the second and the third subsections, respectively.
2.1. Preliminaries
In this subsection, we state and prove several useful lemmas used in the proof of Proposition 2.1. Throughout, D⊂B1 denotes a smooth, bounded, open subset of Rd such that Rd∖D is connected, and ν denotes the unit normal vector field on ∂D, directed into Rd∖D.
The first result is the following simple one:
Lemma 2.1. Let d=2,3, k>0, and let v∈H1(Rd∖D) be such that Δv+ikv=0 in Rd∖D. We have, for R>2,
for some positive constants CR independent of k and v.
Proof. Multiplying the equation by ˉv (the conjugate of v) and integrating by parts, we have
This implies
Here and in what follows, C denotes a positive constant independent of v and k. Since Δv=−ikv in B2∖D, by the trace theory, see, e.g., [7,Theorem 2.5], we have
Combining (2.6) and (2.7) yields
The conclusion follows when k≥1.
Next, consider the case 0<k<1. In the case where d=3, the conclusion is a direct consequence of (2.8) and the Hardy inequality (see, e.g., [18,Lemma 2.5.7]):
We next consider the case where d=2. One just needs to show
By the Hardy inequality (see, e.g., [18,Lemma 2.5.7]),
it suffices to prove (2.10) for R=2 by contradiction. Suppose that there exists a sequence (kn)→0 and a sequence (vn)∈H1(R2∖D) such that
Denote
By (2.8) and (2.11), one might assume that vn converges to v weakly in H1loc(R2∖D) and strongly in L2(B2∖D). Moreover, v∈W1(R2∖D) and v satisfies
and
From (2.12), we have v=0 in R2∖D (see, e.g., [18]) which contradicts (2.13). The proof is complete.
We also have
Lemma 2.2. Let d=2,3, ω>0, 0<ε<1/2, and let v∈H1(Rd∖D) be a solution of Δv+iωε2v=0 in Rd∖D. We have, for 3/2<|x|<R,
for some positive constant C=CR independent of ε, ω and v.
Recall that e(ε,ω,d) is given in (2.3) and (2.4).
Proof. By the trace theory and the regularity theory of elliptic equations, we have
It follows from Lemma 2.1 that
Here and in what follows in this proof, C denotes a positive constant depending only on R and D.
The representation formula gives
where ℓ=eiπ/4εω1/2, and, for x≠y,
Here H(1)0 is the Hankel function of the first kind of order 0. Recall, see, e.g., [15,Chapter 5], that
and
We now consider the case d=3. We have, for 3/2<|x|<R and y∈∂B2,
It follows that, for 3/2<|x|<R and y∈∂B2,
Similarly, one has, for 3/2<|x|<R and y∈∂B2,
Combining (2.17), (2.20) and (2.21) yields
We derive from (2.16) that
which is the conclusion in the case d=3.
We next deal with the case where d=2 and ω>ε−2/4, which is equivalent to |ℓ|>1/2. From (2.19), we derive that, for 3/2<|x|<R and y∈∂B2,
Using (2.16) and combining (2.17) and (2.22), we obtain, since ω>ε−2/4,
which gives the conclusion in this case.
We finally deal with the case where d=2 and 0<ω<ε−2/4, which is equivalent to |ℓ|<1/2. From (2.17), we obtain, for x∈∂B4,
Since d = 2 , we have
It follows from Lemma 2.1 and the trace theory that
Since, by (2.18),
and
we derive from (2.23) and (2.24) that
Again using (2.17), we get, for 3/2 < |x| < R ,
Since, by (2.18), for 0 < \omega < 1/2 ,
and, by (2.19), for 1/2 < \omega < \varepsilon^{-2}/4 ,
we derive from (2.24), (2.25) and (2.26) that, for 3/2 < |x| < R ,
which yields the conclusion in the case 0 < \omega < \varepsilon^{-2}/4 . The proof is complete.
2.2. Proof of Proposition 2.1
In this proof, C denotes a positive constant depending only on \Omega and \Lambda . Multiplying the equation of v_\varepsilon by \bar v_\varepsilon and integrating in \Omega , we derive that
Here we used Poincaré's inequality
It follows from (2.27) that
Similarly, using the equation for v and Poincaré's inequality, we get
Since \Delta v+i\omega v = 0 in B_2 , using Caccioppolli's inequality, we have
By Sobolev embedding, as d\le 3 ,
It follows that
Set
Then w_{\varepsilon} \in H^1(\Omega \setminus B_\varepsilon) and satisfies
Let \widetilde w_{\varepsilon}\in H^1(\mathbb{R}^d \setminus B_{\varepsilon}) be the unique solution of the system
and set
Then \widetilde W_{\varepsilon} \in H^1(\mathbb{R}^d \setminus B_{1}) is the unique solution of the system
Fix r_0 > 2 such that \Omega \subset B_{r_0} . By Lemma 2.2, we have, for 1 \le |x| < r_0 , that
which yields, for x \in B_{r_0} \setminus B_{1} , that
Since \Delta \widetilde w_{\varepsilon} + i \omega \widetilde w_{\varepsilon} = 0 in B_{r_0} \setminus B_{1} , it follows from Caccioppoli's inequality that
Fix \varphi \in C^2(\mathbb{R}^d) such that \varphi = 1 in B_{3/2} and \varphi = 0 in \mathbb{R}^d \setminus B_2 , and set
Then \chi_{\varepsilon}\in H^1_0(\Omega \setminus B_\varepsilon) and satisfies
Multiplying the equation of \chi_{\varepsilon} by \bar \chi_{\varepsilon} and integrating by parts, we obtain, by Poincaré's inequality,
Combining (2.36) and (2.37) yields
The conclusion now follows from (2.28) and (2.32).
2.3. Proof of Theorem 1.1
Let v_\varepsilon = u_\varepsilon - u . Using the fact that v_\varepsilon is real, by the inversion theorem and Minkowski's inequality, we have, for t > 0 ,
Using Proposition 2.1, we get
It follows from (2.39) that, for t > 0 ,
Similarly, we have, for t > 0 ,
The conclusion follows.
Acknowledgments
The second author is funded by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 101.02-2015.21.
Conflict of interest
The authors declare no conflict of interest in this paper.












 DownLoad:
DownLoad: