BCG and IL − 2 model for bladder cancer treatment with fast and slow dynamics based on SPVF method—stability analysis

OPhir Nave; Shlomo Hareli; Miriam Elbaz; Itzhak Hayim Iluz; Svetlana Bunimovich-Mendrazitsky; OPhir Nave; Shlomo Hareli; Miriam Elbaz; Itzhak Hayim Iluz; Svetlana Bunimovich-Mendrazitsky

doi:10.3934/mbe.2019267

Mathematical Biosciences and Engineering

2019, Volume 16, Issue 5: 5346-5379. doi: 10.3934/mbe.2019267

Previous Article Next Article

Research article

BCG and IL − 2 model for bladder cancer treatment with fast and slow dynamics based on SPVF method—stability analysis

1.
Department of Mathematics, Jerusalem College of Technology (JCT)
2.
Department of Mathematics, Ben-Gurion University, Azrieli College of Engineering
3.
Department of Bioinformatics, Jerusalem College of Technology (JCT)
4.
Department of Computer Science, Jerusalem College of Technology (JCT)
5.
Department of Mathematics, Ariel University

Received: 21 November 2018 Accepted: 21 February 2019 Published: 10 June 2019

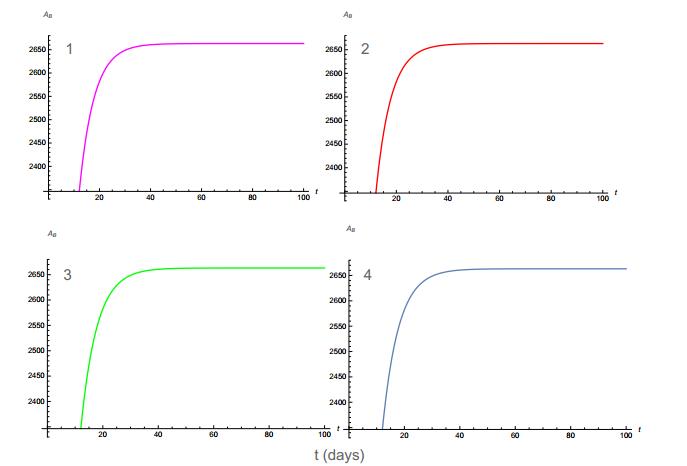
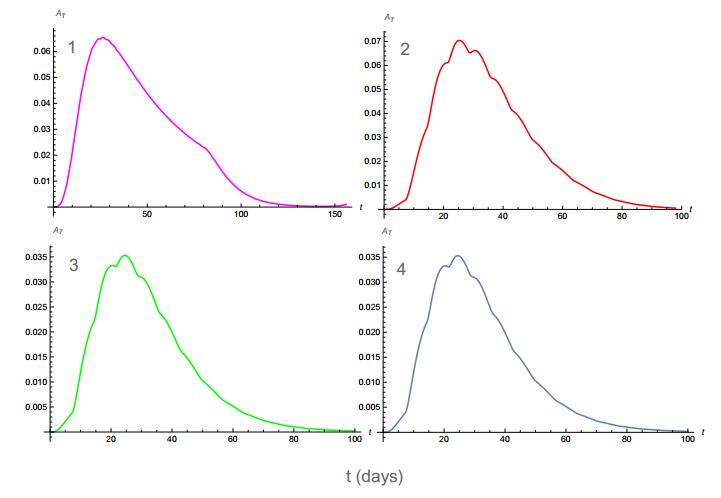
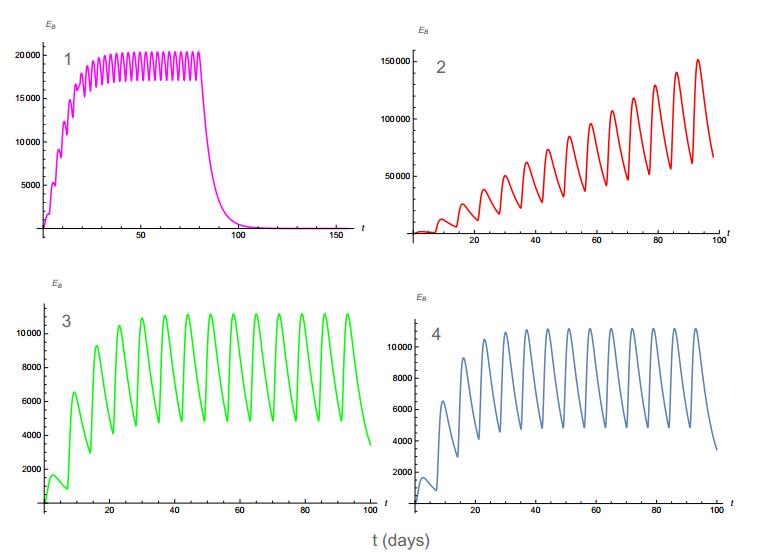
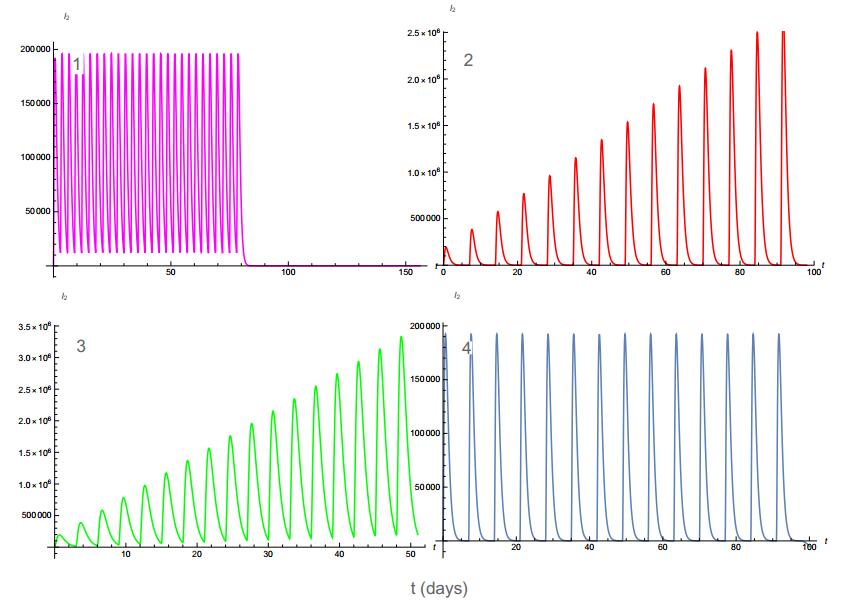
In this study, we apply the method of singularly perturbed vector field (

$SPVF$ ) and its application to the problem of bladder cancer treatment that takes into account the combination of Bacillus Calmette–Guérin vaccine (

$BCG$ ) and interleukin (IL)-2 immunotherapy (

$IL-2$ ). The model is presented with a hidden hierarchy of time scale of the dynamical variables of the system. By applying the

$SPVF$ , we transform the model to

$SPS$ (Singular Perturbed System) form with explicit hierarchy, i.e., slow and fast sub-systems. The decomposition of the model to fast and slow subsystems, first of all, reduces significantly the time computer calculations as well as the long and complex algebraic expressions when investigating the full model. In addition, this decomposition allows us to explore only the fast subsystem without losing important biological/ mathematical information of the original system.The main results of the paper were that we obtained explicit expressions of the equilibrium points of the model and investigated the stability of these points.

Keywords:

Citation: OPhir Nave, Shlomo Hareli, Miriam Elbaz, Itzhak Hayim Iluz, Svetlana Bunimovich-Mendrazitsky. BCG and IL − 2 model for bladder cancer treatment with fast and slow dynamics based on SPVF method—stability analysis[J]. Mathematical Biosciences and Engineering, 2019, 16(5): 5346-5379. doi: 10.3934/mbe.2019267

Related Papers:

[1]	Kongfu Hu, Lei Wang, Jingcao Cai, Long Cheng . An improved genetic algorithm with dynamic neighborhood search for job shop scheduling problem. Mathematical Biosciences and Engineering, 2023, 20(9): 17407-17427. doi: 10.3934/mbe.2023774
[2]	Shaofeng Yan, Guohui Zhang, Jinghe Sun, Wenqiang Zhang . An improved ant colony optimization for solving the flexible job shop scheduling problem with multiple time constraints. Mathematical Biosciences and Engineering, 2023, 20(4): 7519-7547. doi: 10.3934/mbe.2023325
[3]	Yifan Gu, Hua Xu, Jinfeng Yang, Rui Li . An improved memetic algorithm to solve the energy-efficient distributed flexible job shop scheduling problem with transportation and start-stop constraints. Mathematical Biosciences and Engineering, 2023, 20(12): 21467-21498. doi: 10.3934/mbe.2023950
[4]	Cong Zhao, Na Deng . An actor-critic framework based on deep reinforcement learning for addressing flexible job shop scheduling problems. Mathematical Biosciences and Engineering, 2024, 21(1): 1445-1471. doi: 10.3934/mbe.2024062
[5]	Zilong Zhuang, Zhiyao Lu, Zizhao Huang, Chengliang Liu, Wei Qin . A novel complex network based dynamic rule selection approach for open shop scheduling problem with release dates. Mathematical Biosciences and Engineering, 2019, 16(5): 4491-4505. doi: 10.3934/mbe.2019224
[6]	Jianguo Duan, Mengting Wang, Qinglei Zhang, Jiyun Qin . Distributed shop scheduling: A comprehensive review on classifications, models and algorithms. Mathematical Biosciences and Engineering, 2023, 20(8): 15265-15308. doi: 10.3934/mbe.2023683
[7]	Wenqiang Zhang, Chen Li, Mitsuo Gen, Weidong Yang, Zhongwei Zhang, Guohui Zhang . Multiobjective particle swarm optimization with direction search and differential evolution for distributed flow-shop scheduling problem. Mathematical Biosciences and Engineering, 2022, 19(9): 8833-8865. doi: 10.3934/mbe.2022410
[8]	Dan Yang, Zhiqiang Xie, Chunting Zhang . Multi-flexible integrated scheduling algorithm for multi-flexible integrated scheduling problem with setup times. Mathematical Biosciences and Engineering, 2023, 20(6): 9781-9817. doi: 10.3934/mbe.2023429
[9]	Lu-Wen Liao . A branch and bound algorithm for optimal television commercial scheduling. Mathematical Biosciences and Engineering, 2022, 19(5): 4933-4945. doi: 10.3934/mbe.2022231
[10]	Weiguo Liu, Xuyin Wang, Lu Li, Peizhen Zhao . A maintenance activity scheduling with time-and-position dependent deteriorating effects. Mathematical Biosciences and Engineering, 2022, 19(11): 11756-11767. doi: 10.3934/mbe.2022547

Abstract

In this study, we apply the method of singularly perturbed vector field (

$SPVF$ ) and its application to the problem of bladder cancer treatment that takes into account the combination of Bacillus Calmette–Guérin vaccine (

$BCG$ ) and interleukin (IL)-2 immunotherapy (

$IL-2$ ). The model is presented with a hidden hierarchy of time scale of the dynamical variables of the system. By applying the

$SPVF$ , we transform the model to

1. Introduction

Production scheduling problems are very important in manufacturing systems. It could make effective production planning to improve the production efficiency. The job shop scheduling problem (JSP) is one of the most popular scheduling problems existing in practice. This problem consists in assigning a set of operations on a set of machines such as each operation must be processed on one machine. However, as the flexibility of processing in the shop continues to increase, each machine could process multiple operations. That is, each operation could be processed by many different machines. Hence, this problem named flexible job shop scheduling problem (FJSP). FJSP is an extension of the classic JSP. In the FJSP, there are two sub problems: machine selection and operation sequencing. The FJSP is known to be strongly NP-hard. There are many research on swarm intelligence optimization algorithms for the flexible job shop scheduling problems, such as genetic algorithm (GA) ^[1,2,3,4,5], particle swarm optimization (PSO) ^[6,7], ant colony algorithm (ACO) ^[8], shuffled frog-leaping algorithm ^[9], teaching learning based optimization algorithm (TLBO) ^[10], virus optimization algorithm ^[11], and differential evolution ^[12].

This paper studies the FJSP with transportation time for the following reasons. In most of the existing literatures on FJSP, each job could be processed immediately on the next machine after it is completed on the previous machine. In other words, the transportation times between the machines are often neglected. However, the transportation times are possible to affect the quality of the product in some specific production fields. And, transportation times have a direct impact on the production cycle of the product in the actual production process. Hence, in this paper, the transportation time is considered in the mathematic model, and to be solved.

At present, there are some research literatures considering the transportation times. Hurinkab ^[13] applied a novel simulated annealing to consider scheduling hybrid flowshop problems to minimize both total completion time and total tardiness. They integrated two realistic and practical assumptions which are sequence-dependent setup and transportation times into the problem. Naderi et al. ^[14] incorporated the sequence-dependent transportation times with a single-transporter system into the flow-shop. They proposed an adaptation of the simulated annealing algorithm to solve the problem. Boudhar and Haned ^[15] studied scheduling preemptive jobs on the identical parallel machines to minimize the total completion time. Several heuristic algorithms were presented and a high-quality lower-bound one was obtained considering the transportation of an interrupted job from a machine to another machine. Naderi et al. ^[16] considered the transportation times in the permutation flow-shops. They proposed six different models for the problem. Rossi and Andrea ^[17] proposed a swarm intelligence approach based on the disjunctive graph model to to schedule a manufacturing system with resource flexibility and separable setup times. Karimi et al. ^[18] proposed an adaptation of the imperialist competitive algorithm hybridized by a simulated annealing based local search to solve the problem. Overall, more literature about the transportation time focus on flow shop scheduling problem, but few on flexible job shop scheduling problem.

In this paper, we develop a modified GA to solve the FJSP with transportation time. The mathematical model is established to minimize the maximum completion time. The instance from the actual production is solved through the proposed algorithm. The computational results show that the proposed mathematical model and algorithm are valid and feasible.

The remainder of this paper is organized as follows. The problem description and mathematical model are presented in Section 2. The improved genetic algorithm is described in Section 3. The computational results are discussed in Section 4. Finally, Section 5 is the conclusion and addressed several promising research directions.

2. Problem description and mathematics modeling

2.1. Problem description

Flexible job shop scheduling problem (FJSP) could be described as: n jobs should be processed on m machines. Each job may have a different number of operations. Each operation could be processed by any machine out of the set of alternative machine set. Each operation is completed and the job is transported to the next machine. If the two continuous operations are not processed on the same machine, the transportation times between the different machines is necessary to considered. FJSP is an NP-hard combinatorial optimization problem which could not be solved in a polynomial time. The optimization objective is to get the minimum makespan with the processing time and transportation time.

In this paper, further discussion on this problem is based on the following assumptions:

(1) The same job can only be processed by one machine at the same time, and the job cannot be interrupted once it starts processing.

(2) Each job could be processed more than once on the same machine.

(3) Operations belonging to different jobs could be processed in parallel.

(4) All the machine can be used at zero time.

(5) All jobs can be processed at zero time.

(6) The processing route of each job is fixed and known, that is, each operation will be sent to the next processing machine immediately after completion of processing, and the operation can be processed at this time.

(7) The processing time will be different due to the difference of the selected processing machines, and the processing time is known.

(8) The transportation time may be different between the different machines.

2.2. Mathematical model

The mathematical model is described as: The job set J = {J₁, J₂, J₃, ... J_g, ... J_n}, J_g is the g job (g = 1, 2, 3, ... n). Machine set M = {M₁, M₂, M₃, ... M_i, ... M_m}, M_i is the i machine (i = 1, 2, 3, ... m). O_jh denotes the h operation of the job j, and defines the O_j_(h-1) as the previous operation of the O_jh, O_j_'h' represents the previous operation of the machine where O_jh is processed. F_jh expresses the processing completion time of the job j. T_ijh indicates the time required for the h operation of job j on the machine i. S_ijh is the processing start time of the operation h of job j on machine i. C_ijh is the end time of the operation h of the job j on the machine i. TransTime_ie is the transportation time of the job between the machine M_i and the machine M_e. C_j is the completion time of the job j. C_max represents the maximum completion time in the completion time of all jobs. Considering the minimization of makespan, its objective functions and constraints are as follows:

${C_{\max }} = \min (ma{x_{1 \le j \le n}}\left( {{C_j}} \right))$

(1)

${C_{ijh}} = {S_{ijh}} + {T_{ijh}}$

(2)

${C_{ijh}} - {C_{ij'h'}} \ge {T_{ijh}}$

(3)

$\left\{ {\begin{array}{*{20}{c}} {{C_{ej(h - 1)}} + TransTim{e_{ie}}}&{{C_{ij'h'}} \lt {C_{ej(h - 1)}} + TransTim{e_{ie}}}\\ {{C_{ij'h'}}}&{{C_{ij'h'}} \gt {C_{ej(h - 1)}} + TransTim{e_{ie}}} \end{array}} \right.$

(4)

Eq 1 represents the expression of the total objective function, that is, the maximum completion time minimization; Eq 2 indicates that the completion time of the operation is equal to the sum of the operation starting time and the operation time; Eq 3 represents the resource constraints; Eq 4 indicates that the starting time of the machine in the process (the opening time of the gap) is less than that of the process. The transportation time of the last operation is constrained by the transportation time. Otherwise, the processing procedure is constrained by the resources of the current processing machine. Therefore, if the connected operation of the same job is processed on the same machine, it is only constrained by machine resources. For the adjacent two operations in the same job, the transportation time is taken into account, instead of the process sequence constraint in the traditional machining model.

For the convenience of understanding, Table 1 gives an example of a partial flexible job shop scheduling problem. The "-" in Table 1 indicates that the horizontal corresponding operation cannot be processed on a vertical corresponding machine. Table 2 gives the transportation time between the different machines.

Table 1. An example of partial flexible job shop scheduling problem.

Jobs	Operations	Processing time
Jobs	Operations	M₁	M₂	M₃	M₄	M₅
J₁	O₁₁	4	3	-	5	2
J₁	O₁₂	4	-	3	-	5
J₂	O₂₁	-	5	-	4	-
	O₂₂	3	2	6	-	-
	O₂₃	-	7	5	5	4
J₃	O₃₁	3	2	4	3	-
J₃	O₃₂	5	-	3	4	-

| Show Table

DownLoad: CSV

Table 2. The transportation time between different machines.

Machines	Transportation time
Machines	M₁	M₂	M₃	M₄	M₅
M₁	0	2	3	2	4
M₂	2	0	3	4	3
M₃	3	3	0	5	2
M₄	2	4	5	0	1
M₅	4	3	2	1	0

| Show Table

DownLoad: CSV

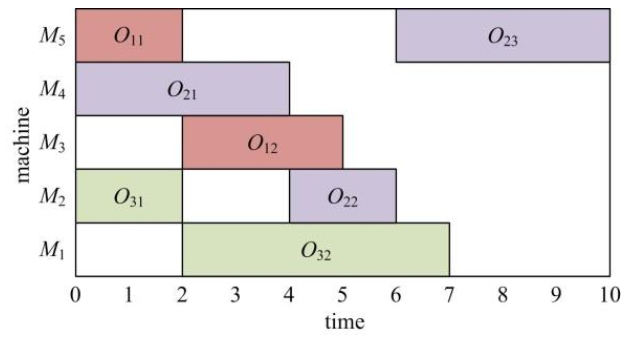
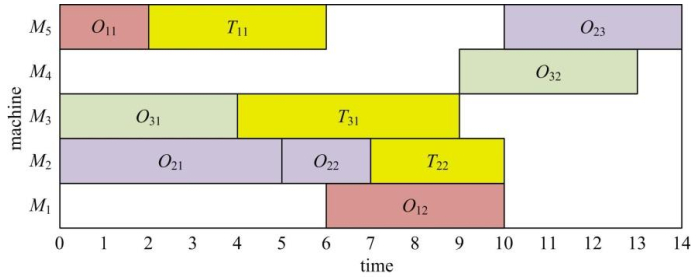
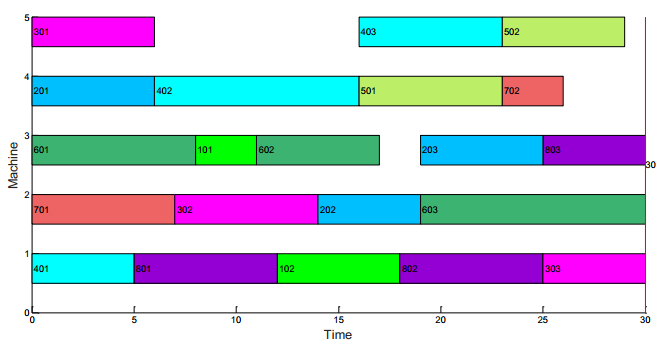
Figures 1, 2 represent Gantt charts without and with the transportation time, respectively according to the Tables 1 and 2. In Figure 2, the yellow box denotes the transportation time between the two different machines. T₁₁ indicates the transportation time of the operation O₁₁ from M₅ to M₁ after the operation O₁₁ is completed on M₅. Obviously, the two figures are different. The makespan of the problem without transportation time is much smaller than that of the problem with transportation time. However, the problem with transportation time is closer to the actual production.

Figure 1. The Gantt chart without transportation time.

DownLoad: Full-Size Img PowerPoint

Figure 2. The Gantt chart with transportation time.

DownLoad: Full-Size Img PowerPoint

3. The proposed improved genetic algorithm

3.1. Encoding and decoding

When the genetic algorithm is used to solve the problem, encoding and decoding are the first problems to be solved in the genetic algorithm. The problem of scheduling jobs in FJSP could be decomposed into two sub-problems: the routing sub-problem, which is assigning each operation to a machine selected out of a set of capable machines and the scheduling sub-problem, which consists of sequencing the assigned operations on all machines in order to obtain a feasible schedule minimizing the predefined objective function. In this paper, we adopted the method of the encoding method in ^[1] to encode two sub problems onto a chromosome, that is, a feasible solution of FJSP.

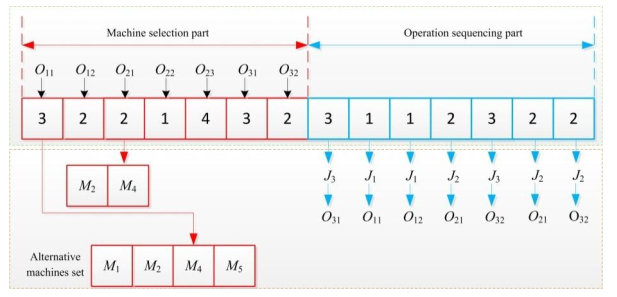
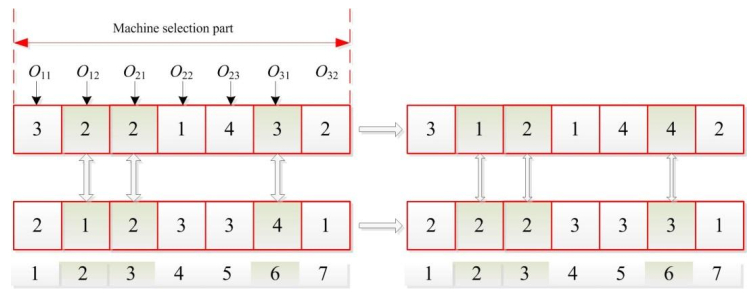
(1) Machine selection part: this part of the chromosome length is equal to the sum number of all operations. Each gene value is presented in integer, from left to right in sequence according to the process sequence of processing jobs. Each integer indicates the sequence number of the current operation of processing the job in the alternative machine set. Taking Table 1 as an example, as shown in the left half of the Figure 3, the gene string 3-2-2-1-4-3-2 indicates that the process O₁₁ is processed on the fourth machine in the alternative machines set, that is, the selected machine is M₅. Operation O₂₁ is processed on the second machine in the alternative machines set, that is, the selected machine is M₄, and so on.

Figure 3. Chromosome encoding.

DownLoad: Full-Size Img PowerPoint

(2) Operation sequencing part: The length of this part of the chromosome is equal to the total operations. Each gene is coded by the job number. The number of job shows the number of the work sequencing. As shown in the right half part of Figure 1, the gene string is 3-1-1-2-3-2-2, and the corresponding processing procedure is O₃₁-O₁₁-O₁₂-O₂₁-O₃₂-O₂₂-O₂₃.

When decoding chromosomes, there are three kinds of scheduling, that is, semi-active scheduling, activity scheduling, and non-delayed scheduling. It has proved that the optimal scheduling values for regular performance measure exist in the active scheduling set. That is, in active scheduling, some processing procedures can be found to make it earlier. Because chromosomes contain two parts, namely machine selection sub problem and operation sequencing sub problem. First, machine selection is decode: Read the machine selection part from left to right, and convert it to machine sequence matrix J_m and time sequence matrix T. J_m_{(j, h)} represents the machine number of the h operation of the j job, J_m(j, ...) represents the arrangement of all machine numbers processed in priority according to the working procedure of the job, and T_{(j, h)} represents the h processing time of the j job. J_m_{(j,
h)} is a one-to-one correspondence with T_{(j, h)}. It is shown that it is decoded in formula 5 and formula 6.

${J_m} = \left[ {\begin{array}{*{20}{c}} 4&3&{}\\ 4&1&5\\ 3&3&{} \end{array}} \right]$

(5)

$T = \left[ {\begin{array}{*{20}{c}} 5&3&{}\\ 4&3&4\\ 4&3&{} \end{array}} \right]$

(6)

Secondly, the operation sequencing is decoded. The chromosome part of the operation is read in turn from left to right. The machine matrix and time matrix are decoded according to the machine selection part. And the processing machine and processing time corresponding to the processing procedure of each operation are obtained in turn. In order to ensure the generation of active scheduling after chromosome decoding, the operation left shift insertion method is applied to operation sequencing. The left shift insertion method is executed as follows:

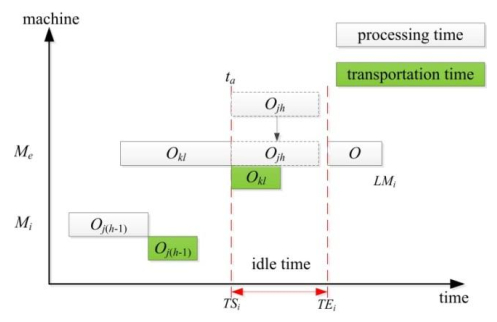
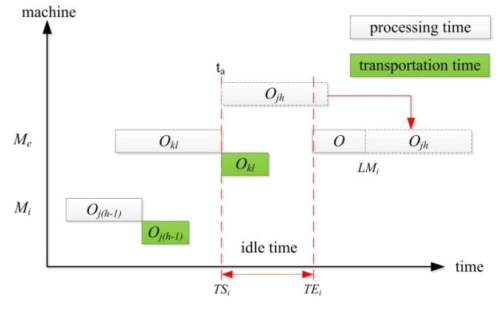
(1) If the job O_jh is the first process in machine M_i, it can be processed directly from the processing time of the previous operation O_j_(h-1) plus the end of the job transportation time.

(2) If operation O_jh is the first processing procedure of the job J, then the machining directly starts from the zero time of the machine M_i. Otherwise, look up all the interval idle time [TS_i, TE_i]. TS_i indicates the start time of the idle time on the machine M_i, and the TE_i indicates the end time of the idle time on the machine M_i.

(3) Taking into account the transportation time, according to the formula 7, the earliest processing start time t_a of the operation O_jh is obtained, which can satisfy the order constraint of the job processing procedure.

${t_a} = \max \{ {F_j}_{(h - 1)} + TransTim{e_{ie}},T{S_i}\}$

(7)

(4) According to the Eq 8, determine whether the interval idle time can satisfy the insertion condition. If the satisfaction is inserted into the current idle time section, as shown in Figure 4; otherwise, the machine M_i is processed on the machine in accordance with the time t_b of Eq 9, in which the TM_i represents the end time of the last machining process of the current machine M_i, as shown in Figure 5.

${t_a} + {T_{ijh}} \le T{E_i}$

(8)

${t_b} = \max \{ {F_j}_{(h - 1)} + TransTim{e_{ie}},T{M_i}\}$

(9)

Figure 4. t_a + T_ijh ≤ TE_i.

DownLoad: Full-Size Img PowerPoint

Figure 5. t_a + T_ijh > TE_i.

DownLoad: Full-Size Img PowerPoint

According to the method presented above, the chromosome of the operation sequencing part is decoded until the end of the chromosome.

3.2. Initialization method

The quality of the initial solution directly affects the solution quality and convergence speed of the genetic algorithm. Because FJSP not only solves machine selection sub-problem, but also solves the operation sequencing sub-problem. In this paper, the machine selection part uses integer random initialization method according to the characteristics of FJSP. That is, the value on each gene position of the machine selection part chromosome is randomly generated from the alternative machine set. The detailed description could be found in ^[2].

The operation sequencing part of each chromosome is also generated by random method.

3.3. Crossover operator

The purpose of crossover is to exchange the information between the parents and retain the excellent information in the parent generation to produce new individuals. In this way, it could effectively reduce the probability of producing the infeasible solutions and search for the new generation. Since each chromosome consists of two parts, different methods are designed for crossover operator.

(1) Machine selection part: In order to ensure that the solution is still feasible solution after crossover operation, the multi-point crossover operation is adopted. That is, multiple crossover points are randomly selected, and two parents are used to exchange gene blocks. Figure 6 gives an example.

Figure 6. The machine selection part crossover.

DownLoad: Full-Size Img PowerPoint

(2) Operation sequencing part: This part is based on operation encoding, and it is easy to produce infeasible solutions by traditional crossover operation. The improved method is to randomly divide the jobs into two groups, and better retain good operation sequence information from the parent individual. The detailed description could be found in ^[2].

3.4. Mutation operator

Mutation operation is to increase the diversity of the population by changing the gene of each chromosome to produce a new individual. To some extent, improve the local search ability of genetic algorithm. Two different mutation operators are adopted for the two parts of the chromosome.

(1) Machine selection part: A gene location is randomly selected from the chromosome, and then a machine is randomly selected from the corresponding alternative machine set to replace the machine at the current gene location.

(2) Operation sequencing part: Interchange method is used. Two genes are randomly selected. Then, the values at the two gene positions are exchanged with each other.

3.5. Selection operator

Through crossover operation and mutation operation, there may be bad solutions in the population. The selection operation is adopted to keep good individuals alive with greater probability. And the number of the population remains unchanged, so as to improve the computational efficiency and accelerate the global convergence. The more commonly used selection operators are rank-based selection, roulette wheel selection, seed selection and tournament selection. The tournament selection method has been proved that it has better or fairly convergence and computational complexity compared with other selection operators. In our proposed algorithm, the tournament selection is adopted. The fitness of a number of individuals was selected from the population to be compared, and the individuals with high fitness were selected and placed in the cross pool to fill the crossover pool.

4. Computational experiments and results

According to the above improved genetic algorithm, we use Matlab7.0 software. The instance from the actual production is executed on a P4 CPU (1.9 GHz) and 4G memory with Window 7 PC operating system. The main parameters of the genetic algorithm are as follows: population size 40, crossover probability 0.8, mutation probability 0.6, and maximum number of iterations is 200.

Table 3 shows the FJSP instance of 9 jobs on 5 machines after an actual instance is simplified. The "-" in Table 3 indicates that the operation of the job cannot be processed on the corresponding machine.

Table 3. An instance of FJSP.

Job	Operation	Processing time
Job	Operation	M₁	M₂	M₃	M₄	M₅
J₁	O₁₁	-	6	3	5	-
J₁	O₁₂	6	-	7	-	10
J₂	O₂₁	-	7	-	6	-
	O₂₂	9	5	4	-	-
	O₂₃	-	8	6	9	7
J₃	O₃₁	11	-	9	9	6
	O₃₂	-	7	6	8	-
	O₃₃	5	-	6	-	5
J₄	O₄₁	5	6	6	9	-
	O₄₂	8	-	11	10	-
	O₄₃	10	13	-	9	7
J₅	O₅₁	-	7	8	7	-
J₅	O₅₂	9	-	6	-	6
J₆	O₆₁	9	-	8	10	11
	O₆₂	6	-	6	-	6
	O₆₃	10	11	7	5	-
J₇	O₇₁	-	7	-	10	8
J₇	O₇₂	6	-	9	3	10
J₈	O₈₁	7	8	8	-	-
	O₈₂	7	-	10	9	8
	O₈₃	-	7	5	-	5

| Show Table

DownLoad: CSV

Table 4 represents the transportation time between the different machines based on the example in Table 3. In Table 4, the number of rows represents the machine corresponding to the operation, and the number of columns represents the processing machine corresponding to the next operation of the job.

Table 4. Transportation time between different machines.

Machine	M₁	M₂	M₃	M₄	M₅
M₁	0	1	1.5	2.5	1.5
M₂	1	0	1	1.5	2
M₃	1.5	1	0	2	2.1
M₄	2.5	1.5	2	0	1.7
M₅	1.5	2	2.1	1.7	0

| Show Table

DownLoad: CSV

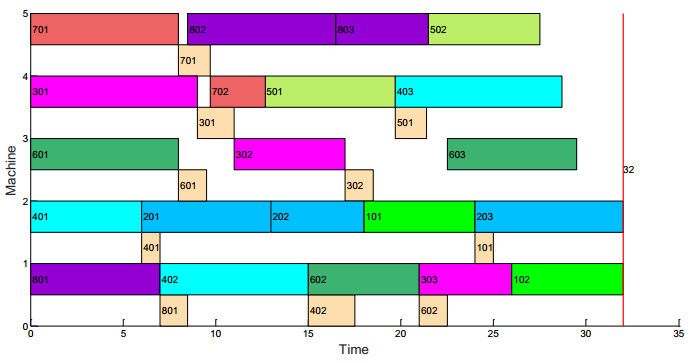
In the actual production process, the transportation time between the different machines is existence. Hence, in this paper, the transportation time is added to the scheduling problem. As shown in Figure 7, the optimal objective with transportation time is 32. And the Figure 8 is the Gantt chart of the FJSP without transportation time. The transportation time should be considered in the actual production for the entire production scheduling. The transportation time has a large impact on the final completion time. The pink box in Figure 7 represents the transportation time of each operation of each job. The other colors in Figure 7 represent the processing time of each operation on the corresponding machine. For example, the pink box of 701 on machine M₅ indicates that the transportation time of the O₇₁. That means that the first operation of the job J₇ is processed on machine M₅ and transported to the machine M₄. The transportation time needs 1.7 unit time.

Figure 7. The Gantt chart with transportation time.

DownLoad: Full-Size Img PowerPoint

Figure 8. The Gantt chart without transportation time.

DownLoad: Full-Size Img PowerPoint

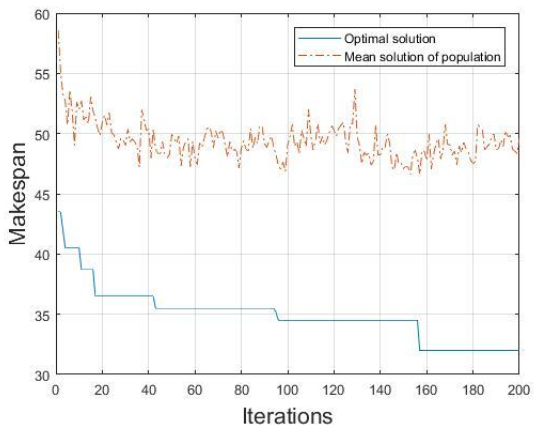
As shown in Figure 9, the improved genetic algorithm is used to solve the FJSP convergence curve with transportation time. The dotted line in Figure 9 represents the mean change curve of each generation of objective values, and the real line represents the change curve of the optimal solution for each generation. The convergence curve of the optimal value is a downward trend. However, the mean value does not clearly reflect the downward trend. This shows that the algorithm needs further improvement in future research.

Figure 9. The convergence curve.

DownLoad: Full-Size Img PowerPoint

5. Conclusion and future research

In this research, the flexible job shop scheduling problem considering transportation time is solved. The mathematical model considering transportation time is established. An improved genetic algorithm based on the traditional genetic algorithm is proposed. In our proposed algorithm, the operation left shift insertion method is applied to decode the operation sequencing part. The improved genetic algorithm is realized by Matlab, and the performance of the computational results show that the proposed algorithm is feasible and effective. In the future research, the more effective optimization algorithm is designed according to characteristics of the flexible job shop scheduling problem with transportation time.

Acknowledgements

This paper presents work funded by the National Natural Science Foundation of China (No. 51705472), Excellent Youth Foundation of Science & Technology Innovation of Henan Province (No.184100510001), Key scientific research projects of Henan Province (No. 182102210457), and Humanities and Social Sciences of Ministry of Education Planning Fund (No. 18YJAZH125).

Conflict of interest

The authors declared that they have no conflicts of interest to this work.

References

[1]	V. M. Gol'dshtein and V. A. Sobolev, Singularity theory and some problems of functional analysis, Amer. Math. Soc., 1 (1992), 73–92.
[2]	V. I. Babushok and V. M. Gol'dshtein, Structure of the thermal explosion limit, Combust. Flame, 72 (1988), 221–226.
[3]	A. C. McIntosh, V. M. Gol'dshtein, I. Goldfarb, et al., Thermal explosion in a combustible gas containing fuel droplets, Combust. Th. Mod., 2 (1998), 153–165.
[4]	I. Goldfarb, V. M. Gol'dshtein, D. Katz, et al., Radiation effect on thermal explosion in a gas containing evaporating fuel droplets, Int. J. Ther. Sci., 46 (2007), 358–370.
[5]	M. R. Roussel and S. J. Fraser, Geometry of the steady-state approximation: perturbation and accelerated convergence methods, J. Chem. Phys., 93 (1990), 1072–1081.
[6]	M. R. Roussel and S. J. Fraser, Accurate steady-state approximations: implications for kinetics experiments and mechanism, J. Chem. Phys., 95 (1991), 8762–8770.
[7]	M. R. Roussel and S. J. Fraser, Global analysis of enzyme inhibition kinetics, textitJ. Chem. Phys., 97 (1993), 8316–8327.
[8]	M. R. Roussel and S. J. Fraser, Invariant manifold methods for metabolic model reduction, Chaos,196 (2001), 196–206.
[9]	A. Zagaris, H. G. Kaper and T. J. Kaper, Analysis of the computational singular perturbation reduction method for chemical kinetics, J. Non. Sci., 14 (2004), 59–91.
[10]	A. Zagaris, H. G. Kaper and T. J. Kaper, Fast and slow dynamics for the computational singular perturbation method, Soc. Indust. App. Math., 2 (2004), 613–638.
[11]	N. Berglunda and B. Gentzd, Geometric singular perturbation theory for stochastic differential equations, J. Diff. Eq., 191 (2003), 1–54.
[12]	N. Fenichel, Geometric singular perturbation theory for ordinary differential equations, J. Diff. Eq., 31 (1979), 53–98.
[13]	C. K. Jones, Geometric singular perturbation theory, 1609 of the series, Lec. Notes Math., Dyn. Syst. (2006), 44-118.
[14]	U. Maas and S. B. Pope, Implementation of simplified chemical kinetics based on intrinsic low-dimensional manifolds (PDF), Symposium (International) on Combustion, Twenty-Fourth Sym-posium on Combustion, (1992), 103–112.
[15]	U. Maas and S. B. Pope, Simplifying chemical kinetics: Intrinsic low-dimensional manifolds in composition space, Combust. Flame, 88 (1992), 239–264.
[16]	H. Bongers, J. A. Van Oijen and L. P. H. De Goey, Intrinsic low-dimensional manifold method extended with diffusion, Proc. Combust. Inst., 291 (2002), 1371–1378.
[17]	S. T. Alison, L. Whitehouse and L. Richard, The Estimation of Intrinsic Low Dimensional Man-ifold Dimension in Atmospheric Chemical Reaction Systems, Air Poll. Modell Simul., (2002), 245–263.
[18]	G. K. Hans and J. K. Tasso, Asymptotic analysis of two reduction methods for systems of chemical reactions, Phys. D, 165 (2002), 66–93.
[19]	V. Bykov, I. Goldfarb and V. Gol'dshtein, Singularly perturbed vector fields, J. Phys. Conf. Ser., 55 (2006), 28–44.
[20]	O. Nave, Singularly perturbed vector field method (SPVF) applied to combustion of monodisperse fuel spray, Diff. Eqs. Dyn. Syst., 27 (2018), 1–18.
[21]	M. Al-Tameemi, M. Chaplain and A. d'Onofrio, Evasion of tumours from the control of the im-mune system: consequences of brief encounters, Biol. Direct, 7 (2012), 1–22.
[22]	I. Kareva, F. Berezovskaya and C. Castillo-Chavez, Myeloid cells in tumour-immune interactions, J. Biol. Dyn., 4 (2010), 315–327.
[23]	L. Derbel, Analysis of a new model for tumor-immune system competition including long time scale effects, Math. Model Methods Appl. Sci., 14 (2004), 1657–1681.
[24]	K. E. Starkov and S. Bunimovich-Mendrazitsky, Dynamical properties and tumor clearance con-ditions for a nine-dimensional model of bladder cancer immunotherapy, Math. Biosci. Eng., 13 (2016), 1059–1075.
[25]	S. Bunimovich-Mendrazitsky, S. Halachmi and N. Kronik, Improving Bacillus Calmette-Guerin (BCG) immunotherapy for bladder cancer by adding interleukin 2 (IL−2): A mathematical model, Math. Med. Biol., 33 (2015), 1–30.
[26]	S. Brandau and H. Suttmann, Thirty years of BCG immunotherapy for non-muscle invasive blad-der cancer: a success story with room for improvement, Biomed. Pharmacother., 61 (2007), 299–305.
[27]	A. N. Tikhonov, Systems of differential equations containing small parameters multiplying the derivatives. Mat. Sborn., 31 (1952), 575–586.
[28]	R. Mahendran, Bacillus Calmette-Guerin immunotherapy-increasing dose as a means of improv-ing therapy?, Trans. Cancer Res., 6 (2017), 168–173.
[29]	A. Kiselyov, S. Bunimovich-Mendrazitsky and V. Startsev, Treatment of non-muscle invasive blad-der cancer with Bacillus Calmette-Guerin (BCG): biological markers and simulation studies, BBA Clin., 10 (2015), 27–34.
[30]	C. Pettenati and M. A.Ingersoll, Mechanisms of BCG immunotherapy and its outlook for bladder cancer, Nat. Rev. Urol., 15 (2018), 615–625.
[31]	A. H. Kitamur and T. Tsukamoto, Immunotherapy for urothelial carcinoma, Current status and perspectives, Cancers, 29 (2011), 3055–3072.
[32]	C. Yee, J. A. Thompson, D. Byrd, et al., Adoptive T cell therapy using antigen-specific CD8+ T cell clones for the treatment of patients with metastatic melanoma: in vivo persistence, migration, and antitumor effect of transferred T cells, Proc. Natl. Acad. Sci. U S A, 10 (2002), 16168–16173.
[33]	N. Kronik, Y. Kogan, P. G. Schlegel, et al., Improving T-cell immunotherapy for melanoma through a mathematically motivated strategy: efficacy in numbers?, J. Immunother., 35 (2012), 116–124.

This article has been cited by:

1.	Guohui Zhang, Jinghe Sun, Xixi Lu, Haijun Zhang, An improved memetic algorithm for the flexible job shop scheduling problem with transportation times, 2020, 53, 0020-2940, 1518, 10.1177/0020294020948094
2.	Xiaoyu Wen, Kanghong Wang, Hao Li, Haiqiang Sun, Haoqi Wang, Liangliang Jin, A two-stage solution method based on NSGA-II for Green Multi-Objective integrated process planning and scheduling in a battery packaging machinery workshop, 2021, 61, 22106502, 100820, 10.1016/j.swevo.2020.100820
3.	Zhuang Huang, Jianjun Yang, 2020, Chapter 35, 978-981-32-9685-5, 295, 10.1007/978-981-32-9686-2_35
4.	Bi Li, Chen Kui, 2020, Research on FJSP with transportation time constraint based on Improved Particle Swarm Optimization, 978-1-7281-6609-4, 130, 10.1109/DASC-PICom-CBDCom-CyberSciTech49142.2020.00035
5.	Binghai Zhou, Xiumei Liao, Particle filter and Levy flight-based decomposed multi-objective evolution hybridized particle swarm for flexible job shop greening scheduling with crane transportation, 2020, 91, 15684946, 106217, 10.1016/j.asoc.2020.106217
6.	Guohui Zhang, Yifan Hu, Jinghe Sun, Wenqiang Zhang, An improved genetic algorithm for the flexible job shop scheduling problem with multiple time constraints, 2020, 54, 22106502, 100664, 10.1016/j.swevo.2020.100664
7.	Yingli Li, Jiahai Wang, 2020, Chapter 39, 978-3-030-53955-9, 435, 10.1007/978-3-030-53956-6_39
8.	Jinghe Sun, Guohui Zhang, Jiao Lu, Wenqiang Zhang, A hybrid many-objective evolutionary algorithm for flexible job-shop scheduling problem with transportation and setup times, 2021, 132, 03050548, 105263, 10.1016/j.cor.2021.105263
9.	Wenxiang Xu, Yongwen Hu, Wei Luo, Lei Wang, Rui Wu, A multi-objective scheduling method for distributed and flexible job shop based on hybrid genetic algorithm and tabu search considering operation outsourcing and carbon emission, 2021, 157, 03608352, 107318, 10.1016/j.cie.2021.107318
10.	Thomas Seidelmann, Jens Weise, Sanaz Mostaghim, 2021, Meeting Demands for Mass Customization: A Hybrid Organic Computing Approach, 978-1-7281-9048-8, 1, 10.1109/SSCI50451.2021.9659946
11.	Elyas Fadakar, 2022, Chapter 12, 978-3-031-21093-8, 157, 10.1007/978-3-031-21094-5_12
12.	M. Hajibabaei, J. Behnamian, Flexible job-shop scheduling problem with unrelated parallel machines and resources-dependent processing times: a tabu search algorithm, 2021, 16, 1750-9653, 242, 10.1080/17509653.2021.1941368
13.	Bo Fang, Ming Feng, Cheng Qiu, Ximing Zhang, Rahman Ali, Rail Multi Vehicle Scheduling Method for Intermediate Depot of Steel Plant Based on Improved Genetic Algorithm, 2022, 2022, 1875-919X, 1, 10.1155/2022/4971638
14.	Junfeng Fang, Jamil Hussain, An Effective Hybrid Multiobjective Flexible Job Shop Scheduling Problem Based on Improved Genetic Algorithm, 2022, 2022, 1875-919X, 1, 10.1155/2022/2120944
15.	Xingwang Shen, Shimin Liu, Can Zhang, Jinsong Bao, Intelligent material distribution and optimization in the assembly process of large offshore crane lifting equipment, 2021, 159, 03608352, 107496, 10.1016/j.cie.2021.107496
16.	S. Vivek, Kishan Rakesh, Biju R. Mohan, 2022, Chapter 21, 978-981-19-1519-2, 271, 10.1007/978-981-19-1520-8_21
17.	Manojkumar Pal, Murari Lal Mittal, Gunjan Soni, Satyendra S. Chouhan, Manish Kumar, A multi-agent system for FJSP with setup and transportation times, 2023, 216, 09574174, 119474, 10.1016/j.eswa.2022.119474
18.	Boxin Yang, Wenhao Yin, Jinghua Li, Qinghua Zhou, Kuruva Lakshmanna, A Multitime Window Parallel Scheduling System for Large-Scale Offshore Platform Project, 2022, 2022, 1530-8677, 1, 10.1155/2022/2352651
19.	Bingtao Quan, Sujian Li, Kuo-Jui Wu, A hybrid metaheuristic algorithm to achieve sustainable production: involving employee characteristics in the job-shop matching problem, 2023, 2168-1015, 1, 10.1080/21681015.2023.2184426
20.	Meng Xu, Fangfang Zhang, Yi Mei, Mengjie Zhang, 2022, Genetic Programming with Multi-case Fitness for Dynamic Flexible Job Shop Scheduling, 978-1-6654-6708-7, 01, 10.1109/CEC55065.2022.9870340
21.	Zhengyu Hu, Wenrui Liu, Shengchen Ling, Kuan Fan, Haibin Lv, Research on multi-objective optimal scheduling considering the balance of labor workload distribution, 2021, 16, 1932-6203, e0255737, 10.1371/journal.pone.0255737
22.	Cenglin Yao, Yongzhou Li, Mohd Dilshad Ansari, Mohammed Ahmed Talab, Amit Verma, Optimization of industrial process parameter control using improved genetic algorithm for industrial robot, 2022, 13, 2081-4836, 67, 10.1515/pjbr-2022-0006
23.	Hangyu Lou, Xianpeng Wang, Zhiming Dong, Yang Yang, Memetic algorithm based on learning and decomposition for multiobjective flexible job shop scheduling considering human factors, 2022, 75, 22106502, 101204, 10.1016/j.swevo.2022.101204
24.	Xixing Li, Xing Guo, Hongtao Tang, Rui Wu, Lei Wang, Shibao Pang, Zhengchao Liu, Wenxiang Xu, Xin Li, Survey of integrated flexible job shop scheduling problems, 2022, 174, 03608352, 108786, 10.1016/j.cie.2022.108786
25.	Qi Zhang, Zhixue He, Wenfeng Liang, 2021, Intelligent Shop Floor Scheduling by an Improved Genetic Algorithm, 978-1-6654-1290-2, 246, 10.1109/ISMII52409.2021.00059
26.	Weiwei Zhang, Speech data system and computer database design based on improved genetic algorithm, 2023, 14727978, 1, 10.3233/JCM-226698
27.	Haoqian Li, Liang Wang, Bingying Tang, 2022, Chapter 7, 978-981-19-6202-8, 67, 10.1007/978-981-19-6203-5_7
28.	Hongliang Zhang, Gongjie Xu, Ruilin Pan, Haijiang Ge, A novel heuristic method for the energy-efficient flexible job-shop scheduling problem with sequence-dependent set-up and transportation time, 2022, 54, 0305-215X, 1646, 10.1080/0305215X.2021.1949007
29.	Mohamed Sayed Al-Ashhab, Abdulrahman Fayez Alhejaili, Shadi M. Munshi, Developing a multi-objective flexible job shop scheduling optimization model using Lexicographic procedure considering transportation time, 2023, 2731-6688, 10.1007/s43995-023-00017-1
30.	Weibo Ren, Yan Yan, Yaoguang Hu, Yu Guan, Joint optimisation for dynamic flexible job-shop scheduling problem with transportation time and resource constraints, 2022, 60, 0020-7543, 5675, 10.1080/00207543.2021.1968526
31.	Qinhui Liu, Nengjian Wang, Jiang Li, Tongtong Ma, Fapeng Li, Zhijie Gao, Research on Flexible Job Shop Scheduling Optimization Based on Segmented AGV, 2023, 134, 1526-1506, 2073, 10.32604/cmes.2022.021433
32.	Siqing Wang, Jian Wang, Xiaowei Hu, Tingting Dong, Zhipeng Niu, Routing Optimization of Regional Flexible Transit Under the Mixed Demand Mode, 2023, 2677, 0361-1981, 662, 10.1177/03611981231162600
33.	Xiaoyu Wen, Yunzhan Fu, Wenchao Yang, Haoqi Wang, Yuyan Zhang, Chunya Sun, An effective hybrid algorithm for joint scheduling of machines and AGVs in flexible job shop, 2023, 56, 0020-2940, 1582, 10.1177/00202940231173750
34.	Lu Zhang, Yi Feng, Qinge Xiao, Yunlang Xu, Di Li, Dongsheng Yang, Zhile Yang, Deep reinforcement learning for dynamic flexible job shop scheduling problem considering variable processing times, 2023, 71, 02786125, 257, 10.1016/j.jmsy.2023.09.009
35.	Aidin Delgoshaei, Mohd Khairol Anuar Mohd Ariffin, Sepehr Maleki, Zulkiflle Leman, Review evolution of dual-resource-constrained scheduling problems in manufacturing systems: modeling and scheduling methods’ trends, 2023, 27, 1432-7643, 18489, 10.1007/s00500-023-09304-4
36.	Hao-Jie Wang, Guang-Yu Zhu, Multiobjective Optimization for FJSP Under Immediate Predecessor Constraints Based OFA and Pythagorean Fuzzy Set, 2023, 31, 1063-6706, 3108, 10.1109/TFUZZ.2023.3245097
37.	Sebastiano Gaiardelli, Damiano Carra, Stefano Spellini, Franco Fummi, Dynamic Job and Conveyor-Based Transport Joint Scheduling in Flexible Manufacturing Systems, 2024, 14, 2076-3417, 3026, 10.3390/app14073026
38.	Khadidja Bakdi, Latéfa Ghomri, Fouad Maliki, 2023, Mathematical Formulation of the Permutation Flow-Shop Scheduling Problem Considering Transport Activity, 979-8-3503-4205-5, 296, 10.1109/DASA59624.2023.10286777
39.	Yifan Gu, Hua Xu, Jinfeng Yang, Rui Li, An improved memetic algorithm to solve the energy-efficient distributed flexible job shop scheduling problem with transportation and start-stop constraints, 2023, 20, 1551-0018, 21467, 10.3934/mbe.2023950
40.	Shupeng Wei, Hongtao Tang, Xixing Li, Deming Lei, Xi Vincent Wang, An improved memetic algorithm for multi-objective resource-constrained flexible job shop inverse scheduling problem: An application for machining workshop, 2024, 74, 02786125, 264, 10.1016/j.jmsy.2024.03.005
41.	Akrem Ben Haj Mouldi, Maroua Nouiri, Integrated Genetic Algorithm with Dispatching Rules to solve the Flexible Job Shop Scheduling Problem under Multi-AMR Transportation Constraints, 2024, 58, 24058963, 652, 10.1016/j.ifacol.2024.09.226
42.	Yuqing Wang, Dequn Zhao, Hongwei Ma, Suming Zhang, Qianhua Deng, Sandeep Saxena, Cairong Zhao, 2023, A simulated annealing genetic algorithm based on reinforcement learning for flexible job shop scheduling problem, 9781510671881, 35, 10.1117/12.3011505
43.	Wenxiang Xu, Shimin Xu, Junyong Liang, Tao Qin, Dezheng Liu, Lei Wang, A discrete water source cycle algorithm design for solving production scheduling problem in flexible manufacturing systems, 2025, 94, 22106502, 101897, 10.1016/j.swevo.2025.101897
44.	Jiapeng Chen, Chun Wang, Binzi Xu, Sheng Liu, Discrete Multi-Objective Grey Wolf Algorithm Applied to Dynamic Distributed Flexible Job Shop Scheduling Problem with Variable Processing Times, 2025, 15, 2076-3417, 2281, 10.3390/app15052281
45.	Yingjie Hou, Xiaojuan Liao, Guangzhu Chen, Yi Chen, Co-Evolutionary NSGA-III with deep reinforcement learning for multi-objective distributed flexible job shop scheduling, 2025, 203, 03608352, 110990, 10.1016/j.cie.2025.110990
46.	Bin Xin, Sai Lu, Qing Wang, Fang Deng, A review of flexible job shop scheduling problems considering transportation vehicles, 2025, 26, 2095-9184, 332, 10.1631/FITEE.2300795
47.	Erlianasha Samsuria, Mohd Saiful Azimi Mahmud, Norhaliza Abdul Wahab, Muhammad Zakiyullah Romdlony, Mohamad Shukri Zainal Abidin, Salinda Buyamin, An improved adaptive fuzzy-genetic algorithm based on local search for integrated production and mobile robot scheduling in job-shop flexible manufacturing system, 2025, 03608352, 111093, 10.1016/j.cie.2025.111093
48.	Yongheng Liu, Fagui Liu, Xing Liu, Hongji Chen, Hongfei Hu, Bin Wang, STCSA: A spatio-temporal collaborative scheduling approach for production–inspection in PCB manufacturing, 2025, 66, 14740346, 103394, 10.1016/j.aei.2025.103394
49.	Wenjie Ding, Hongtao Tang, 2025, An Improved Differential Evolution Algorithm Based on Q-Learning for Solving Flexible Assembly Job Shop Scheduling Problem, 979-8-3315-3508-7, 355, 10.1109/ICAACE65325.2025.11020039
50.	Jatin Trivedi, Shrajal Gupta, Simulative dynamic preventive machine maintenance policy: time efficient stochastic job shops, 2025, 0160-5682, 1, 10.1080/01605682.2025.2515146

Reader Comments

Your name:*

Email:*
© 2019 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)